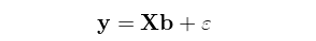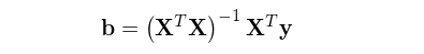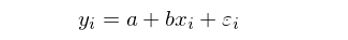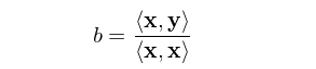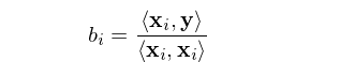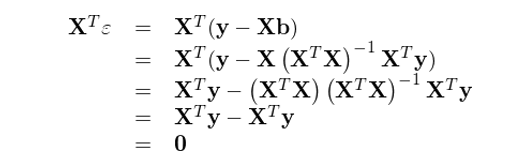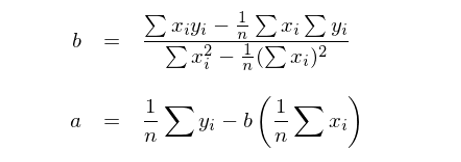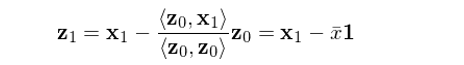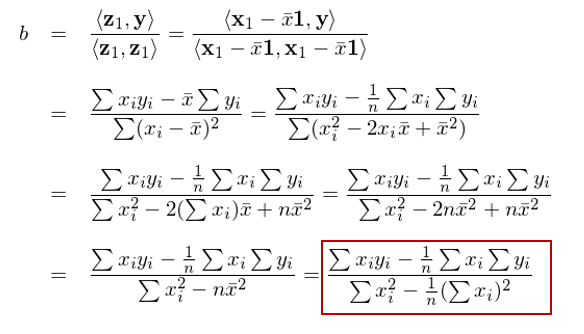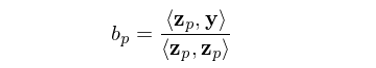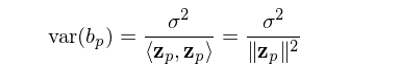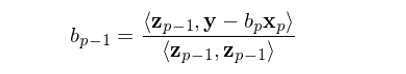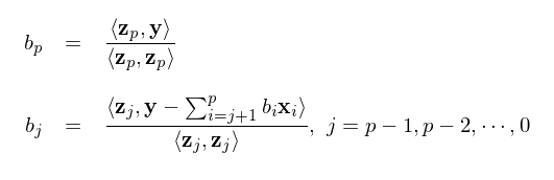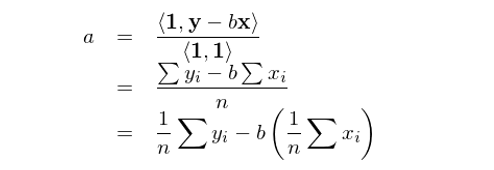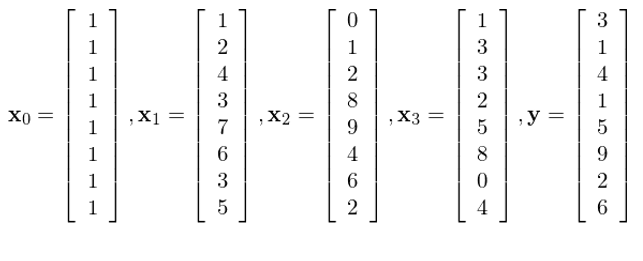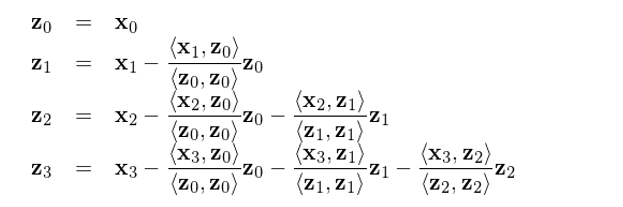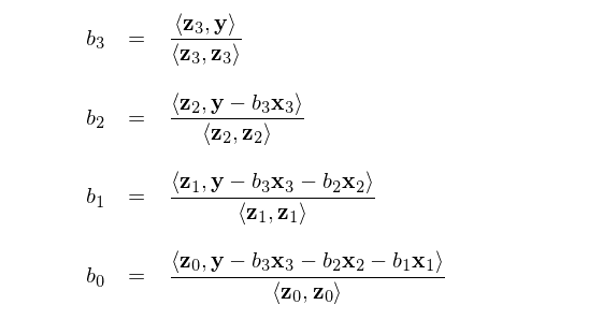爲什(shén)麽要進行因子正交化(huà)處理(lǐ)？

作者：石川

摘要：選股多(duō)因子模型中常進行因子正交化(huà)處理(lǐ)。如果因子之間不滿足正交性，則它們會相互影(yǐng)響各自的(de)回歸系數，這(zhè)可(kě)能造成回歸系數過大(dà)的(de)估計誤差，對(duì)因子的(de)評價産生負面影(yǐng)響。

1 多(duō)因子模型求解

在選股多(duō)因子模型中，人(rén)們常提到的(de)一個(gè)概念是因子正交化(huà)處理(lǐ)。本文就從多(duō)因子截面回歸求解的(de)角度來(lái)簡單說說爲什(shén)麽我們喜歡相互正交的(de)因子，以及如果因子之間不正交對(duì)回歸系數會有什(shén)麽影(yǐng)響。一個(gè)多(duō)因子模型可(kě)以寫成如下(xià)的(de)形式：

其中 y 是 N × 1 階股票(piào)下(xià)一期的(de)收益率向量，X 爲 N × K 階當期的(de)因子暴露矩陣，b 爲 K × 1 階待通(tōng)過回歸求解得(de)到的(de)因子收益率向量，ε 爲 N × 1 階殘差向量。假設 X 滿足列滿秩，則上述模型的(de) OLS（ordinary least squares）解爲：

需要注意的(de)是，在上面這(zhè)個(gè)模型以及 b 的(de)表達式中，因子向量 X 已經包括了(le)所有的(de) regressors，因此回歸模型右側沒有額外的(de)截距項。這(zhè)意味著(zhe)，如果我們假設截距項也(yě)是一個(gè)因子，則它對(duì)應的(de) N × 1 階向量 [1,1,…,1]^T 已經作爲 X 的(de)某一列（通(tōng)常是第一列）存在于 X 之中了(le)；如果我們假設截距項不是一個(gè)因子，則 X 中沒有 [1,1,…,1]^T 這(zhè)一列。

在 Barra 的(de)多(duō)因子模型 CNE5 中考慮了(le)國家因子，所有個(gè)股在該因子上的(de)暴露都是 1，因此它的(de)作用(yòng)就相當于一個(gè)截距因子；[1,1,…,1]^T 這(zhè)個(gè)向量在 Barra 模型中正是 X 的(de)第一列。另外，對(duì)于我們最熟悉的(de) simple regression model，它的(de)右側隻有一個(gè)截距和(hé)一個(gè)解釋變量：

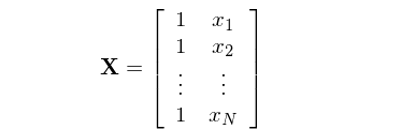
按照(zhào)上述說明(míng)，該模型對(duì)應的(de)矩陣 X 包括兩列：一列對(duì)應截距，一列對(duì)應真正的(de)解釋變量 x：

從 b 的(de)表達式來(lái)看，它和(hé) (X^T)X 有關。當 X 的(de)各列（即回歸模型中的(de)不同解釋變量，或我們研究問題中的(de)不同因子暴露向量）之間不正交時(shí)，則在計算(suàn) (X^T)X 乃至最終的(de) b 時(shí)，X 不同列之間是相互影(yǐng)響的(de)，而這(zhè)種影(yǐng)響不是什(shén)麽好事兒(ér)。

2 簡單一元回歸

讓我們從最簡單的(de)一元回歸（simple univariate regression）說起。假設有一元回歸模型 y = bx + ε（模型右側隻有一個(gè)解釋變量，沒有截距項）。對(duì)于兩個(gè)同階向量 m 和(hé) n，令 <m, n> 表示它們的(de)內積，即 <m, n> = Σ(m_i)(n_i)，則該一元回歸模型的(de) OLS 解爲（求解對(duì)象就是标量 b）：

這(zhè)個(gè)結論非常簡單，但是它十分(fēn)重要。在上一節中，我們給出了(le)多(duō)元回歸 OLS 求解的(de)表達式：

比較一元回歸模型的(de)标量 b 和(hé)多(duō)元回歸模型的(de)向量 b 不難發現如下(xià)現象：在多(duō)元回歸模型中，如果所有的(de)解釋變量兩兩正交，即 <x_i, x_j> = 0, i ≠ j，則向量 b 中的(de)每一個(gè)系數 b_i 恰恰等于：

這(zhè)是因爲 <x_i, x_j> = 0 保證了(le) (X^T)X 的(de)所有非對(duì)角元素都是 0，因此它是一個(gè)對(duì)角陣。對(duì)角陣的(de)逆矩陣就是把該對(duì)角陣對(duì)角線上的(de)元素都取倒數，所以逆矩陣仍然是對(duì)角陣。因此，(X^T)X 的(de)第 i 個(gè)對(duì)角元素爲 1/<x_i, x_i>。另一方面，(X^T)y 是一個(gè) K × 1 向量，它的(de)第 i 個(gè)元素是 x_i 和(hé) y 的(de)內積，即 <x_i, y>。最終，多(duō)元回歸的(de) b_i 正是 <x_i, y>/<x_i, x_i>。怎麽樣？b_i 和(hé)一元回歸中的(de) b 的(de)表達式一模一樣，說明(míng)當所有解釋變量相互正交時(shí)，不同的(de)因子（即 x_i）對(duì)彼此的(de)參數估計（即 b_i，因子收益率）沒有任何影(yǐng)響。這(zhè)便是正交的(de)好處。那麽，當因子（解釋變量）之間不正交時(shí)又會怎樣呢(ne)？爲了(le)回答(dá)這(zhè)個(gè)問題，我們首先來(lái)看看回歸的(de)幾何意義。

3 回歸的(de)幾何意義

将 b 的(de)表達式代入回歸模型得(de)到 ε 的(de)表達式，并計算(suàn) X 和(hé) ε 的(de)內積有

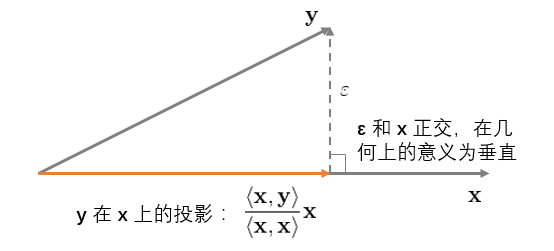
上式說明(míng)，OLS 的(de)殘差 ε 和(hé)解釋變量 X 正交。來(lái)看看這(zhè)在幾何上意味著(zhe)什(shén)麽。首先考慮最簡單的(de)情況，即一元回歸 y = bx + ε（再次提醒，沒有截距項）。它的(de)幾何意義如下(xià)圖所示：

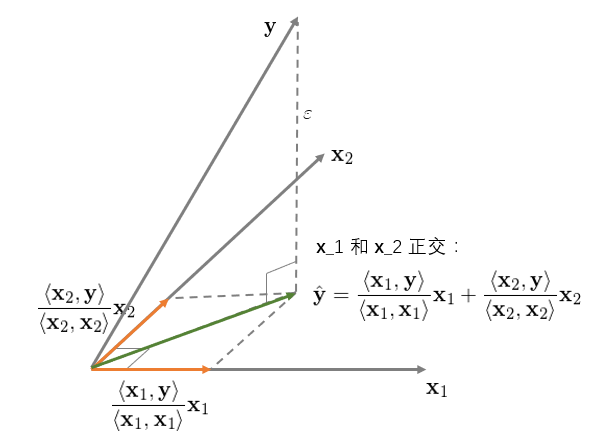
這(zhè)個(gè)圖說明(míng)，OLS 回歸實際上将 y 垂直投影(yǐng)到（orthogonally projected onto）x 之上，使得(de) y 和(hé)其在 x 上的(de)投影(yǐng)之間的(de)距離（ε 的(de)長(cháng)度）最短（殘差平方和(hé)最小）。這(zhè)就是 OLS 的(de)幾何意義。再來(lái)看看二元回歸 y = b_1x_1 + b_2x_2 + ε，并首先假設 x_1 和(hé) x_2 之間是正交的(de)。該回歸的(de)幾何意義如下(xià)：

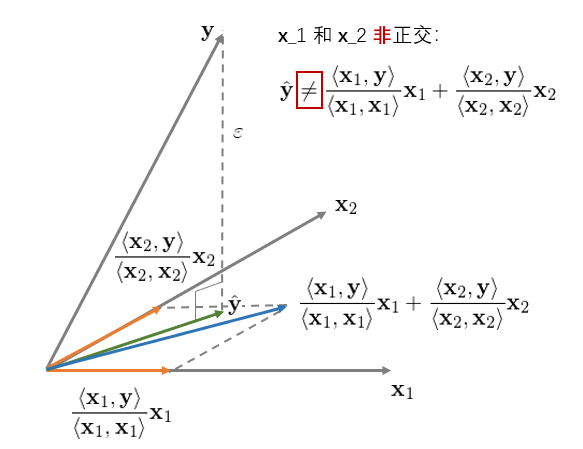
對(duì)于二元回歸，它的(de)幾何意義是将 y 垂直投影(yǐng)到由 x_1 和(hé) x_2 生成的(de)超平面内，其投影(yǐng)正如上圖中綠色向量所示。此外，我們可(kě)以分(fēn)别、獨立的(de)将 y 投影(yǐng)到 x_1 和(hé) x_2 上（圖中兩個(gè)橘黃(huáng)色向量）。在本例中，由于 x_1 和(hé) x_2 相互正交（垂直），因此綠色向量恰好等于兩個(gè)橘黃(huáng)色向量之和(hé)。這(zhè)說明(míng)當 x_1 和(hé) x_2 正交時(shí)，回歸系數 b_i 僅由 x_i 和(hé) y 決定、其他(tā)任何解釋變量 x_j (j ≠ i) 對(duì) b_i 均沒有影(yǐng)響。下(xià)面來(lái)看看 x_1 和(hé) x_2 非正交的(de)情況。該二元回歸的(de)幾何意義如下(xià)：

它和(hé)前一種情況最大(dà)的(de)區(qū)别是，當 x_1 和(hé) x_2 非正交時(shí)，y 在由 x_1 和(hé) x_2 生成的(de)超平面内的(de)投影(yǐng)不等于 y 分(fēn)别在 x_1 和(hé) x_2 上的(de)投影(yǐng)之和(hé)。在這(zhè)種情況下(xià)，解釋變量之間對(duì)各自的(de)回歸系數有不同的(de)作用(yòng)，因此 OLS 的(de)回歸系數 b_i 不再等于 <x_i, y>/<x_i, x_i>。非正交 x_i 之間的(de)相互作用(yòng)如何影(yǐng)響回歸系數 b_i 呢(ne)？通(tōng)過連續正交化(huà)來(lái)求解多(duō)元線性回歸可(kě)以回答(dá)這(zhè)個(gè)問題。

4 用(yòng)正交化(huà)過程求解多(duō)元回歸

還(hái)是拿我們最熟悉的(de) simple regression model 爲例；該模型有兩個(gè)解釋變量 —— 截距項和(hé) x。

令 x_0 表示截距項對(duì)應的(de)解釋變量，即 x_0 = [1,1,…,1]^T；x_1 表示上式中的(de)解釋變量 x。假設 x_0 和(hé) x_1 非正交（正交的(de)話(huà)我們就不用(yòng)費勁了(le)）。對(duì)于簡單回歸模型，回歸系數 a（對(duì)應 x_0）和(hé) b（對(duì)應 x_1）的(de)解爲：

下(xià)面就來(lái)看看如何通(tōng)過正交化(huà)求解 a 和(hé) b。由于 x_0 和(hé) x_1 非正交，首先需要構造出一組正交向量。令 z_0 = x_0 爲其中的(de)一個(gè)向量，将 x_1 用(yòng) z_0 進行一元回歸（不帶截距）得(de)到的(de)殘差就是和(hé) z_0 互相垂直（正交）的(de)向量，記爲 z_1。由一元回歸的(de)性質可(kě)知：

其中 \bar x 表示 x 的(de)均值，1 表示列向量 [1,1,…,1]^T，即 z_0。So far so good？接下(xià)來(lái)，注意了(le)：将 y 用(yòng)上面得(de)到的(de) z_1 進行一元回歸（不帶截距），得(de)到的(de)回歸系數就是上述 simple regression model 中解釋變量 x 的(de)回歸系數 b！

怎麽樣？我們并沒有直接對(duì)該模型求解，而是通(tōng)過正交化(huà)的(de)方式就求出了(le)解釋變量 x_1 的(de)回歸系數 b。反應快(kuài)的(de)小夥伴也(yě)許馬上會問 a 呢(ne)？a 是否等于 <z_0, y>/<z_0, z_0> 呢(ne)？别急，我們一會兒(ér)就聊 a，但是在那之前先來(lái)看一個(gè)通(tōng)過連續正交化(huà)求解多(duō)元回歸的(de)算(suàn)法（Hastie et al. 2016）：

該算(suàn)法的(de)核心是通(tōng)過連續的(de)正交化(huà)計算(suàn)把一組非兩兩正交的(de)向量 x_i 轉換成一組兩兩正交的(de)向量 z_i，并以此方便的(de)求出最後一個(gè)被正交化(huà)的(de)解釋變量的(de)多(duō)元回歸系數。雖然它隻有三步，但是每一步都值得(de)解讀一下(xià)：

看到這(zhè)裏，有的(de)小夥伴可(kě)能會問，這(zhè)個(gè)算(suàn)法确實不錯，但是費了(le)半天勁算(suàn)出了(le)一大(dà)堆相互正交的(de)向量 z_j，但是求解回歸系數的(de)結論僅對(duì)最後一個(gè)被正交化(huà)的(de)解釋變量成立，這(zhè)不是坑爹嗎？答(dá)案是并不坑爹！這(zhè)是因爲上述算(suàn)法中的(de)關鍵一點是，正交化(huà)這(zhè)些解釋變量的(de)順序是任意的(de)。我們可(kě)以選任何一個(gè)來(lái)初始化(huà)，也(yě)可(kě)以選任何一個(gè)作爲最後一個(gè)被正交化(huà)的(de)解釋變量。無論我們怎麽選，上述過程都保證了(le)最後一個(gè)被正交化(huà)的(de)解釋變量的(de)回歸系數滿足 b_p = <z_p, y>/<z_p, z_p>。因此，我們隻需要依次挑選這(zhè)些解釋變量作爲最後一個(gè)被正交化(huà)的(de)，就可(kě)以通(tōng)過上述步驟方便的(de)求出它們的(de)回歸系數。而它所反映出來(lái)的(de)本質是：

這(zhè)個(gè)算(suàn)法叫作多(duō)元回歸的(de) Gram-Schmidt（格拉姆-施密特）正交化(huà)過程。本小節開始的(de) simple regression model 已經驗證了(le)上述結論。我們使用(yòng) x_0 将 x_1 正交化(huà)處理(lǐ)得(de)到 z_1，然後用(yòng) y 和(hé) z_1 回歸得(de)到的(de)正是 x_1 的(de)回歸系數 b；如果将 x_1 選爲 z_0，然後用(yòng)它正交化(huà) x_0 = [1,1,…,1]^T，就可(kě)以方便的(de)求出回歸系數 a。讓我們來(lái)好好審視一下(xià)這(zhè)個(gè)結論，即：

上式說明(míng)，解釋變量 x_p 的(de)回歸系數 b_p 和(hé)正交化(huà)後的(de) z_p 的(de)大(dà)小（z_p 自己的(de)內積爲分(fēn)母）有關。如果 x_p 和(hé)其他(tā)解釋變量高(gāo)度相關（即非常不正交），那麽 z_p 就會很小，則會導緻 b_p 非常不穩定（一點點樣本數據的(de)變化(huà)都會導緻 b_p 的(de)大(dà)幅變化(huà)）。當 y_i 滿足獨立同分(fēn)布時(shí)，假設它的(de)方差爲 σ^2，可(kě)以證明(míng)回歸系數 b_p 的(de)方差和(hé) z_p 的(de)大(dà)小成反比，即 z_p 越小，b_p 的(de)誤差越大(dà)：

在多(duō)因子模型中，b_p 代表的(de)是因子 p 的(de)收益率。爲避免因子收益率的(de)估計非常不穩定，要求不同的(de)因子之間盡量滿足正交化(huà)。舉例來(lái)說，在 Barra 的(de) CNE5 模型中，非線性規模因子和(hé)規模因子之間進行了(le)正交化(huà)處理(lǐ)；殘差波動率因子和(hé)規模以及 BETA 因子也(yě)進行了(le)正交化(huà)處理(lǐ)。

在結束本小節的(de)討(tǎo)論之前，我還(hái)想介紹一個(gè)有意思也(yě)有用(yòng)的(de)特性。本節的(de)論述說明(míng)我們可(kě)以任選一個(gè)解釋變量作爲最後一個(gè)，然後根據連續正交化(huà)方便的(de)求出它的(de)回歸系數。這(zhè)意味著(zhe)如果我們有 20 個(gè)解釋變量，需要進行 20 次上述操作。那麽，是否存在什(shén)麽辦法僅通(tōng)過進行一次連續正交化(huà)就求出所有的(de)回歸系數 b_j, j = 0, 1, …, p 呢(ne)？答(dá)案是肯定的(de)。

假設我們按照(zhào)某給定順序 x_0, x_1, …, x_p 進行了(le)連續正交化(huà)過程，得(de)到了(le) z_0, z_1, …, z_p，且我們現在知道 b_p = <z_p, y>/<z_p, z_p>。由于 b_p 是解釋變量 x_p 的(de)回歸系數，因此 b_p(x_p) 正是 x_p 所解釋的(de) y 的(de)部分(fēn)。如果從 y 中剔除 b_p(x_p)，并把得(de)到的(de) y - b_p(x_p) 用(yòng) x_0, x_1, …, x_{p-1} 回歸，則結果就和(hé) x_p 無關了(le)。在這(zhè)個(gè)新的(de)回歸中，x_{p-1} 就變成了(le)最後一個(gè)被正交化(huà)的(de)解釋變量，其對(duì)應的(de)正交向量爲 z_{p-1}。因此，x_{p-1} 的(de)回歸系數就是用(yòng)新的(de) y - b_p(x_p) 和(hé) z_{p-1} 回歸的(de)結果：

以此類推，我們可(kě)以按照(zhào) b_p, b_{p-1}, …, b_0 的(de)倒序求解出多(duō)元回歸中所有解釋變量的(de)回歸系數 b_j（Drygas 2011）：

最後用(yòng)本小節開始的(de) simple regression model 檢驗一下(xià)。我們用(yòng)上述方法求解截距項的(de)回歸系數 a 看看。根據定義有 z_0 = 1 并假設已知 b。則根據上面的(de)表達式可(kě)得(de)：

這(zhè)正是直接求解 simple regression model 得(de)到的(de)回歸系數 a（請往前滾屏比較看看）。

5 一個(gè)例子

本節用(yòng)一個(gè)例子來(lái)驗證一下(xià)上一節的(de)各種公式。假設有四個(gè)解釋變量 x_0 到 x_3，以及 y：

直接使用(yòng)回歸系數 b 的(de)表達式求解，則它們的(de)回歸系數分(fēn)别爲：b_0 = 0.38548073, b_1 = 0.96332683, b_2 = -0.36300685, b_3 = 0.37189391。按照(zhào) x_0, x_1, x_2, x_3 的(de)順序進行連續正交化(huà)，得(de)到的(de)正交向量爲：

使用(yòng) Drygas (2011) 提出的(de)解法按照(zhào) b_3, b_2, b_1, b_0 的(de)順序求解各個(gè)回歸系數 b_j：

上述公式求出 b_0 = 0.38548073, b_1 = 0.96332683, b_2 = -0.36300685, b_3 = 0.37189391，和(hé)使用(yòng)回歸系數 b 的(de)表達式求解的(de)結果完全一緻。另外，我們也(yě)可(kě)以分(fēn)别選擇 x_0, x_1, x_2 替換 x_3 作爲最後一個(gè)被正交化(huà)的(de)解釋變量（前三個(gè)變量的(de)順序也(yě)不重要），并利用(yòng) b_p = <z_p, y>/<z_p, z_p> 求解，得(de)出的(de) b_j 也(yě)和(hé)上面的(de)完全相同。

6 正交等于不相關？

在我們平常說因子之間正交的(de)時(shí)候，另一個(gè)常用(yòng)的(de)詞彙是因子之間“不相關”（這(zhè)裏不相關指的(de)是不同因子的(de) Pearson 相關系數爲零）。那麽“正交”和(hé)“不相關”是否等價呢(ne)？從定義出發，兩個(gè)因子向量 x_1 和(hé) x_2 正交意味著(zhe)它們的(de)內積，即 <x_1, x_2> 爲零。而 x_1 和(hé) x_2 的(de)相關系數爲零則意味著(zhe) <x_1 – E[x_1]·1, x_2 - E[x_2]·1> 爲零，因爲在計算(suàn)相關系數時(shí)，必須先分(fēn)别減去其均值，這(zhè)就是個(gè) centering 的(de)過程。由于 <x_1, x_2> 爲零不一定意味著(zhe) <x_1 – E[x_1]·1, x_2 - E[x_2]·1> 也(yě)爲零，因此正交不一定等于不相關。

舉個(gè)例子，[4, 2]^T 和(hé) [3, -6]^T 的(de)內積爲零，這(zhè)兩個(gè)向量正交。而各自減去均值後，[4, 2]^T 和(hé) [3, -6]^T 分(fēn)别變爲 [1, -1]^T 和(hé) [4.5, -4.5]^T。這(zhè)兩個(gè)新向量在一條直線上、內積不爲零，因此 [4, 2]^T 和(hé) [3, -6]^T 的(de)相關系數不爲零（事實上，它們的(de)相關系數等于 1）。從多(duō)元回歸求解的(de)角度來(lái)說，我們在乎的(de)是他(tā)們是否正交，而非 centering 之後的(de)內積是否爲零（即是否不相關）。

不過對(duì)于因子暴露向量來(lái)說，因爲個(gè)股在每個(gè)因子上的(de)暴露都經過 demean 處理(lǐ)了(le)，所以每個(gè)因子向量的(de)均值已經是零了(le)（這(zhè)裏考慮的(de)就是簡單等權均值的(de)情況，而不是像 Barra 那種用(yòng)市值作爲權重進行去均值的(de)情況）。從這(zhè)個(gè)意義上說，因子向量之間正交和(hé)它們之間不相關等價。

7 結語

本文掰扯了(le)一大(dà)堆公式其實就是想說明(míng)下(xià)面這(zhè)句話(huà)：在多(duō)元線性回歸中，解釋變量 x_j 的(de)回歸系數 b_j 等于 x_j 在被其他(tā) x_0, x_1, …, x_{j-1}, x_{j+1}, …, x_p 調整之後仍能夠對(duì) y 産生的(de)增量貢獻。如果 x_j 和(hé)其他(tā)解釋變量高(gāo)度相關，則它的(de)回歸系數 b_j 會有很大(dà)的(de)估計誤差。這(zhè)對(duì)于多(duō)因子模型中評價因子收益非常不利。

在計算(suàn)機算(suàn)法進行多(duō)元回歸求解的(de)時(shí)候，并不是試圖按照(zhào) b 的(de)公式計算(suàn) (X^T)X 的(de)逆矩陣，而采用(yòng)的(de)正是正交化(huà)的(de)思路。在正交化(huà)的(de)過程中可(kě)以非常容易的(de)得(de)到 X 的(de) QR 分(fēn)解，其中 Q 是正交陣、R 是上三角陣。這(zhè)也(yě)極大(dà)的(de)化(huà)簡了(le)回歸系數 b 以及 y 預測值的(de)求解。由于篇幅原因（我也(yě)好意思說篇幅……），本文就不給出 QR 分(fēn)解的(de)具體表達式了(le)，感興趣的(de)讀者請參考 Hastie et al. (2016)。

參考文獻

Drygas, H. (2011). On the relationship between the method of least squares and Gram-Schmidt orthogonalization. Acta et Commentationes Universitatis Tartuensis de Mathematica 15(1), 3 – 13.

Hastie, T., R. Tibshirani, and J. Friedman (2016). The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd Ed. Springer.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。