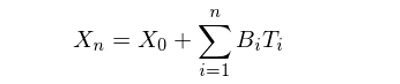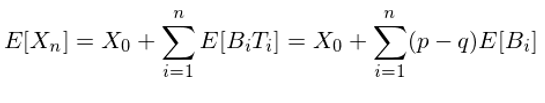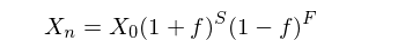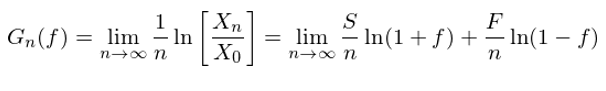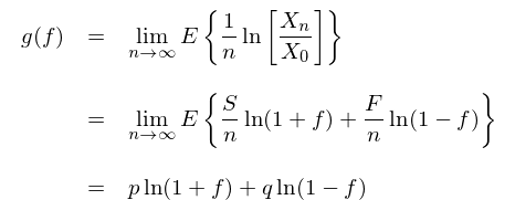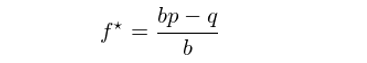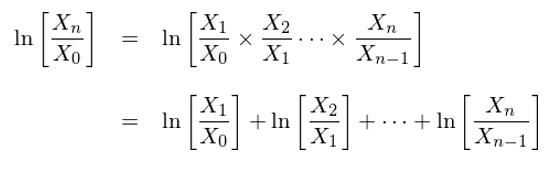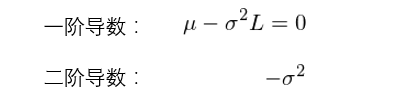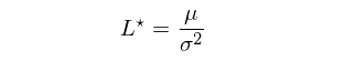凱利公式，從賭場(chǎng)到量化(huà)投資

作者：石川

摘要：從“拉斯維加斯”到“華爾街(jiē)”，凱利公式家喻戶曉。本文揭示凱利公式背後的(de)核心邏輯。

1 引言

今天我們來(lái)聊聊大(dà)名鼎鼎的(de)凱利公式（英文叫 Kelly Formula 或 Kelly Criterion，所以中文也(yě)譯作凱利準則）。

凱利公式由 John R. Kelly, Jr. 于 1956 年提出（Kelly 1956）。它指出在一個(gè)期望收益爲正的(de)重複性賭局或者重複性投資中，每一期應該下(xià)注的(de)最優比例。凱利公式在“拉斯維加斯”和(hé)“華爾街(jiē)”久負盛名。很多(duō)數學天才将它在賭場(chǎng)和(hé)投資中發揚光(guāng)大(dà)，取得(de)了(le)非凡的(de)成就。這(zhè)其中最著名的(de)大(dà)概就是 Dr. Edward Thorp，他(tā)開辟了(le)戰勝 Blackjack（21 點）的(de)策略，并使用(yòng)凱利公式計算(suàn)出來(lái)的(de)比例進行下(xià)注（Thorp 1962）；玩轉賭場(chǎng)後，Thorp 博士将它在統計學和(hé)概率論上的(de)天賦用(yòng)在投資中，他(tā)創建的(de) PNP 對(duì)沖基金曾在近 30 年内取得(de)了(le)年化(huà) 20% 以上的(de)收益率（Thorp 2017）。此外，學術界也(yě)對(duì)凱利公式的(de)各種數學性質以及實踐應用(yòng)進行了(le)大(dà)量的(de)研究，這(zhè)些成果彙總于 MacLean 等人(rén)編輯的(de)論文集 MacLean et al. Eds (2010) 中。

凱利公式的(de)計算(suàn)非常簡單，但它背後所傳達的(de)數學含義至關重要。本文從一個(gè)扔硬币遊戲出發介紹凱利公式以及它的(de)性質，之後會揭示凱利公式背後的(de)實質。最後文章(zhāng)介紹如何把凱利公式推廣到量化(huà)投資中确定投資的(de)最優杠杆比例。鑒于凱利公式的(de)知名度，網上介紹它的(de)文章(zhāng)自不在少數。本文是我和(hé)另一位合夥人(rén)高(gāo)老闆思想碰撞的(de)産物(wù)，雖不求另辟蹊徑，但也(yě)希望能給小夥伴們理(lǐ)解凱利公式提供一些新的(de)思路。

2 從扔硬币到凱利公式

讓我們從扔硬币說起。

假設在一個(gè)賭局遊戲中，我們一直不斷的(de)扔硬币。每局中，硬币出現正面的(de)概率爲 p > 0.5（出現反面的(de)概率爲 q = 1 – p < 0.5）且局與局之間扔硬币的(de)結果獨立。每局中我們下(xià)注一定的(de)金額，如果出現正面我們赢錢（假設賠率爲 1，即不算(suàn)本金，我們赢的(de)錢和(hé)下(xià)注的(de)金額相等），反之我們虧錢。由于 p > 0.5，這(zhè)個(gè)遊戲長(cháng)期的(de)期望收益爲正，因此玩下(xià)去對(duì)我們是有利的(de)。在這(zhè)個(gè)遊戲中，我們需要做(zuò)的(de)決策是決定每局下(xià)注的(de)金額。令 B_i 表示第 i 局的(de)下(xià)注金額；T_i = 1 表示在第 i 局中我們獲勝、T_i = -1 表示在第 i 局中我們失敗。假設我們的(de)初始資金是 X_0，則第 n 局之後的(de)資金量 X_n 滿足：

假設我們的(de)目标是最大(dà)化(huà) X_n 的(de)期望 E[X_n]。由上面的(de)關系時(shí)可(kě)知，E[X_n] 的(de)表達式如下(xià)：

由于 p – q > 0，最大(dà)化(huà) E[X_n] 相當于在每一局都最大(dà)化(huà)當期下(xià)注金額的(de)期望 E[B_i]。這(zhè)意味著(zhe)，每一局中我們都應該有多(duō)少押多(duō)少。舉例來(lái)說，在第一局中，我們應該押注所有的(de)初始資金，因此 B_1 = X_0；如果我們赢了(le)則 X_1 = 2X_0，在第二局中下(xià)注 B_2 = X_1 = 2X_0，以此類推。這(zhè)個(gè)遊戲的(de)期望收益雖然爲正，但我們每局獲勝的(de)概率 p 畢竟不等于 1，而是小于 1。也(yě)許我們能連赢幾次，但總有“運氣用(yòng)盡”的(de)那一局。一旦在某一局中硬币出現反面，由于押注了(le)全部資金，我們将會輸掉所有。由于 p < 1，随著(zhe)賭局數 n 的(de)增加，“輸掉全部”這(zhè)種結果一定會出現。所以，以最大(dà)化(huà) E[X_n] 爲目标的(de)下(xià)注策略（即每把都“滿倉幹”）并不是最優的(de)。

下(xià)面讓我們看另一個(gè)策略 —— 固定比例投注（fixed fraction betting）。假設我們按照(zhào) B_i = f × X_{i-1}，0 < f < 1 的(de)方式投注。每一局中，我們下(xià)注現有資金量的(de)一個(gè)固定比例 f。用(yòng) S 和(hé) F 分(fēn)别表示在 n 局中獲勝和(hé)失敗的(de)次數，S + F = n。n 局後的(de)資金 X_n 爲：

由于 0 < f < 1，那麽我們永遠(yuǎn)不會輸光(guāng)。但是，n 局之後的(de)資金 X_n 顯然和(hé) f 的(de)取值有關。應該如何決定最優的(de) f 呢(ne)？因爲扔硬币有随機性，因此 S 和(hé) F 的(de)取值也(yě)是不确定的(de)，那麽這(zhè)個(gè)最優又是從什(shén)麽意義上來(lái)說的(de)呢(ne)？這(zhè)就是凱利研究的(de)問題。定義函數 G_n(f) 如下(xià)：

這(zhè)個(gè) (1/n)ln[X_n/X_0] 是什(shén)麽呢(ne)？由 exp{n×(1/n)ln[X_n/X_0]} = X_n/X_0 可(kě)知，(1/n)ln[X_n/X_0] 就是單局資金的(de)指數增長(cháng)率（即單局的(de)對(duì)數收益率）。在決定最優的(de)下(xià)注比例 f 時(shí)，凱利選擇最大(dà)化(huà)單局對(duì)數收益率的(de)期望（下(xià)文會解釋爲什(shén)麽），記爲 g(f)：

令 g(f) 的(de)一階導數等于 0 可(kě)以求出最優值 f* = p - q，此外不難驗證在 (0,1) 區(qū)間上 g(f) 的(de)二階導恒爲負，因此 g(f) 在 f = f* 時(shí)有最大(dà)值。f* = p - q 就是最優的(de)下(xià)注比例，它就是凱利公式。在上面的(de)例子中，我們假設每局的(de)賠率等于 1。更一般的(de)，如果用(yòng) b 表示每局賠率，則凱利公式的(de)一般形式爲：

如果我們一直将這(zhè)個(gè)遊戲玩下(xià)去，按 f* 比例下(xià)注将最大(dà)化(huà)對(duì)數收益率的(de)期望。對(duì)于任何給定的(de)局數 n（和(hé)初始資金 X_0），按此比例下(xià)注實際上就是在最大(dà)化(huà) E[ln(X_n)]，即 n 局後資金量的(de)對(duì)數的(de)期望。按照(zhào)凱利公式，我們在每局下(xià)注時(shí)都在最大(dà)化(huà) E[ln(X_n)]；而按照(zhào)之前說的(de)每局都全押，我們是在最大(dà)化(huà) E[X_n]。由對(duì)數函數的(de)特性可(kě)知，E[ln(X_n)] < E[X_n]，所以我們自然會問，爲什(shén)麽要最大(dà)化(huà) E[ln(X_n)]？這(zhè)麽做(zuò)如何就最優了(le)？按照(zhào) f* 比例而非其他(tā)比例下(xià)注有如下(xià)這(zhè)兩點颠覆性的(de)優勢（在數學上都被證明(míng)了(le)，我們隻需要牢記就行了(le)）：

上述兩點是按照(zhào)凱利公式 f* 下(xià)注時(shí)，X_n 的(de)重要性質。尤其是第一條，用(yòng)白話(huà)來(lái)說，它的(de)意思是隻要我們一直玩下(xià)去（n 足夠大(dà)），那麽想赢得(de)最多(duō)的(de)錢（X_n 盡量大(dà)），那麽就應該按照(zhào) f* 下(xià)注。事實上，當 n 小的(de)時(shí)候，X_n(f*) 很有可(kě)能小于 X_n(f) —— 即凱利公式策略的(de)資金額比不過其他(tā)下(xià)注比例的(de)資金額。但隻要 n 足夠大(dà)，凱利公式一定會笑(xiào)到最後，戰勝其他(tā)任何比例。下(xià)面我們就來(lái)解讀凱利公式背後的(de)實質。

3 理(lǐ)解凱利公式 —— 初探

從上一節的(de)數學表達式可(kě)知，凱利公式的(de)推導中考慮的(de)是當局數 n 趨近于無窮時(shí)，資金量 X_n 逼近其極限情況的(de)一些特性。X_n(f*) 一定超過其他(tā) X_n(f) 也(yě)是以 n 足夠大(dà)爲前提的(de)。但是在現實中，足夠大(dà)是多(duō)大(dà)呢(ne)？畢竟無論是在賭場(chǎng)中還(hái)是在投資中，我們的(de)局數（投資期數）n 都是有限的(de)。對(duì)于有限次數的(de)賭局或者投資，無法保證按照(zhào)凱利公式下(xià)注能産生最高(gāo)的(de)期末資金量 X_n；當 n 有限時(shí)，使用(yòng)凱利公式最優比例下(xià)注得(de)到的(de) X_n 在多(duō)大(dà)概率上優于其他(tā)下(xià)注比例？是否有比凱利公式更好的(de)下(xià)注比例呢(ne)？

爲了(le)搞清楚這(zhè)些問題，考慮下(xià)面這(zhè)個(gè)實驗。令 p = 0.6，q = 0.4，b = 1，初始資金爲 1。由凱利公式易知 f* = 0.2。假設我們玩 20 局，即 n = 20。除了(le) f* 外，考慮另一個(gè)下(xià)注比例 f = 0.6。通(tōng)過一百萬次蒙特卡羅仿真來(lái)比較這(zhè)兩個(gè)策略。每次仿真中扔硬币 20 局，并記錄 20 局後這(zhè)兩個(gè)策略的(de)資金額，最後對(duì)這(zhè)一百萬次結果取均值。

結果顯示，按 0.6 比例下(xià)注的(de)策略可(kě)以獲得(de)比按照(zhào)凱利公式下(xià)注更高(gāo)的(de)平均期末資金，即 E[X_n(f=0.6)] > E[X_n(f*=0.2)]。這(zhè)其實不難理(lǐ)解，因爲凱利公式的(de)目标是最大(dà)化(huà) E[ln(X_20)]，而不是爲了(le)最大(dà)化(huà) E[X_20]。每次全押（即 f = 1）的(de)策略最大(dà)化(huà) E[X_20]，任何大(dà)于 f* 的(de)下(xià)注比例的(de)期末期望 E[X_20(f)] 都會大(dà)于凱利公式的(de) E[X_20(f*)]。然而有意思的(de)是，在這(zhè)一百萬次實驗中，按照(zhào) 0.6 比例下(xià)注的(de)策略最終的(de) X_20(f) 取值僅僅在 12.6% 的(de)情況中戰勝了(le)按照(zhào)凱利公式下(xià)注得(de)到的(de) X_20(f*)。在現實中顯然無法将這(zhè) 20 局的(de)賭局進行一百萬次，我們隻能進行一次。雖然按照(zhào) 0.6 下(xià)注的(de)期望更高(gāo)，但就隻進行一次 20 盤的(de)賭局最終能得(de)到的(de)資金 X_20 來(lái)看，使用(yòng)凱利公式下(xià)注戰勝使用(yòng) 0.6 的(de)比例下(xià)注的(de)概率高(gāo)達 87.4%。

這(zhè)是爲什(shén)麽呢(ne)？

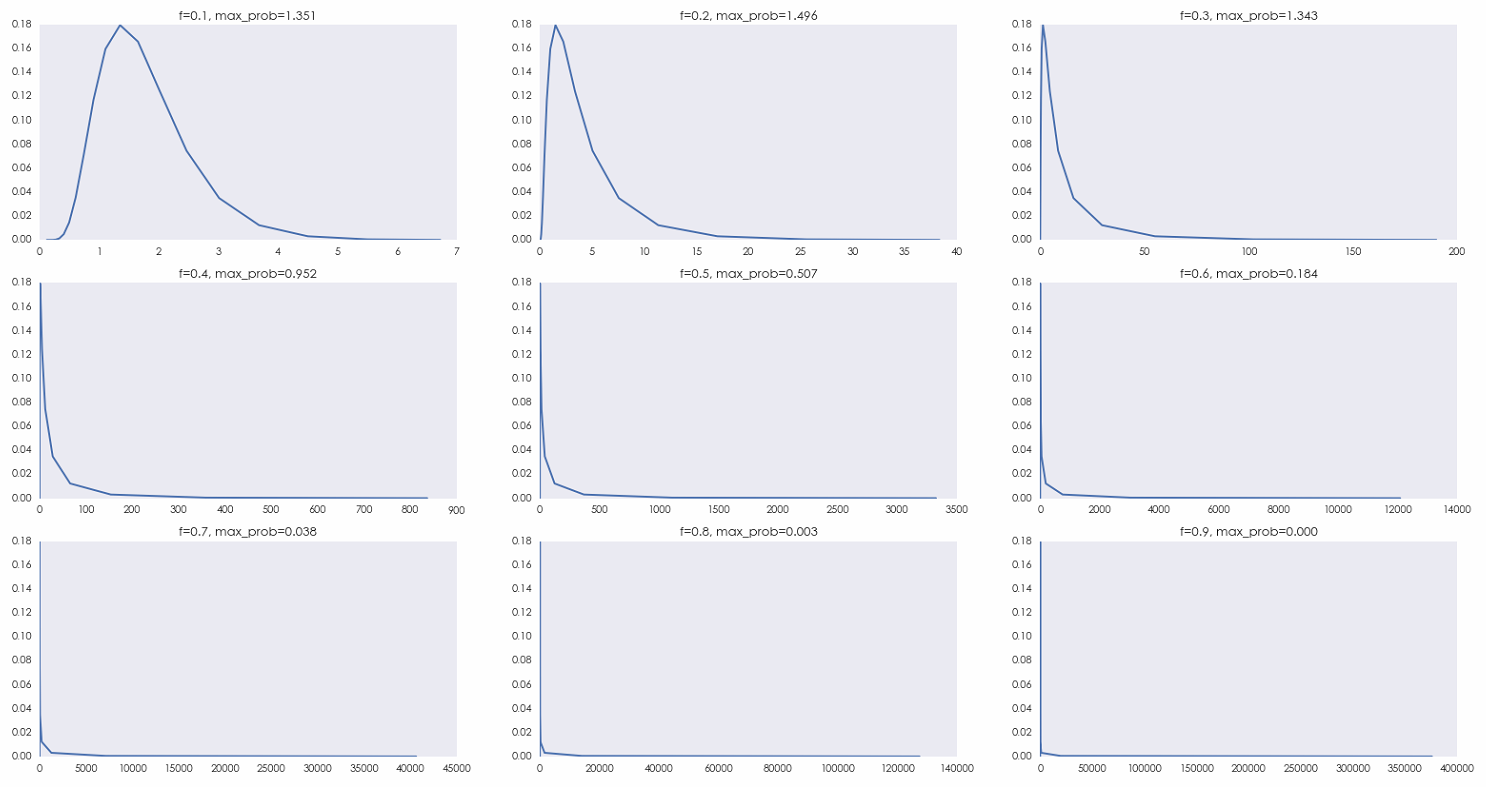
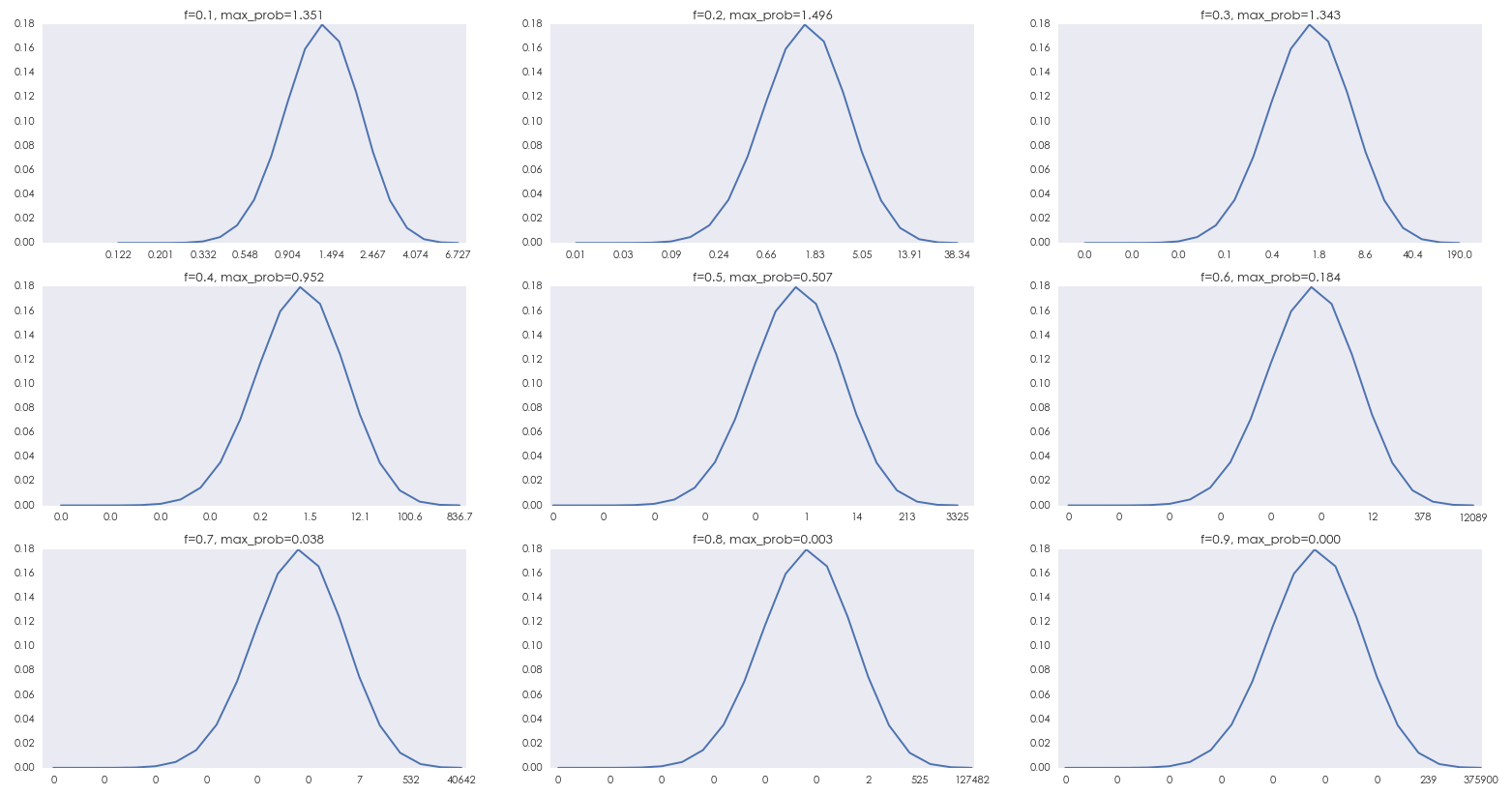
下(xià)圖顯示了(le)當 f 取 0.1，0.2，…，0.9 時(shí)，X_20(f) 的(de)概率質量函數（probability mass function）。扔硬币 20 局，出現正面的(de)次數取值是 0 到 20 這(zhè) 21 個(gè)數，因此對(duì)于每一個(gè) f，X_20(f) 的(de)取值隻有 21 個(gè)。圖中橫坐(zuò)标是 X_20(f) 的(de)可(kě)能取值，縱坐(zuò)标是取值對(duì)應的(de)概率。随著(zhe) f 的(de)增大(dà)，X_20(f) 的(de)取值範圍随指數增長(cháng)，X_20(f) 的(de)最大(dà)、最小值都按指數的(de)速度在橫坐(zuò)标的(de)左右兩端延伸。由于 X_20(f) 無論如何也(yě)不會低于 0，所以它能變小的(de)範圍有限，而它可(kě)能變大(dà)的(de)範圍則要大(dà)得(de)多(duō)（比如 f = 0.2 時(shí)，X_20 的(de)最大(dà)值爲 38.34；而當 f = 0.6 時(shí)，X_20 的(de)最大(dà)值爲 12089.26）。因此，X_20(f) 的(de)分(fēn)布是非常右偏的(de)。這(zhè)種病态的(de)右偏造成了(le) E[X_20(f=0.6)] > E[X_20(f*=0.2)]。由于嚴重的(de)右偏，E[X_n] 在橫坐(zuò)标上的(de)位置非常靠右，但是在現實中根本無法實現。因此以最大(dà)化(huà) E[X_n] 爲目标的(de)下(xià)注一定不是最優的(de)。

随著(zhe) f 的(de)增大(dà)，X_20(f) 分(fēn)布的(de)右偏越來(lái)越嚴重，其越來(lái)越多(duō)的(de)取值被壓縮在整體分(fēn)布的(de)左側，因此 X_20(f) 大(dà)于任何給定常數 C 的(de)概率 —— prob(X_n(f) > C) 随 f 的(de)增大(dà)而快(kuài)速下(xià)降。舉例來(lái)說，當 f = 0.2 時(shí)，X_20 > 1 的(de)概率爲 0.416；而當 f = 0.6 時(shí)，X_20 > 1 的(de)概率驟減到 0.126。這(zhè)暗示著(zhe)在 20 局結束後，X_20(f*=0.2) 比 X_20(f=0.6) 更高(gāo)的(de)概率很大(dà)。即便是對(duì)于有限局數（本例中的(de) 20），凱利公式計算(suàn)出的(de)下(xià)注比例仍然是非凡的(de)。

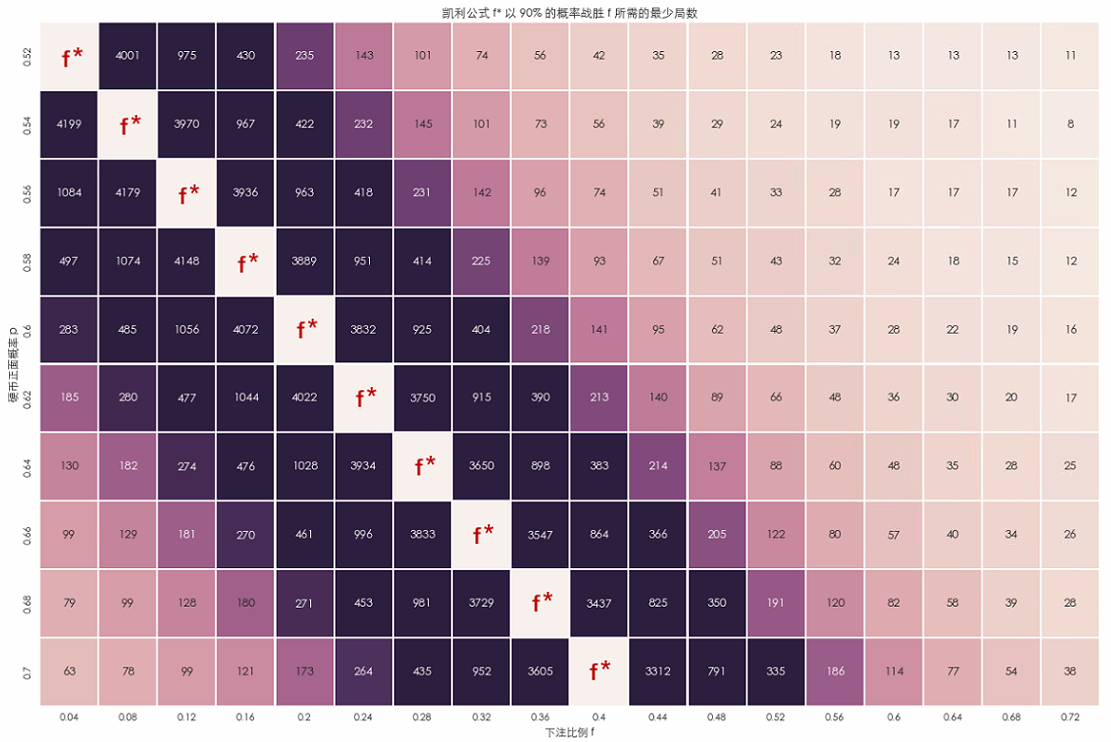
我們将上面的(de)結論推廣到更一般的(de)情況。對(duì)于現實世界中任意給定的(de) p、q 以及賠率 b（下(xià)面假設 b = 1），我們都能利用(yòng)凱利公式算(suàn)出 f*，那麽最少需要玩多(duō)少局我們就能拍(pāi)著(zhe)胸脯說使用(yòng) f* 下(xià)注一定比其他(tā)任何别的(de) f 所獲得(de)的(de)收益更高(gāo)呢(ne)？下(xià)面這(zhè)個(gè)熱(rè)圖爲 f* 以 90% 的(de)概率（足夠拍(pāi)著(zhe)胸脯說了(le)）戰勝其他(tā)f所需要的(de)最小局數。其中每一行左邊的(de)數值爲出現正面概率 p 的(de)取值，每一列最下(xià)方的(de)數字代表下(xià)注比例 f。每個(gè) p 對(duì)應的(de) f* 也(yě)相應的(de)标注在圖中。舉個(gè)例子，如果我們看 p = 0.6 那一行，f* 的(de)格子所在列爲 f = 0.2，說明(míng) f* = 0.2。該行的(de)其他(tā)列中的(de)數字說明(míng)了(le) X_n(f*) 以 90% 的(de)概率打敗 X_n(f) 所需要的(de)最小的(de)局數 n。比如當 f = 0.6 時(shí)，對(duì)應的(de)格子裏的(de)數字是 28，說明(míng)僅僅需要 n = 28 局，X_n(f*=0.2) 就能以 90% 的(de)概率戰勝 X_n(f=0.6)。

當 f 接近 f* 的(de)時(shí)候，f* 打敗 f 所需要的(de)最小局數要高(gāo)一些。但在現實中，如果 f* = 0.2，那麽我們刻意去拿它和(hé) f = 0.24 或者 f = 0.16 這(zhè)些很接近它的(de)比例去比也(yě)沒什(shén)麽意義。f 越接近 f*，X_n(f) 也(yě)就越接近 X_n(f*)，所以我們會用(yòng)一個(gè)和(hé) f* 顯著不同的(de) f 來(lái)對(duì)比。從上面的(de)熱(rè)圖可(kě)以看到，對(duì)于任意給定的(de) p，當 f 和(hé) f* 顯著不同時(shí)，X_n(f*) 僅僅需要很少的(de)局數（一般不超過 50）就可(kě)以以 90% 的(de)概率戰勝 X_n(f)了(le)。50 是一個(gè)什(shén)麽概念？如果我們在賭場(chǎng)待幾天，重複的(de)玩一個(gè)賭局 50 次恐怕很容易。如果我們做(zuò)投資，以周頻(pín)爲單位的(de)話(huà)，50 次隻不過是短短一年，以月(yuè)頻(pín)爲單位的(de)話(huà)，50 次也(yě)不過區(qū)區(qū) 4 年出頭。所以，50 次以内在現實生活中是非常容易達到的(de)次數。因此，對(duì)于現實中的(de) n 有限的(de)情況，凱利公式也(yě)能在很大(dà)的(de)概率上保證是最優的(de)。

第二節直接給出了(le)結論說明(míng)當 n 足夠大(dà)的(de)時(shí)候，X_n(f*) 一定是最高(gāo)的(de)；本節通(tōng)過實證說明(míng)即便在 n 有限的(de)情況下(xià)，X_n(f*) 也(yě)大(dà)概率是最高(gāo)的(de)。那麽，到底是什(shén)麽保證了(le)凱利公式的(de) f* 如此非凡呢(ne)？下(xià)一節就來(lái)給出答(dá)案。

4 理(lǐ)解凱利公式 —— 本質

上一節的(de)介紹讓我們對(duì)凱利公式已經有一定的(de)理(lǐ)解。本節就來(lái)揭示凱利公式背後的(de)實質。

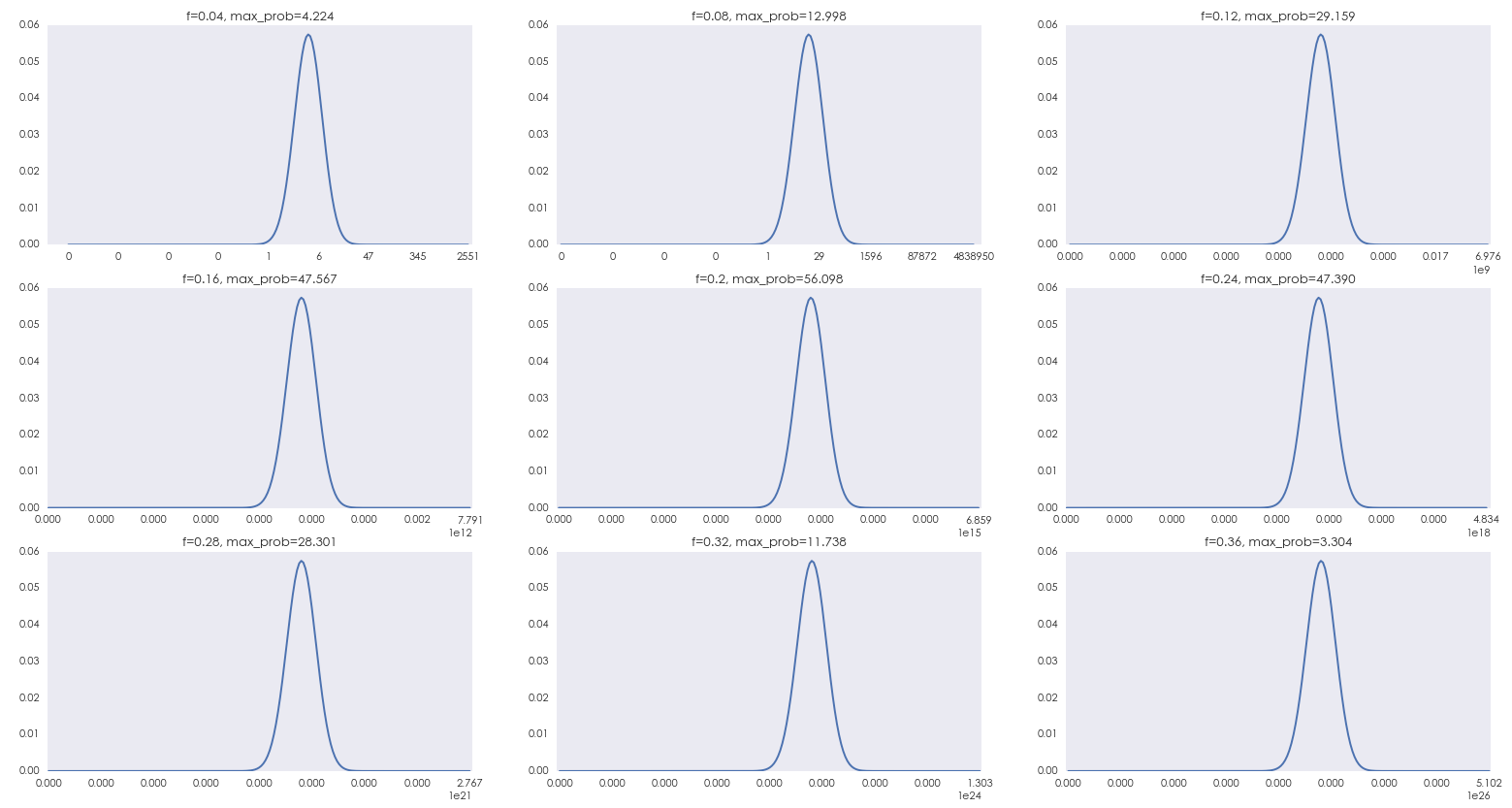
前文說到，以最大(dà)化(huà) E[X_n] 爲目标制定下(xià)注比例根本不靠譜。那麽來(lái)看看靠譜的(de)目标。第二節指出，凱利最大(dà)化(huà)的(de)是單期對(duì)數收益率的(de)期望，對(duì)于任何給定的(de) n，這(zhè)等價于最大(dà)化(huà) E[ln(X_n)]，即 X_n 的(de)對(duì)數的(de)期望。在上一節中，我們給出了(le) n = 20 時(shí)，X_n 的(de)概率質量函數，并指出随著(zhe)f的(de)增大(dà)它呈現出越來(lái)越顯著的(de)病态右偏。但是，如果将上一節中 X_n 的(de)概率質量函數的(de)橫坐(zuò)标變成以 e 爲底的(de)對(duì)數坐(zuò)标，那麽它們就變成了(le)下(xià)面這(zhè)個(gè)樣子。由于進行了(le)坐(zuò)标變換，下(xià)面這(zhè)個(gè)其實就是 ln(X_n) 的(de)概率質量函數。

怎麽樣？ln(X_n)，n = 20 的(de)概率分(fēn)布不再右偏，而是呈現出幾乎左右對(duì)稱的(de)鐘(zhōng)形（bell-shaped）形狀（當然 ln(X_n) 的(de)取值還(hái)是随著(zhe) f 的(de)增大(dà)越來(lái)越寬）。這(zhè)個(gè)鐘(zhōng)形不太平滑是因爲 n 的(de)取值比較小。假如 n = 200，那麽不同比例 f 下(xià) ln(X_n) 的(de)分(fēn)布如下(xià)圖所示，分(fēn)布更加平滑，鐘(zhōng)形左右更加對(duì)稱。

你一定已經猜到了(le)我爲什(shén)麽多(duō)次提到“鐘(zhōng)形”。因爲正态分(fēn)布的(de)形狀就是“鐘(zhōng)形”的(de)。随著(zhe) n 的(de)增大(dà)，ln(X_n) 的(de)分(fēn)布越來(lái)越接近正态分(fēn)布！此外，上面了(le)兩張圖說明(míng)随著(zhe) f 的(de)增大(dà)，ln(X_n) 的(de)衆數（即 ln(X_n) 的(de)所有取值裏面概率最高(gāo)的(de)那一個(gè)，就是圖中概率質量函數的(de)那個(gè)"尖兒(ér)"對(duì)應的(de) ln(X_n) 的(de)取值）先變大(dà)、後變小，在 f = f* 時(shí)達到峰值。對(duì)于正态分(fēn)布來(lái)說，它的(de)衆數就是它的(de)期望。因此，分(fēn)布上這(zhè)個(gè)“尖兒(ér)”對(duì)應的(de) ln(X_n) 的(de)取值向右移動的(de)過程就是 E[ln(X_n)] 向右移動的(de)過程。這(zhè)意味著(zhe) E[ln(X_n)] 在 f = f* 時(shí)最大(dà)，而這(zhè)正是凱利求解 f* 時(shí)的(de)初衷。對(duì)于初始資金 X_0（假設等于 1），ln(X_n) = ln(X_n/X_0) 就是整個(gè) n 局的(de)對(duì)數收益率。對(duì)數收益率的(de)最大(dà)好處是它的(de)可(kě)加性，把單期的(de)對(duì)數收益率相加就得(de)到整體的(de)對(duì)數收益率。

由于不同期之間是相互獨立的(de)，n 期對(duì)數收益率相加相當于 n 個(gè)獨立的(de)随機變量相加。由中心極限定理(lǐ)（Central limit theorem）可(kě)知，它們的(de)和(hé) ln(X_n) 逼近正态分(fēn)布，這(zhè)解釋了(le)爲什(shén)麽上面 ln(X_n) 的(de)概率分(fēn)布呈現出“鐘(zhōng)形”。由于 ln(X_n) 是整個(gè) n 期的(de)對(duì)數收益，因此 (1/n) × ln(X_n) 就是每期對(duì)數收益率的(de)均值。由大(dà)數定律（Law of Large Numbers）可(kě)知，(1/n) × ln(X_n)  随著(zhe) n 的(de)增大(dà)一定會收斂于它的(de)期望，即 E[(1/n) × ln(X_n)]；對(duì)于給定的(de) n，n 期的(de)總收益會收斂于 E[ln(X_n)]。

我們玩一個(gè)賭局或者投資，最終是想讓 X_n 越大(dà)越好，但我們不知道 X_n 最終會變成什(shén)麽樣，或者會收斂到什(shén)麽值。但上面的(de)分(fēn)析說明(míng)隻要 n 足夠大(dà)，大(dà)數定律保證了(le) X_n 的(de)對(duì)數，即 ln(X_n)，一定會非常接近它的(de)期望 E[ln(X_n)]，那麽我們自然就想找到一個(gè)下(xià)注比例使得(de) E[ln(X_n)] 盡可(kě)能的(de)大(dà)。而凱利公式的(de) f* 恰恰就是使 E[ln(X_n)] 最大(dà)的(de)下(xià)注比例。這(zhè)就是凱利公式爲什(shén)麽 NB 的(de)原因。由于中心極限定理(lǐ)和(hé)大(dà)數定律的(de)特性，我們并不要求單期的(de)收益率滿足特定的(de)分(fēn)布。因此即便本文中使用(yòng)扔硬币這(zhè)個(gè)例子 —— 它的(de)單期收益率是個(gè)伯努利分(fēn)布 —— 凱利公式的(de)思想，即最大(dà)化(huà)單期對(duì)數收益率，可(kě)以應用(yòng)到任何不同的(de)分(fēn)布中。

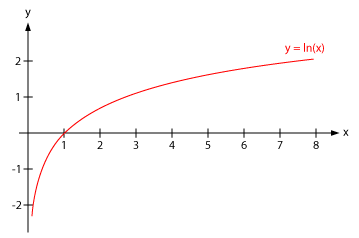
最後想提一句的(de)是，凱利當初選擇使用(yòng)對(duì)數收益率是受了(le)伯努利對(duì)數效用(yòng)函數的(de)啓發。伯努利于 1738 年發表了(le)一篇關于風險下(xià)做(zuò)決策的(de)重要論文（原作不是英文版，後來(lái)爲了(le)推廣，于 1954 年被一個(gè)大(dà)牛教授翻譯成英文出版，見 Bernoulli 1954）。在那篇文章(zhāng)中，伯努利提出了(le)對(duì)數效用(yòng)函數以及著名的(de)聖彼得(de)堡悖論（St. Petersburg paradox）。

ln(X_n) 随 X_n 的(de)變化(huà)如上圖所示。由于對(duì)數函數的(de)特性，它說明(míng)當 X_n > 1 時(shí)（即我們在期末赢錢了(le)），我們掙得(de)越多(duō)，感受到的(de)邊際喜悅越低；當 X_n < 1 時(shí)（即我們在期末虧錢了(le)），我們虧的(de)越多(duō)，感受到的(de)邊際痛苦越高(gāo)，這(zhè)十分(fēn)符合人(rén)在投資時(shí)的(de)主觀感受。所以，從最終收益 X_n 的(de)效用(yòng)的(de)角度來(lái)說，最大(dà)化(huà)期望效用(yòng) E[ln(X_n)] 也(yě)是對(duì)凱利的(de)初衷的(de)一種解釋。當然，對(duì)數收益率可(kě)以相加，這(zhè)樣單期的(de)收益率能和(hé)總體的(de)收益率聯系起來(lái)。因此從業務實際出發，選擇對(duì)數收益率作爲優化(huà)目标實屬必然。

5 凱利公式與量化(huà)投資

最後就來(lái)看看如何将凱利公式應用(yòng)于量化(huà)投資中确定投資品的(de)最佳杠杆比例（倉位）。

首先來(lái)看一種“生搬硬套”的(de)方法。對(duì)于很多(duō)策略（特别是技術分(fēn)析策略），一般都有勝率和(hé)盈虧比的(de)概念。這(zhè)裏勝率就是每次交易賺錢的(de)概率，即 p；盈虧比就相當于賠率 b，即每單位虧損對(duì)應的(de)收益。所以，我們可(kě)以使用(yòng)凱利公式計算(suàn)每次交易的(de)倉位 f* = (b × p – q) / b。當然，考慮到投資者對(duì)于風險的(de)訴求，還(hái)可(kě)以在這(zhè)個(gè)倉位控制上加一個(gè)風險系數，從而進一步降低倉位。但這(zhè)種方法并不是很好。這(zhè)裏的(de)賠率的(de)計算(suàn)方法是所有盈利交易的(de)平均收益除以所有虧損交易的(de)平均虧損。由于每個(gè)交易的(de)開倉、平倉時(shí)間并不固定，因此每次交易的(de)持續時(shí)間都是不同的(de)。這(zhè)種方法在計算(suàn)收益率時(shí)完全不考慮交易時(shí)間這(zhè)個(gè)因素。比如兩次赢錢的(de)交易，一次開倉時(shí)間爲 2 天，收益 1%；而另一次開倉時(shí)間爲 3 小時(shí)，收益爲 1%。它們的(de)平均收益爲 1%，但是顯然這(zhè)兩次交易的(de)風險特性完全不同。所以，這(zhè)個(gè)不考慮交易時(shí)間的(de)賠率計算(suàn)方式是有問題的(de)，以此計算(suàn)的(de) f* 并不合理(lǐ)。

下(xià)面就來(lái)看看更合理(lǐ)的(de)應用(yòng)凱利公式的(de)方法。我們并不是生搬硬套第二節中的(de)那個(gè) f* 公式，而是利用(yòng)凱利公式的(de)思想，即最大(dà)化(huà)單期對(duì)數收益率。由于收益率都是相對(duì)一個(gè)給定的(de)頻(pín)率而言的(de)（如日收益率、周收益率等），因此這(zhè)種方法更加合理(lǐ)。假設一個(gè)投資品的(de)單期的(de)百分(fēn)比收益率（即期末價格 / 期初價格 - 1）滿足均值爲 μ、标準差爲 σ 的(de)正态分(fēn)布。可(kě)以證明(míng)，在這(zhè)個(gè)假設下(xià)，該投資品的(de)單期對(duì)數收益率的(de)期望爲 μ - 0.5σ^2。我們來(lái)看看最大(dà)化(huà)該對(duì)數收益率的(de)杠杆率 L 是多(duō)少。當我們使用(yòng) L 倍的(de)杠杆時(shí)，均值和(hé)标準差分(fēn)别變爲 μL 和(hé) σL，因此對(duì)數收益率變爲 μL - 0.5(σL)^2。以 L 爲自變量來(lái)最大(dà)化(huà) μL - 0.5(σL)^2。對(duì)其求一階導數并使它爲 0，并檢查其二階導數有：

由一階導數等于 0 可(kě)得(de)最優的(de)杠杆率爲 L* = μ / σ^2，由于二階導數恒小于 0，因此對(duì)數收益率在 L = L* 有最大(dà)值。因此，凱利公式确定的(de)最優杠杆率就是：

在實際使用(yòng)中，μ 和(hé) σ 難以估計，此外不同期之間的(de)收益率也(yě)很難保證絕對(duì)獨立，因此業界普遍的(de)觀點是凱利公式的(de)理(lǐ)論杠杆率風險較高(gāo)。爲此，普遍的(de)做(zuò)法是把 L* 看作是杠杆率的(de)上限，而使用(yòng) L*/2 的(de)杠杆率，這(zhè)稱之爲“half-Kelly”。投資者可(kě)根據自己願意承擔的(de)最大(dà)風險來(lái)決定是否進一步降低杠杆率。

最後想說明(míng)的(de)是，無論如何應用(yòng)凱利公式，重複性投資畢竟不是玩一個(gè)有固定且獨立收益特征的(de)賭局。投資的(de)收益參數随時(shí)間不停的(de)變化(huà)，這(zhè)就給我們在投資中應用(yòng)凱利公式帶來(lái)了(le)更多(duō)的(de)障礙。有人(rén)說凱利公式的(de)核心是控制風險，我比較認同這(zhè)句話(huà)。畢竟，控制好風險才能在市場(chǎng)中活得(de)長(cháng)，活得(de)長(cháng)才有可(kě)能獲得(de)更高(gāo)的(de)收益。

參考文獻

Bernoulli, D. (1954). Exposition of a New Theory on the Measurement of Risk. Econometrica 22(1), 23 – 36.

Kelly, J. R. Jr. (1956). A New Interpretation of Information Rate. Bell System Technical Journal 35, 917 – 926.

MacLean, L. C., E. O. Thorp, and W. T. Ziemba, Eds (2010). The Kelly Capital Growth Investment Criterion. World Scientific Handbook in Financial Economics Series, Vol 3.

Thorp, E. O. (1962). Beat the Dealer. Random House, New York.

Thorp, E. O. (2017). A Man for all Markets: from Las Vegas to Wall Street, How I beat the Dealer and the Market. Random House, New York.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。