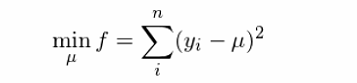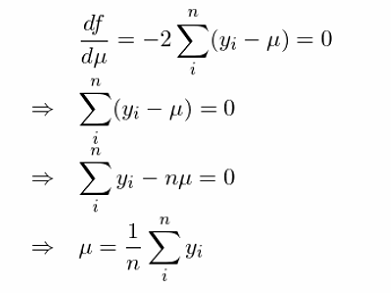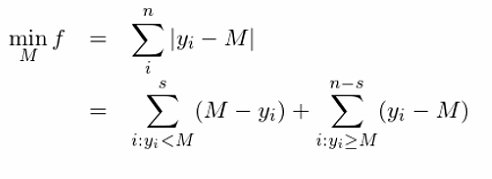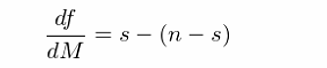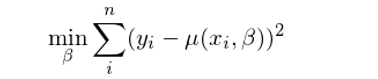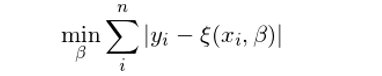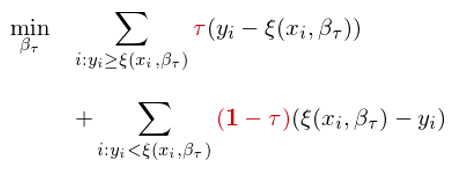用(yòng) Quantile Regression 分(fēn)析變量相關性

作者：石川

摘要：分(fēn)位數回歸根據自變量求出因變量的(de)條件分(fēn)位數，可(kě)以全面地分(fēn)析變量之間的(de)關系。它在量化(huà)投資中的(de)應用(yòng)廣泛。

1 分(fēn)位數和(hé)分(fēn)位數回歸

分(fēn)位數（quantile）是概率中的(de)一個(gè)概念。對(duì)一個(gè)随機變量 X 和(hé)任意一個(gè) 0 到 1 之間的(de)數 τ，如果 X 的(de)取值 x 滿足 prob(X ≤ x) = τ，那麽 x 就是 X 的(de) τ 分(fēn)位數。換句話(huà)說，τ 分(fēn)位數說明(míng)：如果我們按該随機變量的(de)分(fēn)布産生足夠多(duō)的(de)樣本點，那麽在這(zhè)些樣本點的(de)取值中，有 τ × 100% 個(gè)小于該分(fēn)位數；有 (1 - τ) × 100% 個(gè)大(dà)于該分(fēn)位數。最常見的(de)分(fēn)位數非中位數（median）莫屬，它是 50% 分(fēn)位數 —— 在 X 的(de)分(fēn)布中，有一半比中位數小，一半比中位數大(dà)。

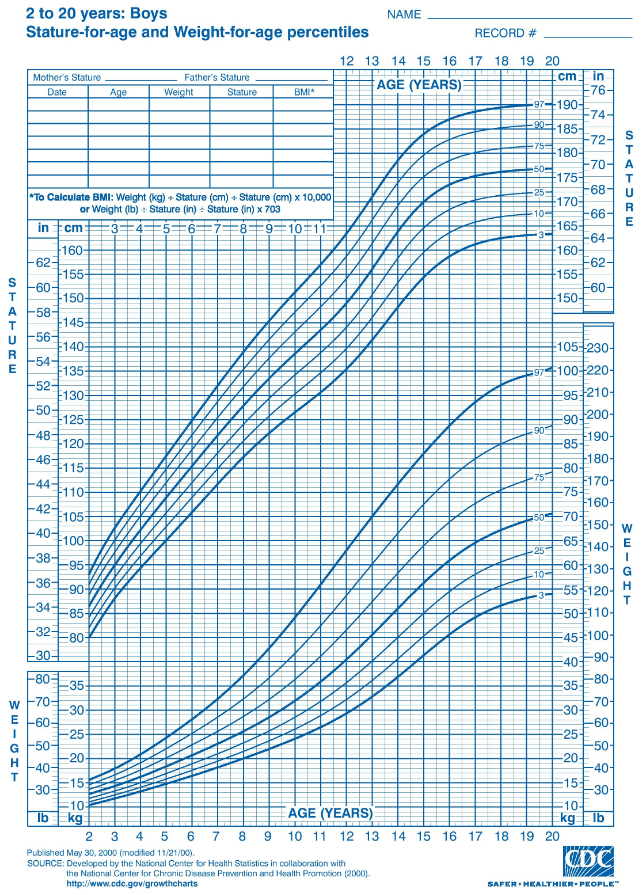
也(yě)許你仍覺著(zhe)上面的(de)定義抽象，但是你對(duì)下(xià)面的(de)兒(ér)童成長(cháng)圖（child growth chart）一定不陌生。它給出了(le)兒(ér)童（這(zhè)個(gè)表中是男(nán)孩）在不同年齡時(shí)身高(gāo)和(hé)體重的(de)不同分(fēn)位數（3%、10%、25%、50%、75%、90% 以及 97%）曲線，這(zhè)有助于兒(ér)醫和(hé)父母判斷寶寶成長(cháng)過程中發育是否正常。如果一個(gè)娃的(de)體重落在 90% 分(fēn)位線上，說明(míng)他(tā)的(de)體重比同齡的(de) 90% 的(de)小夥伴要高(gāo)；如果一個(gè)娃的(de)身高(gāo)或體重在表外了(le)（off the chart），那多(duō)半就說明(míng)他(tā)營養不良或過剩了(le)。分(fēn)位數在生活中作用(yòng)很大(dà)。

上面這(zhè)個(gè)圖說明(míng)兩點：

顯然，這(zhè)兩點向我們展示了(le)身高(gāo)（或體重）與年齡在整個(gè)分(fēn)布上的(de)一些關系。試想一下(xià)，如果我們僅有年齡和(hé)平均身高(gāo)（平均體重）的(de)關系，我們是無法得(de)到上面兩點結論的(de)。分(fēn)位數定量描述了(le)中心趨勢和(hé)統計離散度，這(zhè)有助于更我們全面地分(fēn)析變量之間的(de)關系。

如何得(de)到如上圖中的(de)分(fēn)位數曲線呢(ne)？答(dá)案是分(fēn)位數回歸（quantile regression）。分(fēn)位數回歸由 Koenker and Bassett, Jr. (1978) 提出，是一種回歸分(fēn)析。在傳統回歸中，我們構建回歸模型由自變量求出因變量的(de)條件期望；而在分(fēn)位數回歸中，我們構建回歸模型由自變量求出因變量的(de)條件分(fēn)位數。

近年來(lái)，分(fēn)位數回歸在計量經濟學中的(de)應用(yòng)越來(lái)越廣泛。利用(yòng)分(fēn)位數回歸，Saastamoinen (2008) 研究了(le)芬蘭市場(chǎng)中的(de)羊群效應；Alagidede and Panagiotidis (2012) 討(tǎo)論了(le)通(tōng)貨膨脹和(hé)股票(piào)收益率之間的(de)關系；Badshah (2012) 分(fēn)析了(le)美(měi)股中恐慌指數（VIX）和(hé)收益率分(fēn)布之間的(de)不對(duì)稱性。本文簡要介紹分(fēn)位數回歸，并通(tōng)過一個(gè)簡單的(de)例子說明(míng)它在量化(huà)投資中的(de)潛在作用(yòng)。

2 最優化(huà)視角下(xià)求解均值和(hé)中位數

讓我們先把回歸問題放在一邊，僅僅考慮一個(gè)随機變量 Y 的(de)一組樣本 {y1, y2, …, yn}。在本節中，我們從求解最優化(huà)問題的(de)角度說明(míng)如何求出樣本均值和(hé)中位數。這(zhè)對(duì)于後面介紹分(fēn)位數回歸很有幫助。

我們都知道，這(zhè)組樣本的(de)均值就是這(zhè) n 個(gè)數的(de)平均值。從最優化(huà)的(de)角度來(lái)說，該樣本均值正是下(xià)列最小化(huà)殘差平方和(hé)問題的(de)解：

最優的(de) μ 應滿足 df/dμ = 0。經過簡單的(de)推導不難看出，最小化(huà)殘差平方和(hé)（即我們常說的(de)最小二乘法）得(de)到的(de)解就是樣本均值：

與之類似的(de)，最小化(huà)殘差絕對(duì)值之和(hé)的(de)解就是樣本的(de)中位數（這(zhè)裏的(de)殘差是樣本點相對(duì)于中位數而言的(de)），即這(zhè)組樣本的(de)樣本中位數 M 是如下(xià)最優化(huà)問題的(de)解：

對(duì) M 求導得(de)：

可(kě)見，df/dM 等于 0 的(de)必要條件是 s = n - s，其中 s 是小于 M 的(de)樣本點的(de)個(gè)數，而 n - s 是大(dà)于 M 的(de)樣本點的(de)個(gè)數。這(zhè)意味著(zhe) M 的(de)取值滿足在其兩側的(de)樣本點個(gè)數相同，即 M 是中位數。

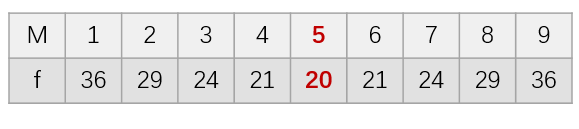
來(lái)看一個(gè)例子。假設随機變量 Y 的(de)一組樣本是 1 到 9 這(zhè) 9 個(gè)數。按照(zhào)上述最優化(huà)的(de)思路，我們想找到 M 使得(de)目标方程 f = Σi|yi - M| 最小。在 1 到 9 内遍曆 M 并求出 f 對(duì)應的(de)值有：

可(kě)見，當 M = 5 時(shí) f 的(de)取值最小，因此這(zhè)組樣本的(de)中位數爲 5。現在我們已經知道如何從求解最優化(huà)問題的(de)角度找到樣本的(de)均值和(hé)中位數（一個(gè)特殊的(de)分(fēn)位數 —— 50% 分(fēn)位數），接下(xià)來(lái)就來(lái)看看如何将這(zhè)個(gè)思路推廣到分(fēn)位數回歸上。

3 分(fēn)位數回歸

推廣上一節的(de)最優化(huà)思路引出分(fēn)位數回歸十分(fēn)簡單，僅需要兩步走。

第一步：引入回歸問題。在上一節中，爲了(le)簡化(huà)討(tǎo)論，我們考慮的(de)是随機變量 Y 自身。在（線性）回歸問題中，我們關注的(de)是因變量 Y 和(hé)某些自變量 X 之間的(de)（線性）關系。（這(zhè)裏，X 可(kě)以代表一個(gè)自變量或者多(duō)個(gè)自變量組成的(de)向量。下(xià)文中爲了(le)簡化(huà)討(tǎo)論，假設自變量隻有一個(gè)。）對(duì)于均值來(lái)說，我們将上一節中的(de)标量 μ 變成自變量 X 的(de)線性方程 μ(X, β) —— 其中 β 是 X 的(de)系數，并将最優化(huà)問題轉化(huà)爲（在這(zhè)個(gè)問題中，求解的(de)對(duì)象是 X 的(de)系數 β）：

求解得(de)到 β 後，線性方程 μ(X, β) 就是因變量 Y 的(de)條件期望方程 E[Y|X]。我們熟悉的(de)求解線性回歸的(de)最小二乘法正是如此找到 Y 和(hé) X 的(de)關系的(de)，它得(de)到的(de) Y 和(hé) X 之間的(de)關系正是 E[Y|X]。

對(duì)于中位數也(yě)可(kě)以做(zuò)相同的(de)推演。令上一節中的(de)标量 M 變爲自變量的(de)線性方程 ξ(X, β)。因此該最優化(huà)問題轉化(huà)爲：

求解得(de)到 β 後，線性方程 ξ(X, β) 就是因變量 Y 的(de)條件中位數方程。

第二步：将中位數推廣到一般分(fēn)位數。在所有分(fēn)位數中間，中位數 —— 又稱 50% 分(fēn)位數 —— 比較特殊是在于在求解最優化(huà)問題中，其兩側樣本點的(de)殘差是等權重的(de)。把上述最小化(huà)殘差絕對(duì)值的(de)問題推廣到一般的(de) τ 分(fēn)位數時(shí)，隻需把 τ 分(fēn)位數兩側的(de)殘差賦予不同的(de)權重即可(kě)。具體的(de)，對(duì)于 τ 分(fēn)位數左側樣本點的(de)殘差，賦予它們 1 - τ 的(de)權重；對(duì)于 τ 分(fēn)位數右側樣本點的(de)殘差，賦予它們 τ 的(de)權重。最優化(huà)問題由此變爲（求解的(de)對(duì)象爲 τ 分(fēn)位數對(duì)應的(de)系數 β，記爲 β_τ）：

使用(yòng)線性規劃求解這(zhè)個(gè)最優化(huà)問題，得(de)到最優解 β_τ 後，線性方程 ξ(X, β_τ) 就是因變量 Y 的(de)條件 τ 分(fēn)位數方程。對(duì)于不同的(de) τ 的(de)取值（如 5%、10%、15%、……、85%、90%、95%），隻需要對(duì)每個(gè) τ 分(fēn)别求解上述最優化(huà)問題，就可(kě)以得(de)到 Y 的(de)不同條件 τ 分(fēn)位數方程。

值得(de)一提的(de)是，如果我們僅有一個(gè)自變量 X，并用(yòng)它來(lái)對(duì) Y 進行分(fēn)位數回歸，那麽任何一個(gè) τ 分(fēn)位數回歸方程都是一條直線（有截距項、斜率爲 β_τ）。但是在第一節的(de)兒(ér)童成長(cháng)圖中，身高(gāo)（體重）的(de)條件 τ 分(fēn)位數方程随年齡的(de)變化(huà)明(míng)顯不是直線。這(zhè)是因爲在構建成長(cháng)曲線時(shí)，通(tōng)常對(duì)年齡先進行了(le)某種非線性變化(huà)以更好的(de)反應它和(hé)兒(ér)童的(de)成長(cháng)的(de)關系。從分(fēn)位數回歸的(de)角度，我們做(zuò)的(de)依然是線性回歸，隻不過這(zhè)時(shí)自變量已經從身高(gāo)變成了(le)身高(gāo)的(de)某個(gè)非線性函數而已。在下(xià)文的(de)第 4、5 節我們考慮兩個(gè)例子，在這(zhè)兩個(gè)例子中我們都不會對(duì)自變量進行任何變換。因此這(zhè)兩個(gè)例子中的(de)條件 τ 分(fēn)位數方程都是線性的(de)。

4 收入和(hé)食物(wù)消費支出的(de)關系

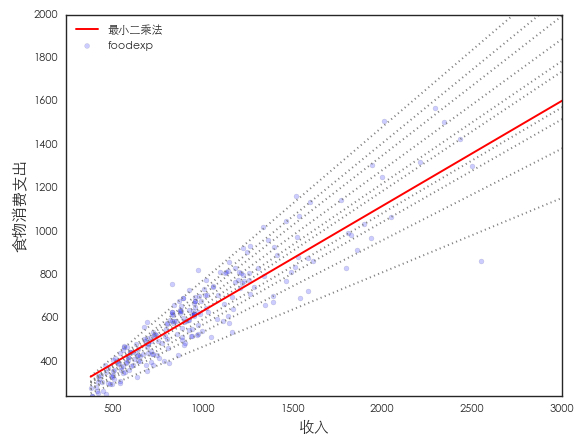
先看一個(gè)生活中的(de)例子。Engel (1857) 研究了(le)家庭收入和(hé)家庭食物(wù)消費支出之間的(de)關系。對(duì)該數據同時(shí)進行最小二乘法回歸（得(de)到條件均值的(de)方程）和(hé)分(fēn)位數回歸（得(de)到 10 個(gè)條件 τ 分(fēn)位數方程，τ 的(de)取值爲 5%，15%，……，95%）如下(xià)圖所示。

從這(zhè)個(gè)圖中可(kě)以觀察到以下(xià)結論：

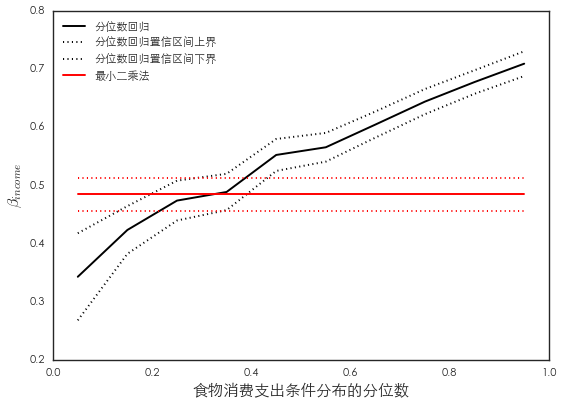
上述分(fēn)位數回歸的(de)結果說明(míng)，在食物(wù)消費支出分(fēn)布的(de)不同位置（不同分(fēn)位數），家庭收入對(duì)其的(de)影(yǐng)響是不同的(de)。下(xià)圖展示了(le)這(zhè)一點。圖中橫坐(zuò)标爲食物(wù)消費支出的(de)分(fēn)位數，縱坐(zuò)标爲不同分(fēn)位數回歸的(de)系數 β_τ，它表示一個(gè)單位的(de)家庭收入變化(huà)帶來(lái)多(duō)大(dà)的(de)食物(wù)消費支出。對(duì)于最小二乘法（紅色）來(lái)說，它假設收入對(duì)食物(wù)消費支出的(de)影(yǐng)響在整個(gè)分(fēn)布上是恒定的(de)；但是分(fēn)位數回歸（黑(hēi)色）正好得(de)到不同的(de)結論。顯然，分(fēn)位數回歸提供了(le)收入和(hé)食物(wù)支出之間更爲豐富的(de)關系。

5 分(fēn)位數回歸在量化(huà)投資中的(de)例子

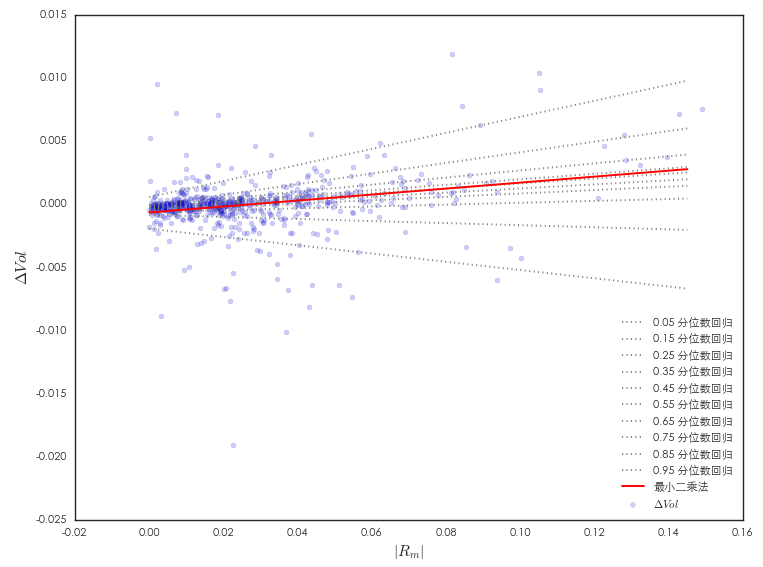
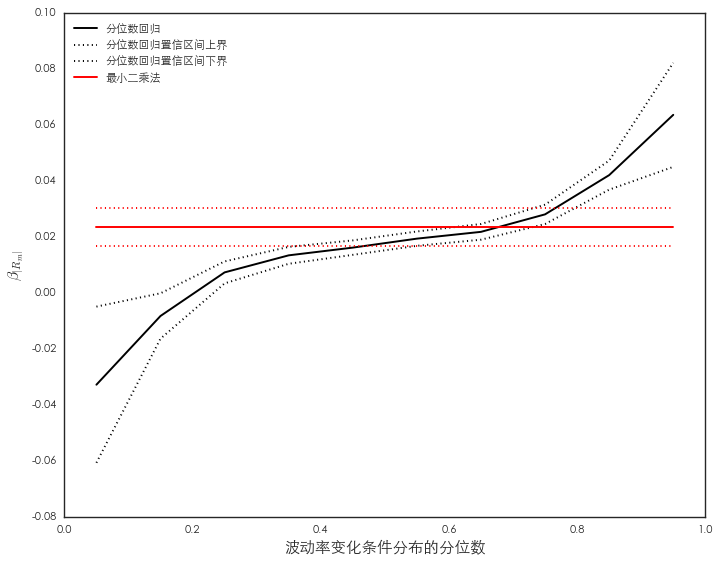
最後通(tōng)過一個(gè)簡單的(de)例子介紹分(fēn)位數回歸在量化(huà)投資中的(de)應用(yòng)。具體的(de)，我們關注風險和(hé)收益之間的(de)關系。爲此，需要給風險和(hé)收益各找一個(gè)代理(lǐ)指标。以上證指數（2005 年 1 月(yuè) 1 日至 2017 年 7 月(yuè) 31 日）爲例，風險的(de)代理(lǐ)指标爲每周已實現波動率（日頻(pín)收益率的(de)平方和(hé)）的(de)變化(huà)率，記爲 ΔVol；收益的(de)代理(lǐ)指标爲周收益率的(de)絕對(duì)值，記爲 |Rm|。對(duì)該數據同時(shí)進行最小二乘法回歸和(hé)分(fēn)位數回歸如下(xià)圖所示。

可(kě)見，對(duì)于 ΔVol 的(de)不同分(fēn)位數，|Rm| 對(duì)其的(de)影(yǐng)響不同。下(xià)圖是 τ 和(hé)系數 β_τ 的(de)關系。當 ΔVol 處于低分(fēn)位數通(tōng)常意味著(zhe)市場(chǎng)一般比較平穩，因此周波動率也(yě)比較穩定、ΔVol 較小。這(zhè)時(shí)收益率的(de)單位變化(huà)對(duì) ΔVol 的(de)影(yǐng)響爲負，有助于進一步維持平穩的(de)市場(chǎng)狀态。當 ΔVol 處于高(gāo)分(fēn)位數通(tōng)常意味著(zhe)市場(chǎng)一般比較震蕩，因此周波動率變化(huà)劇烈、ΔVol 較大(dà)。這(zhè)時(shí)收益率的(de)單位變化(huà)對(duì) ΔVol 的(de)影(yǐng)響爲正，即它會進一步加劇市場(chǎng)的(de)波動。

6 結語

對(duì)于金融投資中的(de)很多(duō)變量，比如收益率，我們往往更關心它在分(fēn)布尾部的(de)特性。在這(zhè)方面，分(fēn)位數回歸是一個(gè)有力的(de)工具，它讓我們研究收益率和(hé)不同的(de)解釋變量在全分(fēn)布上的(de)相關性。當變量的(de)分(fēn)布明(míng)顯偏離正态分(fēn)布或者存在異常值（outliers）時(shí)，傳統的(de)最小二乘法回歸就不那麽有效了(le)。然而分(fēn)位數回歸不受這(zhè)些弊端的(de)影(yǐng)響。此外，分(fēn)位數回歸滿足單調變換不變性（invariant to monotonic transformations）。對(duì)于随機變量 Y 和(hé)它的(de)單調變換 h(Y) —— 比如 log(Y)，h(Y) 的(de)分(fēn)位數正好是 h(Q_τ(Y))，即對(duì) Y 的(de)分(fēn)位數 Q_τ(Y) 直接做(zuò)同樣的(de)變換；而均值并不滿足類似的(de)性質，即 E[h(Y)] ≠ h(E[Y])。投資品收益率的(de)分(fēn)布以不滿足正态性并存在很多(duō)異常值而聞名，因此上述優點使分(fēn)位數回歸在分(fēn)析收益率時(shí)有著(zhe)廣闊的(de)前景。

參考文獻

Alagidede, P. and T. Panagiotidis (2012). Stock returns and Inflation: Evidence from Quantile Regressions. Discussion Paper Series, Department of Economics, University of Macedonia.

Badshah, I. U. (2012). Quantile regression analysis of the asymmetric return-volatility relation. Journal of Futures Markets 33(3), 235 – 265.

Engel, E. (1857). Die Produktions- und Konsumptionverhaltnisse des Konigreichs Sachsen. Reprinted in “Die Lebenkosten Belgischer Arbeiter-Familien Fruher und Jetzt.” International Statistical Institute Bulletin 9, 1 – 125.

Koenker, R. and G. Bassett, Jr. (1978). Regression Quantiles. Econometrica 46(1), 33 – 50.

Saastamoinen, J. (2008). Quantile regression analysis of dispersion of stock returns – evidence of herding? Working paper, Joensuun yliopisto, Taloustieteet.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。