資産配置的(de)源起、中興和(hé)未來(lái)

發布時(shí)間：2024-03-25 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：資産配置是投資中最重要的(de)問題（之一）。本文帶你了(le)解資産配置的(de)源起，中興和(hé)未來(lái)。

1 源起

資産配置是投資中最重要的(de)問題（之一）。

1950 年的(de)某個(gè)下(xià)午，當 Markowitz 在草(cǎo)稿紙上畫(huà)出世界上第一個(gè) mean-variance 有效前沿的(de)時(shí)候，也(yě)正式拉開了(le)使用(yòng)定量化(huà)方法研究資産配置的(de)篇章(zhāng)。MVO 的(de)數學表達式如下(xià)：

$\displaystyle\max_w w^\prime\mu-\frac{1}{2}\delta w^\prime\Sigma w,$

其中 $\mu$ 和(hé) $\Sigma$ 分(fēn)别爲資産的(de)預期收益率向量和(hé)協方差矩陣， $\delta$ 爲風險厭惡系數， $w$ 則表示資産的(de)權重。當不存在無風險資産時(shí)，求解上述方程所得(de)到的(de)抛物(wù)線的(de)上半部分(fēn)就是有效前沿。

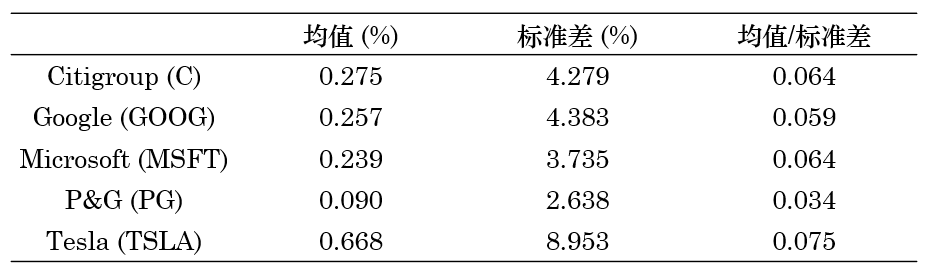
作爲一個(gè)例子，考慮以下(xià)五個(gè)股票(piào)：C、GOOG、MSFT、PG 以及 TSLA。假設樣本内的(de)實證區(qū)間爲 2020/9 到 2023/2。在這(zhè)段區(qū)間内，上述股票(piào)的(de)周收益率均值以及标準差如下(xià)表所示。

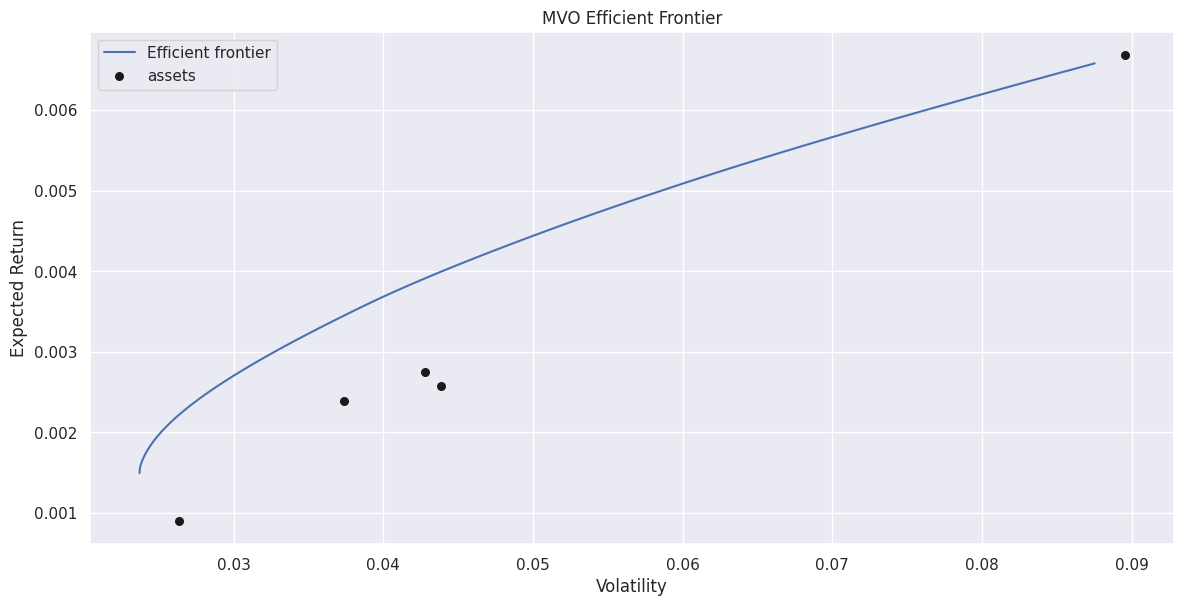
由它們構成的(de)有效前沿爲：

當存在無風險資産時(shí)，我們可(kě)以通(tōng)過無風險資産向該抛物(wù)線做(zuò)切線，得(de)到的(de)切點組合（tangency portfolio）具有最大(dà)的(de)夏普比率。在上述例子中，假設我們使用(yòng)同期 10-year T-note yield 的(de)均值作爲無風險收益率，則得(de)到的(de)最優投資組合權重爲：C：42.43%，GOOG：9.86%，MSFT：19.02%，PG：0%，以及 TSLA：28.69%。

上述結果不難理(lǐ)解。從這(zhè)五個(gè)股票(piào)的(de)風險收益特征來(lái)看，毫無疑問 PG 最沒有吸引力（至少在我們的(de)樣本期内），而其他(tā)幾支股票(piào)不分(fēn)伯仲。另外，C 的(de)相關性和(hé)其他(tā)股票(piào)最低，因此在最優化(huà)中獲得(de)了(le)最高(gāo)的(de)權重。

那麽，這(zhè)個(gè) MVO 組合在樣本外如何呢(ne)？假設考慮 2023/3 到 2023/8 這(zhè)半年作爲樣本外實證區(qū)間。則該投資組合在樣本外的(de)周平均收益率爲 0.50%、标準差爲 3.49%，因此年化(huà)夏普比率爲 0.97 —— not too bad。然而，這(zhè)樣一個(gè)組合和(hé)基準組合（即等權配置五個(gè)股票(piào)）相比又如何呢(ne)？

不出意外的(de)話(huà)，馬上就要出意外了(le)。基準組合在樣本外的(de)周收益率均值爲 0.79%，夏普比率則超過 2.0，遠(yuǎn)超上述 MVO 組合。如果考察股票(piào)在樣本外的(de)表現，這(zhè)樣的(de)結果其實不難理(lǐ)解。在 2023/3 到 2023/8 這(zhè)段時(shí)間，它們的(de)周收益率均值分(fēn)别爲 C：-0.55%，GOOG：1.69%，MSFT：1.10%，PG：0.44% 以及 TSLA：1.25%。其中最令人(rén)大(dà)跌眼鏡的(de)是 C 錄得(de)了(le)負收益。這(zhè)就不難理(lǐ)解重倉 C 的(de) MVO 組合在樣本外跑輸基準組合的(de)結果。

究其原因，都是估計誤差（estimation error）惹的(de)禍，即樣本均值和(hé)協方差矩陣并不是未來(lái)預期收益和(hé)協方差矩陣的(de)準确估計。因此，估計誤差的(de)成本抵消了(le) MVO 的(de)潛在優勢。一般來(lái)說，估計誤差可(kě)能非常大(dà)，以至于在樣本外作爲基準的(de)等權配置往往難以被打敗（DeMiguel, Garlappi and Uppal 2009）。

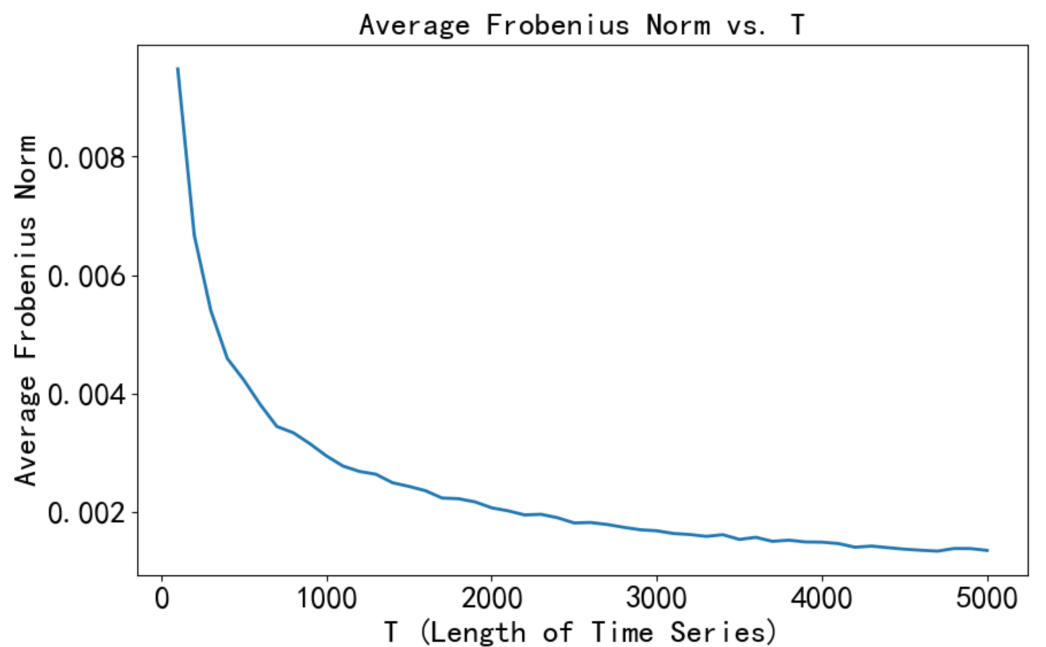
爲了(le)進一步說明(míng)這(zhè)個(gè)問題，以 BetaPlus 小組針對(duì) A 股市場(chǎng)構造的(de) Fama-French 五因子爲配置的(de)标的(de)。假設曆史數據計算(suàn)的(de) $\mu$ 和(hé) $\Sigma$ 就是真實參數，而下(xià)圖中藍線是根據它們計算(suàn)而來(lái)的(de)有效前沿。接下(xià)來(lái)，假設這(zhè)五個(gè)因子的(de)收益率滿足 multivariate normal（參數爲上述 $\mu$ 和(hé) $\Sigma$ ），并生成模拟樣本。對(duì)于每次模拟，使用(yòng)模拟樣本計算(suàn) $\mu^\prime$ 和(hé) $\Sigma^\prime$ ，并使用(yòng)它們計算(suàn)投資組合的(de)最優權重 $w^\prime$ 。得(de)到最優權重 $w^\prime$ 之後，将其和(hé)真實參數 $\mu$ 和(hé) $\Sigma$ 計算(suàn)，便得(de)到了(le)圖中的(de)綠線（一共考慮了(le) 50 組模拟，因此一共有 50 條綠色曲線）。

由于真實的(de)參數是 $\mu$ 和(hé) $\Sigma$ ，而我們計算(suàn)最優權重使用(yòng)的(de)是 $\mu^\prime$ 和(hé) $\Sigma^\prime$ ，因此每個(gè)模拟中的(de)綠色有效前沿都要比藍色曲線差。它們的(de)差異表明(míng)了(le)參數估計誤差對(duì)實際投資組合的(de)影(yǐng)響。此外，另一個(gè)更重要的(de)因素是，資産的(de)預期收益率以及協方差不滿足平穩性。因此，使用(yòng)曆史數據計算(suàn)的(de)均值和(hé)協方差，很難在樣本外構造有效的(de) MVO 組合。

人(rén)們亟需更好的(de)方法。

2 中興

我們可(kě)以至少從兩方面著(zhe)手，降低估計誤差的(de)影(yǐng)響，進而在樣本外構造更好的(de)投資組合。

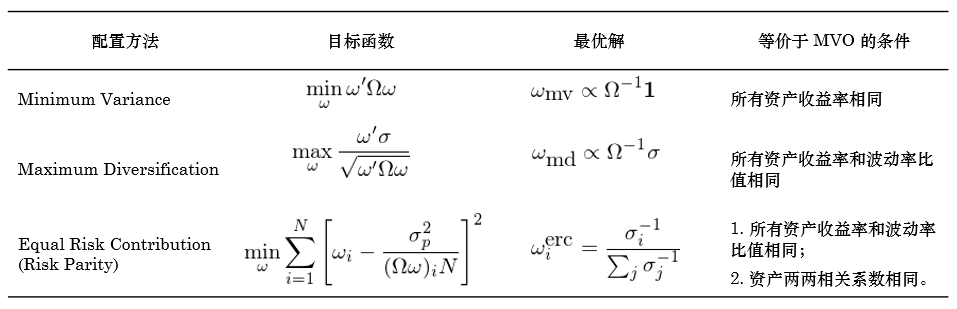
第一個(gè)方面是在合理(lǐ)的(de)假設下(xià)減少需要估計的(de)參數。這(zhè)意味著(zhe)考慮 MVO 之外的(de)資産配置目标，即 minimum variance、maximum diversification 以及 risk parity 等。《淺析資産配置的(de)幾種方法》一文曾經討(tǎo)論過在何種假設下(xià)，上述方法和(hé) MVO 等價。感興趣的(de)小夥伴請自行查閱，此處将結果彙總于下(xià)表。

從上述配置目标來(lái)看，它們和(hé) MVO 最大(dà)的(de)差異是沒有使用(yòng)預期收益率，而聚焦在協方差矩陣上。由于事前難以準确估計預期收益率，且預期收益率的(de)估計誤差對(duì)配置結果影(yǐng)響重大(dà)，這(zhè)些“退而求其次”的(de)做(zuò)法往往能夠比 MVO 獲得(de)更穩健的(de)配置結果。

當然，這(zhè)些配置目标依然需要在事前估計協方差矩陣，而當标的(de)個(gè)數 $N$ 很大(dà)時(shí)，準确估計協方差矩陣也(yě)絕非易事。下(xià)面假設 DGP 已知并通(tōng)過模拟說明(míng)期數 $T$ 和(hé) $N$ 的(de)關系如何影(yǐng)響估計誤差。首先，令 $N=50$ ，并且收益率滿足均值爲零的(de)多(duō)元正态分(fēn)布，并随機生成一個(gè)正定的(de)協方差矩陣作爲真實的(de)協方差矩陣。之後，令 $T$ 的(de)取值從 100 到 5000，且對(duì)每個(gè) $T$ 進行 1000 次模拟。在每次模拟中，計算(suàn)樣本協方差矩陣和(hé)真實協方差矩陣的(de) Frobenius 範數，并取均值作爲該 $T$ 下(xià)的(de)誤差。結果如下(xià)圖所示：區(qū)區(qū) $N=50$ 個(gè)标的(de)也(yě)需要 $T=5000$ 期的(de)數據（對(duì)于日頻(pín)就是差不多(duō) 20 年）才能比較放心的(de)使用(yòng)樣本協方差矩陣。

但顯然，這(zhè)種數據量的(de)需求是奢侈的(de)；而且實際資産配置中，标的(de)個(gè)數也(yě)可(kě)能遠(yuǎn)遠(yuǎn)超過 50。因此，爲了(le)有效地估計協方差矩陣，更常見的(de)做(zuò)法是使用(yòng)多(duō)因子模型 —— 比如 Barra 的(de)一系列風險多(duō)因子模型。通(tōng)過它，能夠大(dà)大(dà)減少需要估計的(de)參數，降低參數估計的(de)統計成本。需要 Barra 多(duō)因子模型背景知識的(de)小夥伴，可(kě)參考《正确理(lǐ)解 Barra 的(de)純因子模型》以及《Barra 因子模型截面回歸求解》。

第二個(gè)方面是通(tōng)過貝葉斯框架融合先驗以及人(rén)對(duì)于資産預期收益率的(de)展望。這(zhè)方面的(de)代表自然要數 Black-Litterman 模型。需要說明(míng)的(de)是，該模型的(de)核心是通(tōng)過納入人(rén)對(duì)資産預期收益率的(de)觀點（成爲 views）得(de)到後驗預期收益率估計以及後驗協方差矩陣，而求解最優投資組合權重時(shí)依然遵循 MVO 框架。

仍然回到本文第一節的(de)例子。假設在 2023/2 的(de)時(shí)點，我們爲這(zhè)五個(gè)股票(piào)提供以下(xià) views：

（1）首先，對(duì)于 GOOG 和(hé) MSFT，考慮到 2023 年 2 月(yuè) 1 日 ChatGPT Pro 的(de)推出會極大(dà)推動 AI 投資熱(rè)潮，因此會利好科技巨頭。對(duì)于這(zhè)兩個(gè)公司而言，GOOG 憑借其龐大(dà)的(de)數據存儲庫和(hé)在機器學習(xí)領域的(de)開拓性工作（例如 DeepMind），處于 AI 的(de)領先位置。另一方面，MSFT 也(yě)擁有強大(dà)的(de)人(rén)工智能框架。比較這(zhè)兩家公司，GOOG 或許稍占優勢。因此，我們認爲 GOOG 的(de)周收益率會比 MSFT 高(gāo)出 0.1％。然而，由于監管和(hé)市場(chǎng)競争，因此上述觀點存在巨大(dà)的(de)不确定性，我們假設這(zhè)個(gè) view 的(de)标準差爲 1％。

（2）再來(lái)看 TSLA。它彼時(shí)的(de)最新财報顯示，無論是 earnings 還(hái)是 revenue 都打敗了(le)分(fēn)析師一緻預期。然而，我們也(yě)注意到了(le)毛利率的(de)明(míng)顯下(xià)降（過去五個(gè)季度中最低）。因此，我們對(duì)其表現持謹慎樂(yuè)觀态度，預計每周平均收益率 0.3％，标準差爲 1％。

（3）對(duì)于 PG，該公司的(de)未來(lái)取決于應對(duì)通(tōng)貨膨脹壓力和(hé)成本挑戰。盡管它以 dividend king 而聞名，但在當時(shí)的(de)時(shí)點其估值已然很高(gāo)。因此，我們假設保持中立，預計未來(lái)周收益率均值爲 0％，标準差 1％。

（4）對(duì)于 C，根據最新财報，盡管其收入增長(cháng)，但淨收入出現了(le)顯著(zhe)下(xià)降，原因是增加的(de)信貸成本和(hé)宏觀經濟衰退等因素。鑒于這(zhè)些挑戰，我們持有負面觀點，預測其周收益率爲 -0.05％，标準差爲 0.5％。

将上述 views 代入 Black-Litterman 模型中的(de) $P$ 、 $Q$ 以及 $\Omega$ :

$Q = \begin{bmatrix} -0.0005 \\ 0.001 \\ 0.0 \\ 0.003 \end{bmatrix},$

$P = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & -1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix},$

$\Omega = \begin{bmatrix} 0.005^2 & 0 & 0 & 0 \\ 0 & 0.01^2 & 0 & 0 \\ 0 & 0 & 0.01^2 & 0 \\ 0 & 0 & 0 & 0.01^2 \end{bmatrix}.$

根據貝葉斯框架，可(kě)得(de)預期收益率的(de)後驗估計：

$\displaystyle\mu_{BL}=[(\tau\Sigma)^{-1}+P'\Omega^{-1}P]^{-1}[(\tau\Sigma)^{-1}\pi+P'\Omega^{-1}Q],$

以及協方差矩陣的(de)後驗估計：

$\displaystyle\Sigma_{BL}=\Sigma+((\tau\Sigma)^{-1}+P'\Omega^{-1}P)^{-1}.$

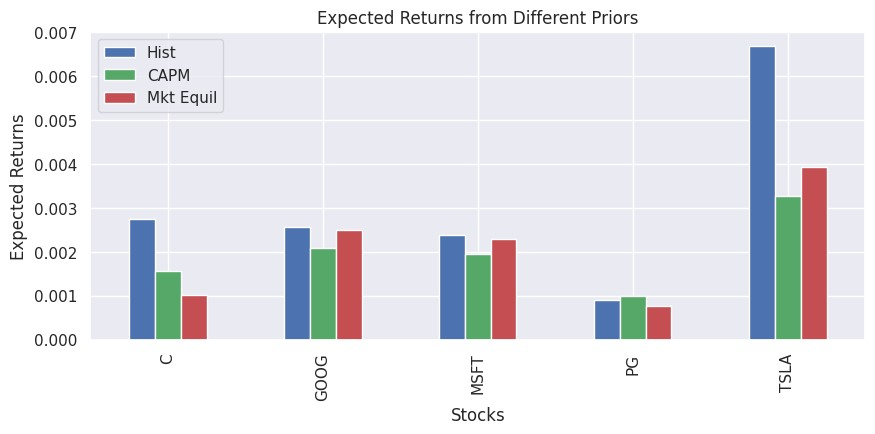
值得(de)一提的(de)是，盡管在原始 Black-Litterman 模型的(de)論文中，兩位作者使用(yòng)市場(chǎng)均衡狀态下(xià)的(de)隐含預期收益率作爲先驗，但在實際應用(yòng)中，我們也(yě)可(kě)以使用(yòng)其他(tā)方法構造先驗，例如使用(yòng)樣本均值或者因子模型（比如 CAPM）所隐含的(de)預期收益率。在本例中，這(zhè)三種方法計算(suàn)的(de)預期收益率先驗如下(xià)圖所示。定性上說，三者的(de)差異并不大(dà)。

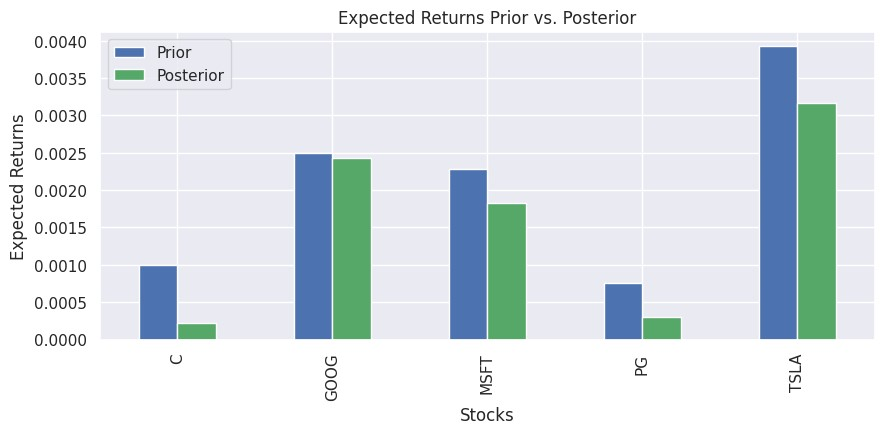
假設我們遵循 Black-Litterman 模型原文，采用(yòng)市場(chǎng)均衡狀态下(xià)隐含的(de)預期收益率作爲先驗，則代入 views 之後就可(kě)計算(suàn)出其後驗。下(xià)圖對(duì)先驗和(hé)後驗進行了(le)對(duì)比。

後驗預期收益率完美(měi)地反映了(le)我們的(de) views。首先，對(duì) C 的(de)負面展望使其後驗預期收益率顯著低于其先驗。其次，GOOG 和(hé) MSFT 的(de)預期收益率差異被放大(dà)，體現了(le)我們更加看好前者的(de)觀點。最後，TSLA 和(hé) PG 的(de)後驗預期收益率均低于它們的(de)先驗。

将後驗預期收益率和(hé)協方差矩陣代入 MVO，得(de)到的(de)最優權重是 C：0％，GOOG：75.07％，MSFT：10.59％，PG：0％，以及 TSLA：14.33％。該投資組合在樣本外的(de)周收益率均值爲 1.56％，夏普比率爲2.80。不僅遠(yuǎn)超原始的(de) MVO 組合，也(yě)輕松的(de)戰勝了(le)基準組合。

（當然，我們的(de) views 隻是爲了(le)說明(míng) Black-Litterman 框架的(de)有效性。在實際投資中，提供正确的(de) views 十分(fēn)困難。）

3 未來(lái)

除了(le)這(zhè)些技術，降噪和(hé)聚類也(yě)是常見的(de)手段。下(xià)面仍然通(tōng)過之前五個(gè)股票(piào)的(de)例子展開討(tǎo)論。

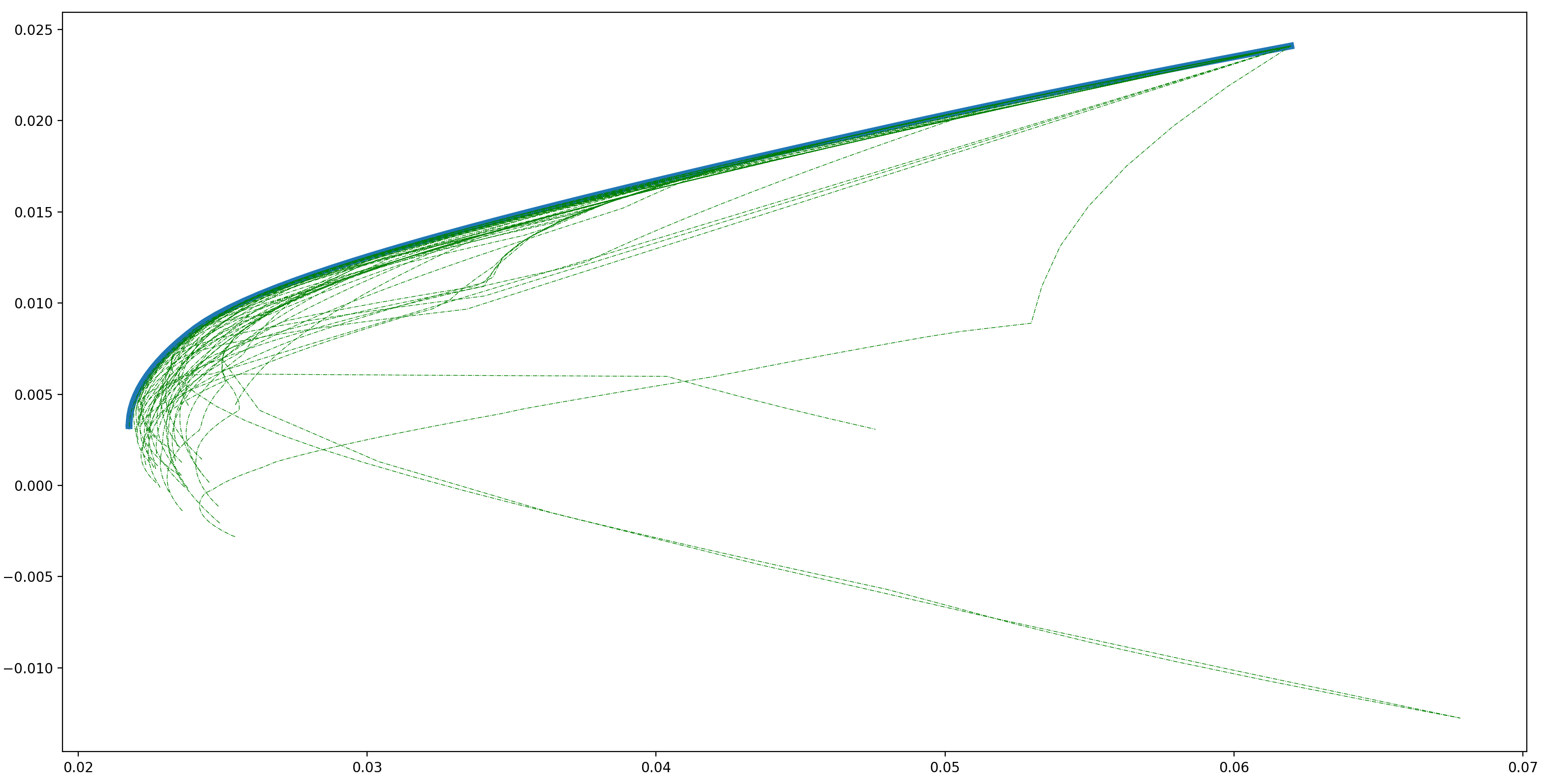
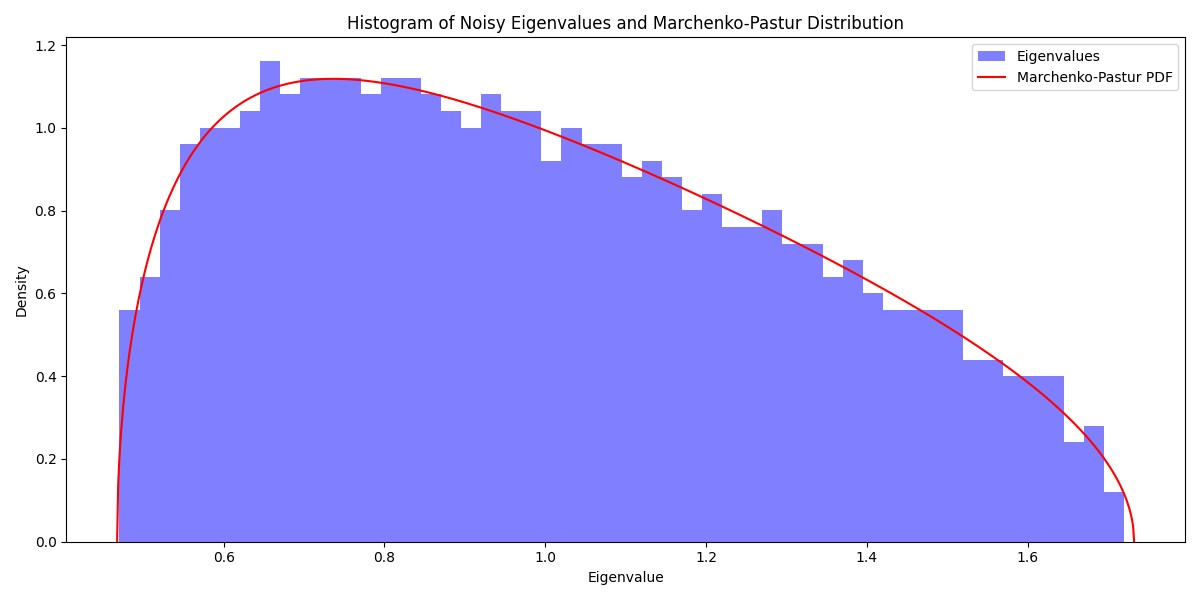
關于降噪，最直觀的(de)方法自然是利用(yòng)随機矩陣理(lǐ)論（RMT），其目标是消除協方差矩陣中的(de)噪聲。根據該理(lǐ)論，噪聲數據協方差矩陣的(de)特征值滿足 Marchenko-Pastur 分(fēn)布。下(xià)圖展示了(le)噪聲數據的(de)協方差矩陣的(de)特征值經驗分(fēn)布以及和(hé)它對(duì)應的(de) Marchenko-Pastur 分(fēn)布。因此，降噪的(de)目标是識别樣本協方差矩陣中位于該分(fēn)布之外的(de)特征值（信号），然後利用(yòng)它們重構協方差矩陣，并用(yòng)于投資組合優化(huà)。

除了(le) RMT，協方差矩陣的(de)收縮方法（例如 Ledoit-Wolf 的(de)很多(duō)研究），也(yě)在某種程度上可(kě)以被視爲是一種降噪。這(zhè)是因爲收縮的(de)目标往往是一個(gè)更具結構化(huà)的(de)矩陣，代表著(zhe)金融理(lǐ)論的(de)先驗知識。通(tōng)過将樣本協方差向該矩陣收縮，可(kě)以有效地減少了(le)原始樣本協方差矩陣中存在的(de)噪聲。

不過需要說明(míng)的(de)是，在降低估計方差的(de)同時(shí)，收縮也(yě)會引入偏差，類似于正則化(huà)在模型拟合中權衡偏差和(hé)方差以防止過拟合。最優的(de)收縮強度可(kě)以被視爲在樣本協方差矩陣的(de)複雜(zá)性和(hé)目标矩陣的(de)簡約性之間找到平衡，最終降低樣本外的(de)估計誤差。在資産配置中，RMT 和(hé)收縮方法可(kě)以互補，從而得(de)到更穩健和(hé)可(kě)靠的(de)優化(huà)結果。

另一方面，聚類也(yě)是改善樣本外資産配置結果的(de)重要工具。通(tōng)過揭示資産的(de)内在關聯，它可(kě)以将具有相似特征的(de)資産分(fēn)組，從而實現分(fēn)散風險的(de)目的(de)。對(duì)于聚類，最近幾年一個(gè)很火的(de)配置方法是層級風險平價（Hierarchical Risk Parity）。該方法通(tōng)過層級聚類對(duì)資産分(fēn)類，并按風險平價來(lái)确定資産權重，優化(huà)投資組合。

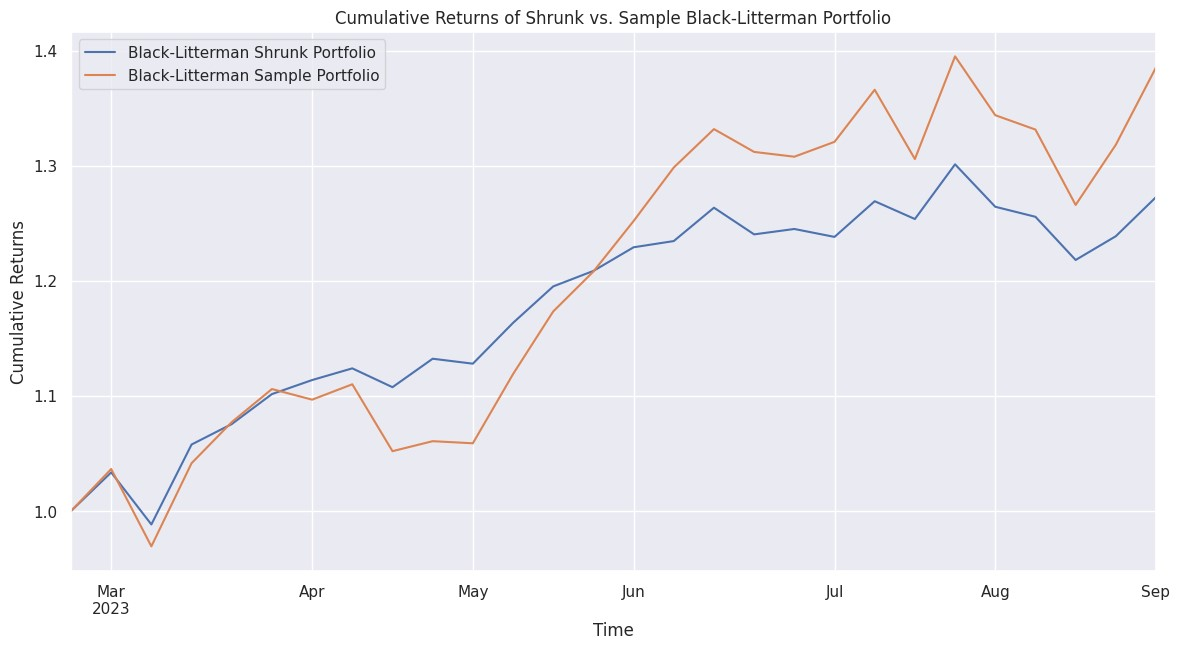
回到我們的(de)例子，下(xià)面試圖将降噪以及聚類融入到 Black-Litterman 模型之中。在實證中我們将通(tōng)過對(duì)樣本協方差矩陣（以及樣本平均收益率）收縮實現降噪，收縮的(de)最優系數通(tōng)過 5-fold CV 确定。因此，作爲比較基準，在非降噪的(de)版本中，直接使用(yòng)樣本收益率均值作爲 Black-Litterman 的(de)先驗，而非像上一節中使用(yòng)市場(chǎng)均衡狀态下(xià)的(de)隐含預期收益率。在收縮時(shí)，對(duì)于預期收益率，五個(gè)股票(piào)的(de)樣本平均收益率均值作爲收縮的(de)目标；而對(duì)于協方差矩陣，則直接使用(yòng) Ledoit-Wolf Shrinkage 估計量。最後，實證的(de)目标是檢驗收縮能否改善先驗，因此在 Black-Litterman 框架中，views 的(de)取值和(hé)上節一樣。

樣本外（2023/3 到 2023/8）的(de)實證結果顯示，加入降噪之後，投資組合的(de)年化(huà)夏普比率爲 2.78，而基準版本爲 2.48。此外，我們也(yě)考察了(le)兩個(gè)風險指标，即最大(dà)回撤和(hé) Expected Shortfall。降噪後，最大(dà)回測從 -9.25% 提升至 -6.39%；ES 從 -5.86% 提升至 -3.68%。下(xià)圖繪制了(le)兩個(gè)組合的(de)累積收益曲線。

接下(xià)來(lái)，将聚類融入到上述過程，看看它能否進一步改善資産配置表現。爲此，我們會将聚類結果作爲約束條件放到最終的(de) MVO 最優化(huà)問題中。對(duì)于本文考慮的(de)這(zhè)個(gè) toy example 而言，由于 GOOG 和(hé) MSFT 都是科技巨頭且相關度最高(gāo)，因此它們被自然的(de)分(fēn)爲一類；其他(tā)三支股票(piào)各自爲一類。MVO 中要求每一類股票(piào)的(de)權重在 0.2 到 0.3 之間。

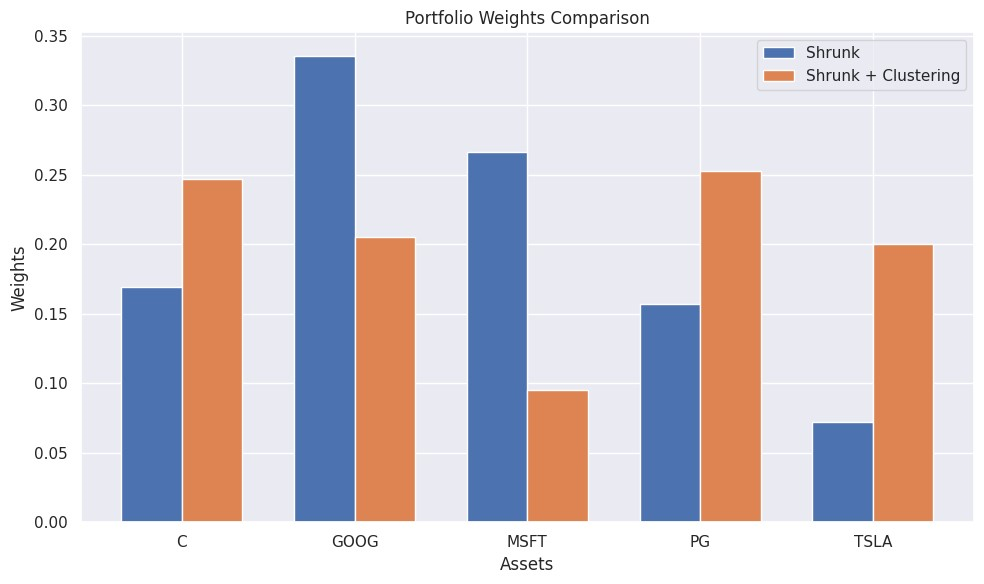
接下(xià)來(lái)，比較降噪 + 聚類和(hé)僅僅降噪兩個(gè)版本。結果顯示，考慮額外的(de)聚類約束後，投資組合的(de)夏普比率從 2.78 下(xià)降到 1.93，且最大(dà)回撤以及 ES 也(yě)有不同程度的(de)變差，表明(míng)至少在這(zhè)個(gè)例子中，聚類約束并沒有帶來(lái)額外的(de)好處。下(xià)圖給出了(le)兩種版本下(xià)的(de)最優投資組合權重。

通(tōng)過比較兩個(gè)投資組合的(de)最優權重，可(kě)以看到附加額外約束的(de)版本在各個(gè)股票(piào)所在的(de)群組上确實更加平衡，達到了(le)預設的(de)目标。這(zhè)導緻投資組合在不同行業之間大(dà)緻均勻暴露，實現了(le)更多(duō)樣化(huà)的(de)配置。然而，作爲代價，上述均衡配置犧牲了(le)某些行業更高(gāo)的(de)預期收益率。在樣本外期間，由于多(duō)樣化(huà)配置的(de)好處未能抵消預期收益率方面的(de)損失，因而導緻夏普比率的(de)下(xià)降。不過需要強調的(de)是，在不同的(de)資産範圍或市場(chǎng)條件下(xià)，多(duō)樣化(huà)能夠發揮更重要的(de)作用(yòng)。因此，我們不應僅僅基于這(zhè)個(gè) toy example 就否定聚類的(de)作用(yòng)。

除了(le)降噪和(hé)聚類之外，将高(gāo)階矩信息 —— 例如 coskewness 和(hé) cokurtosis —— 納入資産配置模型也(yě)是趨勢之一（一個(gè)例子在此）。此時(shí)，配置模型變爲：

$\begin{array}{rl} \max_w & a_1w^\prime M_1\\ &+a_2 w^\prime M_2 w\\ &+a_3 w^\prime M_3(w\otimes w)\\ &+a_4 w^\prime M_4(w\otimes w\otimes w), \end{array}$

其中 $M_i$ 表示收益率的(de)第 $i$ 階中心矩， $a_i$ 表示不同階矩的(de)重要程度。在求解最優化(huà)問題時(shí)，我們也(yě)可(kě)以從金融學理(lǐ)論出發對(duì) $a_i$ 的(de)符号做(zuò)如下(xià)約束：（1） $a_1$ 代表預期收益率的(de)系數，因此 $a_1>0$ ；（2） $a_2$ 代表波動率的(de)系數，因此 $a_2<0$ ；（3） $a_3$ 表示偏度的(de)系數，而投資者往往喜歡 positive skewness，因此 $a_3>0$ ；最後（4） $a_4$ 表示峰度的(de)系數而高(gāo)峰度往往意味著(zhe)更高(gāo)的(de)尾部風險，因此 $a_4<0$ 。

最後，機器學習(xí)也(yě)在近年來(lái)被廣泛應用(yòng)于資産配置當中。例如，de Prado 提倡使用(yòng) combinatorial purged cross-validation（CPCV）方法進行回測，代替傳統的(de) k-fold CV 以及 walk forward 方法。CPCV 是一種金融機器學習(xí)算(suàn)法，能夠生成訓練/測試集合組合來(lái)構建回測路徑，并剔除可(kě)能包含洩露信息的(de)樣本。較傳統方法，CPCV 通(tōng)過生成多(duō)個(gè)訓練/測試拆分(fēn)來(lái)實現多(duō)個(gè)路徑，從而降低過拟合風險、更客觀地評估資産配置結果的(de)表現。

此外，強化(huà)學習(xí)也(yě)被用(yòng)到了(le)資産配置中（雖然我個(gè)人(rén)持謹慎态度）。其主要作用(yòng)是通(tōng)過與環境的(de)交互學習(xí)來(lái)優化(huà)配置結果。例如，強化(huà)學習(xí)算(suàn)法嘗試預測市場(chǎng)動态，并在此基礎上做(zuò)出決策，以最大(dà)化(huà)投資回報。由于該方法不需要先驗知識，且能夠處理(lǐ)複雜(zá)的(de)非線性的(de)投資決策問題，因此成爲了(le)探索資産配置新方法的(de)有力工具。

參考文獻

DeMiguel, V., L. Garlappi, and R. Uppal (2009). Optimal versus naive diversification: How inefficient is the 1/N portfolio strategy? Review of Financial Studies 22(5), 1915-1953.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

資産配置的(de)源起、中興和(hé)未來(lái)