多(duō)重假設檢驗的(de)源起、中興和(hé)未來(lái)

發布時(shí)間：2024-04-17 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：實證資産定價中，多(duō)重假設檢驗容易造成樣本内的(de)僞發現。本文帶你了(le)解多(duō)重假設檢驗的(de)源起，中興和(hé)未來(lái)。

1 源起

多(duō)重假設檢驗（multiple hypothesis testing）指的(de)是同時(shí)檢驗多(duō)個(gè)原假設。在實證資産定價中，使用(yòng)曆史數據挖掘成百上千個(gè)因子正是多(duō)重假設檢驗。當同時(shí)檢驗多(duō)個(gè)假設時(shí)，運氣成分(fēn)（噪聲）會導緻單個(gè)原假設檢驗結果的(de)顯著性被高(gāo)估。當排除了(le)運氣成分(fēn)後，原假設可(kě)能不再顯著。

在單一假設檢驗中，通(tōng)常以 0.05 作爲 p-value 的(de)阈值來(lái)判斷是否接受原假設，其對(duì)應的(de) t-statistic 爲 2.0。這(zhè)也(yě)早已成爲實證資産定價中挖因子的(de)依據。然而多(duō)重假設檢驗的(de)存在使得(de)低 p-value 無法準确說明(míng)因子是否有效。假設我們同時(shí)檢驗 100 個(gè)獨立的(de)因子并發現某個(gè)因子的(de) t-statistic = 2.0。在這(zhè)種情況下(xià)，我們不能說該因子在 0.05 的(de)顯著性水(shuǐ)平下(xià)顯著。這(zhè)是因爲哪怕這(zhè) 100 個(gè)原假設都爲真（即它們的(de)超額收益都爲零），那麽僅僅靠運氣，其中出現 t-statistic 大(dà)于 2.0 的(de)概率高(gāo)達 99%。如果仍然按照(zhào)傳統意義上的(de) 2.0 作爲 t-statistic 的(de)阈值來(lái)評價因子是否顯著，注定會有很多(duō)僞發現（false discoveries 或 false rejections），即第 I 類錯誤。因此，正确處理(lǐ)多(duō)重假設檢驗的(de)影(yǐng)響成爲實證資産定價的(de)關鍵。

在這(zhè)方面，學術界的(de)研究成果可(kě)以被劃分(fēn)爲兩大(dà)類，即頻(pín)率主義方法和(hé)貝葉斯方法。爲了(le)排除運氣（噪聲）的(de)影(yǐng)響，頻(pín)率主義方法以控制第 I 類錯誤爲目标，通(tōng)過增大(dà)标準誤（standard errors）來(lái)修正單個(gè)因子的(de)顯著性水(shuǐ)平。直覺上說，增大(dà)标準誤意味著(zhe)增大(dà)置信區(qū)間，因而這(zhè)使得(de)單個(gè)檢驗的(de)顯著性門檻更加嚴格：隻有當一個(gè)因子原始的(de) t-statistic （遠(yuǎn)）超過傳統意義上的(de) 2.0 水(shuǐ)平，其才有可(kě)能在被修正後依然顯著。

早期的(de)方法多(duō)屬于頻(pín)率主義方法，目标是控制第 I 類錯誤。在統計學中，族錯誤率（family-wise error rate，簡稱 FWER）、僞發現率（false discovery rate，簡稱 FDR）以及僞發現比例（false discovery proportion，簡稱 FDP）是常見的(de)第 I 類錯誤指标。讓我借助下(xià)表來(lái)解釋它們。

假如一共有 $K$ 個(gè)因子，其中 $K_0$ 個(gè)原假設爲真， $K_1$ 個(gè)原假設爲假。根據事先選定的(de)顯著性水(shuǐ)平（比如 0.05），共有 $L$ 個(gè)原假設被拒絕了(le)，其中包括 $T_1$ 個(gè)真實的(de)顯著因子（true discoveries）和(hé) $F_1$ 個(gè)虛假的(de)顯著因子（僞發現）。接下(xià)來(lái)利用(yòng) $F_1$ 和(hé) $L$ 分(fēn)别定義族錯誤率、僞發現率以及僞發現比例。

族錯誤率 FWER 定義爲出現至少一個(gè)僞發現的(de)概率，即 $\text{prob}(F_1\ge 1)$ 。在給定的(de)顯著性水(shuǐ)平 $\alpha_s$ 下(xià)，控制 FWER 的(de)數學表達式爲 $\text{prob}(F_1\ge 1)\le\alpha_s$ 。不難看出，控制族錯誤率對(duì)單個(gè)假設來(lái)說相當嚴格，所以會大(dà)大(dà)提升第 II 類錯誤。針對(duì)族錯誤率，最早的(de)算(suàn)法包括 Bonferroni (1936) 和(hé) Holm (1979) 修正，它們均是直接修正單一假設檢驗的(de) p-value 以實現控制族錯誤率的(de)目的(de)：

$\displaystyle p_i^{\text{Bonferroni}}=\min\{Kp_i,1\},~~i=1,\cdots,K,$

其中 $p_i$ 和(hé) $p_i^{\text{Bonferroni}}$ 分(fēn)别代表第 $i$ 個(gè)因子原始和(hé)經過修正後的(de) p-value；以及

$\displaystyle p_i^{\text{Holm}}=\min\left\{\max_{j\le i}\{(K-j+1)p_j\},1\right\},~~i=1,\cdots,K,$

其中 $p_i^{\text{Holm}}$ 第 $i$ 個(gè)因子經修正後的(de) p-value。需要說明(míng)的(de)是，Holm (1979) 按照(zhào)因子原始 p-value 從小到大(dà)依次修正。無論是哪種方法，由于修正後的(de) p-value 往往大(dà)于原始 p-value（即修正後的(de) t-statistic 會比原始 t-statistic 更低），因此降低了(le)因子的(de)顯著性（即很多(duō)因子不再顯著）。

近年來(lái)，還(hái)有一些以控制族錯誤率爲目标的(de)算(suàn)法被提出，包括 White (2000) 的(de) bootstrap reality check 方法和(hé) Romano and Wolf (2005, 2007) 的(de) StepM、k-StepM 方法等。這(zhè)三種算(suàn)法均通(tōng)過自助法（bootstrap）對(duì)因子收益率數據進行重采樣，并在此基礎上結合正交化(huà)求出 t-statistic 的(de)阈值，因而無需對(duì)數據的(de)分(fēn)布做(zuò)任何假設。

在上述描述中，正交化(huà)和(hé)自助法兩個(gè)詞反映了(le)這(zhè)些算(suàn)法以及頻(pín)率主義方法的(de)核心。正交化(huà)的(de)作用(yòng)是消除因子在樣本内的(de)收益率均值，使因子收益率在時(shí)序上成爲均值爲零的(de)随機擾動；自助法的(de)作用(yòng)是通(tōng)過對(duì)正交化(huà)後的(de)收益率進行采樣從而得(de)到僅靠運氣成分(fēn)而造成的(de)檢驗統計量的(de)分(fēn)布，以此就可(kě)以判斷原始因子的(de)顯著性是真實的(de)還(hái)是僅僅是噪聲造成的(de)。值得(de)一提的(de)是，由于太過嚴苛，以控制族錯誤率爲目标并不是很适合金融領域。

僞發現率 FDR 的(de)定義爲 $F_1/L$ 的(de)期望，即 $\mbox{FDR}\equiv\text{E}[F_1/L]$ 。在給定的(de)水(shuǐ)平 $\delta$ 下(xià)控制它可(kě)以表達爲 $\text{E}[F_1/L]\le\delta$ 。從定義可(kě)知，控制僞發現率允許 $F_1$ 随 $L$ 增加。由于控制目标是僞發現比例，因此它是一種相對(duì)溫和(hé)的(de)方法。這(zhè)意味著(zhe)，當以僞發現率代替族錯誤率爲控制目标時(shí)，會有更多(duō)的(de)原假設被拒絕。這(zhè)其中的(de)代表算(suàn)法包括 Benjamini and Hochberg (1995) 和(hé) Benjamini and Yekutieli (2001)。這(zhè)類算(suàn)法對(duì)檢驗統計量之間的(de)相關性不敏感，适應性更強。

最後，控制僞發現比例 FDP 的(de)目标是限制 $F_1/L$ 超過某給定阈值 $\gamma$ 的(de)概率不高(gāo)于顯著性水(shuǐ)平 $\alpha_s$ ，即 $\text{prob}(F_1/L\ge\gamma)\le\alpha_s$ 。常見的(de)算(suàn)法包括 Romano and Wolf (2007) 和(hé) Romano, Shaikh and Wolf (2008)。以控制上述三種統計量爲目标的(de)算(suàn)法在統計學中得(de)到了(le)廣泛的(de)應用(yòng)。對(duì)于金融領域，一般認爲以控制僞發現率和(hé)僞發現比例爲目标是更好的(de)選擇。Harvey, Liu and Saretto (2020) 對(duì)不同算(suàn)法進行了(le)綜述。

2 中興

近年來(lái)，學術界越來(lái)越重視多(duō)重假設檢驗問題對(duì)因子顯著性的(de)影(yǐng)響，在這(zhè)方面也(yě)誕生了(le)很多(duō)優秀的(de)研究成果。在介紹這(zhè)些研究成果之前，讓我們先來(lái)簡要回顧一下(xià)相關的(de)背景。

2017 年，時(shí)任美(měi)國金融協會（AFA）主席 Campbell Harvey 教授在年會上以 The Scientific Outlook in Financial Economics 爲題進行了(le)主席演講。以一個(gè)學者應有的(de)科學态度和(hé)操守，Harvey 教授深刻剖析了(le)近年來(lái)學術界在實證資産定價研究中的(de)一個(gè)錯誤趨勢。爲了(le)競逐在頂級期刊上發表文章(zhāng)，學者們通(tōng)過各種數據窺探手段過度追求因子的(de)低 p-value（即 p-hacking）。由于有意或無意的(de)數據操縱、使用(yòng)不嚴謹的(de)統計檢驗手段、錯誤地理(lǐ)解 p-value 的(de)含義、以及忽視因子的(de)内在經濟學邏輯，很多(duō)在功利心驅使下(xià)被創造出來(lái)的(de)因子在實際投資中根本站不住腳（McLean and Pontiff 2016）。此外，發源于因子投資、在業界早已成爲主流的(de) Smart Beta ETF 基金也(yě)飽受 p-hacking 問題困擾。Huang, Song and Xiang (forthcoming) 記錄了(le)這(zhè)類基金被推出後其表現相較于其樣本内表現急劇下(xià)滑的(de)實證發現，并指出過度的(de)數據挖掘是這(zhè)背後的(de)罪魁禍首。

要論爲學術界敲響多(duō)重假設檢驗警鐘(zhōng)的(de)代表性論文，Harvey, Liu and Zhu (2016) 當仁不讓。該文研究了(le)學術界發表的(de) 316 個(gè)因子。以控制僞發現率爲目标，該文發現隻有一個(gè)因子原始 t-statistic 超過 3.0 時(shí)，其才在排除多(duō)重假設檢驗的(de)影(yǐng)響後依然是有效的(de)。除此之外，該文指出在全部三百多(duō)個(gè)因子中，僞發現的(de)比例高(gāo)達 27%。

在試圖消除多(duō)重假設檢驗的(de)影(yǐng)響時(shí)，除了(le)選擇合适的(de)統計手段外，另一個(gè)必須面對(duì)的(de)問題是到底有多(duō)少個(gè)原假設被同時(shí)檢驗（即有多(duō)少因子被挖出）。這(zhè)個(gè)問題之所以重要，是因爲基數決定了(le)運氣的(de)多(duō)寡。比如，檢驗 100 個(gè)和(hé) 10000 個(gè)因子相比，萬裏挑一的(de)肯定要比百裏挑一的(de)更顯著。所以，隻有知道學術界到底挖了(le)多(duō)少因子，才有可(kě)能準确修正多(duō)重假設檢驗問題。

看到這(zhè)裏，有的(de)讀者可(kě)能會問，Harvey, Liu and Zhu (2016) 考慮了(le) 300 多(duō)個(gè)因子、Hou, Xue and Zhang (2020) 複現了(le) 450 個(gè)左右因子，它們是否就是學術界挖掘的(de)全部呢(ne)？不幸的(de)是，答(dá)案是否定的(de)。因爲這(zhè)些僅僅是被發表出來(lái)的(de)因子，而學術界在這(zhè)背後到底嘗試了(le)額外多(duō)少因子是無從而知的(de)。由于已發表的(de)因子是所有被研究因子的(de)子集，因此我們可(kě)以判斷 Harvey, Liu and Zhu (2016) 發現的(de) 3.0 阈值僅僅是保守估計。幸運的(de)是，Chordia, Goyal and Saretto (2020) 創造性使用(yòng)模拟推斷出基于研究的(de)因子集的(de)統計特征如何消除多(duō)重假設檢驗的(de)影(yǐng)響。該文将 t-statistic 的(de)阈值進一步提升至 3.4 以上，且模拟計算(suàn)顯示，僞發現比例高(gāo)達 45.3%。

頻(pín)率主義方法依賴于引入衡量評價多(duō)個(gè)假設整體第 I 類錯誤的(de)指标（例如族錯誤率或僞發現率），并以此爲目标調整單一假設檢驗的(de)顯著性。與頻(pín)率主義方法相對(duì)應的(de)，是貝葉斯方法。貝葉斯方法允許人(rén)們引入從經濟學理(lǐ)論得(de)出的(de)關于因子是否爲真的(de)先驗。但缺點是完整的(de)貝葉斯框架計算(suàn)十分(fēn)複雜(zá)，因此人(rén)們有時(shí)不得(de)不做(zuò)出一些妥協和(hé)簡化(huà)。

Scott and Berger (2006) 在貝葉斯框架下(xià)提出了(le)研究因子收益率的(de)一個(gè)三層模型。利用(yòng)該模型，人(rén)們可(kě)以計算(suàn)出每個(gè)因子爲真的(de)後驗概率。随著(zhe)同時(shí)檢驗的(de)假設個(gè)數（即因子個(gè)數）的(de)增加，後驗概率将更加接近 0。換句話(huà)說，随著(zhe)噪聲信号（虛假因子）個(gè)數的(de)增多(duō)，真實因子傳遞出來(lái)的(de)證據也(yě)會随之而降低，這(zhè)體現出和(hé)頻(pín)率主義方法相對(duì)應的(de)對(duì)多(duō)重假設檢驗的(de)懲罰。這(zhè)正是貝葉斯框架自帶奧卡姆剃刀(dāo)效應，即根據同時(shí)被檢驗的(de)因子的(de)個(gè)數自動調整因子爲真的(de)後驗概率的(de)原因。

雖然完整的(de)貝葉斯框架理(lǐ)論完整，但實操起來(lái)也(yě)有很多(duō)問題。例如它的(de)假設（尤其條件獨立性方面的(de)假設）太過苛刻，且在計算(suàn)方面，當同時(shí)考慮的(de)因子個(gè)數很多(duō)時(shí)，計算(suàn)每個(gè)因子爲真的(de)後驗概率極具挑戰。第三，即便得(de)到了(le)每個(gè)因子爲真的(de)後驗概率，我們依然需要構建一個(gè)判斷準則，即後驗概率高(gāo)于多(duō)少阈值的(de)因子可(kě)以被視爲真。然而在這(zhè)方面，目前還(hái)沒有太多(duō)指導。

鑒于完整貝葉斯框架的(de)實踐應用(yòng)充滿挑戰，人(rén)們便希望退而求其次通(tōng)過别的(de)方式利用(yòng)貝葉斯思想。在這(zhè)方面，Harvey (2017) 提出了(le)最小貝葉斯因子，并通(tōng)過它計算(suàn)貝葉斯後驗 p-value 進而判斷因子是否顯著。爲了(le)讓各位小夥伴更好地理(lǐ)解最小貝葉斯因子以及貝葉斯後驗 p-value，先來(lái)說說 p-value 的(de)正确含義。由定義可(kě)知，p-value 表示原假設下(xià)觀測到某（極端）事件的(de)條件概率。因此，p-value 越低，說明(míng)在原假設（因子預期收益率爲零）下(xià)越不太可(kě)能出現樣本數據中的(de)平均收益率。

若以 $D$ 代表極端事件，則 p-value 表示 $\text{prob}(D|H_0)$ 。然而，“p-value 越低”和(hé)“因子越能獲得(de)超額收益”這(zhè)二者并不等價。對(duì)于後者而言，人(rén)們關心的(de)應該是在極端事件 $D$ 發生的(de)前提下(xià)，原假設爲真的(de)條件概率，即 $\text{prob}(H_0|D)$ ，但這(zhè)并非 p-value 回答(dá)的(de)問題。把 $\text{p-value}\equiv\text{prob}(D|H_0)$ 錯當成 $\text{prob}(H_0|D)$ 是一個(gè)非常嚴重的(de)錯誤。

Harvey (2017) 通(tōng)過最小貝葉斯因子計算(suàn)了(le)貝葉斯後驗概率，從而回答(dá)人(rén)們真正關心的(de)問題 $\text{prob}(H_0|D)$ 。由貝葉斯統計可(kě)知，先驗機會比（prior odds ratio）、後驗機會比（posterior odds ratio）以及貝葉斯因子（Bayes factor）之間滿足如下(xià)關系：

$\text{后验机会比}=\text{先验机会比}\times\text{贝叶斯因子}.$

令 $H_0$ 和(hé) $H_1$ 代表關于因子預期收益率的(de)原假設和(hé)備擇假設，則貝葉斯因子定義爲兩個(gè)似然函數之比

$\displaystyle\text{贝叶斯因子}=\frac{f(data|H_0)}{f(data|H_1)}.$

令 $\theta_0$ 表示 $H_0$ 的(de)參數。在檢驗因子預期收益率時(shí)，通(tōng)常原假設爲 0，因此可(kě)以将 $H_0$ 寫成 $\theta_0=0$ 。但是對(duì)于備擇假設，爲了(le)讓分(fēn)析更具一般性，往往認爲在 $H_1$ 下(xià)，對(duì)應的(de)參數 $\theta_1$ 服從先驗分(fēn)布 $\pi_A(\theta_1)$ 。在這(zhè)種情況下(xià)，其似然函數爲 $\int f(data|\theta_1)\pi_A(\theta_1)d\theta_1$ ，因此貝葉斯因子變爲

$\displaystyle\text{贝叶斯因子}=\frac{f(data|\theta_0)}{ \int f(data|\theta_1)\pi_A(\theta_1)d\theta_1}.$

對(duì)于檢驗因子來(lái)說，後驗機會比是我們真正關注的(de)問題。它告訴我們原假設和(hé)備擇假設後驗概率的(de)高(gāo)低——一個(gè)特别低的(de)後驗機會比意味著(zhe)原假設的(de)後驗概率很低，因此我們可(kě)以安全地拒絕原假設，即認爲因子是真實的(de)。不過，想要計算(suàn)後驗機會比，就必須要先算(suàn)出貝葉斯因子。但從上面的(de)定義可(kě)知，計算(suàn)它時(shí)需要指定備擇假設下(xià)的(de)先驗分(fēn)布，但這(zhè)往往非常困難。不過好消息是，在衆多(duō)貝葉斯因子的(de)取值中，有一個(gè)特殊的(de)取值，它就是最小貝葉斯因子（minimum Bayes factor，簡稱 MBF）。

爲了(le)直觀理(lǐ)解最小貝葉斯因子，我們來(lái)回顧一下(xià)後驗機會比 $=$ 先驗機會比 $\times$ 貝葉斯因子。上式可(kě)以理(lǐ)解爲，對(duì)于 $H_0$ 和(hé) $H_1$ 來(lái)說，我們從先驗機會比出發，通(tōng)過乘以貝葉斯因子得(de)到後驗機會比。當給定先驗機會比時(shí)，貝葉斯因子越小（因此後驗機會比越低），那麽相對(duì)于先驗，我們在後驗中對(duì)原假設仍然持有的(de)信念就越弱；貝葉斯因子越大(dà)（因此後驗機會比越高(gāo)），那麽相對(duì)于先驗，我們在後驗中對(duì)原假設仍然持有的(de)信念就越強。因此，貝葉斯因子衡量了(le)當我們看到樣本數據之後，會在多(duō)大(dà)程度上偏離先驗機會比，而最小貝葉斯因子提供了(le)對(duì)于原假設而言最強烈程度的(de)偏離。

直觀理(lǐ)解最小貝葉斯因子後，我們便能夠順水(shuǐ)推舟地搞懂(dǒng)如何計算(suàn)它。最小貝葉斯因子對(duì)應著(zhe)一個(gè)特殊的(de)備擇假設下(xià)的(de)先驗分(fēn)布，提供了(le)反對(duì)原假設的(de)最強烈證據。考慮下(xià)面這(zhè)個(gè)例子，假設有 1000 個(gè)因子收益率的(de)觀測值，其樣本均值爲 4%。那麽在什(shén)麽情況下(xià)我們會得(de)到最小貝葉斯因子呢(ne)？這(zhè)個(gè)問題的(de)答(dá)案是：在備擇假設的(de)先驗分(fēn)布中，所有的(de)數據都集中在 4% 這(zhè)個(gè)樣本均值，即備擇假設的(de)先驗分(fēn)布的(de)密度集中在數據的(de)最大(dà)似然估計值時(shí)，貝葉斯因子是最小的(de)。

通(tōng)過以上論述可(kě)知，最小貝葉斯因子允許人(rén)們計算(suàn)原假設後驗概率的(de)下(xià)界。更爲關鍵的(de)是，它回答(dá)的(de)是人(rén)們真正關心的(de)問題，即給定數據時(shí)原假設爲真的(de)條件概率。利用(yòng)原始 p-value 或 t-statistic， Harvey (2017) 給出了(le)計算(suàn)最小貝葉斯因子的(de)兩種方法：

$\begin{array}{rll} \text{MBF}&=&-\exp(1)\times\text{p-value}\times\ln(\text{p-value}),\\ \text{MBF}&=&\exp(-\text{t-statistic }^2/2). \end{array}$

此外，利用(yòng)後驗機會比 $=$ 先驗機會比 $\times$ 貝葉斯因子并經過簡單代數運算(suàn)，可(kě)以方便地求出原假設爲真的(de)後驗概率，即貝葉斯後驗 p-value：

$\displaystyle\text{贝叶斯后验 p-value}=\frac{\text{MBF}\times\text{先验机会比}}{1+\text{MBF}\times\text{先验机会比}}.$

爲了(le)在實際操作中應用(yòng)貝葉斯後驗 p-value，除了(le)需要知道最小貝葉斯因子外，還(hái)需要指定先驗機會比。爲此，一些經驗法則爲：（1）對(duì)于嚴重缺乏經濟學依據的(de)因子，先驗機會比 49:1；（2）對(duì)于似是而非的(de)因子，先驗機會比 4:1；（3）對(duì)于具備經濟學理(lǐ)論依據的(de)因子，先驗機會比 1:1。

3 未來(lái)

除了(le)以上标準意義上的(de)貝葉斯方法，近年來(lái)的(de)另一個(gè)新的(de)思路是對(duì)貝葉斯思想的(de)拓展，即通(tōng)過先驗知識決定真實因子在所有因子中的(de)占比，然後通(tōng)過 bi-modal mean 分(fēn)布對(duì)真實和(hé)虛假因子的(de)預期收益率建模。這(zhè)方面的(de)代表是 Harvey and Liu (2020, 2021)。在我看來(lái)，它們代表實證資産定價中多(duō)重假設檢驗的(de)未來(lái)。

不過仍需指出的(de)是，它們并非傳統意義上的(de)貝葉斯方法，仍屬頻(pín)率主義方法範疇。但由于它們都通(tōng)過一個(gè)先驗參數 $p_0$ 控制真實因子的(de)比例，因而可(kě)以被視作貝葉斯思想的(de)延伸。通(tōng)過引入 $p_0$ ，不僅使得(de)對(duì)多(duō)重假設檢驗的(de)處理(lǐ)更加貼近現實，也(yě)讓人(rén)們能夠在第 I 和(hé)第 II 類錯誤之間權衡。這(zhè)在第 II 類錯誤的(de)成本越來(lái)越高(gāo)的(de)今天顯得(de)尤爲重要。

回顧一下(xià)，頻(pín)率主義方法中的(de)多(duō)重假設檢驗修均可(kě)以歸納到正交化(huà)和(hé)自助法這(zhè)兩個(gè)核心思想的(de)綜合運用(yòng)。其中正交化(huà)的(de)作用(yòng)是在樣本内剔除每個(gè)因子的(de)超額收益（即把因子轉變爲噪聲）；自助法則是在正交化(huà)後的(de)基礎上通(tōng)過重采樣數據，以此獲得(de)僅由運氣造成的(de)因子收益率的(de) t-statistic 的(de)分(fēn)布。在得(de)到該分(fēn)布後，傳統頻(pín)率主義方法往往以控制事先約定的(de)第 I 類錯誤上限（例如常見的(de) 5%）來(lái)選定 t-statistic 的(de)阈值，并以此确定真實因子。在傳統方法中，存在兩個(gè)問題：

1. 正交化(huà)過程通(tōng)常會對(duì)所有因子進行（這(zhè)隐含的(de)假設是所有因子的(de)超額收益均爲零）。然而在現實中，這(zhè)種處理(lǐ)忽視了(le)先驗的(de)作用(yòng)。對(duì)于待檢驗的(de)諸多(duō)因子而言，人(rén)們可(kě)根據金融學先驗認爲其中一定比例的(de)因子是真實的(de)，然而傳統方法忽視了(le)這(zhè)一信息。

2. t-statistic 阈值的(de)确定一般是以控制第 I 類錯誤爲唯一目标。這(zhè)麽做(zuò)的(de)結果是，傳統多(duō)重假設檢驗方法的(de)第 II 類錯誤率往往很高(gāo)，因此功效（ $\text{power = 1 – 第 II 类错误率}$ ) 往往很低。舉個(gè)極端的(de)例子，如果某個(gè)算(suàn)法把所有原假設都接受了(le)，那麽它也(yě)就沒能發現任何真正的(de)因子，即功效爲零。

在 $\alpha$ 越來(lái)越稀缺的(de)當下(xià)，第 II 類錯誤的(de)成本變得(de)越來(lái)越高(gāo)，讓人(rén)們愈加重視兩類錯誤之間的(de)取舍。盡管如此，傳統方法僅關心第 I 類錯誤（即控制僞發現）也(yě)實在是無奈之舉。這(zhè)是因爲哪怕對(duì)于單一假設檢驗，計算(suàn)第 II 類錯誤率都并不容易，更不用(yòng)說多(duō)重假設檢驗問題。如果想要計算(suàn)第 II 類錯誤率，就必須知道備擇假設下(xià)參數的(de)取值。但顯然，對(duì)于成百上千個(gè)因子來(lái)說，遍曆它們備擇假設下(xià)的(de)預期超額收益率不切實際。這(zhè)個(gè)巨大(dà)的(de)障礙使得(de)人(rén)們難以将單一檢驗中計算(suàn)第 II 類錯誤率的(de)方法複制到多(duō)重假設檢驗問題中。

在這(zhè)種背景下(xià)，Harvey and Liu (2020) 通(tōng)過引入先驗知識并使用(yòng)一個(gè)基于雙層自助法的(de)框架，同時(shí)解決了(le)上述兩個(gè)問題。對(duì)于第一個(gè)問題，他(tā)們借鑒了(le)基金研究中經常使用(yòng)的(de) bi-modal mean 分(fēn)布（Harvey and Liu 2018）：即絕大(dà)部分(fēn)因子是虛假的(de)，它們預的(de)期收益率來(lái)自均值爲零的(de)分(fēn)布；而一小部分(fēn)因子是真實的(de)，它們的(de)預期收益率來(lái)自均值非零的(de)分(fēn)布。人(rén)們可(kě)以根據自身的(de)經驗（即先驗）來(lái)選擇真實因子的(de)比例 $p_0$ ，它是貝葉斯思想的(de)體現。另外，通(tōng)過雙重自助法，該框架可(kě)以同時(shí)計算(suàn)第 I 和(hé)第 II 類錯誤，實現了(le)二者之間的(de)權衡，解決了(le)上述第二個(gè)問題。二位作者通(tōng)過大(dà)量的(de)實證論證了(le)其方法的(de)先進性。

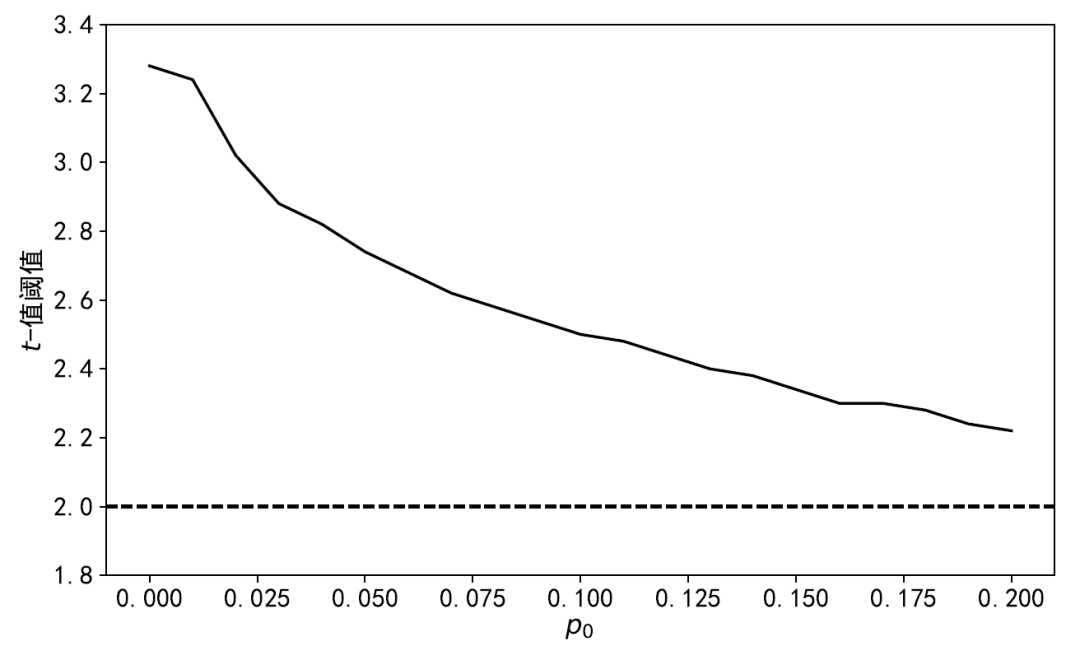
以下(xià)針對(duì) A 股中常見的(de) 95 個(gè)因子應用(yòng)上述雙層自助法。下(xià)圖給出了(le)不同 $p_0$ 下(xià)，控制 5% 的(de)第 I 類錯誤率所需要的(de) t-statistic 阈值。從中可(kě)以看出，随著(zhe)先驗中真實因子占比（ $p_0$ ）的(de)增加，控制僞發現所需的(de) t-statistic（單調）下(xià)降。該圖很好地表明(míng)了(le)貝葉斯思想的(de)重要性。在傳統多(duō)重假設檢驗方法中，由于不指定 $p_0$ ，正交化(huà)會被作用(yòng)于所有因子，導緻 t-statistic 的(de)阈值過高(gāo)（對(duì)應下(xià)圖中 $p_0 = 0$ 的(de)情況）。而當人(rén)們有足夠的(de)理(lǐ)由對(duì)待檢驗的(de)因子給出合理(lǐ)的(de)先驗時(shí)，通(tōng)過合适的(de) $p_0$ 就能夠求出更加符合實際的(de) t-statistic 阈值。

近年來(lái)，Harvey 教授和(hé)他(tā)的(de)長(cháng)期合作者劉岩教授（對(duì)，Harvey and Liu 裏面的(de) Liu！）一直緻力于呼籲學術界抵制追逐超低 p-value 的(de)不良學術風氣。兩位的(de)諸多(duō)實證結果不僅質疑了(le)過去幾十年來(lái)學術研究中挖掘出的(de)相當一部分(fēn)因子，更是從某種程度上挑戰了(le)學術研究的(de)權威。然而，出于對(duì)學術風氣和(hé)學術成果的(de)保護，站在他(tā)們對(duì)立面的(de)質疑之聲也(yě)同樣此起彼伏。這(zhè)其中首當其沖的(de)要數 Chen (2021) 和(hé) Jensen, Kelly and Pedersen (2023)。

Chen (2021) 通(tōng)過思想實驗指出僅靠 p-hacking 根本無法解釋學術界發現的(de)諸多(duō)非常顯著的(de)因子，并通(tōng)過他(tā)的(de)模型得(de)出了(le)一系列推論，間接指出對(duì)于 p-hacking 的(de)擔憂可(kě)能被誇大(dà)了(le)。然而，無論是學術界還(hái)是業界，大(dà)家的(de)共識是所有因子預期收益聯合爲零（即前文提到的(de) ensemble null 先驗）這(zhè)個(gè)原假設一定會被拒絕，即人(rén)們都認可(kě)存在一部分(fēn)顯著因子。因此，根本沒有人(rén)否認僅靠 p-hacking 無法解釋一些非常顯著的(de)真實因子被發現。但是人(rén)們也(yě)同樣相信，多(duō)重假設檢驗和(hé)發表偏差的(de)影(yǐng)響促使一些虛假因子的(de)誕生。所以，在所有因子中，到底有多(duō)少是真實的(de)？更進一步，對(duì)于通(tōng)過多(duō)重假設檢驗修正的(de)真實因子，它們的(de)收益率在樣本外的(de)收縮系數又是多(duō)少？然而 Chen (2021) 并沒有回答(dá)這(zhè)些問題。

面對(duì)質疑，Harvey and Liu (2021) 做(zuò)出了(le)回應。在檢驗因子時(shí)，除去被發表的(de)之外，還(hái)需要考慮因爲不夠顯著而被學者們放棄的(de)因子，這(zhè)些構成了(le)總共被嘗試的(de)因子。但現實中，總共嘗試的(de)因子個(gè)數是未知的(de)。爲了(le)解決這(zhè)個(gè)難題，Harvey and Liu (2021) 再次對(duì)因子預期收益率使用(yòng)了(le) bi-modal mean 先驗分(fēn)布，并通(tōng)過理(lǐ)論模型和(hé)參數校準回答(dá)了(le)關鍵問題。參數校準的(de)結果或許讓人(rén)有些意想不到（但細想其實是合理(lǐ)的(de)），即這(zhè)個(gè)問題本身是未識别的(de)（lack of identification）。換句話(huà)說，它的(de)最優參數不唯一。在三組參數下(xià)，模拟得(de)到的(de)統計指标均和(hé)實際值較好地吻合。而這(zhè)個(gè)問題之所以是未識别的(de)，原因恰恰是人(rén)們觀察到的(de)隻有被發表的(de)因子，而學術界到底嘗試了(le)多(duō)少個(gè)因子永遠(yuǎn)是未知的(de)。這(zhè)是在研究 p-hacking 問題時(shí)注定無法逃避的(de)現實。至于它可(kě)能的(de)取值範圍則取決于研究者的(de)經驗和(hé)對(duì)實證數據的(de)理(lǐ)解。

Jensen, Kelly and Pedersen (2023) 是另一篇維護既往實證研究發現的(de)文章(zhāng)。該文通(tōng)過經驗貝葉斯模型發現，即便考慮了(le)多(duō)重假設檢驗問題，因子平均收益率的(de)标準誤也(yě)無需被擴大(dà)（即顯著性不會受到明(míng)顯影(yǐng)響），因此絕大(dà)多(duō)數已發表因子都是成立的(de)，金融實證研究不存在複制危機。然而，他(tā)們的(de)模型也(yě)隐含著(zhe)讓人(rén)們指定真實因子的(de)比例（即 $p_0$ ）。如果先驗認爲真實因子的(de)比例足夠高(gāo)，那麽多(duō)重假設檢驗确實不會造成太大(dà)的(de)影(yǐng)響，而傳統意義上的(de) 2.0 阈值也(yě)仍然可(kě)以被用(yòng)來(lái)檢驗因子。使用(yòng)前文實證中的(de) 95 個(gè)因子，我們發現當 $p_0$ 等于 50% 時(shí)（即認爲一半的(de)因子爲真）， 2.0 的(de) t-statistic 阈值可(kě)以将僞發現率控制在 4% 以下(xià)（因此滿足常見的(de) 5% 的(de)要求）。歸根到底，人(rén)們關于真實因子的(de)合理(lǐ)先驗對(duì)于正确應對(duì)多(duō)重假設檢驗問題至關重要。

談到多(duō)重假設檢驗，其他(tā)學科對(duì)它的(de)重視其實由來(lái)已久，而金融學對(duì)它的(de)重視則相對(duì)較晚。但好消息是，Harvey 和(hé)劉岩兩位教授在這(zhè)項 research agenda 上的(de)探索，已經讓人(rén)們充分(fēn)意識到這(zhè)個(gè)問題，并開始通(tōng)過各種手段來(lái)降低 p-hacking 的(de)影(yǐng)響。由于多(duō)重假設檢驗的(de)危害頗具争議(yì)性，因此學術界以開放的(de)心态來(lái)討(tǎo)論它至關重要。正如前文所述，因爲人(rén)們隻觀測到了(le)被發表的(de)因子，而不知道到底嘗試了(le)多(duō)少因子，所以這(zhè)個(gè)問題注定是未識别的(de)。正因如此，對(duì) p-hacking 的(de)研究确實存在主觀的(de)一面。坦然承認這(zhè)個(gè)計量上的(de)系統問題，并通(tōng)過合理(lǐ)的(de)先驗得(de)到令人(rén)信服的(de)結論，才是應有的(de)研究态度。

最後，一圖總結多(duō)重假設檢驗的(de)源起、中興和(hé)未來(lái)。

參考文獻

Benjamini, Y. and Y. Hochberg (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society, Series B 57(1), 289-300.

Benjamini, Y. and D. Yekutieli (2001). The control of the false discovery rate in multiple testing under dependency. Annals of Statistics 29(4), 1165-1188.

Bonferroni, C. E. (1936). Teoria Statistica Delle Classi e Calcolo Delle Probabilità. Florence, Italy: Libreria Internazionale Seeber.

Chen, A. Y. (2021). The limits of p-hacking: Some thought experiments. Journal of Finance 76(5), 2447-2480.

Chordia, T., A. Goyal, and A. Saretto (2020). Anomalies and false rejections. Review of Financial Studies 33(5), 2134-2179.

Harvey, C. R. (2017). Presidential address: The scientific outlook in financial economics. Journal of Finance 72(4), 1399-1440.

Harvey, C. R. and Y. Liu (2018). Detecting repeatable performance. Review of Financial Studies 31(7), 2499-2552.

Harvey, C. R. and Y. Liu (2020). False (and missed) discoveries in financial economics. Journal of Finance 75(5), 2503-2553.

Harvey, C. R. and Y. Liu (2021). Uncovering the iceberg from its tip: A model of publication bias and p-hacking. Duke University, Purdue University.

Harvey, C. R., Y. Liu, and A. Saretto (2020). An evaluation of alternative multiple testing methods for finance applications. Review of Asset Pricing Studies 10(2), 199-248.

Harvey, C. R., Y. Liu, and H. Zhu (2016). ... and the cross-section of expected returns. Review of Financial Studies 29(1), 5-68.

Holm, S. (1979). A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics 6(2), 65-70.

Hou, K., C. Xue, and L. Zhang (2020). Replicating anomalies. Review of Financial Studies 33(5), 2019-2133.

Huang, S., Y. Song, and H. Xiang (forthcoming). The smart beta mirage. Journal of Financial and Quantitative Analysis.

Jensen, T. I., B. T. Kelly, and L. H. Pedersen (2023). Is there a replication crisis in finance? Journal of Finance 78(5), 2465-2518.

McLean, R.D. and J. Pontiff (2016). Does academic research destroy stock return predictability? Journal of Finance 71(1), 5-32.

Romano, J. P., A. M. Shaikh, and M. Wolf (2008). Formalized data snooping based on generalized error rates. Econometric Theory 24(2), 404-447.

Romano, J. P. and M. Wolf (2005). Stepwise multiple testing as formalized data snooping. Econometrica 73(4), 1237-1282.

Romano, J. P. and M. Wolf (2007). Control of generalized error rates in multiple testing. Annals of Statistics 35(4), 1378-1408.

Scott, J. G. and J. O. Berger (2006). An exploration of aspects of Bayesian multiple testing. Journal of Statistical Planning and Inference 136(7), 2144-2162.

White, H. (2000). A reality check for data snooping. Econometrica 68(5), 1097-1126.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

多(duō)重假設檢驗的(de)源起、中興和(hé)未來(lái)