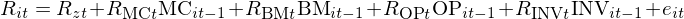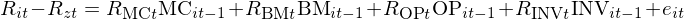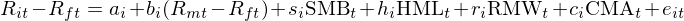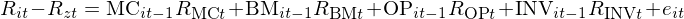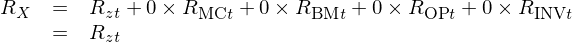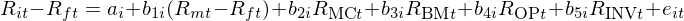Which Beta (II) ?

作者：石川

摘要：Fama and French (2020) 系統的(de)比較了(le)時(shí)序和(hé)截面多(duō)因子定價模型，爲回答(dá) which beta 提供了(le)有力的(de)依據。

1 引言

近日，Eugene Fama 和(hé)他(tā)的(de)老搭檔 Ken French 在 Review of Financial Studies 上發表了(le)一篇題爲 Comparing cross-section and time-series factor models 的(de)最新文章(zhāng)（Fama and French 2020）。顧名思義，該文對(duì)比了(le)截面（CS）和(hé)時(shí)序（TS）兩種因子模型在解釋資産收益率時(shí)的(de)效果。這(zhè)篇文章(zhāng)保留了(le) FF 一貫簡單、直接、從數據出發的(de)文風。但是它在 CS 和(hé) TS 上來(lái)回切換，在時(shí)序回歸 β 爲作爲因子載荷和(hé)以 firm characteristics 作爲因子載荷之間輾轉騰挪，讀來(lái)也(yě)著(zhe)實令人(rén)燒腦(nǎo)。需要對(duì) CS 和(hé) TS 模型，以及使用(yòng)到的(de) Fama and MacBeth (1973) Regression（以下(xià)記爲 FM regression）非常熟悉才不至于在閱讀時(shí)迷失。有小夥伴後台留言希望我們能介紹一下(xià)這(zhè)篇文章(zhāng)，今天就借這(zhè)個(gè)機會對(duì)它進行解讀。

Fama and French (2020) 的(de)目的(de)是爲了(le)從 TS 和(hé) CS 的(de)比較中找出更好的(de)定價模型（empirical asset pricing model）。它的(de)結論對(duì)于進行因子投資非常有價值，因爲更好的(de)模型意味著(zhe)在截面上能更好區(qū)分(fēn)股票(piào)預期收益率的(de)差異。在 Fama and French (2020) 一文中，兩位作者先後考慮了(le)四個(gè)模型，進行了(le)全方位系統的(de)對(duì)比，從實證數據中得(de)出了(le)非常符合預期的(de)結論，而這(zhè)個(gè)結論也(yě)剛好能回答(dá)前文《Which Beta ?》所關注的(de)核心問題。爲此，我給本文起名爲《Which Beta (II) ?》。

2 Fama-MacBeth Regression

Fama and French (2020) 一文以 Fama and French (2015) 五因子模型（下(xià)文記爲 FF5）爲 benchmark 構建了(le)不同 TS、CS 版本的(de)因子模型。爲構建 CS 模型，他(tā)們采用(yòng)了(le) FM regression。傳統的(de) FM regression 分(fēn)爲兩步：

最初，Fama and MacBeth (1973) 一文是爲了(le)檢驗 CAPM。因此，它的(de)第一步是爲了(le)得(de)到個(gè)股的(de) market β 值。而如今無論是學術界還(hái)是業界的(de)應用(yòng)中，在使用(yòng) FM regression 時(shí)，往往跳過第一步，而直接運用(yòng)它第二步中“先單期截面回歸、再從時(shí)序上取平均”的(de)思想，以排除殘差收益率的(de)截面相關性帶來(lái)的(de)影(yǐng)響。既然跳過了(le)第一步，那麽用(yòng)什(shén)麽來(lái)做(zuò) factor loading 呢(ne)？對(duì)，正是 firm characteristics。比如我們熟悉的(de) Barra 模型，其本質是一個(gè) FM regression。它沒有使用(yòng)第一步時(shí)序回歸計算(suàn) factor loading，而是直接使用(yòng)了(le) firm characteristics，并進行第二步的(de)截面回歸計算(suàn) factor risk premium。

Fama and French (2020) 也(yě)正是使用(yòng) firm characteristics 作爲 factor loadings，并通(tōng)過 FM regression 來(lái)提出截面因子模型。考慮 FF5 中的(de)五個(gè)因子，除了(le)市場(chǎng)因子外，其餘四個(gè)風格因子用(yòng)到的(de) firm characteristics 包括 Market Cap（MC）、Book-to-Market（BM）、Operating Profitability（OP）以及 Change of Total Assets（INV）。以這(zhè)四個(gè)指标作爲 RHS，以資産下(xià)期收益率作爲 LHS，可(kě)以寫出 FM regression：

在每一期 t – 1， 通(tōng)過使用(yòng)該期的(de)指标和(hé) t 期資産收益率進行截面回歸，就可(kě)以得(de)到 t 期這(zhè)些指标的(de)因子收益率。上式中，所有 R 代表的(de)變量均表示不同的(de)收益率，其中 R_zt 爲截距項（會在本文第三節重點說明(míng)），e_it 爲殘差項。由截面回歸的(de)性質可(kě)知，這(zhè)些收益率對(duì)應的(de)投資組合均爲純因子組合。以 R_MCt 爲例，它是 MC 因子純因子組合的(de)收益率，該組合滿足在 MC 因子上一個(gè)單位的(de)暴露，而在其他(tā)三個(gè)因子上零暴露。而截距項對(duì)應的(de)投資組合則滿足其中資産的(de)權重之和(hé)爲 1，而在任何風格因子上均沒有暴露。将上式中 R_zt 挪到等式左側得(de)到：

不妨把這(zhè)個(gè)式子稱爲（*）式，它是構建 CS 定價模型的(de)關鍵，我們會留在第三節進行說明(míng)。

3 三個(gè)模型

Fama and French (2020) 一文共考慮了(le)四個(gè)多(duō)因子定價模型，兩個(gè) TS 模型，兩個(gè) CS 模型。其中第二個(gè) TS 模型是在其更早的(de) working paper 版本中并沒有出現，它裏面考慮了(le)交叉項。但老實說這(zhè)第二個(gè) TS 模型并不是對(duì)比的(de)重點，所以下(xià)文中不做(zuò)考慮。本文僅介紹三個(gè)模型：一個(gè) TS 模型和(hé)兩個(gè) CS 模型。TS 模型就是我們熟悉的(de) FF5：

其中 R_mt 是 t 期市場(chǎng)收益率，R_ft 爲 t 期無風險收益率，SMB、HML、RMW 以及 CMA 這(zhè)些是使用(yòng)相應 firm characteristics 通(tōng)過 2 × 3 double sort 構建的(de)多(duō)空對(duì)沖組合的(de)收益率，代表了(le)因子的(de)收益率（具體方法可(kě)參考 Fama and French 2015），而小寫字母 b_i、s_i、h_i、r_i、c_i 則代表了(le)公司 i 在這(zhè)些因子上的(de)暴露，通(tōng)過時(shí)序回歸得(de)到；a_i 是截距項，即該模型無法解釋的(de)超額收益。

說完了(le) TS 模型，再來(lái)說 CS 模型。還(hái)記得(de)（*）式嗎？它是 CS 模型的(de)基礎，但它看起來(lái)不像個(gè)定價模型，原因是它是一個(gè)單期的(de)截面回歸。如果我們把全部 T 期的(de)截面回歸跨時(shí)間堆疊在一起（用(yòng) FF 的(de)話(huà)叫 stacked across time），并在（*）等号右邊的(de)表達中将收益率和(hé)作爲 loading 的(de) firm characteristics 位置對(duì)調，就可(kě)以得(de)到下(xià)面這(zhè)個(gè)式子：

通(tōng)過這(zhè)個(gè)變化(huà)，FM regression 搖身一變，成爲一個(gè)定價模型，這(zhè)就是第一個(gè) CS 定價模型（記爲 CS 模型一）。它是一個(gè)四因子模型，因子爲 R_MC、R_BM、R_OP 以及 R_INV，factor loading 爲這(zhè)些因子各自對(duì)應的(de) firm characteristics。特别需要強調的(de)是，該因子模型解釋的(de)并不是 TS 模型中 R_it 相對(duì) R_f 的(de)超額收益，而是 R_it 相對(duì) R_zt 的(de)超額收益。

R_zt 是什(shén)麽呢(ne)？從（*）式可(kě)知，R_zt 是每個(gè)截面上 FM regression 回歸的(de)截距項，因此它顯然和(hé) FM regression 中 LHS 的(de)那些資産的(de)收益率有關。那麽，用(yòng)什(shén)麽資産放在 LHS 呢(ne)？Fama and French (2020) 的(de)目的(de)是以 FF5 爲基礎比較 TS 和(hé) CS 定價模型。因此，顯然不能随便挑一些無關資産放在 FM regression 的(de) LHS，那樣的(de)話(huà) CS 模型的(de)因子就和(hé) FF5 的(de)因子不具備可(kě)比性。

從上面的(de)描述中，你大(dà)概已經猜到了(le)（用(yòng)紅筆劃重點已經劃到那個(gè)份兒(ér)上了(le)），被放在 FM regression 的(de) LHS 的(de)資産必須和(hé) FF5 的(de)因子密切相關；事實上，這(zhè)些 LHS 資産正是構建 FF5 因子的(de)那些投資組合。在 FF5 中，除去市場(chǎng)因子，其他(tā)四個(gè)因子均是由市值和(hé)某個(gè)指标 2 × 3 double sort 得(de)到的(de) 6 個(gè)投資組合來(lái)構建。由于在 SMB 之外還(hái)有三個(gè)因子，因此一共有 6 × 3 = 18 個(gè)投資組合。Fama and French (2020) 正是用(yòng)這(zhè) 18 個(gè)投資組合作爲 FM regression 的(de) LHS，從而求出（*）式中的(de)因子收益率 R_MCt、R_BMt、R_OPt、R_INVt 以及截距項 R_zt。

上述 LHS 資産的(de)選擇在 Fama and French (2020) 中至關重要，它也(yě)對(duì)應著(zhe)該文中很重要的(de)一段話(huà)：Using the same portfolios (those from the 2×3 sorts) to produce TS and CS factors is important. The cross-section regressions that generate the CS factors optimize the month-by-month description of returns of these portfolios. In contract, the TS factor definitions are arbitrary. Since the same portfolios produce the TS and CS factors, one central issue in our tests is whether the optimization of the CS factors enhances the description of average returns for test assets beyond those that produce the factors.

上面這(zhè)段話(huà)的(de)意思就是，CS 模型中，每個(gè)因子都是截面回歸最優化(huà)得(de)到的(de)純因子組合，保證了(le)在目标因子上的(de)單位暴露和(hé)在非目标因子無暴露；而在 TS 模型中，2 × 3 double sort 得(de)到的(de)因子則沒有這(zhè)樣的(de)性質，每個(gè)因子都可(kě)能在其他(tā)因子上有時(shí)變的(de)暴露。基于這(zhè)種差異，Fama and French (2020) 想要通(tōng)過實證分(fēn)析回答(dá)的(de)問題是，構建因子組合時(shí)的(de)這(zhè)種優化(huà)能否更好的(de)解釋截面預期收益率差異？由于 LHS 資産是這(zhè) 18 個(gè)投資組合，那麽在 FM regression RHS 的(de) firm characteristics 顯然也(yě)隻能是這(zhè)些投資組合的(de)。這(zhè)些投資組合的(de) firm characteristics 由每個(gè)組合中個(gè)股的(de)相應指标按市值加權得(de)到。此外，對(duì) CS 模型中的(de)每個(gè)因子，Fama and French (2020) 将這(zhè) 18 個(gè)組合的(de)指标在截面上進行了(le)常規的(de)标準化(huà)，讓它們截面均值爲 0，标準差爲 1。

下(xià)面我們終于能夠回答(dá) R_zt 是什(shén)麽了(le)。假設我們有一個(gè)投資組合（稱爲 X）是上述 18 個(gè)組合的(de)等權平均。令 R_X 代表這(zhè)個(gè)組合的(de)收益率。依據上述标準化(huà)方法，由于 X 組合是這(zhè) 18 個(gè)組合的(de)平均，因此它在 CS 模型中的(de)全部四個(gè)因子上的(de)暴露均爲零。把 R_X 和(hé)這(zhè)些零暴露（factor loading = 0）代入到（*）式中有：

R_zt = R_X 意味著(zhe) R_zt 正是這(zhè) 18 個(gè)投資組合收益率的(de)均值；這(zhè)就是 R_zt 的(de)含義。熟悉 Barra 模型的(de)小夥伴也(yě)不妨回想一下(xià)，R_zt 的(de)作用(yòng)和(hé) CNE5 中的(de)國家因子是一樣的(de)。由于在 Barra 模型中風格因子用(yòng)市值權重來(lái)做(zuò)的(de)标準化(huà)，因此 CNE5 中的(de)國家因子代表了(le)市值加權的(de)個(gè)股收益率，也(yě)就正好是市場(chǎng)因子。這(zhè)裏的(de) R_zt 和(hé) CNE5 中的(de)國家因子有異曲同工之妙。之所以花費了(le)如此多(duō)的(de)筆墨解釋 R_zt，是因爲在上述 CS 定價模型中，四因子解釋的(de)是 R_it 相對(duì) R_zt 的(de)超額收益（即 R_it – R_zt）的(de)截面差異。因此，從業務上搞清楚 R_zt 的(de)含義至關重要。

Fama and French (2020) 在上述 CS 定價模型的(de)基礎上又提出了(le)第二個(gè) CS 模型（記爲 CS 模型二）：

相比前者，這(zhè)個(gè)版本的(de) CS 模型就非常好理(lǐ)解了(le)。它實際上是用(yòng)了(le)時(shí)序回歸 + CS 因子。在這(zhè)個(gè)模型中，作爲因子的(de)仍然是通(tōng)過 FM regression 得(de)到的(de) R_MCt、R_BMt、R_OPt、R_INVt；除此之外還(hái)加入了(le) R_mt – R_ft 這(zhè)個(gè)市場(chǎng)因子，因此該模型是一個(gè)五因子模型。它解釋的(de)也(yě)是 R_it 相對(duì) R_ft 的(de)超額收益 —— 在這(zhè)個(gè)模型中沒有 R_zt 什(shén)麽事兒(ér)！最重要的(de)是，這(zhè)個(gè)模型也(yě)是通(tōng)過時(shí)序回歸求出上述五個(gè)因子的(de) factor loadings。從上面的(de)描述不難看出，第二個(gè) CS 模型直接對(duì)标了(le) FF5。這(zhè)二者唯一的(de)區(qū)别就是在四個(gè)風格因子的(de)構建上：FF5 使用(yòng) 18 個(gè) 2 × 3 double sort 的(de)投資組合構建；而在 CS 模型二中，使用(yòng) FM regression 求解純因子模型來(lái)構建。

作爲回顧，下(xià)表總結了(le)這(zhè)三個(gè)不同的(de)定價模型：

4 CS 因子做(zuò)定價模型？

看到這(zhè)裏，有的(de)小夥伴也(yě)許會困惑：FF5 和(hé) CS 模型二非常好理(lǐ)解，它們隻是 factor returns 的(de)差異，從定價模型的(de)角度來(lái)說，以這(zhè)些 factor returns 作爲解釋變量，隻需要對(duì)每個(gè) LHS 資産單獨進行時(shí)序回歸就能得(de)到其無法被模型解釋的(de)超額收益（時(shí)序回歸中的(de)截距 a_i）。而 CS 模型一則有所不同，它的(de) factor loadings 是 firm characteristics，它隻不過是把不同的(de)截面回歸跨時(shí)間堆疊在一起使它看起來(lái)像一個(gè)定價模型。但它從始至終都不進行時(shí)序回歸，如何獲得(de) pricing error 呢(ne)？

It is important to be clear about how model (2) is applied in the asset pricing tests of panels B5 and B6 of Table 3. Panels B5 and B6 do not test model (2) with time-series regressions.

上面這(zhè)段話(huà)出自 Fama and French (2020)，其中 model (2) 就是本文的(de) CS 模型一。爲了(le)使用(yòng)該模型進行 asset pricing 并求出 pricing error，該文采用(yòng)了(le)如下(xià)兩步：

按照(zhào)上述兩步就可(kě)以得(de)到每個(gè)資産每期的(de) pricing error；将它們在時(shí)序上平均就得(de)到該資産在 CS 模型一下(xià)的(de)平均 pricing error。爲了(le)比較這(zhè)三個(gè)定價模型，需要使用(yòng)足夠多(duō)有代表性的(de)資産放在因子模型的(de) LHS。Lewellen, Nagel, and Shanken (2010) 指出應使用(yòng)足夠多(duō)的(de)投資組合作爲 LHS 以避免這(zhè)些 LHS 資産有非常強的(de) factor structure、造成檢驗失效；而 Jegadeesh et al. (2019) 更是倡導使用(yòng)個(gè)股作爲 LHS 檢驗定價模型。

在 Fama and French (2020) 中，二位作者（自然）沒有使用(yòng)個(gè)股作爲 LHS，但是使用(yòng)了(le)多(duō)達 210 個(gè)投資組合。構建這(zhè)些投資組合背後的(de)指标即來(lái)自構建因子的(de)指标，也(yě)來(lái)自學術界常見的(de)異象。比如，對(duì)于 BM、OP、INV 這(zhè)些指标，他(tā)們分(fēn)别使用(yòng)市值和(hé)這(zhè)些指标進行 5 × 5 double sort 構建了(le) 25 個(gè)組合（因此 3 個(gè)指标一共有 75 個(gè)組合），此外 Fama and French (2020) 還(hái)考慮了(le)動量指标，也(yě)構建了(le) 25 個(gè)組合。在異象方面，他(tā)們考慮了(le)諸如 Black, Jensen, and Scholes (1972) 的(de) market β 和(hé) Ang et al. (2006) 的(de)低波動異象，構建了(le)一共 110 個(gè)組合。關于這(zhè)些 LHS 組合的(de)具體描述，請參考原文，下(xià)面來(lái)看實證結果。

5 實證結果

爲對(duì)比不同的(de) TS 和(hé) CS 定價模型，Fama and French (2020) 使用(yòng)了(le)大(dà)量的(de)實證并進行了(le)充分(fēn)的(de)穩健性檢驗。此外，在評價模型時(shí)，他(tā)們采用(yòng)了(le)不同的(de) metrics，如 Gibbons, Ross, and Shanken (1989) test statistic 以及 pricing error 絕對(duì)值均值等。本小節僅以 Table 3 爲例介紹實證結果。首先來(lái)看 Table 3 的(de) Panel A。

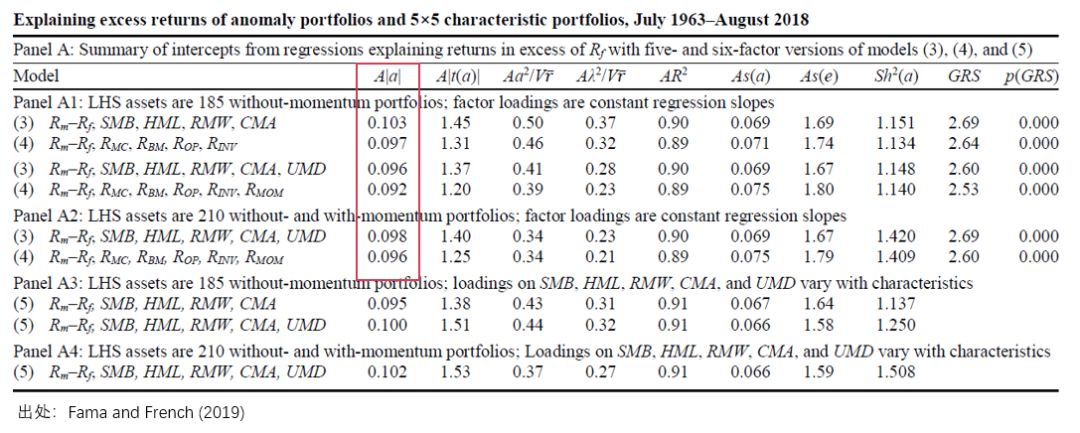
雖然僅僅是 Panel A，但它又細分(fēn)爲 A1 到 A4，包含的(de)信息量非常大(dà)。我把最關鍵的(de)用(yòng)紅框标出來(lái)了(le)。這(zhè)裏，我們隻需要關注 Panels A1 和(hé) A2（因爲 A3 和(hé) A4 是關于那個(gè)帶交叉項的(de)模型，本文并不涉及）。Panels A1 和(hé) A2 的(de)區(qū)别隻是在于 LHS 投資組合的(de)數量差異，除此之外它們均是比較了(le) Fama and French (2020) 中的(de)模型（3）和(hé)模型（4），分(fēn)别對(duì)應本文中的(de) TS 模型（FF5）和(hé) CS 模型二（對(duì)标 FF5 的(de)那個(gè)）。

另外值得(de)一提的(de)是，在 FF5 的(de)基礎上，Fama and French (2020) 也(yě)考慮了(le) UMD 動量因子。當加入動量因子後，其 TS 模型便加入了(le) UMD 因子，而 CS 模型就加入了(le) R_MOM 因子。上表中，紅框标出來(lái)的(de) metric（A|α|）是給定定價模型下(xià)，所有 LHS 資産的(de) pricing errors 絕對(duì)值的(de)均值。這(zhè)個(gè)值越接近零說明(míng)定價模型越出色。從結果不難看出，無論是五因子還(hái)是加入了(le) UMD 和(hé) R_MOM 的(de)六因子模型，無論是考慮 185 個(gè)還(hái)是 210 個(gè) LHS 資産，CS 模型二均優于其對(duì)應的(de) TS 模型。

接下(xià)來(lái)再看看 Panel B。相比于 Panel A 對(duì)比了(le) TS 模型和(hé) CS 模型二，Panel B 僅僅關注 CS 模型一，但它巨大(dà)的(de)信息量卻更令人(rén)“懵逼”。

爲了(le)解釋它，我不得(de)不先回顧一下(xià) CS 模型一：

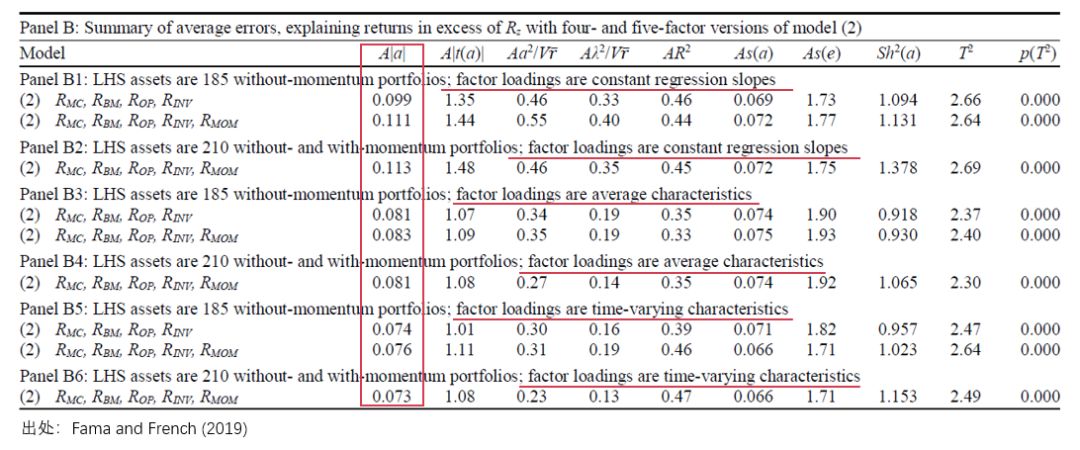
首先，這(zhè)個(gè)模型解釋的(de)是 R_it 相對(duì) R_zt 而非 R_ft 的(de)超額收益；其次，該模型中作爲 factor loadings 的(de)是 firm characteristics，而且它們是時(shí)變的(de)，而非常數。記住了(le)這(zhè)兩條，就可(kě)以來(lái)看 Panel B 了(le)：

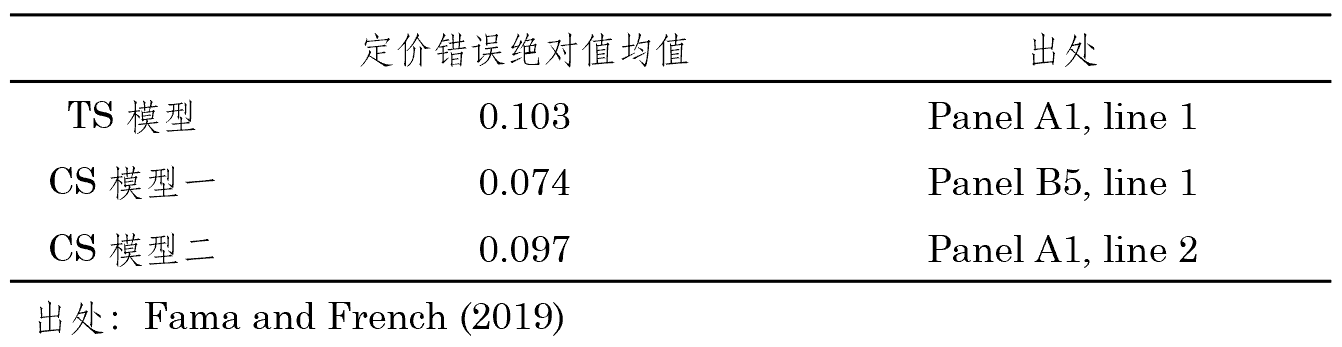
有了(le)上述說明(míng)就可(kě)以來(lái)看結果了(le)。上表顯示，無論采用(yòng)哪些 LHS 資産來(lái)評價不同模型，我們都可(kě)以觀察到這(zhè)樣的(de)結果：Panels B5/6 優于 Panels B3/4 優于 Panels B1/2。進一步的(de)，比較 Panels B5/6 和(hé) Panel A 中的(de) TS 和(hé) CS 模型二可(kě)知，CS 模型一的(de)效果是最好的(de)。比如，當采用(yòng) 185 個(gè) LHS 資産時(shí)，這(zhè)三個(gè)模型的(de)平均定價錯誤絕對(duì)值爲：

從以上各種對(duì)比的(de)結果中可(kě)以得(de)到 Fama and French (2020) 一文的(de)核心結論：

最後用(yòng) Fama and French (2020) 原文對(duì)上述結論做(zuò)一個(gè)總結：

We close by addressing a central question: What explains the dominance of model (2)? All the models we consider target cross-section variation in average returns related to the same size, value, profitability, investment, and momentum characteristics. And the CS factors of model (2) are constructed from returns on the same 2 × 3 MC-BM, MC-OP, MC-INV, and MC-MOM portfolios that produce the TS factors of model (3). The way these returns are related to produce the TS factors is, however, arbitrary. In contrast, monthly cross-section FM OLS regressions combine returns and characteristics on the 2 × 3 portfolios to produce CS factors that optimize the month-by-month description of returns on these portfolios.

一句話(huà)概括：截面回歸得(de)到的(de)純因子組合的(de) factor returns 比各種 double sort 得(de)到的(de) factor returns 能夠更好的(de)解釋資産的(de)截面差異。Barra 大(dà)概要笑(xiào)出聲了(le)。

6 結語

Fama and French (2020) 是一篇典型的(de) Eugene Fama 的(de)文章(zhāng)，它把 empirical analysis 做(zuò)到了(le)極緻并得(de)出了(le)非常清晰的(de)結論。不過，我最初精讀完它的(de) working paper 版本的(de)時(shí)候感受也(yě)是懵逼的(de)，因爲它的(de)信息量太大(dà)，而且在各種模型之間切換，給人(rén)一種腦(nǎo)容量不夠的(de)感覺。而後來(lái)得(de)知這(zhè)篇文章(zhāng)被 RFS 接受後也(yě)是懵逼的(de)。我想大(dà)概隻有 FF 寫這(zhè)麽一篇文章(zhāng)才能被頂刊接受吧。它實在是太 empirical 了(le)，最終的(de)結論 —— 雖然異常清晰 —— 也(yě)僅僅是建立在 empirical results 之上的(de)。

當然，不管怎樣，該文回答(dá)了(le)無論是學術界還(hái)是業界都非常關心的(de)問題，即到底應該用(yòng)什(shén)麽作爲 factor returns 以及用(yòng)什(shén)麽作爲 factor loadings。從 Fama and French (2020) 的(de)研究結果來(lái)看，CS 純因子組合或大(dà)有可(kě)爲。也(yě)許在不久的(de)将來(lái)，我們就能看到用(yòng) CS 因子來(lái)構建的(de)因子模型來(lái) PK 掉所有靠各種 sort 獲得(de)的(de) TS 因子模型了(le)（學術界主流 TS 因子模型見 Hou et al. 2019）。So, which beta? 我們也(yě)許已經有了(le)答(dá)案。

參考文獻

Ang, A., R. J. Hodrick, Y. Xing, and X. Zhang (2006). The cross-section of volatility and expected returns. Journal of Finance 61(1), 259 – 299.

Black, F., M. C. Jensen, and M. Scholes (1972). The Capital Asset Pricing Model: Some Empirical Tests. In Studies in the Theory of Capital Markets. M. C. Jensen (ed), New York: Praeger, 79 – 121.

Fama, E. F. and K. R. French (2015). A Five-Factor Asset Pricing Model. Journal of Financial Economics 116(1), 1 – 22.

Fama, E. F. and K. R. French (2020). Comparing cross-section and time-series factor models. Review of Financial Studies 33(5), 1891 – 1926.

Fama, E. F. and J. D. MacBeth (1973). Risk, Return, and Equilibrium: Empirical Tests. Journal of Political Economy 81(3), 607 – 636.

Gibbons, M. R., S. A. Ross, and J. Shanken (1989). A test of the efficiency of a given portfolio. Econometrica 57(5), 1121 – 1152.

Hou, K., H. Mo, C. Xue, and L. Zhang (2019). Which factors? Review of Finance 23(1), 1 – 35.

Jegadeesh, N., J. Noh, K. Pukthuanthong, R. Roll, and J. Wang (2019). Empirical tests of asset pricing models with individual assets: Resolving the errors-in-variables bias in risk premium estimation. Journal of Financial Economics 133(2), 273 – 298.

Lewellen, J., S. Nagel, and J. Shanken (2010). A skeptical appraisal of asset pricing tests. Journal of Financial Economics 96(2), 175 – 194.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。