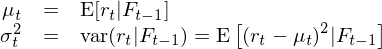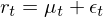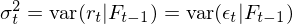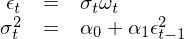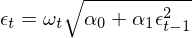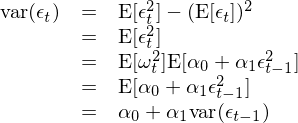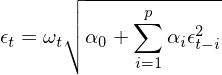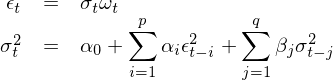寫給你的(de)金融時(shí)間序列分(fēn)析：補完篇

作者：石川

摘要：本文介紹時(shí)間序列分(fēn)析中的(de) GARCH 模型，闡述使用(yòng) mean model 和(hé) volatility model 對(duì)收益率序列聯合建模的(de)方法。

1 引言

兩年前，我們推出了(le)《寫給你的(de)金融時(shí)間序列分(fēn)析》系列，通(tōng)過四篇文章(zhāng)介紹了(le)金融數據時(shí)序分(fēn)析建模的(de)基礎知識。這(zhè)四篇文章(zhāng)的(de)内容分(fēn)别爲：

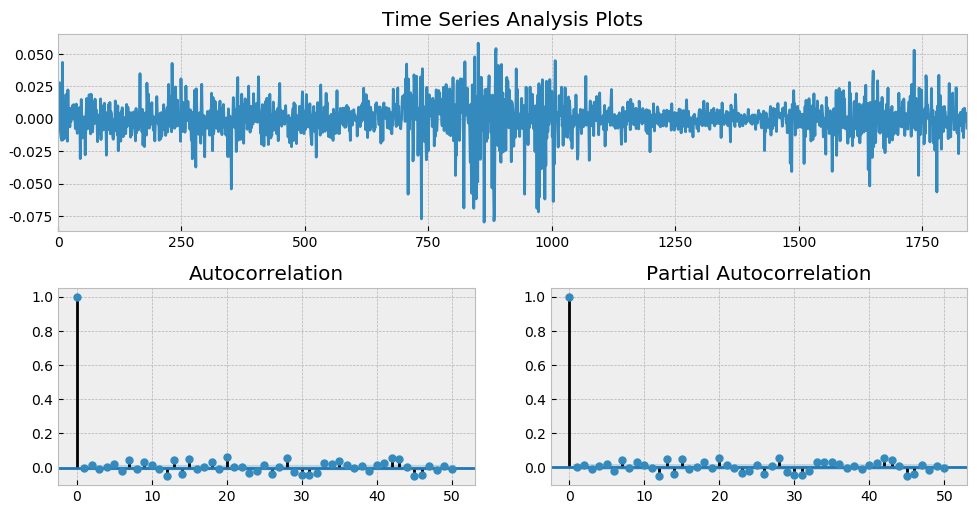
通(tōng)過前述四篇文章(zhāng)的(de)介紹可(kě)知，金融時(shí)間序列分(fēn)析的(de)核心是找到資産收益率序列的(de)自相關性，并利用(yòng)它。以 2012 年 1 月(yuè) 1 日到 2019 年 7 月(yuè) 31 日上證指數日頻(pín)對(duì)數收益率爲例，假設使用(yòng) ARMA(3, 2) 對(duì)其建模，并考察其殘差。下(xià)圖展示了(le)殘差時(shí)序以及它的(de) ACF 和(hé) Partial ACF（PACF）。

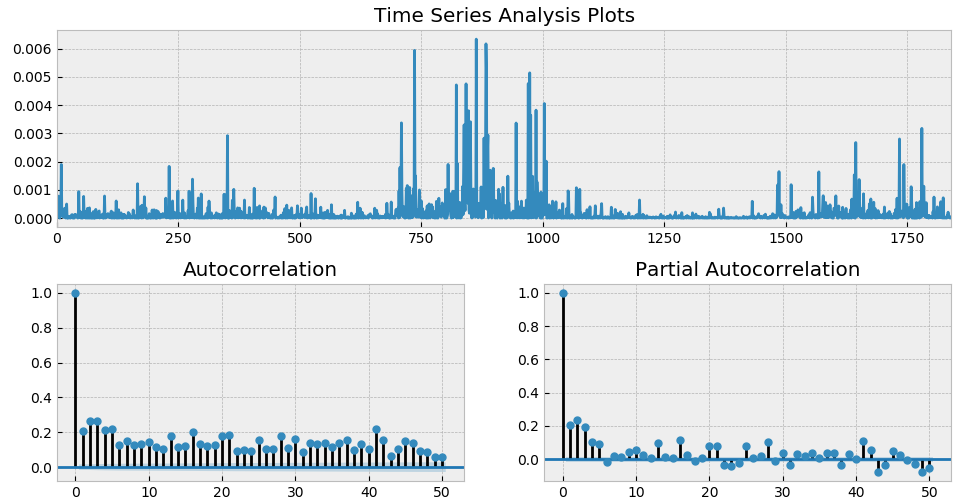
從 ACF 和(hé) PACF 上不難看出，在很多(duō) lags 上，自相關系數是超過 95% 的(de)置信區(qū)間的(de)；而從最上面一副圖中也(yě)能明(míng)顯看出收益率序列的(de)一大(dà)特征 —— 波動率聚類。如果把殘差取平方，并再次作圖，上述波動率聚類則會變得(de)更加直觀。它在數學上被稱爲條件異方差（conditional heteroskedasticity）。

上述結果意味著(zhe)，僅使用(yòng) ARMA 對(duì)收益率序列建模是不夠的(de)，它對(duì)條件異方差無能爲力。爲了(le)解決這(zhè)個(gè)問題需要對(duì)波動率建模，即使用(yòng) Generalized Autoregressive Conditional Heteroskedasticity（GARCH）模型。不介紹 GARCH 的(de)時(shí)間序列分(fēn)析系列大(dà)抵是不完整的(de)；此外也(yě)有小夥伴留言說能不能寫寫 GARCH。所以今天就來(lái)補作業了(le)，也(yě)因此給這(zhè)篇文章(zhāng)起了(le)個(gè)“補完篇”的(de)名字。

考慮到本系列前四篇“狠狠”的(de)參考了(le) quantstart.com 上相關文章(zhāng)的(de)“優良傳統”，我在本文第 3 小節介紹 GARCH 的(de)數學模型時(shí)也(yě)會再次借鑒（參考文獻中有鏈接）。最後，再給 quantstart.com 打個(gè) call（必須給足它 credits），它上面的(de)所有文章(zhāng)都非常值得(de)一讀。下(xià)文以資産收益率序列作爲研究對(duì)象，介紹相關概念：第 2 節解釋模型的(de)結構；第 3 節介紹 ARCH 和(hé) GARCH 的(de)數學背景知識；第 4 節說明(míng)如何使用(yòng) ARMA 和(hé) GARCH 對(duì)收益率的(de)條件均值和(hé)條件方差進行聯合建模；第 5 節針對(duì)上證指數做(zuò)簡單實證；第 6 節總結全文。

2 模型的(de)結構

首先來(lái)看看“條件異方差”一詞。波動率聚類說明(míng)不同階段收益率的(de)方差是不同的(de)，這(zhè)就是異方差性（heteroskedastic）。而很多(duō)時(shí)候，資産收益率表現出高(gāo)波動伴随著(zhe)高(gāo)波動時(shí)期（大(dà)牛市或者股災的(de)時(shí)候），而低波動又往往伴随著(zhe)低波動，因此波動率之間是存在序列相關性的(de)，這(zhè)就是“條件”一詞的(de)來(lái)源。将二者結合就有了(le)條件異方差。

使用(yòng) GARCH 建模，是爲了(le)在 r_t 的(de)線性自相關性之上考慮其方差之間的(de)相關性，即把均值模型和(hé)波動率模型放在一個(gè)整體框架中考慮（Tsay 2010）。假設 t – 1 時(shí)刻所有已知的(de)信息爲 F_{t-1}，則當給定 F_{t-1} 時(shí)，t 時(shí)刻收益率的(de)條件均值和(hé)條件方差可(kě)寫爲：

對(duì)于條件均值 μ_t，它可(kě)以是一個(gè)常數，也(yě)可(kě)以使用(yòng)我們已經掌握的(de) ARMA 模型對(duì)其建模。一旦有了(le) μ_t 的(de)模型，r_t 可(kě)以寫作：

上式中 ε_t 是 t 時(shí)刻的(de)擾動或者新息。結合上式和(hé)條件方差的(de)定義可(kě)知，t 時(shí)刻收益率 r_t 的(de)條件方差由 ε_t 的(de)方差決定：

從模型結構不難看出，爲了(le)考慮條件異方差則需要對(duì) ε_t 建模，而這(zhè)正是 GARCH 的(de)目标。

3 ARCH 和(hé) GARCH

在介紹 GARCH 之前不妨先來(lái)看看 ARCH，畢竟 GARCH 隻是在它前面加了(le)一個(gè) G（generalized）從而将其推廣了(le)。ARCH 由 Engle (1982) 提出，它是第一個(gè)對(duì)波動率建模的(de)系統性框架。對(duì)于 ε_t，考慮如下(xià)模型（其中 ω_t 表示均值爲 0、方差爲 1 的(de)白噪聲）：

把 σ_t 的(de)表達式帶回到 ε_t 中可(kě)得(de)：

這(zhè)個(gè)關于序列 {ε_t} 的(de)模型稱作一階自回歸條件異方差模型，也(yě)就是最簡單的(de) ARCH(1) 過程 —— 括号裏的(de)系數 1 表明(míng)自回歸模型中隻考慮了(le) lag = 1 階。爲了(le)直觀看出方差序列之間的(de)關系，将上式兩邊平方：

上式清晰的(de)顯示了(le) var(ε_t) 和(hé) var(ε_{t-1}) 之間的(de)關系。前面我們提到，{ε_t} 的(de)模型是一個(gè) ARCH(1) 過程。從 var(ε_t) 和(hé) var(ε_{t-1}) 的(de)關系可(kě)知，一個(gè) ARCH(1) 過程的(de)方差 —— 即 var(ε_t) —— 正是一個(gè) AR(1)，即一階自回歸過程。接下(xià)來(lái)我們照(zhào)貓畫(huà)虎，将 ARCH(1) 簡單推廣到多(duō)階 lags，就得(de)到 ARCH(p) 過程：

類似的(de)，我們可(kě)以說一個(gè) ARCH(p) 過程的(de)方差是一個(gè) AR(p)，即 p 階自回歸過程；這(zhè)相當于對(duì)方差使用(yòng) AR(p) 來(lái)建模。既然能對(duì)方差用(yòng) AR(p) 來(lái)建模，那麽很自然的(de)一個(gè)問題就是，爲什(shén)麽不把 MA(q) 也(yě)加上得(de)到方差的(de) ARMA(p, q) 模型呢(ne)？如此便引出了(le) GARCH(p, q)。對(duì)于 ε_t，考慮如下(xià)模型：

這(zhè)就是大(dà)名鼎鼎的(de) GARCH(p, q) 模型 —— (p, q) 階的(de)廣義自回歸條件異方差模型。有了(le) GARCH 我們就可(kě)以用(yòng)它對(duì)收益率建模了(le)。

4 使用(yòng) ARMA + GARCH 建模

本小節來(lái)看看如何在第二節介紹的(de)體系下(xià)使用(yòng) ARMA(p, q) 和(hé) GARCH(p', q') 來(lái)對(duì) r_t 進行聯合建模。爲了(le)區(qū)分(fēn)條件均值模型和(hé)條件方差模型中的(de)自回歸階數，我特意用(yòng)了(le) (p, q) 和(hé) (p', q') 表示。将前面的(de)内容整合到一起得(de)到關于 r_t 的(de)模型如下(xià)：

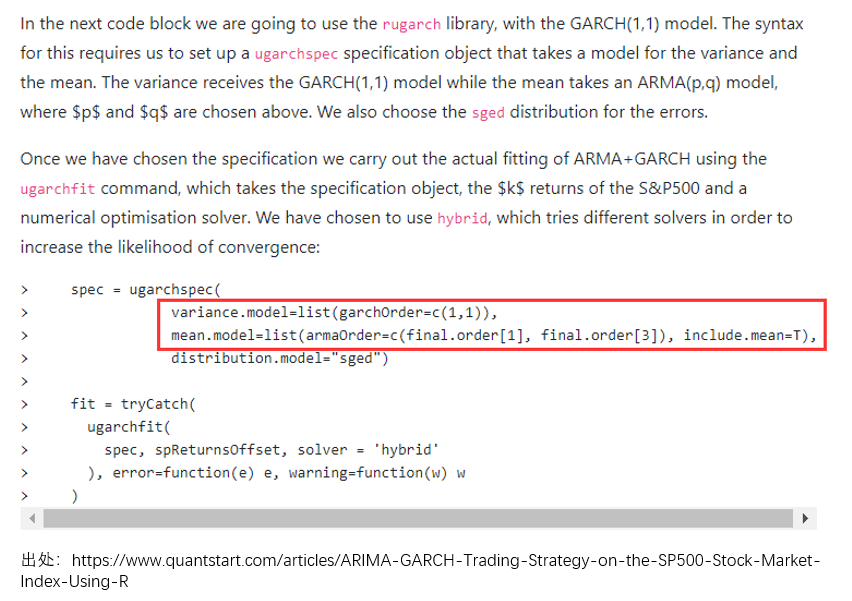
當我們對(duì) r_t 建模時(shí)，需要同時(shí)指定 mean model（對(duì) μ_t 建模）以及 volatility model（對(duì) ε_t 建模）。上式使用(yòng)了(le) ARMA(p, q) 作爲 mean model，但根據實際問題也(yě)可(kě)以使用(yòng)更簡單的(de)模型，比如 μ_t = 常數；使用(yòng)了(le) GARCH(p', q') 作爲 volatility model。最後使用(yòng)已有的(de)數據對(duì)這(zhè)兩個(gè)模型的(de)參數進行聯合估計。在實際應用(yòng)中，無論使用(yòng) python 還(hái)是 R 的(de)相關 package，在調用(yòng)時(shí)都要指定 mean model 和(hé) volatility model。舉個(gè)例子，在 quantstart.com 上一篇使用(yòng) ARMA 對(duì) mean 建模、用(yòng) GARCH 對(duì) volatility 建模來(lái)交易 S&P500 指數的(de)例子中，作者對(duì)兩個(gè)模型同時(shí)進行了(le)設定。

在具體 GARCH 建模時(shí)可(kě)以遵如下(xià)步驟（Tsay 2010）：

以上五步構成了(le)對(duì)條件均值和(hé)條件方差的(de)聯合建模，使用(yòng)得(de)到的(de)模型就可(kě)以對(duì)未來(lái)的(de) r_t 以及 var(r_t) 進行預測。在離開本節之前，我們再來(lái)介紹兩個(gè)使用(yòng) GARCH 建模時(shí)不十分(fēn)正确的(de)做(zuò)法（希望能幫你排雷）。

錯誤做(zuò)法一：用(yòng) ARMA(p, q) 的(de)階數作爲 GARCH(p', q') 的(de)階數

網上一些資料中提過這(zhè)樣的(de)做(zuò)法：首先是用(yòng) ARMA 對(duì) r_t 建模、确定最優的(de)參數 p 和(hé) q；然後将它們作爲波動率模型的(de)階數，即 GARCH(p, q)，同時(shí)在聯合建模時(shí)僅假設 mean model = constant。這(zhè)種做(zuò)法使用(yòng)從 r_t 線性關系找到的(de) p 和(hé) q 去對(duì) r_t 的(de)波動率的(de)關系建模，然後又假設 mean model 是常數，著(zhe)實令人(rén)費解。

錯誤做(zuò)法二：将 mean model 和(hé) volatility model 拆開估計

這(zhè)種做(zuò)法聽(tīng)上去更“靠譜”一些。首先是用(yòng) ARMA 對(duì) r_t 建模，确定最優參數 p 和(hé) q；然後使用(yòng) ARMA 模型的(de)殘差爲被解釋變量，對(duì)其進行 GARCH(p', q') 建模；第二步中因爲被解釋變量是殘差，因此 GARCH 模型的(de) mean model = 0，即假設殘差均值爲零。這(zhè)種做(zuò)法看似合理(lǐ)，但是從條件均值角度來(lái)說，它也(yě)僅僅是利用(yòng)了(le) ARMA 這(zhè)一步（第二步的(de) GARCH 建模由于假設 mean model = 0 因此對(duì)條件均值不再有影(yǐng)響），而沒有利用(yòng) ARMA + GARCH 的(de)聯合估計考察異方差對(duì)收益率序列的(de)影(yǐng)響。通(tōng)常來(lái)說，就 ARMA 的(de)參數而言，僅使用(yòng) ARMA 和(hé)聯合使用(yòng) ARMA + GARCH 的(de)結果是有差異的(de)。

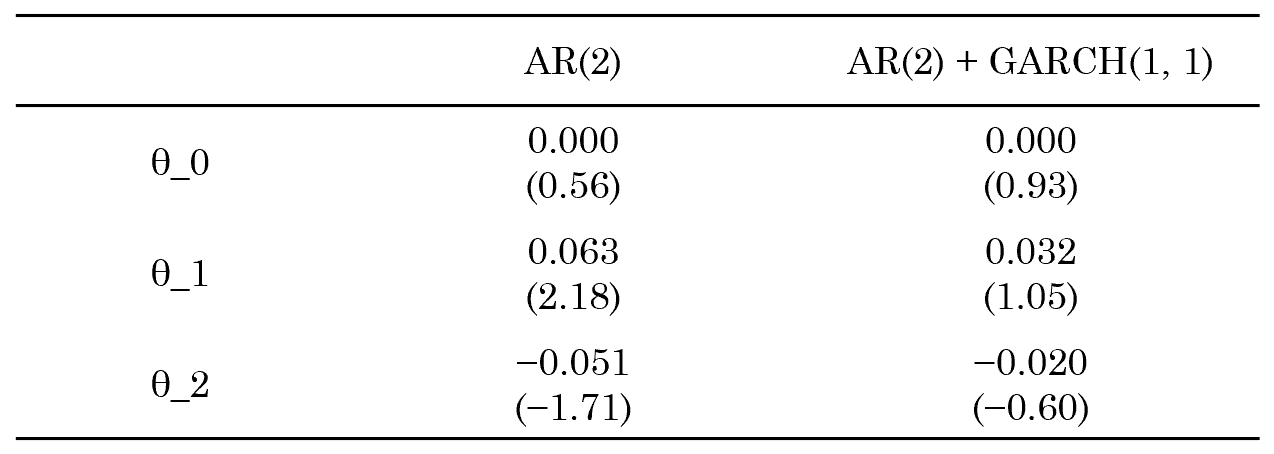
舉個(gè)例子：使用(yòng) AR(2) 和(hé) AR(2) + GARCH(1, 1) 兩種方法對(duì)收益率建模。

OK，回到例子。下(xià)表展示了(le)兩種方法建模時(shí)，AR(2) 的(de)參數，可(kě)以看出它們之間的(de)差異。

所以，GARCH 模型雖好，但是 use with care。我們應時(shí)刻搞清楚是在對(duì)什(shén)麽建模、怎麽建模，mean model 是什(shén)麽、volatility model 又是什(shén)麽。

5 簡單實證

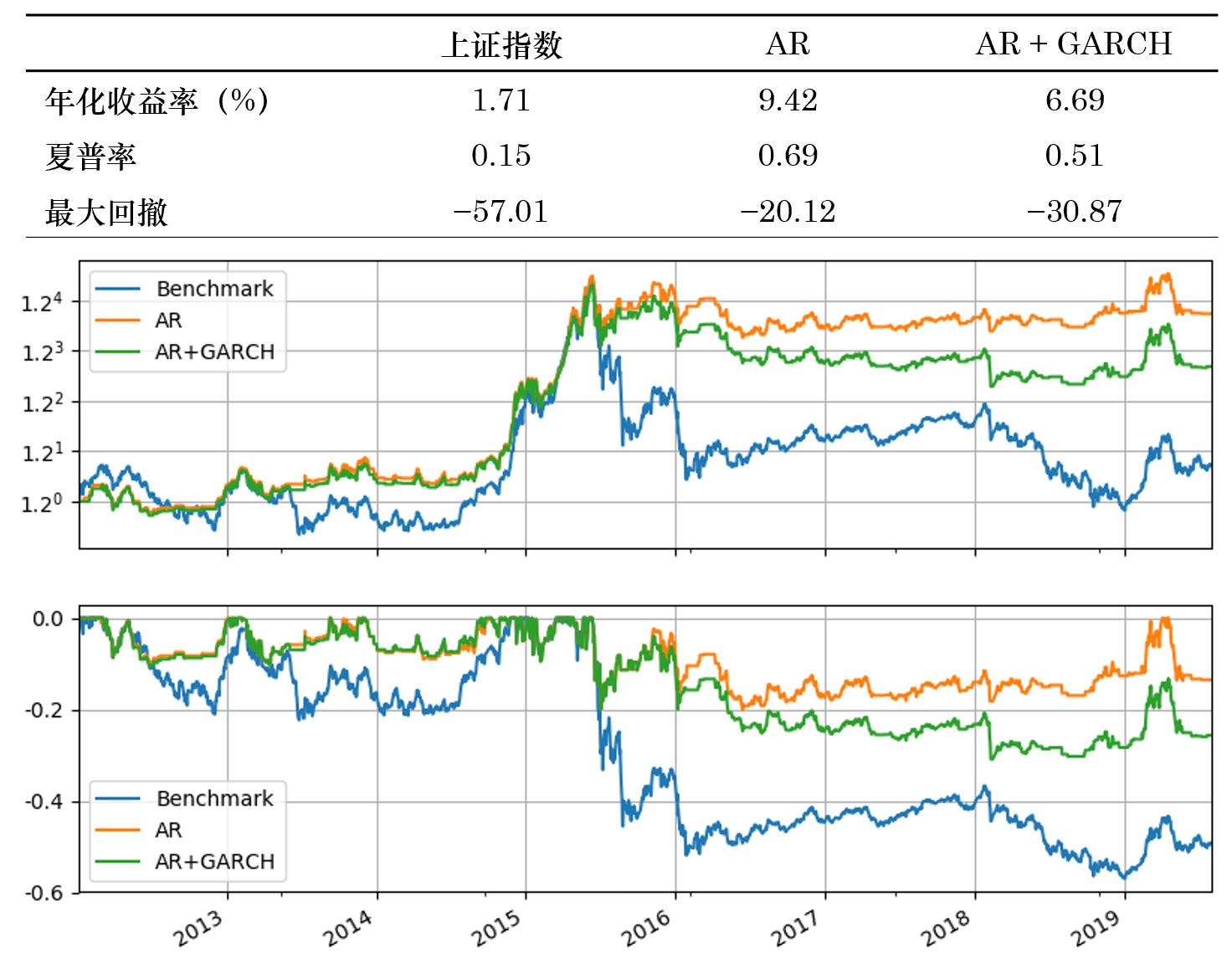
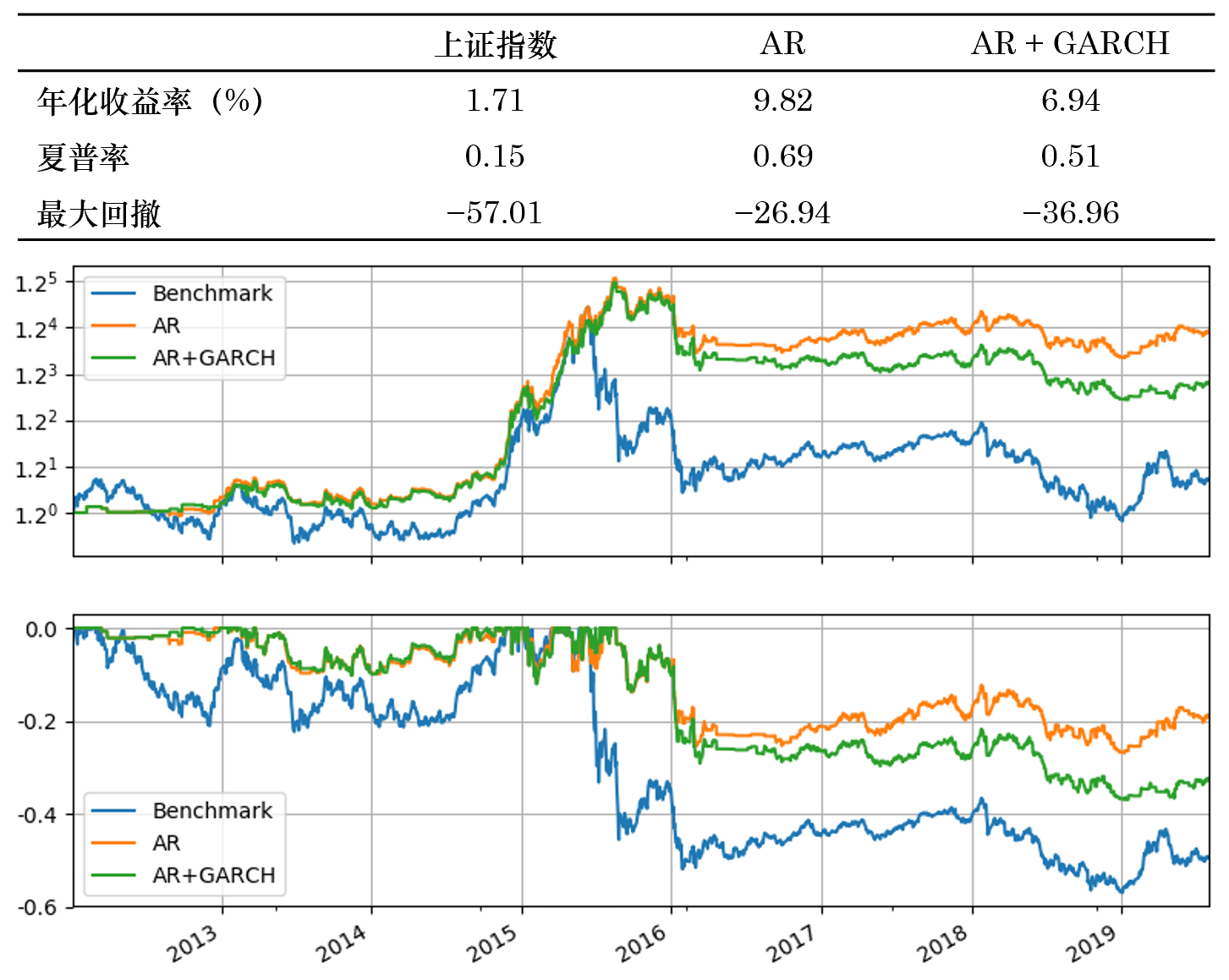
最後通(tōng)過一個(gè) toy example 來(lái)介紹 ARMA + GARCH 的(de)應用(yòng)。以下(xià)對(duì)上證指數自 2012 年 1 月(yuè)到 2019 年 7 月(yuè)的(de)日頻(pín)對(duì)數收益率進行時(shí)間序列建模，并使用(yòng)該模型預測下(xià)一個(gè)交易的(de)收益率。如果預測爲正則選擇持有上證指數，反之則空倉；假設以收盤價成交且不考慮任何交易成本。在構建策略時(shí)，采用(yòng)長(cháng)度爲 T 的(de)滾動窗(chuāng)口曆史數據。首先是用(yòng) AR 對(duì)收益率建模（因爲 python arch package 不支持 ARMA 作爲 mean model，所以僅使用(yòng) AR(p) 模型），并根據 AIC 選擇最優 p 值（p 取值範圍爲 0 到 5）；然後以該 AR(p) 作爲 mean model，并使用(yòng) GARCH(1, 1) 模型爲 volatility model，進行聯合參數估計。使用(yòng)最終的(de)模型預測下(xià)一個(gè)交易日收益率。此外作爲比較，我們也(yě)考慮僅采用(yòng) AR(p) 來(lái)對(duì)收益率建模，而不考慮條件異方差的(de)影(yǐng)響。

首先來(lái)看 T = 60 個(gè)交易日的(de)情況。下(xià)圖展示了(le) AR 和(hé) AR + GARCH 兩種策略的(de)淨值和(hé)回撤曲線。就表現而言，它們均戰勝了(le)上證指數本身（benchmark）。但是在股災之後（波動率變大(dà)了(le)），這(zhè)兩種模型的(de)表現發生了(le)分(fēn)化(huà)，就這(zhè)個(gè)簡單實證而言，AR 的(de)效果比 AR + GARCH 更好。

再來(lái)看看把滾動窗(chuāng)口長(cháng)度換到 T = 252 的(de)情況。結果和(hé)上面接近，依然是 AR 戰勝了(le) AR + GARCH 的(de)組合。

從本小節的(de)例子來(lái)看，加入了(le) GARCH 的(de)策略似乎并沒有僅使用(yòng) AR 的(de)策略優異。我在最後的(de)結語部分(fēn)對(duì)此做(zuò)簡單評價。

6 結語

作爲“補完篇”，本文填了(le)《寫給你的(de)金融時(shí)間序列分(fēn)析》最後一個(gè)大(dà)坑 —— GARCH；寫作的(de)重點在于闡述使用(yòng) mean model 和(hé) volatility model 對(duì)收益率序列聯合建模，以及在一個(gè)整合的(de)框架下(xià)對(duì)兩種模型的(de)參數進行聯合估計。本文的(de)第 5 節給出了(le)一個(gè)簡單實證。因 python arch package 的(de)功能所限，實證中的(de) mean model 僅采用(yòng)了(le) AR 模型。感興趣的(de)小夥伴不妨嘗試 R 的(de)相關 packages。從實證結果來(lái)看，加入 GARCH 似乎沒什(shén)麽效果。但不要忘了(le)，我們并沒有對(duì) GARCH 的(de)參數進行任何優化(huà)，也(yě)沒有額外利用(yòng)其對(duì)波動率的(de)建模來(lái)添加更加複雜(zá)的(de)規則 —— 比如 volatility scaling。因此，僅僅基于這(zhè)個(gè)簡單的(de)例子難以對(duì) GARCH 的(de)貢獻做(zuò)出任何正确的(de)評判。

對(duì)于量化(huà)投資的(de)研究來(lái)說，構建出策略并看到回測出來(lái)的(de)淨值曲線無疑是最令人(rén)激動的(de)。然而，真正研究工作的(de)核心卻在于搞懂(dǒng)每個(gè)模型的(de)原理(lǐ)以及它的(de)作用(yòng)，而這(zhè)個(gè)過程注定是枯燥的(de)。Quantstart Team 在其時(shí)間序列分(fēn)析系列文章(zhāng)（以及其他(tā)系列）中不厭其煩的(de)介紹每個(gè)基礎模型，從簡單到複雜(zá)，像搭積木(mù)一樣爲讀者構建知識體系，令人(rén)敬佩。現在，我們有了(le)時(shí)間序列分(fēn)析的(de)各個(gè) building blocks。但是，能夠用(yòng)它們做(zuò)什(shén)麽、如何去更科學的(de)對(duì)收益率分(fēn)析、預測，還(hái)需有經驗的(de)積累。最後，我想以下(xià)面這(zhè)段出自 Quantstart 的(de)話(huà)作爲本系列的(de)結束，也(yě)希望與各位共勉。

True quantitative trading research is careful, measured and takes significant time to get right. There is no quick fix or "get rich scheme" in quant trading.

參考文獻

Engle, R. F. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 50(4), 987 – 1008.

Tsay, R. S. (2010). Analysis of Financial Time Series (3rd ed). Wiley.

https://www.quantstart.com/articles/Generalised-Autoregressive-Conditional-Heteroskedasticity-GARCH-p-q-Models-for-Time-Series-Analysis

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。