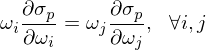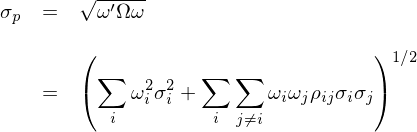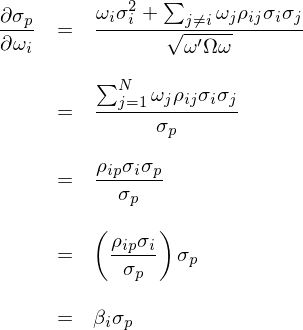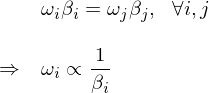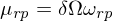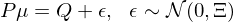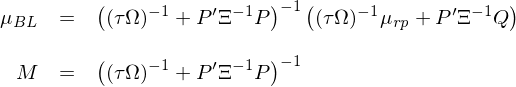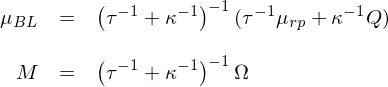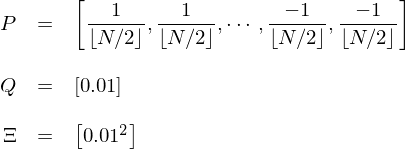基于 Risk Parity + Black-Litterman 的(de)因子擇時(shí)

作者：石川

摘要：Risk Parity 能夠有效分(fēn)散風險；而 Black-Litterman 是貝葉斯思想的(de)完美(měi)體現。二者的(de)結合是值得(de)持續探索的(de)資産配置方法。

1 引言

之前我寫了(le)一些文章(zhāng)介紹海外因子擇時(shí)的(de)先進觀點。然後有小夥伴問我“你怎麽看因子擇時(shí)？”。于是就有了(le)本文。本文将使用(yòng) Risk Parity + Black-Litterman 模型進行股票(piào)風格因子的(de)擇時(shí)實證。需要特别強調的(de)是，本文的(de)目的(de)不是宣稱 RP + BL 就一定會比不擇時(shí)（即按簡單多(duō)樣化(huà)配置）更好 —— 從實證結果來(lái)看也(yě)确實并非如此。本文更多(duō)的(de)是介紹 RP + BL 這(zhè)種思想。

Risk Parity（風險平價）是一種 volatility weighting；volatility weighting 被證明(míng)在長(cháng)期來(lái)看可(kě)以獲得(de)更高(gāo)的(de) Sharpe Ratio（Hallerbach 2012），是一個(gè)優秀的(de)配置方法。另一方面，Black-Litterman 是基于貝葉斯思想的(de)資産配置框架。它讓使用(yòng)者非常容易把自己的(de)主觀判斷（稱爲 views）和(hé)先驗結合起來(lái)，得(de)到待配置資産的(de)後驗收益率分(fēn)布。較直接使用(yòng) mean-variance optimization 來(lái)說，BL 模型給出的(de)配置結果更加符合人(rén)們的(de)預期。

将 RP 和(hé) BL 結合起來(lái)的(de)方法是把 Risk Parity 配置下(xià)的(de)收益率分(fēn)布作爲 Black-Litterman 框架下(xià)的(de)先驗，同時(shí)摒棄原方法中的(de)所謂市場(chǎng)均衡狀态下(xià)的(de)先驗。RP + BL 可(kě)以看成是 volatility weighting 和(hé)貝葉斯思想的(de)完美(měi)結合。下(xià)面就來(lái)看看它們能擦出怎樣的(de)火花。下(xià)文假設讀者熟悉 Risk Parity 和(hé) Black-Litterman 模型。需要背景知識的(de)小夥伴請參考《你真的(de)搞懂(dǒng)了(le)風險平價嗎？》以及《Black-Litterman 模型 —— 貝葉斯框架下(xià)的(de)資産配置利器》。

2 再談 Risk Parity

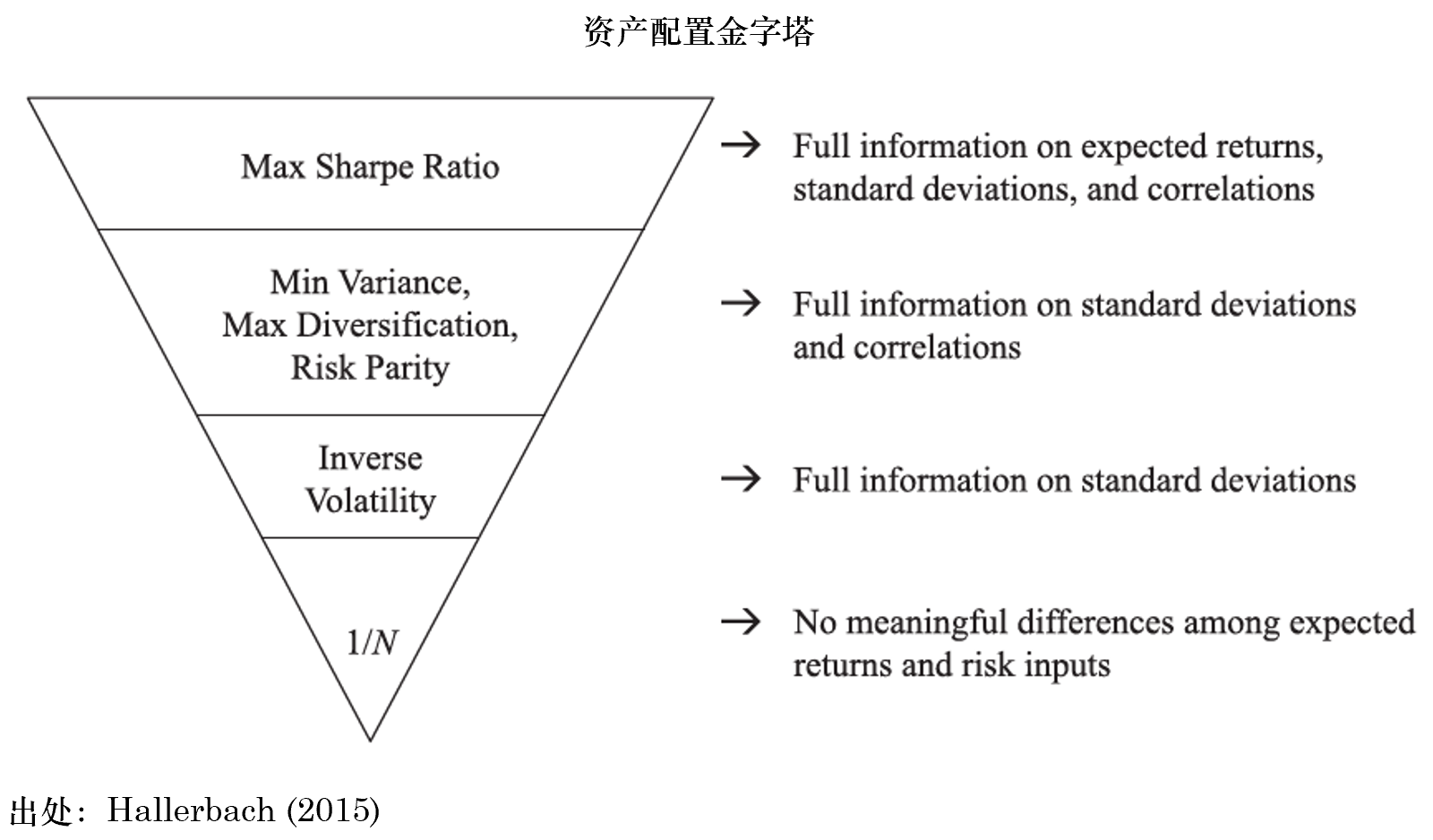
《淺析資産配置的(de)幾種方法》一文曾對(duì)比了(le)一些常見的(de)資産配置方法。随著(zhe)我們對(duì)資産間收益率分(fēn)布的(de) μ_i、σ_i 以及 ρ_ij 的(de)信息的(de)減少，不同資産配置方法的(de)關系如下(xià)圖所示。當我們有 μ_i、σ_i、ρ_ij 全部信息時(shí)，應充分(fēn)利用(yòng)它們、以最大(dà)化(huà)投資組合夏普率爲目标做(zuò)配置；而在另一個(gè)極端，如果所有信息都是未知的(de)，那麽簡單多(duō)樣化(huà)（等權配置）是唯一的(de)選擇。Risk Parity 介于兩者之間，它假設我們充分(fēn)掌握投資品之間的(de)協方差矩陣。

令 ω_i 代表資産 i 的(de)權重。由 Risk Parity 的(de)定義有：

其中 σ_p 代表投資組合的(de)波動率，它的(de)表達式爲：

上式中，ω 是全部 N 個(gè)資産的(de)權重向量；Ω 是 N 個(gè)資産收益率的(de)協方差矩陣。将 σ_p 的(de)表達式代入到其對(duì) ω_i 的(de)偏導數有：

在上面的(de)推導中，第三步使用(yòng)了(le)資産 i 收益率 r_i 和(hé)投資組合收益率 r_p 之間的(de)協方差的(de)定義；最後一步使用(yòng)了(le) β 的(de)定義 —— 資産 i 收益率相對(duì)于投資組合收益率的(de) β。将該關系式代回到 Risk Parity 的(de)條件可(kě)知：

在 Risk Parity 中，投資組合的(de)權重和(hé)它于資産的(de) β 成反比；一個(gè)資産和(hé)組合的(de) β 越高(gāo)，其權重越低，從而有效的(de)分(fēn)散了(le)風險，每個(gè)資産對(duì)投資組合的(de)風險貢獻相同。從 β 的(de)定義出發可(kě)以看到，波動低（σ_i 小）且和(hé)其他(tā)資産相關性低（ρ_ij 低，因此 ρ_ip 才可(kě)能低）的(de)資産會獲得(de)更高(gāo)的(de)權重。通(tōng)常來(lái)說，波動率低的(de)資産收益率也(yě)更低，因此 Risk Parity 通(tōng)常使用(yòng)杠杆來(lái)提高(gāo)低波動資産的(de)權重以使組合的(de)風險達到給定的(de)風險水(shuǐ)平（現實中是否能加杠杆則是另一個(gè)問題）。當然，上面的(de)求解并沒有考慮任何約束條件，僅是定性說明(míng) Risk Parity 的(de)性質。在實際投資中，ω_i 應滿足各種限制（比如能否做(zuò)空；或者能使用(yòng)多(duō)高(gāo)的(de)杠杆）。本文的(de)實證要求 ω_i 滿足非負且 Σω_i = 1 兩個(gè)約束條件。

3 結合 Black-Litterman 框架

作爲應用(yòng)貝葉斯思想的(de)資産配置方法，Black-Litterman 使用(yòng)先驗和(hé)新息的(de)線性加權計算(suàn)出 N 個(gè)資産收益率的(de)後驗分(fēn)布。首先使用(yòng) Risk Parity 的(de)權重反推出的(de)預期收益率先驗分(fēn)布 N(μ_rp, τΩ)：

其中 δ 是風險厭惡系數，ω_rp 代表使用(yòng) Risk Parity 配置權重；模型假設預期收益率的(de)協方差矩陣和(hé)收益率的(de)協方差矩陣 Ω 有同樣的(de)結構，但是數量級要小很多(duō)，因此用(yòng) τΩ 表示（τ 是縮放尺度）。另一方面，Black-Litterman 模型将新息定義爲投資者對(duì)于資産收益率相對(duì)強弱的(de)主動判斷（views），每個(gè) view 由其所涉及的(de)資産的(de)線性組合表示。假設投資者一共有 K 個(gè) views，則它們的(de)關系如下(xià)：

其中，P（K × N 矩陣）的(de)每一行表示某個(gè) view 中涉及資産的(de)權重（換句話(huà)說，每個(gè) view 是一個(gè)投資組合，它可(kě)涉及一個(gè)或多(duō)個(gè)資産）；μ（K 階向量）表示未知新息預期收益率（該變量最終并未出現在 BL 公式中）；Q（K 階向量）表示 P 中的(de) K 個(gè)投資組合的(de)收益率。由于投資者對(duì)于這(zhè)些 views 并不是 100% 确定，因此模型中使用(yòng) Ξ（K × K 矩陣）表示 views 的(de)不确定性；假設 views 之間相互獨立，因此 Ξ 是一個(gè)對(duì)角陣。新息的(de)方差爲 P’(Ξ^-1)P。根據貝葉斯思想，後驗預期收益率是先驗和(hé)新息的(de)加權，權重和(hé)這(zhè)二者各自的(de)不确定性成反比。因此，Black-Litterman 模型中的(de)預期收益率後驗滿足分(fēn)布 N(μ_BL, M)：

由于預期收益率也(yě)是一個(gè)随機變量，因此資産的(de)收益率波動是預期收益率的(de)波動和(hé)收益率圍繞預期收益率波動之和(hé)。最終，N 個(gè)資産收益率的(de)後驗分(fēn)布滿足 N(μ_BL, Ω + M)。将收益率的(de)後驗分(fēn)布代入到 mean-variance optimization（MVO）中就可(kě)以求出基于 Black-Litterman 的(de)最優配置權重。在使用(yòng) Black-Litterman 框架時(shí)，一種簡化(huà)處理(lǐ)方式（出自 Haesen et al. 2017）是讓 P = I，即對(duì)于 N 個(gè)資産新息預期收益率有 K = N 個(gè)判斷（每個(gè) view 涉及單獨一個(gè)資産）；此外，進一步假設這(zhè) K = N 個(gè) views 的(de)不确定性和(hé) Ω 有同樣的(de)結構，記爲 Ξ = κΩ。将上述假設代入到模型中可(kě)知預期收益率後驗分(fēn)布爲 N(μ_BL, M)：

在上述假設下(xià)，μ_BL 是 μ_rp 和(hé) Q 的(de)簡單線性加權。同樣的(de)，N 個(gè)資産收益率的(de)後驗分(fēn)布滿足 N(μ_BL, Ω + M)。在使用(yòng) Black-Litterman 框架時(shí)必須要回答(dá)的(de)一個(gè)問題就是如何提供 views。實證中将使用(yòng)過去一段時(shí)間内資産收益率（即動量）作爲确定 views 的(de)依據，并采取上面兩種方法 —— 标準版和(hé)簡化(huà)版 —— 計算(suàn) views 的(de)參數。此外，由于 M 較 Ω 來(lái)說很小，因此在實證中忽略 M，仍使用(yòng) Ω 作爲資産收益率分(fēn)布的(de)協方差矩陣。求出後驗收益率分(fēn)布後，采用(yòng) MVO 計算(suàn)最終的(de)資産權重；在優化(huà)時(shí)，要求權重 ω_i 滿足非負及 Σω_i = 1 兩個(gè)約束條件。在因子擇時(shí)問題中，每個(gè)因子投資組合是一個(gè)資産。按照(zhào)上述設定可(kě)以動态計算(suàn)出每一期因子的(de)權重，從而達到擇時(shí)的(de)效果。以上設定的(de)步驟總結如下(xià)：

4 一個(gè)例子

本節使用(yòng)一個(gè)例子說明(míng)使用(yòng) Risk Parity + Black Litterman 的(de)因子擇時(shí)效果。實證中（本節和(hé)下(xià)一節）的(de)全部因子投資組合均是基于中證 500 成分(fēn)股構建的(de)多(duō)、空對(duì)沖組合，收益率頻(pín)率爲月(yuè)頻(pín)。對(duì)于給定的(de)因子，每月(yuè)末按其業務邏輯排序，做(zuò)多(duō)排名最高(gāo)的(de) 50 支，做(zuò)空排名最低的(de) 50 支，等權配置，不考慮任何成本。實證中的(de)因子均來(lái)自聚寬因子庫。該因子庫包含質量、基礎、情緒、成長(cháng)、風險以及每股因子六大(dà)類因子。由于情緒類因子的(de)收益率受漲跌停、停牌影(yǐng)響較大(dà)，實證中僅考慮其他(tā)五類（共 120 個(gè)）因子。

實證中使用(yòng)長(cháng)度爲 18 個(gè)月(yuè)的(de)滾動窗(chuāng)計算(suàn)協方差矩陣 Ω，并以此作爲 Risk Parity 的(de)輸入求出 ω_rp。此外，假設風險厭惡系數 δ = 10，計算(suàn) μ_rp。對(duì)于新息，采用(yòng)每個(gè)因子過去 12 個(gè)月(yuè)内的(de)動量計算(suàn) views 的(de)取值，并針對(duì)标準版和(hé)簡化(huà)版 Black-Litterman 模型有兩種處理(lǐ)方法。在簡化(huà)版中，使用(yòng)每個(gè)因子在過去 12 個(gè)月(yuè)的(de)平均收益率直接作爲 Q，并假定 μ_rp 和(hé) Q 的(de)權重分(fēn)别爲 0.8 和(hé) 0.2。在标準版中，假設 τ = 0.1。對(duì)于 views 的(de)處理(lǐ)則沒那麽直截了(le)當。在這(zhè)種情況下(xià)，實證中僅考慮一個(gè) view：将這(zhè) N 個(gè)資産按過去 12 個(gè)月(yuè)的(de)動量從高(gāo)到低排序，并等權做(zuò)多(duō)前 N/2 個(gè)、等權做(zuò)空後 N/2 個(gè)（如果 N 爲奇數則丢棄掉中間那個(gè)）；假設該組合下(xià)個(gè)月(yuè)的(de)收益率爲 1%（即強者恒強），且該判斷的(de)标準差爲 1%。在上述條件下(xià)，該 view 的(de)參數爲：

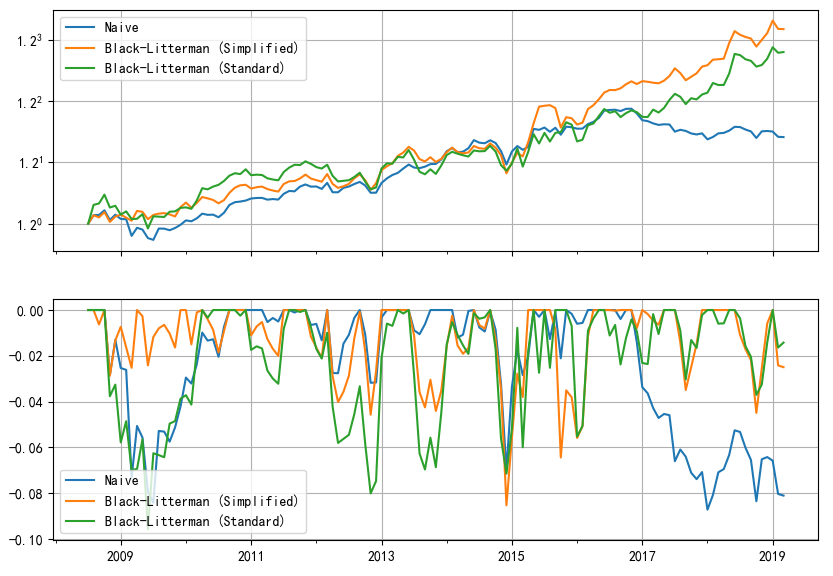
有了(le)這(zhè)些參數就可(kě)以按照(zhào)标準版的(de) Black-Litterman 公式計算(suàn)這(zhè)些因子收益率的(de)後驗分(fēn)布。每個(gè)月(yuè)末，采用(yòng)上述兩種方法計算(suàn)下(xià)個(gè)月(yuè)的(de)最新權重，以此實現因子擇時(shí)。在實證期内，這(zhè)兩種 Black-Litterman 配置方法和(hé)簡單多(duō)樣化(huà)（naive）的(de)淨值如下(xià)圖所示。

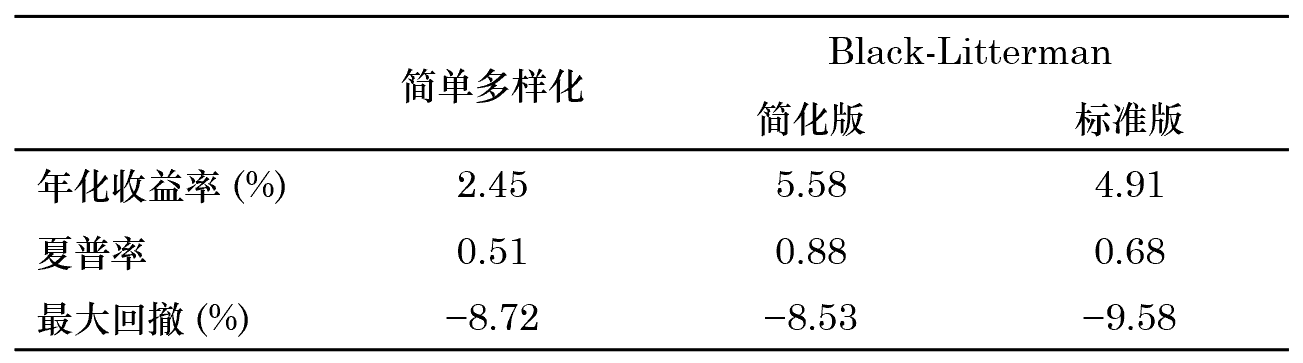
下(xià)表彙總了(le)這(zhè)三種配置方法的(de)風險收益情況。

從圖中和(hé)表中看到，使用(yòng) Black-Litterman 将 Risk Parity 和(hé)因子動量“揉在”一起擇時(shí)戰勝了(le)簡單多(duō)樣化(huà)。此外，簡化(huà)版 BL 戰勝了(le)标準版 BL。這(zhè)可(kě)能說明(míng)标準版中使用(yòng)的(de) view 并不十分(fēn)靠譜。先别急著(zhe)激動。這(zhè)個(gè)例子當然是 Cherry Picking！下(xià)一小節會有更多(duō)的(de)實證結果來(lái)客觀的(de)評判這(zhè)個(gè)擇時(shí)方法的(de)效果。然而，這(zhè)個(gè)例子也(yě)有可(kě)取之處。實證中故意挑選了(le)走勢不同的(de)因子，而非那些多(duō)空對(duì)沖後穩健上行的(de)因子。對(duì)沖後在樣本内穩健上行的(de)因子基本上都是 data mining 的(de)産物(wù)，無論怎麽配置或者擇時(shí)效果都不會差。本文雖然題爲因子擇時(shí)，但上述方法也(yě)可(kě)以用(yòng)于大(dà)類資産擇時(shí)，而大(dà)類資産難以出現穩健上行的(de)走勢。所以，對(duì)于這(zhè)樣的(de)一組樣本，比較主動擇時(shí)方法和(hé)簡單多(duō)樣化(huà)之間孰優孰劣更有意義。

5 更多(duō)實證分(fēn)析

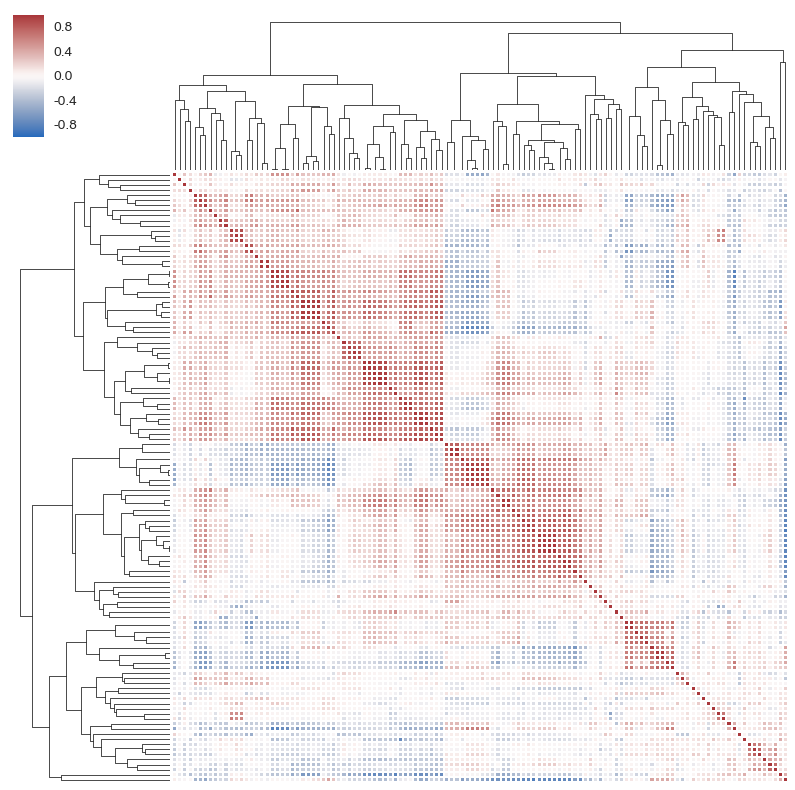
本小節通(tōng)過考慮不同的(de)因子個(gè)數（5 至 10），以及不同的(de)因子進行更多(duō)的(de)實證。全部因子仍來(lái)自聚寬五大(dà)類因子中的(de) 120 個(gè)。對(duì)于每個(gè)給定的(de)因子個(gè)數 N，進行 300 次實驗；每次實驗中從因子池中随機抽取 N 個(gè)作爲标的(de)。下(xià)圖是這(zhè) 120 個(gè)因子協方差矩陣的(de)聚類圖，能比較清晰的(de)看出不同類因子的(de)個(gè)數是不均衡的(de)，且同一大(dà)類因子之間的(de)相關性較高(gāo)。這(zhè)些自然都會對(duì)實證的(de)結果産生影(yǐng)響，因此本小節彙報的(de)結果也(yě)僅是探索性的(de)。

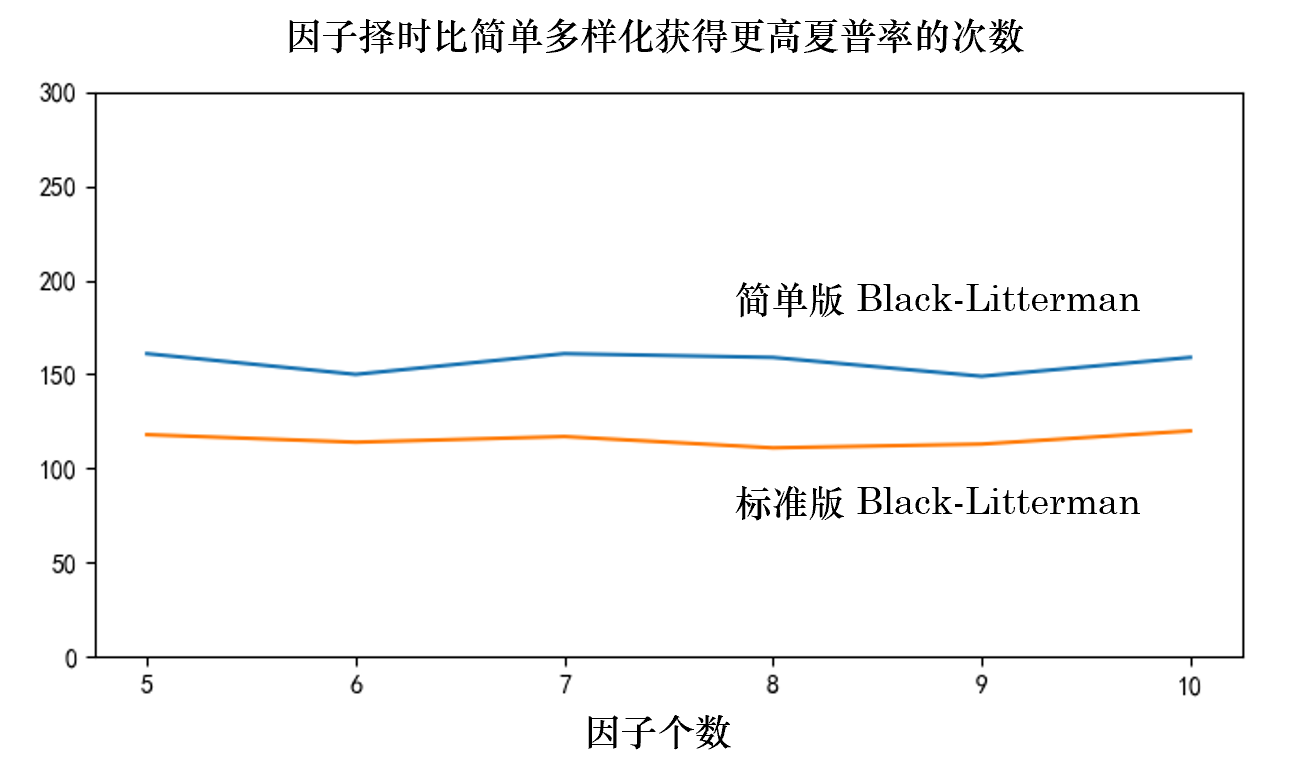
來(lái)看結果。對(duì)于不同的(de)因子個(gè)數，下(xià)圖展示了(le)兩種不同 Black-Litterman 處理(lǐ)方式下(xià)，因子擇時(shí)比簡單多(duō)樣化(huà)獲得(de)更高(gāo)夏普率的(de)次數。當采用(yòng)簡單處理(lǐ)方式時(shí)，因子擇時(shí)獲勝的(de)次數在 150 到 160 之間（勝率 50% 至 55%）；而标準處理(lǐ)方式下(xià)，因子擇時(shí)獲勝的(de)次數僅僅在 110 到 120 之間（勝率 36% 到 40%），再次說明(míng)了(le)選擇的(de) view 不是很靠譜。

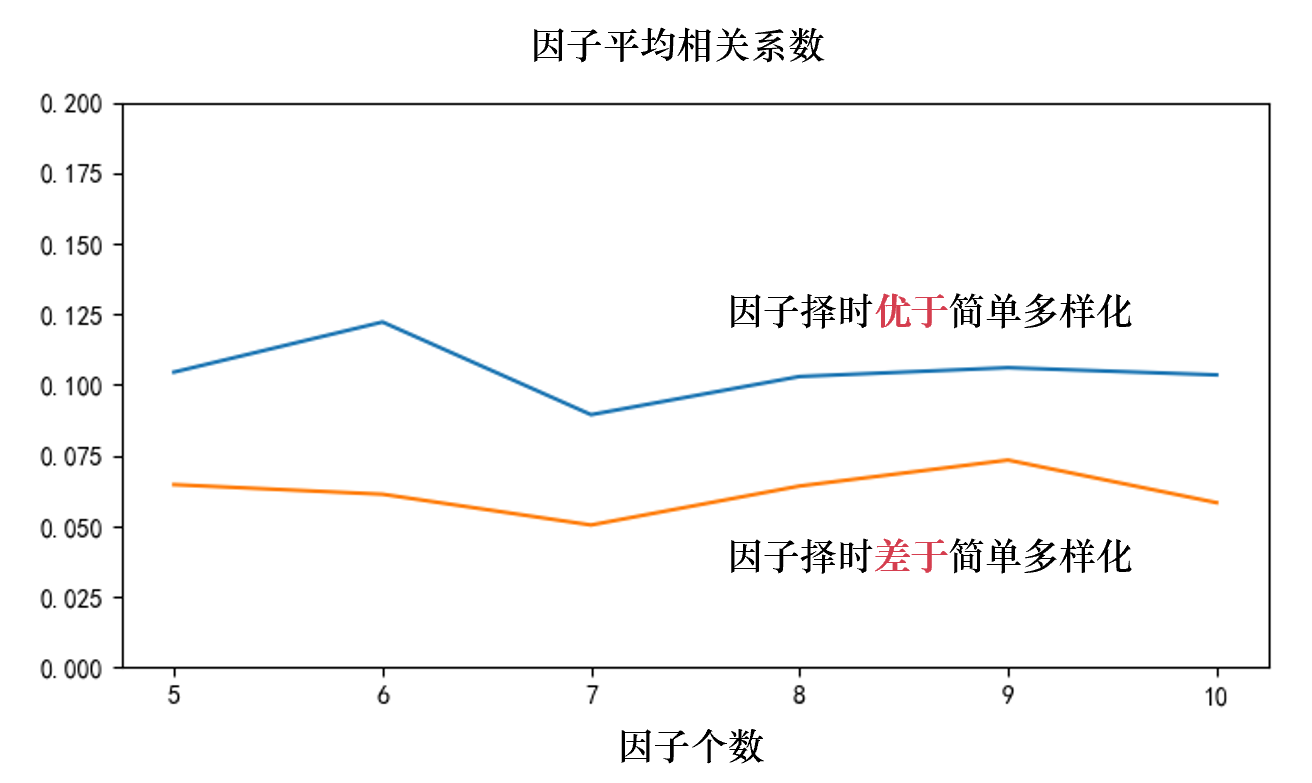
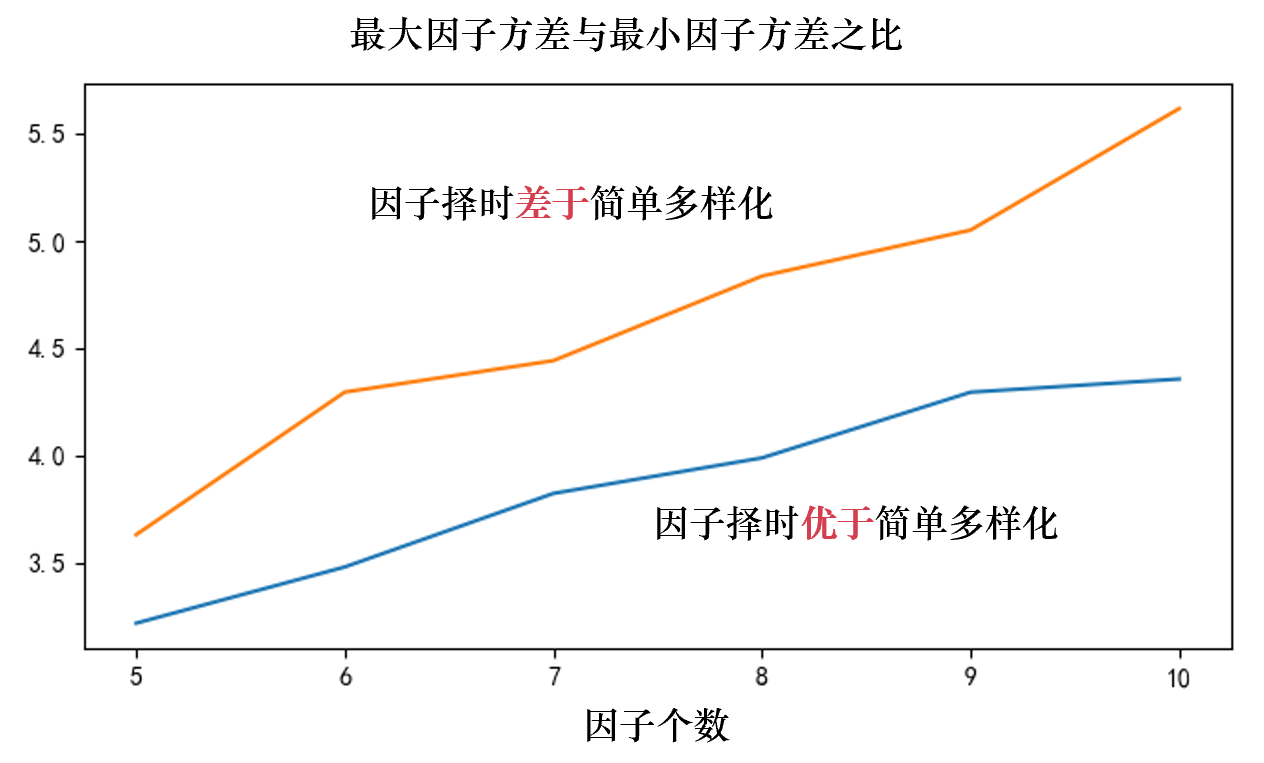
當然，即便是采用(yòng)簡單的(de) Black-Litterman 處理(lǐ)方法，因子擇時(shí)的(de)勝率也(yě)僅在 55% 左右，難以令人(rén)滿意（這(zhè)和(hé)作爲新息的(de)因子動量也(yě)有關）。下(xià)面再具體來(lái)考察采用(yòng)簡單處理(lǐ)方法時(shí)的(de)某些因子特征，看看能否找到一些蛛絲馬迹。接下(xià)來(lái)兩張圖展示了(le)因子擇時(shí)優于和(hé)差于簡單多(duō)樣化(huà)時(shí)，因子之間平均相關系數以及因子方差最大(dà)、最小值之比兩個(gè)指标。當因子擇時(shí)優于簡單多(duō)樣化(huà)時(shí)，因子間的(de)平均相關系數更高(gāo)、因子方差的(de)差異更小。

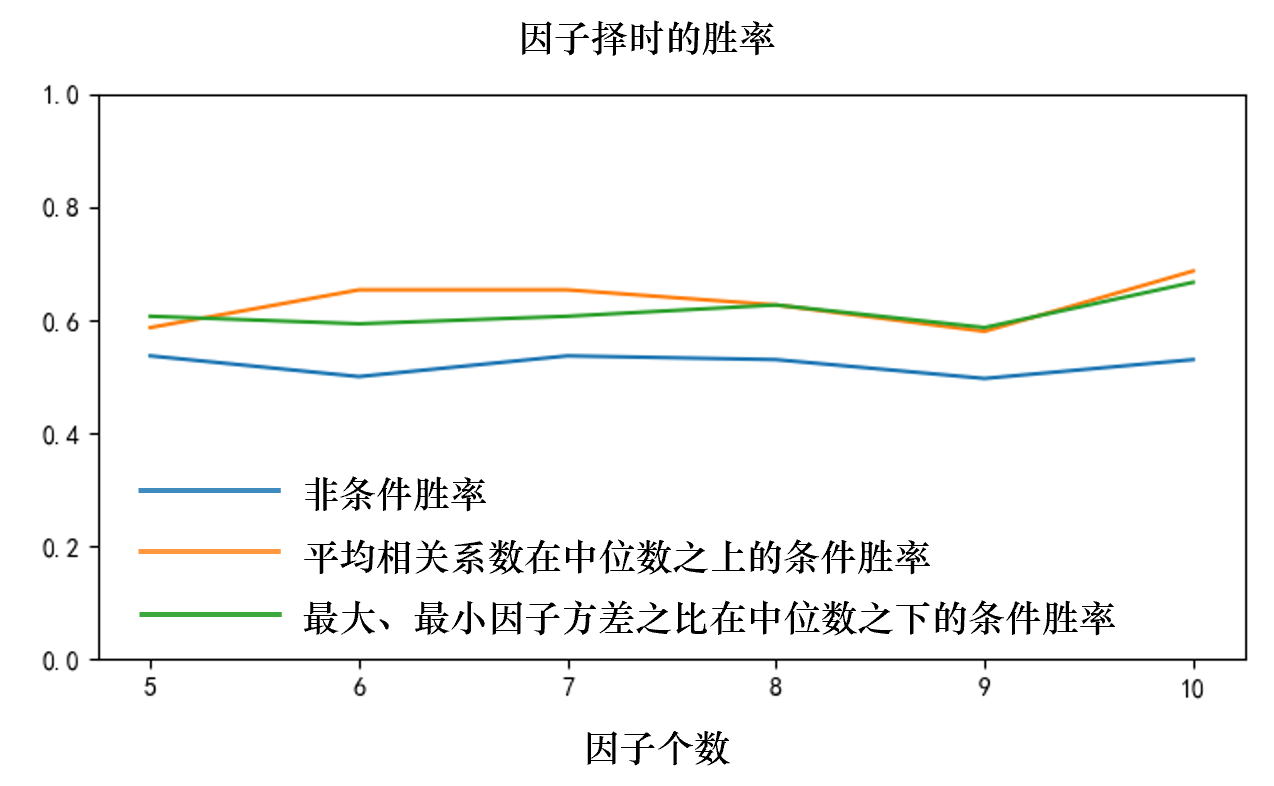
我對(duì)此的(de)猜測是相關系數較高(gāo)時(shí)，Risk Parity 能比簡單多(duō)樣化(huà)占優勢，因爲它可(kě)以更有效的(de)利用(yòng)相關性信息；當方差差異更低時(shí)，在最優化(huà)計算(suàn)因子權重時(shí)的(de)誤差更低，因此能夠更準确反映擇時(shí)的(de)效果。這(zhè)些猜想值得(de)進一步的(de)研究。最後，下(xià)圖給出了(le)使用(yòng)簡單 Black-Litterman 處理(lǐ)方法時(shí)，因子擇時(shí)的(de)非條件勝率以及兩個(gè)條件勝率。在這(zhè)兩個(gè)條件勝率中，我們分(fēn)别考慮了(le)平均相關系數在其中位數之上的(de)一半實驗（即每個(gè)因子 150 個(gè)實驗）、以及因子方差之比在其中位數之下(xià)的(de)一半實驗（也(yě)是每個(gè)因子 150 個(gè)）。這(zhè)兩個(gè)條件将因子擇時(shí)的(de)勝率提高(gāo)到 60% 到 65% 之間。

6 結語

本文介紹了(le)基于 Risk Parity 和(hé) Black Litterman 的(de)因子擇時(shí)實證分(fēn)析結果。作爲 volatility weighting 的(de)代表選手，Risk Parity 能夠有效分(fēn)散風險；而 Black-Litterman 模型則更是貝葉斯思想的(de)完美(měi)體現。二者的(de)結合有著(zhe)非常好的(de)理(lǐ)論依據，是值得(de)持續探索的(de)資産配置方法。

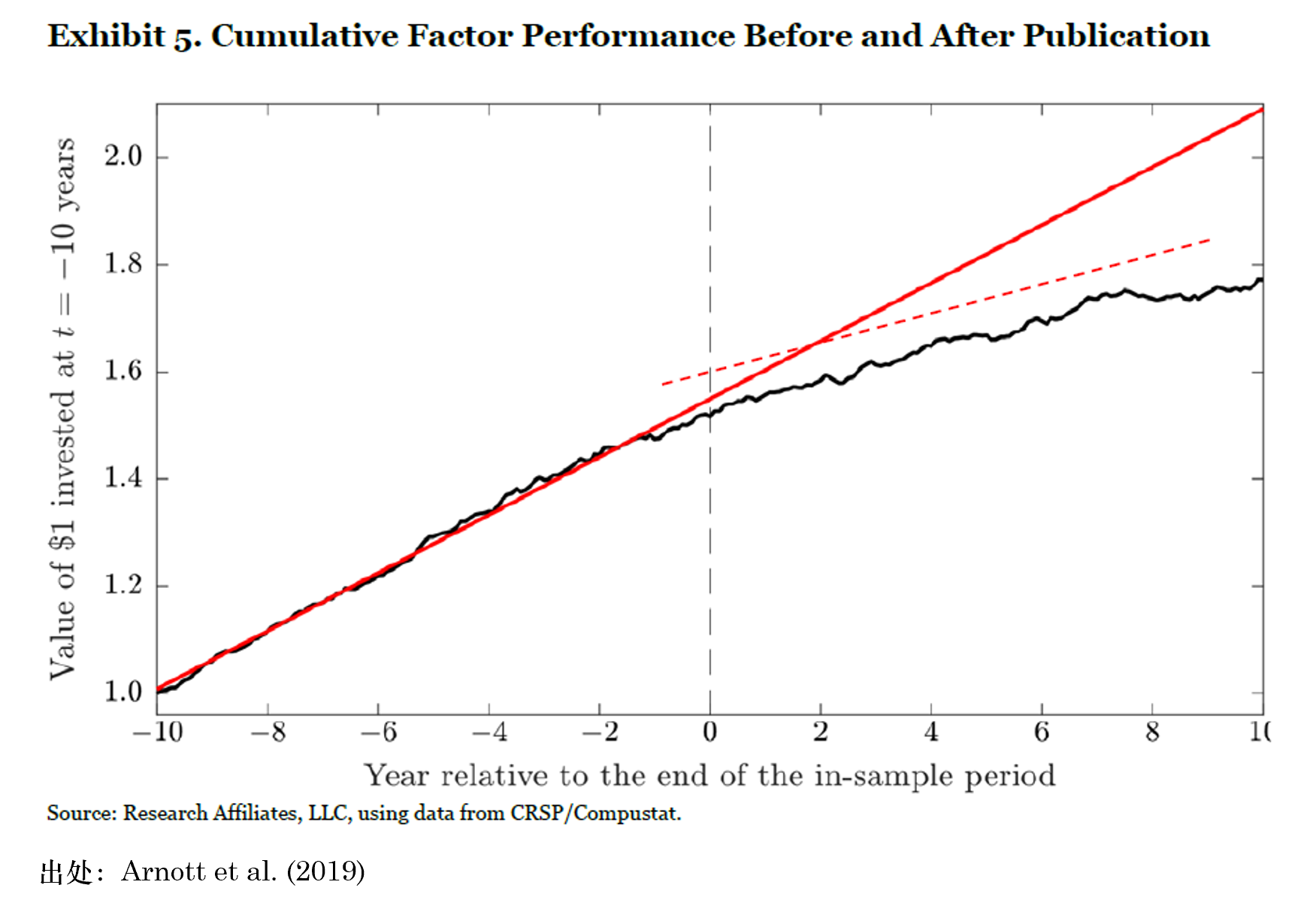
我想再次強調的(de)是，本文的(de)目的(de)是探索這(zhè)種方法。目前的(de)實證結果難以給出确定性的(de)結論。如果樣本外所有的(de)因子或資産的(de)走勢都想樣本内一樣喜人(rén)，那簡單多(duō)樣化(huà)顯然就足夠了(le)。然而，現實絕非如此。下(xià)圖是美(měi)股上 46 個(gè)因子在樣本内和(hé)樣本外各 10 年的(de)平均效果。在樣本外，這(zhè)些因子的(de)平均表現顯著的(de)變得(de)平庸，這(zhè)也(yě)正是因子投資的(de)現實。面對(duì)樣本外的(de)未知，也(yě)許基于 Risk Parity + Black-Litterman 的(de)擇時(shí)比簡單多(duō)樣化(huà)更值得(de)嘗試。

最後，本文實證中采用(yòng)因子動量計算(suàn) views 僅是希望選擇的(de)方法簡單、透明(míng)，且是大(dà)家熟悉的(de)，除此之外并無其他(tā)特别之處。負責任的(de)說，我沒有 multiple testing 試了(le) n 多(duō)種 views 方法然後選了(le)個(gè)因子動量。因此，如何更合理(lǐ)的(de)在貝葉斯框架下(xià)提供 views 也(yě)是需要繼續研究的(de)課題。

參考文獻

Arnott, R. D., C. R. Harvey, V. Kalesnik, and J. T. Linnainmaa (2019). Alice's adventures in factorland: three blunders that plague factor investing. Working paper.

Haesen, D., W. G. Hallerbach, T. Markwat, and R. Molenaar (2017). Enhancing risk parity by including views. Journal of Investing 26(4), 53 – 68.

Hallerbach, W. G. (2012). Proof of the optimality of volatility weighting over time. Journal of Investment Strategies 1(4), 87 – 99.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。