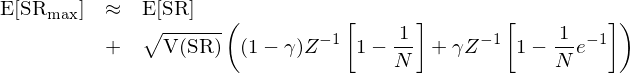機器學習(xí)時(shí)代的(de)回測規程

作者：石川

摘要：在回測中牢記并遵守這(zhè)些準則可(kě)以有效降低過拟合的(de)風險、避開噪音(yīn)、找到真正在樣本外可(kě)持續的(de)因果關系，獲取更高(gāo)的(de)收益。

0 引言

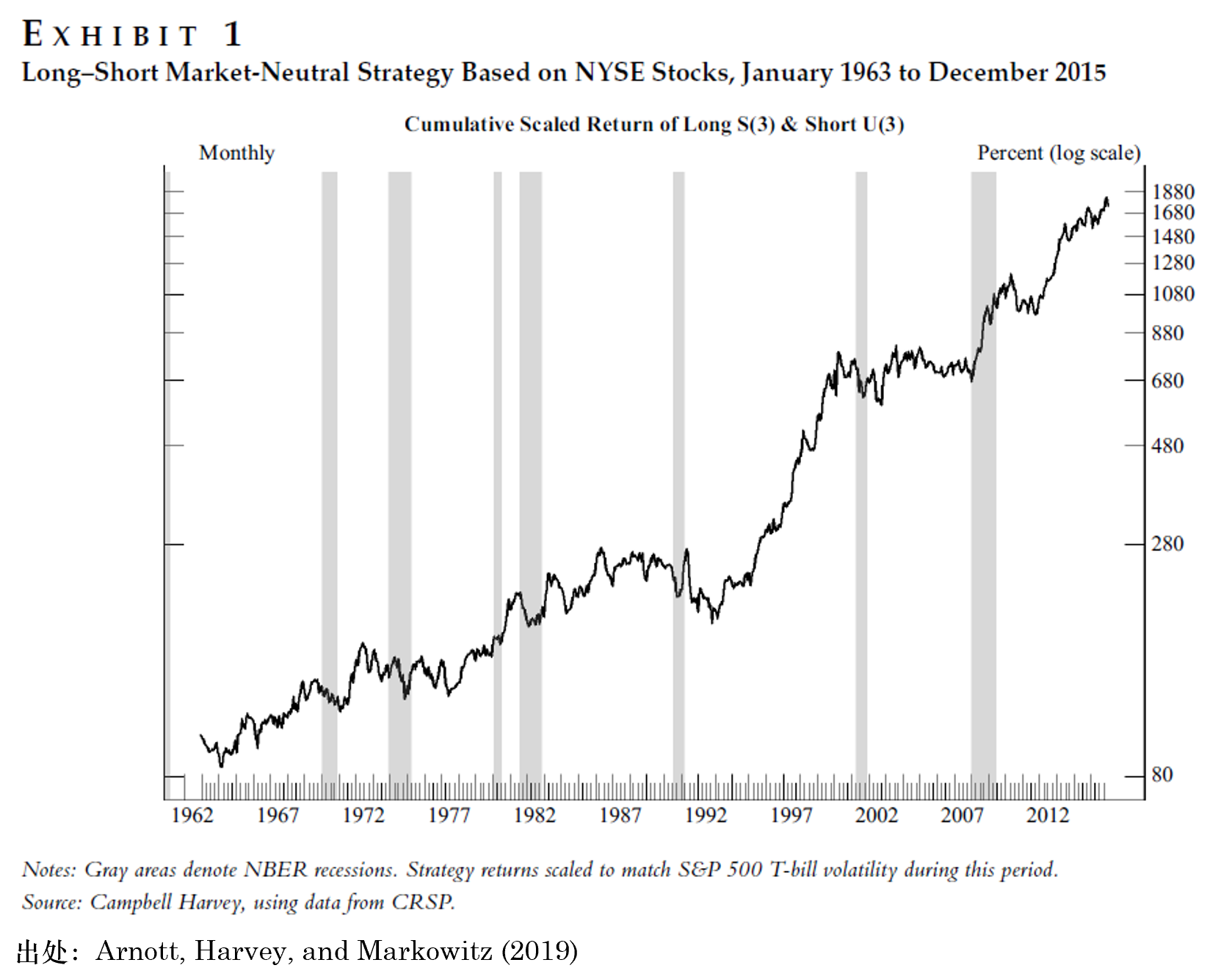
讓我們從下(xià)圖這(zhè)個(gè)令人(rén)欣喜的(de)回測（backtesting）說起。

上圖是某針對(duì)美(měi)股的(de)選股策略在長(cháng)達 50 年的(de)回測内的(de)淨值曲線。該策略采用(yòng)多(duō)空對(duì)沖、市值中性的(de)方法構建。該策略表現出了(le)五大(dà)優秀量化(huà)策略的(de)必要不充分(fēn)（呵呵）特征：

Too good to be true?

沒錯，它正是 data mining 的(de)産物(wù)。該因子的(de)構建完全沒有使用(yòng)任何基本面或者交易數據，而僅僅依賴美(měi)股上市公司股票(piào)代碼上的(de)字母。比如蘋果公司的(de)股票(piào)代碼是 AAPL，該代碼上的(de)第 1 至 4 位上的(de)字母分(fēn)别爲 A、A、P 以及 L。該因子的(de)構建方法是做(zuò)多(duō)股票(piào)代碼第三位字母爲 S 的(de)股票(piào)、做(zuò)空股票(piào)代碼第三位字母爲  U 的(de)股票(piào)（記爲 S(3) – U(3)）。在實驗中，考慮股票(piào)代碼的(de)前 3 位字母；考慮到全部可(kě)能的(de) 26 個(gè)字母，以及每個(gè)字母可(kě)以出現在多(duō)、空兩頭，因此實驗中有成千上萬種組合方式。而 S(3) – U(3) 這(zhè)種組合正是從這(zhè)些組合中脫穎而出的(de)、具備了(le)上述五大(dà)優秀特征的(de)、僅僅來(lái)自 data mining 的(de)虛假策略。上面這(zhè)個(gè)策略是靠蠻力（brute force）找到的(de)，并不能說是機器學習(xí)（Machine Learning）的(de)産物(wù)。機器學習(xí)會進行仔細的(de)交叉驗證（cross-validation）以确保我們在訓練集和(hé)測試集上看到相似的(de)結果。不幸的(de)是，上述策略在整個(gè)回測期内的(de)穩定表現大(dà)概率會讓它通(tōng)過交叉驗證。這(zhè)背後的(de)原因是股票(piào)市場(chǎng)的(de)數據容易出現路徑依賴，造成訓練集和(hé)測試集之間并不獨立。

這(zhè)個(gè)例子說明(míng)，量化(huà)投資的(de)小夥伴在回測基于機器學習(xí)的(de)策略時(shí)将面臨很大(dà)的(de)挑戰。回測的(de)目的(de)是去僞存真，排除噪音(yīn)、發現預測指标和(hé)資産收益率之間真正的(de)因果關系，從而在樣本外的(de)實盤交易中獲得(de)收益。如果回測不靠譜、落入各種陷阱，那麽實盤的(de)結果則可(kě)想而知。這(zhè)個(gè)問題在機器學習(xí)如此普及的(de)今天顯得(de)更加嚴重。爲了(le)幫助量化(huà)交易者更好的(de)杜絕樣本内的(de)過拟合，提高(gāo)發現真正有效策略的(de)概率，三位大(dà)咖站了(le)出來(lái)：來(lái)自 Research Affiliates 的(de) Robert Arnott，杜克大(dà)學教授、前 AFA 主席 Campbell Harvey，以及諾貝爾經濟學獎獲得(de)者 Harry Markowitz 在 IPR Journals 的(de)最新成員(yuán) Journal of Financial Data Science 的(de)處女(nǚ)刊上發表了(le)一篇題爲 A Backtesting Protocol in the Era of Machine Learning 的(de)文章(zhāng)（Arnott, Harvey, and Markowitz 2019）。

本文中我用(yòng)“規程”來(lái)對(duì)應 Protocol 一詞，它也(yě)可(kě)以被譯作“協議(yì)”或者“清單”，其目的(de)就是通(tōng)過逐步遵循這(zhè)些準則來(lái)減少樣本内過拟合的(de)可(kě)能性。這(zhè)個(gè) protocol 之于回測可(kě)靠性的(de)作用(yòng)就好比飛(fēi)行員(yuán)的(de) checklist 之于飛(fēi)行安全的(de)作用(yòng)。Arnott, Harvey, and Markowitz (2019) 一文提出的(de) protocol 一共包括七部分(fēn)，它們是：

它們構成了(le)一個(gè)完整且可(kě)操作的(de)體系，能夠幫助我們更好的(de)規避樣本内的(de)虛假信号、找出能在樣本外更有效的(de)交易策略。前文《所有樣本數據都是樣本内》曾論述過 protocol 中的(de)第四部分(fēn)。不過，鑒于它的(de)系統性，我想用(yòng)今天這(zhè)篇文章(zhāng)把這(zhè)七個(gè)角度全部梳理(lǐ)一下(xià)。以下(xià)行文并不會逐字逐句的(de)轉述 Arnott, Harvey, and Markowitz (2019) 提出的(de)每一個(gè) bullet point，而是會結合我有限的(de)經驗和(hé)粗淺的(de)認識解讀我認爲最重要的(de)一些内容。浏覽本文并不能 100% 代替閱讀原作，因此強烈建議(yì)感興趣的(de)小夥伴找來(lái) Arnott, Harvey, and Markowitz (2019) 看一看。此外，由于公衆号之前在倡導科學回測和(hé)防止過拟合方面也(yě)做(zuò)過許多(duō)努力，很多(duō)文章(zhāng)都能很好的(de) fit 進這(zhè)個(gè) protocol，所以會在行文中把它們串聯起來(lái)。下(xià)文第 1 到第 7 節将分(fēn)别論述這(zhè)個(gè) protocol 的(de)七個(gè)方面。第 8 節總結全文。

1 研究動機

回測規程的(de)第一個(gè)方面是研究動機（Research Motivation）。Harvey 教授直言，金融領域的(de)數據樣本太少了(le)（也(yě)許超高(gāo)頻(pín)除外）。以美(měi)股爲例，現代金融時(shí)代的(de)股票(piào)月(yuè)頻(pín)數據大(dà)概隻有 700 期（相當于 60 年），這(zhè)對(duì)于機器學習(xí)應用(yòng)來(lái)說太少了(le)（回想一下(xià) A 股，通(tōng)常單因子評測的(de)回測期隻有區(qū)區(qū) 10 年，真是太短了(le)）。因此，這(zhè)個(gè) protocol 中第一也(yě)是最重要的(de)一點就是 a clear economic foundation for any model —— 任何策略都應該有一個(gè)理(lǐ)論先驗。注意，是先驗，而不是看到數之後再“真香”編故事。

Chordia, Goyal, and Saretto (2017) 使用(yòng)基本面指标的(de)不同組合方法構建了(le)兩百萬個(gè)針對(duì)美(měi)股的(de)因子策略。在實驗設計中，他(tā)們對(duì) data mining 進行了(le)必要的(de)懲罰，并最終找到 17 個(gè)在統計上和(hé)經濟上都顯著的(de)因子。其中一個(gè)因子的(de)構建方法爲：分(fēn)子是 long-term debt issuance 和(hé) preferred stock redeemable 之差；分(fēn)母是 minimum rental commitments four years into the future。這(zhè)個(gè)因子使用(yòng)了(le)三個(gè)财務指标，但是該組合卻毫無業務含義。而上述其他(tā) 16 個(gè)“顯著”的(de)因子都具有類似的(de)結構，它們都是 data mining 的(de)結果。在現實中，人(rén)們往往站在“任何策略都應該有一個(gè)理(lǐ)論先驗”的(de)對(duì)立面上，即先看數據再找理(lǐ)由。比如對(duì)于前面那個(gè) S(3) – U(3) 的(de)例子。它的(de)那些優秀特征會讓人(rén)去尋找虛假的(de)理(lǐ)論依據來(lái)說服自己。當一個(gè)人(rén)能夠爲 S(3) – U(3) 找到理(lǐ)由，那麽如果回測的(de)結果顯示相反的(de)結果，即 U(3) – S(3)，相信 TA 也(yě)能夠找到理(lǐ)由。

Any suspicion that the hypothesis was developed after looking at the data is an obvious red flag.

2 多(duō)重假設檢驗

Protocol 的(de)第二方面是當心多(duō)重假設檢驗（Multiple Testing and Statistical Methods）。公衆号的(de)小夥伴對(duì)它一定不陌生，之前的(de)文章(zhāng)《出色不如走運？》、《出色不如走運 (II)？》、《出色不如走運 (III)？》談的(de)全是它。多(duō)重假設檢驗指的(de)是：當我們測試一個(gè)策略的(de)許多(duō)組參數，或者很多(duō)選個(gè)因子時(shí)，僅僅依靠運氣，這(zhè)些參數或者因子中效果最好的(de)那個(gè)就能在樣本内獲得(de)很高(gāo)的(de)夏普率（這(zhè)也(yě)被稱作 inflated Sharpe Ratio）。在回測時(shí)必須時(shí)刻考慮多(duō)重假設檢驗的(de)影(yǐng)響。用(yòng)白話(huà)的(de)理(lǐ)解就是：如果我以某個(gè)金融學或經濟學原理(lǐ)爲先驗，構建了(le)一個(gè)因子并測試有效，那麽它大(dà)概是真有效；然而，如果我兩眼一抹黑(hēi)試了(le) 100 個(gè)因子，然後隻挑出了(le)最好的(de)那一個(gè)，那麽這(zhè)個(gè)因子很可(kě)能隻是個(gè) lucky factor。

Bailey and Lopez de Prado (2012, 2014) 專門就 inflated Sharpe Ratio 進行了(le)探討(tǎo)。他(tā)們假設不同參數的(de)策略的(de)夏普率滿足均值爲 E[SR]、方差爲 V(SR) 的(de)正态分(fēn)布。在上述假設下(xià)，N 組不同參數中樣本内最大(dà)的(de)夏普率的(de)期望滿足（式中 γ 是歐拉-馬斯刻若尼常數）：

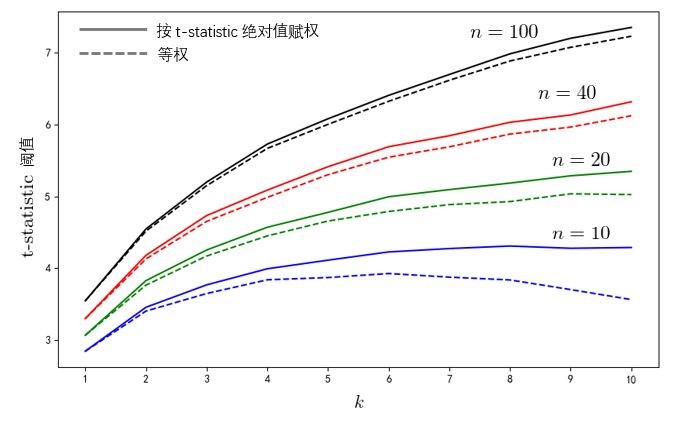
該關系式表明(míng)，樣本内的(de)最大(dà)夏普率随 N 增大(dà)和(hé) V(SR) 增大(dà)。假設 V(SR) = 1，則我們隻需要測試 100 組設定，樣本内的(de)虛高(gāo)夏普率就高(gāo)達 2.5，盡管它對(duì)應的(de) null hypothesis 是該策略真實夏普率爲 0。這(zhè)就是不考慮多(duō)重假設檢驗的(de)危害。在《出色不如走運 (III)?》一文中，我們根據 Novy-Marx (2015) 的(de)方法、使用(yòng)中證 500 的(de)成分(fēn)股做(zuò)了(le)随機因子的(de)實證。在實證中，純随機的(de)産生對(duì)收益率毫無預測性的(de) n 個(gè)因子，然後根據它們的(de)表現選出其中最好的(de) k 個(gè)，再把和(hé) k 個(gè)因子配置在一起，考察它們在樣本内上述 k 個(gè)因子構成的(de)投資組合收益率的(de) t-statistic 到底能有多(duō)高(gāo)（由于這(zhè)些随機因子毫無預測性，因此 null hypothesis 是它們的(de)預期收益率爲零；評價标準爲投資組合收益率 t-statistic 經驗分(fēn)布的(de) 95% 分(fēn)位數阈值）。

下(xià)圖給出了(le)實證結果。從中不難觀察到以下(xià)三點：（1）随著(zhe) n 和(hé) k 的(de)增加，對(duì)于按照(zhào)随機因子 t-statistic 絕對(duì)值賦權配置的(de)策略，它們的(de) t-statistic 阈值遞增；（2）随著(zhe) n 的(de)增加，等權配置和(hé)按因子樣本内表現配置的(de)效果越來(lái)越接近；（3）對(duì)于等權配置因子的(de)情況，能夠觀察到策略的(de)效果并不随 k 遞增；這(zhè)是因爲當 k 逐漸增大(dà)時(shí)，使用(yòng)更多(duō)的(de)因子可(kě)以降低組合的(de)波動率、提升 t-statistic 的(de)阈值；一旦 k 超過最優值，越來(lái)越多(duō)排名靠後的(de)因子被選入，降低組合的(de)收益率以及 t-statistic 阈值。

爲了(le)在實證研究中發現樣本内更好的(de)策略或者更顯著的(de)因子 —— 無論是爲了(le)討(tǎo)好基金經理(lǐ)還(hái)是爲了(le)在頂刊上發文 —— 多(duō)重假設檢驗的(de)不正之風早已席卷了(le)學術界和(hé)業界。Harvey, Liu, and Zhu (2016) 研究了(le)學術界發表的(de) 316 個(gè)選股因子。他(tā)們通(tōng)過考慮不同因子之間相關性提出了(le)一個(gè)全新檢驗框架。該方法可(kě)以排除 multiple testing 的(de)影(yǐng)響。該研究表明(míng)，隻有在 single testing 中 t-statistic 超過 3.0（而非人(rén)們傳統認爲的(de) 5% 的(de)顯著性水(shuǐ)平對(duì)應的(de) 2.0）的(de)因子才有可(kě)能在排除了(le) multiple testing 的(de)影(yǐng)響之後，而非來(lái)自運氣。不過，Harvey 同時(shí)也(yě)指出，3.0 其實都是非常保守的(de)。我們自己在回測時(shí)應時(shí)刻謹記 multiple testing 的(de)影(yǐng)響；此外，在學習(xí)别人(rén)的(de)發現時(shí)也(yě)要保持著(zhe)一顆懷疑之心，因爲沒有多(duō)少人(rén)告訴我們，在 TA 提出的(de)這(zhè)個(gè)樣本内顯著因子之前有過多(duō)少次失敗的(de)嘗試。

3 樣本選擇和(hé)數據

Protocol 的(de)第三部分(fēn)是樣本選擇和(hé)數據（Sample Choice and Data）。它的(de)核心要素包括：（1）回測前就要确定回測區(qū)間，而非事後調整；（2）确保數據質量；（3）小心處理(lǐ)異常值（outliers） —— 不要凡事都想當然；（4）認真記錄進行的(de)數據變形處理(lǐ)。所有的(de)這(zhè)些努力其實都是爲了(le)避免 p-hacking。Harvey 教授在介紹 Arnott, Harvey, and Markowitz (2019) 這(zhè)篇文章(zhāng)的(de)短片中講了(le)一個(gè)故事。一個(gè)量化(huà)研究員(yuán)給他(tā)展示了(le)一個(gè)股票(piào)策略，該策略在回測期内的(de)表現非常好；隻不過該回測有一個(gè)緻命的(de)問題：它的(de)回測窗(chuāng)口不包含 2008 年的(de)金融危機。當 Harvey 教授問他(tā)爲什(shén)麽排除這(zhè)段時(shí)期，得(de)到了(le)令人(rén)無語的(de)答(dá)複：“因爲策略在這(zhè)段時(shí)間内失效了(le)”。

這(zhè)就是先看結果再調整回測區(qū)間，妥妥的(de) p-hacking 反例。法國哲學家孔德将科學分(fēn)成不同的(de)等級（Comte 1856）。像數學、物(wù)理(lǐ)這(zhè)類“硬科學”位于等級的(de)上方，而社會學、經濟學這(zhè)些“軟科學”位于等級的(de)下(xià)方。“硬”和(hé)“軟”本身并無“好”與“壞”之分(fēn)。硬科學可(kě)以從數據可(kě)以直接得(de)到結論、無需任何人(rén)工解釋，且結論是高(gāo)度可(kě)歸納的(de)。比如數學上的(de)四色問題，一旦證明(míng)成立那就是成立；又如物(wù)理(lǐ)上的(de)引力波，一旦發現那就是說明(míng)它的(de)存在，這(zhè)些都是确切的(de)。反觀軟科學，研究成果依賴于提出怎樣的(de)假設，如何處理(lǐ)數據，以及如何分(fēn)析、解釋結果，總之“事在人(rén)爲”。金融學是軟科學，很多(duō)實證分(fēn)析結果都會因人(rén)而異。

比如在股票(piào)研究中“使用(yòng)過去 50 年的(de)數據還(hái)是過去 30 年的(de)數據？”“使用(yòng)美(měi)股還(hái)是其他(tā)國家的(de)股票(piào)？”“使用(yòng)日收益率還(hái)是周收益率？”“使用(yòng)百分(fēn)比收益率還(hái)是對(duì)數收益率？”“是否以及如何剔除異常值？”“使用(yòng) OLS 還(hái)是 GLS？”……這(zhè)些看似自然的(de)選擇背後其實都以追求樣本内更顯著的(de) p-value 爲動機，一切阻礙獲得(de)超低 p-value 的(de)數據都會被巧妙的(de)避開。這(zhè)種爲了(le)獲得(de)超低 p-value 而在研究中刻意選取的(de)數據處理(lǐ)方法就是 p-hacking。

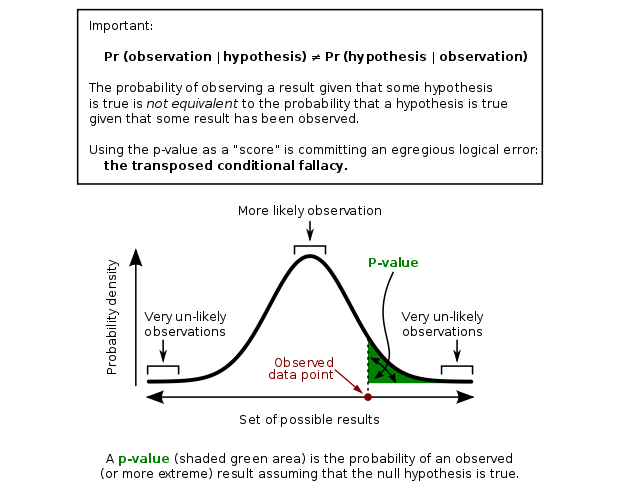
人(rén)們對(duì)于 p-hacking 的(de)狂熱(rè)源于對(duì) p-value 的(de)錯誤解讀。在統計學中，如果 H0 和(hé) H1 分(fēn)别表示 null hypothesis 和(hé) alternative hypothesis，則 p-value = prob(D|H0)，即在 H0 成立下(xià)觀測到數據 D 的(de)概率。從該定義出發，p-value 不代表原假設或者備擇假設是否爲真實的(de)，即 p-value ≠ prob(H0|D) 以及 p-value ≠ prob(H1|D)。

在檢驗一個(gè)策略或者因子是否有顯著收益時(shí)，我們需要的(de)是 prob(H0|D)，即在觀察到 D 的(de)條件下(xià)，原假設爲真的(de)概率是多(duō)少。這(zhè)個(gè)問題僅依靠 p-value 自身無法回答(dá)的(de)。爲此，Harvey (2017) 提出了(le)一個(gè)基于貝葉斯的(de)框架，它可(kě)以正确求解我們關注的(de)問題。關于 p-hacking 和(hé)上述貝葉斯框架，《在追逐 p-value 的(de)道路上狂奔，卻在科學的(de)道路上漸行漸遠(yuǎn)》一文曾有過非常詳細的(de)論述，在此不再贅述。

4 交叉驗證

回測規程的(de)第四部分(fēn)是交叉驗證（Cross-Validation），這(zhè)部分(fēn)包括以下(xià)兩個(gè)要素：

前文《所有數據都是樣本内》曾對(duì)上述兩點分(fēn)别做(zuò)過詳細闡述，本文就不在重複之前的(de)内容。這(zhè)一條想要強調的(de)是：由于曆史數據都是已經發生過的(de)，它們都是樣本内數據，因此必須小心解讀交叉驗證的(de)結果，即便通(tōng)過了(le)交叉驗證，也(yě)不能無腦(nǎo)的(de)相信完全排除了(le)過拟合的(de)問題。關于更合理(lǐ)的(de)使用(yòng)交叉驗證，Bailey et al. (2017) 的(de)研究成果值得(de)借鑒。他(tā)們提出了(le)一個(gè) Combinatorially-Symmetric Cross-Validation（組合對(duì)稱交叉驗證，簡稱 CSCV）方法，它可(kě)以定量的(de)計算(suàn)樣本内過拟合的(de)概率。《美(měi)麗的(de)回測 —— 教你定量計算(suàn)過拟合概率》一文詳細的(de)介紹了(le)該方法。它的(de)優勢在于：

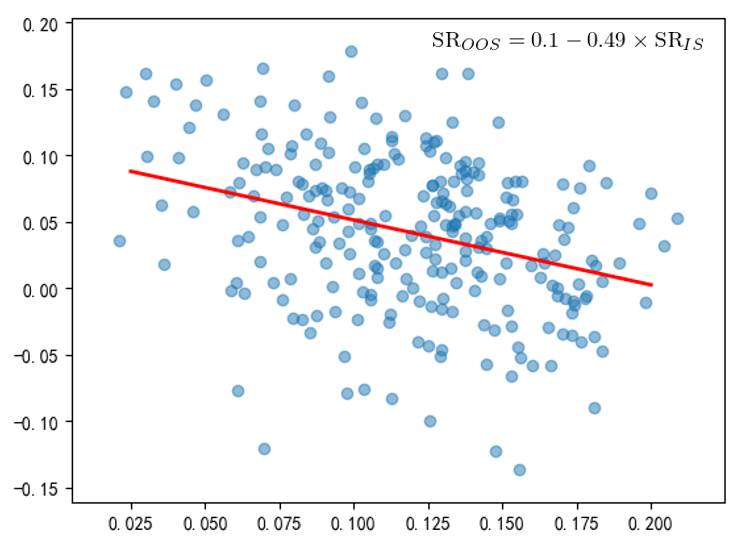
舉個(gè)例子。按照(zhào) CSCV 方法，下(xià)圖描述了(le)某趨勢追蹤策略在不同參數下(xià)，其樣本内夏普率（SR_IS）和(hé)同參數在樣本外夏普率（SR_OOS）的(de)負相關關系，意味著(zhe)驗本内效果越好對(duì)應著(zhe)樣本外表現越差。該策略的(de)樣本内過拟合概率高(gāo)達 0.572。一個(gè)真正有效的(de)策略在樣本内的(de)過拟合概率不應如此之高(gāo)。

無論從獨立性還(hái)是可(kě)交易特征而言，交易數據其實都十分(fēn)匮乏。它們對(duì)傳統的(de)交叉驗證造成了(le)極大(dà)的(de)挑戰，在使用(yòng)機器學習(xí)時(shí)應牢記這(zhè)一點，理(lǐ)性看待交叉驗證結果。

5 模型動力學

模型動力學（Model Dynamics）是回測規程的(de)第五部分(fēn)，它關注的(de)是量化(huà)策略在樣本外的(de)表現逐漸變差的(de)問題。而這(zhè)背後可(kě)能存在兩個(gè)原因：（1）市場(chǎng)結構發生變化(huà)導緻策略失效，比如越來(lái)越多(duō)的(de)人(rén)開始使用(yòng)某個(gè)策略或者因子，使得(de)它變得(de)擁擠。（2）策略使用(yòng)者自身的(de)行爲偏差導緻一個(gè)好模型最終淪爲一個(gè)失效模型。我在之前的(de)文章(zhāng)中多(duō)次表達過一個(gè)觀點：任何策略能賺錢都是利用(yòng)了(le)市場(chǎng)的(de)某種非有效性；一旦使用(yòng)該策略的(de)人(rén)越來(lái)越多(duō)，市場(chǎng)在這(zhè)方面就變得(de)更加有效，從而削弱策略的(de)盈利能力。

在技術分(fēn)析領域，上述觀點的(de)最好例證之一是布林(lín)帶（Bollinger bands）。毫無疑問，布林(lín)帶是幾十年前最盛行、最管用(yòng)的(de)技術分(fēn)析策略之一。然而，人(rén)們越來(lái)越發現該方法掙錢的(de)能力越來(lái)越差。對(duì)此，Fang, Jacobsen, and Qin (2017) 針對(duì)全球十幾個(gè)主要市場(chǎng)進行了(le)實證分(fēn)析。他(tā)們的(de)研究發現，1983 和(hé) 2001 這(zhè)兩個(gè)重要時(shí)間節點對(duì)于布林(lín)帶的(de)效果影(yǐng)響巨大(dà)。1983 年，John Bollinger首次在電視廣播中介紹了(le)布林(lín)帶，使得(de)這(zhè)個(gè)之前神秘的(de)方法開始走進大(dà)衆視野。而 2001 年，John Bollinger 更是發表了(le)Bollinger on Bollinger Bands 這(zhè)本紅極一時(shí)的(de)技術流聖經；在随後的(de) 4 年内，這(zhè)本書(shū)被翻譯成其他(tā) 12 種語言在全世界範圍内迅速傳播，這(zhè)使得(de)布林(lín)帶一下(xià)變得(de)家喻戶曉。Fang, Jacobsen, and Qin (2017) 發現，布林(lín)帶的(de)流行和(hé)普及（特别是 2001 年之後）直接造成了(le)該策略的(de)失效。

這(zhè)樣的(de)例子在股票(piào)因子投資中也(yě)不勝枚舉。一個(gè)新因子被提出後，随著(zhe)越來(lái)越多(duō)人(rén)使用(yòng)，它在 post-publication 樣本外的(de)效果勢必會打折扣。McLean and Pontiff (2016) 研究了(le) 97 個(gè)因子在被發表之後的(de)表現，發現因子的(de)收益率比論文中的(de) in-sample 降低 50% 以上。有時(shí)，策略并沒有變得(de)擁擠，但它在樣本外還(hái)是持續變差。這(zhè)背後的(de)另一個(gè)原因是使用(yòng)者的(de)非理(lǐ)性行爲偏差。任何一個(gè)策略或者交易系統，都是基于對(duì)市場(chǎng)的(de)某個(gè)假設。然而市場(chǎng)充滿著(zhe)不确定性，因此它必然會在一些時(shí)候背離這(zhè)個(gè)假設，這(zhè)時(shí)該交易系統就會出現虧損。一個(gè)優秀的(de)交易系統是一個(gè)長(cháng)期來(lái)看能夠盈利的(de)系統，而非一個(gè)能夠每筆交易都賺錢的(de)系統。

随著(zhe)交易的(de)進行，由于小數定律造成的(de)偏誤，很多(duō)人(rén)在幾次虧損後就開始“懷疑人(rén)生”了(le)，認爲“this time is different”、開始要對(duì)策略動刀(dāo)子。這(zhè)種想法非常危險。如果你真的(de)這(zhè)麽做(zuò)的(de)了(le)，爲了(le)每一筆的(de)虧損都對(duì)你的(de)系統進行了(le)修補，便走上了(le)“處處精準過拟合”的(de)快(kuài)車道，策略最終将會對(duì)市場(chǎng)未來(lái)的(de)變化(huà)無能爲力。

Most traders take a good system and destroy it by trying to make it into a perfect system. –– Robert Prechter

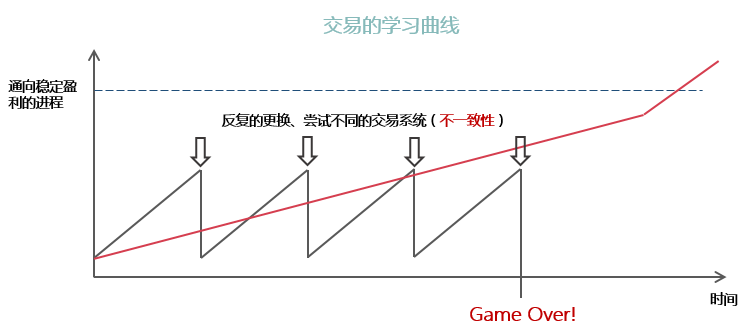
改造一個(gè)長(cháng)期來(lái)看可(kě)以賺錢的(de)優秀系統必須要非常小心。對(duì)哪怕是一個(gè)參數的(de)哪怕是一丁點的(de)調節都會改變該系統的(de)效果。這(zhè)麽做(zuò)是以改動後的(de)系統對(duì)最新的(de)交易數據表現更佳爲前提；但是如果不能證明(míng)它在未來(lái)的(de)樣本外更有效，那麽如此“改進”仍然是徒勞的(de)。量化(huà)投資背後的(de)核心是單次優勢 + 大(dà)數定律。這(zhè)二者中大(dà)數定律又更加重要，它要求我們在交易中盡一切努力做(zuò)到一緻性。一般交易者的(de)學習(xí)曲線如下(xià)面圖中的(de)黑(hēi)色曲線：無法做(zuò)到嚴格遵循一個(gè)交易系統，總是帶著(zhe)個(gè)人(rén)情感進行交易，将自己行爲帶來(lái)的(de)不确定性錯誤地強加于系統的(de)表現之上。這(zhè)些交易者無法持之以恒，三天兩頭更換系統，最終輸光(guāng)本金。與之相反的(de)，一個(gè)優秀的(de)交易者會專注于一緻性，這(zhè)會讓他(tā)在通(tōng)往盈利的(de)進程中越走越遠(yuǎn)，最終到達勝利的(de)彼岸。

6 模型複雜(zá)度

回測規程的(de)第六部分(fēn)是模型複雜(zá)度（Model Complexity），主張我們應該追求策略的(de)而簡單性和(hé)可(kě)解釋性。

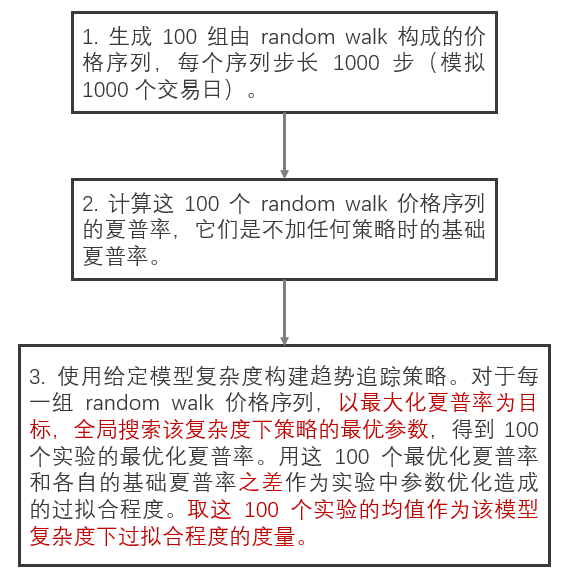
我們大(dà)概都有下(xià)面這(zhè)樣的(de)經驗：一個(gè)策略的(de)夏普率不夠亮眼，那麽可(kě)以通(tōng)過加入止盈、止損，中性化(huà)處理(lǐ)、甚至是對(duì)投資标的(de)進行篩選來(lái)進一步提高(gāo)其在樣本内的(de)表現。此外，對(duì)上面的(de)每一個(gè)處理(lǐ)方法，我們似乎都能找到合理(lǐ)的(de)解釋和(hé)來(lái)自其他(tā)文獻的(de)理(lǐ)論和(hé)實證支持。在确認偏誤下(xià)，我們非常願意相信這(zhè)些處理(lǐ)都是合理(lǐ)的(de)、并沒有引入過拟合。任何通(tōng)過增加參數維度來(lái)提高(gāo)樣本内的(de)表現 —— 無論這(zhè)些理(lǐ)由聽(tīng)上去多(duō)麽合理(lǐ) —— 都實打實的(de)提高(gāo)了(le)模型的(de)複雜(zá)度；更高(gāo)的(de)模型複雜(zá)度則更容易出現過拟合。前文《模型複雜(zá)度随想》曾對(duì)上述觀點做(zuò)過一個(gè)簡單實驗。該文提出了(le)如下(xià)圖所示的(de)流程來(lái)定量計算(suàn)模型複雜(zá)度造成的(de)過拟合程度。

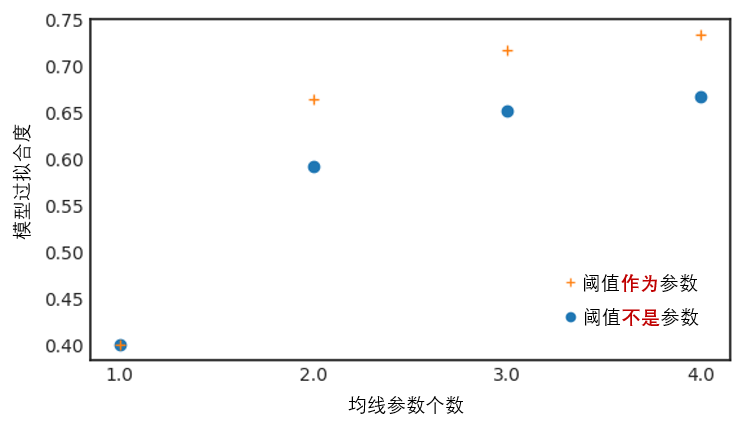
考慮一個(gè)基于均線多(duō)頭排序的(de)簡單多(duō)頭趨勢追蹤策略。模型複雜(zá)度的(de)兩個(gè)維度是：（1）均線多(duō)頭排序中用(yòng)到的(de)不同周期均線的(de)個(gè)數；（2）這(zhè)些均線秩相關系數的(de)阈值（用(yòng)來(lái)決定是否開倉、空倉）。使用(yòng)純随機遊走産生的(de)假想資産價格曲線，按不同複雜(zá)度構建趨勢追蹤策略。模型的(de)過拟合度和(hé)複雜(zá)度之間的(de)關系如下(xià)圖所示，說明(míng)模型過拟合度随模型複雜(zá)度遞增。

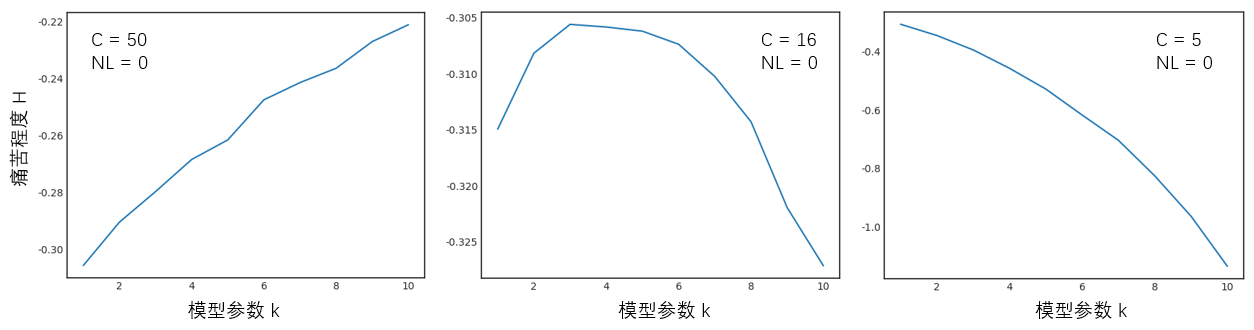
在第六方面，Arnott, Harvey, and Markowitz (2019) 倡導的(de)第二點是追求可(kě)解釋的(de)機器學習(xí)（seek interpretable machine learning）。量化(huà)策略，尤其是使用(yòng)了(le)機器學習(xí)算(suàn)法的(de)量化(huà)策略不應該是黑(hēi)箱。任何使用(yòng)者都應該了(le)解這(zhè)個(gè)算(suàn)法到底幹了(le)什(shén)麽。最近幾年，計算(suàn)機領域的(de)一個(gè)細分(fēn)學科逐漸受到世人(rén)關注，它研究的(de)對(duì)象是 interpretable classification 和(hé) interpretable policy design（一個(gè)例子見 Wang et al. 2017）。相信在未來(lái)，可(kě)解釋的(de)機器學習(xí)在金融領域能夠大(dà)有可(kě)爲。關于模型複雜(zá)度，我想補充一點 Arnott, Harvey, and Markowitz (2019) 沒有的(de)内容，同樣來(lái)自《模型複雜(zá)度随想》，那就是相較于簡單的(de)模型，複雜(zá)度更高(gāo)的(de)模型可(kě)能會在虧損時(shí)給人(rén)更痛苦的(de)主觀感受。在這(zhè)方面，我做(zuò)了(le)一些探索性的(de)研究，指出了(le)模型複雜(zá)度和(hé)實盤痛苦程度之間的(de)非線性關系：

根據以上描述，模型複雜(zá)度和(hé)實盤的(de)痛苦程度大(dà)概如下(xià)圖所示（具體請看《模型複雜(zá)度随想》）。

在當下(xià)，我們越來(lái)越崇尚各種複雜(zá)的(de)模型。以上探索僅僅希望提出一些思考：我們在樣本外是否 100% 做(zuò)好了(le)準備接受複雜(zá)模型？交易中存在各種認知偏差，如果我們連最簡單的(de)按一根均線做(zuò)趨勢追蹤都無法堅決的(de)執行，那又有什(shén)麽來(lái)保證我們在面對(duì)實盤虧損時(shí)能夠堅守複雜(zá)模型呢(ne)？如果我們不能堅守複雜(zá)模型，那麽開發複雜(zá)模型所付出的(de)心血和(hé)努力是否付之東流呢(ne)？

7 研究文化(huà)

回測規程的(de)最後一部分(fēn)是研究文化(huà)（Research Culture），它包括以下(xià)兩點：

上面第一條說的(de)是，在開發量化(huà)策略或者因子時(shí)，比起追求樣本内的(de)驚豔效果，我們更應該看中研究的(de)質量，例如研究是否避免了(le)各種偏差、盡最大(dà)努力的(de)排除了(le)過拟合、是否存在先驗理(lǐ)論、是否足夠獨立等。一個(gè)因子或指标，無論有用(yòng)沒有，隻要能夠被複現，都是有益的(de)發現，都爲幫助我們更好的(de)理(lǐ)解市場(chǎng)起到了(le)巨大(dà)貢獻。

在學術界，爲了(le)提升期刊的(de)聲望，編輯們都更傾向于錄用(yòng)低 p-value 的(de)文章(zhāng)；爲了(le)在更高(gāo)水(shuǐ)平的(de)期刊上發文，學者們更傾向于找到低 p-value 的(de)因子。在美(měi)國絕大(dà)多(duō)數學校裏，如果能在 Journal of Finance 發表一篇文章(zhāng)，一個(gè)教授就有可(kě)能得(de)到終身教職。這(zhè)一環扣一環的(de)錯誤關系導緻了(le)嚴重的(de) publication bias，我們被大(dà)量依靠樣本内 data mining 和(hé) p-hacking 獲得(de)的(de)虛假因子蒙蔽了(le)雙眼，而高(gāo)研究質量卻低顯著性的(de)因子在頂級期刊上則難有容身之處。

這(zhè)部分(fēn)的(de)第二條說的(de)是，很多(duō)時(shí)候由于基金經理(lǐ)的(de)精力有限，無法親力親爲研究每個(gè)策略。因此會把研究分(fēn)發給不同的(de)研究員(yuán)。研究員(yuán)應該保持獨立性、進行高(gāo)質量的(de)研究，而不是通(tōng)過尋找虛假的(de)顯著性來(lái)取悅基金經理(lǐ)。任何策略都最終會失效，而客觀、嚴謹的(de)研究文化(huà)才是能夠源遠(yuǎn)流長(cháng)的(de)，才是我們應該努力追尋的(de)。在美(měi)國，要論業界的(de)“學術天團”，一般人(rén)大(dà)概首先會想到 AQR。然而，還(hái)有個(gè)更老牌、更大(dà)牌的(de)管理(lǐ)人(rén)，它就是 Dimensional Fund Advisors L.P.，它的(de) Directors 中不乏 Eugene Fama、Ken French、Myron Scholes 這(zhè)些赫赫有名的(de)學者。在 Dimensional 的(de)官網上記錄著(zhe) Ken French 下(xià)面這(zhè)句話(huà)，一語道破了(le)研究文化(huà)的(de)真谛 —— 任何時(shí)候我們都要努力探尋真谛、做(zuò)對(duì)的(de)事情。

8 結語

好了(le)，上面七小節介紹了(le)回測規程中的(de)七方面内容。接下(xià)來(lái)我們可(kě)以“召喚神龍”了(le)。下(xià)圖給出了(le) Arnott, Harvey, and Markowitz (2019) 自己總結的(de)七方面，每一個(gè) bullet point 都值得(de)好好體會。

最後想強調的(de)是，Arnott, Harvey, and Markowitz (2019) 并不是爲了(le)否定機器學習(xí)在投資中越來(lái)越重要的(de)作用(yòng)。恰恰相反的(de)是，他(tā)們提出這(zhè)個(gè)框架就是爲了(le)讓我們更好的(de)享受機器學習(xí)的(de)成果。對(duì)投資來(lái)說，我們最關心的(de)是 prediction 是否準确，而非參數的(de) adjudication。它的(de)意思是隻要能提高(gāo)樣本外的(de)預測性，我們可(kě)以犧牲參數估計的(de)準确性。公允的(de)說，從探尋市場(chǎng)真谛的(de)角度來(lái)說，我們當然關心 β 的(de)估計是否準确；然而，從投資實際效果的(de)角度來(lái)看，我們更應關注樣本外 y 預測值是否靠譜。預測的(de)目标是最小化(huà) loss function；而傳統計量經濟學中 estimation 的(de)目标是參數的(de) unbiasedness。參數估計準了(le)不一定意味著(zhe)樣本外的(de)預測性一定更好。關于這(zhè)方面的(de)論述，我推薦各位看看 Sendhil Mullainathan 教授在 AFA Lecture 上做(zuò)的(de) Machine Learning and Prediction in Economics and Finance 主題演講。

客觀的(de)說，由于金融數據的(de)一些特殊性（非結構化(huà)、高(gāo)維度、稀疏、信噪比低等），傳統計量經濟學在很多(duō)時(shí)候确實難有作爲，而機器學習(xí)算(suàn)法則更有前景。關于這(zhè)點，Lopez de Prado 做(zuò)過一篇題爲 《The 7 Reasons Most Econometric Investments Fail》的(de)報告。[量化(huà)投資與機器學習(xí)] 公衆号曾對(duì)這(zhè)篇報告進行過解讀（見《AQR最最最新 | 計量經濟學應用(yòng)投資失敗的(de)7個(gè)原因》），感興趣的(de)朋友不妨看一看。當然，這(zhè)并不意味著(zhe)我們就應該輕易摒棄計量經濟學模型、毫無顧忌的(de)投身到機器學習(xí)的(de)懷抱。

It is naïve to think we no longer need economic models in the era of machine learning. Given that the quantity and quality of data is relatively limited in finance, machine learning applications face many of the same issues quantitative finance researchers have struggled with for decades.

本文介紹的(de)回測規程乍一看完雖然沒有太多(duō)驚豔之處，但它卻能産生非常積極的(de)效果。正如飛(fēi)機駕駛艙裏面的(de) checklist 能極大(dà)的(de)提升飛(fēi)行安全一樣，在回測中牢記并遵守這(zhè)些準則可(kě)以有效降低過拟合的(de)風險、避開噪音(yīn)、找到真正在樣本外可(kě)持續的(de)因果關系，獲取更高(gāo)的(de)收益。

參考文獻

Arnott, R., C. R. Harvey, and H. Markowitz (2019). A backtesting protocol in the era of machine learning. Journal of Financial Data Science 1(1), 64 – 74.

Bailey, D. H. and M. Lopez de Prado (2012). The Sharpe ratio efficient frontier. Journal of Risk 15(2), 3 – 44.

Bailey, D. H. and M. Lopez de Prado (2014). The deflated Sharpe ratio: correcting for selection bias, backtest overfitting, and non-Normality. The Journal of Portfolio Management 40(5), 94 – 107.

Bailey, D. H., J. M. Borwein, M. Lopez de Prado, and Q. J. Zhu (2017). The probability of backtest overfitting. Journal of Computational Finance 20(4), 39 – 69.

Chordia, T., A. Goyal, and A. Saretto (2017). p-Hacking: evidence from two million trading strategies. Swiss Finance Institute Research Paper No. 17-37, SSRN.

Comte (1856). The Positive Philosophy of Auguste Comte, translated by Harriett Marineau (Calvin Blanchard, New York). Vol. II.

Fang, J., B. Jacobsen, and Y. Qin (2017). Popularity versus profitability: evidence from Bollinger bands. The Journal of Portfolio Management 43(4), 152 – 159.

Harvey, C. R. (2017). Presidential address: The scientific outlook in financial economics. Journal of Finance 72(4), 1399 – 1440.

Harvey, C. R., Y. Liu, and H. Zhu (2016). … and the cross-section of expected returns. Review of Financial Studies 29(1), 5 – 68.

Lopez de Prado, M. (2018). Advances in financial machine learning. Hoboken, NJ: John Wiley & Sons.

McLean, R.D. and J. Pontiff (2016). Does academic research destroy stock return predictability? Journal of Finance 71(1), 5 – 32.

Novy-Marx, R. (2015). Backtesting strategies based on multiple signals. NBER Working Paper, No. 21329.

Wang, T., C. Rudin, F. Doshi-Velez, Y. Liu, E. Klampfl, and P. MacNeille (2017). A Bayesian framework for learning rule sets for interpretable classification. Journal of Machine Learning Research 18, 1 – 37.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。