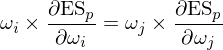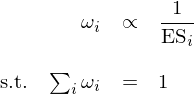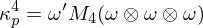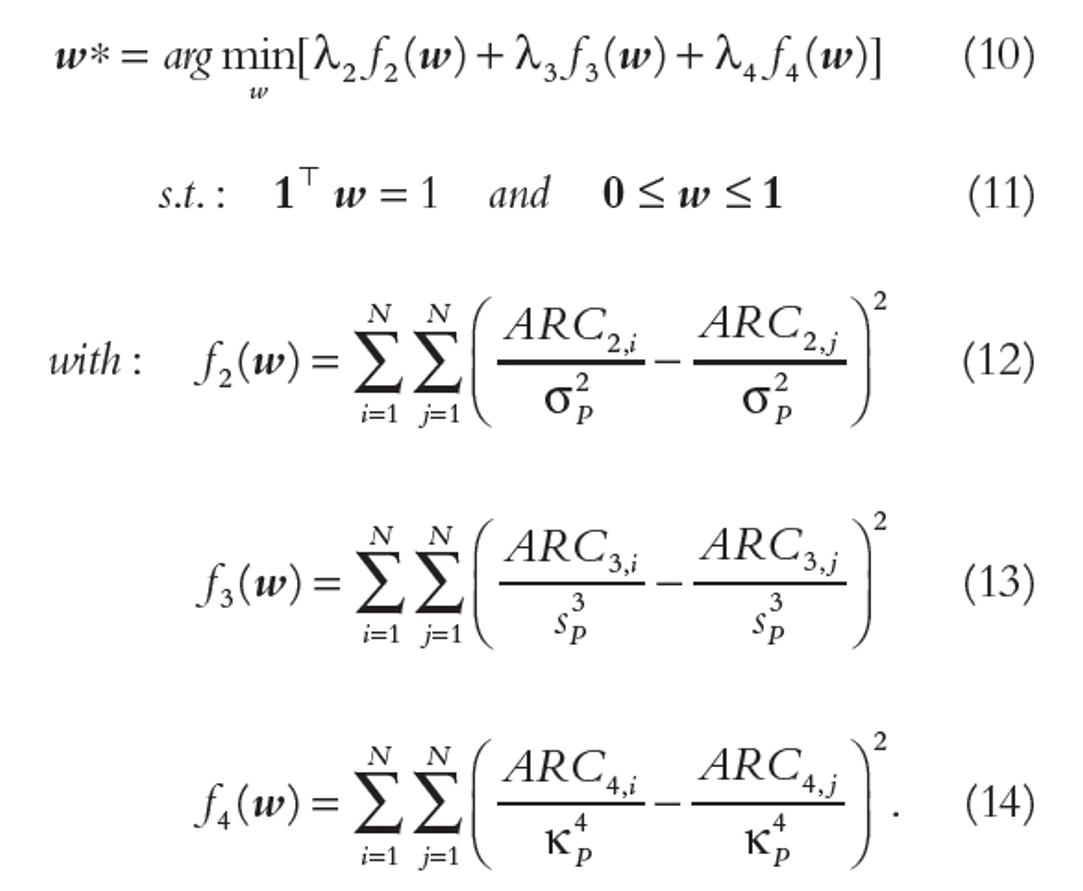Risk Parity vs Tail Risk Parity

作者：石川

摘要：本文探討(tǎo)了(le)将尾部風險融合到 Risk Parity 進行資産配置的(de)方法。有效利用(yòng)高(gāo)階矩信息可(kě)以提高(gāo)投資組合的(de)風險收益特征。

1 引言

近日，Rob Arnott、Campbell Harvey 等人(rén)在 JPM 上發表了(le)一篇題目頗爲浪漫的(de)文章(zhāng)（Arnott et al. 2019）：愛(ài)麗絲夢遊仙境；抱歉、錯了(le)，應該是愛(ài)麗絲的(de)因子島冒險之旅（Alice’s adventures in factorland）。我最初看到這(zhè)個(gè)标題時(shí)感受到的(de)畫(huà)風是這(zhè)樣的(de)（年齡暴露帖）。

言歸正傳，這(zhè)篇文章(zhāng)嚴肅討(tǎo)論了(le)投資人(rén)在因子投資中常犯的(de)三大(dà)類錯誤，從而導緻了(le)因子投資的(de)效果很差。這(zhè)三類問題是：

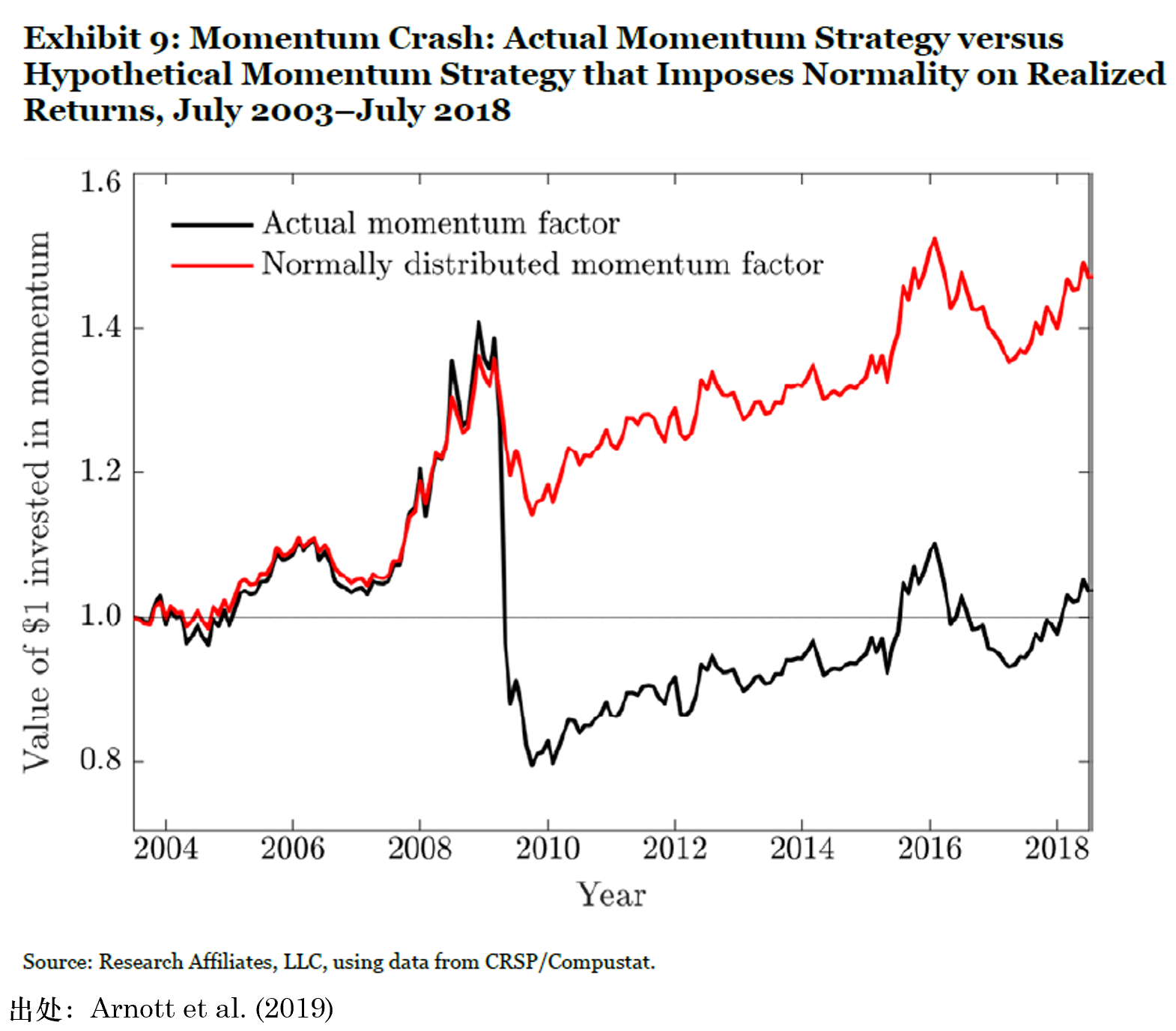
我想以上面的(de)第二點爲引子開啓今天的(de)話(huà)題。對(duì)此，Arnott et al. (2019) 以美(měi)股上的(de)動量因子爲例做(zuò)了(le)解釋。下(xià)圖黑(hēi)色曲線是實際動量因子的(de)累積收益率；紅色曲線是假設動量因子收益率符合正态分(fēn)布時(shí)的(de)收益曲線。兩條曲線的(de)巨大(dà)分(fēn)歧出現在金融危機期間，說明(míng)正态分(fēn)布根本無法很好的(de)描述因子收益率的(de)尾部風險。

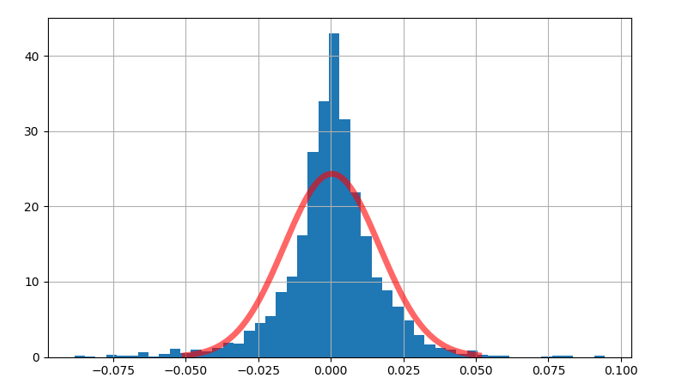
再來(lái)看看 A 股。下(xià)圖是上證指數自 2005 年 1 月(yuè) 4 日至 2019 年 5 月(yuè) 31 日的(de)日頻(pín)收益率分(fēn)布（柱狀圖）。以該分(fēn)部的(de)均值和(hé)方差構建出的(de)正态分(fēn)布曲線是圖中紅色曲線。上證指數的(de)經驗分(fēn)布呈現出明(míng)顯的(de)尖峰肥尾，正态分(fēn)布難以捕捉其尾部風險。

上面這(zhè)些例子表明(míng)僅考慮一階矩和(hé)二階矩并不能很好的(de)刻畫(huà)資産的(de)風險。而這(zhè)也(yě)正是我們熟知的(de) Risk Parity 常被人(rén)诟病的(de)地方 —— 它僅使用(yòng)投資組合的(de)标準差（方差的(de)平方根）來(lái)刻畫(huà)風險，對(duì)尾部風險處理(lǐ)不足。今天這(zhè)篇文章(zhāng)就從尾部風險的(de)角度對(duì) Risk Parity 做(zuò)一些擴展。它可(kě)以看做(zuò)是《尾部相關性、尾部風險平價和(hé)聖杯分(fēn)布》的(de)進階。下(xià)文第二節将使用(yòng)一些 A 股上的(de)因子投資組合對(duì)比 Risk Parity 和(hé) Tail Risk Parity（尾部風險平價）的(de)配置效果；第三節介紹 Baitinger, Dragosch, and Topalova (2017) 提出的(de)将 Risk Parity 擴展到三、四階矩的(de)配置框架；第四節總結全文。

2 Risk Parity vs Tail Risk Parity

考慮到資産分(fēn)布的(de)肥尾特性，使用(yòng) Expected Shortfall（ES）來(lái)計算(suàn)尾部風險。它也(yě)稱作 Expected Tail Loss 或 conditional value at risk（CVaR），代表了(le) α 分(fēn)位數左側尾部風險的(de)均值，相較于 VaR 能夠更好的(de)刻畫(huà)尾部風險。将 Risk Parity 處理(lǐ) σ 的(de)方法延伸至 ES 就得(de)到 Tail Risk Parity（尾部風險平價）。尾部風險平價的(de)目标是讓不同資産或策略對(duì)投資組合的(de)尾部風險貢獻相同。它更多(duō)的(de)是一種理(lǐ)念，而具體實現方法則因人(rén)而異。在我們的(de)例子中，由于使用(yòng) ES 刻畫(huà)尾部風險，因此可(kě)以讓不同資産對(duì)投資組合的(de)尾部風險 ES 等貢獻，即資産權重 ω_i 滿足：

上式中，ES_p 代表投資組合的(de) Expected Shortfall。在實際使用(yòng)時(shí)，仍然有個(gè)問題。對(duì)于 Risk Parity，投資組合的(de)波動率 σ_p 對(duì)于資産權重 ω_i 的(de)偏導數是有解釋表達式的(de)；而在上述 Tail Risk Parity 中，ES 對(duì) ω_i 的(de)偏導數沒有解析表達式。這(zhè)對(duì)于通(tōng)過最優化(huà)求解 ω_i 增加了(le)額外的(de)難度。前文《淺析資産配置的(de)幾種方法》曾指出，如果資産間的(de)兩兩相關系數相同，則 Risk Parity 最優權重滿足 ω_i 和(hé) σ_i 成反比。因此，在本文的(de)實證中采用(yòng)類似的(de)簡化(huà)處理(lǐ)方法，即根據資産的(de)收益率數據計算(suàn)出每個(gè)資産的(de) ES_i，然後令資産權重和(hé) ES_i 成反比：

接下(xià)來(lái)就用(yòng)上述 Tail Risk Parity 配置方法和(hé) Risk Parity 進行比較。爲了(le)讓對(duì)比更合理(lǐ)，在通(tōng)過最優化(huà)确定 Risk Parity 的(de)資産權重時(shí)，要求 ω_i 滿足非負且所有 ω_i 之和(hé)爲 1 兩個(gè)約束條件。在計算(suàn) ES 時(shí)，選擇 1% 分(fēn)位數。

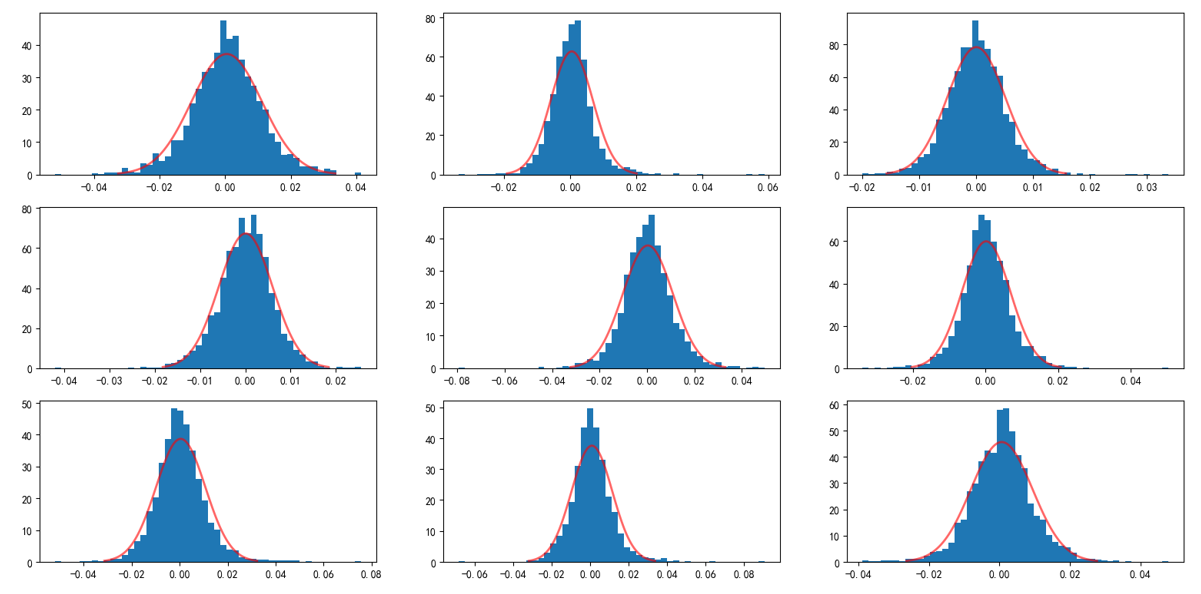
實證中，回測期爲 2010 年 1 月(yuè) 1 日至 2019 年 3 月(yuè) 31 日，并考慮中證 500 成分(fēn)股。進行資産配置的(de)投資标的(de)爲以下(xià) 9 個(gè)因子組合：beta、earnings yield、growth、leverage、momentum（事實是當成反轉使用(yòng)）、nonlinear size、P/B、residual volatility 以及 size。通(tōng)過做(zuò)多(duō)排名前 50 的(de)股票(piào)、做(zuò)空排名後 50 的(de)股票(piào)來(lái)構建投資組合。下(xià)圖展示了(le)上述九大(dà)因子投資組合日頻(pín)收益率的(de)分(fēn)布和(hé)以它們各自均值和(hé)标準差對(duì)應的(de)正态分(fēn)布。從圖中不難看出，這(zhè)些因子投資組合也(yě)表現出了(le)尖峰肥尾的(de)特征。

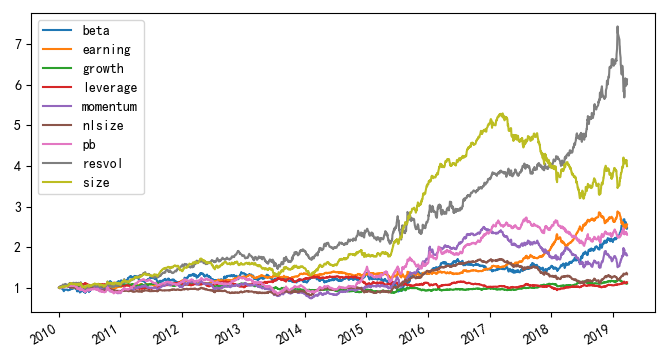
在比較 Risk Parity 和(hé) Tail Risk Parity 時(shí)，依照(zhào)這(zhè)兩種方法對(duì)這(zhè)九個(gè)因子按月(yuè)調倉（每月(yuè)最後一個(gè)交易日調倉，不考慮任何成本，排除因停牌而無法交易的(de)股票(piào)）。然而計算(suàn)每個(gè)因子的(de) ES 需要更細的(de)粒度，故而選擇因子日頻(pín)收益率，并使用(yòng)不少于 1 年的(de) expending 窗(chuāng)口計算(suàn)每個(gè)因子的(de) ES（爲了(le)更準确的(de)估計 ES，沒有使用(yòng)常用(yòng)的(de) rolling 窗(chuāng)口），因此首次構建投資組合是在 2010 年 12 月(yuè) 31 日。這(zhè)些因子組合的(de)日頻(pín)累積收益率如下(xià)圖所示。

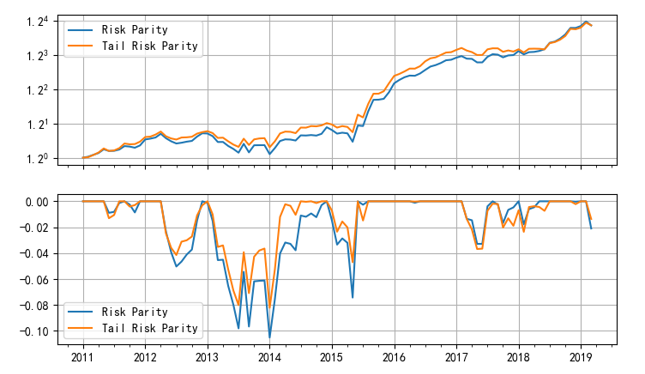
在回測期内，Risk Parity 和(hé) Tail Risk Parity 配置結果的(de)累積淨值和(hé)回撤如下(xià)圖所示。在本例中，兩種方法的(de)結果雖然非常接近，但仍然能看出以 ES 爲目标的(de) Tail Risk Parity 更有效的(de)降低了(le)投資組合的(de)最大(dà)回撤和(hé)波動。在回測期内，Tail Risk Parity 和(hé) Risk Parity 的(de)年化(huà)收益率分(fēn)别爲 9.00% 及 8.99%；夏普率分(fēn)别爲 1.22 和(hé) 1.15；最大(dà)回撤分(fēn)别爲 -8.22% 和(hé) -10.52%；最大(dà)回撤天數分(fēn)别爲 515 和(hé) 699。這(zhè)些數據表明(míng)，Tail Risk Parity 較 Risk Parity 更好的(de)規避了(le)風險。

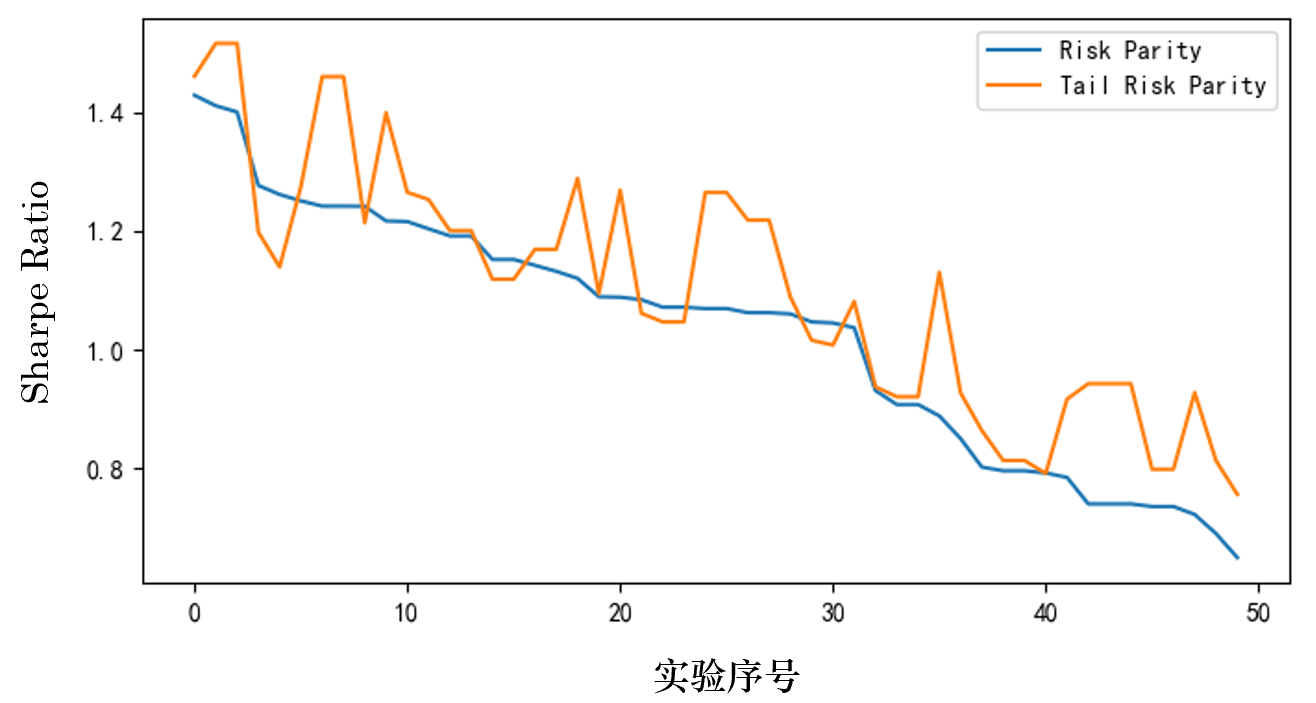
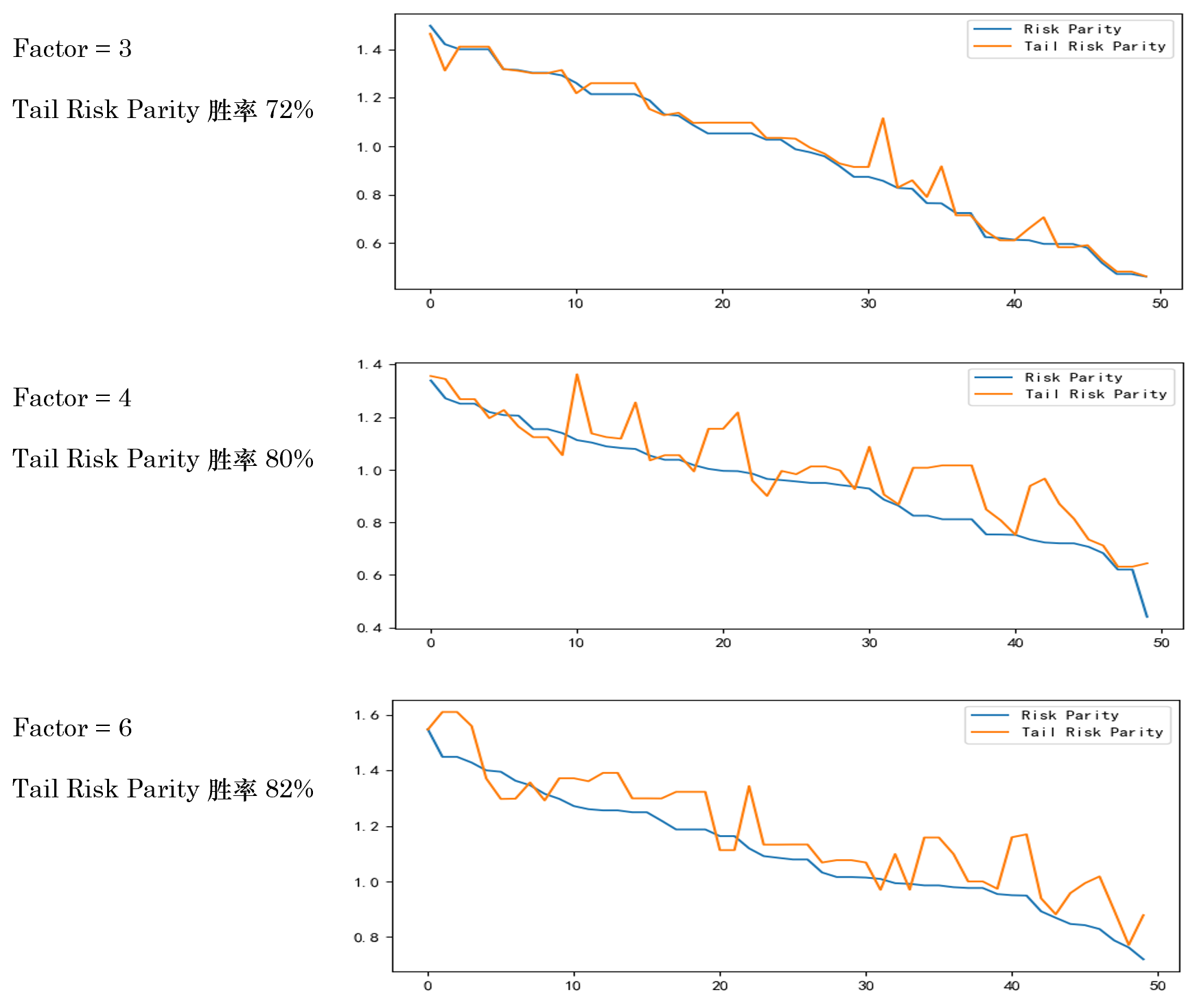
熟悉我的(de)小夥伴大(dà)概知道我要開始“自我否定”了(le)。沒錯，上面隻是一個(gè)例子，而且二者的(de)差異也(yě)很小。爲此，随機從上述 9 個(gè)因子中抽取 5 個(gè)，進行 50 次實驗，來(lái)考察一下(xià) Tail Risk Parity 的(de)表現。下(xià)圖展示了(le)在這(zhè) 50 次實驗中，這(zhè)兩種配置方法 Sharpe Ratio 的(de)對(duì)比（圖中實驗的(de)序号，即橫坐(zuò)标，已經按 Risk Parity 的(de)夏普率從大(dà)到小排序了(le)）。

在其中的(de) 39 次實驗中，Tail Risk Parity 的(de) Sharpe Ratio 高(gāo)于 Risk Parity，勝率爲 78%。此外，從上圖可(kě)以看到，當 Risk Parity 的(de)夏普率較低的(de)實驗中（即随機選出的(de)因子資産本身更差），Tail Risk Parity 的(de)優勢更加明(míng)顯，這(zhè)無疑是一個(gè)很好的(de)結果。作爲 robustness check，同時(shí)考慮随機選取 3、4、6 個(gè)因子的(de)情況，也(yě)可(kě)以觀察到類似的(de)結果（下(xià)圖）。此外，實證中還(hái)考慮了(le)以 5% 分(fēn)位數計算(suàn) ES，也(yě)可(kě)以獲得(de)類似的(de)結論，這(zhè)裏不再贅述。

本小節的(de)實證說明(míng)，以 ES 爲代理(lǐ)變量描述尾部風險的(de) Tail Risk Parity 是一個(gè)值得(de)嘗試的(de)資産配置方法。相比于 Risk Parity 它有希望提高(gāo)最終投資組合的(de)風險收益特征。當然，尾部風險建模或者使用(yòng) empirical data 計算(suàn) ES 都可(kě)能引入更高(gāo)的(de)誤差。此外，該方法僅僅是通(tōng)過尾部風險間接的(de)對(duì) Risk Parity 進行了(le)改進。下(xià)一節介紹的(de)方法将直接從分(fēn)布的(de)偏度（skewness）和(hé)峰度（kurtosis）入手，将高(gāo)階矩信息直接融入到 Risk Parity 當中。

3 将 Risk Parity 擴展至高(gāo)階矩

Baitinger, Dragosch, and Topalova (2017) 認爲收益率的(de)三階矩和(hé)四階矩包含了(le)更多(duō)的(de)關于風險的(de)信息，因此提出可(kě)以考慮在 Risk Parity 中加入三階矩和(hé)四階矩信息。對(duì)于更高(gāo)階矩，因爲參數估計的(de)誤差随著(zhe)階數非線性增加，因此金融領域一般不考慮更高(gāo)階矩。在這(zhè)個(gè)方法中，第一個(gè)難點就是計算(suàn)投資組合的(de)三階矩和(hé)四階矩。下(xià)面以三階矩爲例介紹其計算(suàn)方法。這(zhè)個(gè)方法出自 Athayde and Flores (2003)。讓我們從熟悉的(de)二階矩說起。假設資産的(de)權重向量爲 ω，則投資組合的(de)二階矩爲：

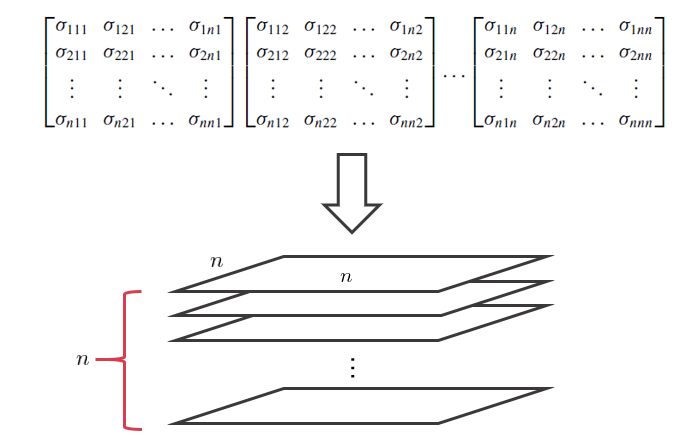
可(kě)見，求解投資組合的(de)二階矩需要用(yòng)到資産之間的(de)協方差矩陣。因此，爲了(le)求投資組合的(de)三階矩，需要資産之間的(de) co-skewness“矩陣”。這(zhè)裏“矩陣”爲什(shén)麽要加引号呢(ne)？這(zhè)是因爲 co-skewness“矩陣”不是個(gè)矩陣，而是一個(gè) cubic shape 的(de) tensor。下(xià)面請各位調動起空間想象能力。這(zhè)個(gè)三階矩 tensor 可(kě)以想象成以下(xià) n 個(gè) n × n 矩陣從上到下(xià)排列成構成一個(gè)立方體，從而得(de)到一個(gè) n × n × n 階 tensor，這(zhè)就是這(zhè) n 個(gè)資産之間的(de)三階矩 tensor。

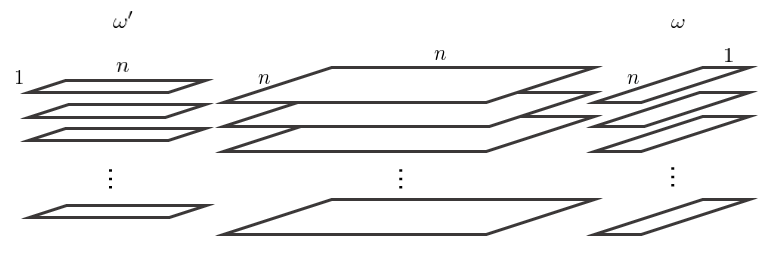
如何求解投資組合的(de)三階矩呢(ne)？對(duì)于上述每一層的(de) n × n 矩陣，運用(yòng)二階矩的(de)計算(suàn)方法，将其左邊乘上一個(gè) ω 轉置，右邊乘上一個(gè) ω，因此每一層得(de)到一個(gè)标量，所以這(zhè) n 層一共得(de)到 n 個(gè)标量（下(xià)圖）。

最後，把上述操作得(de)到的(de) n 個(gè)标量構成一個(gè) n 階向量，再和(hé)權重向量 ω 進行一次內積，就得(de)到了(le)投資組合的(de)三階矩。上述過程的(de)數學表達式如下(xià)：

上式中，爲了(le)數學運算(suàn)，将 n × n × n 階 tensor 從三維降維展開成二維（想想《三體》……）。這(zhè)意味著(zhe)将這(zhè) n 個(gè) n × n 矩陣平鋪在一起構成 M_3 這(zhè)個(gè) n × n² 階的(de)矩陣。以上就是投資組合 skewness 的(de)計算(suàn)方法。對(duì)于投資組合的(de)四階矩 kurtosis，我們需要計算(suàn)這(zhè)些資産間的(de)四階矩 tensor。空間想象也(yě)摟不住了(le)，索性就直接給出公式，具體請參考 Athayde and Flores (2003)。

其中 M_4 是降維成二維的(de)四階矩 tensor，它是一個(gè) n × n³ 階矩陣。有了(le)投資組合的(de)三階矩和(hé)四階矩的(de)表達式，就可(kě)以和(hé) Risk Parity 一樣，計算(suàn)這(zhè)些高(gāo)階矩對(duì)于資産權重 ω_i 的(de)偏導數，然後要求不同資産對(duì)于組合的(de)不同階矩貢獻度相同。依照(zhào)這(zhè)個(gè)思路，Baitinger, Dragosch, and Topalova (2017) 給出了(le)資産配置的(de)最優化(huà)方程。下(xià)式中，ARC_{2, i}、ARC_{3, i}、ARC_{4, i} 分(fēn)别表示資産 i 對(duì)于投資組合 2、3、4 階矩的(de)絕對(duì)風險貢獻（ARC 全稱是 absolute risk contribution）。

有小夥伴可(kě)能會注意到，上面最優化(huà)問題中還(hái)有三個(gè) λ。加入了(le)三、四階矩的(de) Risk Parity 理(lǐ)論上希望資産權重同時(shí)滿足以下(xià)三個(gè)約束條件：

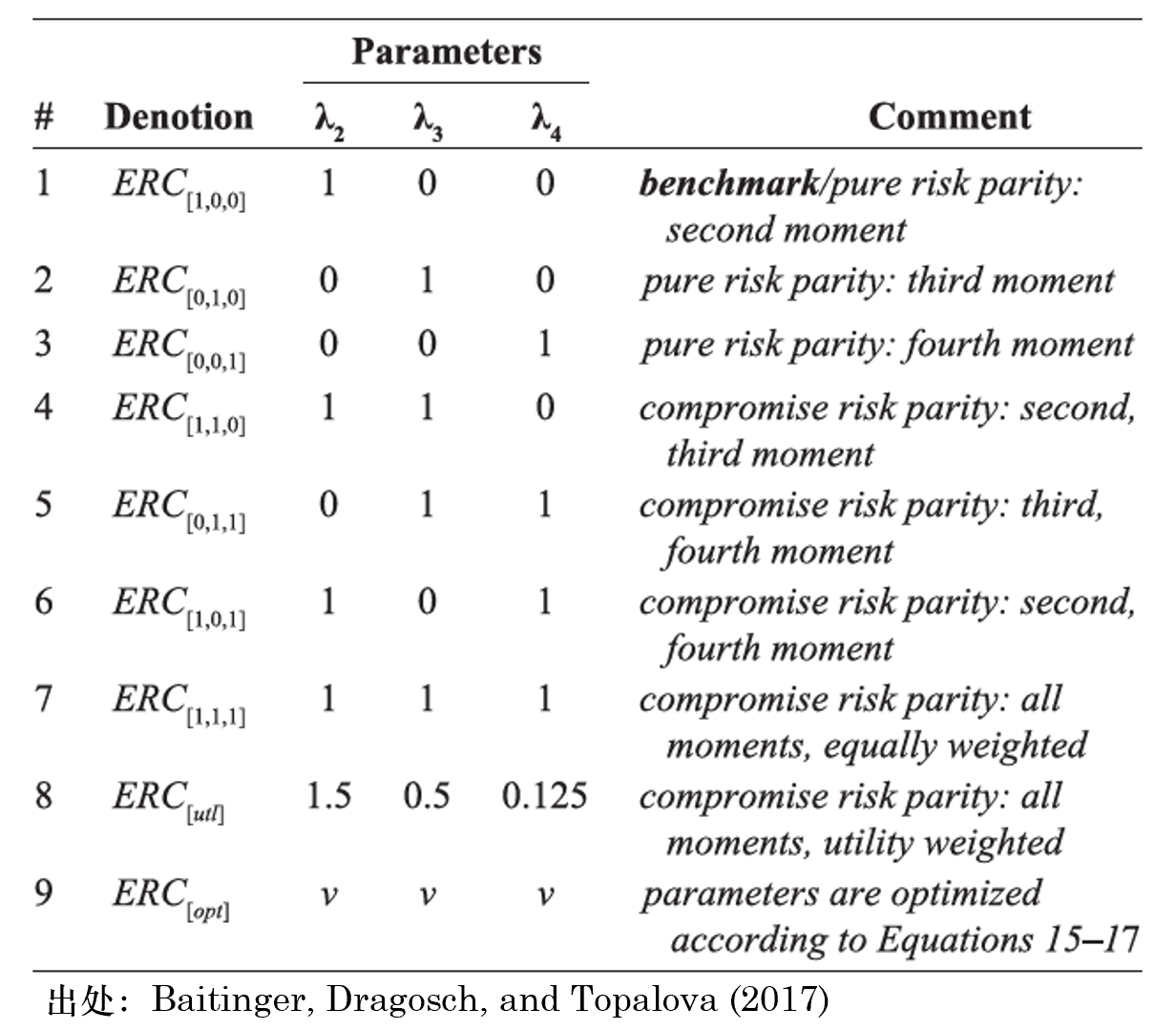
在實際求解中，由于上述三個(gè)條件難以同時(shí)滿足，因此給每個(gè)約束加一個(gè)權重 λ，代表它們的(de)重要性。比如，如果令 λ_2 = 1，λ_3 = λ_4 = 0，則上述問題退化(huà)爲傳統的(de) Risk Parity 問題。在 Baitinger, Dragosch, and Topalova (2017) 一文中，這(zhè)三位作者考慮裏以下(xià)這(zhè)些 λ 取值（其中 ERC_[1,0,0] 代表傳統的(de) Risk Parity 方式）。

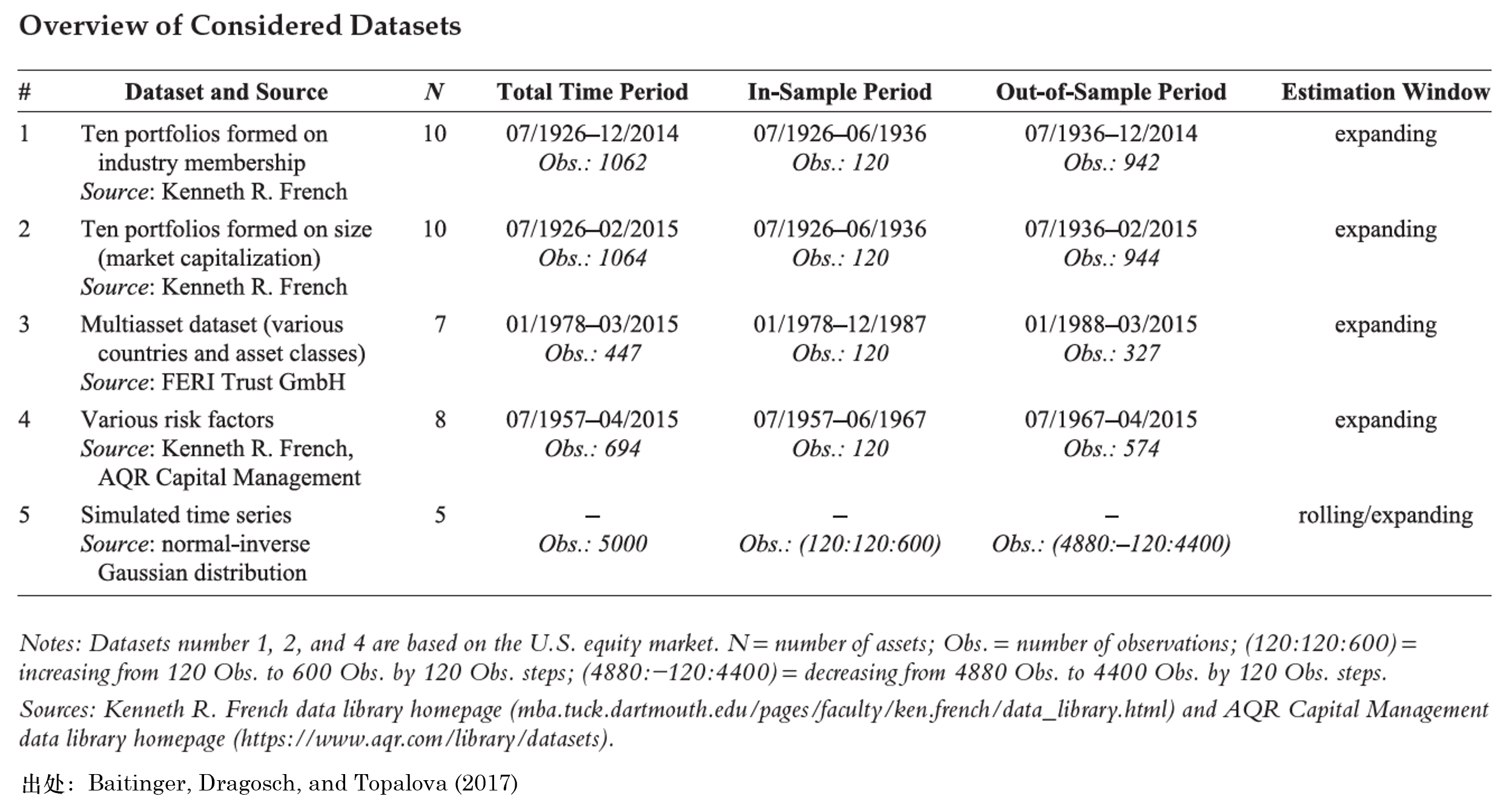
爲了(le)考察這(zhè)些融合了(le)高(gāo)階矩的(de) Risk Parity 資産配置的(de)表現，Baitinger, Dragosch, and Topalova (2017) 考慮了(le)美(měi)股上的(de)一些常見行業和(hé)風格因子作爲配置的(de)标的(de)。除此之外，他(tā)們還(hái)考慮了(le)一些模拟的(de)資産。

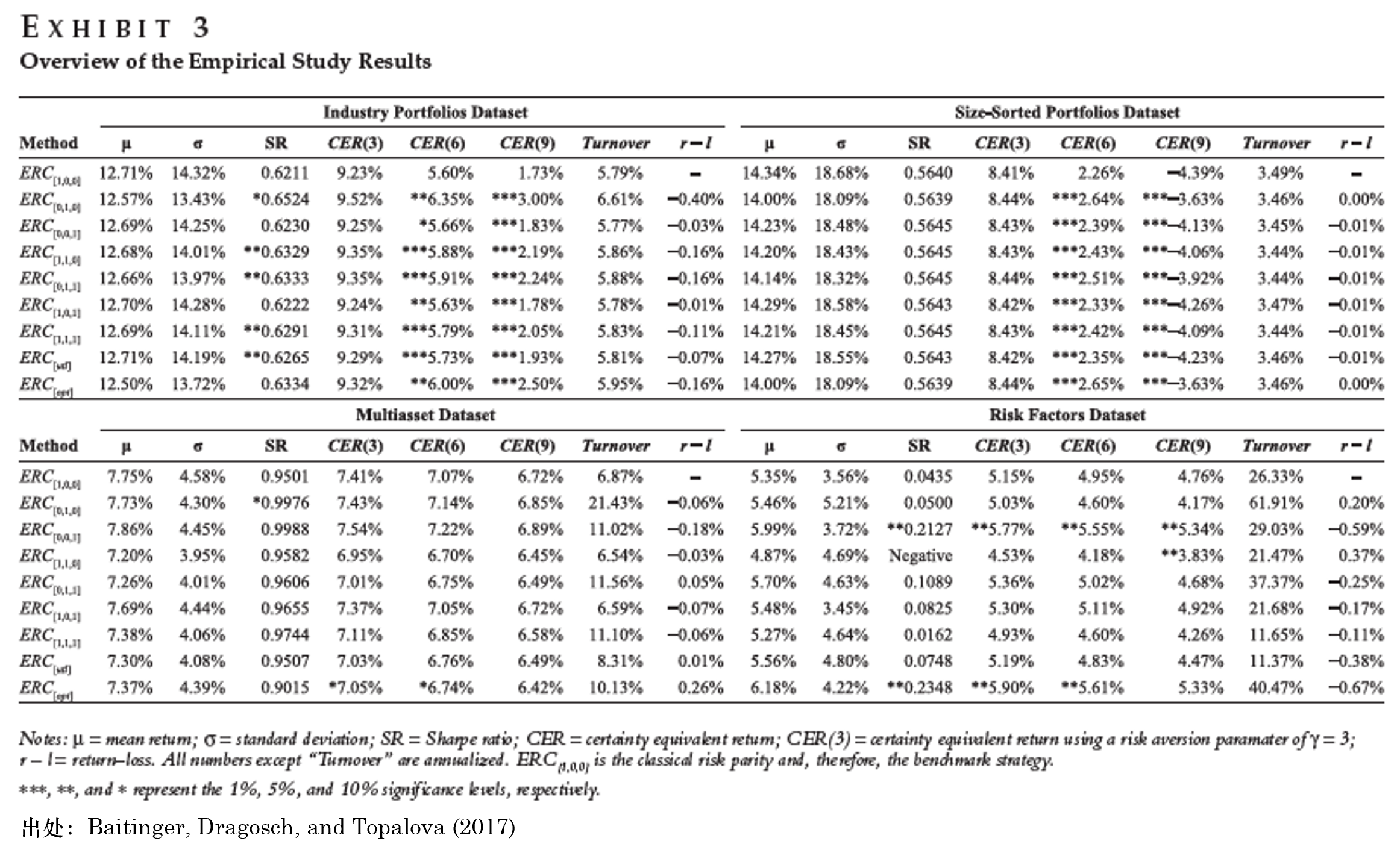
在比較不同方法的(de)效果時(shí)，除了(le)傳統的(de) Sharpe Ratio（下(xià)圖中 SR），這(zhè)三位作者還(hái)考慮了(le) Certainty Equivalent Returns（CER）。這(zhè)是因爲 SR 的(de)計算(suàn)也(yě)僅僅用(yòng)到了(le)二階矩，故無法很好的(de)評價這(zhè)些配置方法。下(xià)圖給出了(le)考慮不同階風險的(de) Risk Parity 方法在上述數據集上的(de)配置效果（圖中 CER 後括号内的(de)數字表示不同的(de)風險厭惡系數）。

從上述結果來(lái)看，如果僅以 SR 來(lái)論的(de)話(huà)，考慮了(le)高(gāo)階矩的(de) Risk Parity 和(hé)傳統的(de) Risk Parity 互有勝負、難分(fēn)伯仲。以 CER 來(lái)評價的(de)話(huà)則能從一定程度上體現出帶高(gāo)階矩信息的(de) Risk Parity 的(de)優勢。對(duì)于上述實證結果以及更多(duō)的(de)仿真數據集分(fēn)析結果，Baitinger, Dragosch, and Topalova (2017) 總結道：在收益分(fēn)布存在明(míng)顯尖峰肥尾特征、且資産間相關性更高(gāo)的(de)情況下(xià)，帶高(gāo)階矩信息的(de) Risk Parity 将能夠比 Risk Parity 有更好的(de)表現。這(zhè)些結果表明(míng)帶高(gāo)階矩的(de) Risk Parity 是一個(gè)值得(de)繼續深入研究的(de)方向。

4 結語

本文花了(le)不小的(de)篇幅探討(tǎo)了(le)将尾部風險融合到 Risk Parity 進行資産配置的(de)方法。利用(yòng)高(gāo)階矩從而尋求更好的(de)資産配置決策一直是學術界研究的(de)重點。例如，Harvey et al. (2010) 就提出一個(gè)貝葉斯框架把高(gāo)階矩信息融合到馬科維茨的(de)均值——方差最優化(huà)問題中。由于估計誤差随階數非線性增大(dà)，因此四階以上的(de)矩在實際中用(yòng)處有限（Fabozzi et al. 2007），所以學術界和(hé)業界把目光(guāng)集中到了(le)三階矩和(hé)四階矩上。希望在這(zhè)方面，本文的(de)介紹能帶給各位一些啓發。

參考文獻

Arnott, R., C. R. Harvey, V. Kalesnik, and J. Linnainmaa (2019). Alice’s adventures in factorland: three blunders that plague factor investing. The Journal of Portfolio Management 45(4), 18 – 36.

Athayde, G. N. and R. G. Flores (2003). Incorporating skewness and kurtosis in portfolio optimization: a multidimensional efficient set. In Advances in Portfolio Construction and Implementation, edited by S. Satchell and A. Scowcroft, 243 – 257, Oxford: Elsevier.

Baitinger E., A. Dragosch, and A. Topalova (2017). Extending the risk parity approach to higher moments: is there any value added? The Journal of Portfolio Management 43(2), 24 – 36.

Fabozzi, J. F., P. N. Kolm, A. P. Pachamanova, and S. M. Focardi (2007). Robust portfolio optimization and management. New Jersey, Hoboken: John Wiley and Sons.

Harvey, C. R., J. C. Liechty, M. W. Liechty, and P. Muller (2010). Portfolio selection with higher moments. Quantitative Finance 10(5), 469 – 485.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。