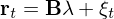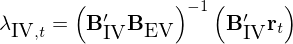Which Beta ?

作者：石川

摘要：爲檢驗因子是否有顯著的(de)風險溢價，首先需要正确計算(suàn)因子暴露。本文討(tǎo)論了(le)收益率時(shí)序回歸 β 和(hé) firm characteristics 作爲 β 時(shí)的(de)差異，并給出了(le)一些建議(yì)。

1 引言

這(zhè)篇文章(zhāng)關注的(de)是 empirical asset pricing test 中的(de) test。它既不介紹異象，也(yě)不講述因子，而是著(zhe)眼于檢驗。本文的(de)内容雖然重要，但行文非常 technical 且結論又看似 boring；以“真香”論來(lái)看，搞清楚文中的(de)解讀不如記住最後的(de)結論。另外，本文篇幅較長(cháng)。鑒于撰寫本文花費了(le)較大(dà)精力（包括精讀了(le)幾篇 2019 年發表于頂刊的(de)論文以及進行了(le)大(dà)量實證），下(xià)周将暫停一次創作，屆時(shí)會轉載一篇優質文章(zhāng)。最後，llang lli 和(hé)刀(dāo)疤連對(duì)本文的(de)寫作提出了(le)許多(duō)寶貴意見，在此特别感謝。正是因爲和(hé)他(tā)們的(de)反複討(tǎo)論，才使得(de)本文最終變成了(le)我滿意的(de)樣子。

OK，如果你沒有被上述劇透打敗，那讓我們開始吧。

在檢驗因子是否有顯著的(de) risk premium 時(shí)，常用(yòng)的(de)工具是 Fama-MacBeth Regression；而該方法首先需要明(míng)确股票(piào)在每個(gè)因子上的(de)因子暴露（factor exposure，即我們常說的(de) β）。計算(suàn)因子暴露有兩種方法：

比較這(zhè)兩種方法的(de)差異就是本文的(de)目标，這(zhè)也(yě)是本文取名 which beta 的(de)原因。由于篇幅較長(cháng)，爲避免各位小夥伴在閱讀過程中 get lost，下(xià)面先給出文章(zhāng)的(de)思維導圖。

下(xià)面讓我們從 Fama-MacBeth Regression 說起。

2 Fama-MacBeth Regression

Fama-MacBeth Regression 是學界和(hé)業界檢驗因子 risk premium 的(de)主流方法之一（Fama and MacBeth 1973，見《股票(piào)多(duō)因子模型的(de)回歸檢驗》）。它的(de)檢驗過程分(fēn)爲兩步：

上述過程的(de)第一步是爲了(le)第二步服務，而第二步具備兩個(gè)優點：（1）在截面上使用(yòng)多(duō)因子回歸可(kě)以考察每個(gè)因子對(duì)解釋資産預期收益率差異的(de)增量貢獻；（2）“先單期截面回歸、再從時(shí)序上取平均”可(kě)以排除殘差收益率的(de)截面相關性帶來(lái)的(de)影(yǐng)響。然而，上述兩步走的(de)過程存在一個(gè)不可(kě)避免的(de)問題，即第一步通(tōng)過時(shí)序回歸得(de)到的(de)因子暴露僅僅是真實但未知的(de) β 的(de)估計，因而存在誤差；将這(zhè)個(gè) estimate 直接作爲解釋變量用(yòng)在第二步就引入了(le) errors-in-variables 問題（EIV）。

Fama and MacBeth (1973) 自然意識到了(le)這(zhè)個(gè)問題。爲此，在這(zhè)篇以檢驗 CAPM 爲初衷的(de)文章(zhāng)中，他(tā)們并沒有使用(yòng)個(gè)股的(de)收益率，而是将個(gè)股按照(zhào)曆史 β 的(de)大(dà)小構成了(le)不同的(de)投資組合，然後使用(yòng)這(zhè)些投資組合作爲資産，放在回歸中的(de) LHS 檢驗 CAPM。Black, Jensen, and Scholes (1972) 以及 Fama and MacBeth (1973) 指出：當使用(yòng)投資組合時(shí)，個(gè)股 β 的(de)估計誤差會相互抵消，因此對(duì)投資組合的(de) β 估計會更準确，從而在一定程度上降低 EIV 的(de)影(yǐng)響。自此以後，在進行 Fama-MacBeth Regression 檢驗因子時(shí)，使用(yòng)投資組合而非個(gè)股放在 LHS 就成爲了(le)學術界的(de)标配。但有大(dà)佬對(duì)此頗有微詞，這(zhè)其中就包括 Fama 的(de)弟(dì)子 Richard Roll。

Roll 和(hé)他(tā)的(de) co-authors 在 Jegadeesh et al. (2019) 這(zhè)篇最新發表于 Journal of Financial Economics 的(de)文章(zhāng)指出将個(gè)股按照(zhào)某種屬性分(fēn)組實際上是一種降維處理(lǐ)，投資組合會丢掉很多(duō)個(gè)股截面上的(de)特征。如果待檢驗的(de)因子和(hé)這(zhè)些 LHS 組合的(de)分(fēn)組屬性正交，用(yòng)它們作爲 LHS 進行 Fama-MacBeth Regression 是無法發現這(zhè)些因子的(de) risk premium 的(de)。因此，Jegadeesh et al. (2019) 建議(yì)使用(yòng)個(gè)股收益率放在 LHS。

除此之外，學術界對(duì)于投資組合的(de)過度使用(yòng)還(hái)有另一個(gè)不好的(de) side effect。Fama and French (1993) 三因子的(de)橫空出世，不僅讓人(rén)們從此接受了(le) SMB 和(hé) HML 兩個(gè)因子，更讓使用(yòng) Size 和(hé) B/M 進行 double sort 得(de)到的(de) 5 × 5 一共 25 個(gè)投資組合成爲了(le)評價不同因子模型時(shí)的(de)标配。很多(duō)模型以能夠在截面上很好的(de)解釋這(zhè) 25 個(gè)資産的(de)預期收益率爲依據，說明(míng)提出的(de)新因子是有效的(de)。對(duì)此，另外兩位大(dà)佬 Stefan Nagel 和(hé) Jay Shanken 認爲這(zhè)是極大(dà)的(de)誤解。

Nagel 和(hé) Shanken 在 Lewellen, Nagel, and Shanken (2010) 一文中指出，使用(yòng) Size 和(hé) B/M double sort 的(de)這(zhè) 25 個(gè)組合有非常強的(de) factor structure。任何一個(gè)待檢驗的(de)因子，如果它們和(hé) HML 或 SMB 的(de)相關性大(dà)于它和(hé)這(zhè) 25 個(gè)組合被 HML 和(hé) SMB 解釋後的(de)殘差的(de)相關性的(de)話(huà)，這(zhè)個(gè)新因子就能在這(zhè)些投資組合的(de)截面上獲得(de)很高(gāo)的(de) R²，換句話(huà)說，這(zhè)些組合的(de) α 會很接近零。因此，哪怕一個(gè)因子能夠很好的(de)解釋這(zhè) 25 個(gè)投資組合的(de)截面預期收益率差異，它也(yě)未必是有效的(de)。

以上兩個(gè)問題均說明(míng)在檢驗因子以及因子模型時(shí)，僅使用(yòng)有限個(gè)投資組合作爲 test assets 不再合适。Lewellen, Nagel, and Shanken (2010) 提出的(de)解決方法之一正是使用(yòng)更多(duō)的(de)投資組合。比如，在 Fama and French (2019) 這(zhè)篇最新的(de)研究中，他(tā)們二位就使用(yòng)不同的(de)公司指标兩兩 double sort 構建了(le) 200+ 個(gè)投資組合，檢驗了(le)時(shí)序和(hé)截面因子模型的(de)效果。

如今，距離 Fama and MacBeth (1973) 的(de)提出已經過去了(le)快(kuài) 50 年。無論是計量經濟學的(de)發展還(hái)是學術界因子挖掘的(de)日趨嚴重（factor zoo），都促使我們摒棄投資組合、轉而使用(yòng)個(gè)股收益率放在回歸方程的(de) LHS。當使用(yòng)個(gè)股收益率放在 LHS 時(shí)，必須盡量排除 EIV 問題、獲得(de)盡可(kě)能準确的(de)因子暴露的(de)估計。爲此，Jegadeesh et al. (2019) 提出在 Fama-MacBeth Regression 的(de)第一步時(shí)序回歸中引入 Instrumental Variables（IV），它将是下(xià)一節的(de)内容。

對(duì) EIV 問題，業界有著(zhe)不同的(de)做(zuò)法。我們熟悉的(de) Barra 的(de)純因子模型本質上正是 Fama-MacBeth Regression。但是它沒有使用(yòng)第一步時(shí)序回歸計算(suàn)因子暴露，而是使用(yòng)了(le) firm characteristics 作爲因子暴露，然後進行截面回歸。由于不需要估計 β，Barra 在回歸方程的(de) LHS 使用(yòng)了(le)個(gè)股收益率。當然，Barra 多(duō)因子模型的(de)目的(de)是爲了(le)計算(suàn)個(gè)股的(de)協方差矩陣，從這(zhè)個(gè)意義上說，LHS 使用(yòng)投資組合也(yě)沒什(shén)麽道理(lǐ)。當把個(gè)股收益率放在 LHS 時(shí)，比較學術界和(hé)業界的(de)在計算(suàn)因子暴露時(shí)的(de)不同做(zuò)法正是本文背後的(de)動機。

3 工具變量

在 Fama-MacBeth Regression 中，第二步截面回歸的(de)數學表達式爲：

由于采用(yòng)了(le)個(gè)股收益率放在 LHS，因此上式中 r_t 是個(gè)股收益率向量；B 是第一步時(shí)序回歸得(de)到的(de)因子暴露估計矩陣，它是一個(gè) N × K 階矩陣（N 支個(gè)股；K 個(gè)因子）；λ 是帶求解的(de)因子 risk premium 向量；ξ_t 是殘差向量。爲減少 EIV 問題的(de)影(yǐng)響，Jegadeesh et al. (2019) 在上述 OLS 回歸中引入了(le) Instrumental Variables，因此得(de)到 λ 的(de) IV 估計量爲：

上式中，B_IV 和(hé) B_EV 分(fēn)别爲 instrumental 和(hé) explanatory variables：B_EV 是對(duì) β 的(de) estimate；B_IV 是 B_EV 的(de)工具變量。Jegadeesh et al. (2019) 使用(yòng)互不重疊的(de)曆史數據分(fēn)别進行時(shí)序回歸求解 B_IV 和(hé) B_EV，并指出正因如此，它們在截面上是不相關的(de)，可(kě)以減少 EIV 問題。具體來(lái)說，在每個(gè)月(yuè)末，爲了(le)計算(suàn)最新的(de) B_IV 和(hé) B_EV，Jegadeesh et al. (2019) 使用(yòng)過去三年個(gè)股的(de)日頻(pín)收益率和(hé)多(duō)因子模型的(de)日頻(pín)收益率進行時(shí)序 multivariate regression：

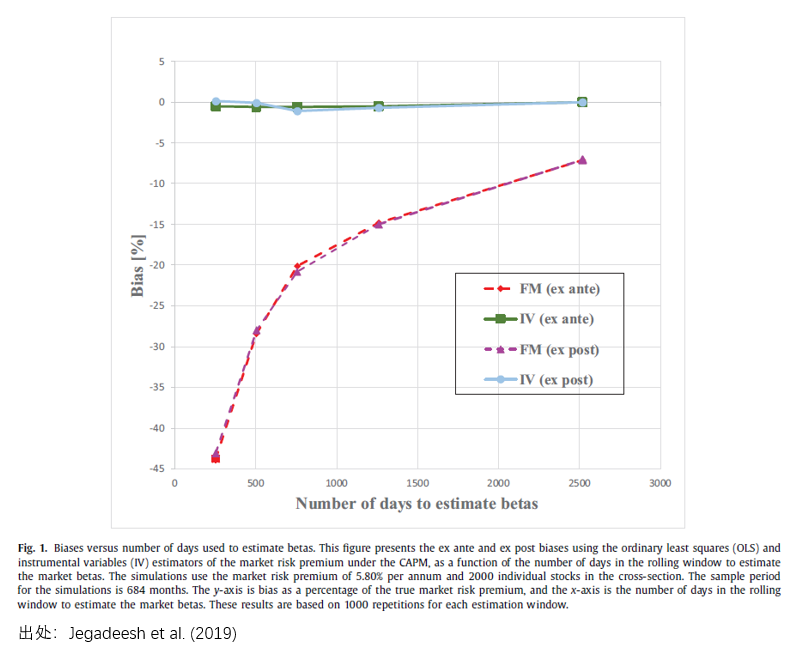
由于 EIV 問題，Fama-MacBeth Regression 中第二步截面上的(de) OLS 計算(suàn)得(de)到的(de) risk premium 往往是 biased，而多(duō)個(gè)因子一起的(de)多(duō)元截面回歸使得(de)我們無法确定每個(gè)因子溢價上 bias 的(de)方向。Jegadeesh et al. (2019) 指出，上述 IV estimate 可(kě)以獲得(de) risk premium 的(de)無偏估計。以 CAPM 單因子爲例，下(xià)圖給出了(le) Jegadeesh et al. (2019) 的(de)分(fēn)析結果。當使用(yòng)傳統的(de) OLS 時(shí)，對(duì) market risk premium 的(de)估計的(de) bias 随著(zhe)計算(suàn) β 的(de)時(shí)序窗(chuāng)口增加而減少，但即便是使用(yòng)了(le)長(cháng)達 10 年的(de)數據（2500 個(gè)交易日），bias 仍然高(gāo)達 -7% 左右；若采用(yòng) IV 估計量，對(duì) market risk premium 的(de)估計是 unbiased。

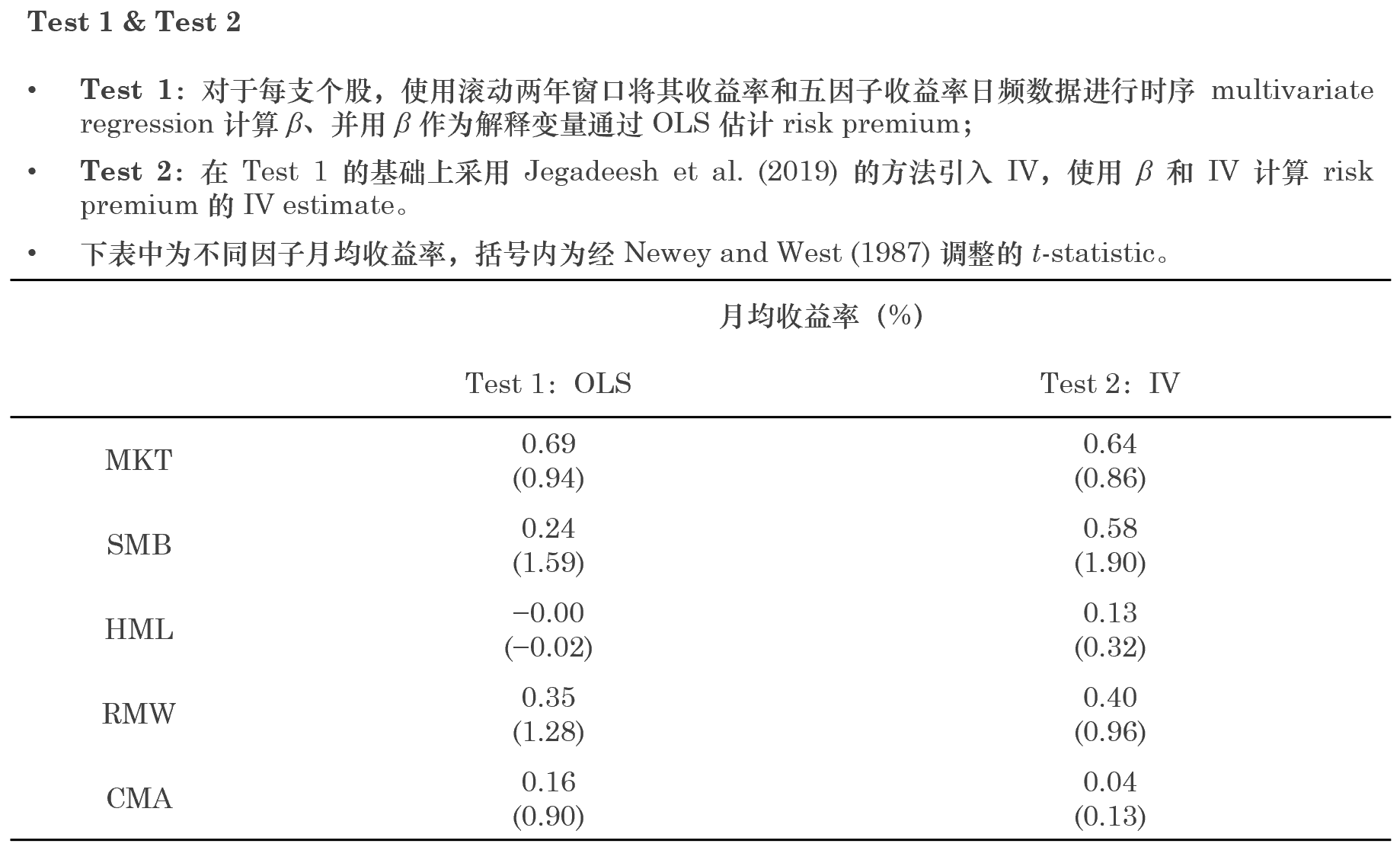
顯然，即便是對(duì)于美(měi)股，使用(yòng)十年滾動窗(chuāng)口來(lái)估計 β 都是相當奢侈的(de)（況且它還(hái)無法消除 bias），更不要提大(dà) A 股了(le)。因此，IV 估計量在估計 risk premium 時(shí)優勢明(míng)顯。下(xià)面以中證 500 成分(fēn)股爲例（将它們放在回歸方程的(de) LHS），檢驗 Fama and French (2015) 的(de)五因子模型中的(de)因子是否有 risk premium。實證期爲 2010 年 1 月(yuè)至 2019 年 4 月(yuè)。在每月(yuè)末，使用(yòng)過去兩年的(de)日頻(pín)收益率序列估計 B_EV 和(hé) B_EV。作爲對(duì)比，同時(shí)使用(yòng)不引入 IV 的(de)方法，即使用(yòng)兩年滾動窗(chuāng)口的(de)全部數據估計 β 并将它用(yòng)在 Fama-MacBeth Regression 的(de)第二步。下(xià)表給出了(le)這(zhè)五個(gè)因子的(de)檢驗結果（其中 Test 1 爲未引入 IV 的(de)方法；Test 2 爲使用(yòng) IV estimate 的(de)方法）。

結果顯示，當使用(yòng)個(gè)股作爲資産放在 LHS 時(shí)，由于 EIV 的(de)問題，Fama-MacBeth Regression 給出的(de)結論是全部五個(gè)因子均沒有顯著的(de) risk premium —— 即五因子不能有效的(de)解釋個(gè)股截面預期收益的(de)差異。當采用(yòng) IV estimate 時(shí)，SMB 因子變得(de)顯著（其他(tā)四個(gè)因子仍然不顯著）。這(zhè)個(gè)簡單的(de)結果表明(míng)消除 EIV 問題，即使用(yòng)更準确的(de) β estimate，對(duì)于評判一個(gè)因子是否有效至關重要。從上面的(de)結果可(kě)以得(de)到本文 which beta 之問的(de)第一個(gè)觀點：在 β 估計時(shí)引入 IV 消除 EIV 的(de)影(yǐng)響比直接使用(yòng) β 做(zuò) OLS 截面回歸能夠獲得(de)更準确的(de) risk premium estimate。如果討(tǎo)論就此結束實在意猶未盡。事實上，Jegadeesh et al. (2019) 的(de)實證分(fēn)析也(yě)未止步于此；他(tā)們在 β 的(de)基礎上加入了(le) firm characteristics。使用(yòng)時(shí)序回歸系數和(hé) firm characteristics 同時(shí)作爲 β 也(yě)是這(zhè)兩種方法的(de)直接 PK。

4 公司特征

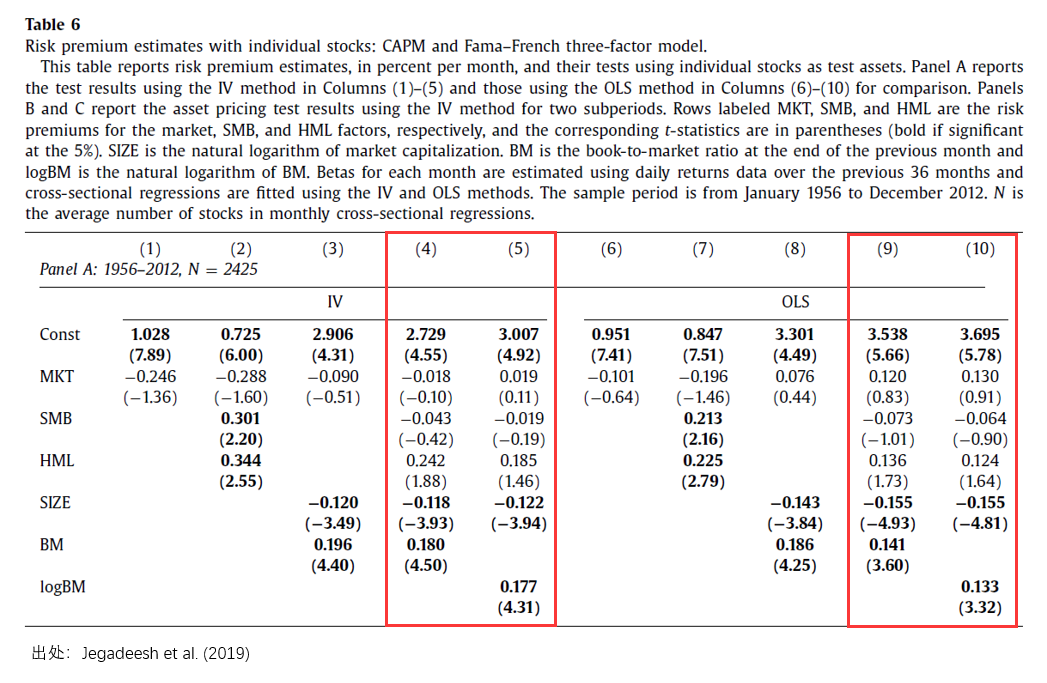
Jegadeesh et al. (2019) 在美(měi)股上使用(yòng)他(tā)們提出的(de) IV 估計量檢驗 Fama and French (1993) 三因子模型并發現 SMB 和(hé) HML 确實有顯著的(de) risk premium。不過，他(tā)們同時(shí)指出，以上顯著的(de)結果可(kě)能源自被忽視的(de)變量偏差，即在截面回歸時(shí)沒有控制 Size 和(hé) B/M 這(zhè)些用(yòng)來(lái)構建 SMB 和(hé) HML 的(de)公司特征（firm characteristics）。爲此，他(tā)們将 Size 和(hé) B/M 加入到 Fama-MacBeth Regression 的(de)第二步，和(hé) HML 以及 SMB 的(de) β estimate 一起進行了(le)截面回歸。令人(rén)吃(chī)驚的(de)是，Jegadeesh et al. (2019) 的(de)實證結果（下(xià)圖）顯示，當 Size 和(hé) B/M（或 logB/M） 被加入後，這(zhè)兩個(gè) firm characteristics 可(kě)以獲得(de)顯著的(de) risk premium，而 SMB 和(hé) HML 的(de) risk premium 不再顯著。

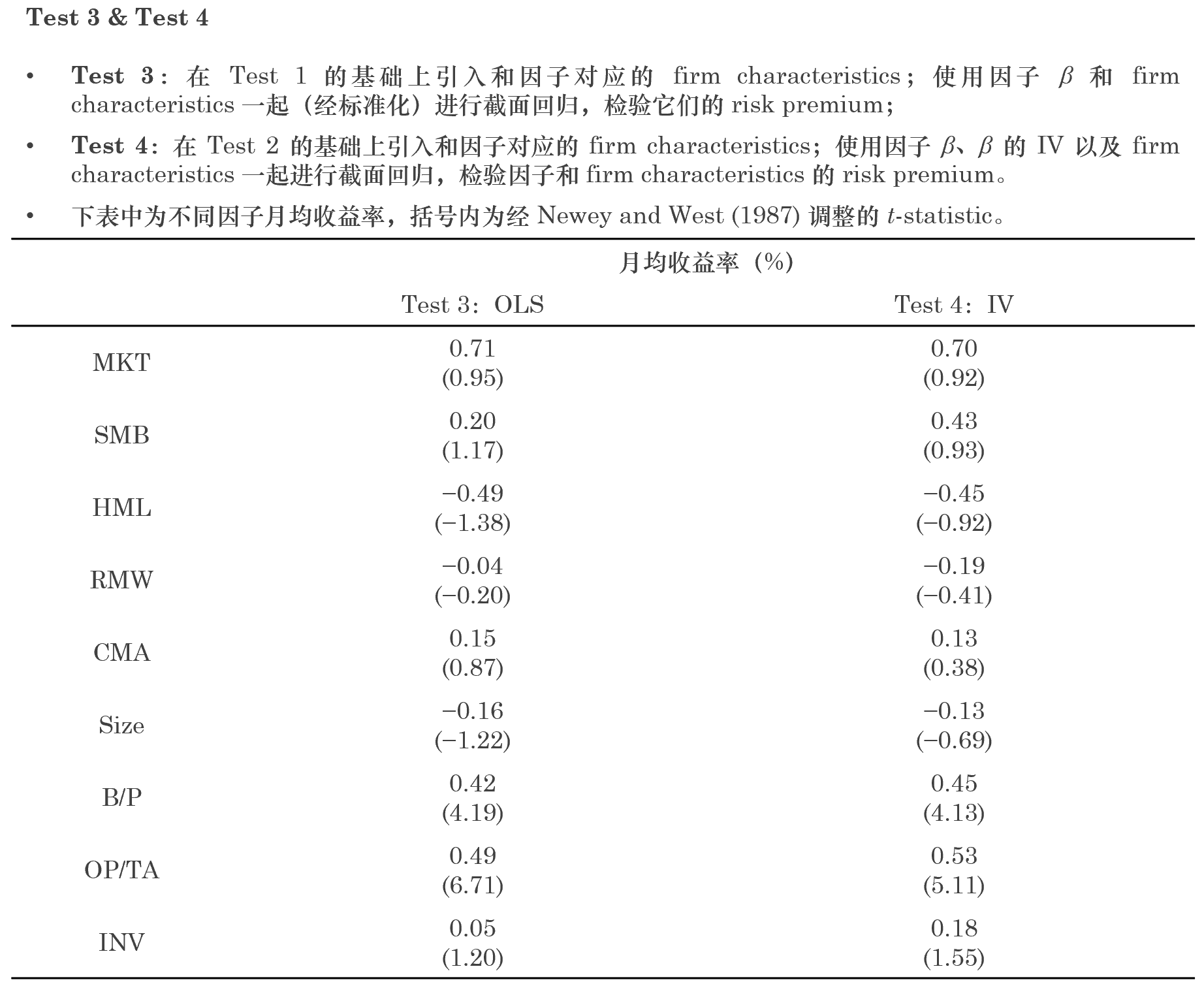
我們同樣來(lái)看看 A 股的(de)實證結果。考慮 firm characteristics 之後，把上一節 Test 1 和(hé) Test 2 中分(fēn)别加入對(duì)應 SMB、HML、RMW、CMA 四因子的(de)公司指标得(de)到 Test 3 和(hé) Test 4。在這(zhè)兩個(gè) tests 中，相應的(de)公司指标記爲 Size（使用(yòng)的(de)對(duì)數流通(tōng)市值）、B/P、OP/TA 以及 INV。

引入 firm characteristics 之後，Fama and French (2015) 五因子在中證 500 上均不顯著；而 B/P 和(hé) OP/TA 這(zhè)兩個(gè)公司指标可(kě)以獲得(de)顯著的(de) risk premium。Firm characteristics“戰勝”時(shí)序回歸 β 的(de)結果和(hé) Jegadeesh et al. (2019) 在美(měi)股上的(de)實證結果十分(fēn)相似（他(tā)們針對(duì)美(měi)股也(yě)檢驗了(le)五因子模型和(hé) Hou, Xue, and Zhang 2015 的(de) q-factor 模型，均有類似的(de)發現）。當使用(yòng)投資組合作爲檢驗因子的(de)資産時(shí)，這(zhè)些學術界的(de)因子的(de)确可(kě)以獲得(de)顯著的(de) risk premium。然而，當使用(yòng)個(gè)股收益率、并考慮了(le) firm characteristics 後，它們均不再顯著。這(zhè)背後的(de)原因是什(shén)麽呢(ne)？Jegadeesh et al. (2019) 給出了(le)它們的(de)嘗試，無奈最後的(de)結論是“remains a puzzle”；我們也(yě)要給出自己的(de)思考。接下(xià)來(lái)從以下(xià)兩個(gè)角度思考這(zhè)個(gè)問題：

5 時(shí)序回歸 vs 公司特征

前文中 Test 1 和(hé) Test 2 的(de)結果說明(míng)，當 LHS 使用(yòng)個(gè)股收益率時(shí)，五因子幾乎都無法獲得(de)顯著 risk premium。我們知道，一個(gè)随機因子是無法獲得(de) risk premium 的(de)。從這(zhè)個(gè)觀點出發反推，可(kě)以猜測時(shí)序回歸得(de)到的(de) β 在截面上非常不穩定，使得(de)這(zhè)些因子的(de)行爲就像随機因子一樣。這(zhè)可(kě)能是由于日頻(pín)收益率數據的(de)高(gāo)噪音(yīn)和(hé)多(duō)元回歸中因子之間的(de)相互影(yǐng)響所緻。另一方面，使用(yòng) firm characteristics 比使用(yòng)時(shí)序回歸 β 能獲得(de)更顯著的(de) risk premium，這(zhè)說明(míng) firm characteristics 對(duì)應的(de) pure factor portfolio 能獲得(de)更高(gāo)的(de)收益率。這(zhè)意味著(zhe)與時(shí)序回歸的(de) β 相比，當期 firm characteristics 和(hé)下(xià)一期個(gè)股收益率之間的(de) IC 以及 ICIR 更高(gāo)。下(xià)列實證結果也(yě)證實了(le)這(zhè)個(gè)猜想。

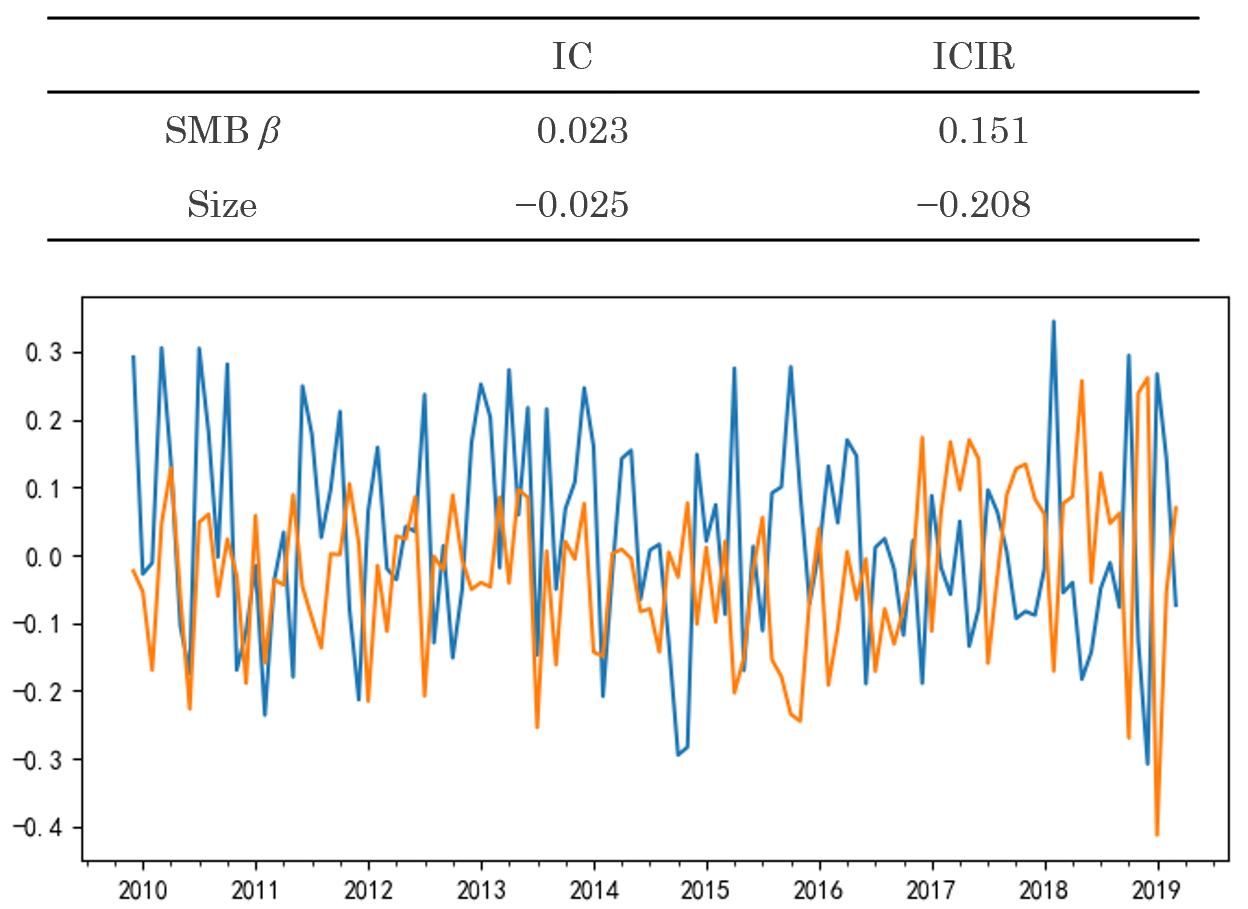
下(xià)圖是 SMB 因子的(de)時(shí)序回歸 β 和(hé) Size 這(zhè)兩個(gè)解釋變量和(hé)個(gè)股未來(lái)收益率之間的(de) rank IC 時(shí)序圖（藍色爲時(shí)序回歸 β；黃(huáng)色爲 Size），圖中同時(shí)給出了(le)這(zhè)兩個(gè)變量的(de) IC 均值以及 ICIR（Size 的(de) IC 均值及 ICIR 爲負說明(míng)小市值更好）。結果顯示，時(shí)序回歸得(de)到的(de) SMB 的(de) β 和(hé)個(gè)股收益率的(de) IC 均值（絕對(duì)值）沒有 Size 高(gāo)；說明(míng) Size 比 SMB β 對(duì)于未來(lái)收益率更具有預測性。此外 Size 的(de) ICIR（絕對(duì)值）更高(gāo)也(yě)說明(míng)它作爲因子暴露，要比 SMB 的(de) β 更加穩定。

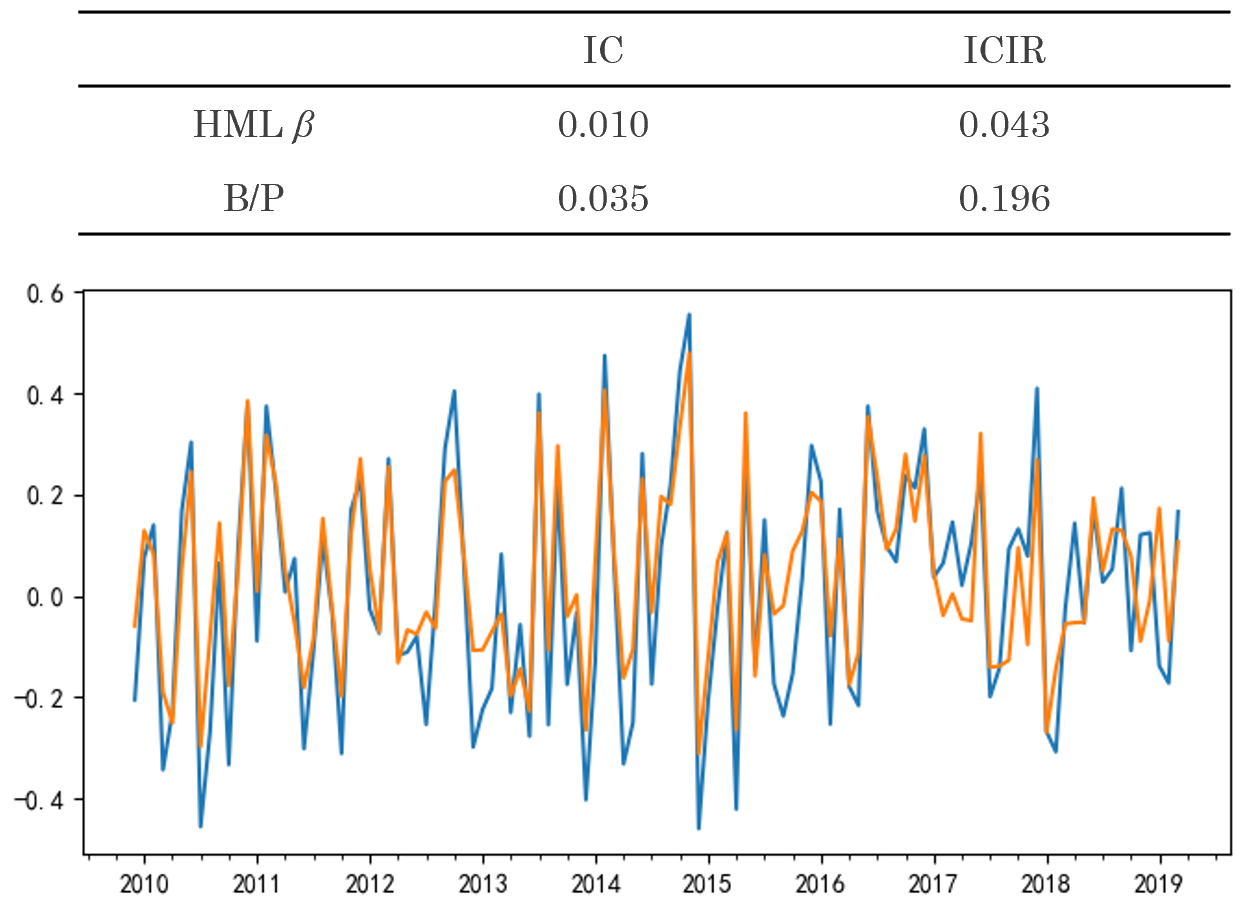
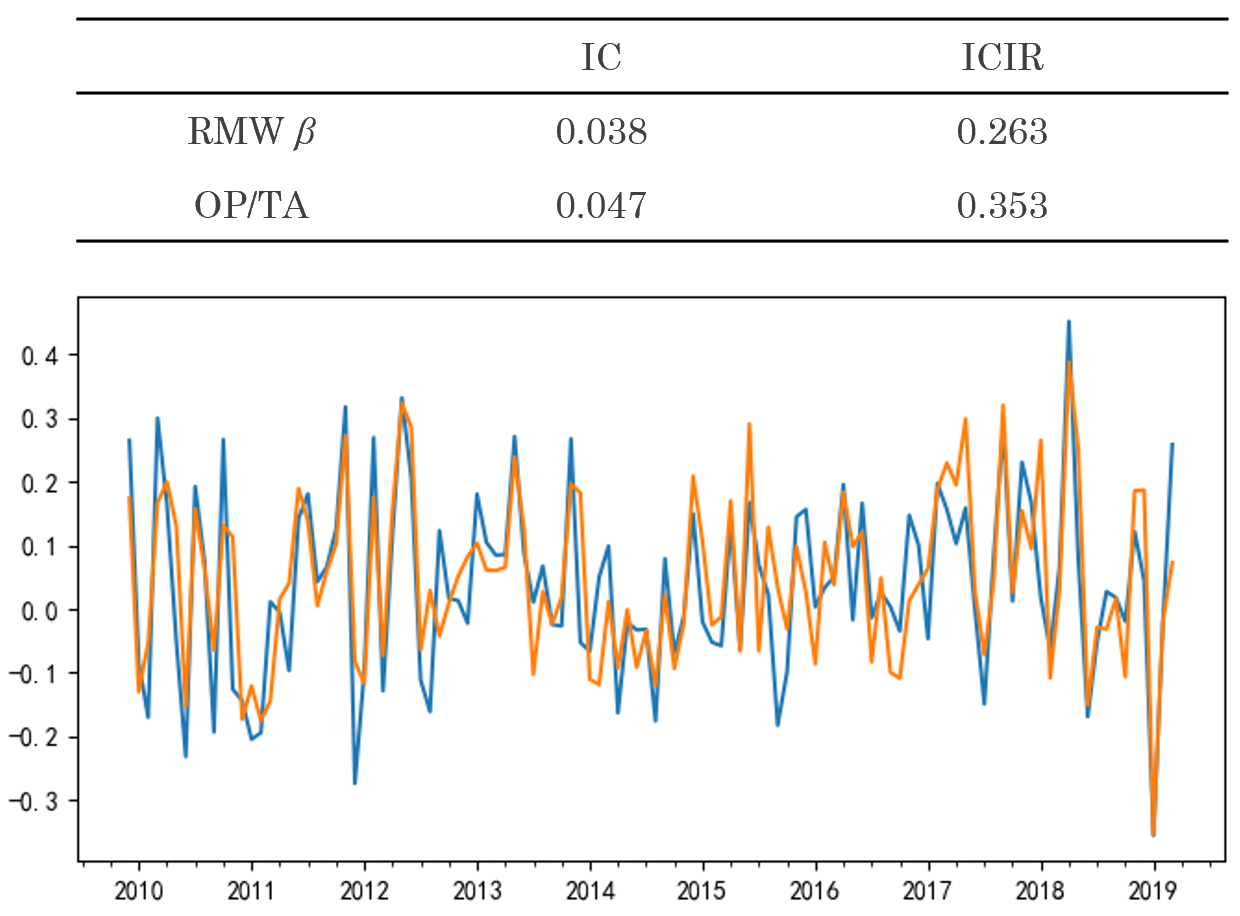
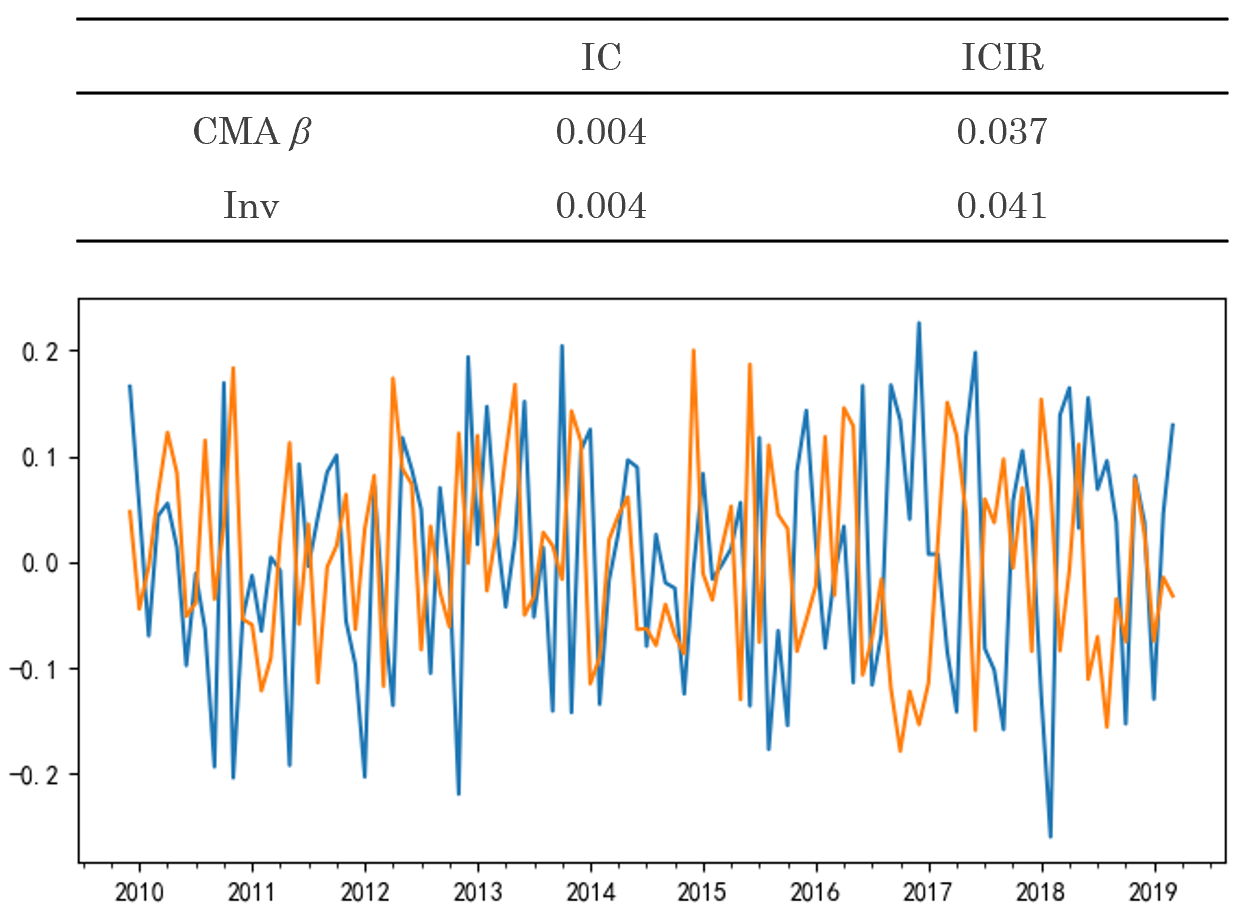
在其他(tā)三個(gè)因子 HML、RMW 以及 CMA 上也(yě)能觀察到類似的(de)結果，這(zhè)裏不再贅述，結果彙總于以下(xià)三張圖。

以上實證結果說明(míng)，作爲因子暴露，firm characteristics 确實比它們對(duì)應的(de)因子 β 有更好的(de)預測性。但這(zhè)背後的(de)原因是什(shén)麽呢(ne)？近日，Richard Roll 和(hé)他(tā)的(de) co-authors 在 Review of Financial Studies 上發表了(le)一篇題爲 A protocol for factor identification 的(de)文章(zhāng)（Pukthuanthong, Roll, and Subrahmanyam 2019），闡述了(le)一個(gè)系統識别因子的(de)規程。這(zhè)篇文章(zhāng)本身非常值得(de)一讀，不過我提它是因爲一個(gè) side note。

這(zhè)篇文章(zhāng)最早寫于 2015 年并獲得(de)了(le) The Q Group 的(de) Jack Treynor 獎；Richard Roll 也(yě)于 2016 年應邀做(zuò)了(le)該文的(de)報告。在報告中，他(tā)指出因子本身的(de)運動是難以預測的(de)，因此像 firm characteristics 這(zhè)些可(kě)以提前知道的(de)指标不能成爲因子。它們能夠獲得(de)風險溢價可(kě)能有兩個(gè)原因：（1）它們是未知因子暴露的(de) good proxy；（2）它們代表了(le)套利機會。

我們知道如果以 B/P 來(lái)構建一個(gè)多(duō)空組合，該組合的(de)波動其實是很大(dà)的(de)，它并不代表某種無風險套利機會，因此上述第二個(gè)原因難以說通(tōng)。所以，更有可(kě)能的(de)是這(zhè)些 firm characteristics 有效的(de)代表了(le)因子暴露。需要強調的(de)是，“firm characteristics 是更好的(de)因子暴露”這(zhè)個(gè)觀點仍然是一種猜測。Jegadeesh et al. (2019) 就這(zhè)一點構建了(le)一個(gè)假設，但很遺憾實證數據并沒有支持這(zhè)個(gè)觀點。我們在此給出 which beta 之問的(de)第二個(gè)觀點：同時(shí)考慮 firm characteristics 和(hé)時(shí)序回歸系數時(shí)，後者無法獲得(de)顯著 risk premium；從實證結果來(lái)看，firm characteristics 确實是更好使的(de)因子暴露，但背後的(de)原因依然未知。

6 結語

如今，無論是檢驗單個(gè)因子還(hái)是因子模型，僅使用(yòng)有限個(gè)投資組合作爲 LHS 都難以令人(rén)滿意。正因如此，學者們提出使用(yòng)個(gè)股的(de)收益率作爲 LHS。但由于 EIV 的(de)問題，如何計算(suàn)個(gè)股的(de)因子暴露 β 至關重要。本文就 which beta 問題進行了(le)系統的(de)闡述。

文章(zhāng)從 Jegadeesh et al. (2019) 提出的(de) IV estimate 出發，考慮了(le)時(shí)序回歸估計 β，并引入 firm characteristics 作爲控制變量，構建了(le)一共 4 個(gè) tests 檢驗了(le) Fama and French (2015) 五因子模型在中證 500 上是否能夠獲得(de)顯著 risk premium。作爲回顧，這(zhè) 4 個(gè) tests 的(de)設定總結于下(xià)表。

綜合本文的(de)實證結果，關于 which beta 的(de)探討(tǎo)得(de)到以下(xià)兩個(gè)觀點：

正确計算(suàn)因子暴露至關重要。例如，在業績歸因時(shí)，如果不知道具體的(de)持倉明(míng)細，就隻能把待歸因的(de)收益率作爲被解釋變量、把因子收益率作爲解釋變量進行時(shí)序回歸，以回歸系數 β 作爲評價的(de)依據（AQR 用(yòng)自家的(de)多(duō)個(gè)風格因子對(duì)美(měi)股上多(duō)位傳奇大(dà)佬的(de)收益進行過業績歸因）。又如，在構建宏觀因子模型（macroeconomic factor models）時(shí)，由于宏觀經濟數據不是公司财務指标，因此隻能通(tōng)過時(shí)序回歸計算(suàn)股票(piào)在這(zhè)些因子上的(de)因子暴露（比如常見的(de)對(duì) GDP、利率的(de)敏感度等）。

在 Fama and French (1996) 這(zhè)篇著名的(de)解讀三因子模型的(de)文章(zhāng)中，兩位作者指出，解釋一支股票(piào)的(de)截面收益應該關注的(de)是它和(hé)因子之間的(de) β，而非公司指标上的(de)取值 —— 比如 B/P 小的(de)公司如果在 HML 上的(de)暴露大(dà)，那麽該公司實際上會被認爲是價值股，而非成長(cháng)股。

以上例子都說明(míng)，使用(yòng)時(shí)序回歸 β 是符合我們認知的(de)。但實證數據顯示的(de)卻又是另一個(gè)故事。當個(gè)股收益率被放在 LHS 時(shí)，firm characteristics 完勝時(shí)序回歸系數：前者能獲得(de) risk premium，但後者卻不行。而 Jegadeesh et al. (2019) 的(de)分(fēn)析表明(míng)，firm characteristics 作爲因子暴露時(shí)，它們和(hé)未來(lái)因子暴露之間的(de)相關性甚至還(hái)低于使用(yòng)曆史數據時(shí)序回歸的(de) β 和(hé)未來(lái)因子暴露的(de)相關性。這(zhè)就是爲什(shén)麽他(tā)們把這(zhè)個(gè)現象稱作未解之謎。

對(duì)于到底該使用(yòng)時(shí)序回歸系數還(hái)是 firm characteristics 作爲因子暴露，《股票(piào)多(duō)因子模型的(de)回歸檢驗》的(de)第六節曾有過簡單討(tǎo)論（今天算(suàn)是個(gè)進階版）。盡管在實證中 firm characteristics 獲得(de)了(le)顯著的(de) risk premium，用(yòng)它作爲因子暴露也(yě)不能說 100% 有道理(lǐ)。從多(duō)因子模型來(lái)說，股票(piào)在因子上的(de)收益正比于它們的(de)因子暴露。但像對(duì)數市值或 P/B 這(zhè)些指标，即使公司 A 的(de)指标是公司 B 的(de)兩倍，也(yě)不能說 A 在該因子上獲得(de)的(de)收益率就是 B 的(de)兩倍；從因子模型的(de)本質來(lái)說，收益率時(shí)序回歸系數作爲因子暴露更加合理(lǐ)。但另一方面，當公司基本面發生較大(dà)變化(huà)時(shí)，回歸系數的(de)變化(huà)又不能及時(shí)、準确的(de)反映股票(piào)在因子上暴露的(de)變化(huà)。無論如何，選擇正确的(de)因子暴露是我們需要解決的(de)問題。

從“真香”的(de)角度來(lái)說，似乎使用(yòng) firm characteristics 無可(kě)厚非；但是從真相的(de)角度來(lái)說，我們還(hái)有很長(cháng)的(de)路要走。

So, which beta?

參考文獻

Black, F., M. C. Jensen, and M. Scholes (1972). The capital asset pricing model: Some empirical tests. In Studies in the Theory of Capital Markets. M. C. Jensen (ed), New York: Praeger, 79 – 121.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K. R. French (1996). Multifactor explanations of asset pricing anomalies. Journal of Finance 51(1), 55 – 84.

Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.

Fama, E. F. and K. R. French (2019). Comparing Cross-Section and Time-Series Factor Models. Chicago Booth Research Paper No. 18-08; Fama-Miller Working Paper.

Fama, E. F. and J. D. MacBeth (1973). Risk, Return, and Equilibrium: Empirical Tests. Journal of Political Economy 81(3), 607 – 636.

Hou, K., C. Xue, L. Zhang (2015). Digesting anomalies: an investment approach. Review of Financial Studies 28(3), 650 – 705.

Jegadeesh, N., J. Noh, K. Pukthuanthong, R. Roll, and J. Wang (2019). Empirical tests of asset pricing models with individual assets: Resolving the errors-in-variables bias in risk premium estimation. Journal of Financial Economics 133(2), 273 – 298.

Lewellen, J., S. Nagel, and J. Shanken (2010). A skeptical appraisal of asset pricing tests. Journal of Financial Economics 96(2), 175 – 194.

Newey, W. K. and K. D. West (1987). A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 55(3), 703 – 708.

Pukthuanthong, K., R. Roll, and A. Subrahmanyam (2019). A protocol for factor identification. Review of Financial Studies 32(4), 1573 – 1607.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。