使用(yòng)正交化(huà)和(hé)自助法尋找顯著因子

作者：石川

摘要：本文在 A 股上複現 Harvey and Liu (2018) 提出的(de)方法，使用(yòng)正交化(huà)和(hé)自助法尋找顯著的(de)因子。

1 引言

《出色不如走運 (II)》一文曾介紹了(le) Harvey and Liu (2018) 提出的(de)基于回歸的(de)因子有效性檢驗方法。該方法避免了(le)因 multiple testing 造成的(de)運氣成分(fēn)、從而鑒别出能顯著解釋資産截面預期收益率差異的(de)因子。考慮到《出色不如走運 (II)》涉及的(de)内容理(lǐ)論有餘、實證不足，本文以中證 500 指數成分(fēn)股爲例，做(zuò)一些實證分(fēn)析，同時(shí)也(yě)指出在大(dà) A 股中應用(yòng) Harvey and Liu (2018) 時(shí)遇到的(de)一些坑。

首先簡單回歸一下(xià) Harvey and Liu (2018) 提出的(de)方法。當大(dà)量因子同時(shí)被用(yòng)做(zuò) empirical asset pricing 分(fēn)析時(shí)，它們之中效果最顯著的(de)因子中一定包含了(le)運氣的(de)成分(fēn)。Harvey and Liu (2018) 巧妙之處在于通(tōng)過正交化(huà)和(hé)自助法（Bootstrap）得(de)到了(le)僅靠運氣能夠得(de)到的(de)顯著性的(de)經驗分(fēn)布；如果當排除了(le)運氣造成的(de)顯著性之後某個(gè)因子依然顯著，那它就是真正有效的(de)因子。下(xià)圖高(gāo)度概括了(le)該方法的(de)邏輯（正交化(huà)和(hé) Bootstrap 是核心）。

值得(de)一提的(de)是，Harvey and Liu (2018) 提出的(de)方法既可(kě)以用(yòng)針對(duì) empirical asset pricing 找出顯著因子；也(yě)可(kě)以用(yòng)于更一般的(de) predictive regression —— 即考察解釋變量 X 能否預測被解釋變量 Y。面對(duì)不同的(de)問題，正交化(huà)和(hé) Bootstrap 的(de)核心思想是一緻的(de)，但在具體處理(lǐ)方法上存在差異。《出色不如走運 (II)》 一文以 predictive regression 爲例詳細介紹了(le)該方法，本文不再贅述。以下(xià)行文将假設讀者了(le)解 Harvey and Liu (2018)。但是，我會針對(duì) empirical asset pricing 問題，說明(míng)使用(yòng)正交化(huà)和(hé) Bootstrap 時(shí)的(de)各種細節。這(zhè)篇實證的(de)目的(de)更多(duō)的(de)是介紹在 A 股上如何複現 Harvey and Liu (2018)。相反的(de)，由于實證中的(de)因子以及用(yòng)來(lái)檢驗這(zhè)些因子的(de)一組資産，均無法避免的(de)存在主觀成分(fēn)（本文最後一節會再聊聊這(zhè)點），因此實證結果僅是示例性的(de)。

2 Block Bootstrap

先來(lái)說說 Bootstrap。本來(lái) Bootstrap 無需多(duō)言（需要背景知識的(de)朋友請點這(zhè)裏），但是數據的(de)特殊性決定了(le) Bootstrap 的(de)特殊性。在 Harvey and Liu (2018) 的(de)方法中，需要進行 Bootstrap 的(de)數據是資産的(de)收益率和(hé)正交化(huà)後的(de)因子收益率時(shí)間序列。由于時(shí)間序列存在自相關性，因此在重采樣的(de)時(shí)候應使用(yòng) Block Bootstrap。顧名思義，Block Bootstrap 就是每次從序列中有放回的(de)抽取一個(gè)由連續 n 個(gè)相鄰數據點構成的(de) block（大(dà)小由 block size 決定）。主流的(de) Block Bootstrap 算(suàn)法包括以下(xià)三種：

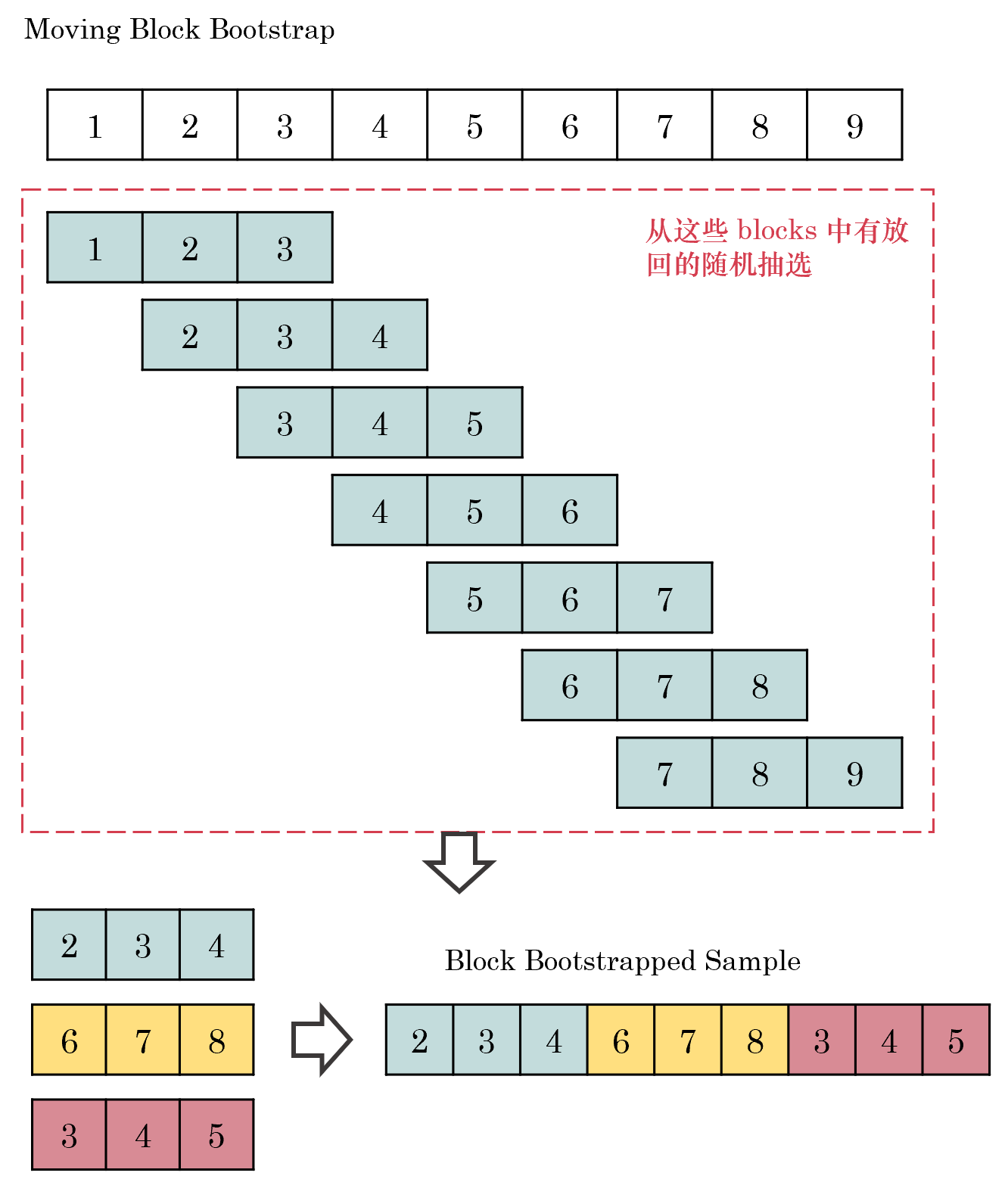
下(xià)圖說明(míng)了(le) Moving Block Bootstrap（MBB）的(de)原理(lǐ)。假設原始數據由 1 – 9 組成，且令 block size = 3。MBB 依次以序列中的(de)每個(gè)數字爲起點構建長(cháng)度爲 3 的(de) blocks（本例中一共 7 個(gè)），然後從這(zhè) 7 個(gè) blocks 中有放回的(de)随機抽取，直至構成和(hé)原始序列長(cháng)度一樣的(de) bootstrapped sample。

從上圖的(de)原理(lǐ)可(kě)知，MBB 最大(dà)的(de)問題是對(duì)于原始序列首尾兩端樣本采樣不足。爲了(le)規避這(zhè)個(gè)問題，Circular Block Bootstrap（CBB）被提出。顧名思義，它是将原始數據的(de)首尾相連，構成一個(gè)圓圈（Circular 一詞的(de)出處），然後再按照(zhào)給定的(de) block size 進行重采樣，避免首尾兩端采樣不足。

最後一種方法是 Stationary Bootstrap（SB），它和(hé)前兩者最大(dà)的(de)區(qū)别是使用(yòng)非固定的(de) block size。SB 中的(de) block size 滿足幾何分(fēn)布；作爲輸入而給定的(de) block size 是它的(de)期望。該方法得(de)到的(de) bootstrapped 樣本可(kě)以更好的(de)滿足平穩性的(de)要求，因此當原始時(shí)間序列難以滿足平穩性時(shí)有更好的(de)效果。

本文的(de)實證采用(yòng) stationary bootstrap，并在第四節說明(míng)原因。

3 因子模拟和(hé)投資組合

Harvey and Liu (2018) 的(de)目的(de)是找到能夠真正解釋資産截面預期收益率差異的(de)顯著因子。因此在實證中，我們需要選定多(duō)因子模型，以及用(yòng)來(lái)檢驗這(zhè)些因子的(de)一組資産。在因子方面，實證中選擇 Fama and French (2015) 五因子以及 Carhart (1997) 的(de)動量因子，一共六個(gè)因子：MKT、HML、SMB、RMW、CMA 和(hé) UMD。構建這(zhè)些因子的(de)标的(de)均爲中證 500 的(de)成分(fēn)股；實證區(qū)間爲 2008 年 10 月(yuè)到 2019 年 2 月(yuè)。每個(gè)月(yuè)最後一個(gè)交易日排除停牌的(de)股票(piào)，使用(yòng)剩餘成分(fēn)股構建多(duō)空投資組合（多(duō)、空兩邊均等權配置），以此計算(suàn)每個(gè)因子下(xià)個(gè)月(yuè)的(de)收益率，全部數據均來(lái)自 JoinQuant。具體的(de)，這(zhè)些因子定義如下(xià)：

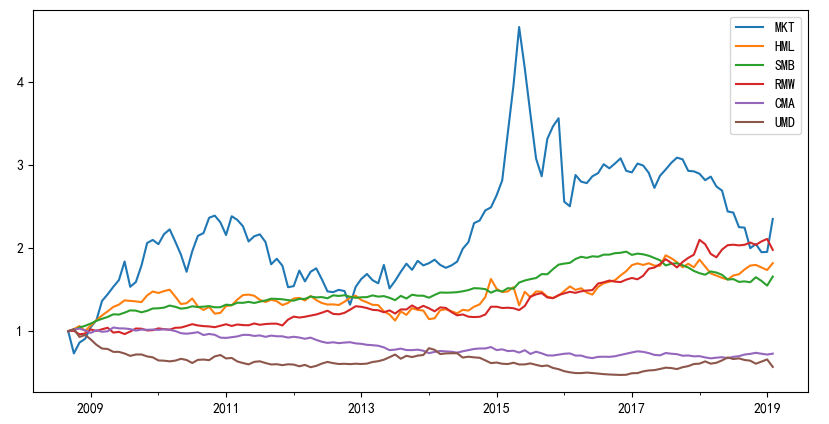
這(zhè)六個(gè)因子在實證區(qū)間内的(de)累積淨值如下(xià)圖所示。

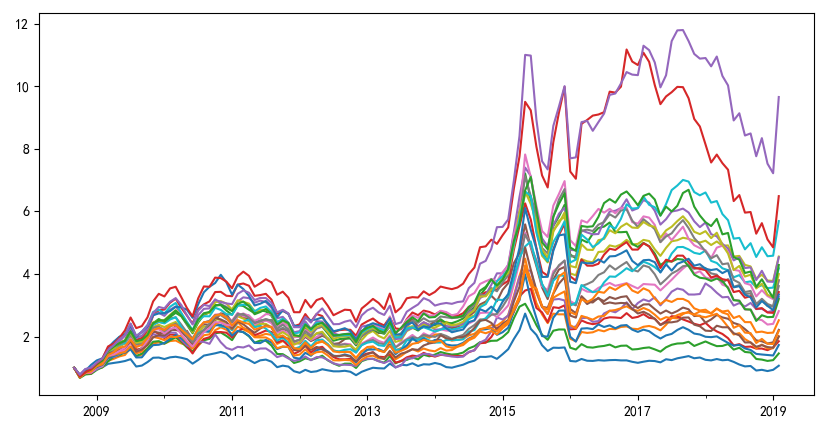
下(xià)面再來(lái)看看用(yòng)來(lái)檢驗因子的(de)一組資産。由于多(duō)因子模型是用(yòng)來(lái)給個(gè)股的(de)超額收益定價的(de)，因此最純粹的(de)實證是使用(yòng)個(gè)股。考慮到本文更多(duō)的(de)是爲了(le)說明(míng)如何複現 Harvey and Liu (2018)、實證結果僅是示例性的(de)，因此我們也(yě)像 Harvey and Liu (2018) 一樣，考慮使用(yòng) BP 和(hé)流通(tōng)市值 double sort 得(de)到的(de)投資組合作爲資産。具體的(de)，将中證 500 成分(fēn)股按照(zhào) BP 和(hé)流通(tōng)市值的(de)大(dà)小各分(fēn)成五檔，并按照(zhào)個(gè)股在兩個(gè)指标上的(de)檔位取值将它們歸類于 5 × 5 = 25 個(gè)投資組合中的(de)某一個(gè)，由此構建 25 個(gè)純多(duō)頭投資組合。這(zhè) 25 個(gè)投資組合在實證區(qū)間内的(de)累積淨值如下(xià)圖所示。

下(xià)面用(yòng)這(zhè) 25 個(gè)投資組合檢驗上述六個(gè)因子。

4 挑選有效因子

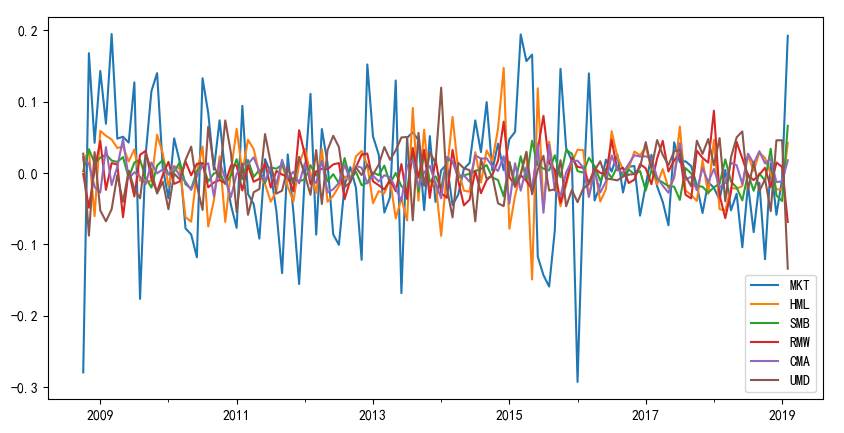
在檢驗有效因子時(shí)，Harvey and Liu (2018) 的(de)思路是反複使用(yòng)正交化(huà) + 自助法，逐一找到顯著的(de)因子，直到所有剩餘因子中沒有任何顯著的(de)。下(xià)面就來(lái)進行這(zhè)個(gè)過程。在第一輪中，這(zhè)六個(gè)因子是否顯著都是未知的(de)。首先對(duì)它們進行正交化(huà)處理(lǐ)。正交化(huà)的(de)目的(de)是排除因子對(duì)資産截面預期收益差異的(de)解釋能力；正交化(huà)的(de)手段是對(duì)因子收益率序列在時(shí)序上去均值（demean）。時(shí)序上 demean 不改變這(zhè)些因子對(duì)于資産收益率波動的(de)解釋力度（時(shí)序回歸的(de) R-squared 不變），但由于 demean 之後因子收益率期望爲零，使用(yòng) demean 因子對(duì)資産進行時(shí)序回歸得(de)到的(de)截距恰好等于資産本身的(de)時(shí)序均值，說明(míng) demean 因子在截面上不再具備解釋能力。這(zhè)六個(gè)因子 demean 之後的(de)時(shí)序如下(xià)圖所示。

由于 A 股上旗幟鮮明(míng)的(de)牛熊市，demean 之後的(de) MKT 因子（以及其他(tā)一些因子）難以滿足平穩性，如不加以處理(lǐ)，将會影(yǐng)響 Harvey and Liu (2018) 的(de)使用(yòng)。該方法的(de)本質是 demean 之後的(de)因子無法解釋資産預期收益率的(de)截面差異（能解釋的(de)都是運氣），因此在 bootstrap 時(shí)應保證 bootstrapped 樣本中這(zhè)些 demean 之後的(de)因子的(de)收益率依然爲零。如果使用(yòng) MBB，由于對(duì)原始序列兩端采樣不足，則會使 bootstrapped 樣本中 demean 後因子的(de)收益率均值對(duì)于實證窗(chuāng)口的(de)選擇異常敏感。例如上圖中，原始序列兩端 demean 之後的(de) MKT 收益率一個(gè)很小、一個(gè)巨大(dà)，如果采樣不足會影(yǐng)響 bootstrapped 樣本。爲此，在實證中選擇将原始序列首尾相連的(de) Stationary Bootstrap。這(zhè)是在 A 股中複現 Harvey and Liu (2018) 時(shí)的(de)第一個(gè)坑。

下(xià)面再來(lái)說說第二個(gè)。我在一開始選擇的(de)實證窗(chuāng)口是 2010 年 1 月(yuè)到 2019 年 2 月(yuè)，而非從 2008 年 10 月(yuè)開始。然而，由于中證 500 指數在這(zhè)段時(shí)間内漲上去又跌回來(lái)，導緻 MKT 因子的(de)收益率期望接近零。這(zhè)就意味著(zhe)，哪怕不 demean，由于 E[MKT] ≈ 0，MKT 因子對(duì)于資産截面收益率的(de)解釋力度也(yě)十分(fēn)有限。對(duì)于一個(gè)真正有效的(de)因子，demean 的(de)目的(de)是排除它的(de)截面解釋能力，把它暫時(shí)視作一個(gè)随機因子（随機因子的(de)期望收益爲零），從而僅考察由于多(duō)個(gè)因子 multiple testing 中的(de)運氣成分(fēn)能造成的(de)解釋力度。不幸的(de)是，如果選擇從 2010 年 1 月(yuè)開始的(de)實證區(qū)間，我們這(zhè)位 MKT 因子都不需要 demean 就 E[MKT] ≈ 0 了(le)，剩下(xià)再怎麽檢驗，它也(yě)難言有效，從而造成錯誤的(de)結論。這(zhè)就是第二個(gè)坑。OK，坑挖完了(le)也(yě)填完了(le)，下(xià)面繼續實證。

分(fēn)别使用(yòng)這(zhè)六個(gè)因子和(hé) 25 個(gè)投資組合收益率做(zuò)時(shí)序回歸。對(duì)于每個(gè)因子，得(de)到 25 個(gè)回歸截距，它們是這(zhè)些投資組合在使用(yòng)該因子時(shí)的(de)定價錯誤。使用(yòng)這(zhè) 25 個(gè)截距絕對(duì)值的(de)中位數作爲該因子解釋這(zhè)些投資組合的(de)能力。定價錯誤低意味著(zhe)解釋力度高(gāo)，因此該中位數越小說明(míng)因子越有效。此外，爲了(le)計算(suàn)僅憑運氣能夠獲得(de)的(de)顯著性，将原始 25 個(gè)投資組合的(de)收益率序列和(hé) demean 之後六個(gè)因子的(de)收益率序列放在一起（T × 31 階矩陣），令 block size = 4，進行 1000 次 stationary bootstrap，得(de)到 1000 個(gè) bootstrapped 樣本。對(duì)于每個(gè)樣本，分(fēn)别使用(yòng)每個(gè) demean 因子對(duì)這(zhè) 25 個(gè)投資組合進行時(shí)序回歸、得(de)到 6 個(gè)截距絕對(duì)值中位數，将這(zhè) 6 個(gè)中位數中的(de)最小值作爲 test statistic，它就是在這(zhè)個(gè) bootstrapped 樣本中，僅靠運氣能夠獲得(de)的(de)最低定價錯誤。

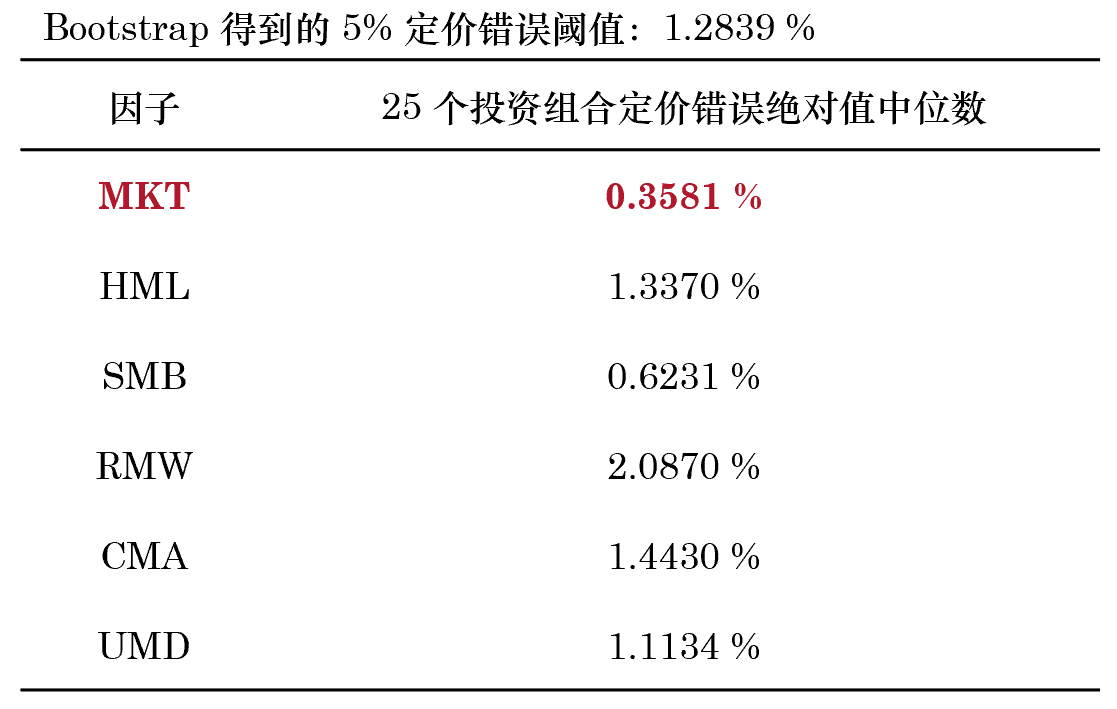
從 1000 個(gè) bootstrapped 樣本中得(de)到 1000 個(gè) test statistic，便構成了(le)它的(de)分(fēn)布，這(zhè)就是僅靠運氣能夠得(de)到的(de)定價錯誤分(fēn)布。使用(yòng)該分(fēn)布 5% 分(fēn)位數作爲阈值，如果原始因子獲得(de)的(de)定價錯誤小于該阈值，我們就說該因子在 5% 的(de)顯著性水(shuǐ)平下(xià)有效。在第一輪中，這(zhè)六個(gè)因子對(duì) 25 個(gè)投資組合定價錯誤絕對(duì)值的(de)中位數、以及使用(yòng) 1000 次 stationary bootstrap 獲得(de)的(de) test statistic 阈值如下(xià)表所示。不難看出，MKT 的(de)解釋力度最高(gāo)且小于阈值，因此 MKT 被選爲第一個(gè)有效的(de)因子。第一輪正交化(huà) + 自助法結束。

下(xià)面來(lái)看第二輪（後面的(de)以此類推）。在第二輪中，已選出的(de) MKT 将會出現在時(shí)序回歸方程的(de)右側，這(zhè)麽做(zuò)是爲了(le)考察剩餘待檢驗因子對(duì)于解釋資産預期收益截面差異的(de)增量貢獻。首先，對(duì)于 SMB、HML、RMW、CMA、UMD 的(de)每一個(gè)，将它們和(hé)已經選定的(de) MKT 一起（如果是第 n 輪正交化(huà) + 自助法，則使用(yòng)前 n – 1 輪中選出的(de) n – 1 個(gè)因子），對(duì)那 25 個(gè)投資組合進行時(shí)序回歸，得(de)到的(de)截距項絕對(duì)值的(de)中位數作爲這(zhè)五個(gè)因子的(de)解釋力度。

接下(xià)來(lái)，使用(yòng) MKT（again，如果是第 n 輪正交化(huà) + 自助法，則使用(yòng)前 n – 1 輪中選出的(de)全部因子）對(duì)待檢驗因子正交化(huà)。具體做(zuò)法爲，将待檢驗因子依次放在回歸方程左側，将已經選出的(de)因子放在回歸方程的(de)右側，時(shí)序回歸得(de)到截距項；使用(yòng)原始待檢驗因子減去截距項（也(yě)是一種 demean 處理(lǐ)），得(de)到的(de)就是其正交化(huà)之後的(de)因子。該方法保證了(le)使用(yòng) demean 的(de)待檢驗因子和(hé)已選出因子一起對(duì)資産時(shí)序回歸時(shí)得(de)到的(de)截距和(hé)僅使用(yòng)已選出因子對(duì)資産時(shí)序回歸時(shí)得(de)到的(de)截距相同，從而說明(míng) demean 後的(de)待檢驗因子無增量貢獻。

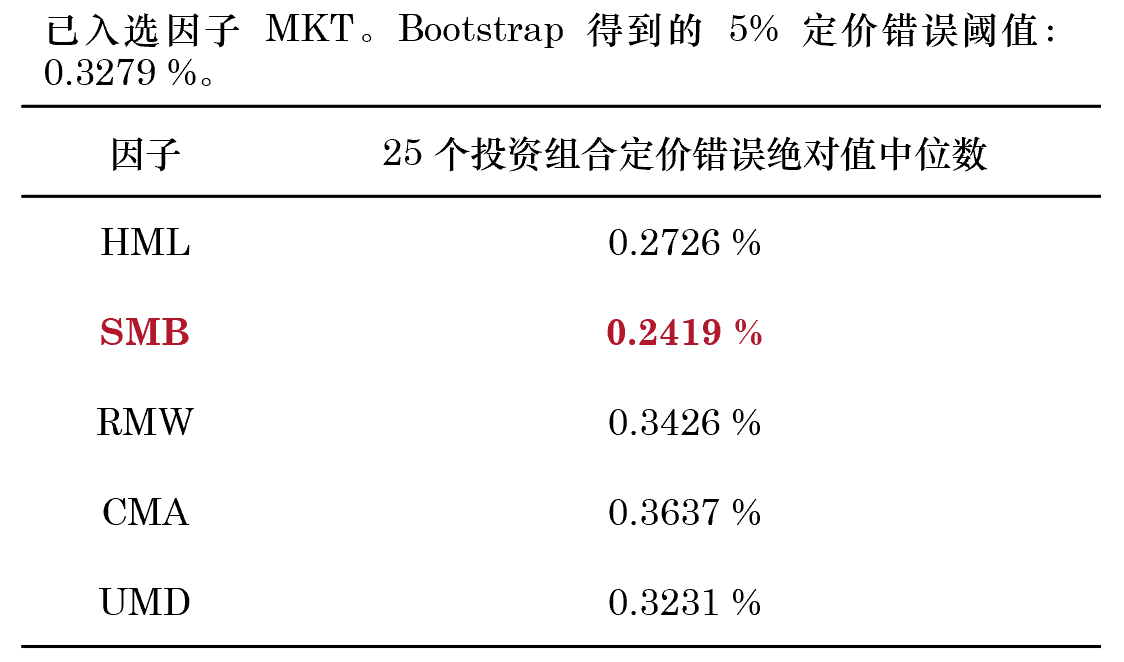
将正交化(huà)後的(de)五個(gè)因子和(hé)原始 MKT 因子一起，和(hé) 25 個(gè)投資組合收益率序列放在一起，構成一個(gè) T × 31 階矩陣。對(duì)其并進行 1000 次 stationary bootstrap 的(de)到 1000 個(gè) bootstrapped 樣本。對(duì)于每一個(gè)樣本，逐一使用(yòng) demean 後的(de)因子，将它和(hé)已選出的(de)因子一起（這(zhè)裏是 MKT），對(duì)這(zhè) 25 個(gè)投資組合回歸，得(de)到截距絕對(duì)值中位數；然後從這(zhè)五個(gè)因子中挑出中位數最低的(de)，它就是該 bootstrapped 樣本的(de) test statistic。這(zhè) 1000 個(gè) bootstrapped 樣本的(de) test statistic 取值便構成了(le)它的(de)分(fēn)布。下(xià)表是第二輪中這(zhè)五個(gè)因子的(de)解釋能力以及 test statistic 的(de) 5% 分(fēn)位數阈值。其中，SMB 的(de)解釋力度最高(gāo)且小于阈值，因此 SMB 被選爲第二個(gè)有效因子。第二輪正交化(huà) + 自助法結束。

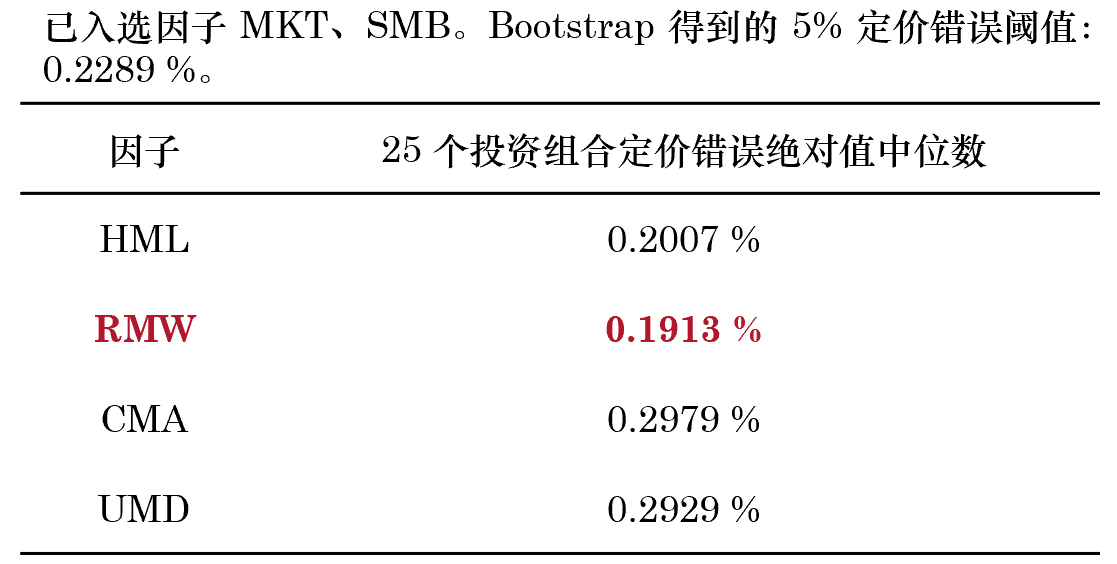
按上述說明(míng)，反複使用(yòng)正交化(huà) + 自助法，直至沒有顯著的(de)因子。在第三輪中的(de)結果如下(xià)，RMW 因子被選出。

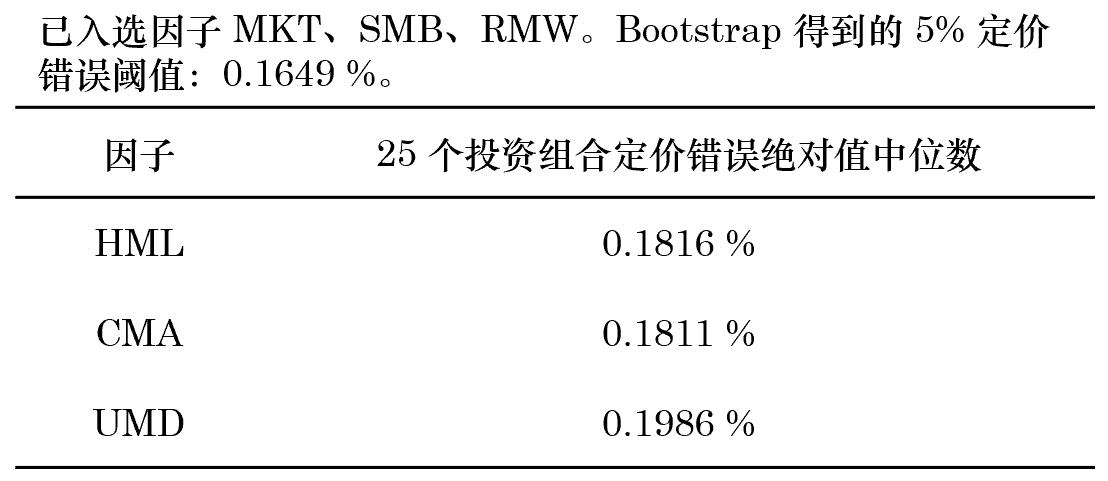
第四輪的(de)結果如下(xià)，剩餘三個(gè)因子的(de)解釋力度均無法超過 test statistic 阈值，因此全部被拒絕、檢驗結束。最終選出的(de)因子爲：MKT + SMB + RMW。

以上就是對(duì) Harvey and Liu (2018) 的(de)實證研究。

5 結語

Harvey and Liu (2018) 這(zhè)篇文章(zhāng)十分(fēn) technical。我在《出色不如走運 (II)》對(duì)它的(de)理(lǐ)論部分(fēn)做(zuò)了(le)介紹，但是不甚滿意，因此便有了(le)這(zhè)篇實證，希望這(zhè)篇沒那麽晦澀（但我覺著(zhe)也(yě)挺晦澀的(de)……）。想對(duì)它進一步加深理(lǐ)解的(de)小夥伴，我推薦翻牆去 YouTube 上看 Prof. Harvey 在 Jacobs Levy Center 年會上題爲 Lucky Factors 的(de)演講，它能幫我們跳出細節、從全局掌握該方法的(de)實質。從我的(de)實證體會來(lái)說，最難的(de)不是方法本身，而是如何盡可(kě)能客觀的(de)選擇多(duō)因子模型以及用(yòng)來(lái)檢驗該模型的(de)資産。

在 empirical asset pricing 的(de)研究中，最著名的(de)文章(zhāng)當屬 Fama 和(hé) French 的(de)一系列文章(zhāng)。無疑，這(zhè)和(hé)他(tā)們開創性的(de)研究密不可(kě)分(fēn)，但不容忽視的(de)一點是，人(rén)家 marketing 做(zuò)的(de)好！Ken French 在其網站上定期更新因子收益率序列供所有人(rén)免費下(xià)載。這(zhè)些高(gāo)質量且被市場(chǎng)廣泛認可(kě)的(de)數據爲美(měi)股研究的(de)蓬勃發展奠定了(le)堅實的(de)基礎。反觀 A 股，很難找到大(dà)家都認可(kě)的(de)标準化(huà)因子收益率數據，這(zhè)造成不同人(rén)對(duì)于哪怕是對(duì)同一因子的(de)研究結果都有可(kě)能大(dà)相徑庭。（就我有限的(de)所知，中央财經大(dà)學維護了(le)針對(duì)全 A 股的(de) Fama-French 五因子 + Carhart 動量因子數據。）究其原因是因爲處理(lǐ)因子數據背後的(de)細節太過紛繁 —— 按什(shén)麽頻(pín)率調倉；具體使用(yòng)什(shén)麽指标（比如當期還(hái)是 TTM）；依何種權重配置多(duō)空組合；如何處理(lǐ) ST、漲跌停、停牌、退市等股票(piào)。

但即便有各種困難，爲了(le)在 A 股上得(de)到更加客觀、公允的(de)實證分(fēn)析結果（無論某個(gè)因子是有效還(hái)是無效都是有價值的(de)發現），構建标準化(huà)因子數據的(de)努力都必不可(kě)少。（最近，我在構思寫一篇比較學術界主流多(duō)因子模型在 A 股上的(de)效果分(fēn)析文章(zhāng)，但是第一步就是要獲得(de)客觀、标準的(de)因子收益率。）希望未來(lái)能有更多(duō)的(de)你、我（特别是市面上的(de)各種量化(huà)平台）能爲此努力，這(zhè)将是造福量化(huà)多(duō)因子研究的(de)大(dà)功績。

參考文獻

Carhart, M. M. (1997). On Persistence in Mutual Fund Performance. Journal of Finance 52(1), 57 – 82.

Fama, E. F. and K. R. French (2015). A Five-Factor Asset Pricing Model. Journal of Financial Economics 116(1), 1 – 22.

Harvey, C. R. and Y. Liu (2018). Lucky Factors. Working paper, available at SSRN: https://ssrn.com/abstract=2528780.

Kunsch, H. R. (1989). The jackknife and the bootstrap for general stationary observations. The Annals of Statistics 17(3), 1217 – 1241.

Liu, R. Y. and K. Singh (1992). Moving blocks jackknife and bootstrap capture weak dependence. In Exploring the Limits of Bootstrap (R. Lepage and L. Billard, eds.), 225 – 248. Wiley, New York.

Politis, D. N. and J. P. Romano (1992). A circular block resampling procedure for stationary data. In Exploring the Limits of Bootstrap (R. Lepage and L. Billard, eds.), 263 – 270. Wiley, New York.

Politis, D. N. and J. P. Romano (1994). The stationary bootstrap. Journal of the American Statistical Association 89(428), 1303 – 1313.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。