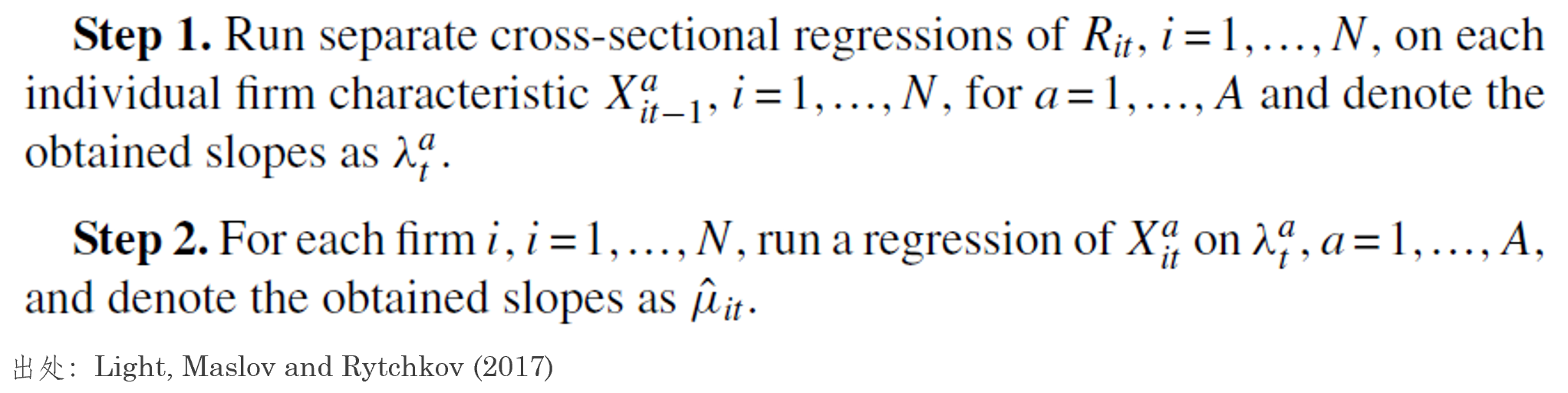更有效的(de)信息聚合方法 ?

發布時(shí)間：2022-06-16 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：協變量的(de)高(gāo)維數時(shí)代，數不勝數的(de)公司特征都和(hé)預期收益相關，然而它們之間存在不能忽視的(de)相關性。在這(zhè)個(gè)背景下(xià)，如何更好地聚合協變量包含的(de)預測信息?

對(duì)于資産定價而言，相信到現在你已經接受了(le)協變量的(de)高(gāo)維數時(shí)代（Kozak, Nagel and Santosh 2020，Giannone, Lenza and Primiceri 2021）。需要補充背景知識的(de)小夥伴請參考《稀疏性幻覺》。然而，面對(duì)層出不窮的(de) factor zoo（Cochrane 2011，Harvey, Liu and Zhu 2016）背後的(de)公司特征，一個(gè)自然的(de)問題是：如何有效地聚合它們所包含的(de)預測信息，從而形成關于預期收益率更好的(de)預測？

在這(zhè)方面，學界和(hé)業界的(de)嘗試從未停止過。比如，最直接的(de)方法是 Fama-MacBeth regression。當然，一旦協變量個(gè)數激增後，這(zhè)個(gè)方法就會受到各種計量經濟學問題的(de)困擾。又比如 rank-based approach，即根據取值高(gāo)低将股票(piào)在每個(gè)公司特征上排名，然後求均值得(de)到綜合排名。這(zhè)個(gè)方法在 Stambaugh, Yu and Yuan (2015) 以及 Stambaugh and Yuan (2017) 中大(dà)放異彩，也(yě)同時(shí)出現在 Asness, Frazzini and Pedersen (2019) 的(de) QMJ 因子構造之中。再比如各種機器學習(xí)算(suàn)法，這(zhè)其中以 PCA 爲代表（Kelly, Pruitt and Su 2019，Kozak, Nagel and Santosh 2020），也(yě)在聚合預測信息的(de)時(shí)候發揮了(le)很大(dà)的(de)作用(yòng)。另外，Lettau and Pelger (2020a, b) 的(de) risk premium PCA 也(yě)是這(zhè)類方法的(de)拓展。《實證資産定價理(lǐ)論新進展》一文的(de)聚合因子信息一節對(duì)上述方法有更多(duō)的(de)介紹。

除此之外，Light, Maslov and Rytchkov (2017) 通(tōng)過将預期收益率視爲隐性變量（latent variable），利用(yòng) partial least squares（PLS）提出了(le)一種新的(de)方法。該方法實操起來(lái)方便，在直覺上也(yě)頗具吸引力。

令 $\mathcal{F}_t$ 表示 $t$ 時(shí)刻所有的(de)信息，則 $t$ 時(shí)刻關于股票(piào)收益率的(de)最佳預測爲：

$\displaystyle \mu_{it}=\mathbb{E}[R_{it+1}|\mathcal{F}_t].$

由已實現收益率和(hé)預期收益率之間的(de)關系，我們進而有：

$\displaystyle R_{it+1}=\mu_{it}+\varepsilon_{it+1}.$

對(duì)于進行分(fēn)析的(de)計量經濟學家而言，預期收益率 $\mu_{it}$ 是無法觀測的(de)，而且他(tā)也(yě)不具備 $\mathcal{F}_t$ 所包含的(de)全部信息。取而代之的(de)是，他(tā)能夠觀測并收集大(dà)量的(de)公司特征 $X_{it}^a, a=1,\cdots,A$ 。在此基礎上，Light, Maslov and Rytchkov (2017) 方法的(de)核心假設是隐性變量 $\mu_{it}$ 是公司特征空間中唯一和(hé)未來(lái)收益率有關的(de)變量，即公司特征和(hé)預期收益率滿足如下(xià)關系（在擴展的(de)模型中，他(tā)們假設預期收益率由多(duō)個(gè)隐性因子 span 而成，感興趣的(de)小夥伴請閱讀原文）： $\displaystyle X_{it}^a=\delta_t^a(\mu_{it}-\bar{\mu}_t)+u_{it}^a.$ 在該模型中， $\bar{\mu}_t$ 爲 $t$ 時(shí)刻預期收益率在截面上的(de)均值，而 $\delta_t^a$ 刻畫(huà)了(le)公司特征和(hé) demean 之後預期收益率的(de)關系。

由于預期收益率是隐性變量，因此計量經濟學家的(de)任務就變成如何通(tōng)過可(kě)觀測到的(de)已實現收益率 $R$ 和(hé)公司特征 $X$ 來(lái)估計 $\mu$ 。爲此，Light, Maslov and Rytchkov (2017) 使用(yòng)了(le) PLS。從直覺上說，PLS 類似 PCA，也(yě)是從一大(dà)堆變量（公司特征）中提取公共的(de)信息。然而，它們之間的(de)差異是，PCA 提取的(de)目标是最能解釋這(zhè)些變量共同運動的(de)信息，而 PLS 的(de)目标則是從這(zhè)些變量之中提取出信息，使得(de)該信息和(hé)目标（即被預測的(de)）變量之間的(de)協方差最大(dà)化(huà)。

The main objective of PLS is the extraction of a common factor from a set of predictive variables that has the highest covariance with the predicted (target) variable. In contrast to PCA and factor analysis, which also extract one or few factors that concisely describe the variability of data and correlations between predictors, respectively, PLS identifies a factor with the best ability to predict the target variable even though this factor may not be the most important source of common variation in the predictors.

按照(zhào) Light, Maslov and Rytchkov (2017) 自己的(de)話(huà)說，PLS 的(de)這(zhè)個(gè)特點正是它相比于 PCA 的(de)優勢所在。因爲有些公共信息僅僅解釋了(le)特征的(de)共同波動但是卻和(hé)預期收益率無關，這(zhè)些信息對(duì)于解釋資産的(de)預期收益率來(lái)說是沒有幫助的(de)，因此會影(yǐng)響 PCA 的(de)結果，而 PLS 卻不會。爲此，該文提出了(le)一個(gè)兩步截面回歸來(lái)估計預期收益率：

在第一步中，用(yòng) $t$ 期已實現收益率分(fēn)别對(duì) $t-1$ 期每個(gè)公司特征獨立進行截面回歸，得(de)到每個(gè)特征各自的(de)斜率 $\lambda_t^a$ 。在第二步中，對(duì)每個(gè)公司 $i$ ，将 $t$ 時(shí)刻的(de)公司特征 $X_{it}^a$ 對(duì)第一部得(de)到的(de) $\lambda_t^a$ 進行回歸，得(de)到斜率 $\hat{\mu}_{it}$ 。Light, Maslov and Rytchkov (2017) 證明(míng)了(le)第二步回歸所得(de)到的(de)斜率的(de)統計特性，指出它就是 $t$ 時(shí)刻截面上 demean 之後預期收益率的(de)估計（up to a scaling factor）。

值得(de)一提的(de)是，在上述兩步估計中，第一步僅用(yòng)到了(le) $t$ 和(hé) $t-1$ 時(shí)刻的(de)信息，而第二步僅用(yòng)到了(le) $t$ 時(shí)刻的(de)信息。因此這(zhè)不僅僅是一個(gè)事後的(de) in-sample test，而且還(hái)是在實際投資中可(kě)以用(yòng)來(lái)構造樣本外投資組合的(de)方法。在樣本外使用(yòng)時(shí)，有兩點需要注意。首先，上述估計值和(hé)真實 demean 預期收益率差了(le)一個(gè) scaling factor。第二，即便沒有 scaling factor 的(de)顧慮，上述估計也(yě)是截面上 demean 的(de)預期收益率。所以如果基于該預期收益率的(de)估計來(lái)進行樣本外選股，那麽 portfolio sort 無疑就是最自然的(de)選擇，因爲它不受 scaling 或者 shift 的(de)影(yǐng)響。這(zhè)也(yě)正是 Light, Maslov and Rytchkov (2017) 在實證中采用(yòng)的(de)方法。此外，在實操層面，還(hái)有另外一個(gè)技巧。上述兩步法的(de)第一步類似 Fama-MacBeth 的(de)第二步，使用(yòng)單期收益率對(duì)單期公司特征回歸（FM 是對(duì) beta 回歸），得(de)到 $t$ 期的(de) $\lambda_t^a$ 。考慮到單期數據噪聲比較大(dà)，因此可(kě)以使用(yòng)過去一段時(shí)間的(de)數據，并在每一期 $s\le t$ 進行估計，并将它們的(de) $\lambda_s^a$ 取平均得(de)到更準确的(de) $\lambda$ 。

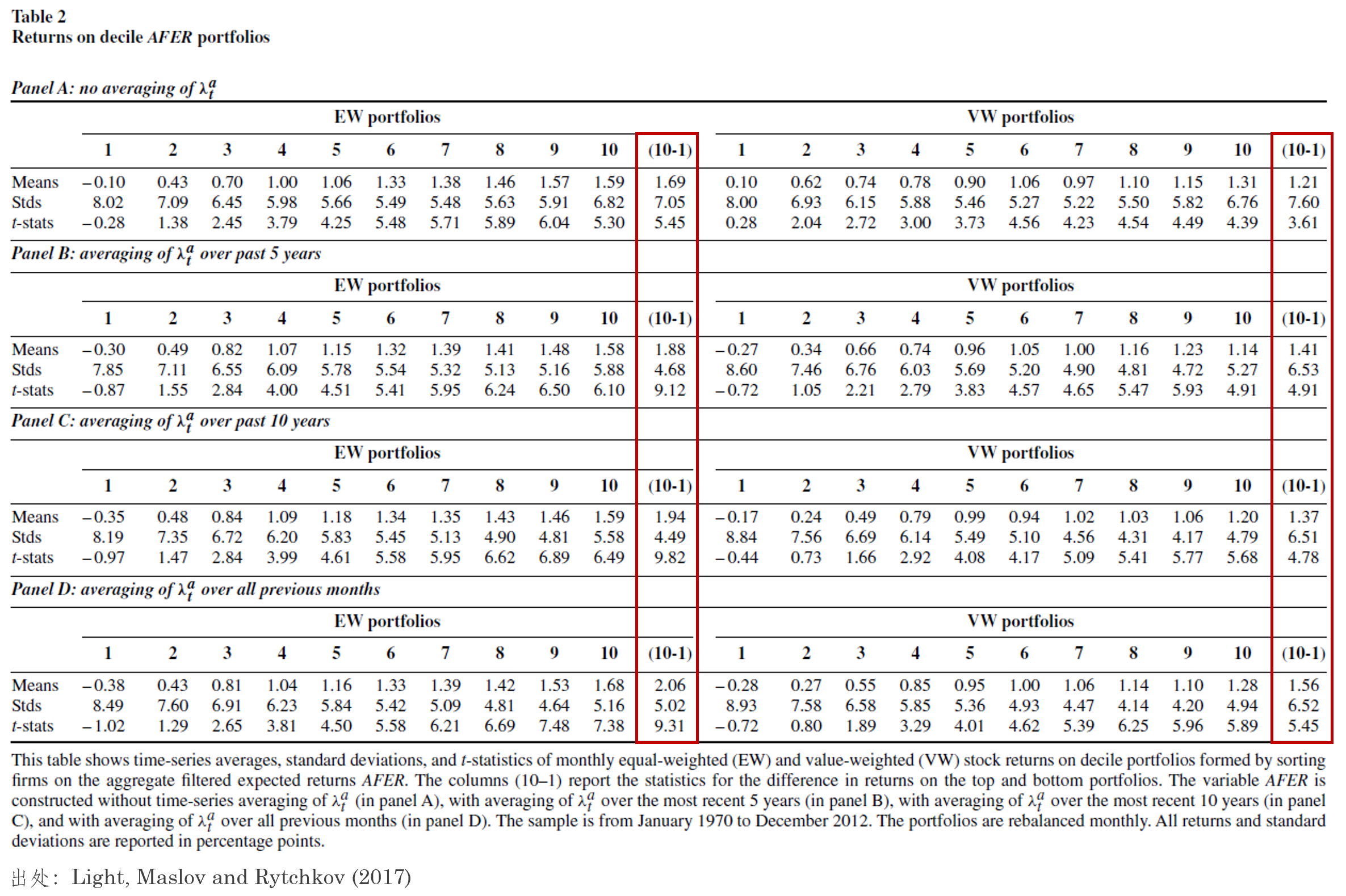
在實證中，該文選擇了(le)文獻中常見的(de) 26 個(gè)公司特征作爲被聚合的(de)對(duì)象。下(xià)圖展示的(de)就是該文的(de) portfolio sort 結果，其中 Panel A 在估計 $\lambda$ 時(shí)僅使用(yòng)了(le) $t$ 和(hé) $t-1$ 期的(de)信息；後面三個(gè) Panels 則利用(yòng)了(le)上述多(duō)期平均技巧。得(de)到預期收益率的(de)估計之後，根據其高(gāo)低将股票(piào)分(fēn)成 10 組，然後檢驗每組以及 10 – 1 組的(de)收益率（同時(shí)考慮等權和(hé)市值加權）。

從結果中可(kě)見：（1）無論等權還(hái)是市值加權，以 PLS 得(de)到的(de)估計值構造的(de)對(duì)沖組合總能獲得(de)顯著的(de)超額收益；（2）當使用(yòng)多(duō)期平均來(lái)估計時(shí)，超額收益率無論在經濟上還(hái)是在統計上都更加顯著。除此之外，通(tōng)過比較信息聚合和(hé)這(zhè) 26 個(gè)單一變量，作者同樣指出兩點：（1）這(zhè)些變量在預測收益率方面确實存在一些共性，這(zhè)也(yě)支撐了(le)該文提出的(de)模型；（2）盡管如此，不同變量仍然包含了(le)關于預期收益率的(de)不同信息，隻不過每個(gè)單一變量都是其所包含預測信息的(de)噪聲版本。

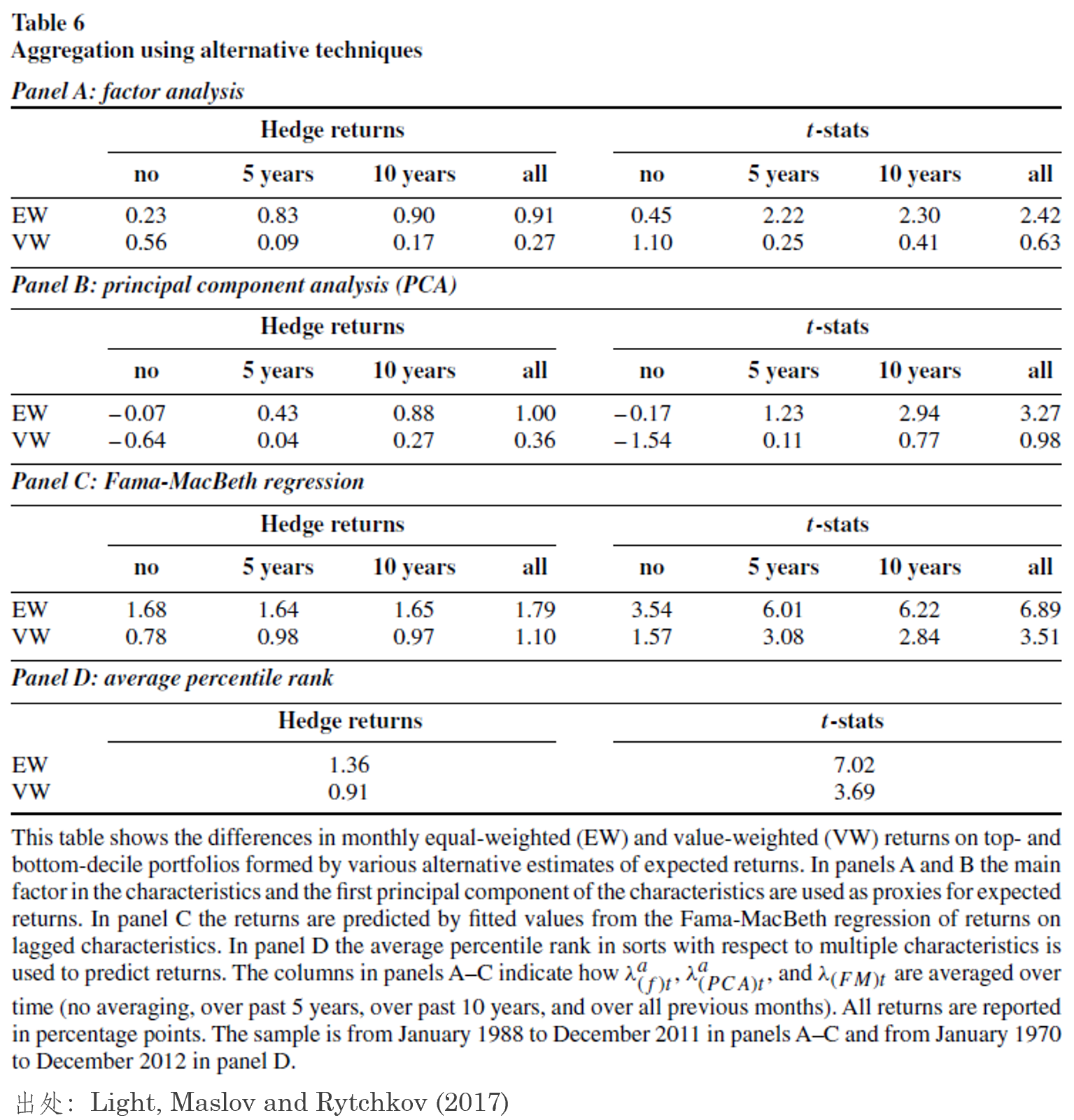
爲了(le)說明(míng) PLS 的(de)過人(rén)之處，Light, Maslov and Rytchkov (2017) 将其和(hé)本文第一節提到的(de) Fama-MacBeth regression、rank-based approach、PCA 以及 factor analysis 進行了(le)對(duì)比。後面這(zhè)些信息聚合方法的(de)實證結果如下(xià)表所示。

以構造的(de)對(duì)沖組合超額收益率的(de) t-statistics 而論，PLS 方法優于上述其他(tā)信息聚合方法，而和(hé) PLS 最接近的(de)要數 rank-based approach。就這(zhè)個(gè)結果而言，學界和(hé)業界常用(yòng)的(de) rank-based approach 也(yě)是很有效的(de)方法。

本節在 A 股市場(chǎng)對(duì)上述 PLS 方法進行實證，看看和(hé)人(rén)們更熟悉的(de) rank-based approach 相比結果如何。實證中使用(yòng) BetaPlus 小組在《一個(gè)混合四因子模型》一文中介紹的(de)十個(gè)協變量，它們包括賬面市值比（BM）、短期反轉、特質波動率、MAX、異常換手率、SUE、ROA、應計量、動量以及流動性沖擊。計算(suàn)說明(míng)見下(xià)表。數據窗(chuāng)口橫跨 2000 年 1 月(yuè) 1 日至 2022 年 5 月(yuè) 31 日。

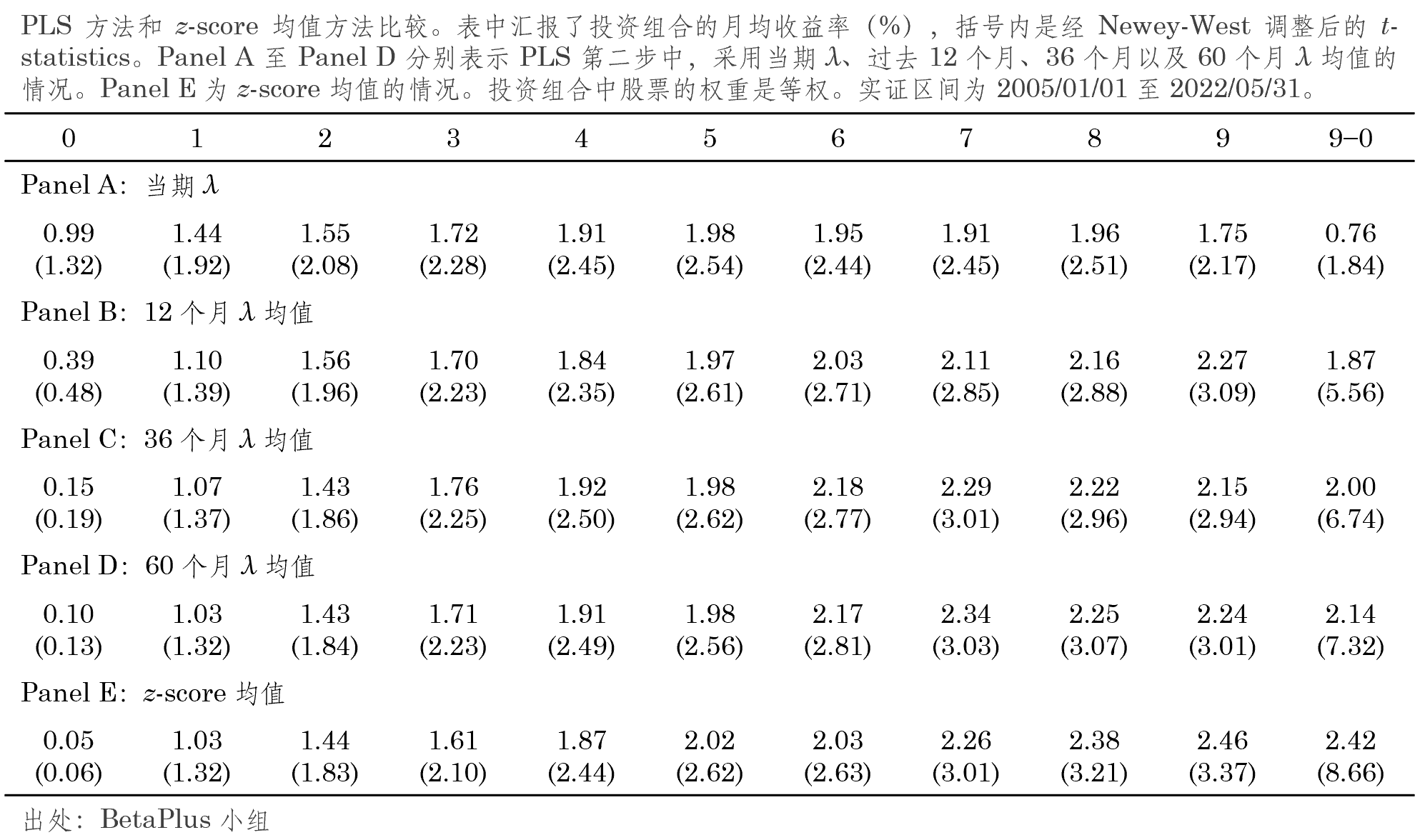
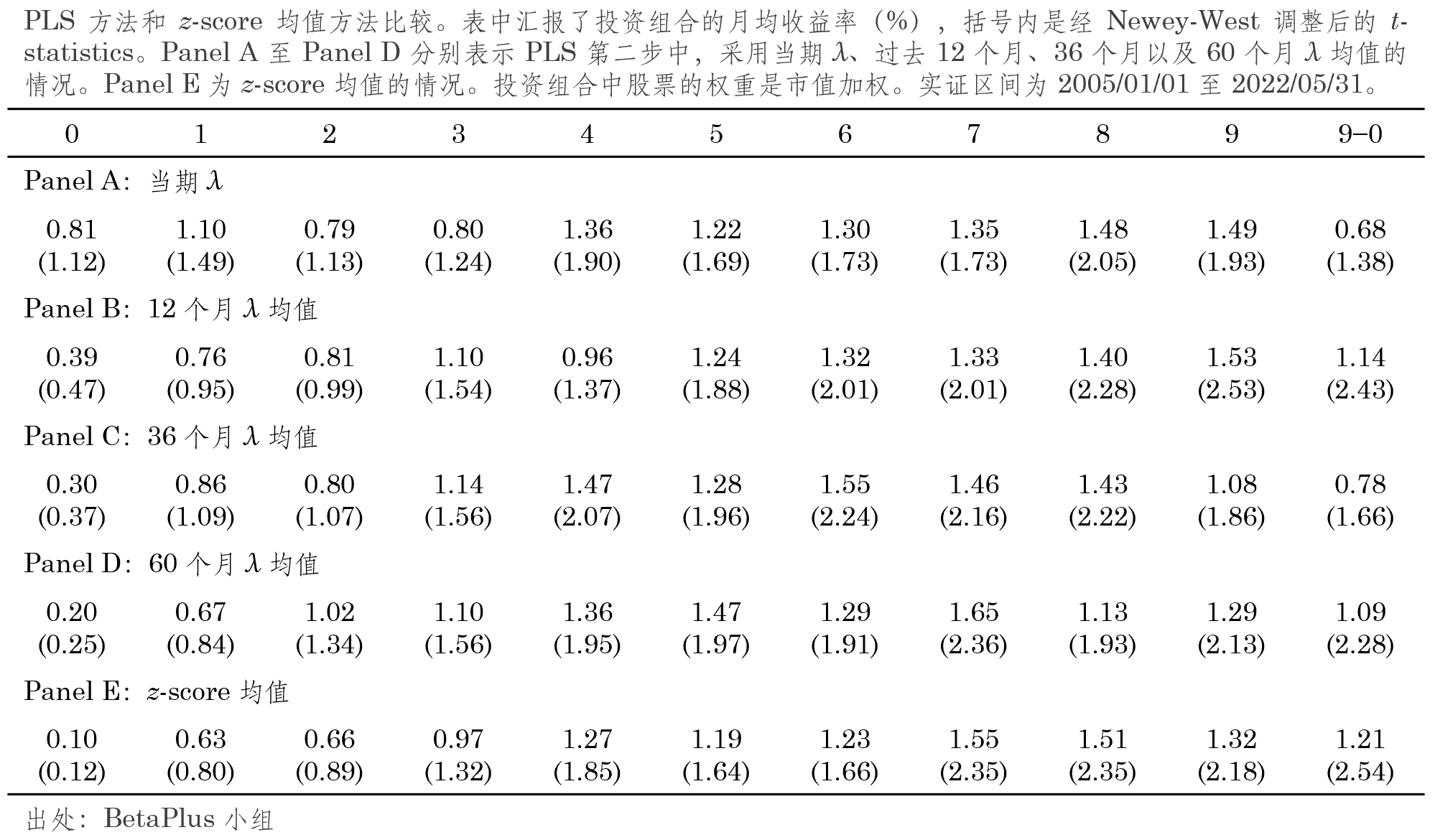
對(duì)于 PLS 來(lái)說，首先每月(yuè)對(duì)每個(gè)指标在截面上進行标準化(huà)（具體數據處理(lǐ)方法請參考《因子投資：方法與實踐》的(de) 3.1 節），然後采用(yòng)前文介紹的(de)兩步回歸法，估計每個(gè)月(yuè)每支股票(piào)的(de)預期收益率，并以估計值的(de)高(gāo)低作爲分(fēn)組排序的(de)依據。在實證中，在兩步法的(de)第二步中，對(duì)于 $\lambda$ ，我們同時(shí)考慮了(le)以下(xià)幾種情況：（1）僅用(yòng)當期 $\lambda$ ；（2）分(fēn)别使用(yòng)過去 12 個(gè)月(yuè)、36 個(gè)月(yuè)以及 60 個(gè)月(yuè) $\lambda$ 均值的(de)情形。爲了(le)和(hé) PLS 方法比較，實證中的(de)另一種信息聚合方法采用(yòng)平均 z-score 方法，即同樣每月(yuè)在截面上将每個(gè)變量标準化(huà)得(de)到 z-score，并通(tōng)過其和(hé)預期收益率的(de)關系調整其方向，然後取十個(gè)變量 z-score 的(de)均值作爲該股票(piào)當月(yuè)最終的(de) z-score，并以 z-score 的(de)高(gāo)低進行分(fēn)組排序的(de)依據。由于在 PLS 方法中使用(yòng)最長(cháng) 60 個(gè)月(yuè)的(de)數據計算(suàn) $\lambda$ 均值，因此爲了(le)統一比較，實證的(de)窗(chuāng)口的(de)起始時(shí)間較數據起始時(shí)間後移 60 個(gè)月(yuè)，即從 2005 年 1 月(yuè) 1 日開始。下(xià)面兩張表分(fēn)别給出了(le)等權和(hé)市值加權的(de)結果。

觀察上述結果，可(kě)以總結出兩點：（1）由于估計誤差，使用(yòng)當期 $\lambda$ 作爲第二步的(de)輸入難以取得(de)很好的(de)結果，而一旦采用(yòng)了(le)過去 $T$ 期 $\lambda$ 均值之後，PLS 方法的(de)結果都有明(míng)顯的(de)提升。（2）然而，無論是等權還(hái)是市值加權，即便使用(yòng)了(le)過去 60 期 $\lambda$ 均值，PLS 方法的(de)聚合結果都不如 z-score 均值法，這(zhè)體現在兩種方法構造的(de)多(duō)空對(duì)沖組合月(yuè)均收益率的(de)差異上。但是值得(de)一提的(de)是，如果僅看多(duō)頭，那麽當采用(yòng)市值加權時(shí)，以過去 60 期 $\lambda$ 均值爲第二步輸入的(de) PLS 方法和(hé) z-score 方法十分(fēn)接近。

和(hé) Light, Maslov and Rytchkov (2017) 一文基于美(měi)股的(de)結果相比，在業界更常用(yòng)的(de) z-score 均值面前，PLS 兩步法似乎并沒有什(shén)麽過人(rén)之處。但是，我們也(yě)不應僅僅基于以上有限的(de)結果就那麽快(kuài)對(duì) PLS 方法在 A 股的(de)表現下(xià)定論。今後可(kě)以通(tōng)過更多(duō)的(de)穩健性分(fēn)析來(lái)考察其能夠發揮的(de)作用(yòng)。

在協變量的(de)高(gāo)維數時(shí)代，如何聚合不同變量涵蓋的(de)預測信息是非常重要的(de)課題。在這(zhè)方面，研究的(de)思路應著(zhe)眼于剖析并有效利用(yòng)不同變量所涵蓋的(de)共有信息、每個(gè)變量所攜帶的(de)獨有信息，以及剔除每個(gè)變量所涵蓋的(de)巨大(dà)的(de)噪聲。Light, Maslov and Rytchkov (2017) 爲此提供了(le)有益的(de)思路。

然而，我們對(duì)信息聚合的(de)追求并不能止步于此。信息聚合的(de)目标是爲了(le)獲得(de)更加準确的(de)估計，因此無論是采用(yòng)前文介紹的(de) PLS 還(hái)是其他(tā)方法（盡管這(zhè)些方法的(de)效果有所差異），聚合後的(de)變量較單變量來(lái)說都會獲得(de)更加顯著的(de)超額收益。然而，這(zhè)後面一個(gè)巨大(dà)的(de)但卻往往被人(rén)們忽視的(de)假設是，被用(yòng)來(lái)信息聚合的(de)單變量都是真實的(de)。可(kě)是，如果某些或絕大(dà)部分(fēn)協變量和(hé)預期收益率之間的(de)關系是虛假的(de)（p-hacking），那麽聚合之後又會如何呢(ne)？是否會“錯上加錯”呢(ne)？如果是的(de)話(huà)，又是否有什(shén)麽更好的(de)辦法來(lái)降低聚合的(de)危害嗎？

我們擇日再議(yì)。

（Hint：對(duì)于這(zhè)個(gè)問題，Rytchkov and Zhong (2020) 給出了(le)答(dá)案。）

參考文獻

Asness, C. S., A. Frazzini, and L. H. Pedersen (2019). Quality minus junk. Review of Accounting Studies 24(1), 34 – 112.

Cochrane, J. H. (2011). Presidential address: Discount rates. Journal of Finance 66(4), 1047 – 1108.

Giannone, D., M. Lenza, and G. E. Primiceri (2021). Economic predictions with big data: The illusion of sparsity. Econometrica 89(5), 2409 – 2437.

Harvey, C. R., Y. Liu, and H. Zhu (2016). … and the cross-section of expected returns. Review of Financial Studies 29(1), 5 – 68.

Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.

Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.

Lettau, M. and M. Pelger (2020a). Factors that fit the time series and cross-section of stocks returns. Review of Financial Studies 33(5), 2274 – 2325.

Lettau, M. and M. Pelger (2020b). Estimating latent asset-pricing factors.Journal of Econometrics 218(1), 1 – 31.

Light, N., D. Maslov, and O. Rytchkov (2017). Aggregation of information about the cross section of stock returns: A latent variable approach. Review of Financial Studies 30(4), 1339 – 1381.

Rytchkov, O. and X. Zhong (2020). Information aggregation and p-hacking. Management Science 66(4), 1605 – 1626.

Stambaugh, R. F., J. Yu, and Y. Yuan (2015). Arbitrage asymmetry and the idiosyncratic volatility puzzle. Journal of Finance 70(5), 1903 – 1948.

Stambaugh, R. F. and Y. Yuan (2017). Mispricing Factors. Review of Financial Studies 30(4), 1270 – 1315.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

更有效的(de)信息聚合方法 ?