Missing Financial Data

作者：石川

摘要：在因子投資中，當協變量存在缺數問題時(shí)，除了(le)填充截面或行業均值/中位數，是否還(hái)有更好的(de)方法？

1

協變量缺數是因子投資中繞不過的(de)坎兒(ér)，而這(zhè)個(gè)問題在另類數據中尤甚。缺數，顧名思義，就是在特定的(de)曆史時(shí)刻、對(duì)特定的(de)股票(piào)來(lái)說、某個(gè)協變量的(de)取值是缺失的(de)。這(zhè)個(gè)問題廣泛存在于因子投資和(hé)實證資産定價研究之中。在面對(duì)缺數問題時(shí)，常見的(de)做(zuò)法是填充截面均值/中位數，或者行業均值/中位數，或者上一期的(de)值（假設上一期沒有缺數）。這(zhè)些似乎是人(rén)們約定俗成的(de)做(zuò)法，從來(lái)也(yě)沒有人(rén)去質疑上述處理(lǐ)方式的(de)合理(lǐ)性。（另外一種更加粗暴的(de)方式是，把缺數的(de)資産排除在分(fēn)析之外，但這(zhè)會造成 sample selection bias。）然而，它們真的(de)合理(lǐ)嗎？

要想搞清楚這(zhè)個(gè)問題，就必須回答(dá)一系列具體的(de)問題：數據缺失在時(shí)序和(hé)截面上是随機的(de)嗎？還(hái)是有何種相關性（比如小市值的(de)股票(piào)更容易缺失某些變量）？不同公司的(de)協變量之間是否存在截面上和(hé)時(shí)序上相關性，能否利用(yòng)它們更好的(de)填充缺失的(de)數據？無腦(nǎo)排除缺數的(de)股票(piào)，對(duì)實證資産定價有怎樣的(de)影(yǐng)響（比如在因子溢價估計方面）？對(duì)現實世界中的(de)投資機會又有怎樣的(de)影(yǐng)響（比如是否會損害可(kě)能構造的(de)最大(dà)夏普比率）？

當意識到存在如此之多(duō)尚待回答(dá)的(de)問題時(shí)，就很難再對(duì)“約定俗成”做(zuò)法可(kě)能存在的(de)潛在危害無動于衷。好消息是，學界在這(zhè)方面的(de)一些最新研究成果，有助于幫助人(rén)們回答(dá)上述問題（雖然是針對(duì)美(měi)股）。在應對(duì)實證資産定價的(de)缺數問題方面，近期兩篇頗有代表性的(de) working papers 是 Freyberger et al. (2021) 以及 Bryzgalov et al. (2022)。由于 Svetlana Bryzgalova 和(hé) Markus Pelger 兩位都是我非常欣賞的(de)新生代學者，今天就來(lái)簡要介紹 Bryzgalov et al. (2022) 一文。本文的(de)題目也(yě)照(zhào)搬了(le)該文的(de)标題，特此說明(míng)。

2

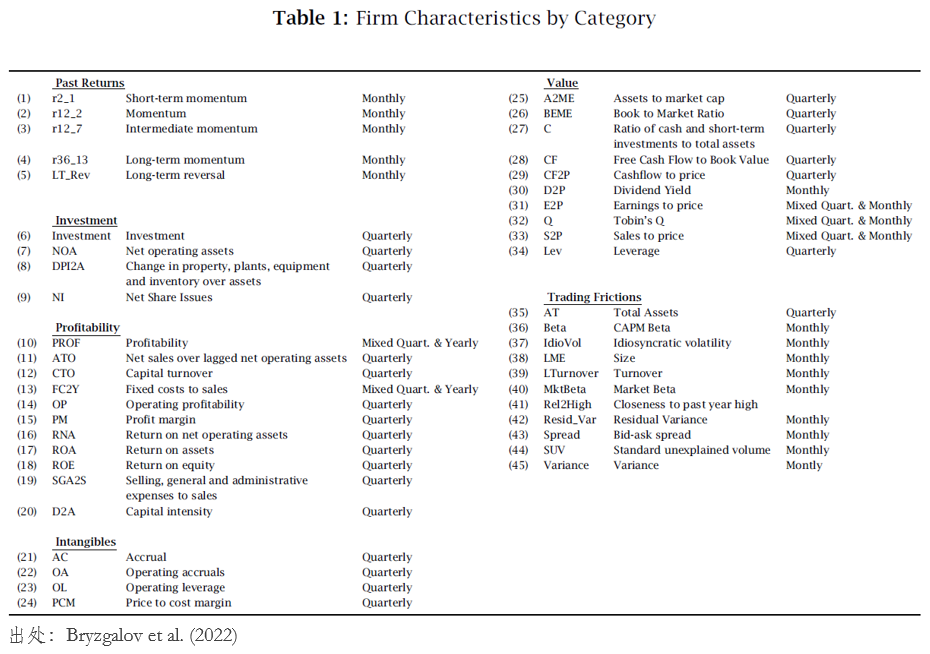
Bryzgalov et al. (2022) 考察了(le)美(měi)股中最常用(yòng)的(de) 45 個(gè)公司特征（下(xià)表），缺數存在 4 點 stylized facts。

Fact 1：缺數問題廣泛存在于上市公司之中，受影(yǐng)響的(de)公司占據了(le)一半的(de)市場(chǎng)總市值。無論公司市值是高(gāo)是低，無論公司的(de)曆史是長(cháng)是短，又無論公司的(de)經營情況是好是壞，都有可(kě)能出現缺數的(de)問題。

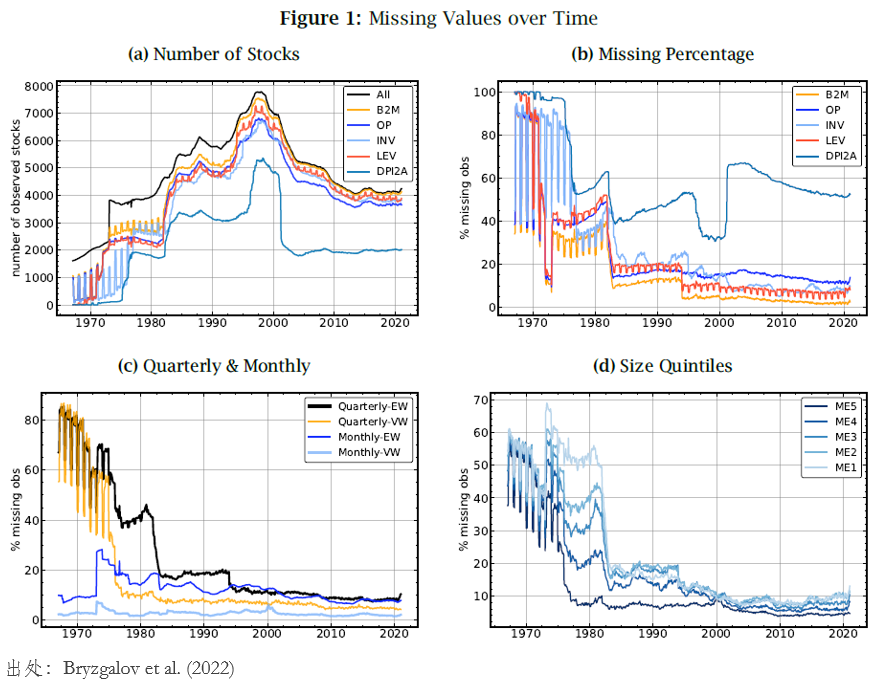
以美(měi)股中重要的(de) 5 個(gè)變量爲例——賬面市值比（B2M）、operating profitability（OP）、investment（INV）、leverage（LEV）以及real investment to book value（DPI2A）——下(xià)圖展示了(le)它們在時(shí)序上的(de)缺數變化(huà)情況。從（a）和(hé)（b）中不難看出，随著(zhe)時(shí)間的(de)推移，缺數的(de)比例在下(xià)降，不過仍然存在于所有變量。而（c）和(hé)（d）表明(míng)，無論是考察季度數據還(hái)是月(yuè)度數據變量，以及無論考察大(dà)市值公司還(hái)是小市值公司，缺數問題都是存在的(de)。

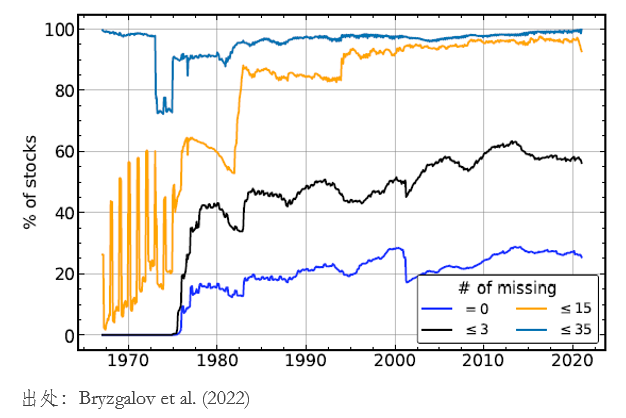
Fact 2：當分(fēn)析中需要用(yòng)到衆多(duō)協變量時(shí)（比如利用(yòng)機器學習(xí)算(suàn)法），缺數問題的(de)影(yǐng)響更加嚴重。

同樣是上述 45 個(gè)變量，下(xià)圖展示了(le)不同允許缺數變量個(gè)數下(xià)，公司占比随時(shí)間的(de)變化(huà)。比如，圖中藍色曲線代表 = 0 的(de)情況，即要求不存在任何變量的(de)缺失。在這(zhè)個(gè)約束下(xià)，滿足條件的(de)公司僅占不到 30%。換句話(huà)說，如果研究中同時(shí)使用(yòng)上述 45 個(gè)協變量且要求僅使用(yòng)沒有任何缺數的(de)公司，那麽 70% 的(de)公司都會被排除在外。

Fact 3：公司特征的(de)缺失并非随機的(de)。比如，很多(duō)基本面變量可(kě)能用(yòng)到了(le)同樣的(de)會計學條目來(lái)計算(suàn)，那麽一旦該條目缺數，就會影(yǐng)響基本面變量的(de)計算(suàn)；又比如，對(duì)于曆史時(shí)間較短的(de)公司，一些長(cháng)周期的(de)量價變量（比如中期動量和(hé)長(cháng)期反轉）自然也(yě)就無法計算(suàn)。

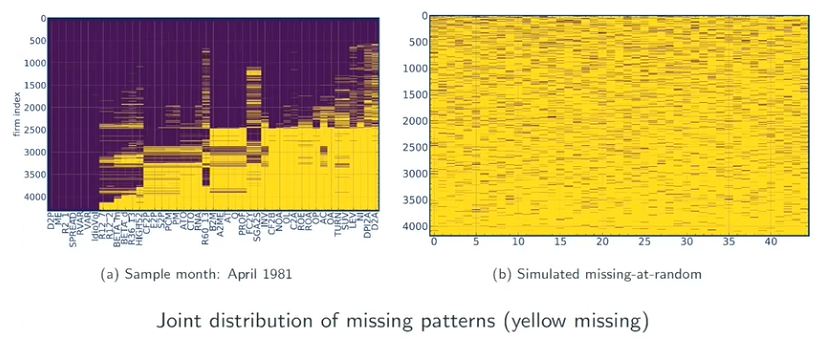
下(xià)圖（a）展示了(le) 1981 年 4 月(yuè)實際的(de)缺書(shū)情況，其中橫軸爲 45 個(gè)公司特征，縱軸爲公司 index。圖（b）展示了(le)假想的(de)随機缺失的(de)情況。如果缺數是随機的(de)，那麽我們在不同的(de)變量上應該觀察到無序的(de)随機性，如圖（b）所示。而真實情況下(xià)（圖（a））則顯示了(le)截然不同的(de)情況，很多(duō)公司在不同的(de)變量上均存在缺數的(de)情況。

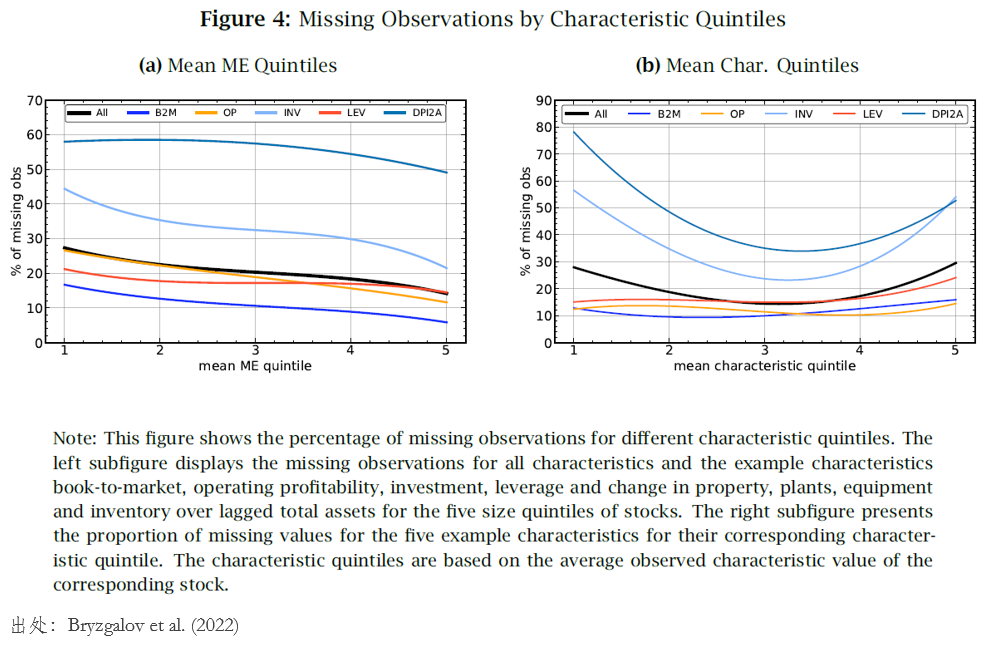
仍以前述 5 個(gè)公司特征爲例，下(xià)圖（a）考察了(le)不同市值分(fēn)組下(xià)的(de)缺失比例，可(kě)見小市值（第 1 組）相對(duì)大(dà)市值組（第 5 組）的(de)缺數問題更加嚴重；圖（b）則以變量本身進行分(fēn)組，考察了(le)每組的(de)缺數程度。看到這(zhè)裏有的(de)小夥伴也(yě)許會問：如果變量都缺數了(le)還(hái)怎麽分(fēn)組？這(zhè)裏的(de)處理(lǐ)方法是利用(yòng)股票(piào)在該變量上取值的(de)均值作爲分(fēn)組的(de)依據。結果顯示，當按照(zhào)變量排序時(shí)，最小的(de)組（第 1 組）和(hé)最大(dà)的(de)組（第 5 組）往往缺數問題最爲嚴重。由于因子或異象通(tōng)常是通(tōng)過這(zhè)兩組多(duō)空對(duì)沖構造的(de)，因此這(zhè)兩組缺失嚴重無疑是進行實證資産定價或因子投資的(de)夢魇。

另一方面，由于變量本身的(de)構造機制以及使用(yòng)的(de)數據的(de)差異，不同變量的(de)缺數存在異質性。這(zhè)些問題均使得(de)“約定俗成”的(de)中位數或均值填充不再合理(lǐ)（因爲均值或中位數是有偏的(de)）。

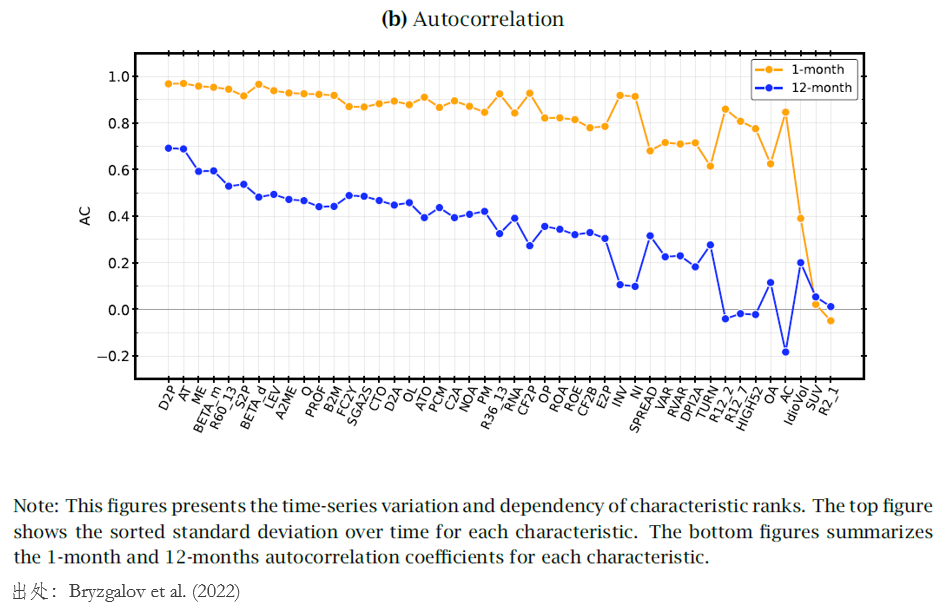
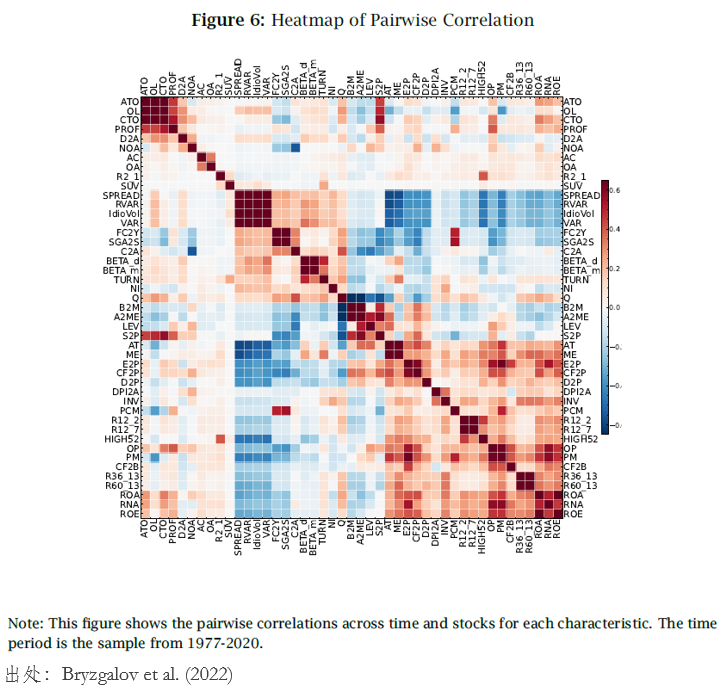
下(xià)面兩圖分(fēn)别展示了(le)每個(gè)變量自身的(de)時(shí)序自相關性以及不同變量的(de)截面相關性。從中不難發現，一些變量在時(shí)序上的(de)自相關性非常高(gāo)（比如市值），有些則爲零（比如特質波動率 iVol）；此外，很多(duō)變量的(de)截面相關性很高(gāo)。這(zhè)些結果表明(míng)，不同變量的(de)缺數問題存在特質性，而爲了(le)找到比“約定俗成”更好的(de)填數方法，需要充分(fēn)利用(yòng)變量在時(shí)序和(hé)截面上的(de)信息。

Fact 4：股票(piào)的(de)收益率與公司是否缺數有關，對(duì)實證資産定價的(de)研究結果（比如簡單如 portfolio sort）造成了(le)複雜(zá)的(de)影(yǐng)響。

3

爲了(le)利用(yòng)變量的(de)截面和(hé)時(shí)序信息，Bryzgalov et al. (2022) 針對(duì)公司特征協變量構造了(le)一個(gè)隐性多(duō)因子模型。以截面信息爲基礎，該模型的(de)重要因素如下(xià)面這(zhè)張 slide 所示（其中  表示公司特征，上标  表示時(shí)間，  表示股票(piào)，  表示變量）。該文利用(yòng) PCA 估計隐性多(duō)因子模型，并使用(yòng) Xiong and Pelger (forthcoming) 的(de)方法應對(duì)估計中的(de)缺數問題。

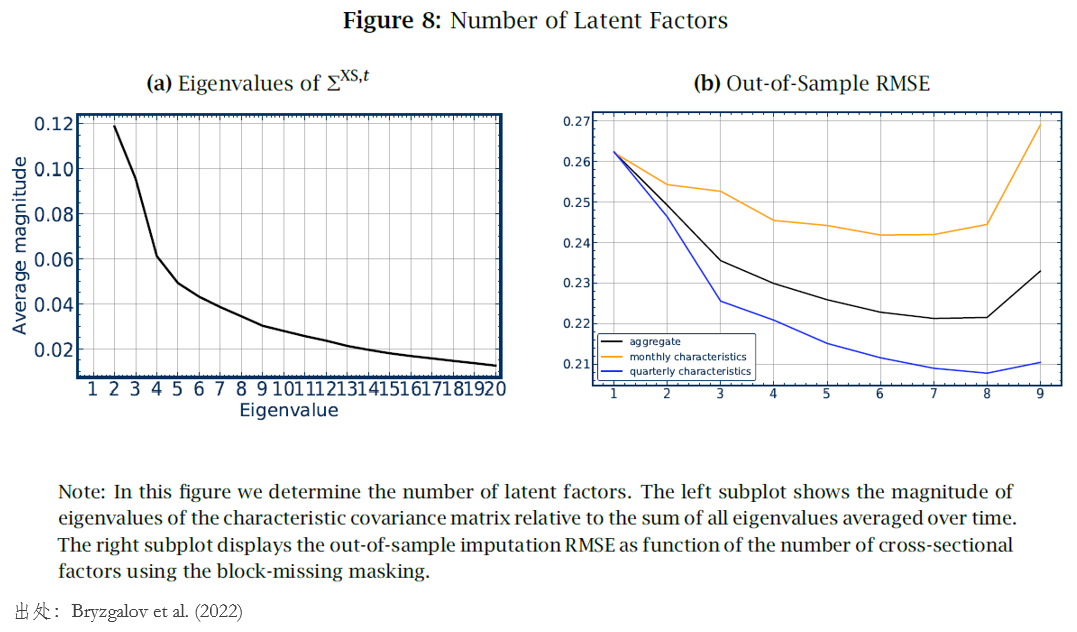
PCA 結果顯示，公司特征之間表現出了(le)很強的(de)因子結構；使用(yòng) 6 個(gè)因子就可(kě)以捕捉絕大(dà)部分(fēn)截面上的(de)變化(huà)。此外，這(zhè)些因子也(yě)有很強的(de)經濟學解釋。圖（b）展示了(le)樣本外填充的(de)公司特征的(de) RMSE 随隐性因子個(gè)數的(de)變化(huà)。

有了(le)基礎的(de)截面模型，Bryzgalov et al. (2022) 進一步添加了(le)時(shí)序的(de)公司特征，構造了(le)同時(shí)包括截面和(hé)時(shí)序信息的(de)隐性因子模型。

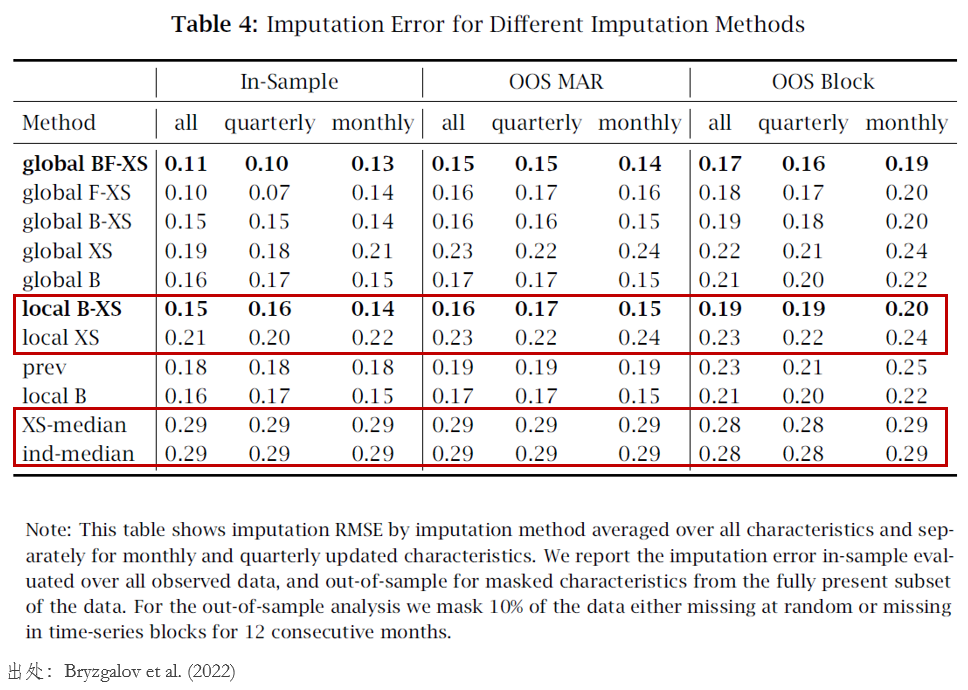
最後我們來(lái)看看不同模型和(hé)“約定俗成”模型在樣本外的(de)表現。不過這(zhè)裏先插一句，在前述的(de)介紹中，就提到了(le)樣本外 RMSE 的(de)計算(suàn)。有小夥伴可(kě)能會問：既然是缺數，怎麽算(suàn)是“樣本外”？這(zhè)裏的(de)處理(lǐ)方法是，刻意隐去（masking）一部分(fēn)觀測到的(de)公司特征（随機選擇，記爲 OOS MAR 或者在選擇上保留時(shí)序連續性，記爲 OOS Block），用(yòng)剩餘觀測數據進行建模，然後用(yòng)這(zhè)部分(fēn)隐去的(de)數據進行樣本外評估。評估結果如下(xià)表。

以我标出的(de) local B-XS 和(hé) local XS 兩個(gè)模型爲例，它們都是單期條件模型，其中 B-XS 用(yòng)到了(le)截面信息和(hé)曆史時(shí)序信息，XS 僅用(yòng)到了(le)截面信息。另外兩個(gè)“約定俗成”模型是 XS-median，即截面中位數填充和(hé) ind-median，即行業中位數填充。結果顯示，無論是在樣本内還(hái)是在樣本外（OOS MAR 或 OOS Block），通(tōng)過主成分(fēn)分(fēn)析得(de)到的(de)預測均優于“約定俗成”模型，即它們的(de)預測誤差更低，且改進非常明(míng)顯。另外，從 local B-XS 和(hé) local XS 兩個(gè)模型結果的(de)差異可(kě)知，補充了(le)時(shí)序信息後能夠進一步提高(gāo)預測準确性，說明(míng)時(shí)序和(hé)截面信息對(duì)于填充缺數來(lái)說同樣重要。對(duì)于一些時(shí)序上自相關性很強的(de)變量，上述隐性因子模型能夠更多(duō)地利用(yòng)時(shí)序信息；而對(duì)于那些截面上信息更重要的(de)變量，該模型則更多(duō)地利用(yòng)截面信息。換句話(huà)說，該模型并不依賴于人(rén)們對(duì)于 missing patterns 的(de)假設，而是能夠從數據中發現并加以利用(yòng)。

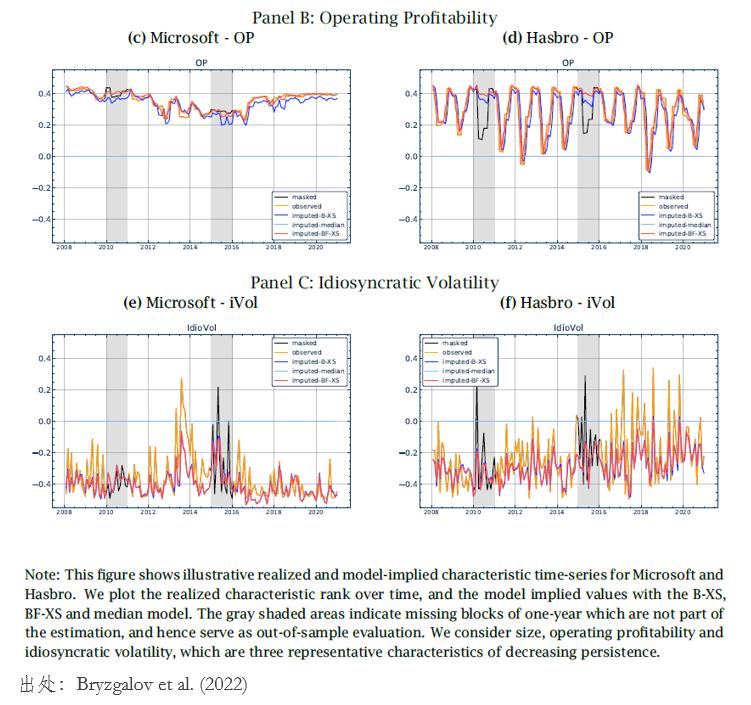
最後來(lái)看兩個(gè)具體的(de)例子。考慮 Microsoft 和(hé) Hasbro 兩個(gè)公司，考慮 operating profitability 和(hé) iVol 兩個(gè)變量。圖中灰色的(de)區(qū)間是留出的(de) OOS 區(qū)間，圖中 0.0 的(de)水(shuǐ)平線表示“約定俗成”做(zuò)法的(de)填充。從這(zhè)兩個(gè)例子中可(kě)以看到，無論是對(duì)于 OP 這(zhè)種比較穩定的(de)變量，還(hái)是對(duì)于 iVol 這(zhè)種上蹿下(xià)跳的(de)變量，模型都能給出不錯的(de)填充結果，遠(yuǎn)遠(yuǎn)優于填充 0.0。

4

以上和(hé)各位一起簡要浏覽了(le) Bryzgalov et al. (2022) 一文的(de)核心内容和(hé)結果。在近日的(de)一個(gè) talk 中，Bryzgalov 提到她們後續會把填充好的(de)數據挂出來(lái)，供學界和(hé)業界使用(yòng)。當有了(le)更合理(lǐ)填充後的(de)公司特征後，一些傳統的(de)異象或因子的(de)表現是否會發生颠覆性的(de)改變？答(dá)案令人(rén)期待。另一方面，Bryzgalov et al. (2022) 對(duì)于缺數的(de)研究還(hái)給了(le)我另外的(de)一個(gè)強烈的(de)感受。近年來(lái)，機器學習(xí)算(suàn)法已經被廣泛應用(yòng)于實證資産定價和(hé)因子投資之中。然而，越來(lái)越多(duō)的(de)研究表明(míng)，在如此低信噪比的(de)金融領域，指望“數據發聲”的(de)粗暴做(zuò)法是不切實際的(de)。反而是小到數據如何标準化(huà)、不同的(de)協變量如何進行縮放，如何選擇正則化(huà)的(de)方式等每一個(gè)具體的(de)細節決定著(zhe)應用(yòng)機器學習(xí)算(suàn)法的(de)成敗。

Bryzgalov et al. (2022) 關于缺數的(de)研究毫無疑問再次說明(míng)了(le)這(zhè)一點。一個(gè)看似不起眼的(de)填充決定，也(yě)許就會改變應用(yòng)機器學習(xí)的(de)結果。而到底應該使用(yòng)哪種數據處理(lǐ)方式（例如“約定俗成” vs. 該文同時(shí)利用(yòng)時(shí)序和(hé)截面信息構造的(de)隐性模型）背後顯然也(yě)應該有足夠的(de)經濟學推導作爲指引。這(zhè)些看似很小的(de)差異，也(yě)許在其他(tā)高(gāo)信噪比的(de)機器學習(xí)應用(yòng)領域難以産生太大(dà)的(de)影(yǐng)響，但對(duì)于實證資産定價的(de)成功來(lái)說，可(kě)能正是必不可(kě)少的(de)一環。

More to come …

參考文獻

Bryzgalov, S., S. Lerner, M. Lettau, and M. Pelger (2022). Missing financial data. Working paper.

Freyberger, J., B. Hoppner, A. Neuhierl, and M. Weber (2021). Missing data in asset pricing panels. Working paper.

Xiong, R. and M. Pelger (forthcoming). Large dimensional latent factor modeling with missing observations and applications to causal inference. Journal of Econometrics.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。