沒有 β、都是 α ?

發布時(shí)間：2022-08-23 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：Not Really!

金融學會議(yì)的(de)每篇論文通(tōng)常都有一個(gè) discussant，負責對(duì)論文提出建設性意見。在金融學頂會上，discussant 的(de)發言比原報告更加精彩的(de)情況也(yě)并不罕見。而如果當 discussant 是 Bryan Kelly 時(shí)，上述情形就幾乎一定會出現。近日，Kelly 又“火力全開”了(le)（對(duì)了(le)，我老早之前又被 Kelly 圈粉了(le)）。

在前不久的(de) NBER SI 2022 的(de) Asset Pricing Session 中，Lopez-Lira and Roussanov (2022) 彙報了(le)一篇題爲 Do common factors really explain the cross-section of stock returns? 的(de)文章(zhāng)。文章(zhāng)的(de)結論非常抓人(rén)眼球，他(tā)們拒絕了(le) APT：

他(tā)們是怎麽得(de)出這(zhè)樣的(de)結論呢(ne)？分(fēn)三步：

1. 從 APT 出發，解釋預期收益的(de)因子應該和(hé)資産收益率的(de) COV 矩陣有關，因此 Lopez-Lira and Roussanov (2022) 使用(yòng)日收益率并通(tōng)過 PCA 構造了(le)隐性風險因子；

2. 該文進而基于大(dà)量公司特征并使用(yòng) Random Forest 構造了(le) test assets；

3. 最後，該文利用(yòng) test assets 構造了(le)關于隐性因子中性（即無暴露）的(de)投資組合，獲得(de)了(le)顯著的(de)超額收益，因此他(tā)們拒絕了(le) APT。

上述邏輯似乎看上去沒有什(shén)麽毛病。而如果這(zhè)個(gè)結論成立，那就意味著(zhe)“沒有 $\beta$ ，都是 $\alpha$ ”。有意思的(de)是，這(zhè)并不是兩位作者第一次彙報這(zhè)項研究。然而“不幸的(de)是”，這(zhè)回等待著(zhe)他(tā)們的(de)是 Bryan Kelly。

本節我們就跟著(zhe) Kelly 的(de) slides 看看這(zhè)篇論文的(de)實證結果和(hé)結論到底有什(shén)麽問題。Kelly 首先用(yòng)三頁 slides 總結了(le)該文的(de)結果（如下(xià)）。這(zhè)部分(fēn)沒啥可(kě)說的(de)，我也(yě)不多(duō)做(zuò) comment。

接下(xià)來(lái)就是關鍵的(de)，Kelly 開始討(tǎo)論該文的(de)結論。首先，他(tā)指出所有人(rén)（尤其是研究資産定價的(de)人(rén)）都知道，我們總能找到 benchmark model 無法解釋的(de) test assets 從而拒絕 benchmark model，所以這(zhè)并不新鮮。但是，拒絕 APT 這(zhè)個(gè)表述是不準确的(de)，可(kě)以說拒絕了(le)某個(gè)多(duō)因子模型，但是不能說拒絕了(le) APT。此外，在 Lopez-Lira and Roussanov (2022) 的(de)實證結果中，最令他(tā)擔憂的(de)并非 benchmark model 無法解釋 test assets 的(de)預期收益率，而是通(tōng)過 PCA 構造的(de)這(zhè)個(gè) benchmark model 裏面的(de)因子的(de) risk premium 全都是零。

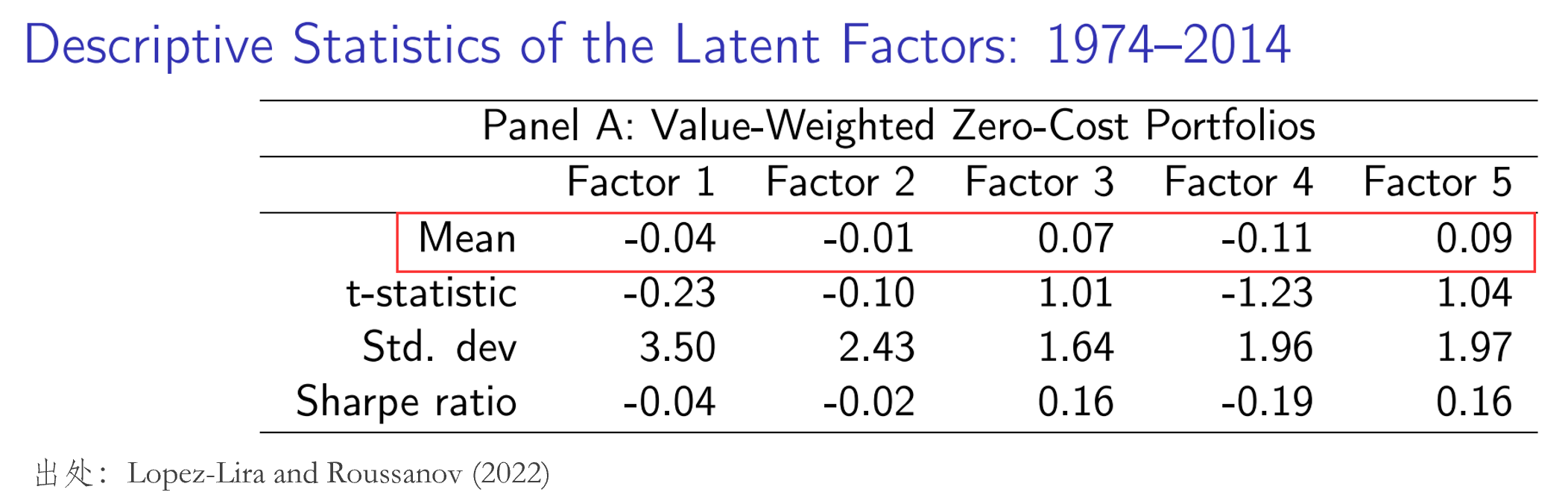
下(xià)表展示了(le) Lopez-Lira and Roussanov (2022) 中因子的(de) risk premium。

在 Kelly 看來(lái)，factor risk premium 都是零（if true）才是 real main result。可(kě)惜的(de)是，這(zhè)個(gè) if 要打一個(gè)大(dà)大(dà)的(de)問号。之前大(dà)量的(de)實證結果已經表明(míng)，很多(duō)能夠解釋資産共同運動的(de)因子的(de) risk premium 都顯著不爲零。難道是那些文章(zhāng)錯了(le)嗎？還(hái)是這(zhè)篇文章(zhāng)的(de) PCA 實證有什(shén)麽問題？對(duì)此，Kelly 認爲該文的(de)因子存在 inconsistent conditioning information 問題（這(zhè)絕對(duì)是 Kelly 這(zhè)個(gè) discussion 的(de) WOW moment）。

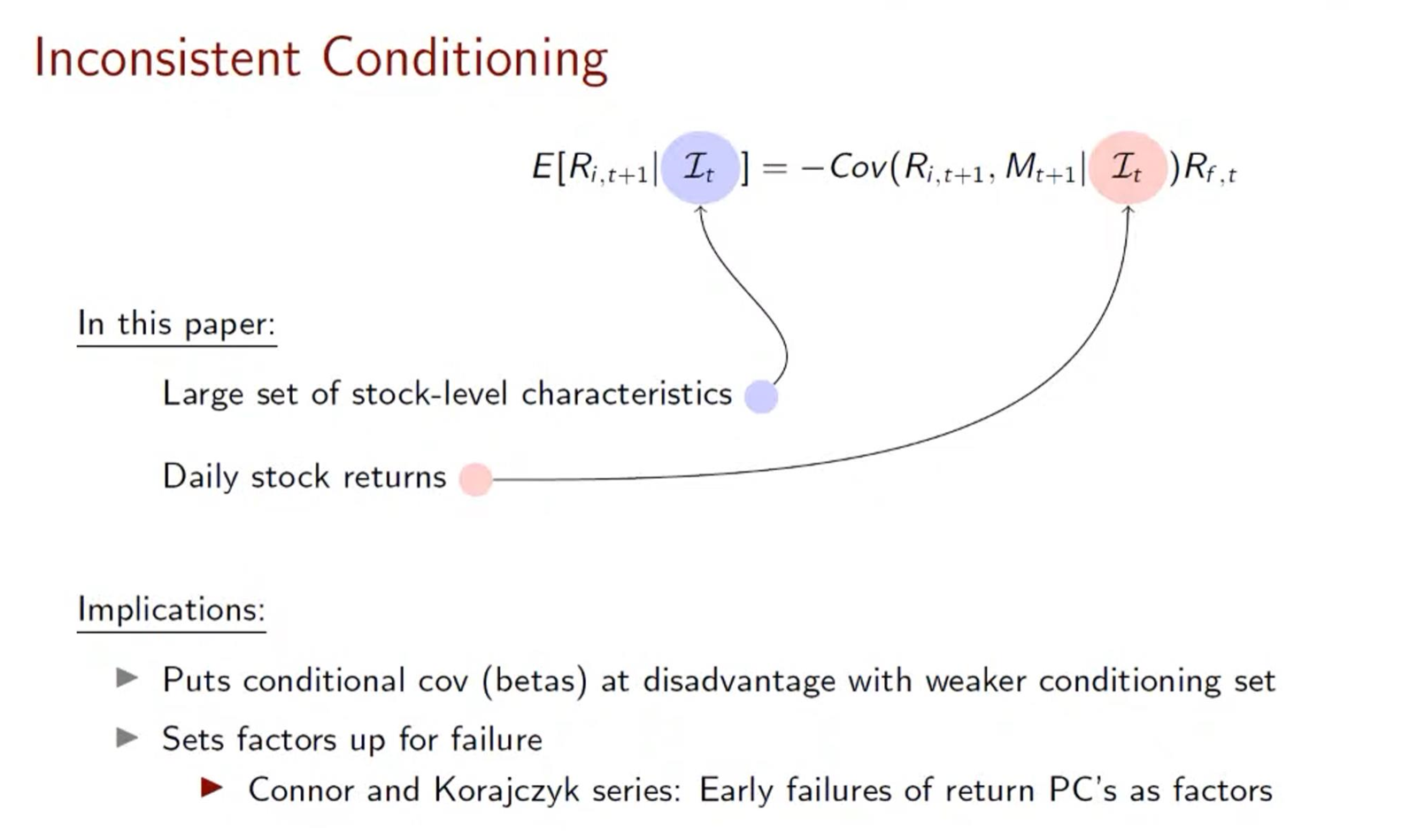
結合下(xià)面這(zhè)張 slide 來(lái)理(lǐ)解一下(xià) inconsistent conditioning。由資産定價理(lǐ)論可(kě)知，資産的(de)條件預期收益率由資産和(hé) SDF 的(de)條件協方差決定（下(xià)圖中的(de)公式）。而在 Lopez-Lira and Roussanov (2022) 一文中，用(yòng)來(lái)預測預期收益率（即構造 test assets）的(de) information set 是大(dà)量的(de)公司特征，反觀用(yòng)來(lái)計算(suàn)隐性因子的(de)信息僅僅是日收益率。這(zhè)就是不一緻性所在。

單純利用(yòng)日收益率并通(tōng)過 PCA 來(lái)構造隐性因子，這(zhè)是得(de)到 factor risk premium 爲零這(zhè)個(gè)錯誤結論的(de)直接原因。具體而言，這(zhè)裏面存在兩個(gè)問題：（1）估計因子溢價時(shí)存在大(dà)量誤差；（2）公司特征中涵蓋了(le)大(dà)量預測未來(lái) $\beta$ （對(duì)，這(zhè)裏關注的(de)是 $\beta$ ，而不是預期收益率）的(de)預測信息，如果僅僅使用(yòng)日收益率則完全忽視了(le)它們。

關于第一點，感興趣的(de)小夥伴可(kě)以找一些 random matrix theory（RMT）的(de)資料看看（比如 Lettau and Pelger 2020）。簡單的(de)說就是基于日收益率的(de) PCA 很難準确估計因子的(de) risk premium。關于這(zhè)點，我做(zuò)過一個(gè)小實驗，在實驗中假設已知收益率的(de) data generating process 并利用(yòng)樣本數據估計 30 個(gè)資産的(de) COV 矩陣。由于 DGP 已知，因此 population COV 矩陣已知，這(zhè)允許我們計算(suàn)樣本 COV 矩陣和(hé) population COV 矩陣的(de)誤差。實驗結果顯示，對(duì)于僅僅 30 個(gè)資産的(de) COV 矩陣的(de)估計，需要 $10^4$ 這(zhè)個(gè)量級的(de) sample size 才能準确估計。

更關鍵的(de)是，上面這(zhè)個(gè)還(hái)僅僅是 COV 矩陣的(de)估計誤差，而非基于樣本 COV 矩陣進行 PCA 分(fēn)析的(de)誤差。RMT 的(de)相關研究表明(míng)，當 sample size 有限的(de)時(shí)候，基于樣本 COV 進行 PCA 得(de)到的(de)特征向量和(hé)總體特征向量之間的(de)夾角在 80 度以上（幾乎垂直了(le)）。PCA 了(le)個(gè)寂寞。

另外，Kelly 關于第一點的(de)討(tǎo)論也(yě)讓我想起了(le) Bryzgalova, Huang, and Julliard (2020) 的(de) Bayesian estimator，而估計誤差正是她們提出 Bayesian estimator 的(de)動機。感興趣的(de)小夥伴請參考《Bayesian Two-Pass Regression》。

對(duì)于第二個(gè)問題，Kelly, Moskowitz, and Pruitt (2021) 指出，公司特征能夠有效預測未來(lái)的(de) $\beta$ ，因此僅僅基于日收益率會丢失掉大(dà)量的(de)信息。關于如何解決 inconsistent conditioning 問題，Kelly 建議(yì)參考他(tā)和(hé)合作者提出的(de) IPCA 方法（Kelly, Pruitt, and Su 2019）。

最後，Kelly 對(duì)該文的(de)結論進行了(le)總結。在他(tā)看來(lái)，聲稱拒絕了(le) APT 爲時(shí)尚早（且是錯誤的(de)），而該文最大(dà)的(de)問題 —— 正如上面所述 —— 是 risk factor 的(de) risk premium 爲零。對(duì)于任何一篇實證資産定價研究來(lái)說，這(zhè)樣的(de)結果應該是一個(gè) red flag，它表明(míng) latent factor estimator 并沒有想象的(de)那麽美(měi)好。

如果 Lopez-Lira and Roussanov (2022) 的(de)實證結果沒問題，那麽它意味著(zhe)人(rén)們可(kě)以找到并利用(yòng)解釋預期收益而和(hé)資産波動無關的(de)因子，即“全是 $\alpha$ ，沒有 $\beta$ ”，這(zhè)将和(hé) Kozak, Nagel, and Santosh (2018) 基于“市場(chǎng)中不存在近似無風險套利機會”這(zhè)一假設得(de)出的(de)結論相左，也(yě)和(hé)過去幾十年大(dà)量的(de)實證結果相矛盾。

最後，Kelly 以“Extremely thought provoking paper! I learned a lot.” 結束了(le)他(tā)的(de)討(tǎo)論。和(hé) Lopez-Lira and Roussanov (2022) 這(zhè)篇文章(zhāng)相比，Kelly 的(de)觀點無疑更加精彩，而大(dà)佬之間思維的(de)碰撞和(hé)毫不敷衍的(de)深刻討(tǎo)論也(yě)正是推動金融學發展的(de)驅動力。

Kelly rocks!

參考文獻

Bryzgalova, S., J. Huang, and C. Julliard (2020). Bayesian solutions for the factor zoo: We just run two quadrillion models. Working paper.

Kelly, T. B., T. J. Moskowitz, and S. Pruitt (2021). Understanding momentum and reversal. Journal of Financial Economics 140(3), 726 – 743.

Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.

Kozak, S., S. Nagel, and S. Santosh (2018). Interpreting factor models. Journal of Finance 73(3), 1183 – 1223.

Lopez-Lira, A. and N. Roussanov (2022). Do common factors really explain the cross-section of stock returns? Working paper.

Lettau, M. and M. Pelger (2020). Estimating latent asset-pricing factors. Journal of Econometrics 218(1), 1 – 31.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

沒有 β、都是 α ?