Low-Risk Anomalies

作者：石川

摘要：本文從發展曆程、實證以及投資實務三方面詳解 Low-Risk（類）異象。

寫在前面：在《因子投資：方法與實踐》中，我們以特質性波動率爲代表，闡述了(le) low-risk anomaly（見 5.3 節）。鑒于此類異象的(de)普遍存在且飽受争議(yì)、以及其背後涵蓋了(le)衆多(duō)不同的(de)構造變量，因此有必要将它們進行一個(gè)系統的(de)梳理(lǐ)。本文對(duì) [因子動物(wù)園] 和(hé)本公衆号關于此話(huà)題的(de)多(duō)篇文章(zhāng)進行了(le)整合和(hé)提煉。下(xià)面就讓我們一起從發展曆程、實證以及投資實務三方面再探 low-risk anomalies。

1 起源、發展、争議(yì)、歸宿（?）

自打被提出以來(lái)，low-risk anomalies 身上從來(lái)不缺乏争議(yì)；随著(zhe)理(lǐ)論的(de)發展和(hé)實證的(de)深入，人(rén)們對(duì)于不同變量構造的(de) anomalies 的(de)觀點不但沒有收斂，反倒是持續的(de)交鋒。發展脈絡和(hé)思想碰撞的(de)相互糾纏也(yě)使得(de)本文注定無法像書(shū)中介紹主流因子那樣把起源和(hé)解釋一分(fēn)爲二。索性，我們就把它們融合在一起，分(fēn)代表性變量并按照(zhào)時(shí)間梳理(lǐ)異象背後的(de)種種。

Low-risk anomalies 并非某一個(gè)變量，而是代表了(le)一大(dà)類變量，它又可(kě)以看成更廣義下(xià)的(de) defensive factors / anomalies 大(dà)類下(xià)的(de)一個(gè)子類（French and Gartner forthcoming）。而在層出不窮的(de)構造變量之中，最知名也(yě)是最重要的(de)要數 Ang et al. (2006) 的(de)特質性波動率（Idiosyncratic Volatility，簡稱 IVOL）以及 Frazzini and Pedersen (2014) 的(de) Betting Against Beta（BAB）。然而，它們均飽受争議(yì)。讓我們從 IVOL 說起。（本文第 3.2 節将會介紹其他(tā)構造變量。）

1.1 Idiosyncratic Volatility

股票(piào)的(de)風險分(fēn)爲系統性風險和(hé)特質性風險兩部分(fēn)，後者可(kě)通(tōng)過特質性波動率來(lái)衡量，其中特質性波動率可(kě)由資産收益率對(duì)定價模型回歸的(de)殘差所計算(suàn)的(de)波動率來(lái)代表（實證中常用(yòng)的(de)定價模型包括 FF3 和(hé) FF5）。傳統金融理(lǐ)論認爲特質性波動率可(kě)以通(tōng)過分(fēn)散化(huà)投資而被抵消，因此它和(hé)資産預期收益之間不應有什(shén)麽關聯。然而，Ang et al. (2006) 打破了(le)這(zhè)個(gè)觀點。該文指出特質性波動率高(gāo)的(de)股票(piào)在未來(lái)預期收益率更低，即二者負相關。這(zhè)篇文章(zhāng)自發表以來(lái)，即成爲 JF 上的(de)（最）高(gāo)引文章(zhāng)之一，足見學術界對(duì)其的(de)關注程度。三年後，Ang et al. (2009) 又在 JFE 上發文，通(tōng)過來(lái)自美(měi)國和(hé)全球的(de)更多(duō)實證結果證實上述實證結果的(de)穩健性。

Ang et al. (2006) 引發了(le)學術界大(dà)討(tǎo)論。而和(hé)該文觀點相反的(de)研究也(yě)不在少數。例如，Fu (2009) 提出特質性波動率和(hé)收益率之間存在正相關，并認爲 Ang et al. (2006) 發現的(de)負相關性源于一小撮高(gāo)特質性波動率股票(piào)收益率的(de)反轉。此外，Anderson, Bianchi, and Goldberg (2015) 也(yě)對(duì)特質性波動率和(hé)預期收益率之間的(de)負相關性提出了(le)質疑之聲。

實證研究往往容易踏入 data snooping 的(de)陷阱，所以出現相互矛盾的(de)結果也(yě)并不令人(rén)意外。對(duì)于特質性波動率和(hé)預期收益率的(de)關系，學術界的(de)結論尚無定論，無論是正相關、負相關還(hái)是沒有顯著關系，都有研究結果所支持。但是，更多(duō)的(de)結果還(hái)是發現特質性波動率和(hé)收益率之間的(de)負相關。這(zhè)個(gè)現象被稱作特質性波動率之謎。

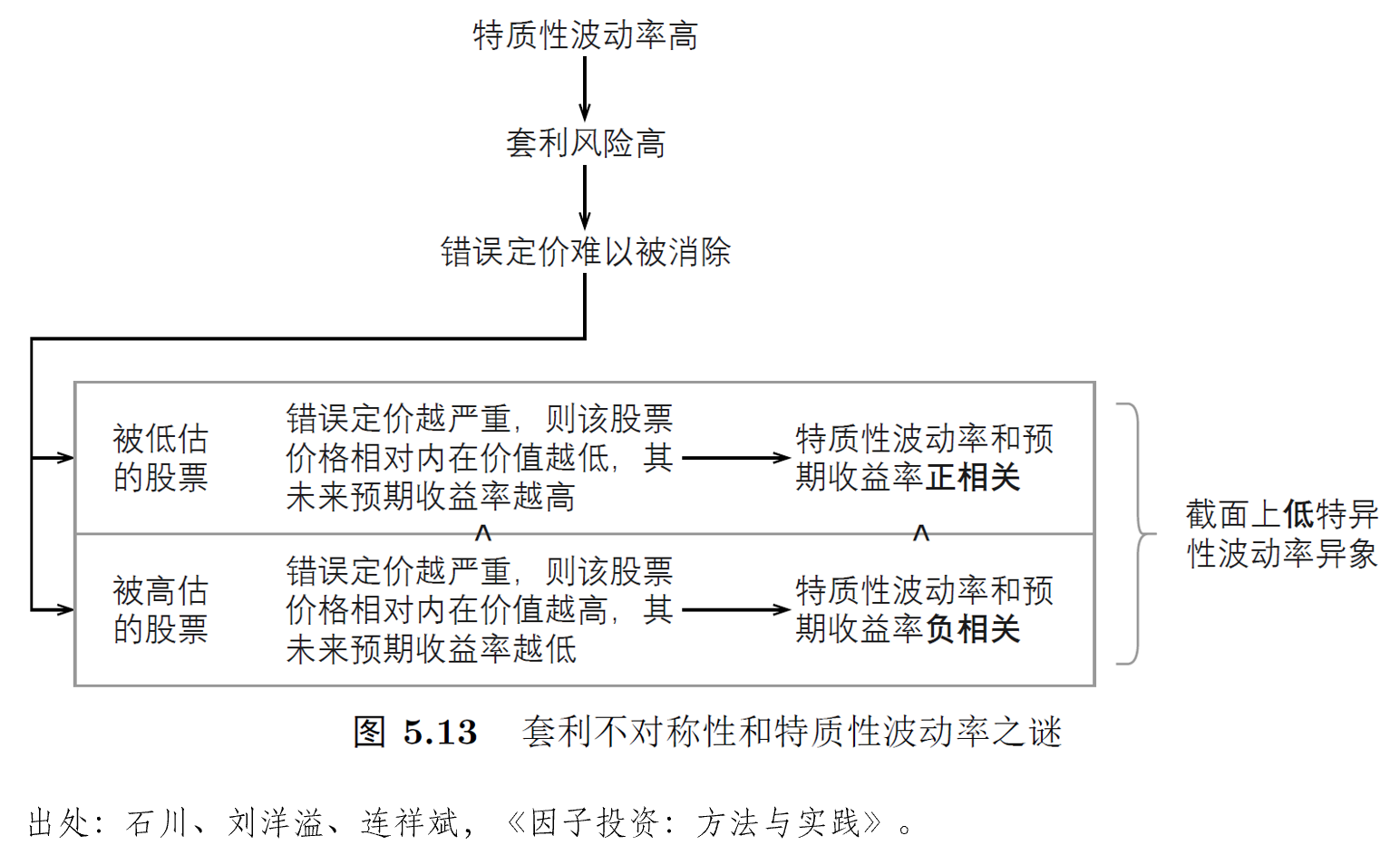
爲了(le)破解特質性波動率之謎，Stambaugh, Yu, and Yuan (2015) 從套利不對(duì)稱性（arbitrage asymmetry）的(de)角度進行了(le)研究，實證結果非常漂亮。該文把股票(piào)按照(zhào)估值高(gāo)低分(fēn)成五組，并發現在最被高(gāo)估的(de)一組中，特質性波動率和(hé)收益率呈現負相關；而在最被低估的(de)一組中，特質性波動率和(hé)收益率呈現正相關。接下(xià)來(lái)就是最精彩的(de)部分(fēn)：套利不對(duì)稱性導緻市場(chǎng)對(duì)最被高(gāo)估的(de)股票(piào)套利不充分(fēn)，因此這(zhè)一組内特質性波動率和(hé)收益率的(de)負相關強于最被低估組内特質性波動率和(hé)收益率的(de)正相關。這(zhè)導緻最終從截面上看，特質性波動率和(hé)收益率呈現負相關，即和(hé) Ang et al. (2006) 發現相符的(de)特質性波動率異象。下(xià)圖展示了(le)上文所描述的(de)邏輯。

除此之外， Liang and Tang (2018) 将 IVOL 拆解成不确定性和(hé)殘差波動率兩部分(fēn)，并指出 IVOL 和(hé)收益率的(de)負相關主要由前者造成，爲理(lǐ)解 IVOL 之謎提供了(le)新的(de)視角。本文第二節将以 IVOL 爲變量，針對(duì) A 股進行 low-risk anomaly 實證分(fēn)析。

1.2 Betting Against Beta

說到 low-risk anomalies，另一條不得(de)不提的(de)研究脈絡當屬 Betting Against Beta 系列。

我們不妨從 Black CAPM 模型說起。1972 年，Black, Jensen, and Scholes (1972) 從實際市場(chǎng)數據中觀察到證券市場(chǎng)線（SML）遠(yuǎn)比 CAPM 預測的(de)要更平緩，這(zhè)說明(míng)風險和(hé)收益的(de)關系不能很好的(de)滿足 CAPM。Black, Jensen, and Scholes (1972) 從時(shí)間序列回歸和(hé)截面回歸兩個(gè)維度實證了(le)上述猜想，提出了(le)新的(de) CAPM 模型。

該文将股票(piào)按照(zhào)其 market β 大(dà)小分(fēn)成十組，并通(tōng)過時(shí)序回歸檢驗發現，在不同的(de)曆史時(shí)期，α 顯著不爲 0 且和(hé) β 呈負相關：高(gāo) β 的(de)股票(piào)往往有負 α。在此基礎上，他(tā)們在 CAPM 中加入了(le)另一個(gè)因子。該模型被後人(rén)稱爲 Black CAPM。

在 Black CAPM 被提出的(de) 40 年之後，來(lái)自 AQR 的(de) Frazzini and Pedersen (2014) 在 JFE 上發表了(le)一篇題爲 Betting Against Beta 的(de)文章(zhāng)，從另外的(de)角度解釋了(le) α 和(hé) β 之間的(de)負相關。Frazzini and Pedersen（2014）指出杠杆約束是 BAB 形成的(de)重要因素。利用(yòng) TED 衡量融資寬松程度，該文發現如果 TED 擴大(dà)，則融資比較輕松，未來(lái) BAB 收益變現會變差；如果 TED 價差縮小，則融資難度變大(dà)，未來(lái) BAB 表現會變好。此外，該文檢驗了(le)不同杠杆約束程度如何影(yǐng)響投資者的(de)偏好，發現約束較高(gāo)的(de)投資者（如共同基金和(hé)個(gè)人(rén)投資）會傾向于持有高(gāo) β 股票(piào)，而約束較少的(de)投資者（如對(duì)沖基金、LBO 和(hé)伯克希爾）會更偏愛(ài)低 β 股票(piào)。令 ψ 來(lái)表示資金約束強弱程度，Frazzini and Pedersen (2014) 指出 α 和(hé) β 的(de)關系滿足  。因此，他(tā)們通(tōng)過做(zuò)多(duō)低 β 的(de)股票(piào)、做(zuò)空高(gāo) β 的(de)股票(piào)構造了(le) BAB 異象，獲得(de)了(le)可(kě)觀的(de)超額收益（at least on paper）。

除此之外，Blitz, Falkenstein, and van Vliet (2014) 從 CAPM 基本假設的(de)角度討(tǎo)論了(le)杠杆約束。CAPM 假設投資者沒有杠杆限制，每個(gè)投資者都追求單位風險下(xià)收益最大(dà)化(huà)（即切點組合），投資者可(kě)以通(tōng)過資金的(de)靈活借貸實現自己的(de)目标收益水(shuǐ)平。然而在實際情形中，杠杆是有約束的(de)，借貸資金成本較高(gāo)或者條款不允許加杠杆，導緻投資者無法随意增加或降低杠杆水(shuǐ)平。因此，投資者爲了(le)獲得(de)更高(gāo)的(de)收益，隻能通(tōng)過暴露更多(duō)的(de)市場(chǎng)風險，追逐高(gāo) β 股票(piào)，導緻其被高(gāo)估。Blitz and van Vliet (2007) 則認爲，同樣由于使用(yòng)杠杆限制或者害怕使用(yòng)杠杆，緻使聰明(míng)的(de)投資者無法超配低 β 股票(piào)，導緻這(zhè)種異象難以消失。

來(lái)自不同市場(chǎng)的(de)實證結果均實證了(le) Frazzini and Pedersen (2014) 的(de)猜想。由于低 β 早已深入人(rén)心，該文一經發表，便在學術界和(hé)業界産生了(le)巨大(dà)的(de)反響，它也(yě)自然而然的(de)成爲了(le) JFE 的(de)高(gāo)引文章(zhāng)之一。在業界，BAB 成爲防禦型投資策略的(de)代表之一，得(de)到了(le)大(dà)量機構投資者的(de)追捧。

由于 BAB 和(hé) CAPM 不符，因此它的(de)存在是不亞于特質性波動率的(de)另一個(gè)謎團。而正所謂“人(rén)紅是非多(duō)”，BAB 自提出以來(lái)所受到的(de)争議(yì)則要比 IVOL 多(duō)的(de)多(duō)的(de)多(duō)的(de)多(duō)（重要的(de)事情一不留神說了(le)三遍）。多(duō)到什(shén)麽程度？多(duō)到我必須從三個(gè) subsections 來(lái)分(fēn)别論述。

到底是理(lǐ)論需要“修正”還(hái)是實證出了(le)“纰漏”？盡管來(lái)自不同市場(chǎng)的(de) BAB 看上去非常充分(fēn)，但是我們不禁仍然要問，BAB 是否真的(de)存在？學界至少從兩方面回答(dá)了(le)這(zhè)個(gè)問題，其一是從 BAB 内部直接擊破，其二則是從風險和(hé)收益的(de)角度出發重新解構 β。下(xià)面兩個(gè) subsections 先討(tǎo)論以上兩個(gè)視角，最後一個(gè) subsection 討(tǎo)論杠杆約束 vs 彩票(piào)偏好這(zhè)兩種 BAB 背後的(de)潛在成因。

1.2.1 Is it there in the first place? (I)

前者的(de)代表是 Novy-Marx and Velikov (2022)，該文以 Betting Against Betting Against Beta （BABAB）爲題對(duì) BAB 進行了(le)抨擊，指出 BAB 構造中存在三個(gè)異常之處，而這(zhè)些異常造就了(le)這(zhè)個(gè)異象。這(zhè)三個(gè)異常之處是：（1）構造組合時(shí)使用(yòng) rank weighting；（2）通(tōng)過杠杆進行 β 對(duì)沖；（3）計算(suàn) β 時(shí)分(fēn)别使用(yòng)了(le)不同的(de)窗(chuāng)口來(lái)估計相關系數的(de)标準差。

Novy-Marx and Velikov (2022) 指出：關于（1），BAB 原文使用(yòng) rank 作爲權重近似等價于等權，從而大(dà)大(dà)提升了(le)小市值和(hé)微小市值股票(piào)在構造投資組合中起到的(de)作用(yòng)，而非像 Frazzini and Pedersen (2014) 所預期的(de)那樣賦予極端 β 取值股票(piào)更高(gāo)的(de)權重；關于（2），BAB 原文對(duì)低 β 多(duō)頭進行了(le)加杠杆，對(duì)高(gāo) β 空頭進行了(le)降杠杆，從而構造零 β 的(de)對(duì)沖組合（市場(chǎng)中性組合），這(zhè)種做(zuò)法也(yě)在一定程度上和(hé)等權近似。結合上述兩點，Novy-Marx and Velikov (2022) 認爲 BAB 因子的(de)構造方法造成其在超小市值公司上的(de)權重過高(gāo)且在盈利和(hé)投資因子上有很高(gāo)的(de)暴露。由于規模、盈利和(hé)投資三個(gè)因子在美(měi)股上已經被證明(míng)是有效的(de)，因此 BAB 毫無疑問是沾了(le)光(guāng)，表現被大(dà)幅提升。

關于（3），該文認爲 Frazzini and Pedersen (2014) 在計算(suàn) β 時(shí)使用(yòng)不同的(de)時(shí)間窗(chuāng)口計算(suàn)波動率和(hé)相關系數，這(zhè)種估計方法是有偏的(de)，從而它陰差陽錯的(de)支持了(le)他(tā)們提出的(de)理(lǐ)論。一旦修正這(zhè)個(gè)偏差，該理(lǐ)論則不再成立。具體來(lái)說，Frazzini and Pedersen (2014) 分(fēn)别使用(yòng) 1 年和(hé) 5 年計算(suàn)波動率和(hé)相關系數，簡單的(de)代數運算(suàn)指出  和(hé)傳統方法計算(suàn)的(de) market β 之間的(de)關系： 

式中下(xià)标 1 和(hé) 5 分(fēn)别代表一年和(hé)五年的(de)滾動窗(chuāng)口，上标 i 表示資産。該關系式說明(míng)，  等價于傳統方法得(de)到的(de) β 乘以一個(gè)系數；即資産的(de)  與市場(chǎng)的(de)  之比。Novy-Marx and Velikov (2022) 通(tōng)過實證研究發現當市場(chǎng)自身處于高(gāo)波動時(shí)，資産的(de)  和(hé)市場(chǎng)的(de)  之間的(de)彈性小于 1；反之，當市場(chǎng)自身處于低波動時(shí)，二者之間的(de)彈性大(dà)于 1。這(zhè)意味著(zhe)當市場(chǎng)處于高(gāo)波動時(shí)，  比傳統 β 更低；而當市場(chǎng)處于低波動時(shí)，  比傳統 β 更高(gāo)。因此，使用(yòng)  作爲單一資産的(de) β，那麽按照(zhào)市值加權後得(de)到的(de)全市場(chǎng) β 并不等于 1（其取值随時(shí)間波動，且時(shí)序均值略高(gāo)于 1），說明(míng)  不夠合理(lǐ)的(de)證據。

1.2.2 Is it there in the first place? (II)

面對(duì)和(hé)經典 CAPM 模型背道而馳的(de) BAB，Bollerslev, Patton, and Quaedvlieg (2022) 指出，相比于波動本身，投資者更在意資産的(de)下(xià)行風險，并據此将資産與市場(chǎng)因子的(de)協方差進行了(le)更細緻的(de)拆分(fēn)，提出了(le) semibeta 的(de)概念。不過對(duì)于拆 β 這(zhè)件事兒(ér)，該文并非始作俑者。因此，在介紹它之前，讓我們先 detour 一下(xià)，解讀一篇更早的(de)文章(zhāng)：Ang, Chen, and Xing (2006)。

Ang, Chen, and Xing (2006) 的(de)核心觀點是，下(xià)行風險高(gāo)的(de)資産在投資者收益較低（從而邊際效用(yòng)最高(gāo)）的(de)時(shí)期，有最低的(de)收益。因此，投資者需要風險補償，因此下(xià)行風險高(gāo)的(de)資産有更高(gāo)的(de)預期收益。爲計算(suàn)下(xià)行風險，該文使用(yòng)如下(xià)方法計算(suàn)下(xià)行 β：

式中，  和(hé)  分(fēn)别爲資産和(hé)市場(chǎng)的(de)超額收益，而  爲樣本期内的(de)市場(chǎng)超額收益均值。換言之，下(xià)行 β 被定義爲市場(chǎng)超額收益小于均值時(shí)的(de)條件 β。用(yòng)類似的(de)方式，也(yě)可(kě)以計算(suàn)的(de)上行 β。實證結果顯示，已實現下(xià)行 β 較高(gāo)的(de)股票(piào)，未來(lái)收益顯著更高(gāo)，即二者正相關，進而驗證了(le)下(xià)行風險對(duì)股票(piào)溢價的(de)重要性。換句話(huà)說，如果能篩選出那些未來(lái)下(xià)行風險更大(dà)的(de)股票(piào)，則有機會獲得(de)顯著的(de)超額收益。

下(xià)面再讓我們回到 Bollerslev, Patton, and Quaedvlieg (2022)。相比于 Ang, Chen, and Xing (2006)，該文同時(shí)考慮資産收益率和(hé)市場(chǎng)收益率的(de)符号（而非僅僅 conditioning on 市場(chǎng)收益率的(de)符号），從而對(duì)原始 β 進行了(le)更加細緻的(de)切分(fēn)。從協方差出發，同時(shí)考慮二者的(de)符号，可(kě)以将原始協方差劃分(fēn)爲四個(gè)部分(fēn)（忽略均值）： 

因此，根據 β 的(de)定義，其可(kě)以被拆分(fēn)爲四個(gè)部分(fēn)： 

注意，上式中爲了(le)表述的(de)方便，定義  以及  。這(zhè)就是爲什(shén)麽上式中最後兩項前面的(de)符号爲減号。邏輯上，與上/下(xià)行風險的(de)分(fēn)解一緻，投資者厭惡下(xià)行風險，因而市場(chǎng)下(xià)跌時(shí)，  和(hé)  更容易被定價，且（1）  代表風險，因此應該有正溢價；（2）  代表著(zhe)對(duì)沖資産（市場(chǎng)下(xià)行時(shí)有好的(de)表現），因而應有負溢價。

在實證方面，上述 semibetas 都是隐變量，不可(kě)直接觀測，隻能基于樣本計算(suàn) realized semibetas。但根據 Bollerslev, Patton, and Quaedvlieg (2020) 的(de)發現，已實現 semibetas 是真實 semibetas 的(de)一緻估計。實證結果證實了(le)作者的(de)猜想：（1）兩個(gè)下(xià)行 β 顯著被定價但方向不同（和(hé)預期的(de)方向一緻），而兩個(gè)上行 β 則沒有被定價；（2）平均 R-squared 較 CAPM 模型顯著提升。在此基礎上，該文最後構造了(le) Betting On and Against Semi-Betas 組合（BOASB）。顧名思義，它由兩部分(fēn)構成：（1）做(zuò)多(duō)高(gāo)  、做(zuò)空低  标的(de)；以及（2）做(zuò)多(duō)低  、做(zuò)空高(gāo)  标的(de)；第一部分(fēn)是 On；第二部分(fēn)是 Against。實證結果顯示，BOASB 及其兩個(gè)組成部分(fēn)均能獲得(de) FF5 無法解釋的(de)顯著超額收益，然而 BAB 卻不能。

1.2.3 杠杆約束 vs 彩票(piào)偏好

從前面的(de)描述可(kě)知，Frazzini and Pedersen (2014) 認爲 BAB 主要是由投資者的(de)杠杆約束所驅動。Bali et al. (2017) 對(duì)此提出了(le)不同的(de)意見。故事要從 Bali, Cakici, and Whitelaw (2011) 提出的(de) MAX 效應說起。所謂 MAX，是指過去一段時(shí)間内股票(piào)的(de)最大(dà)單日收益；MAX 越大(dà)的(de)股票(piào)，未來(lái)收益顯著更低。MAX 效應也(yě)被稱爲彩票(piào)偏好（lottery preference）。

利用(yòng) MAX，Bali et al. (2017) 對(duì) BAB 的(de)原因提出了(le)不同的(de)看法。該文首先考察了(le) MAX 和(hé) β 的(de)雙重排序分(fēn)組，發現在每一個(gè) MAX 分(fēn)組中，BAB 的(de)超額收益都不再顯著。相反，MAX 效應在每一個(gè) β 分(fēn)組中卻高(gāo)度顯著。此外平均 MAX 效應甚至比 MAX 單變量分(fēn)組下(xià)還(hái)要顯著。接著(zhe)，Fama-MacBeth 回歸結果顯示，在考慮了(le) MAX 以及其他(tā)控制變量後，β 的(de)溢價顯著爲正。最後，該文通(tōng)過市值和(hé) MAX 雙重排序構造了(le) FMAX 因子，并比較了(le) FMAX 和(hé) BAB 是否可(kě)以解釋對(duì)方。結果顯示，在 Carhart 四因子模型中加上 FMAX 可(kě)以解釋 BAB ，但反過來(lái) FMAX 因子卻總能獲得(de)顯著的(de)負超額收益。綜上，Bali et al. (2017) 認爲，BAB 隻是 MAX 效應的(de)反映，彩票(piào)偏好而非杠杆約束才是 BAB 的(de)合理(lǐ)解釋。

當然，AQR 天團可(kě)不會甘心被怼。Asness et al. (2020) 一文針鋒相對(duì)地進行回應，認爲 BAB 有效是因爲 Betting Against Correlation（BAC）而非彩票(piào)偏好的(de)原因。爲了(le)構建 BAC 因子，該文首先在每月(yuè)末将股票(piào)按照(zhào)波動率分(fēn)爲 5 組，然後在每組内進一步按照(zhào)相關性分(fēn)爲兩組，接著(zhe)用(yòng)與 BAB 相同的(de)排序加權法構建多(duō)空兩端，最後構建 β 中性多(duō)空組合。他(tā)們也(yě)用(yòng)類似的(de)方法構建了(le) Betting Against Volatility（BAV）。結果發現，BAC 和(hé) BAV 都可(kě)以獲得(de)顯著且穩健的(de)超額收益。爲了(le)檢驗杠杆約束假說，Asness et al. (2020) 考察了(le)保證金借款餘額對(duì) BAB 和(hé) BAC 因子的(de)影(yǐng)響。當事前的(de)保證金借款較低，即杠杆約束較高(gāo)時(shí)，BAB 和(hé) BAC 因子的(de)表現都顯著更好。這(zhè)是支持杠杆約束假說的(de)有力證據。

爲了(le)檢驗彩票(piào)偏好的(de)影(yǐng)響，該文則引入了(le)（經 GDP 标準化(huà)的(de)）賭場(chǎng)的(de)季度分(fēn)紅變化(huà)來(lái)表征博彩偏好。結果表明(míng)，它對(duì) MAX 效應有顯著影(yǐng)響，但對(duì) BAB 因子卻沒有顯著的(de)影(yǐng)響。由這(zhè)些結果可(kě)知，杠杆約束假說是 BAB 的(de)合理(lǐ)解釋之一，而關于彩票(piào)偏好假說，則沒有一緻的(de)結論。

1.3 歸宿?

就馬上要介紹的(de)文獻而言，它似乎宣告了(le) low-risk anomalies 研究的(de)終點。但是，對(duì)任何實證現象來(lái)說，恐怕都很難因爲某個(gè)結果就下(xià)一個(gè)非常确切的(de)結論，這(zhè)就是本小節标題加問号的(de)原因。下(xià)面就讓我們來(lái)看看 low-risk anomalies 的(de)終結之旅 —— Schneider, Wagner, and Zechner (2020)。

Schneider, Wagner, and Zechner (2020) 指出，剩餘協偏度是所有 low-risk anomalies（自然包括上面的(de) IVOL 和(hé) BAB）的(de)歸宿。Again，在介紹它之前，一點點曆史依然會很有幫助。

早在上世紀 70 年代，Kraus and Litzenberger (1976) 便指出，由投資者遞減的(de)絕對(duì)風險厭惡可(kě)以推出效用(yòng)函數的(de)三階導大(dà)于零 ，從而隐含著(zhe)投資者對(duì)正偏度的(de)偏好。Harvey and Siddique (2000) 進一步将上述觀點表達爲正式的(de)模型，并指出偏度溢價爲負。經過理(lǐ)論推導可(kě)知，資産的(de)剩餘協偏度同其 CAPM-α 負相關，其中剩餘協偏度定義爲資産的(de) CAPM-α 和(hé)市場(chǎng)組合超額收益平方的(de)協方差。

前述理(lǐ)論模型意味著(zhe)，當投資者在意偏度時(shí)，CAPM-α 同剩餘協偏度密切相關。因而，剩餘協偏度可(kě)能是解釋低風險異象的(de)一個(gè)關鍵因素。但問題來(lái)了(le)，我們需要的(de)是事前無法獲得(de)的(de)未來(lái)剩餘協偏度。那麽，該用(yòng)什(shén)麽變量來(lái)代表呢(ne)？一個(gè)自然的(de)選擇是隐含偏度。與隐含波動率類似，隐含偏度根據期權價格倒推而得(de)。下(xià)面就輪到 Schneider, Wagner, and Zechner (2020) 出場(chǎng)。

該文首先通(tōng)過模拟分(fēn)析檢驗了(le)隐含偏度對(duì)預期的(de)真實剩餘協偏度的(de)代表性。他(tā)們生成了(le) 2000 家公司的(de)數據，然後分(fēn)别依據隐含偏度和(hé)預期已實現偏度将股票(piào)分(fēn)爲 10 組，并計算(suàn)不同分(fēn)組的(de)平均剩餘協偏度和(hé) α。結果表明(míng)，基于兩種偏度指标的(de)結果高(gāo)度相似，即隐含偏度對(duì)預期偏度有很強的(de)代表性。實證方面，該文基于 1996 至 2014 年間的(de)美(měi)股數據進行了(le)實證分(fēn)析。選擇 1996 年開始是因爲完整的(de)期權數據從這(zhè)一時(shí)間開始。結果顯示，（1）各種 low-risk anomalies 均能獲得(de)顯著的(de)超額收益，但是它們的(de)剩餘協偏度均顯著爲負；（2）隐含偏度因子能夠獲得(de)顯著的(de)超額收益，且與低風險一緻，剩餘協偏度爲負；（3）将隐含偏度因子加入定價模型，low-risk anomalies 的(de)超額收益不再顯著。

Schneider, Wagner, and Zechner (2020) 進一步利用(yòng)主成分(fēn)分(fēn)析和(hé)回歸分(fēn)析，檢驗了(le)隐含偏度因子和(hé) low-risk anomalies 的(de)關聯。具體而言，他(tā)們首先提取了(le)四個(gè)低風險異象的(de)第一主成分(fēn)，然後考察隐含偏度因子是否可(kě)以解釋該主成分(fēn)。結果顯示，隐含偏度因子幾乎可(kě)以完全解釋該主成分(fēn)。豐富的(de)實證結果表明(míng)，隐含偏度因子可(kě)以解釋低風險異象，并不僅僅是巧合，而的(de)确是因爲它同低風險異象的(de)核心驅動因素有關，這(zhè)也(yě)印證了(le)前文的(de)理(lǐ)論模型的(de)寓意。

對(duì)于 low-risk anomalies 而言，Schneider, Wagner, and Zechner (2020) 也(yě)許提供了(le)一個(gè)可(kě)能終結其争論的(de)答(dá)案：當考慮了(le)剩餘協偏度 / 隐含偏度後，低風險異象不再存在。當然，我們最終能否去除本節标題中的(de)問号，不妨就留給時(shí)間去評判。

2 實證

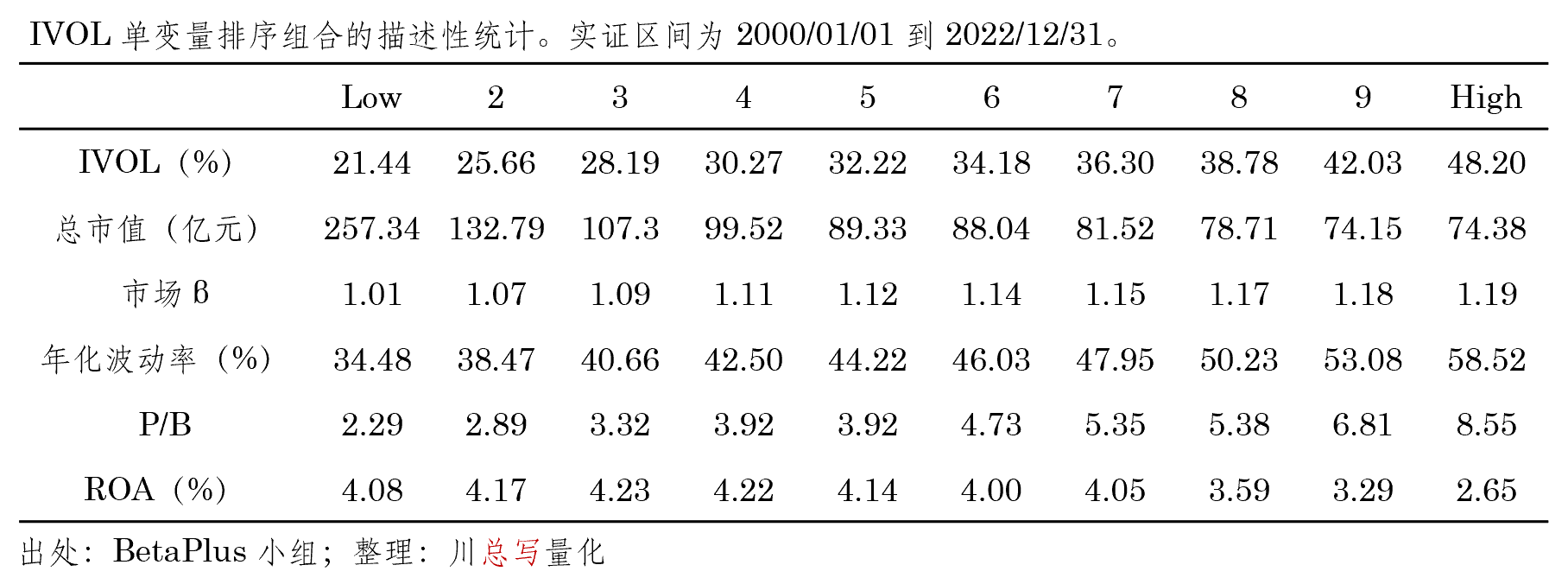
本節針對(duì) A 股市場(chǎng)，以基于 FF3 無法解釋的(de)殘差所計算(suàn)的(de)波動率來(lái)進行 IVOL 實證。實證區(qū)間爲 2000 年 1 月(yuè)至 2022 年 12 月(yuè)。每月(yuè)末将股票(piào)按照(zhào) IVOL 的(de)取值從低到高(gāo)分(fēn)成 10 組，表 1 彙報了(le)描述性統計。不難發現，IVOL 在十組截面上和(hé)總市值負相關；此外，IVOL 和(hé)年化(huà)波動率以及 market β 正相關，進而符合預期。除此之外不難發現，随著(zhe) IVOL 的(de)增大(dà)，P/B 呈現單調上升，說明(míng)高(gāo)波動的(de)股票(piào)估值更高(gāo)。最後，在盈利方面，前幾組的(de) ROA 差異不大(dà)，但是最後高(gāo) IVOL 的(de)幾組 ROA 明(míng)顯更低。因此 IVOL 和(hé)盈利因子也(yě)有一定的(de)聯系。本文第三章(zhāng)将闡述 low-risk anomalies 和(hé)常見風格因子的(de)關系。

表 1 描述性統計

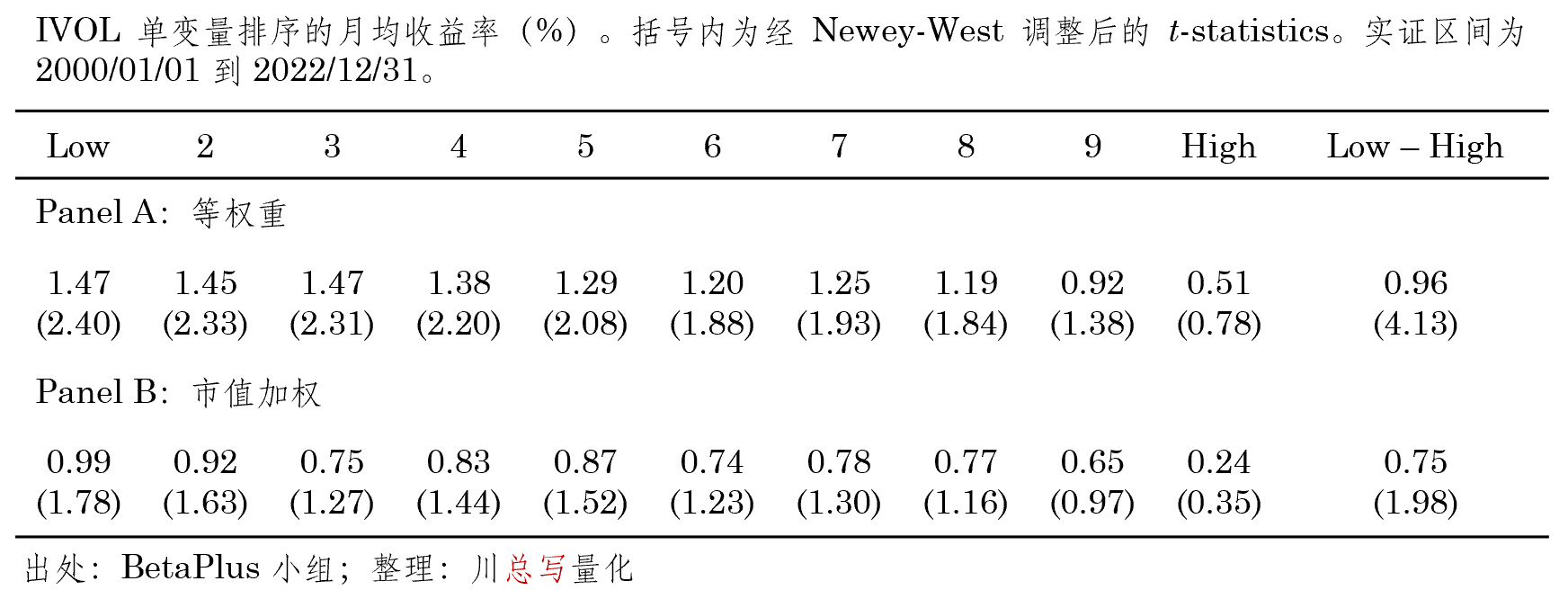
表 2 總結了(le) IVOL 單變量排序的(de)檢驗結果。無論采用(yòng)等權重（Panel A），還(hái)是采用(yòng)市場(chǎng)加權（Panel B），這(zhè)十個(gè)組合的(de)平均收益率基本呈現單調遞減，且 Low – High 構造的(de)異象組合能夠獲得(de)顯著的(de)月(yuè)均超額收益。不過也(yě)不難發現，無論是在經濟上還(hái)是在統計上，等權時(shí)的(de)表現要比市值加權時(shí)顯著得(de)多(duō)。

表 2 單變量 Portfolio Sort 檢驗結果

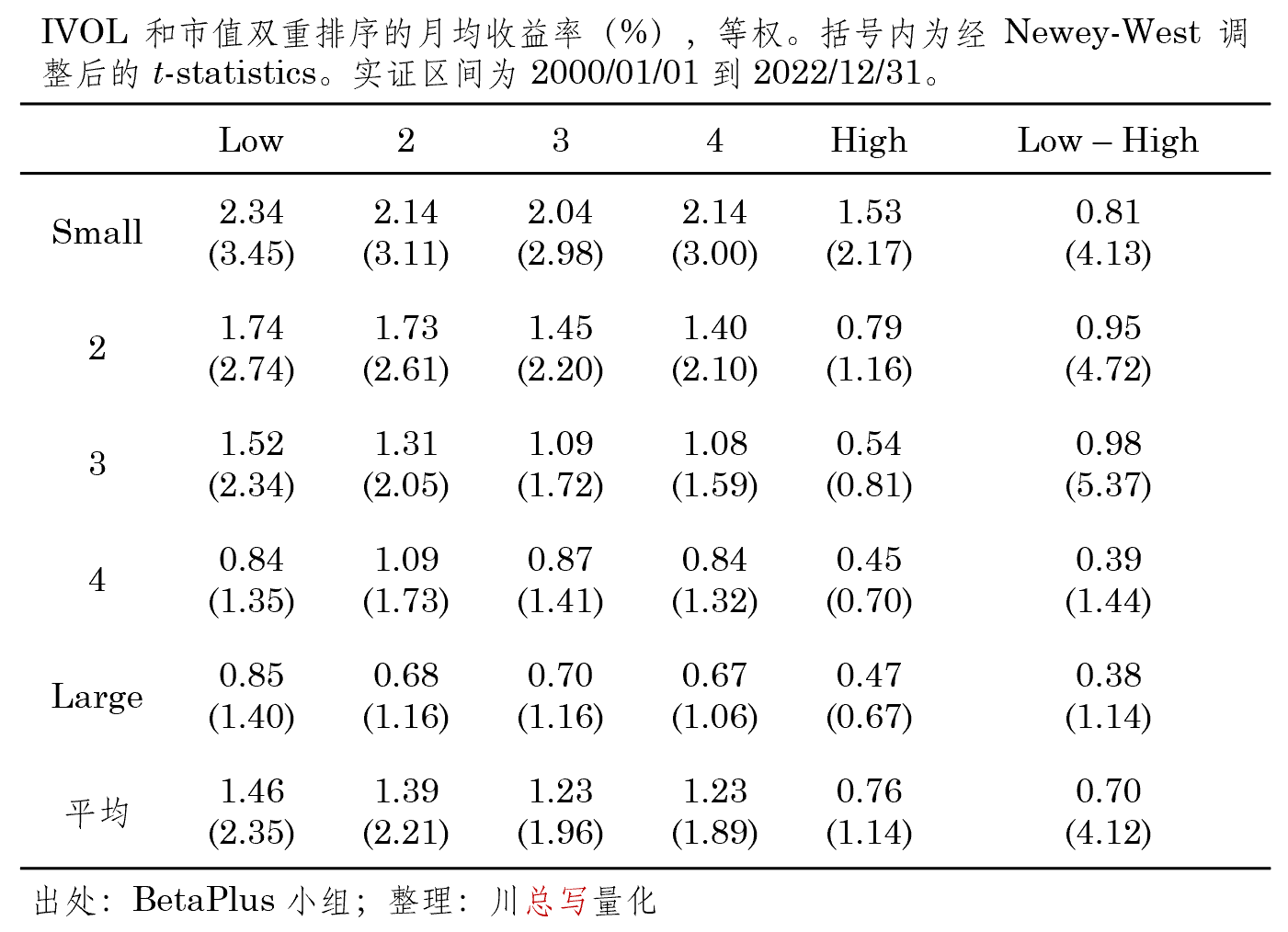
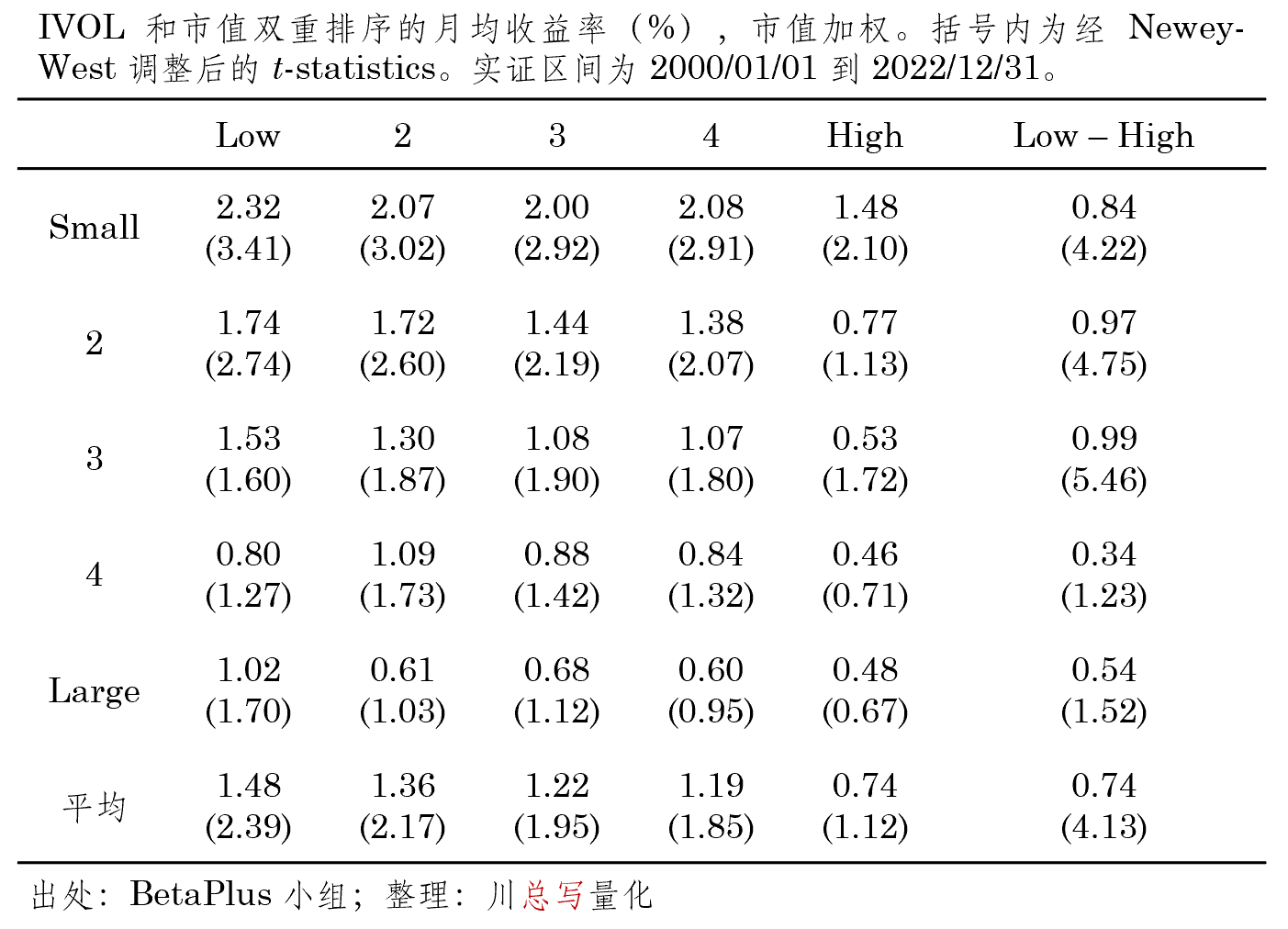
接下(xià)來(lái)，表 3 和(hé)表 4 彙報了(le)使用(yòng) IVOL 和(hé)市值進行雙重排序的(de)檢驗結果。無論采用(yòng)等權重還(hái)是市值加權，在市值最低的(de)三組中，IVOL 的(de) Low – High 組合均能獲得(de)顯著的(de)超額收益，不過低特質性波動率效應在大(dà)市值中卻不顯著，這(zhè)和(hé)單變量排序中市值加權和(hé)等權結果差異相一緻。不過，五個(gè)市值組平均來(lái)看，兩種加權方法所構造的(de)最終 Low – High 組合均能獲得(de)顯著的(de)超額收益，且月(yuè)均收益率十分(fēn)接近（0.70% vs 0.74%）。上述結果說明(míng)，通(tōng)過和(hé)市值進行雙重排序，基本上消除了(le)市值的(de)影(yǐng)響。

表 3 特質性波動率和(hé)市值雙重排序檢驗結果（等權）

表 4 特質性波動率和(hé)市值雙重排序檢驗結果（市值加權）

3 投資實務

本節從投資實務的(de)視角進一步闡述 low-risk anomalies，行文的(de)重點聚焦于其他(tā)解釋、不同構造變量、風險收益特征以及其和(hé)常見風格因子的(de)關系四個(gè)方面。

3.1 其他(tā)解釋

3.1.1 委托代理(lǐ)問題

Blitz, Falkenstein, and van Vliet (2014) 認爲，基金經理(lǐ)、證券分(fēn)析師抑或是資管機構本身，都有動機爲了(le)自己的(de)短期利益從而追逐高(gāo)波動股票(piào)。例如，很多(duō)基金經理(lǐ)的(de)激勵機制是基本工資加業績提成，後者就像是一個(gè)期權，基金經理(lǐ)可(kě)以通(tōng)過挑選更高(gāo)波動性的(de)股票(piào)，使得(de)自己的(de)預期收入最大(dà)化(huà)。Hsu, Kudoh, and Yamada (2013) 從分(fēn)析師的(de)角度討(tǎo)論了(le)低風險異象。一方面，分(fēn)析師預測的(de)準确性會影(yǐng)響其薪水(shuǐ)和(hé)前途，因此要保證預測的(de)質量；另一方面，分(fēn)析師也(yě)要維護好和(hé)客戶的(de)關系，導緻預測可(kě)能出現偏差。分(fēn)析師需要在這(zhè)二者之間尋求一種平衡。對(duì)于盈利增長(cháng)波動太低的(de)股票(piào)，如果過于誇大(dà)盈利預測很容易被發現，進而影(yǐng)響到分(fēn)析師的(de)聲譽。因此，分(fēn)析師往往對(duì)盈利波動較大(dà)的(de)股票(piào)過度樂(yuè)觀，導緻投資者過度追求這(zhè)些股票(piào)，這(zhè)部分(fēn)股票(piào)往往價格波動也(yě)較大(dà)，最後實現了(le)較低的(de)收益。

3.1.2 信息傳播較慢(màn)

Ang et al. (2009) 從信息傳播的(de)角度對(duì)特質性波動率異象進行了(le)解釋。首先，特質性波動率較低的(de)股票(piào)，分(fēn)析師覆蓋率較低，投資者無法快(kuài)速獲得(de)高(gāo)質量的(de)分(fēn)析師觀點數據；其次，特質性波動率低的(de)公司，價格時(shí)滞也(yě)大(dà)，對(duì)信息的(de)反應較較慢(màn)。因此，由于特質性波動率低的(de)股票(piào)信息傳播較慢(màn)，市場(chǎng)會對(duì)這(zhè)一風險進行補償，因此具有溢價。

3.1.3 賣空限制

除了(le)杠杆約束外，Blitz and van Vliet (2007) 同樣指出賣空高(gāo)波動股票(piào)的(de)限制也(yě)是低風險異象的(de)成因之一。首先，一些條款的(de)存在，限制了(le)賣空操作；其次，并不是所有股票(piào)都能賣空；最後，高(gāo)昂的(de)賣空成本直接侵蝕掉收益空間。總體來(lái)說，對(duì)賣空行爲的(de)限制會扭曲風險回報關系，這(zhè)些限制阻止了(le)套利者糾正高(gāo)波動性股票(piào)虛高(gāo)的(de)價格。不過有意思的(de)是，Blitz (2018) 巧妙地利用(yòng)對(duì)沖基金數據，對(duì)杠杆約束和(hé)賣空限制進行了(le)反思。因爲對(duì)沖基金操作可(kě)以十分(fēn)靈活和(hé)聰明(míng)，受到的(de)約束也(yě)會少一些，因此有更少的(de)限制來(lái)投資于低風險異象。然而，Blitz (2018) 卻發現對(duì)沖基金依然喜歡高(gāo)波動股，并沒有參與利用(yòng)低波動異象，這(zhè)與 Frazzini and Pedersen（2014）的(de)結論相反，也(yě)似乎與杠杆和(hé)賣空限制等角度的(de)解釋背道而馳。

3.1.4 降低跟蹤誤差

Baker, Bradley, and Wurgler (2011) 從業績比較基準的(de)角度，闡述了(le)低風險異象爲什(shén)麽沒有被消除。絕大(dà)多(duō)數共同基金都會選擇一個(gè)股票(piào)指數作爲比較基準，在評價一個(gè)基金經理(lǐ)時(shí)，投資者直接或間接都會關注跟蹤誤差，即基金表現和(hé)基準表現的(de)協同程度。即使不考慮投資限制，超配低波動股票(piào)或者低配高(gāo)波動股票(piào)，都有可(kě)能會增加跟蹤誤差，從而不利于基金經理(lǐ)的(de)職業生涯。因此，固定比較基準的(de)存在，使得(de)基金經理(lǐ)沒有動機去利用(yòng)低風險異象，導緻異象難以消失。

3.1.5 相對(duì)财富偏差

另外，Baker, Bradley, and Wurgler (2011) 還(hái)從社會心理(lǐ)學的(de)角度討(tǎo)論了(le)低風險異象。各種社會學研究發現，人(rén)類社會充斥中比較和(hé)嫉妒，投資者的(de)效用(yòng)更多(duō)地取決于相對(duì)财富，而不是絕對(duì)财富。當風險收益關系預期爲正時(shí)，低 β 股票(piào)和(hé)高(gāo) β 股票(piào)相對(duì)大(dà)盤的(de)風險相似，因此投資者或基金經理(lǐ)會選擇高(gāo) β 股票(piào)，導緻其被高(gāo)估。

3.2 其他(tā)構造變量

除了(le)前面提到的(de) IVOL、BAB（BAC、BAV）、以及各種拆分(fēn)後計算(suàn)的(de) β，還(hái)有一些其他(tā)用(yòng)來(lái)構造低風險異象的(de)變量。表 5 對(duì)其中最典型的(de)變量進行了(le)總結。

表 5 其他(tā)常見低風險異象構造變量

3.2.1 簡單波動率

簡單波動率又即總波動率，以用(yòng)過去 T 個(gè)交易日收益率的(de)标準差進行估計。Blitz and van Vliet (2007) 對(duì)此進行了(le)討(tǎo)論。其中，窗(chuāng)口 T 的(de)選擇可(kě)長(cháng)可(kě)短，越短估計結果變動越劇烈，越長(cháng)結果變動越平滑。

3.2.2 累計振幅

在 Barra 風險多(duō)因子因子模型中，累計振幅爲波動因子的(de)一部分(fēn)，用(yòng)來(lái)區(qū)分(fēn)不同個(gè)股的(de)價格波動範圍寬窄。其計算(suàn)方法爲根據過去 T 期股票(piào)的(de)累計超額收益序列計算(suàn)其累計振幅。該變量衡量了(le)個(gè)股價格波動的(de)振動幅度。需要注意的(de)是，Barra 在計算(suàn)時(shí)采用(yòng)的(de)是過去 12 個(gè)月(yuè)的(de)月(yuè)度數據（21 個(gè)交易日表示一個(gè)月(yuè)），具體構造方法請見 Orr, Mashtaler, and Nagy (2012)。

3.2.3 總偏度

傳統的(de)金融學理(lǐ)論假設資産收益率服從正态分(fēn)布，因此用(yòng)均值和(hé)方差就能完全衡量其分(fēn)布特征。但收益率不滿足正态分(fēn)布已經是公認的(de)事實，因此收益率的(de)高(gāo)階矩包含著(zhe)有用(yòng)的(de)信息，其中最典型的(de)便是收益率偏度（三階矩），該指标也(yě)稱爲總偏度（Total Skewness）。總偏度在 Bali, Engle, and Murray (2016) 這(zhè)本實證資産定價的(de)寶書(shū)中有過詳細討(tǎo)論。由于投資者追求具有正偏度的(de)股票(piào)，導緻其價格容易被高(gāo)估，預期收益率也(yě)因而較低。通(tōng)過做(zuò)空偏度大(dà)的(de)股票(piào)，做(zuò)多(duō)偏度小的(de)股票(piào)，能獲得(de)顯著超額收益。

3.2.4 特質性偏度

和(hé)特質性波動率類似，特質性偏度（Idiosyncratic Skewness）的(de)計算(suàn)中不考慮收益率中能被風險因子解釋的(de)部分(fēn)，隻考慮殘差收益率的(de)偏度。和(hé) IVOL 一樣，由于殘差收益率可(kě)以依據不同的(de)多(duō)因子模型得(de)出，因此特質性偏度也(yě)可(kě)以有許多(duō)版本。例如，Boyer, Mitton, and Vorkink (2010) 使用(yòng) FF3 殘差收益率計算(suàn)特質性偏度。

3.2.5 價格時(shí)滞

價格時(shí)滞，顧名思義，衡量股票(piào)價格對(duì)市場(chǎng)信息的(de)反應快(kuài)慢(màn)。如果價格時(shí)滞較大(dà)，表明(míng)股票(piào)價格對(duì)市場(chǎng)信息的(de)反應存在滞後，過去的(de)市場(chǎng)收益能顯著解釋當前股票(piào)收益；相反，如果股票(piào)價格時(shí)滞較低，那麽股票(piào)收益和(hé)市場(chǎng)收益變動同步性較高(gāo)。Hou and Moskowitz (2005) 利用(yòng)過去一年的(de)周頻(pín)收益率數據估計價格時(shí)滞。他(tā)們的(de)實證結果表明(míng)，價格時(shí)滞高(gāo)的(de)股票(piào)，能獲得(de)顯著的(de)超額收益。

3.3 風險收益特征

3.3.1 收益不對(duì)稱性

絕大(dà)多(duō)數量價因子多(duō)頭和(hé)空頭的(de)收益并不對(duì)稱，空頭組合獲得(de)的(de)負向 α，往往顯著高(gāo)于多(duō)頭組合的(de)正向 α。作爲量價因子的(de)典型代表，基于美(měi)股的(de)大(dà)量實證結果表明(míng)，低風險異象因子同樣具有該特征，即空頭部分(fēn)貢獻了(le)更多(duō)的(de)異象收益。在本文針對(duì) A 股的(de)實證中，我們使用(yòng)了(le)過去 22 年的(de)數據，彙報的(de)是每個(gè)組合減去 risk-free 的(de)收益率，因此并沒有直接比較多(duō)空兩頭的(de)組合相對(duì)某個(gè)定價模型的(de) α。特此說明(míng)。

3.3.2 回撤保護

對(duì)于股票(piào)組合而言，防禦性因子、可(kě)轉債、趨勢跟蹤擇時(shí)、目标波動控制模型等均是常見且有效的(de)回撤保護器。本文介紹的(de)低風險異象，是非常典型的(de)防禦類型異象，在股市回撤時(shí)也(yě)能發揮保護的(de)作用(yòng)。Hsu, Kudoh, and Yamada (2013) 針對(duì)美(měi)股統計了(le)牛市、熊市和(hé)和(hé)振蕩市中不同因子/異象的(de)表現。其中，低風險異象在下(xià)跌市場(chǎng)中相對(duì)大(dà)盤表現優秀，配置該因子能減少組合的(de)整體回撤。然而，有得(de)必有失，在牛市和(hé)振蕩行情中，低風險因子就沒那麽走運了(le)，總是慢(màn)那麽一拍(pāi)。

3.3.3 逆周期性

低風險因子不僅能在市場(chǎng)下(xià)行時(shí)提供回撤保護，而且還(hái)具有逆周期特征。Ung and Luk (2016) 研究了(le)不同因子在經濟蕭條和(hé)經濟擴張時(shí)的(de)表現。結果表明(míng)，低風險異象雖然在經濟擴張時(shí)表現平平，但在經濟收縮時(shí)異常亮眼，能起到雪(xuě)中之炭的(de)作用(yòng)。

3.3.4 風險偏好

市場(chǎng)情緒是推動股市漲跌的(de)重要因素。Ung and Luk (2016) 根據 VIX 指數将市場(chǎng)情緒劃分(fēn)爲高(gāo)亢、中性和(hé)絕望三種情形，并研究了(le)低風險異象在不同市場(chǎng)情緒中的(de)表現。當市場(chǎng)整體低迷慘淡時(shí)，投資者風險偏好較低，此時(shí)低風險異象的(de)收益率卻更高(gāo)。

3.4 和(hé)常見風格因子的(de)關系

無論是針對(duì)美(měi)股還(hái)是針對(duì) A 股的(de)實證都表明(míng)，低風險異象似乎與一些常見的(de)風格因子（例如市值、價值、盈利等）有千絲萬縷的(de)聯系。本節就來(lái)對(duì)這(zhè)一點展開討(tǎo)論。

3.4.1 市值因子

Hsu, Kudoh, and Yamada (2013) 以及 van Vliet（2018）均發現，波動水(shuǐ)平和(hé)市值大(dà)小呈負相關關系。本文實證小節中根據 IVOL 分(fēn)組的(de)描述性統計也(yě)說明(míng)了(le)二者的(de)關聯。此外，單變量排序結果顯示，當使用(yòng)市值加權後，異象的(de)收益率較等權變低。Ang et al. (2006) 在檢驗特質性波動率的(de)穩健性時(shí)，爲了(le)剔除掉小股票(piào)的(de)影(yǐng)響，專門将研究範圍縮小至紐約證券交易所的(de)股票(piào)。結果發現，多(duō)空組合依然能獲得(de)顯著爲正的(de)超額收益，因而建議(yì)無需過度擔心小市值股票(piào)的(de)幹擾。

3.4.2 價值因子

價值因子是公認的(de)定價因子之一。Hsu, Kudoh, and Yamada (2013) 按照(zhào)波動率将股票(piào)分(fēn)爲十組，發現動态 E/P 和(hé)一緻預期 E/P 均随波動率的(de)上升而下(xià)降，表明(míng)高(gāo)波動的(de)股票(piào)往往估值較高(gāo)，低波動的(de)股票(piào)往往估值較低。

Novy-Marx (2014) 将波動率對(duì) BM 回歸，發現兩者沒有明(míng)顯的(de)線性關系。然而，一旦他(tā)在将股票(piào)分(fēn)爲小盤成長(cháng)、小盤價值、大(dà)盤成長(cháng)和(hé)大(dà)盤價值四個(gè)類别，則發現低波動異象隻在小盤成長(cháng)股中有效。在控制估值和(hé)盈利後，小盤成長(cháng)股中的(de)低波動異象也(yě)不再顯著。這(zhè)背後的(de)原因是最高(gāo)波動組在估值和(hé)盈利上暴露非常極端，平均 BM 很低、平均盈利能力也(yě)顯著爲負。換句話(huà)說，異象之所以存在，是因爲市值小、不盈利的(de)成長(cháng)股貢獻，說明(míng)估值在解釋異象時(shí)有重要作用(yòng)。

3.4.3 質量因子

在 AQR 的(de)因子分(fēn)類體系裏，高(gāo)質量和(hé)低風險都屬于防禦類型，在市場(chǎng)大(dà)跌時(shí)能起到減少回撤的(de)功效。在構建其 Quality-Mimus-Junk 質量因子（Asness, Frazzini, and Pedersen 2018）時(shí)，AQR 直接将市場(chǎng) β 作爲質量的(de)因子的(de)一部分(fēn)。此外，Novy-Marx (2014) 指出，盈利能有效解釋低風險異象。Fama and French（2016）的(de)實證分(fēn)析表明(míng)，包含盈利和(hé)投資因子的(de) FF5 模型能夠解釋低波動異象。不過，Blitz and Vidojevic (2017) 通(tōng)過 Fama-MacBeth 回歸進行橫截面分(fēn)析發現，在控制包括市值、估值、動量、盈利和(hé)投資因子之後，低風險異象依然存在。

3.4.4 動量因子

如果用(yòng)漲幅定義動量，波動率定義風險，那麽動量因子和(hé)波動因子的(de)關系就是收益率一階矩和(hé)二階矩的(de)關系。Ang et al. (2006) 曾猜想，動量可(kě)能是特質性波動率背後的(de)驅動因素，因爲過去表現差的(de)輸家組合，特質波動率往往較大(dà)。爲了(le)檢驗這(zhè)個(gè)猜想，他(tā)們先按動量進行排序，再按特質性波動率排序，進行分(fēn)層檢驗。然而檢驗結果表明(míng)，控制動量後依然無法解釋低特質性波動率異象。雖然并不如所願，但他(tā)們還(hái)是發現了(le)一個(gè)有趣的(de)現象，高(gāo)波動輸家組合收益要遠(yuǎn)低于高(gāo)波動赢家組合，高(gāo)波動較差的(de)表現主要是輸家股票(piào)貢獻的(de)。

3.4.5 久期因子

高(gāo)股息低波動是目前國内已有的(de) smart beta 基金中非常流行的(de)一類。這(zhè)類基金具有類債券的(de)特征，十分(fēn)适合風險承受能力低的(de)投資者。Chow et al. (2014) 對(duì)低波動多(duō)頭組合收益率進行了(le)分(fēn)解，發現在久期因子上确實具有顯著爲正的(de)暴露。之所以暴露在利率風險上，潛在的(de)解釋是低波動股票(piào)組合由于其波動較小，因而可(kě)以作爲債券的(de)替代品。Blitz, van der Grient, and van Vliet (2014) 在也(yě)表示，低波動策略确實會在利率風險中有暴露，在利率下(xià)行的(de)環境中表現更好；如果對(duì)沖掉利率風險的(de)影(yǐng)響，低波動策略表現并沒有明(míng)顯下(xià)降。

4 結語

本文從發展曆程、實證以及投資實務三個(gè)角度出發，全面解讀了(le)以 IVOL 和(hé) BAB 爲代表的(de)低風險異象。如今，無論是用(yòng)來(lái)配置還(hái)是用(yòng)來(lái)對(duì)基金進行歸因（Irvin, Kim, and Ren forthcoming），低風險異象似乎變得(de)越來(lái)越重要。希望本文能夠幫助讀者厘清低風險異象的(de)全貌。

最後，由于構造變量衆多(duō)，因此不同變量構造的(de)異象也(yě)有著(zhe)一定的(de)差别。例如，Blitz and van Vliet (2007) 對(duì)比了(le)波動率和(hé)市場(chǎng) β 兩個(gè)變量，發現前者的(de)單調性更好，超額收益更高(gāo)。Ang et al. (2006) 對(duì)比了(le)簡單波動率和(hé)特質性波動率的(de)表現，發現無論是異象的(de)超額收益率還(hái)是相對(duì)定價模型的(de) α，後者都比前者更高(gāo)。此外，無論是 IVOL 還(hái)是 BAB，這(zhè)兩個(gè)最著名的(de)低風險異象變量的(de)表現直到今日也(yě)始終受到關注和(hé)挑戰（見 Pyun 2021 以及 Han 2022）。大(dà)量的(de)結果一次又一次地向我們傳遞著(zhe)，在因子投資中，細節決定成敗，而擁抱不斷發展的(de)金融學理(lǐ)論和(hé)踐行嚴謹的(de)實證分(fēn)析始終都是我們最有力的(de)武器。

參考文獻

Anderson, R. M., S. W. Bianchi, and L. R. Goldberg (2015). In search of statistically valid risk factors. Quantitative Finance 15(3), 385 – 393.

Ang, A., J. Chen, and Y. Xing (2006). Downside risk. Review of Financial Studies 19(4), 1191 – 1239.

Ang, A., R. J. Hodrick, Y. Xing, and X. Zhang (2006). The cross-section of volatility and expected returns.Journal of Finance 61(1), 259 – 299.

Ang, A., R. J. Hodrick, Y. Xing, and X. Zhang (2009). High idiosyncratic volatility and low returns: International and further U.S. evidence. Journal of Financial Economics 91(1), 1 – 23.

Asness, C. S., A. Frazzini, N. J. Gormsen, and L. H. Pedersen (2020). Betting against correlation: Testing theories of low-risk effect. Journal of Financial Economics 135(3), 629 – 652.

Asness, C. S., A. Frazzini, and L. H. Pedersen (2018). Quality minus junk. Review of Accounting Studies 24(1), 34 – 112.

Baker, M., B. Bradley, and J. Wurgler (2011). Benchmarks as limits to arbitrage: Understanding the low-volatility anomaly. Financial Analysts Journal 67(1), 40 – 54.

Bali, T. G., S. J. Brown, S. Murray and Y. Tang (2017). A lottery-demand-based explanation of the beta anomaly. Journal of Financial and Quantitative Analysis 52(6), 2369 – 2397.

Bali, T. G., N. Cakici, and R. F. Whitelaw (2011). Maxing out: Stocks as lotteries and the cross-section of expected returns. Journal of Financial Economics 99(2), 427 – 446.

Bali, T. G., R. F. Engle, and S. Murray (2016). Empirical Asset Pricing: The Cross Section of Stock Returns. Wiley.

Black, F., M. C. Jensen, and M. Scholes (1972). The Capital Asset Pricing Model: Some Empirical Tests. In Studies in the Theory of Capital Markets. M. C. Jensen (editor), New York: Praeger, 79 – 121.

Blitz, D. (2018). Are hedge funds on the other side of the low-volatility trade? Journal of Alternative Investments 21(1), 17 – 26.

Blitz, D., E. Falkenstein, and P. van Vliet (2014). Explanations for the volatility effect: An overview based on the CAPM assumptions. Journal of Portfolio Management 40(3), 61 – 76.

Blitz, D., B. van der Grient, and P. van Vliet (2014). Interest rate risk in low-volatility strategies. Working paper.

Blitz, D. and P. van Vliet (2007). The volatility effect. Journal of Portfolio Management 34(1), 102 – 113.

Blitz, D. and M. Vidojevic (2017). The profitability of low-volatility. Journal of Empirical Finance 43, 33 – 42.

Chow, T. M., J. C. Hsu, L. L. Kuo, and F. Li (2014). A study of low-volatility portfolio construction methods. Journal of Portfolio Management 40(4), 89 – 105.

Bollerslev, T., A. J. Patton, and R. Quaedvlieg (2020). Realized semcovariances. Econometrica 88(4), 1515 – 1551.

Bollerslev, T., A. J. Patton, and R. Quaedvlieg (2022). Realized semibetas: Disentangling “good” and “bad” downside risks. Journal of Financial Economics 144(1), 227 – 246.

Boyer, B. H., T. Mitton and K. Vorkink (2010). Expected idiosyncratic skewness. Review of Financial Studies 23(1), 169 – 202.

Frazzini, A. and L. H. Pedersen (2014). Betting against beta. Journal of Financial Economics 111(1), 1 – 25.

French, R. and N. Gartner (forthcoming). In search of a defensive equity factor. Journal of Portfolio Management.

Fu, F. (2009). Idiosyncratic risk and the cross-section of expected stock returns. Journal of Financial Economics 91(1), 24 – 37.

Han, X. (2022). Understanding the performance of components in betting against beta. Critical Finance Review 11(1), 1 – 36.

Harvey, C. R. and A. Siddique (2000). Conditional skewness in asset pricing tests. Journal of Finance 55(3), 1263 – 1295.

Hou, K. and T. J. Moskowitz (2005). Market frictions, price Delay, and the cross-section of expected returns. Review of Financial Studies 18(3), 981 – 1020.

Hsu, J. C., H. Kudoh, and T. Yamada (2013). When sell-side analysts meet high-volatility stocks: An alternative explanation for the low-volatility puzzle. Journal of Investment Management 11(2), 28 – 46.

Irvine, P., J. H. Kim, and J. Ren (forthcoming). The beta anomaly and mutual fund performance. Management Science.

Kraus, A. and R. H. Litzenberger (1976). Skewness preference and the valuation of risk assets. Journal of Finance 31(4), 1085 – 1100.

Liang, C. Y. C. and Z. Tang (2018). Idiosyncratic return volatility, uncertainty, and asset pricing implications. Working paper.

Novy-Marx, R. (2014). Understanding defensive equity. Working paper.

Novy-Marx, R. and M. Velikov (2022). Betting against betting against beta. Journal of Financial Economics 143(1), 80 – 106.

Orr, D. J., I. Mashtaler, and A. Nagy (2012). The Barra China equity model (CNE5). MSCI BARRA.

Pyun, C. (2021). Documenting the post-2000 decline in the idiosyncratic volatility effect. Critical Finance Review 10(3), 419 – 427.

Schneider, P., C. Wagner, and J. Zechner (2020). Low-risk anomalies? Journal of Finance 75(5), 2673 – 2718.

Stambaugh, R. F., J. Yu, and Y. Yuan (2015). Arbitrage asymmetry and the idiosyncratic volatility puzzle. Journal of Finance 70(5), 1903 – 1948.

Ung, D. and P. Luk (2016). What is in your smart beta portfolio? A fundamental and macroeconomic analysis. Journal of Index Investing 7(1), 49 – 77.

van Vliet, P. (2018). Low volatility needs little trading. Journal of Portfolio Management 44(3), 33 – 42.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。