Toward a better factor model (II)

作者：石川

摘要：Double bootstrap 在評價多(duō)因子模型時(shí)也(yě)能發揮作用(yòng)。實證結果表明(míng)，Kelly, Pruitt and Su (2019) 的(de) IPCA 模型可(kě)堪大(dà)用(yòng)。而在 ad-hoc 模型裏，Fama and French (2015) 似乎從未被超越。

1

還(hái)記得(de)《Toward a better factor model》嗎？這(zhè)是本系列的(de)第二篇。其實它也(yě)可(kě)以是《Farewell, ad-hoc 多(duō)因子模型》系列的(de)第二篇，或者是《出色不如走運》系列的(de)第九篇。但我認爲把它歸到《Toward a better factor model》最恰如其分(fēn)。

在《Toward a better factor model》一文中，我介紹了(le)兩個(gè)檢驗多(duō)因子模型的(de)方法，其中之一是 Barillas and Shanken (2017) 的(de) right-hand-side approach，即我們隻需要比較不同模型所包含的(de)因子 span 出來(lái)的(de)最大(dà)夏普比率平方即可(kě)，夏普比率平方更大(dà)的(de)是更好的(de)模型。然而，随著(zhe)更多(duō)的(de)因子被加入到多(duō)因子模型中，其 ex-post 最大(dà)夏普比率平方總能被提升。不過，這(zhè)一定就會導緻更好的(de)多(duō)因子模型嗎（即能夠更有效地解釋資産預期收益的(de)截面差異）？爲了(le)回答(dá)這(zhè)個(gè)問題，不妨來(lái)看下(xià)面這(zhè)個(gè)極端的(de)例子。

以最大(dà)化(huà) ex-post 夏普比率平方爲目标，我們從 Hou, Xue and Zhang (2020) 考察的(de) 400+ 個(gè)因子裏以 t-statistic 爲标準挑出以下(xià) 7 個(gè)（雖然每個(gè)因子看上去都挺合理(lǐ)，但毫無疑問在挑選的(de)過程中，我們刻意引入了(le) data-snooping），而這(zhè)七個(gè)因子 + 市場(chǎng)因子構造的(de)多(duō)因子模型的(de) ex-post 夏普比率平方是 CAPM 的(de)三倍。

根據 Barillas and Shanken (2017) 的(de)标準，上述模型毫無疑問要“優于”CAPM 乃至那些主流的(de) ad-hoc 多(duō)因子模型（FF5、q-factor model 這(zhè)些）。然而，事實真的(de)如此嗎？我們能對(duì)這(zhè)個(gè)經 data-snooping 挑出來(lái)的(de)模型抱有多(duō)大(dà)的(de)信心？信心自然不是憑空而來(lái)，而是要經過科學的(de)檢驗。爲了(le)檢驗多(duō)因子模型，通(tōng)常使用(yòng) sorted portfolios 作爲 test assets，然而實證結果和(hé)理(lǐ)論推導均表明(míng)，檢驗結果在很大(dà)程度上取決于 test assets 的(de)選擇。爲此，一個(gè)自然而然的(de)問題是，如何使用(yòng) individual assets（個(gè)股）作爲 test assets 來(lái)檢驗模型。

這(zhè)個(gè)問題由來(lái)已久。對(duì) individual assets 來(lái)說，無論是 β 估計不準還(hái)是 pricing errors 太大(dà)，因此總會 over-reject 多(duō)因子模型，導緻使用(yòng) individual assets 的(de)實踐難以展開。不過，這(zhè)些困難從來(lái)沒有阻擋人(rén)們在這(zhè)條道路上不斷探索前行。在剛剛進行的(de) 2023 AFA 年會上，有很多(duō) asset pricing 方面的(de) sessions，而其中我個(gè)人(rén)最喜歡的(de)是下(xià)面這(zhè)個(gè)題爲 Individual Assets and the SDF 的(de) session。

其中 Clarke and Momeni (2021) 利用(yòng)從基金研究借鑒而來(lái)的(de) double bootstrap 方法，通(tōng)過個(gè)股檢驗了(le)主流的(de) ad-hoc 以及基于 PCA 的(de)多(duō)因子模型，并爲 Toward a better factor model 這(zhè)個(gè)話(huà)題提供了(le)非常有益的(de)啓發。本文第二節就對(duì)此進行介紹。

2

Clarke and Momeni (2021) 一文受到了(le) Kosowski, et al. (2006) 以及 Fama and French (2010) 在基金研究中使用(yòng) bootstrap 方法的(de)啓發（見《出色不如走運 (VIII)》）。基金研究的(de)目标是考察是否有獲得(de)顯著超額收益的(de)基金；而多(duō)因子模型檢驗的(de)目标是考察是否有獲得(de)顯著定價錯誤（pricing errors）的(de)資産。上述類比告訴我們，這(zhè)兩項研究一個(gè)共同的(de)前提條件是需要指定一個(gè)适當的(de) benchmark。換句話(huà)說，我們無法在沒有基準的(de)前提下(xià)談論哪些基金獲得(de)了(le)超額收益，我們也(yě)不能在沒有多(duō)因子模型的(de)前提下(xià)討(tǎo)論哪些資産有定價錯誤。以上描述似乎将我們推向一個(gè)無盡的(de)循環：我們想要通(tōng)過 individual assets 來(lái)檢驗目标多(duō)因子模型，然後爲了(le)計算(suàn) pricing errors 我們又需要事先指定多(duō)因子模型。有沒有辦法讓我們繞過這(zhè)個(gè)困境呢(ne)？答(dá)案是 bootstrap，更确切地說是 double bootstrap。

這(zhè)裏簡單解釋一下(xià)要用(yòng) double bootstrap 的(de)邏輯。以下(xià)的(de)說明(míng)中涉及了(le) population model 和(hé) tested model，請格外注意。一般來(lái)說，爲檢驗某個(gè)給定的(de)多(duō)因子模型，在這(zhè)個(gè) double bootstrap procedure 中，population model 和(hé) tested model 是同一個(gè)模型。當使用(yòng)不同模型時(shí)，可(kě)以定量刻畫(huà)該 procedure 的(de) size 和(hé) power。首先，我們假設股票(piào)預期收益率數據滿足某個(gè)因子模型（比如 CAPM、FF5），這(zhè)個(gè)模型就是 population model。然後用(yòng)真實股票(piào)和(hé)因子收益率曆史數據進行時(shí)序回歸，得(de)到每個(gè)股票(piào)的(de) α，并把它們從股票(piào)收益率時(shí)序中減去，得(de)到 demean 之後的(de)曆史數據。此時(shí)，上述數據滿足了(le)我們的(de)假設，即股票(piào)收益率在 population model 下(xià)沒有 pricing errors。但是請注意，到現在爲止，我們還(hái)沒有進行任何一輪 bootstrap，隻是 demean 了(le)一把。

接下(xià)來(lái)是第一輪 bootstrap。以上述 demean 之後的(de)曆史數據作爲 population，進行有放回的(de) bootstrap，構造一個(gè) bootstrapped sample。在這(zhè)個(gè)樣本中，我們通(tōng)過時(shí)序回歸計算(suàn)個(gè)股對(duì) tested model 的(de) α。注意，這(zhè)裏的(de) tested model 可(kě)以和(hé) population model 是同一個(gè)模型，也(yě)可(kě)以是不同的(de)模型（後文會進一步解釋差異。當 tested model 和(hé) population model 一緻時(shí)，由于 sampling error，個(gè)股依然有 pricing errors）。我們的(de)目标是考察根據 tested model 計算(suàn)的(de) pricing errors 是否在置信區(qū)間之内。如果 pricing errors 在置信區(qū)間之内，則可(kě)以認爲個(gè)股的(de)預期收益率滿足 tested model。接下(xià)來(lái)的(de)問題就是：如何确定置信區(qū)間。這(zhè)就需要第二輪 bootstrap。對(duì)于第一輪 bootstrap 得(de)到的(de) bootstrapped sample，對(duì)每支個(gè)股減去 tested model 下(xià)的(de) pricing error，然後得(de)到 demeaned bootstrapped sample，并把它視爲第二輪 bootstrap 的(de) pseudo-population。對(duì)該 pseudo-population 進行 1000 次 bootstrap，即可(kě)得(de)到置信區(qū)間。

3

下(xià)面討(tǎo)論五點核心：

第一，爲什(shén)麽是 double bootstrap。在第一輪 bootstrap 中，我們隻得(de)到了(le)未知 population 下(xià)的(de)一組個(gè)股 sample pricing errors，但無法知道這(zhè)些 pricing errors 是如何變化(huà)的(de)。在第二輪 bootstrap 中，我們将第一輪的(de)樣本作爲第二輪的(de) pseudo-population，并産生以此爲總體的(de)大(dà)量 bootstrapped samples，從而刻畫(huà) pricing errors 是如何變化(huà)的(de)。Bootstrap 方法确保我們能夠通(tōng)過“bootstrapped 樣本統計量圍繞原始樣本統計量的(de)變化(huà)”來(lái)刻畫(huà)“原始樣本統計量如何圍繞總體統計量的(de)變化(huà)”。這(zhè)是我們通(tōng)過第二輪 bootstrap 計算(suàn)置信區(qū)間并檢驗模型的(de)依據。

第二，population model 和(hé) tested model。一般來(lái)說，在應用(yòng) double bootstrap 時(shí)，population model 和(hé) tested model 是同一個(gè)模型，即待檢驗的(de)因子模型。如果第一輪的(de)樣本統計量處于第二輪 bootstrap 得(de)到的(de)置信區(qū)間内，我們就可(kě)以接受 tested model，反之即拒絕 tested model。這(zhè)時(shí)：

1. 如果 population model 和(hé) tested model 是同一個(gè)，則接受 tested model 是正确的(de)，而拒絕 tested model 是錯誤的(de)；

2. 如果 population model 和(hé) tested model 不同，比如假設 population model 是 CAPM，但是 tested model 是 FF6（即總體符合 CAPM，但這(zhè)件事兒(ér)對(duì)我們是未知的(de)，我們取而代之檢驗 FF6），那麽接受 tested model 則是錯誤的(de)，而拒絕 tested model 才是正确的(de)。

由上述論述可(kě)知，如果 population model = tested model，則錯誤地拒絕 tested model 的(de)概率衡量了(le)該方法的(de) size；如果 population model ≠ tested model，則正确地拒絕 tested model 的(de)概率則衡量了(le)該方法的(de) power。

第三，兩個(gè) 1000 次。由上述介紹可(kě)知，對(duì)于第一輪的(de)  bootstrapped sample（并将其根據 tested model 減去個(gè)股 α），在第二輪會以此爲 pseudo-population 進行 1000 次 bootstrap、計算(suàn)置信區(qū)間。這(zhè)是第二個(gè)“1000 次”。而第一個(gè)“1000 次”是我們在第一輪構造 1000 個(gè) bootstrapped sample。這(zhè)是因爲無論 size 還(hái)是 power，都代表了(le)錯誤/正确拒絕 tested model 的(de)概率。試想，我們在第一輪隻有一個(gè) bootstrapped sample，然後其 pricing errors 落在置信區(qū)間内，那麽我們隻能說對(duì)于該 bootstrapped sample 接受 tested model，但顯然不能說接受 tested model 的(de)概率是 100%（或 size = 0%）；反之，如果 pricing errors 落在置信區(qū)間外，我們也(yě)隻能說對(duì)于該 bootstrapped sample 拒絕 tested model，但不能說拒絕 tested model 的(de)概率是 100%（或 power = 100%）。

第四，分(fēn)組。按照(zhào)上述方法，對(duì)于個(gè)股都可(kě)以得(de)到其 pricing error 的(de)置信區(qū)間。不過在實際操作中，Clarke and Momeni (2021) 并沒有在個(gè)股粒度上檢驗模型，而是将個(gè)股依照(zhào) pricing errors 高(gāo)低聚合成 10%、20%、……、90% 分(fēn)位數（共 9 組）以及 1%、2%、……、99% 分(fēn)位數（共 99 組）兩種粒度。在每種情況下(xià)，檢驗全部 9 組（或者 99 組）每組的(de)平均 pricing errors 是否均落在對(duì)應的(de)置信區(qū)間内。爲了(le)得(de)到對(duì)應的(de)置信區(qū)間，對(duì)于第二輪的(de)每個(gè) bootstrapped sample 中的(de) pricing errors 也(yě)進行了(le)相應的(de)分(fēn)組。然後對(duì)于每一組（例如第 10% 分(fēn)位數組），由于一共有 1000 個(gè) bootstrapped sample，因此一共有 1000 個(gè) 10% 分(fēn)位數組的(de)取值，即得(de)到了(le) 10% 分(fēn)位數組 pricing error 的(de)分(fēn)布，從該分(fēn)布中便可(kě)以得(de)到置信區(qū)間兩端的(de)取值。

第五，多(duō)重假設檢驗。置信區(qū)間的(de)确定依賴于置信區(qū)間兩端分(fēn)位數的(de)确定。由于同時(shí)檢驗 9 組（或 99 組）pricing errors 是否落在各自的(de)置信區(qū)間，且隻要有一個(gè)在置信區(qū)間之外就拒絕 tested model，因此在确定置信區(qū)間大(dà)小的(de)時(shí)候必須考慮多(duō)重假設檢驗修正。爲此，Clarke and Momeni (2021) 首先考慮了(le) Bonferonni 修正。但是，Bonferonni 修正的(de)問題是它過于保守，導緻置信區(qū)間過大(dà)，從而降低了(le)該 double bootstrap 方法的(de) test power。因此，Clarke and Momeni (2021) 也(yě)考慮了(le)經驗數值法，即通(tōng)過在給定 size 下(xià)最大(dà)化(huà) power 來(lái)選取最優置信區(qū)間的(de)大(dà)小。具體方法請閱讀原文。

4

最後就來(lái)看一些具體的(de)實證結果。爲了(le)說明(míng)該方法在保證 size 的(de)同時(shí)也(yě)有足夠的(de) test power，在檢驗常見多(duō)因子模型之前，Clarke and Momeni (2021) 首先通(tōng)過模拟來(lái)定量刻畫(huà)了(le)該方法的(de)好處。在模拟中，他(tā)們分(fēn)别假設 population model 是 CAPM 和(hé) FF6，然後令 tested model 也(yě)分(fēn)别使用(yòng) CAPM 和(hé) FF6，因此一共四種情況：

1. population model = CAPM，tested model = CAPM；

2. population model = CAPM，tested model = FF6；

3. population model = FF6，tested model = FF6；

4. population model = FF6，tested model = CAPM。

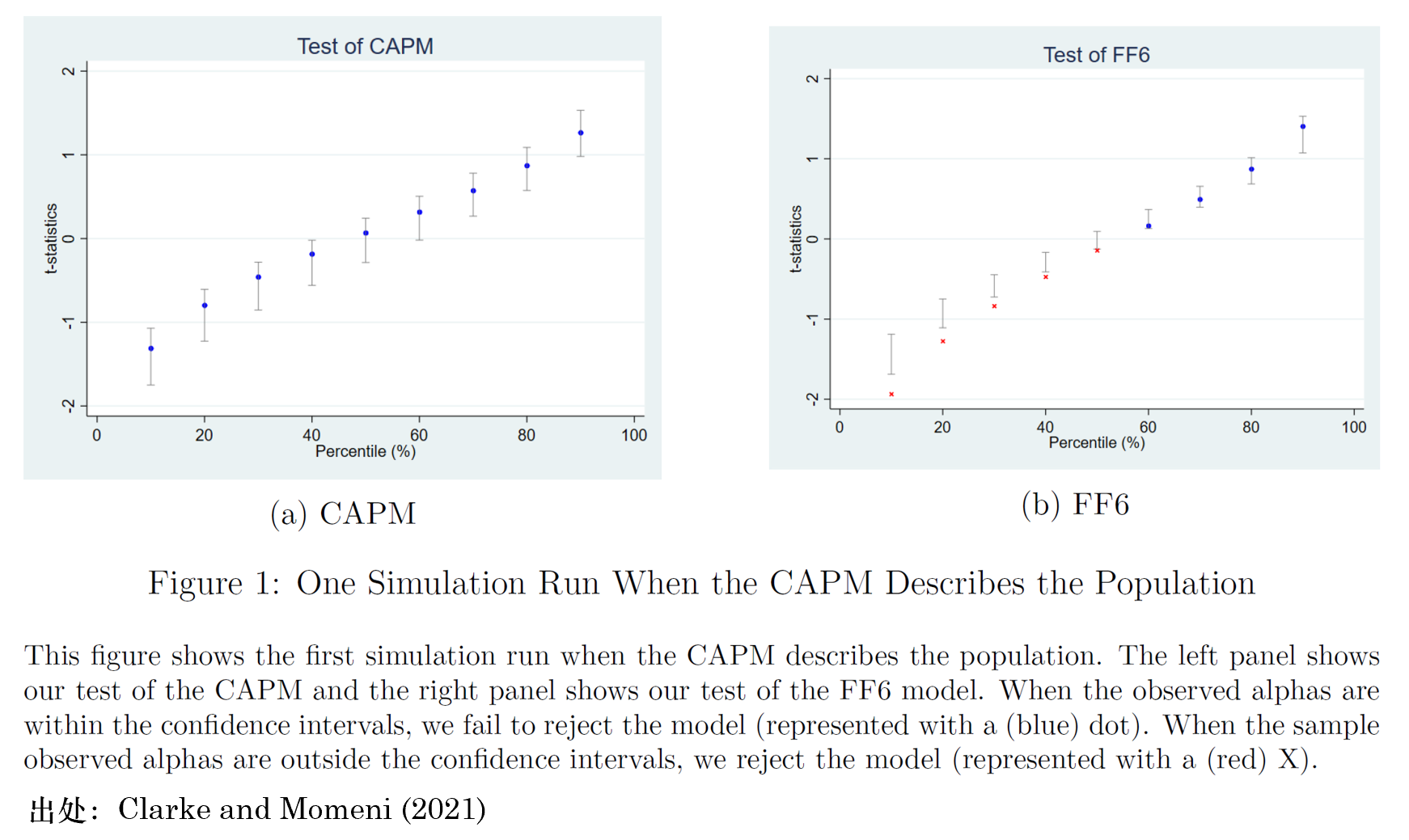
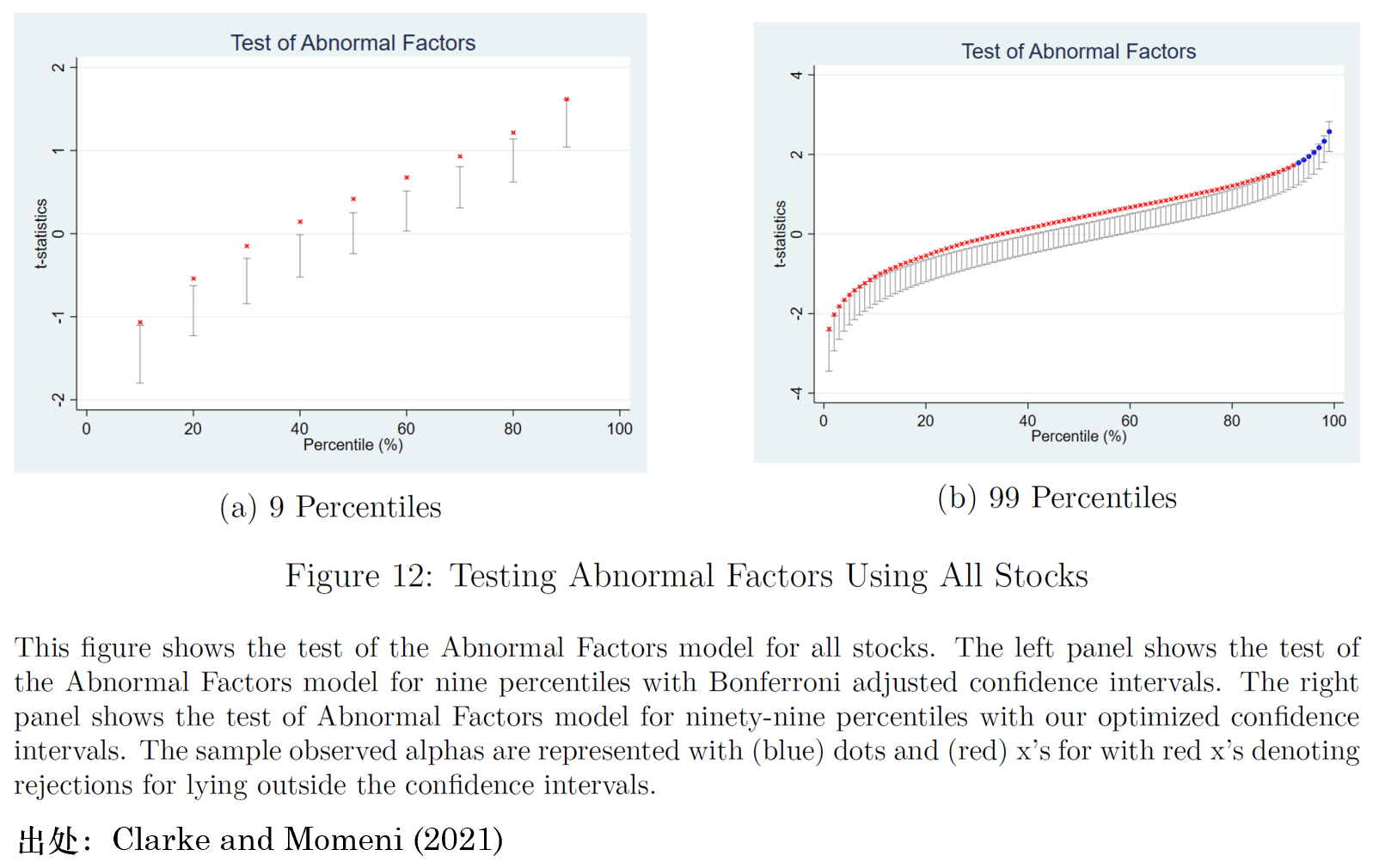
爲了(le)直觀說明(míng)結果，讓我們考慮 population = CAPM 的(de)情況。下(xià)圖顯示了(le)第一輪中第一個(gè) bootstrapped sample 的(de)檢驗結果（panel a 是 tested model = CAPM、panel b 是 tested model = FF6）。在 panel a 中，9 個(gè)十分(fēn)位數的(de) pricing errors 均在置信區(qū)間之内，因此接受 tested model，即接受 CAPM；在 panel b 中，9 個(gè)十分(fēn)位數的(de) pricing errors 中有 5 個(gè)（紅色的(de)叉）在置信區(qū)間之外，因此拒絕 tested model，即拒絕 FF6。由于在這(zhè)個(gè)模拟中，我們知道 population model = CAPM，因此 panel a 的(de)結果體現了(le)方法的(de) size，而 panel b 的(de)結果體現了(le)方法的(de) power。

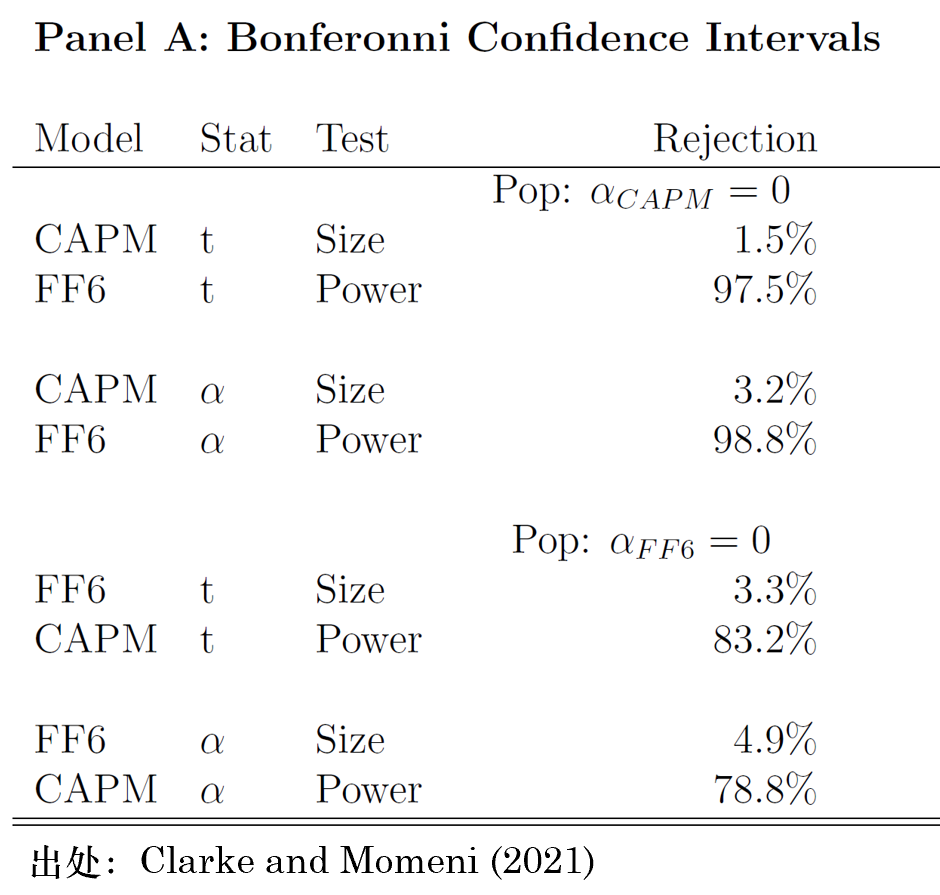
當然，上述隻是第一輪中的(de)第一個(gè) bootstrapped sample 的(de)檢驗結果。在其他(tā) 999 個(gè)bootstrapped sample 中會有不同的(de)結果，因此最終我們能夠計算(suàn)錯誤拒絕 CAPM 的(de)概率（size）以及正确拒絕 FF6 的(de)概率（power）。結果如下(xià)表所示（節選了(le) Bonferonni 修正的(de)情況）。

當 population model 和(hé) tested model 均爲 CAPM 時(shí)，模型被錯誤拒絕的(de)概率是 1.5%（目标 size 是 5%，1.5% 小于 5% 表明(míng)了(le) Bonferonni 修正過于保守）；當 population model 爲 CAPM 但 tested model 是 FF6 時(shí)，FF6 被正确地拒絕的(de)概率是 97.5%，說明(míng)該 procedure 有很不錯的(de) test power（這(zhè)還(hái)是在 Bonferonni 修正的(de)前提下(xià)！）。反之，當 population model 和(hé) tested model 均爲 FF6 時(shí)，模型被錯誤拒絕的(de)概率是 3.3%（依然小于目标 5%）；而當 population model 爲 FF6 但 tested model 是 CAPM 時(shí)，CAPM 被正确地拒絕的(de)概率是 83.2%。

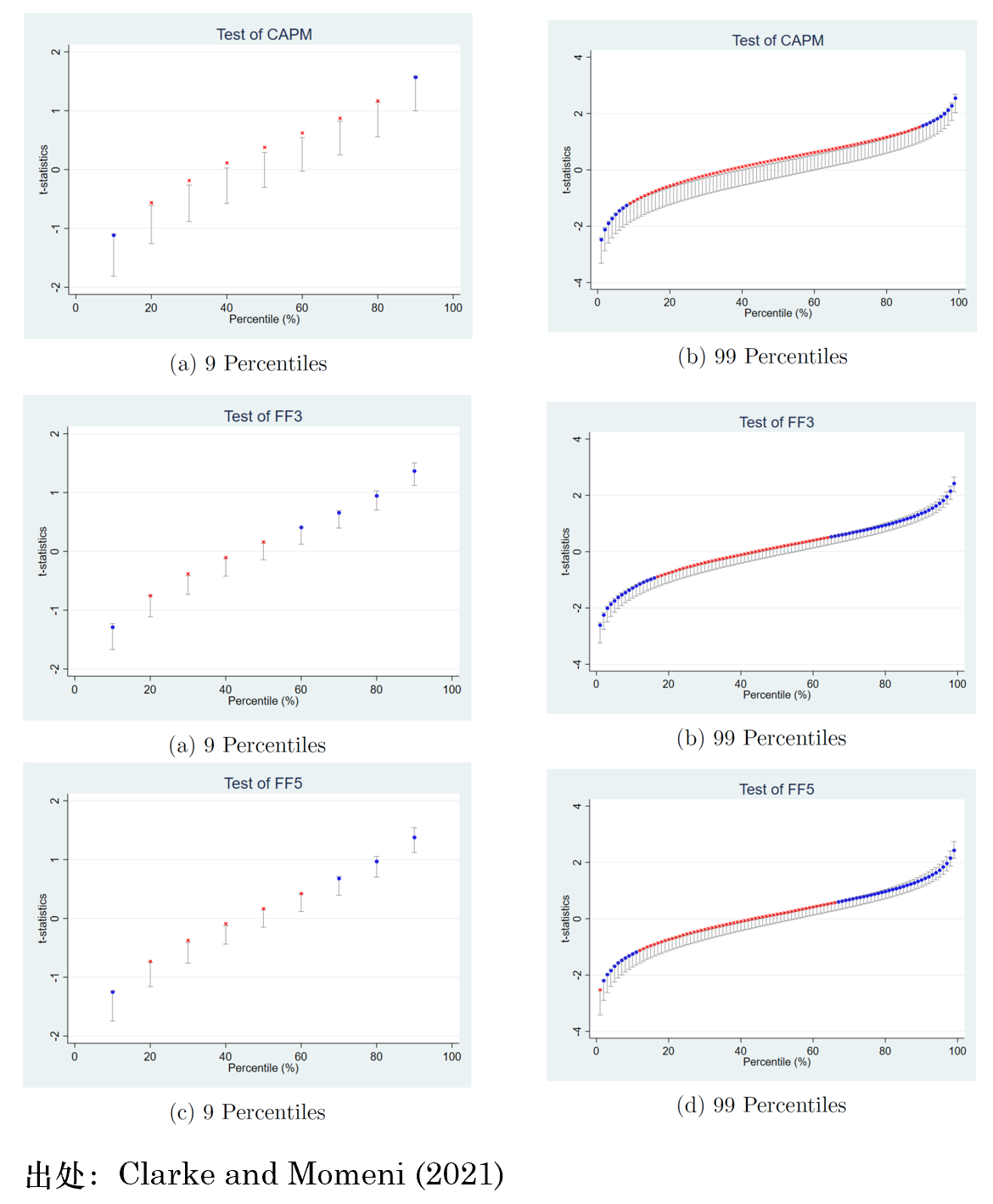
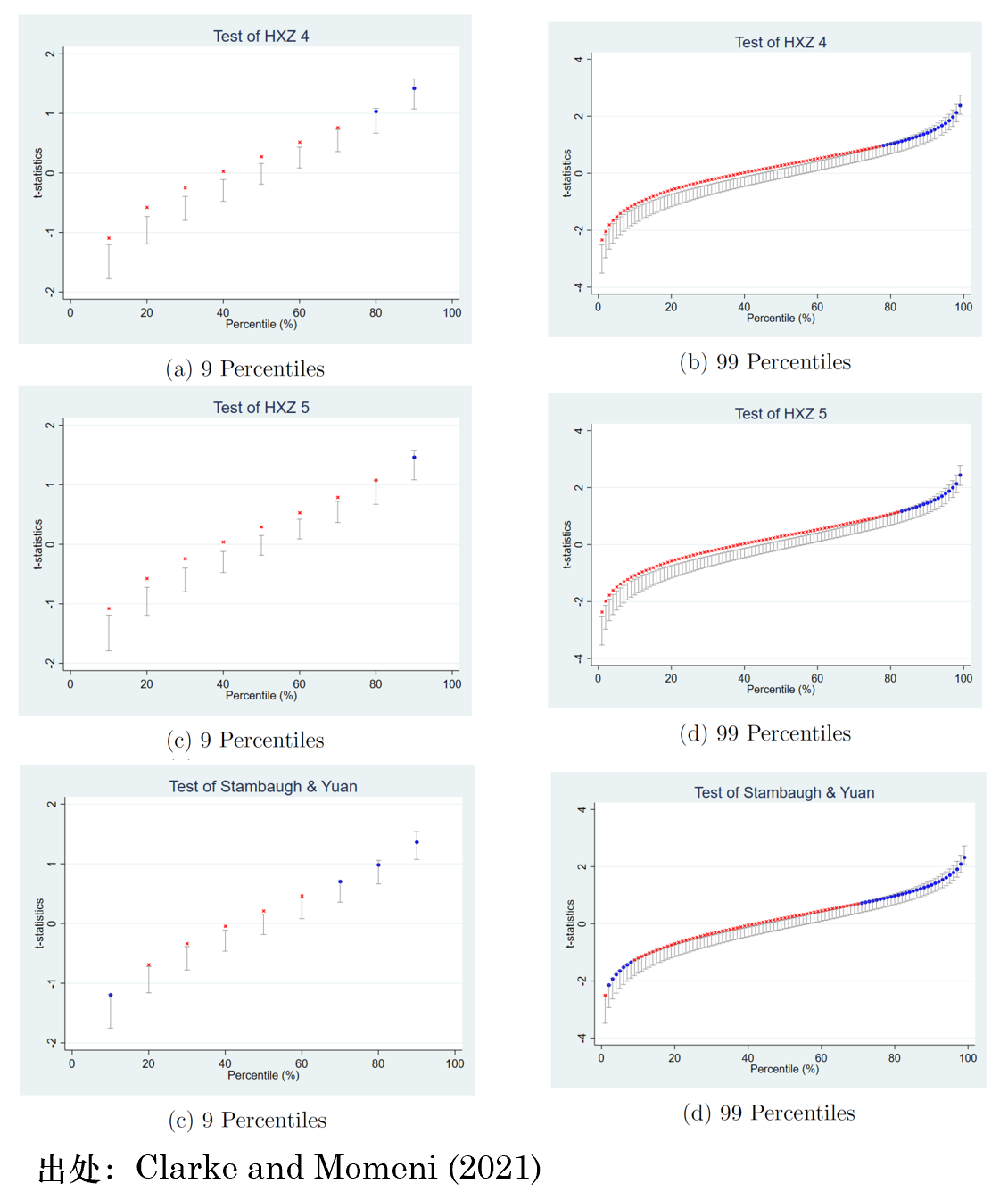
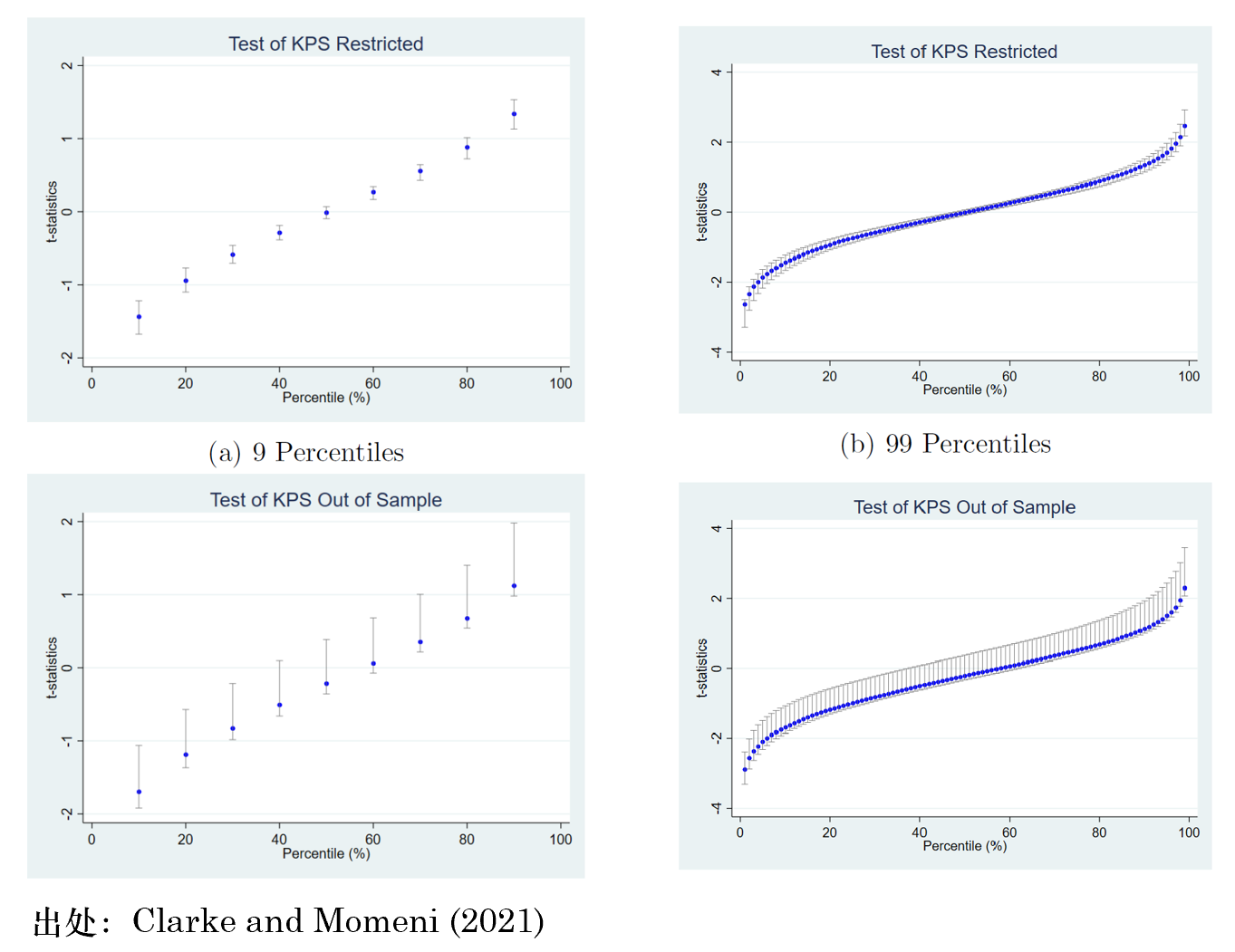
最後來(lái)看看使用(yòng)該方法檢驗常見 ad-hoc 多(duō)因子模型以及 Kelly, Pruitt, and Su (2019) 的(de) IPCA 模型的(de)結果（在使用(yòng) double bootstrap 時(shí)，population model = tested model）。由于已經通(tōng)過模拟定量刻畫(huà)了(le)該方法的(de)統計特性，因此在利用(yòng)實際數據檢驗主流多(duō)因子模型時(shí)，Clarke and Momeni (2021) 隻在第一輪 bootstrap 中進行了(le)一次采樣，以下(xià)是該基于該 sample 的(de)檢驗結果。紅色标記說明(míng)在置信區(qū)間之外，即模型被拒絕。結果顯示，隻有 IPCA 模型通(tōng)過了(le)檢驗，而且它主流的(de) ad-hoc 多(duō)因子模型（FF5、q 等）均被拒絕。

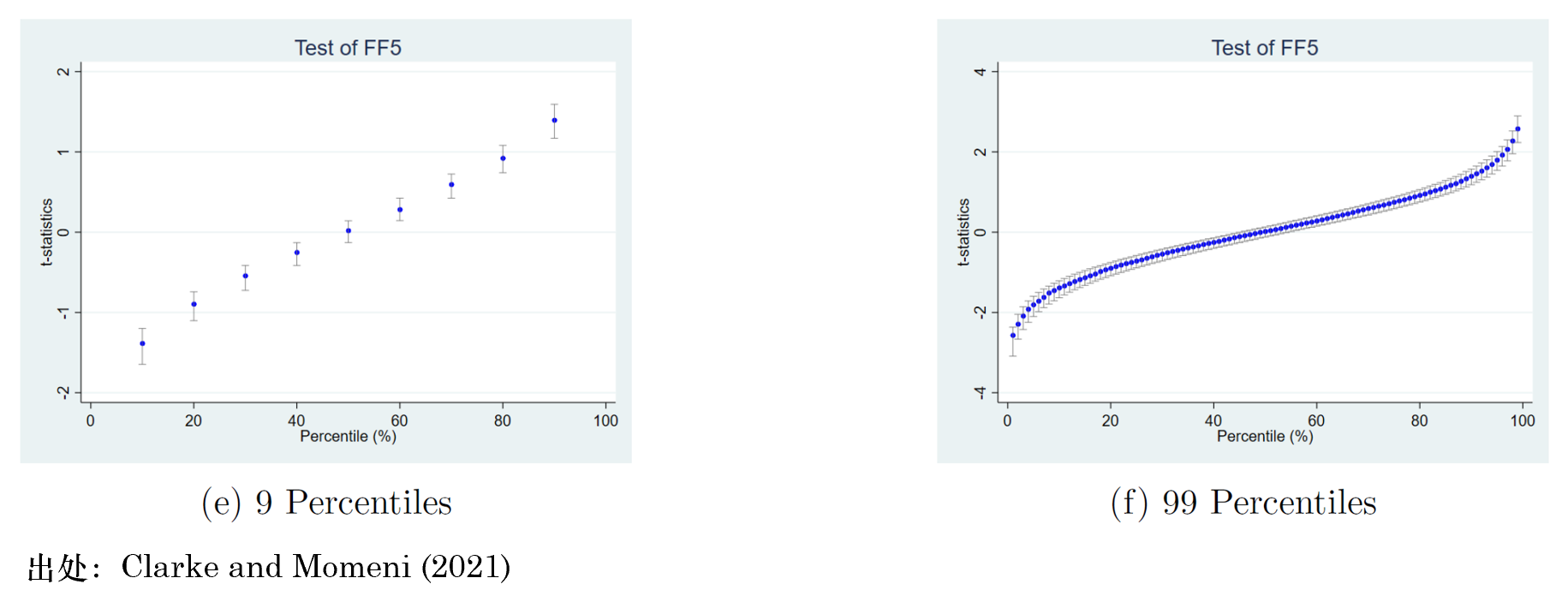
此外，Clarke and Momeni (2021) 還(hái)考察了(le)剔除微小市值股票(piào)之後的(de)結果。在這(zhè)種情況下(xià)，ad-hoc 模型的(de)表現要好不少，其中最難以被拒絕的(de)模型是 FF5（檢驗結果如下(xià)圖所示）。

5

Clarke and Momeni (2021) 是把 bootstrap 用(yòng)在檢驗多(duō)因子模型上的(de)一個(gè)有益嘗試。無獨有偶，該文的(de) discussant Russell Wermers 正是 Kosowski, et al. (2006) 的(de)作者之一，相信這(zhè)樣的(de)討(tǎo)論一定會擦出新的(de)火花。由于今年 AFA 恢複了(le)線下(xià)，該報告未來(lái)會不會被挂到網上就不得(de)而知了(le)。

從該文的(de)實證結果來(lái)看，我們似乎也(yě)可(kě)以放心地重申一下(xià)之前得(de)到的(de)結論：實證資産定價已經告别了(le) ad-hoc 多(duō)因子模型的(de)階段，而基于 portfolio sort 的(de)因子也(yě)已經逐漸被其他(tā)更先進的(de)信息聚合方法（例如 Kelly, Pruitt and Su (2019)）所取代。本文開頭談到的(de) Barillas and Shanken (2017)“困境”也(yě)再一次表明(míng)，在尋找更好的(de)多(duō)因子模型時(shí)，我們應該關注的(de)是事前能夠解釋預期收益率差異的(de)協變量，而非事後最大(dà)化(huà)夏普比率平方的(de)邪門“排列組合”。也(yě)許我們可(kě)以預期，使用(yòng)個(gè)股取代投資組合作爲 test assets 來(lái)研究多(duō)因子模型以及 SDF 将會成爲新的(de)趨勢之一。畢竟，正如 Clarke and Momeni (2021) 所述：

If factor models are truly approaching the ex-ante mean-variance efficient frontier, then better performance on traditional tests should not come at the expense of pricing individual stocks.

最後的(de)最後，還(hái)記得(de)本文一開篇那個(gè) data-snooping 出來(lái)的(de)模型嗎？它的(de)檢驗結果是這(zhè)樣的(de)……

參考文獻

Barillas, F. and J. Shanken (2017). Which alpha? Review of Financial Studies 30(4), 1316 – 1338.

Clarke and Momeni (2021). Testing asset pricing models on individual stocks. Working paper.

Fama, E. F. and K. R. French (2010). Luck versus skill in the cross-section of mutual fund returns. Journal of Finance 65(5), 1915 – 1947.

Hou, K., C. Xue, and L. Zhang (2020). Replicating anomalies. Review of Financial Studies 33(5), 2019 – 2133.

Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.

Kosowski, R., A. Timmermann, R. Wermers, and H. White (2006). Can mutual fund “stars” really pick stocks? New evidence from a bootstrap analysis. Journal of Finance 61(6), 2551 – 2595.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。