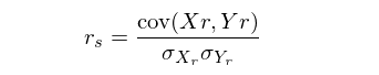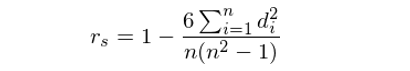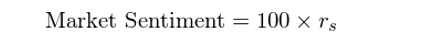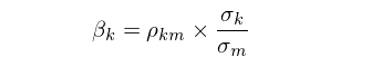從 Spearman 秩相關看市場(chǎng)情緒
發布時(shí)間:2017-08-23 | 來(lái)源: 川總寫量化(huà)
作者:石川
摘要:秩相關系數用(yòng)來(lái)計算(suàn)兩個(gè)變量之間的(de)單調相關性。本文采用(yòng)秩相關系數進行市場(chǎng)情緒分(fēn)析。
1 Spearman 秩相關系數
人(rén)們對(duì)相關系數(correlation coefficient)并不陌生,它是統計學中的(de)一個(gè)概念,用(yòng)來(lái)表示兩個(gè)随機變量共同運動的(de)程度,即線性相關性(linear correlation)。秩相關系數(rank correlation coefficient)和(hé)我們常說的(de)相關系數類似,不同的(de)是它考察的(de)是兩個(gè)随機變量之間的(de)單調相關性(monotonic correlation)。秩相關系數的(de)計算(suàn)公式和(hé)相關系數的(de)類似,隻不過在前者中,使用(yòng)的(de)并不是觀測值本身的(de)數值,而是它們在各自樣本中的(de)排序。
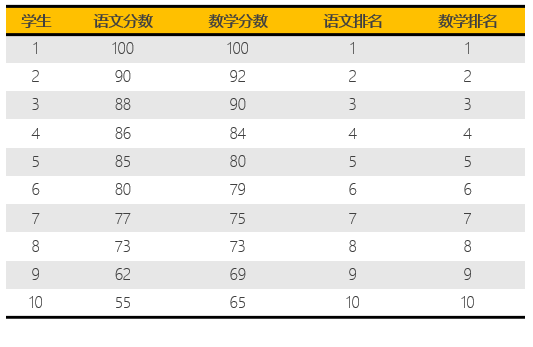
來(lái)看兩個(gè)例子。假設某班裏有 10 名學生,他(tā)們的(de)語文和(hé)數學分(fēn)數如下(xià)。這(zhè)裏,語文和(hé)數學就是兩個(gè)變量,我們想考察它們的(de)秩相關性。特别的(de),假設這(zhè)個(gè)班的(de)所有學生都沒有偏科,學霸通(tōng)吃(chī)語文數學、學渣則兩門都不靈。因此,如果我們分(fēn)别按語文和(hé)數學成績來(lái)排名,并用(yòng)排名代替這(zhè)些學生的(de)原始得(de)分(fēn)時(shí),每個(gè)學生的(de)語文和(hé)數學排名總能完美(měi)的(de)對(duì)應起來(lái)。比如,語文最高(gāo)分(fēn)的(de)學生的(de)數學成績也(yě)是第一。在這(zhè) 10 名學生中(觀測值),語文和(hé)數學的(de)排序(兩個(gè)序列變量,ranked variables)高(gāo)度一緻(單調性完全相同),因此我們說它們的(de)秩相關系數爲 1。
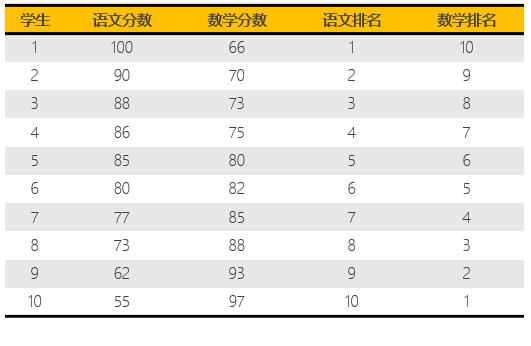
再來(lái)看另外一個(gè)班。這(zhè)個(gè)班裏的(de) 10 名學生都存在一定程度的(de)偏科,且某一科學得(de)越好,另外一科學的(de)越差。他(tā)們的(de)語文數學成績和(hé)分(fēn)别的(de)排名如下(xià)表所示。例如,語文第一名的(de)學生,數學考分(fēn)墊底(第 10 名)。在這(zhè) 10 名學生中,語文和(hé)數學排序的(de)單調性完全相反,這(zhè)說明(míng)它們存在完美(měi)的(de)負的(de)秩相關。事實上,在這(zhè)個(gè)例子中,語文和(hé)數學的(de)秩相關系數爲 -1。
從這(zhè)兩個(gè)例子可(kě)以看出:
當兩個(gè)變量在觀測值序列中有相似的(de)排序時(shí),這(zhè)兩個(gè)變量的(de)秩相關性很高(gāo);而當它們在觀測值中有明(míng)顯不同的(de)排序時(shí),這(zhè)兩個(gè)變量的(de)秩相關性很低。極端的(de)情況發生在當兩個(gè)變量的(de)排序完全一緻或者完全相反。秩相關系數的(de)取值爲 -1 到 1 之間。
秩相關性的(de)取值僅與變量的(de)排序有關,而與具體的(de)觀測值無關,因此它描繪的(de)是變量之間的(de)單調相關性。我們之所以關心秩相關性是因爲傳統的(de)相關系數僅考察兩個(gè)變量之間是否存在線性相關性。而秩相關性對(duì)變量之間的(de)線性或非線性相關性不做(zuò)假設,而将考察的(de)重點放在單調相關性上。
在統計學中,有多(duō)種計算(suàn)秩相關系數的(de)方法,其中最流行的(de)要數 Spearman 秩相關系數,它以 Charles Spearman 命名。假設有兩個(gè)随機變量 X 和(hé) Y 的(de) n 個(gè)觀測值,Spearman 秩相關系數,記爲 r_s,的(de)計算(suàn)過程如下(xià):
1. 首先将 X 和(hé) Y 的(de)觀測值轉換成它們對(duì)應的(de)排序 X_r 和(hé) Y_r。
2. 對(duì) X_r 和(hé) Y_r 采用(yòng)傳統的(de)線性相關系數公式,則可(kě)得(de)到 r_s:
特别的(de),如果 X 和(hé) Y 各自的(de)取值沒有重複——即排序後的(de) X_r 和(hé) Y_r 中沒有任何兩個(gè)觀測值有同樣的(de)排序,則 r_s 還(hái)可(kě)以通(tōng)過下(xià)面這(zhè)個(gè)更簡單的(de)公式計算(suàn):
其中 d_i = X_r(i) – Y_r(i),它表示第 i 個(gè)觀測值中 X 和(hé) Y 的(de)排序之差;n 爲觀測值的(de)總數。
由上面這(zhè)個(gè)簡單的(de)公式很容易驗證,在上面兩個(gè)例子中,第一個(gè)班級中語文和(hé)數學的(de)秩相關爲 1 - 0 = 1;而第二個(gè)班級中語文和(hé)數學的(de)秩相關系數爲 1 - 6 × (9²+7²+5²+3²+1²+1²+3²+5²+7²+9²) / (10 × (10²-1)) = 1 – (6 × 330)/990 = -1。
2 秩相關和(hé)市場(chǎng)情緒
在量化(huà)投資領域,我們可(kě)以使用(yòng) Spearman 秩相關性做(zuò)市場(chǎng)情緒分(fēn)析。市場(chǎng)情緒(market sentiment)是個(gè)很主觀的(de)定義。在我們的(de)用(yòng)例中,對(duì)它的(de)解釋如下(xià):
市場(chǎng)情緒的(de)高(gāo)、低由風險資産的(de)收益率和(hé)它的(de)風險水(shuǐ)平的(de)一緻程度所反應。市場(chǎng)情緒高(gāo)漲時(shí),高(gāo)風險資産應該比低風險資産有更高(gāo)的(de)收益率;市場(chǎng)情緒低落的(de)時(shí)候,高(gāo)風險資産應比低風險資産有更大(dà)的(de)跌幅。
在上述解釋下(xià),我們可(kě)以使用(yòng)風險資産的(de)收益率和(hé)其風險水(shuǐ)平之間的(de)單調相關性來(lái)定量評價市場(chǎng)情緒。這(zhè)裏使用(yòng)秩相關性的(de)好處是,我們并不需要假設收益和(hé)風險水(shuǐ)平之間到底應該是線性的(de)還(hái)是非線性的(de)關系。上述解釋符合人(rén)們對(duì)市場(chǎng)的(de)認知。通(tōng)常在一波漲幅有偃旗息鼓迹象時(shí),我們看到最後一波的(de)瘋狂往往由大(dà)盤股(如銀行、石油和(hé)傳統低 β 闆塊)拉升,反而之前漲幅較好的(de)高(gāo) β 闆塊(如 TMT、有色金屬)出現回調,給人(rén)造成不舒服的(de)感覺。
如何選取風險資産并描述它們的(de)風險水(shuǐ)平呢(ne)?一個(gè)合理(lǐ)的(de)選擇是使用(yòng)不同的(de)行業指數作爲風險資産,并使用(yòng)它們的(de) β 系數來(lái)代表風險水(shuǐ)平。爲此,選用(yòng)申萬一級的(de) 28 個(gè)行業作爲風險資産,并使用(yòng)東方财富全 A 指數作爲市場(chǎng)的(de)代表,以此計算(suàn)不同行業的(de) β。有了(le)不同行業的(de) β 之後,我們便可(kě)以計算(suàn)這(zhè)些行業指數的(de)收益率與它們的(de) β 的(de)秩相關系數,以此來(lái)定量說明(míng)市場(chǎng)情緒的(de)大(dà)小。特别的(de),假設收益率和(hé) β 的(de)秩相關系數爲 r_s,則我們定義市場(chǎng)情緒如下(xià):
因此,市場(chǎng)情緒的(de)取值在 -100 和(hé) 100 之間,越高(gāo)說明(míng)情緒越高(gāo)漲。
3 計算(suàn) β 系數
爲了(le)計算(suàn)市場(chǎng)情緒,必須知道每個(gè)行業的(de) β 系數。由定義可(kě)知,對(duì)于任意行業 k,其 β 系數,記爲 β_k 的(de)計算(suàn)公式爲:
其中,ρ_km 爲行業 k 和(hé)市場(chǎng)收益率的(de)相關系數;σ_k 和(hé) σ_m 分(fēn)别爲行業 k 和(hé)市場(chǎng)收益率的(de)波動率(标準差)。根據 Frazzini and Pedersen (2013),在上式中分(fēn)别計算(suàn)相關系數和(hé)波動率的(de)原因是:
1. 較波動率而言,兩個(gè)變量的(de)相關性的(de)變化(huà)更加緩慢(màn)。因此,應該使用(yòng)更長(cháng)的(de)曆史數據來(lái)計算(suàn)相關系數,而可(kě)以用(yòng)更短的(de)數據計算(suàn)波動率(考慮到波動率聚類,這(zhè)是有必要的(de))。這(zhè)要求計算(suàn)時(shí)把波動率和(hé)相關系數區(qū)分(fēn)對(duì)待。
2. 對(duì)于波動率和(hé)相關系數的(de)計算(suàn)可(kě)以使用(yòng)不同粒度的(de)收益率數據。例如,對(duì)于波動率我們可(kě)以使用(yòng)日收益率;而對(duì)于相關系數我們可(kě)以使用(yòng)三日收益率或者周收益率數據,以消除非同步交易的(de)影(yǐng)響。(當然,由于我們都是使用(yòng)行業指數而非個(gè)股,并沒有這(zhè)個(gè)問題。)
在所有相關的(de)計算(suàn)中,使用(yòng)的(de)都是對(duì)數收益率。在計算(suàn)波動率時(shí),使用(yòng)過去 1 年的(de)日對(duì)數收益率;在計算(suàn)相關系數時(shí),使用(yòng)過去 2 年的(de)三日對(duì)數收益率。這(zhè)樣,我們可(kě)以計算(suàn)出這(zhè) 28 個(gè)申萬一級行業在每個(gè)交易日的(de) β 系數。
4 實證分(fēn)析
本節将市場(chǎng)情緒分(fēn)析在 A 股上進行實證。假設考察的(de)時(shí)間區(qū)間爲 2011 年 1 月(yuè) 1 日到 2017 年 8 月(yuè) 18 日。此外,爲了(le)避免日收益率的(de)噪聲,以周五進行 β 系數采樣并使用(yòng)周收益率計算(suàn)秩相關系數和(hé)每周的(de)市場(chǎng)情緒。需要說明(míng)的(de)是,在實證分(fēn)析中,我們僅僅想考察這(zhè)個(gè)本文介紹的(de)這(zhè)種基于秩相關的(de)計算(suàn)方法在描述市場(chǎng)情緒時(shí)是否合理(lǐ)。因此計算(suàn) β 和(hé)秩相關系數時(shí)采用(yòng)的(de)都是當期的(de)最新數據。換句話(huà)說,計算(suàn)中假設每周收益率已知後(比如等到周五收盤後),再計算(suàn)最新的(de)市場(chǎng)情緒。本文不試圖使用(yòng)市場(chǎng)情緒指标對(duì)未來(lái)的(de)收益率進行任何預測。
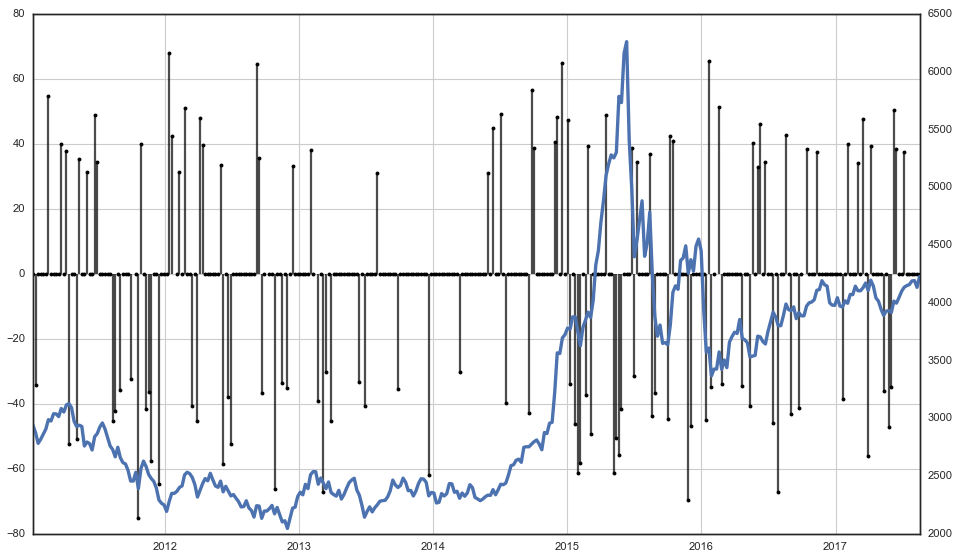
和(hé)相關系數類似,如果秩相關系數在 0 附近這(zhè)說明(míng)兩個(gè)變量的(de)單調相關性不明(míng)顯,因此我們重點關注秩相關系數——市場(chǎng)情緒——超過一定正、負阈值的(de)情況。爲此,在計算(suàn)出的(de)每周原始市場(chǎng)情緒序列中,将數值在 -30 到 30 之内的(de)以 0 代替,表示在那些周市場(chǎng)情緒不溫不火。最終,下(xià)圖顯示了(le)市場(chǎng)情緒和(hé)東财全 A 指數在實證期窗(chuāng)口内的(de)變化(huà)。
觀察上圖,我們可(kě)以大(dà)緻得(de)到以下(xià)幾個(gè)結論:
1. 由于我們計算(suàn)的(de)是事後市場(chǎng)情緒,因此它和(hé)市場(chǎng)的(de)漲跌走勢在一定程度上相符合:市場(chǎng)上漲時(shí),情緒一般高(gāo)漲;市場(chǎng)下(xià)跌時(shí),情緒則在 0 水(shuǐ)位以下(xià);在市場(chǎng)糾結時(shí),情緒也(yě)比較糾結(圖中對(duì)應的(de)是那些市場(chǎng)情緒爲 0 的(de)周)。
2. 比較有意思的(de)一點是在 2015 年牛市結束前的(de)一到兩個(gè)月(yuè),市場(chǎng)情緒出現過連續的(de)幾周非常負面的(de)情況。雖然現在下(xià)任何結論還(hái)爲時(shí)尚早(我不能不負責任的(de)說什(shén)麽“市場(chǎng)情緒有預示牛市中風險累積過高(gāo)的(de)作用(yòng)”這(zhè)種觀點),但這(zhè)種現象絕對(duì)值得(de)進一步研究。
3. 最近幾個(gè)月(yuè),市場(chǎng)情緒逐漸得(de)到修複。雖然 3300 點似乎已經成爲了(le)上證指數的(de)一個(gè)無法逾越的(de)阻力位,但從情緒的(de)角度看,市場(chǎng)并沒有太過悲觀。
5 結語
對(duì)市場(chǎng)情緒的(de)量化(huà)對(duì)投資來(lái)說無疑會有益處。計算(suàn)市場(chǎng)情緒有不同的(de)方法。例如,對(duì)于流量大(dà)的(de)投資公衆号或者平台,可(kě)以定期統計投資者的(de)倉位并以此來(lái)計算(suàn)市場(chǎng)情緒(情緒高(gāo)漲時(shí)倉位應該重;反之倉位應該輕)。本文從秩相關的(de)概念出發,介紹了(le)券商中流行的(de)一種定量計算(suàn)市場(chǎng)情緒的(de)方法。
這(zhè)種方法是否有效是個(gè)見仁見智的(de)問題。我個(gè)人(rén)的(de)感受總結如下(xià):
1. 基于秩相關的(de)市場(chǎng)情緒是一個(gè)事後分(fēn)析手段。和(hé)技術分(fēn)析指标類似,市場(chǎng)情緒是對(duì)曆史數據所傳達的(de)信息的(de)二次加工。是一種信息濃縮、提煉過程,讓人(rén)們可(kě)以通(tōng)過單一指标對(duì)情緒有一個(gè)認知。
2. 由于它是一個(gè)曆史信息提取手段,因此它是否對(duì)未來(lái)的(de)收益率有預測性仍然存疑。客觀來(lái)說,不可(kě)能存在單一的(de)指标或者因子和(hé)某個(gè)投資品未來(lái)的(de)收益率高(gāo)度相關(那就發财了(le)),因此市場(chǎng)情緒指标也(yě)許更适合來(lái)作爲一個(gè)輔助判斷的(de)手段。在一些研究報告中,存在使用(yòng)市場(chǎng)情緒預測未來(lái)收益率而構建投資策略,并取得(de)了(le)不錯的(de)效果。但是我甘願相信那就是數據操縱的(de)産物(wù)。由于大(dà) A 股獨特的(de)牛熊周期,隻要抓住牛市、躲開熊市,那麽回測的(de)淨值就不會太差。因此,通(tōng)過選擇參數和(hé)标的(de),使用(yòng)市場(chǎng)情緒來(lái)在回測中擇時(shí)遠(yuǎn)沒有想象的(de)困難。
3. 計算(suàn)時(shí)完全可(kě)以不使用(yòng)本文提到的(de)申萬一級行業,而使用(yòng)其他(tā)的(de)風險資産。事實上,我也(yě)嘗試了(le)使用(yòng)滬深兩市的(de)個(gè)股進行同樣的(de)計算(suàn)。在那種情況下(xià),由于股票(piào)的(de)波動率較大(dà)且個(gè)數太多(duō),使用(yòng)所有的(de)股票(piào)對(duì)于秩相關系數的(de)計算(suàn)會産生較大(dà)的(de)噪聲。爲此,可(kě)以考慮按照(zhào) β 值或者行業對(duì)個(gè)股進行采樣,以排除相似的(de)股票(piào),把研究的(de)重點放在風險水(shuǐ)平差異較大(dà)的(de)那些股票(piào)中。
4. 情緒分(fēn)析的(de)頻(pín)率可(kě)以因分(fēn)析目的(de)而異。本文僅僅以周頻(pín)來(lái)做(zuò)實證并做(zuò)彙報而已。我也(yě)使用(yòng)日線和(hé)分(fēn)鐘(zhōng)線進行了(le)情緒分(fēn)析。綜合不同時(shí)間尺度上的(de)市場(chǎng)情緒結果也(yě)許能提供新的(de)視角。
5. 能否準确計算(suàn) β 系數十分(fēn)重要。計算(suàn)中,本文采用(yòng)了(le)日收益率數據,這(zhè)是因爲計算(suàn)相關系數的(de)準确性随著(zhe)采樣頻(pín)率的(de)增加而增加(Merton 1980)。同時(shí),分(fēn)别計算(suàn)風險資産和(hé)市場(chǎng)指數的(de)相關系數和(hé)它們的(de)波動率也(yě)是爲了(le)更準确的(de)計算(suàn) β。
參考文獻
Merton (1980). On estimating the expected return on the market: An exploratory investigation. Journal of Financial Economics 8(4), 323 – 361.
Frazzini and Pedersen (2014). Betting against beta. Journal of Financial Economics 111(1), 1 – 25.
免責聲明(míng):入市有風險,投資需謹慎。在任何情況下(xià),本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外,文中圖表均直接或間接來(lái)自于相應論文,僅爲介紹之用(yòng),版權歸原作者和(hé)期刊所有。