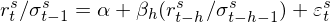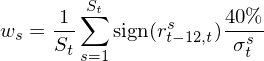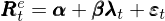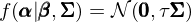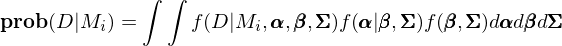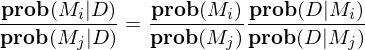建設性“怼人(rén)”
發布時(shí)間:2020-04-14 | 來(lái)源: 川總寫量化(huà)
作者:石川
摘要:在頂刊上發文“怼人(rén)”是種什(shén)麽樣的(de)體驗?
0 引言
上世紀 60 年代,Treynor、Sharpe、Lintner 和(hé) Mossin 分(fēn)别獨立提出了(le) CAPM —— 資本資産定價模型(見《CAPM 的(de)一小段曆史》)。然而這(zhè)其中又以 Sharpe 和(hé) Lintner 的(de)版本最爲著名,因此 CAPM 又被稱爲 Sharpe-Lintner CAPM。在 Sharpe 和(hé) Lintner 兩個(gè)版本中,Sharpe (1964) 先于 Lintner (1965) 發表,兩篇文章(zhāng)都發表于 Journal of Finance。不過 Lintner 将自己的(de)模型和(hé) Sharpe 的(de)版本進行了(le)比較,并指出它們并不相同,且自己的(de)适用(yòng)性更強。在一段時(shí)期内,Sharpe 被說服了(le),并在 Journal of Finance 上發文對(duì) Lintner 進行了(le)回複(Sharpe 1966),承認 Lintner 的(de)模型優于自己的(de)。
故事到這(zhè)裏似乎就結束了(le)。但是最後的(de)結果我們都知道了(le),Sharpe 于 1990 年因 CAPM 獲得(de)了(le)諾貝爾經濟學獎(與 Harry Markowitz 和(hé) Merton Miller 分(fēn)享),而 Lintner 由于英年早逝無緣獲獎。但這(zhè)至少說明(míng) Sharpe 版本的(de) CAPM 的(de)重要性絲毫不比 Lintner 的(de)版本低。事實上,另一位大(dà)佬 Eugene Fama 在 1968 年的(de)文章(zhāng) Fama (1968) 指出,經過仔細比較,這(zhè)兩個(gè)版本的(de) CAPM 是等價的(de)。
之所以回顧上面這(zhè)段曆史,是爲了(le)引出今天的(de)主題 —— 學術研究中的(de)建設性“怼人(rén)”。在這(zhè)裏,我們給怼人(rén)一詞加了(le)引号,而且在前面加上了(le)褒義的(de)修飾詞建設性,都是爲了(le)說明(míng)這(zhè)種質疑是對(duì)學科發展有促進作用(yòng)的(de),是科學而積極的(de)。在實證資産定價和(hé)因子投資領域,自然也(yě)不乏這(zhè)種精彩的(de)“怼”與“被怼”,其中還(hái)有不少是發表在金融學三大(dà)頂刊上的(de),讓人(rén)高(gāo)呼過瘾的(de)同時(shí)更加加深了(le)對(duì)市場(chǎng)的(de)理(lǐ)解。今天這(zhè)篇小文就來(lái)梳理(lǐ)七對(duì)兒(ér)“怼”與“被怼”。對(duì)于每一個(gè)主題,以下(xià)把提出觀點的(de)論文稱爲提出篇、把後續提出反對(duì)觀點的(de)文章(zhāng)稱爲怼人(rén)篇。
1 BAB vs BABAB
作爲熱(rè)身,先來(lái)看第一對(duì)兒(ér):
提出篇:Betting against beta(Frazzini and Pedersen 2014),JFE
怼人(rén)篇:Betting against betting against beta(Novy-Marx and Velikov 2018),SSRN(納尼??)
Novy-Marx and Velikov (2018) 大(dà)概是這(zhè)七對(duì)兒(ér)中唯一沒有正是發表的(de)文章(zhāng),但因爲它“怼”的(de)對(duì)象太有名,因此不妨礙把它納入。公衆号之前的(de)文章(zhāng)《BAB vs BABAB》系統介紹過相關研究。來(lái)自 AQR 的(de) Frazzini and Pedersen (2014) 在 Journal of Financial Economics 上發表了(le)一篇題爲 Betting Against Beta 的(de)文章(zhāng),站在 Black CAPM 的(de)肩膀上指出低 β 的(de)股票(piào)能獲得(de)更高(gāo)的(de)超額收益。該文認爲在實際投資中,不同的(de)投資者受到不同資金使用(yòng)的(de)限制。爲了(le)追求更高(gāo)的(de)收益,一些投資者(特别是機構)會把有限的(de)資金投資于高(gāo)風險的(de)投資品,比如高(gāo) β 的(de)股票(piào),這(zhè)便造成了(le)它們 α 的(de)下(xià)降。他(tā)們在股票(piào)、商品、債券、外彙等市場(chǎng)中均發現了(le)該現象,并由此提出了(le)如今早已家喻戶曉的(de) Betting Against Beta(BAB)因子。
作爲“怼人(rén)篇”,Novy-Marx and Velikov (2018) 以 Betting Against Betting Against Beta (BABAB)對(duì) BAB 進行了(le)抨擊。他(tā)們不僅質疑了(le) BAB 因子 on paper 的(de)超高(gāo)收益,也(yě)質疑了(le)其背後的(de)理(lǐ)論。對(duì)于前者,Novy-Marx and Velikov (2018) 指出 BAB 因子的(de)構造方法造成其在超小市值公司上的(de)權重過高(gāo)、且在盈利和(hé)投資因子上有很高(gāo)的(de)暴露。由于規模、盈利和(hé)投資三個(gè)因子在美(měi)股上已經被證明(míng)是有效的(de),因此 BAB 毫無疑問是沾了(le)光(guāng)。對(duì)于後者,該文認爲 BAB 因子在計算(suàn) β 時(shí)使用(yòng)不同的(de)時(shí)間窗(chuāng)口計算(suàn)波動率和(hé)相關系數,這(zhè)種估計方法是有偏的(de),而它陰差陽錯的(de)支持了(le) Frazzini and Pedersen (2014) 提出的(de) β 和(hé)流動性風險之間的(de)關系。一旦修正這(zhè)個(gè)偏差,該理(lǐ)論則不再成立。
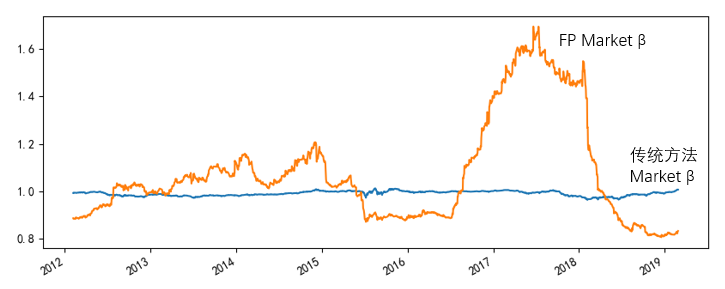
對(duì)于 Frazzini and Pedersen (2014) 使用(yòng)的(de) β 計算(suàn)方法(記爲 β_FP),值得(de)多(duō)說兩句。他(tā)們分(fēn)别使用(yòng) 1 年和(hé) 5 年計算(suàn)波動率和(hé)相關系數,簡單的(de)代數運算(suàn)指出 β_FP 和(hé)傳統 β 方法之間的(de)關系:
式中下(xià)标 1 和(hé) 5 分(fēn)别代表一年和(hé)五年的(de)滾動窗(chuāng)口。該關系式說明(míng),β_FP 等價于傳統 β 乘以一個(gè)系數;即個(gè)股的(de) (σ_1/σ_5) 與市場(chǎng)的(de) (σ_1/σ_5) 之比。Novy-Marx and Velikov (2018) 通(tōng)過實證研究發現當市場(chǎng)自身處于高(gāo)波動時(shí),個(gè)股的(de) σ_1/σ_5 和(hé)市場(chǎng)的(de) σ_1/σ_5 之間的(de)彈性小于 1;反之,當市場(chǎng)自身處于低波動時(shí),二者之間的(de)彈性大(dà)于 1。這(zhè)意味著(zhe)當市場(chǎng)處于高(gāo)波動時(shí),β_FP 比 β 更低;而當市場(chǎng)處于低波動時(shí),β_FP比 β 更高(gāo)。因此,若使用(yòng) β_FP 作爲股票(piào)的(de) beta 值,則按市值加權後得(de)到的(de)全市場(chǎng) beta 并不等于 1(下(xià)圖)。這(zhè)就是 β_FP 不夠合理(lǐ)的(de)證據。
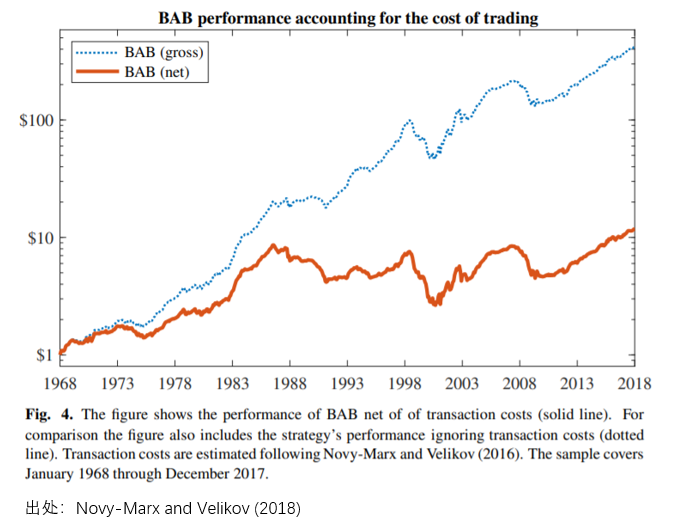
公允的(de)說,低 β 異象早已被學術界和(hé)業界接受。但是 BAB 因子 on paper 的(de)超高(gāo)收益确實值得(de)警惕,因爲在考慮了(le)交易成本之後,BAB 因子的(de)實際效果要打很大(dà)的(de)折扣,正如 Novy-Marx and Velikov (2018) 展示的(de)那樣。
2 BAB: 杠杆約束 or 彩票(piào)偏好
BABAB 并非關于 BAB 的(de)唯一争議(yì)。另一組學術達人(rén)也(yě)爲了(le)到底如何解釋 BAB 而和(hé) AQR 争得(de)“面紅耳赤”。隻不過這(zhè)一回,AQR 反擊了(le)。
提出篇:Betting against beta(Frazzini and Pedersen 2014),JFE —— 對(duì),還(hái)是它……
怼人(rén)篇:A lottery-demand-based explanation of the beta anomaly(Bali et al. 2017),JFQA
反怼人(rén)篇:Betting against correlation: Testing theories of low-risk effect(Asness et al. 2020),JFE
由前一節可(kě)知,Frazzini and Pedersen (2014) 認爲 BAB 主要是由投資者的(de)杠杆約束所驅動。Bali et al. (2017) 對(duì)此提出了(le)不同的(de)意見。故事要從 Bali, Cakici, and Whitelaw (2011) 提出的(de) MAX 效應說起。所謂 MAX,是指過去一段時(shí)間内股票(piào)的(de)最大(dà)單日收益。MAX 越大(dà)的(de)股票(piào),未來(lái)收益顯著更低,且該效應非常穩健。即便控制了(le)規模、BM 和(hé)動量,以及特質性波動率等,都無法解釋 MAX。MAX 效應也(yě)被稱爲彩票(piào)偏好(lottery preference 或 lottery demand)。
利用(yòng) MAX,Bali et al. (2017) 通(tōng)過四個(gè)步驟狠狠怼了(le) BAB 一把。在開始之前,他(tā)們首先承認,低 β 異象可(kě)以獲得(de)顯著的(de)超額收益,但之後便正式開怼。該文首先考察了(le) MAX 和(hé) β 的(de)雙重排序分(fēn)組,發現在每一 MAX 分(fēn)組中,低 β 異象的(de)超額收益都不再顯著。相反,MAX 效應在每一 β 分(fēn)組中卻高(gāo)度顯著。此外平均 MAX 效應甚至比 MAX 單變量分(fēn)組下(xià)還(hái)要顯著。
接著(zhe),他(tā)們利用(yòng) Fama-MacBeth regression 考察了(le)額外控制其他(tā)變量時(shí)的(de)情況。結果顯示,當加入 MAX 後,β 的(de)溢價顯著爲正(注意,是正喲,這(zhè)和(hé) BAB 完全滿擰!)。而 MAX 則在所有模型中都高(gāo)度顯著爲負。在此基礎上,他(tā)們利用(yòng)市值和(hé) MAX 雙重排序構造了(le) FMAX 因子,并表明(míng) FMAX 因子有助于解釋 β 組合的(de)表現。最後,他(tā)們祭出了(le)大(dà)招,比較了(le) FMAX 和(hé) BAB 是否可(kě)以解釋對(duì)方。結果顯示,FMAX(加上 Fama-French 三因子以及 Carhart 的(de)動量因子)可(kě)以解釋 BAB ,但反過來(lái),FMAX 因子卻總能獲得(de)顯著的(de)負超額收益。綜上,Bali, et al. (2017) 認爲,BAB 隻是 MAX 效應的(de)反應,而彩票(piào)偏好才是 BAB 的(de)合理(lǐ)解釋。
在 2014 年的(de) working paper 中,該文直接被取名爲 Betting against Beta or Demand for Lottery,火藥味要濃得(de)多(duō)。而在正式發表的(de)版本中,題目變爲了(le) A Lottery-Demand-Based Explanation of the Beta Anomaly,已然溫和(hé)許多(duō)。
當然,AQR 天團可(kě)不會甘心被怼。Asness et al. (2020) 一文針鋒相對(duì)地進行回應,認爲 BAB 有效是因爲 BAC —— Betting against correlation(BAC)—— 而非彩票(piào)偏好的(de)原因。這(zhè)篇文章(zhāng)剛在 Journal of Financial Economics 正式見刊,仔細考察了(le)在控制了(le)波動率(即也(yě)就控制了(le)與其相關的(de) MAX)之後的(de) BAC 因子是否可(kě)以獲得(de)顯著的(de)超額收益。
爲了(le)構建 BAC 因子,Asness et al. (2020) 首先在每月(yuè)末将股票(piào)按照(zhào)波動率分(fēn)爲 5 組,然後在每組内進一步按照(zhào)相關性分(fēn)爲兩組,接著(zhe)用(yòng)與 BAB 相同的(de)排序加權法構建多(duō)空兩端,最後構建 β 中性多(duō)空組合。他(tā)們也(yě)用(yòng)類似的(de)方法構建了(le)低波動因子 BAV —— betting against volatility。結果發現,BAC 和(hé) BAV 都可(kě)以獲得(de)顯著且穩健的(de)超額收益。
最爲精彩的(de)是,爲了(le)檢驗杠杆約束假說,Asness et al. (2020) 考察了(le)保證金借款餘額對(duì) BAB 和(hé) BAC 因子的(de)影(yǐng)響。當事前的(de)保證金借款較低,即杠杆約束較高(gāo)時(shí),BAB 和(hé) BAC 因子的(de)表現都顯著更好。這(zhè)是支持杠杆約束假說的(de)有力證據。
爲了(le)檢驗彩票(piào)偏好的(de)影(yǐng)響,該文則做(zuò)了(le)一項非常有創造性的(de)研究,引入了(le)(經 GDP 标準化(huà)的(de))賭場(chǎng)的(de)季度分(fēn)紅變化(huà)來(lái)表征博彩偏好。結果表明(míng),它對(duì) MAX 效應有顯著影(yǐng)響,但對(duì) BAB 因子卻沒有顯著的(de)影(yǐng)響。由這(zhè)些結果可(kě)知,杠杆約束假說是 BAB 的(de)合理(lǐ)解釋之一,而關于彩票(piào)偏好假說,則沒有一緻的(de)結論。
此外,其他(tā)學者也(yě)就這(zhè)個(gè)問題插了(le)一腳。Schneider, Wagner, and Zechner (2020) 這(zhè)篇 Journal of Finance 的(de)文章(zhāng)認爲所有低風險異象都是因爲忽略了(le)協偏度所緻。他(tā)們力圖将低風險異象一網打盡。但顯然,相關的(de)研究和(hé)争論并不會就此終結。
3 特質性波動率之謎
說起“怼”與“被怼”,就自然不得(de)不提和(hé) BAB 同屬于低風險異象一族的(de)另一個(gè)異象 —— 特質性波動率。
提出篇:The cross-section of volatility and expected returns(Ang et al. 2006),JF
怼人(rén)篇:Idiosyncratic risk and the cross-section of expected stock returns(Fu 2009),JFE
解惑篇:Arbitrage asymmetry and the idiosyncratic volatility puzzle(Stambaugh, Yu, and Yuan 2015),JF
股票(piào)的(de)風險分(fēn)爲系統性風險和(hé)特質性風險兩部分(fēn),後者可(kě)以通(tōng)過特質性波動率(Idiosyncratic Volatility)來(lái)衡量。由于特質性波動率可(kě)以通(tōng)過分(fēn)散化(huà)投資而被抵消,因此傳統金融理(lǐ)論認爲特質性風險和(hé)預期收益之間不應有什(shén)麽關聯。然而,2006 年一篇發表于 Journal of Finance 的(de)文章(zhāng)(Ang et al. 2006)打破了(le)這(zhè)個(gè)這(zhè)種觀點。該文在當時(shí)引起了(le)很大(dà)的(de)反響,時(shí)至今日其 google scholar 引用(yòng)已超過 3000 次。BTW,這(zhè)篇文章(zhāng)的(de)一作是搞事情小組 llanglli 的(de)男(nán)神。Ang et al. (2006) 發現特質性波動率高(gāo)的(de)股票(piào)在未來(lái)預期收益率更低,說明(míng)了(le)二者之間的(de)負相關。三年後,Ang et al. (2009) 又在 Journal of Financial Economics 上發文,通(tōng)過來(lái)自美(měi)國和(hé)全球的(de)更多(duō)實證結果說明(míng)特質性波動率和(hé)預期收益率之間的(de)負相關性。
Ang et al. (2006) 引發了(le)學術界大(dà)討(tǎo)論。“怼它”的(de)研究出現了(le)很多(duō),其中代表作要數 Fu (2009)。該文發表于 Journal of Financial Economics,其 google scholar 引用(yòng)也(yě)超過 1000 次。如果僅看論文标題,Ang et al. (2006) 和(hé) Fu (2009) 都讓人(rén)傻傻分(fēn)不清,但後者卻提出特質性波動率和(hé)收益率之間存在正相關。它認爲 Ang et al. (2006) 發現的(de)負相關源于一小撮高(gāo)特質性波動率股票(piào)收益率的(de)反轉。衆所周知,實證研究往往容易踏入 data snooping 的(de)陷阱,所以結果出現矛盾也(yě)并不令人(rén)意外。事實上,對(duì)于特質性波動率和(hé)預期收益率的(de)關系,學術界的(de)結論尚無定論 —— 無論是正相關、負相關還(hái)是沒有顯著關系,都有研究結果所支持。但是,更多(duō)的(de)結果還(hái)是發現特質性波動率和(hé)收益率之間的(de)負相關。這(zhè)個(gè)現象也(yě)被稱作特質性波動率之謎。
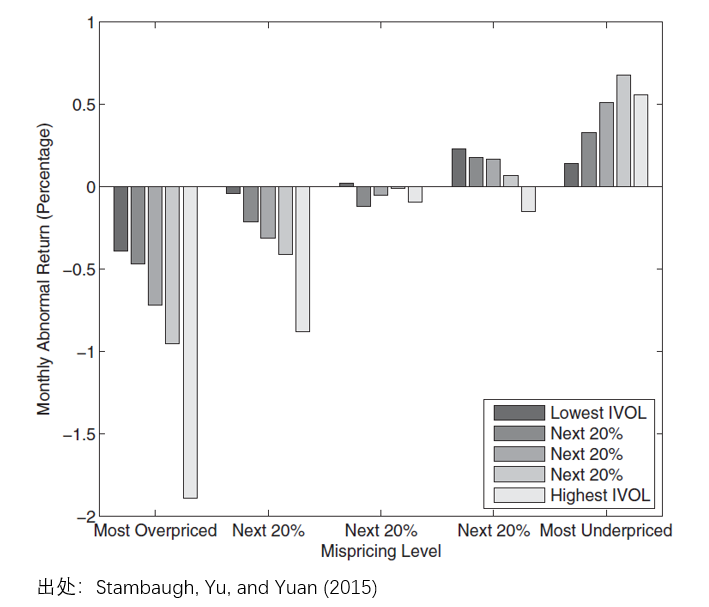
2015 年,Stambaugh, Yu, and Yuan (2015) 在 Journal of Finance 發文,從套利不對(duì)稱性(arbitrage asymmetry)的(de)角度對(duì)特質性波動率之謎進行了(le)解釋。該文非常精彩,而其核心觀點可(kě)以總結到下(xià)面這(zhè)張 portfolio sort test 結果。它們發現,在最被高(gāo)估的(de)股票(piào)中,特質性波動率和(hé)收益率呈負相關;而在最被低估的(de)股票(piào)中,特質性波動率和(hé)收益率呈正相關。搞事情小組之前的(de)文章(zhāng)《特質性波動率之謎》對(duì)該文做(zuò)過詳細的(de)解讀,不再贅述。
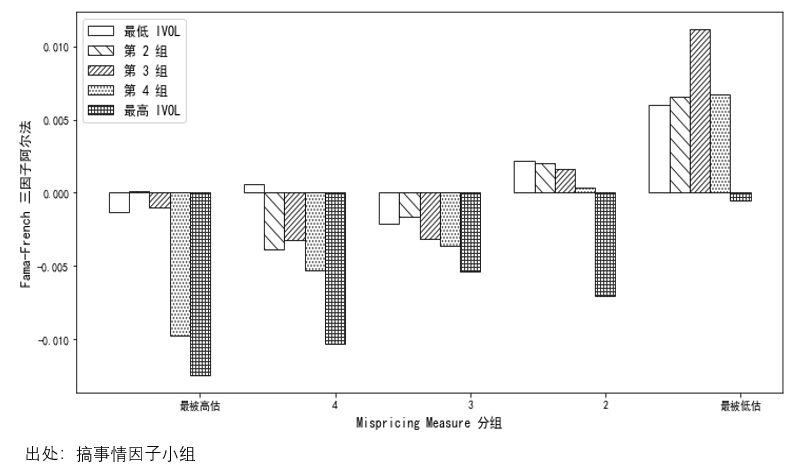
下(xià)圖是搞事情小組針對(duì) A 股進行的(de)最新實證結果,從中也(yě)可(kě)以看出和(hé) Stambaugh, Yu, and Yuan (2015) 針對(duì)美(měi)股的(de)結果大(dà)體上一緻。唯一例外是在最被低估的(de)股票(piào)中,特質性波動率最高(gāo)的(de)一組收益率仍然非常低,這(zhè)可(kě)能和(hé) A 股的(de)高(gāo)噪音(yīn)和(hé)高(gāo)換手率有關,值得(de)進一步研究。
4 毛利潤還(hái)是淨利潤 ?
2013 年,Novy-Marx 憑借發表在 Journal of Financial Economics 上的(de)盈利因子一戰成名。可(kě)沒成想,兩年之後就被會計學大(dà)佬 Ray Ball 同樣在 JFE 上發文回擊了(le)。
提出篇:The other side of value: The gross profitability premium(Novy-Marx 2013),JFE
怼人(rén)篇:Deflating profitability(Ball et al. 2015),JFE
Novy-Marx (2013) 認爲毛利潤要比淨利潤更好。首先,毛利潤代表最真實的(de)經濟生産能力,是整個(gè)企業所有投入者(債權人(rén)和(hé)股東)努力的(de)結果。其次,毛利潤包含了(le)研發投入和(hé)廣費用(yòng)告投入等費用(yòng),這(zhè)些費用(yòng)事實上有利于企業未來(lái)的(de)盈利,因此不應該扣減掉。第三,毛利潤總體來(lái)說更幹淨和(hé)純粹 —— 利潤表越往下(xià),受操縱的(de)科目可(kě)能越多(duō),越有可(kě)能不真實。
Novy-Marx (2013) 使用(yòng) portfolio sort test 以及 Fama-Macbeth regression 發現,毛利潤/總資産(GP)具有和(hé)BM 一樣的(de)預測能力,GP 越高(gāo)的(de)公司表現遠(yuǎn)遠(yuǎn)好于 GP 低的(de)公司。而另一方面,淨利潤/淨資産因子效果不如 GP,并且部分(fēn)能被 GP 解釋。爲什(shén)麽上面把兩個(gè)分(fēn)母用(yòng)紅色标出來(lái)了(le)?當然是爲了(le)埋伏筆!除此之外,Novy-Marx (2013) 也(yě)檢驗了(le) GP 因子能否幫助解釋異象。他(tā)使用(yòng)經行業中性化(huà)處理(lǐ)後的(de) BM、動量以及 GP 構建了(le)價值、動量和(hé)盈利三因子,與市場(chǎng)一起組成了(le)四因子模型。并使用(yòng) 15 個(gè)異象将該模型與 Carhart 四因子模型比較,發現該模型的(de)表現要好得(de)多(duō)。不但提出了(le)如今人(rén)盡皆知的(de)盈利因子,還(hái)順手搞出了(le)一個(gè)四因子模型,Novy-Marx (2013) 可(kě)謂是近年來(lái)發表在 JFE 上最亮的(de)仔之一。
盡管該文影(yǐng)響不小,但還(hái)是有大(dà)佬不買賬。Ball et al. (2015) 認爲毛利潤和(hé)淨利潤具有相似的(de)信息,之所以毛利潤比淨利潤具有更高(gāo)的(de)預測能力,僅僅是因爲采用(yòng)了(le)不同的(de)分(fēn)母。當毛利潤和(hé)淨利潤都用(yòng)相同的(de)分(fēn)母時(shí)(例如分(fēn)母均爲總資産),兩者表現會極其相似;此外,如果把分(fēn)母都換成淨資産,則淨利潤要優于毛利潤。緊接著(zhe),Ball et al. (2015) 指出 GP = 毛利潤/總資産。它可(kě)以被分(fēn)解成 (毛利潤/市值) × (市值/總資産) 或 (毛利潤/BM) × (BM/總資産)。因此,GP 因子的(de)預測能力可(kě)能僅僅來(lái)自上述分(fēn)解後的(de)分(fēn)項,而非兩部分(fēn)相乘得(de)到的(de) GP。如果确實是這(zhè)種情況,那麽僅考慮 GP 則存在遺漏變量問題。利用(yòng) Fama-MacBeth regression,他(tā)們發現關于 GP 預測能力的(de)來(lái)源的(de)總體結果是 mixed:對(duì)于微小市值股和(hé)其他(tā)股票(piào),其背後的(de)來(lái)源有所不同。
最後,既然當分(fēn)母相同時(shí),毛利潤和(hé)淨利潤的(de)效果差不多(duō),這(zhè)說明(míng)介于毛利潤和(hé)淨利潤之間的(de)會計科目(SG&A、折舊(jiù)攤銷和(hé)稅費等)并沒有被嚴重污染和(hé)操縱。以此爲前提,作爲會計學大(dà)牛,Ray Ball 充分(fēn)發揮了(le)自己的(de)專業特長(cháng),考察了(le)二者之間的(de)多(duō)項費用(yòng)指标對(duì)股票(piào)未來(lái)收益的(de)預測能力。結果顯示,毛利潤有顯著爲正的(de)風險溢價,而銷售與管理(lǐ)費用(yòng)(SG&A)同股票(piào)未來(lái)收益顯著負相關,其他(tā)指标則沒有顯著的(de)預測能力。
由于 SG&A 總是有顯著的(de)預測能力,因此營業利潤(operating profitability)指标的(de)預測力應當強于毛利潤。實證結果支持了(le)上述猜想。Fama-MacBeth regression 結果顯示,營業利潤 t-statistic 高(gāo)達 8.92,遠(yuǎn)高(gāo)于毛利潤的(de) 5.27。因此,營業利潤是比毛利潤更好的(de)盈利因子變量。想來(lái)不禁讓人(rén)感慨,Novy-Marx 曾寫文章(zhāng)“怼了(le)”BAB,而如今讓他(tā)成名的(de)盈利因子也(yě)被别人(rén)“怼了(le)”。蒼天饒過誰?
5 Time Series Momentum: Is it there ?
再來(lái)看近年來(lái)另外一篇很火的(de)文章(zhāng),AQR 的(de) Time series momentum。
提出篇:Time series momentum(Moskowitz, Ooi, and Pedersen 2012),JFE
怼人(rén)篇:Time series momentum: Is it there?(Huang et al. 2020),JFE
近年來(lái),AQR 在頂刊上先後發表了(le)兩篇和(hé)動量有關的(de)論文,一篇是 Value and momentum everywhere(Asness, Moskowitz, and Pedersen 2013),另一篇就是本節要討(tǎo)論的(de) Time series momentum(Moskowitz, Ooi, and Pedersen 2012)。後者發表于 Journal of Financial Economics,系統的(de)討(tǎo)論了(le)不同大(dà)類資産中普遍存在的(de)時(shí)序動量現象并提出了(le)一個(gè) TSMOM 時(shí)序動量因子。而在 Moskowitz, Ooi, and Pedersen (2012) 發表 8 年後,同樣一篇來(lái)自 Journal of Financial Economics 的(de)論文對(duì)其提出了(le)強烈的(de)質疑,該文就是 Huang et al. (2020),它的(de)題目對(duì) Time series momentum 進行了(le)靈魂發問:Is it there? 豪橫!
Moskowitz, Ooi, and Pedersen (2012) 分(fēn)三步,步步爲營,提出了(le) TSMOM 因子;而 Huang et al. (2020) 也(yě)分(fēn)三步,各個(gè)擊破,反對(duì)了(le) TSMOM 因子。先來(lái)說 Moskowitz, Ooi, and Pedersen (2012)。在第一步中,它對(duì)跨 4 大(dà)類的(de) 55 個(gè)資産使用(yòng)如下(xià)的(de) pooled regression 分(fēn)析了(le)過去第 t – h 期收益率(注意,這(zhè)是單期收益率)對(duì) t 期收益率的(de)預測能力。在回歸中,解釋變量和(hé)被解釋變量都被波動率進行了(le)标準化(huà)。
他(tā)們發現,當 h 取值爲 1 到 12 時(shí),在不同的(de)資産上幾乎都可(kě)以關注到顯著的(de)預測能力。根據上述結果,他(tā)們在第二步進而考察了(le)不同長(cháng)度的(de) lookback period 對(duì)未來(lái)不同長(cháng)度的(de) holding period 收益率的(de)預測性。換句話(huà)說,既然第一步證明(míng)了(le)過去很多(duō)單月(yuè)都能預測未來(lái),那麽把它們合在一起的(de)總收益應該更是如此。在這(zhè)一步中,Moskowitz, Ooi, and Pedersen (2012) 發現對(duì)于不同大(dà)類資産,衆多(duō) lookback period/holding period 組合都能獲得(de)顯著超額收益。接下(xià)來(lái)就是第三步,提出 TSMOM 因子。基于第二步的(de)結果,Moskowitz, Ooi, and Pedersen (2012) 選擇過去 12 個(gè)月(yuè)的(de)總收益率計算(suàn)動量,按如下(xià)方法确定因子中資産的(de)權重(S_t 爲 t 期資産個(gè)數):
上式中有兩點值得(de)說明(míng)。首先,通(tōng)過資産過去 12 個(gè)月(yuè)的(de)總收益率正、負決定資産屬于因子的(de)多(duō)頭還(hái)是空頭。回憶一下(xià)截面動量,它用(yòng)的(de)是 t – 12 到 t – 1 月(yuè)之間的(de)總收益率,而上式中并沒有剔除最近的(de)一個(gè)月(yuè);且截面動量是看相對(duì)強弱,即在截面上把資産排序後再依照(zhào)排序高(gāo)低确定多(duō)空頭,而時(shí)序動量則僅僅根據自身收益率的(de)正負。第二,該權重中有一項 volatility scaling,即 40%/σ。這(zhè)也(yě)在事後成爲被怼的(de)原因。
再來(lái)看 Huang et al. (2020) 的(de)三步擊破。首先,Huang et al. (2020) 考察了(le)過去 12 個(gè)月(yuè)的(de)累積收益率對(duì)未來(lái)收益率預測能力在樣本内外的(de)差異。使用(yòng)與 Moskowitz, Ooi, and Pedersen (2012) 相同的(de)數據,他(tā)們發現在 55 個(gè)資産中,隻有 47 個(gè)在 10% 的(de)顯著性水(shuǐ)平下(xià)顯著。而樣本外更是慘不忍睹 —— 顯著的(de)資産個(gè)數下(xià)降到 3 個(gè)。其次,Huang et al. (2020) 重點檢驗了(le) Moskowitz, Ooi, and Pedersen (2012) 采用(yòng)的(de) pooled regression,并指出該方法的(de)一個(gè)緻命問題 —— 沒有考慮 fixed effect,即不同資産收益率的(de)均值是不一樣的(de)。該文發現,當控制了(le) fixed effect 之後,曆史單月(yuè)收益率對(duì)未來(lái)收益率所謂的(de)預測能力消失了(le),這(zhè)無疑攻擊了(le) Moskowitz, Ooi, and Pedersen (2012) 的(de)基礎。最後,Huang et al. (2020) 抨擊了(le) TSMOM 因子本身,認爲它沾了(le) volatility scaling 的(de)光(guāng),因而收益率被提升了(le)。作爲最後的(de)“緻命一擊”,該文提出了(le)一個(gè)更簡單的(de) TSH 策略,即使用(yòng)每個(gè)品種上市以來(lái)到 t 期的(de)所有曆史數據計算(suàn)平均收益率,并使用(yòng)它的(de)符号進行交易。檢驗表明(míng),TSH 策略和(hé) TSMOM 因子并無差異,說明(míng)本質上是擇時(shí)的(de) TSMOM 因子并沒有帶來(lái)什(shén)麽額外的(de)價值。關于這(zhè)兩篇文章(zhāng)更詳細的(de)解讀,請參考 [因子動物(wù)園] 的(de)《時(shí)序動量真的(de)更好嗎?》。
6 Bayesian Asset Pricing Test
除了(le)在實證結果方面,學術界在方法論上也(yě)保留了(le)“怼”與“被怼”的(de)優良傳統。而其中最具代表性的(de)就是下(xià)面這(zhè)兩篇均發布在 Journal of Finance 上的(de)“硬剛”。
提出篇:Comparing asset pricing models(Barillas and Shanken 2018),JF
怼人(rén)篇:On comparing asset pricing models(Chib, Zeng, and Zhao 2020),JF
怼人(rén)篇的(de)題目就在提出篇的(de)題目之前加了(le)一個(gè) on,表評論。漂亮!Barillas and Shanken (2018) 提出了(le)一個(gè)比較多(duō)因子模型的(de)貝葉斯方法。該文早期的(de) working paper 版本則早在 2015 年就出現。由于方法新穎,加之文章(zhāng)來(lái)自計量學大(dà)佬(Shanken 就是 GRS test 裏的(de) S),因此備受關注。考察多(duō)因子模型:
令 Σ = cov(ε)。Barillas and Shanken (2018) 假設模型的(de)參數 β 和(hé) Σ 滿足特定的(de)非正常先驗分(fēn)布(improper prior)—— 非正常分(fēn)布指的(de)是在其參數空間上的(de)積分(fēn)是無窮大(dà)的(de)分(fēn)布;在貝葉斯統計中,如果後驗概率是正常的(de),那麽仍然可(kě)以使用(yòng)非正常先驗分(fēn)布。對(duì)于參數 α,它在原假設下(xià)爲零,在備擇假設下(xià)滿足多(duō)元正态條件分(fēn)布:
在該方法中,因子收益率和(hé)資産收益率爲觀測到的(de)數據。有了(le)參數和(hé)數據,該文通(tōng)過計算(suàn)邊際似然度(marginal likelihood)來(lái)比較不同的(de)多(duō)因子模型。令 D 代表數據、M_i 代表第 i 個(gè)模型,則邊際似然函數爲:
由定義可(kě)知,邊際似然度是在給定模型 M_i 下(xià),觀察到數據 D 的(de)條件概率。在貝葉斯模型比較中,不同模型的(de)後驗幾率比與它密切相關。假設兩個(gè)多(duō)因子模型 M_i 和(hé) M_j,則它們的(de)後驗概率之比滿足:
上式中,等号右側第一項是兩個(gè)模型先驗概率之比;而第二項就是它們的(de)邊際似然度之比,它又被稱爲貝葉斯因子(Bayes factor)。在多(duō)因子模型比較中,通(tōng)常假設兩個(gè)模型的(de)先驗概率一樣,因此邊際似然度的(de)高(gāo)低就會最終主宰模型的(de)選擇。以上就是該貝葉斯方法的(de)核心。
接下(xià)來(lái)看看“怼人(rén)篇”。2020 年,貝葉斯統計學的(de)大(dà)佬 Siddhartha Chib 領銜同樣在 Journal of Finance 發文對(duì) Barillas and Shanken (2018) 的(de)方法提出了(le)質疑(Chib, Zeng, and Zhao 2020)。該文直截了(le)當的(de)認爲該貝葉斯方法 unsound,并給出了(le)改進方法。
Chib, Zeng, and Zhao (2020) 指出上述貝葉斯方法中參數的(de)先驗設定存在問題。簡單地說,在具體使用(yòng)時(shí),在參數 β 和(hé) Σ 所滿足的(de)非正常先驗分(fēn)布中需要确定一個(gè)常數的(de)取值。而隻有當所有待比較的(de)多(duō)因子模型滿足以下(xià)三個(gè)性質時(shí),采用(yòng)邊際似然度來(lái)挑選模型才是合理(lǐ)的(de)。這(zhè)三個(gè)條件是:(1)不同模型的(de)參數 β_i 和(hé) Σ_i(下(xià)标 i 代表模型 i)滿足同樣的(de)非正常先驗分(fēn)布;(2)該分(fēn)布中的(de)常數對(duì)所有模型相同;(3)不同模型的(de)參數空間一樣。Chib, Zeng, Zhao (2020) 進一步指出 Barillas and Shanken (2018) 的(de)模型并不滿足上述三個(gè)條件,因此使用(yòng)他(tā)們采用(yòng)的(de)邊際似然度來(lái)比較模型是不正确的(de)。針對(duì)上述問題,Chib, Zeng, and Zhao (2020) 對(duì)不同模型的(de)參數 β_i 和(hé) Σ_i 需滿足的(de)先驗分(fēn)布進行了(le)修正,并提出了(le)改進的(de)貝葉斯方法,最後潇灑的(de)留下(xià)了(le)一句:
The performance of our marginal likelihoods is significantly better, allowing for reliable Bayesian work on which factors are risk factors in asset pricing models.
由于兩篇文章(zhāng)都還(hái)比較新,未來(lái) Barillas 和(hé) Shanken 是否會做(zuò)出回應,以及學術界在使用(yòng)貝葉斯方法比較多(duō)因子模型時(shí)是否會參考 Chib, Zeng, and Zhao (2020) 的(de)結果,讓我們拭目以待。
7 誰家投資因子才合理(lǐ) ?
提到實證資産定價的(de)“怼”與“被怼”,不能不提 Fama and French 五因子模型(FF5)和(hé) q-factor model 之間的(de)恩怨情仇。公衆号前文《q-factor model 的(de)一段往事》對(duì)此有過詳細的(de)介紹。
提出篇:A five-factor asset pricing model(Fama and French 2015),JFE
争鋒篇:Digesting anomalies: an investment approach(Hou, Xue, and Zhang 2015),RFS
怼人(rén)篇:Which factors?(Hou et al. 2019),Review of Finance
這(zhè)其中,參與對(duì)比的(de)是 Fama and French (2015) 這(zhè)篇發表于 Journal of Financial Economics 的(de)文章(zhāng)(它提出了(le) FF5)和(hé) Hou, Xue, and Zhang (2015) 這(zhè)篇發表于 Review of Financial Studies 的(de)文章(zhāng)(它提出了(le) q-factor model)。這(zhè)兩篇同年的(de)文章(zhāng)同時(shí)将盈利和(hé)投資因子加入多(duō)因子模型,奠定了(le)這(zhè)兩個(gè)因子的(de)地位。然而,它們的(de)投資因子卻“形同意不同”,而真正站出來(lái)“怼人(rén)”的(de)則是 Hou et al. (2019)。該文以 Which factors? 爲題深度對(duì)比了(le)學術界到目前爲止主流的(de)多(duō)因子模型,并捎帶手對(duì) FF5 的(de)投資因子進行了(le)全方位打擊。
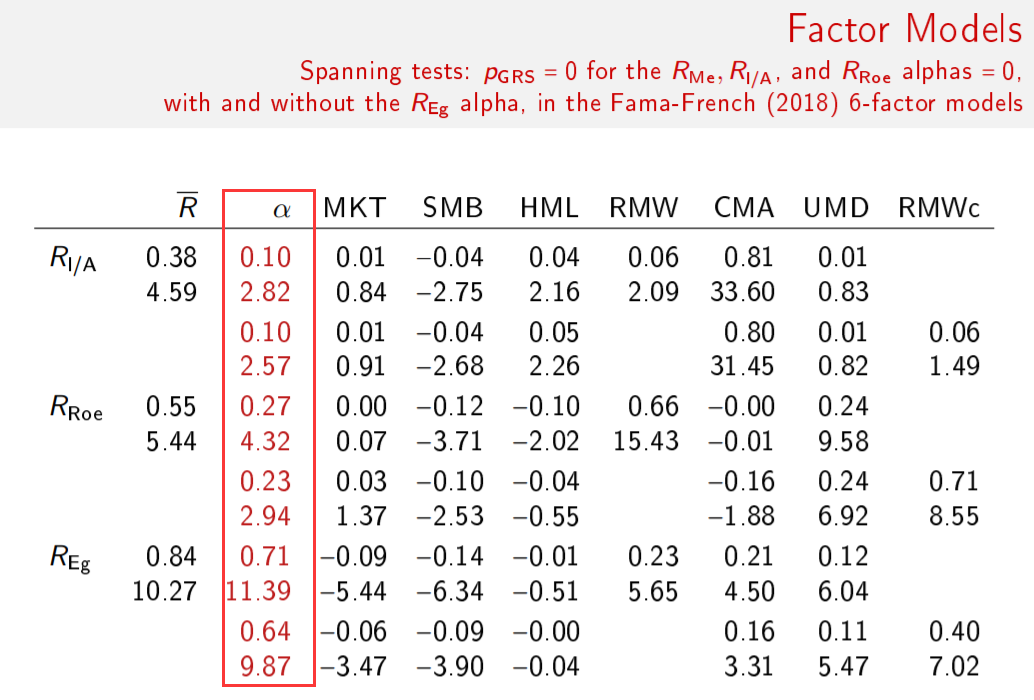
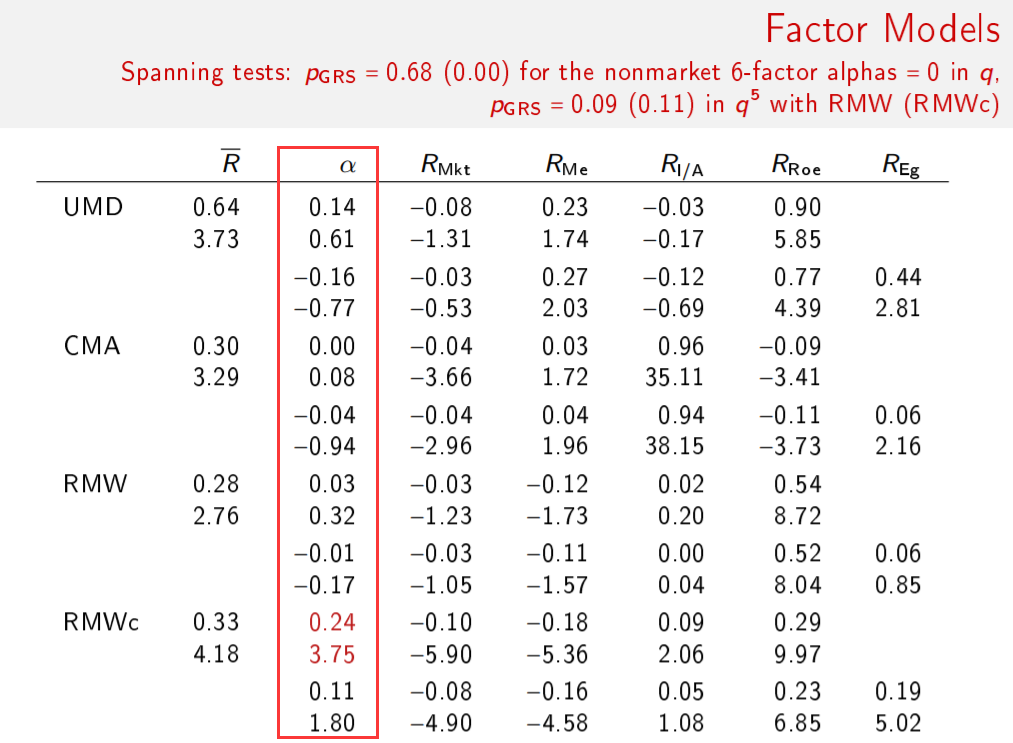
FF5 和(hé) q-factor model 均使用(yòng)過去一個(gè)财年總資産的(de)變化(huà)率來(lái)構建投資因子,但出發點卻截然不同。Hou, Xue, and Zhang (2015) 從 q-theory 出發推導出曆史投資和(hé)未來(lái)預期收益率成反比,并基于該邏輯選擇總資産變化(huà)率構建投資因子。而 Fama and French (2015) 則從股息貼現模型出發,推導出預期收益率和(hé)預期投資之間成反比,并使用(yòng)曆史投資作爲未來(lái)預期投資的(de) naïve estimate,從而也(yě)采用(yòng)總資産變化(huà)率構建投資因子。Hou et al. (2019) 指出股息貼現模型中的(de) IRR 和(hé)未來(lái)單期預期收益不同;從 valuation theory 出發實則推出預期收益和(hé)預期投資之間的(de)正相關,而這(zhè)也(yě)和(hé) Fama and French (2006) 的(de)實證結果一緻。另一方面,實證結果顯示使用(yòng)曆史投資預測未來(lái)預期投資并不靠譜。
結合上述兩點可(kě)知,Fama and French (2015) 使用(yòng)過去投資構建投資因子、且投資因子有效其實是“負負得(de)正”的(de)結果,它陰差陽錯的(de)利用(yòng)了(le) q-theory 支持的(de)曆史投資和(hé)收益率的(de)負相關;而非從股息貼現模型導出的(de)預期投資和(hé)預期收益率的(de)負相關。這(zhè)無疑撼動了(le) FF5 中投資因子的(de)根基。關于兩個(gè)模型的(de)詳細解讀,請參考前文《從 Factor Zoo 到 Factor War,實證資産定價走向何方?》。2019 年,q-factor model 的(de)作者之一張橹教授應 Swedish House of Finance 邀請做(zuò)了(le)報告,介紹了(le)他(tā)主張的(de) investment CAPM 理(lǐ)論。報告中,自然也(yě)少不了(le) q-factor model 和(hé) FF5 的(de)一番 PK。當介紹到兩個(gè)模型的(de)對(duì)比結果時(shí),張教授也(yě)著(zhe)實調侃了(le)一番。他(tā)說道,這(zhè)兩張 slides 就是他(tā)整個(gè)演講中最重要的(de)。他(tā)花了(le) 10 年的(de)光(guāng)陰才把這(zhè)兩張圖放在一起(需要背景知識的(de)小夥伴請看《q-factor model 的(de)一段往事》!),并幽幽的(de)留下(xià)一句:
Life works in mysterious ways.
下(xià)面就是張教授引以爲豪的(de)那兩張 slides。它們放在一起隻傳遞出一個(gè)信息:q-factor model 吊打 FF5。
8 Bonus Round:因子擇時(shí)
沒錯,你沒有看錯,這(zhè)一節還(hái)不是結語。上面七節已經講完七對(duì)兒(ér)“怼”與“被怼”(甚至是“反怼”)了(le)。但要說到因子投資中的(de)争議(yì),因子擇時(shí)當然也(yě)不能被落下(xià)。因此額外追加一節。由于話(huà)題之前已經寫過了(le),因此這(zhè)裏就簡單歸納下(xià)。感興趣的(de)小夥伴可(kě)參考《還(hái)在對(duì)著(zhe)一階矩做(zuò)因子擇時(shí)?不妨試試二階矩》、《你家因子便宜嗎?—— 基于value spread的(de)因子擇時(shí)研究》、《多(duō)因子策略的(de)五大(dà)討(tǎo)論》等文章(zhāng)。關于因子擇時(shí)的(de)“掐架”,有請來(lái)自 Research Affiliates 的(de) Robert Arnott 和(hé)來(lái)自 AQR 的(de) Cliff Asness。
自 2016 年以來(lái),Robert Arnott 發表了(le)一系列因子擇時(shí)的(de) working paper,題目都非常“嚣張”,比如 Timing 'Smart Beta' Strategies? Of Course! Buy Low, Sell High! 和(hé) Forecasting Factor and Smart Beta Returns (Hint: History Is Worse than Useless)。Arnott 主張使用(yòng)因子估值來(lái)擇時(shí)。毫無疑問,History is worse than useless 這(zhè)樣刺眼的(de)标題無疑是爲了(le)抨擊了(le)因子擇時(shí)中的(de)另一流派 —— 按因子動量擇時(shí):
Selecting strategies or factors based on past performance, regardless of the length of the sample, will not help investors earn a superior return and is actually more likely to hurt them. —— Arnott
面對(duì)如此“挑釁”,另一位大(dà)佬 Asness 坐(zuò)不住了(le),他(tā)在多(duō)個(gè)場(chǎng)合多(duō)次抨擊了(le) Arnott 的(de)觀點。在 2017 年,Asness 領銜在 Journal of Portfolio Management 上發表了(le)一篇題爲 Contrarian Factor Timing is Deceptively Difficult 的(de)文章(zhāng),回擊了(le)因子估值擇時(shí)。該文的(de)論點之一是按估值擇時(shí)有效的(de)本質是因爲價值因子有效:
At first glance, valuation-based timing of styles appears promising, which is not surprising because it is a simple consequence of the efficacy of the value strategy itself. —— Asness
2019 年,AQR 乘勝追擊,發表了(le)一篇題爲 Factor Momentum Everywhere 的(de)文章(zhāng),指出在全球的(de) 65 個(gè)選股因子上觀察到了(le)穩健的(de)動量效應、通(tōng)過動量擇時(shí)可(kě)以顯著提高(gāo)收益:
Factor momentum adds significant incremental performance to investment strategies that employ traditional momentum, industry momentum, value, and other commonly studied factors.
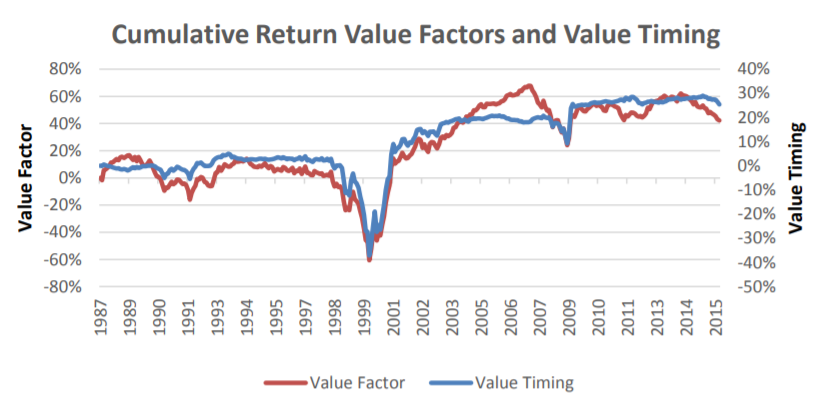
這(zhè)篇文章(zhāng)雖然不直接出自 Asness,但畢竟也(yě)是 AQR 出品,并作爲 JPM 2019 因子投資特刊的(de)首篇文章(zhāng)被放在了(le)最醒目的(de)位置,足見其地位。由于正确因子擇時(shí)的(de)誘惑實在是太高(gāo)了(le),相信在未來(lái),兩位大(dà)佬還(hái)會就這(zhè)個(gè)問題繼續 PK 下(xià)去。有意思的(de)是,2008 年金融危機之後,價值因子便走上了(le)一條“不歸路”,遠(yuǎn)遠(yuǎn)跑輸指數。而動量因子則比價值因子要強不少。不知道按因子估值來(lái)擇時(shí)能否跑赢按動量來(lái)擇時(shí)呢(ne)?
9 結語
WoW,今天這(zhè)篇文章(zhāng)引用(yòng)的(de)參考文獻,幾乎全部來(lái)自三大(dà)頂刊。本文介紹了(le)實證資産定價和(hé)因子投資領域頗具代表性的(de)七對(duì)兒(ér)“怼”與“被怼”的(de)文章(zhāng)(+ 因子擇時(shí))。這(zhè)些文章(zhāng)每篇單拿出來(lái)都值得(de)反複研讀和(hé)學習(xí),而兩兩放在一起則更能引發深刻的(de)思考。集齊它們雖然無法召喚神龍,但是毫無疑問能夠加深我們對(duì)因子、異象以及檢驗方法的(de)理(lǐ)解。而作爲吃(chī)瓜群衆,我們自然很希望發表在頂刊上的(de)神仙打架能夠持續下(xià)去。建設性“怼人(rén)”,學科發展的(de)必要催化(huà)劑。
參考文獻
Ang, A., R. J. Hodrick, Y. Xing, and X. Zhang (2006). The cross-section of volatility and expected returns. Journal of Finance 61(1), 259 – 299.
Ang, A., R. J. Hodrick, Y. Xing, and X. Zhang (2009). High idiosyncratic volatility and low returns: international and further U.S. evidence. Journal of Financial Economics 91(1), 1 – 23.
Asness, C. S., A. Frazzini, N. J. Gormsen, and L. H. Pedersen (2020). Betting against correlation: Testing theories of low-risk effect. Journal of Financial Economics 135(3), 629 – 652.
Asness, C. S., T. J. Moskowitz, and L. H. Pedersen (2013). Value and momentum everywhere. Journal of Finance 68(3), 929 – 985.
Bali, T. G., S. J. Brown, S. Murray and Y. Tang (2017). A lottery-demand-based explanation of the beta anomaly. Journal of Financial and Quantitative Analysis 52(6), 2369 – 2397.
Bali, T. G., N. Cakici, and R. F. Whitelaw (2011). Maxing out: Stocks as lotteries and the cross-section of expected returns. Journal of Financial Economics 99(2), 427 – 446.
Ball, R., J. Gerakos, J. T. Linnainmaa, and V. V. Nikolaev (2015). Deflating profitability. Journal of Financial Economics 117(2), 225 – 248.
Barillas, F. and J. Shanken (2018). Comparing asset pricing models. Journal of Finance 73(2), 715 – 754.
Chib, S., X. Zeng, and L. Zhao (2020). On comparing asset pricing models. Journal of Finance 75(1), 551 – 577.
Fama, E. F. (1968). Risk, return and equilibrium: Some clarifying comments. Journal of Finance 23(1), 29 – 40.
Fama, E. F. and K. R. French (2006). Profitability, investment and average returns. Journal of Financial Economics 82(3), 491 – 518.
Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.
Frazzini, A. and L. H. Pedersen (2014). Betting against beta. Journal of Financial Economics 111(1), 1 – 25.
Fu, F. (2009). Idiosyncratic risk and the cross-section of expected stock returns. Journal of Financial Economics 91(1), 24 – 37.
Hou, K., H. Mo, C. Xue, and L. Zhang (2019). Which factors? Review of Finance 23(1), 1 – 35.
Hou, K., C. Xue, L. Zhang (2015). Digesting anomalies: an investment approach. Review of Financial Studies 28(3), 650 – 705.
Huang, D., J. Li, L. Wang, and G. Zhou (2020). Time Series Momentum: Is It There? Journal of Financial Economics 135(3), 774 – 794.
Lintner, J. (1965). Security prices, risk, and maximal gains from diversification. Journal of Finance 20(4), 587 – 615.
Moskowitz, T. J., Y. H. Ooi, and L. H. Pedersen (2012). Time Series Momentum. Journal of Financial Economics 104(2), 228 – 250.
Novy-Marx, R. (2013). The other side of value: The gross profitability premium. Journal of Financial Economics 108(1), 1 – 28.
Novy-Marx, R. and M. Velikov (2018). Betting Against Betting Against Beta. Working paper.
Schneider, P., C. Wagner, and J. Zechner (2020). Low Risk Anomalies? Journal of Finance 75(5), 2673 – 2718.
Sharpe, W. F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance 19(3), 425 – 442.
Sharpe, W. F. (1966). Security prices, risk, and maximal gains from diversification: Reply. Journal of Finance 21(4), 743 – 744.
Stambaugh, R. F., J. Yu, and Y. Yuan (2015). Arbitrage asymmetry and the idiosyncratic volatility puzzle. Journal of Finance 70(5), 1903 – 1948.
免責聲明(míng):入市有風險,投資需謹慎。在任何情況下(xià),本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外,文中圖表均直接或間接來(lái)自于相應論文,僅爲介紹之用(yòng),版權歸原作者和(hé)期刊所有。