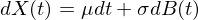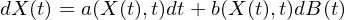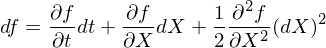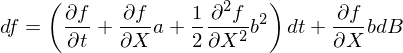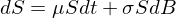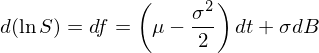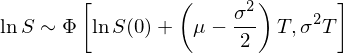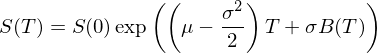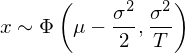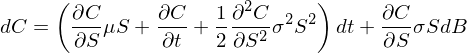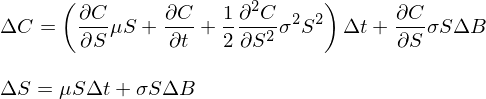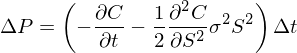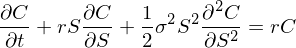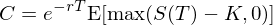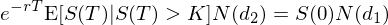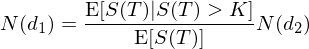布朗運動、伊藤引理(lǐ)、BS 公式（後篇）

作者：石川

1 前文回顧

本系列的(de)前篇從布朗運動出發，介紹了(le)布朗運動的(de)性質并解釋了(le)爲什(shén)麽使用(yòng)幾何布朗運動來(lái)描述股價是被投資界廣泛接受的(de)。此外，前文給出了(le)伊藤引理(lǐ)的(de)最基本形式，它是随機分(fēn)析的(de)基礎，爲分(fēn)析衍生品定價提供了(le)堅實的(de)武器。

作爲本系列的(de)後篇，本文将從擴展伊藤引理(lǐ)出發，并用(yòng)它求解幾何布朗運動，然後推導 BS 微分(fēn)方程以及 BS 公式（也(yě)稱 Black-Scholes-Merton 公式）。在介紹 BS 公式時(shí)，論述的(de)重點會放在衍生品定價中的(de)一個(gè)核心方法，即風險中性定價理(lǐ)論。此外，我們會花一定的(de)筆墨來(lái)解釋 BS 公式中的(de)兩個(gè)核心要素（即 N(d_1) 和(hé) N(d_2) 的(de)業務含義），明(míng)白它們對(duì)理(lǐ)解 BS 公式至關重要。

在那之前，先來(lái)點輕松的(de)，看看 Black，Scholes 和(hé) Merton 三位大(dà)咖長(cháng)什(shén)麽樣子。Scholes 和(hé) Merton 因在衍生品定價方面的(de)傑出工作于 1997 年獲得(de)諾貝爾經濟學獎。Black 沒有在列的(de)原因是他(tā)不幸地于 1995 年去世，而諾貝爾獎不追授給頒獎時(shí)已故 6 個(gè)月(yuè)以上的(de)學者。

2 伊藤引理(lǐ)的(de)一般形式

在前篇中，我們介紹了(le)帶有漂移（drift）和(hé)擴散（diffusion）的(de)布朗運動有如下(xià)形式的(de)随機微分(fēn)方程。在這(zhè)裏，μ 和(hé) σ 被假定爲常數。

更一般的(de)，漂移和(hé)擴散的(de)參數均可(kě)以是随機過程 X(t) 以及時(shí)間 t 的(de)函數。假設我們令 a(X(t),t) 和(hé) b(X(t),t) 表示漂移和(hé)擴散參數（則在上面這(zhè)個(gè)例子中，a(X(t),t) = μ 而 b(X(t),t) = σ）。我們稱滿足如下(xià)随機微分(fēn)方程（stochastic differential equation，或 SDE）的(de)随機過程爲伊藤漂移擴散過程（Itō drift-diffusion process，下(xià)稱伊藤過程）：

令 f(X(t), t) 爲 X(t) 的(de)二階連續可(kě)導函數（并對(duì) t 一階可(kě)導），由伊藤引理(lǐ)可(kě)知（省略自變量以簡化(huà)表達）：

将 dX = a(X(t),t)dt + b(X(t),t)dB 帶入上式，并且略去所有比 dt 更高(gāo)階的(de)小量，最終可(kě)以得(de)到伊藤引理(lǐ)的(de)一般形式：

由 f 的(de) SDE 可(kě)知，作爲 X 和(hé) t 的(de)函數，f 本身也(yě)是一個(gè)伊藤過程。更重要的(de)是，伊藤引理(lǐ)說明(míng)，df 表達式右側的(de)布朗運動 dB 恰恰正是 dX 表達式中的(de)那個(gè)布朗運動。換句話(huà)說，在 f 和(hé) X 的(de)随機性由同一個(gè)布朗運動決定，而非兩個(gè)獨立的(de)布朗運動。這(zhè)一點在下(xià)文中推導 BS 微分(fēn)方程時(shí)至關重要。下(xià)面我們就利用(yòng)伊藤引理(lǐ)求解幾何布朗運動。

3 幾何布朗運動

對(duì)于股票(piào)價格 S，可(kě)以用(yòng)滿足如下(xià) SDE 的(de)幾何布朗運動來(lái)描述。

上式中 μ 是股票(piào)的(de)期望年收益率，σ 是股票(piào)年收益率的(de)标準差。顯然，這(zhè)是一個(gè)伊藤過程（a = μS，b = σS）。爲了(le)求解 S，令 f = lnS（S 的(de)自然對(duì)數）并對(duì) df 使用(yòng)伊藤引理(lǐ)（注：爲了(le)保持符号和(hé)前篇的(de)一緻性，我們用(yòng) S 而非 X 代表股票(piào)價格的(de)随機過程）得(de)到 lnS 的(de) SDE：

這(zhè)個(gè)式子說明(míng)，lnS 是一個(gè)帶漂移的(de)布朗運動，它的(de)漂移率爲 μ – 0.5σ^2，波動率爲 σ。由布朗運動的(de)性質可(kě)知，在任何時(shí)間 T，lnS 的(de)變化(huà)符合正态分(fēn)布：

如果一個(gè)随機變量的(de)對(duì)數滿足正态分(fēn)布，我們說這(zhè)個(gè)随機變量本身滿足對(duì)數正态分(fēn)布（lognormal distribution）。因此，當我們用(yòng)幾何布朗運動來(lái)描述股價波動時(shí)，得(de)到的(de)股價滿足對(duì)數正态分(fēn)布。通(tōng)過對(duì) lnS 的(de) SDE 兩邊積分(fēn)，再對(duì)等式兩邊取指數，便可(kě)很容易的(de)寫出股價随時(shí)間變化(huà)的(de)解析式：

上式乍一看好像有悖于我們的(de)直覺。我們已知股票(piào)的(de)年收益率期望爲 μ。但在上式中，抛開 B(T) 帶來(lái)的(de)随機性不談而僅看時(shí)間 T 的(de)系數，股價的(de)增長(cháng)速率是 μ – 0.5σ^2 而不是 μ。這(zhè)意味著(zhe)什(shén)麽呢(ne)？數值 μ – 0.5σ^2 又是否是什(shén)麽别的(de)收益率呢(ne)？正确答(dá)案是，μ – 0.5σ^2 恰恰是股票(piào)每年的(de)連續複利期望收益率。利用(yòng)股價 S 的(de)對(duì)數正态特性可(kě)以說明(míng)這(zhè)一點。假設 x 代表股票(piào)每年的(de)連續複利收益率。因此有 S(T) = S(0)e^(xT)，或 x = (1/T)×(lnS(T) - lnS(0))。由上面的(de)分(fēn)析可(kě)知，lnS(T) – lnS(0) 符合均值爲 (μ – 0.5σ^2)T、方差爲 (σ^2)T 的(de)正态分(fēn)布。因此每年的(de)連續複利收益率 x 也(yě)是正态分(fēn)布并且滿足：

直觀比較股票(piào)的(de)每年期望收益率 μ 和(hé)每年連續複利期望收益率 μ – 0.5σ^2，後者考慮了(le)波動 σ，它們的(de)區(qū)别就是年收益率序列算(suàn)數平均值和(hé)幾何平均值的(de)區(qū)别。來(lái)看一個(gè)例子。假設某股票(piào)在過去五年的(de)年收益率分(fēn)别爲 15%，20%，30%，-20% 和(hé) 25%。這(zhè)個(gè)序列的(de)算(suàn)數平均值爲 14%，因此該股票(piào)的(de)每年的(de)（樣本）期望收益率 μ = 14%。再來(lái)看看它每年連續複利期望收益率是多(duō)少。假設我們在五年前花 100 塊買入它并持有 5 年，那麽在 5 年後我們的(de)回報是 100×1.15×1.20×1.30×0.80×1.25 = 179.4。因此每年（樣本）連續複利期望收益率（即這(zhè)個(gè)收益率序列的(de)幾何平均值）爲 12.4%，顯然它低于算(suàn)數平均值。

4 Black-Scholes 微分(fēn)方程

本節介紹 Black-Scholes 期權定價微分(fēn)方程。細心如你一定已經發現了(le)，“随機”兩個(gè)字被拿掉了(le)，而 BS 方程是一個(gè)微分(fēn)方程，說明(míng)它不再具備任何随機因素，這(zhè)是喜聞樂(yuè)見的(de)，因爲沒有多(duō)少人(rén)喜歡随機性。讀完本節你就會明(míng)白這(zhè)是爲什(shén)麽。首先來(lái)看推導 BS 微分(fēn)方程時(shí)用(yòng)到的(de)假設：

顯然，有些假設在真實交易中是不可(kě)能出現的(de)，但是在确定期權的(de)理(lǐ)論價值時(shí)，這(zhè)些假設還(hái)是普遍被接受的(de)。當然，自 BS 模型發明(míng)以來(lái)，衍生品定價也(yě)有了(le)長(cháng)足的(de)發展。很多(duō)改進的(de)模型相繼被提出，用(yòng)于修正 BS 模型中各種假設。下(xià)面以歐式看漲期權（European call option）爲例介紹 BS 微分(fēn)方程。

令 C 代表歐式看漲期權的(de)價格，顯然它是标的(de)股票(piào)價格 S 和(hé)時(shí)間 t 的(de)函數，記爲 C(S, t)。對(duì) C 運用(yòng)伊藤引理(lǐ)可(kě)得(de)：

讓我們來(lái)看看在一個(gè)微小的(de)時(shí)間區(qū)間 Δt 内股價 S 和(hé)期權價格 C 如何變化(huà)。爲此，将 S 和(hé) C 的(de)随機微分(fēn)方程離散化(huà)：

在本文第二節我們曾經強調過，一個(gè)伊藤過程 X 的(de)函數 f 也(yě)是一個(gè)伊藤過程，且 f 和(hé) X 這(zhè)兩個(gè)随機過程中的(de)不确定性來(lái)自同一個(gè)布朗運動。根據這(zhè)個(gè)性質可(kě)知，股價和(hé)期權價格的(de)變化(huà)，即 ΔC 和(hé) ΔS 中，的(de)布朗運動也(yě)是同一個(gè)。認識到這(zhè)一點是非常關鍵的(de)，因爲我們可(kě)以使用(yòng)股票(piào)和(hé)期權來(lái)構建一個(gè)投資組合把這(zhè)個(gè)布朗運動完全幹掉。考慮下(xià)面這(zhè)個(gè)投資組合：

該組合做(zuò)空 1 份期權，并做(zuò)多(duō) ∂C/∂S 份股票(piào)。将期權和(hé)股票(piào)的(de)權重帶入 ΔC 和(hé) ΔS 可(kě)以很容易的(de)驗證，布朗運動 ΔB 被完美(měi)的(de)對(duì)沖掉了(le)。這(zhè)種構建投資組合以消除随機性的(de)方法稱爲 Delta 對(duì)沖。用(yòng) P 表示該投資組合的(de)價值，則它在時(shí)間 Δt 内的(de)變化(huà)爲：

不出意外，ΔB 不存在于 ΔP 的(de)表達式中，它僅有一個(gè)時(shí)間項。換句話(huà)說，通(tōng)過賣出 1 份期權并同時(shí)買入 ∂C/∂S 份股票(piào)，我們在 Δt 内完美(měi)的(de)消除了(le)任何風險，構建了(le)一個(gè)無風險的(de)投資組合。在不存在無風險套利的(de)市場(chǎng)中，該投資組合在 Δt 内的(de)收益率必須等于無風險收益率 r，即 ΔP = rPΔt。将 ΔP 和(hé) P = -C + (∂C/∂S)S 帶入該式并進過簡單的(de)代數運算(suàn)就推導出：

這(zhè)便是大(dà)名鼎鼎的(de) Black-Scholes 微分(fēn)方程。由于我們通(tōng)過 Delta 對(duì)沖消除了(le)随機性，該方程中沒有任何随機變量，所以它是一個(gè)一般的(de)（偏）微分(fēn)方程，而非随機微分(fēn)方程。求解這(zhè)個(gè)微分(fēn)方程需要給定的(de)邊界條件。對(duì)于歐式看漲期權，它的(de)邊界條件爲當時(shí)間 t = T（行權時(shí)刻）時(shí)，期權的(de)價格 C 必須滿足 C = max(S(T) - K, 0)，這(zhè)裏 K 是行權價格。

最後引用(yòng)衍生品研究領域的(de)著名學者約翰 • 赫爾（John C. Hull）在其著作 Options, Futures, and Other Derivatives 中的(de)一段話(huà)來(lái)總結 BS 微分(fēn)方程的(de)推導過程：

我們之所以可(kě)以建立無風險交易組合是由于股票(piào)價格與期權價格均受同一種不定性的(de)影(yǐng)響：股票(piào)價格的(de)變動。在任意一段短時(shí)期内，衍生産品的(de)價格與股票(piào)價格有完美(měi)的(de)相關性；在建立了(le)一個(gè)适當的(de)股票(piào)與期權的(de)組合後，由股票(piào)所帶來(lái)的(de)盈虧總是可(kě)以抵消由期權所帶來(lái)的(de)盈虧。這(zhè)樣一來(lái)，交易組合在一個(gè)短時(shí)間内的(de)價值變化(huà)也(yě)就成爲已知而沒有不确定性。

5 風險中性定價

其實，使用(yòng)給定的(de)邊界條件求解 BS 微分(fēn)方程就可(kě)以得(de)到歐式看漲期權的(de)價格 C。然而，在衍生品的(de)定價理(lǐ)論中還(hái)有一個(gè)非常重要的(de)方法怎麽強調都不爲過，這(zhè)就是風險中性定價理(lǐ)論（Risk-neutral valuation）。使用(yòng)風險中性定價可(kě)以繞過求解 BS 微分(fēn)方程，更加方便的(de)求出 C。

僅僅看到這(zhè)裏也(yě)許你會誤解：既然不用(yòng)求解BS微分(fēn)方程，那麽費那麽大(dà)力氣推導它幹什(shén)麽？然而，風險中性定價理(lǐ)論恰恰來(lái)自 BS 微分(fēn)方程中的(de)一個(gè)關鍵性質：

BS 微分(fēn)方程不涉及任何受投資者風險偏好影(yǐng)響的(de)變量，在方程中出現的(de)變量包括股票(piào)的(de)當前價格、時(shí)間、股票(piào)價格波動率和(hé)無風險利率，而它們均與風險選擇無關。

從 BS 微分(fēn)方程可(kě)知，标的(de)股票(piào)的(de)期望收益率 μ 沒有出現在方程中。顯然，μ 與投資者的(de)風險偏好有關：投資者對(duì)風險的(de)厭惡程度越高(gāo)，對(duì)任何股票(piào)，相應的(de) μ 也(yě)會越高(gāo)。可(kě)喜的(de)是在采用(yòng) Delta 對(duì)沖構投資組合并推導 BS 微分(fēn)方程時(shí)，μ 也(yě)正好消失了(le)！我們通(tōng)過 Delta 對(duì)沖想要幹掉布朗運動，結果發現不僅布朗運動被幹掉了(le)，連 μ 也(yě)一起被拿下(xià)了(le)，這(zhè)真是一個(gè) happy accident！既然風險偏好在方程中不出現，那麽意味著(zhe)它的(de)任何取值都不會影(yǐng)響方程的(de)解。因此，在計算(suàn) C 時(shí)，我們可(kě)以使用(yòng)任意的(de)風險偏好，那麽顯然我們想要一個(gè)最簡單的(de)，即假設所有的(de)投資者都是風險中性的(de)。

對(duì)于任何衍生品定價來(lái)說，我們無外乎需要知道以下(xià)兩點：

1. 在到期（行權日）時(shí)它的(de)期望價格。由于衍生品的(de)價格是标的(de)價格的(de)函數，這(zhè)顯然和(hé)标的(de)投資品的(de)收益率參數 μ 有關。

2. 我們需要根據衍生品在行權日的(de)價格推算(suàn)出在當前時(shí)刻該衍生品的(de)價格，這(zhè)意味著(zhe)必須知道适合于該衍生品的(de)折現率。

不幸的(de)是，在現實世界中，這(zhè)兩個(gè)參數都很難被準确的(de)估計。因此能夠假設風險中性對(duì)于衍生品定價至關重要。正如約翰 • 赫爾所論述的(de)那樣：

在每一個(gè)投資者都是風險中性的(de)世界裏，所有投資的(de)回報率期望均爲無風險利率 r，原因是對(duì)風險中性的(de)投資者而言，不需要額外的(de)回報而使他(tā)們承受風險。另外，在一個(gè)風險中性世界裏，任何現金流的(de)現值都可(kě)以通(tōng)過對(duì)其期望值以無風險利率貼現來(lái)得(de)到。因此，在假設世界是風險中性時(shí)能夠大(dà)大(dà)地簡化(huà)對(duì)衍生産品的(de)分(fēn)析。

利用(yòng)風險中性定價原理(lǐ)對(duì)衍生品定價的(de)過程如下(xià)：

風險中性定價是獲得(de)期權定價公式的(de)一個(gè)人(rén)爲工具，但它所得(de)到的(de)解不僅在這(zhè)個(gè)虛拟的(de)風險中性世界中成立，而且在所有世界裏（自然也(yě)就包括真是世界）也(yě)都是成立的(de)。當我們從風險中性世界換到風險厭惡世界時(shí)，兩件事會發生：股票(piào)價格變動的(de)增長(cháng)率期望以及對(duì)衍生産品收益所必需使用(yòng)的(de)貼現率都将會變化(huà)，而這(zhè)兩種變化(huà)剛好相互抵消。下(xià)面介紹如何使用(yòng)風險中性定價理(lǐ)論求解歐式看漲期權的(de)價格 C。

6 Black-Scholes 期權定價公式

歐式看漲期權在行權日 T 的(de)期望價值爲 E[max(S(T) – K, 0)]，其中 S(T) 爲股票(piào)在 T 時(shí)刻的(de)價格，K 爲行權價。股價 S 滿足對(duì)數正态分(fēn)布，在風險中性定價理(lǐ)論下(xià)，S 的(de)期望收益率爲無風險收益率 r，且期權的(de)折現率也(yě)等于無風險收益率 r。因此，期權在當前時(shí)刻的(de)價格 C 爲：

根據對(duì)數正态分(fēn)布的(de)性質可(kě)以方便的(de)計算(suàn)出 E[max(S(T) – K, 0)]，從而得(de)到著名的(de) BS 期權定價公式（同時(shí)給出看漲期權價格 C 和(hé)看跌期權價格 P）：

根據公式并利用(yòng)計算(suàn)機，隻要輸入五個(gè)變量——當前股價 S(0)、行權價格 K，行權日距現在的(de)時(shí)間（按年計算(suàn)）T，無風險收益率 r，以及标的(de)股票(piào)的(de)年收益率的(de)标準差 σ —— 就可(kě)以計算(suàn)出歐式看漲（看跌）期權的(de)理(lǐ)論價格，這(zhè)無疑非常方便。然而我們需要了(le)解定價公式背後的(de)含義。

對(duì)于任何一個(gè)期權，在定價時(shí)有兩個(gè)不确定性需要考慮：

這(zhè)兩個(gè)不确定性恰恰就對(duì)應著(zhe)由 BS 定價公式中的(de) N(d_1) 和(hé) N(d_2)。以看漲期權爲例來(lái)解釋這(zhè)一點。在 BS 公式中，N 代表了(le)标準正态分(fēn)布的(de)累積密度函數，因此 N(d_1) 和(hé) N(d_2) 就代表兩個(gè)概率。其中，N(d_2) 正是在風險中性世界中期權被行權的(de)概率，即 prob(S(T) > K)。因此 C 公式中的(de)第二項 Ke^(-rT)N(d_2) 就是在當前時(shí)點、考慮了(le)行權概率後的(de)行權費的(de)期望（即爲了(le)在 T 購(gòu)買股票(piào)所需的(de)期望成本）。

至于 N(d_1)，對(duì)于它的(de)理(lǐ)解遠(yuǎn)沒有 N(d_2) 直觀。先抛開 N(d_1) 不說，而來(lái)看看 C 公式中的(de)第一項。由于第二項代表著(zhe)期望成本，那麽第一項必然代表著(zhe)行權得(de)到股票(piào)的(de)期望收益。由于隻有 S(T) 大(dà)于 K 才會行權，因此在行權的(de)條件下(xià)，股票(piào)在行權時(shí)的(de)期望價值是一個(gè)條件期望，即 E[S(T) | S(T) > K]。用(yòng)這(zhè)個(gè)條件期望乘以行權的(de)概率 N(d_2) 再把它折現到今天（乘以 e^(-rT)）就應該是 C 公式中的(de)第一項。因此有：

将 S(0) 替換爲 e^(-rT)E[S(T)] 并帶入上式可(kě)知：

由于 E[S(T) | S(T) > K] > E[S(T)]，因此 N(d_1) > N(d_2)（這(zhè)從 d_1 大(dà)于 d_2 且 N 是單調增函數也(yě)可(kě)以驗證）。根據這(zhè)個(gè)關系，我們可(kě)以把 N(d_1) 理(lǐ)解爲風險中性世界中、按照(zhào)股票(piào)價格加權的(de)行權概率。這(zhè)是因爲和(hé)固定的(de)行權成本 K 不同（K 是獨立于股價 S 的(de)），收益和(hé)股價之間不是獨立的(de)。N(d_1) 在數學上還(hái)有另外的(de)解釋，它是“以股票(piào)波動率 σ 爲市場(chǎng)風險定價，并在以股票(piào)爲計價單位時(shí)，期權被行權的(de)概率”。如果你覺著(zhe)這(zhè)句話(huà)是天書(shū)也(yě)沒有任何問題，因爲要解釋它需要涉及到測度變換、等價鞅、以及計價單位變換等高(gāo)深的(de)數學知識。這(zhè)些顯然超出本文的(de)範疇。

如果我們使用(yòng) C 的(de)公式對(duì) S 求偏導數，那麽不難發現 N(d_1) 恰恰等于 ∂C/∂S。因此在現實中，投資者把 N(d_1) 理(lǐ)解爲看歐式漲期權價格 C 對(duì)标的(de)股票(piào)價格 S 的(de)變化(huà)的(de)敏感程度。

看到這(zhè)裏，也(yě)許你會發問：BS 定價公式僅僅給出了(le)一個(gè)基于各種嚴格假設的(de)理(lǐ)論價格，它在現實中到底有沒有用(yòng)？真的(de)會有人(rén)因爲理(lǐ)論價格和(hé)實際交易價格不同來(lái)構建策略并且賺錢嗎？BS 定價公式的(de)核心價值在于它構建了(le)一個(gè)數學模型，以此我們可(kě)以求出期權的(de)各種風險敞口，這(zhè)對(duì)于将期權（或任何衍生品）作爲配置資産的(de)投資者至關重要。由 BS 公式出發可(kě)以方便的(de)求出期權價格對(duì)标的(de)資産、時(shí)間、利率、波動率的(de)偏導數，從而确定期權在這(zhè)些因素上的(de)風險敞口。在投資中，常用(yòng)的(de)風險敞口有五類（通(tōng)常用(yòng)希臘字母來(lái)表示），它們是：

我們會在後續的(de)文章(zhāng)中進一步介紹這(zhè)些風險敞口。除此之外，BS 公式的(de)另一個(gè)核心作用(yòng)是計算(suàn)标的(de)資産的(de)隐含波動率。在 BS 公式中，除去 σ 之外的(de)輸入參數的(de)取值都比較确定，唯有 σ 可(kě)能會随著(zhe)使用(yòng)者的(de)不同而不同。根據期權的(de)實際交易價格，可(kě)以利用(yòng) BS 公式反推出标的(de)波動率 σ，稱爲隐含波動率，這(zhè)往往代表著(zhe)市場(chǎng)對(duì)于标的(de)資産風險的(de)普遍觀點。隐含波動率最有名的(de)應用(yòng)大(dà)概是芝加哥(gē)交易所針對(duì)标普 500 指數，利用(yòng)未來(lái) 30 天的(de)看漲和(hé)看跌期權計算(suàn)的(de) VIX 指标，又稱爲恐慌指數。它被投資者廣泛參考。

7 結語

和(hé)本系列前篇一樣，再次恭喜你看到這(zhè)裏……下(xià)面，讓我們來(lái)簡單總結一下(xià)本文都說了(le)點啥。本文首先定義了(le)伊藤過程，并給出了(le)伊藤引理(lǐ)的(de)一般形式，通(tōng)過它可(kě)以方便的(de)寫出伊藤過程的(de)函數的(de)随機微分(fēn)方程。伊藤引理(lǐ)說明(míng)伊藤過程的(de)函數也(yě)是一個(gè)伊藤過程，且它的(de)随機性和(hé)原始的(de)伊藤過程來(lái)自同一個(gè)布朗運動，這(zhè)對(duì)于推演 BS 微分(fēn)方程至關重要。

利用(yòng)伊藤引理(lǐ)，可(kě)以很容易的(de)求解幾何布朗運動，從而得(de)到股價的(de)描述模型。在幾何布朗運動的(de)假設下(xià)，股價滿足對(duì)數正态分(fēn)布，這(zhè)也(yě)是 BS 定價模型的(de)假設之一。在股價模型中，年收益率期望和(hé)連續複利收益率期望是兩個(gè)不同的(de)概念，它們的(de)區(qū)别相當于收益率序列的(de)算(suàn)數平均值和(hé)幾何平均值的(de)區(qū)别。

最後利用(yòng) Delta 對(duì)沖，利用(yòng)标的(de)股票(piào)和(hé)期權構建投資組合從而完美(měi)的(de)消除了(le)布朗運動的(de)随機性，從而得(de)到了(le) BS 微分(fēn)方程，這(zhè)是衍生品定價的(de)基礎。此外，在 Delta 對(duì)沖下(xià)，和(hé)投資者風險偏好相關的(de)參數 μ 也(yě)從 BS 方程中消失了(le)。由此引出了(le)衍生品定價中的(de)一個(gè)非常重要的(de)方法：風險中性定價理(lǐ)論。根據該理(lǐ)論求出了(le)歐式期權的(de)價格，并以看漲期權爲例解釋了(le)價格表達式中每一項的(de)業務含義。文章(zhāng)最後介紹了(le) BS 公式在實際投資中的(de)核心作用(yòng)：它可(kě)以量化(huà)期權的(de)各種風險敞口，這(zhè)對(duì)于配置期權的(de)投資者至關重要。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。