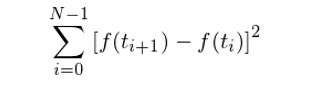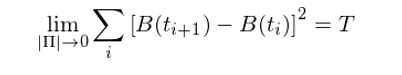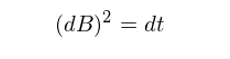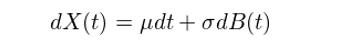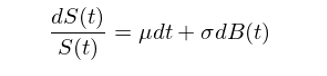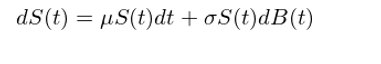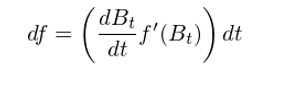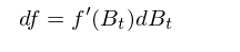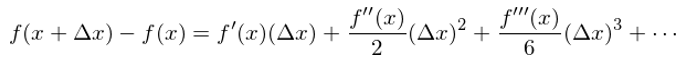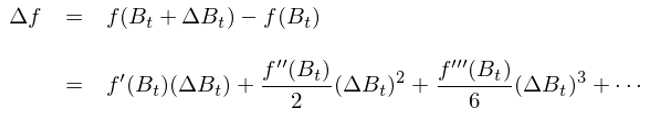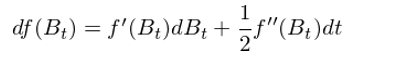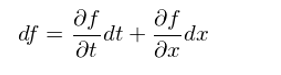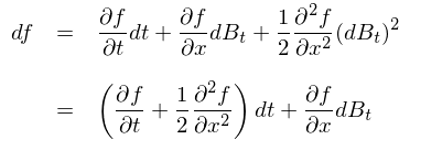布朗運動、伊藤引理(lǐ)、BS 公式（前篇）

作者：石川

摘要：随機分(fēn)析是近代金融數學發展的(de)基礎。本文介紹布朗運動及其重要性質并引出伊藤引理(lǐ)的(de)最基本形式。

1 引言

對(duì)量化(huà)投資感興趣的(de)人(rén)大(dà)概都聽(tīng)說過的(de) Black-Scholes 期權定價公式（又稱 Black-Scholes-Merton 公式，下(xià)稱 BS 公式）。它大(dà)概是将數學中随機過程（stochastic process）的(de)概念運用(yòng)到實際金融産品中的(de)最著名的(de)一個(gè)例子。美(měi)國華爾街(jiē)的(de) Quant 職位面試中更是無一例外的(de)會問到 BS 公式及其引申出來(lái)的(de)相關問題，足見其地位。然而黑(hēi)天鵝之父納西姆·塔雷伯（Nassim Nicholas Taleb，以《黑(hēi)天鵝效應》一書(shū)聞名于世）卻對(duì)它嗤之以鼻，更是寫過一篇題爲 Why we have never used the Black-Scholes-Merton option pricing formula（爲什(shén)麽我們從來(lái)不用(yòng)BS期權定價公式）來(lái)抨擊它。

誠然，BS 公式在投資實踐中能夠起到多(duō)大(dà)的(de)作用(yòng)見仁見智。但我們想說的(de)是，BS 公式僅僅是一結果，是随機分(fēn)析（stochastic calculus）經過嚴謹的(de)層層推演得(de)到的(de)産物(wù)。透過現象看本質，它背後蘊含著(zhe)強大(dà)的(de)數學體系，使得(de)我們可(kě)以運用(yòng)随機過程對(duì)股價、期權價格以及其他(tā)衍生品價格進行量化(huà)建模。掌握這(zhè)套分(fēn)析體系對(duì)于有志于在量化(huà)投資領域有所建樹的(de)人(rén)來(lái)說十分(fēn)必要。

想要摸清楚這(zhè)套随機分(fēn)析體系并不容易。如果你在搜索引擎上查詢 BS 公式的(de)推導體系，一定會看到諸如“布朗運動”、“伊藤引理(lǐ)”、“随機微分(fēn)方程”這(zhè)些概念。它們都是這(zhè)套分(fēn)析體系中必不可(kě)少的(de)組成部分(fēn)，環環相扣，在随機分(fēn)析的(de)大(dà)框架下(xià)完美(měi)的(de)聯系在一起。熟悉這(zhè)套分(fēn)析框架的(de)人(rén)可(kě)以充分(fēn)的(de)感受到這(zhè)些基本模塊無縫的(de)組合在一起所展示出來(lái)的(de)數學的(de)魅力。而對(duì)于不熟悉它的(de)人(rén)來(lái)說，這(zhè)之中每一個(gè)概念都可(kě)能仿佛天書(shū)一般；即便是具有高(gāo)等數學知識的(de)人(rén)，想要很快(kuài)的(de)梳理(lǐ)出它們之間的(de)邏輯聯系也(yě)并不容易。

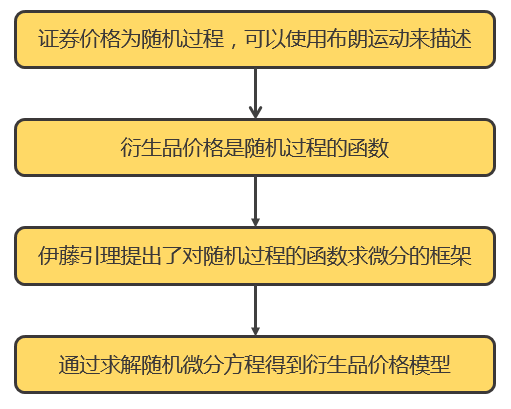
簡單的(de)說，（标準）布朗運動是一種最簡單的(de)連續随機過程，它是描述證券價格随機性的(de)基本模型。而對(duì)于期權或其他(tā)衍生品這(zhè)些金融工具，它們的(de)價格是相關證券資産價格的(de)函數。因此可(kě)以說證券價格是一個(gè)随機過程，而衍生品價格是該随機過程的(de)函數。伊藤引理(lǐ)提供了(le)對(duì)随機過程的(de)函數做(zuò)微分(fēn)的(de)框架；這(zhè)對(duì)于衍生品的(de)定價意義非凡（在此之前，人(rén)們是不知道如何對(duì)随機過程的(de)函數做(zuò)微分(fēn)的(de)）。通(tōng)過伊藤引理(lǐ)，可(kě)以寫出金融衍生品價格的(de)随機微分(fēn)方程，通(tōng)過對(duì)其求解便可(kě)以得(de)到衍生品價格的(de)模型。BS 公式就是一個(gè)最簡單的(de)例子。

鑒于随機分(fēn)析的(de)重要性，我們決定用(yòng)兩期的(de)量化(huà)核武研究專題來(lái)介紹它。行文會力争深入淺出，但也(yě)會包括必要的(de)數學推導（這(zhè)對(duì)理(lǐ)解相關概念至關重要）。作爲前篇，本文介紹布朗運動及其重要性質，同時(shí)指出使用(yòng)幾何布朗運動描述股價的(de)合理(lǐ)性，最後會引出伊藤引理(lǐ)的(de)最基本形式。此外，爲避免将本文寫成偏數學的(de)技術性文章(zhāng)，文中也(yě)花了(le)很多(duō)篇幅揭示布朗運動的(de)性質對(duì)于股票(piào)投資的(de)重要含義。下(xià)一篇會進一步介紹伊藤引理(lǐ)的(de)一般形式，并用(yòng)它求解幾何布朗運動，最後推導 BS 模型以及介紹 BS 公式（注：BS 模型是一個(gè)偏微分(fēn)方程，而 BS 公式是一個(gè)解析形式的(de)表達式）。希望通(tōng)過這(zhè)兩篇文章(zhāng)的(de)介紹，讓感興趣的(de)讀者直觀的(de)理(lǐ)解這(zhè)個(gè)分(fēn)析框架，并且能夠感受到各個(gè)模塊無縫地組合到一起而最終得(de)到一個(gè)優雅的(de)定價公式的(de)數學之美(měi)。

2 布朗運動的(de)發展和(hé)定義

1827 年英國植物(wù)學家羅伯特 • 布朗（Robert Brown）在使用(yòng)顯微鏡觀察水(shuǐ)中花粉微粒運動時(shí)發現了(le)微粒的(de)無規則運動，但是當時(shí)并不能從物(wù)理(lǐ)學角度上很好的(de)解釋其成因。1905 年，愛(ài)因斯坦詳細解釋了(le)布朗發現的(de)這(zhè)種運動：微粒的(de)無規則運動是由水(shuǐ)分(fēn)子的(de)撞擊形成的(de)。從那以後，布朗運動在物(wù)理(lǐ)學上的(de)發展日臻完善。相比之下(xià)，數學上對(duì)布朗運動的(de)描述發展的(de)要慢(màn)一些。嚴謹的(de)定義并描述布朗運動由諾伯特 • 維納（Norbert Wiener）在 1918 年提出，因此布朗運動（Brownian motion）又稱爲維納過程（Wiener process）。

布朗運動是一個(gè)連續随機過程。一個(gè)随機過程是定義在時(shí)域或者空間域上的(de)依次發生的(de)一系列随機變量的(de)集合。以時(shí)域爲例，如果這(zhè)些随機變量在整個(gè)實數時(shí)域上都有定義，那麽這(zhè)個(gè)随機過程爲連續随機過程；反之，如果這(zhè)些随機變量僅僅在時(shí)域上一些離散的(de)點有定義，那麽該随機過程爲離散随機過程。

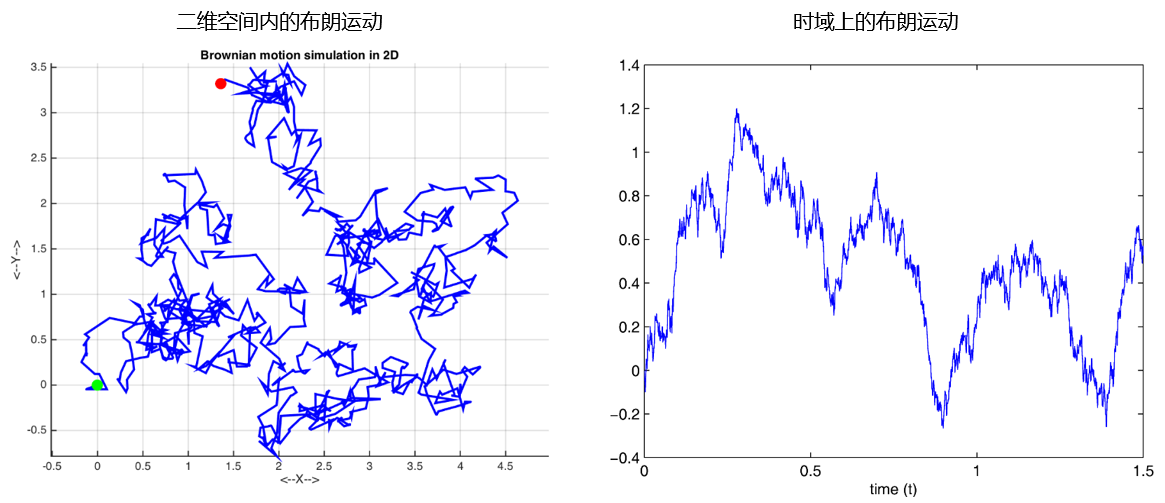
上面兩張圖分(fēn)别爲二維空間内和(hé)時(shí)域上的(de)（一維）布朗運動軌迹。時(shí)域上的(de)這(zhè)個(gè)一維布朗運動走勢和(hé)股票(piào)價格曲線的(de)走勢看著(zhe)非常相似，這(zhè)便引起了(le)人(rén)們利用(yòng)它來(lái)描述股票(piào)價格走勢的(de)興趣。事實上，早在 1900 年一個(gè)名叫路易斯 • 巴舍利耶（Louis Bachelier）的(de)法國小夥就在他(tā)的(de)博士論文《投機理(lǐ)論》（Théorie de la spéculation）中使用(yòng)布朗運動分(fēn)析股票(piào)和(hé)期權的(de)價格。說幾句題外話(huà)，這(zhè)個(gè)法國小夥的(de)研究比愛(ài)因斯坦給出布朗運動的(de)物(wù)理(lǐ)解釋還(hái)要早 5 年！比維納提出布朗運動的(de)數學定義更是早了(le) 18 年！據說由于他(tā)把數學應用(yòng)到了(le)在當時(shí)比較未知的(de)領域——股票(piào)研究——他(tā)在答(dá)辯時(shí)的(de)反響并不好。但是現在看來(lái)，這(zhè)個(gè)小夥才是研究金融數學的(de)先驅！

下(xià)文會進一步解釋爲什(shén)麽使用(yòng)布朗運動來(lái)描述股價運動是合适的(de)。現在，首先給出（一維）标準布朗運動（即維納過程）的(de)定義。如果一個(gè)定義在非負實數（時(shí)域）t 上的(de)連續随機過程 ｛B(t), t ≥ 0｝ 滿足如下(xià)三個(gè)性質：

1. B(0) = 0；

2. 平穩性：對(duì)于所有的(de) 0 < s < t，增量 B(t) – B(s) 符合均值爲 0，方差爲 t - s 的(de)正态分(fēn)布；

3. 獨立增量性：對(duì)于不重疊的(de)區(qū)間 [s_i, t_i]，随機變量 B(t_i) – B(s_i) 之間是相互獨立的(de)；

則 B(t) 是一個(gè)标準的(de)布朗運動。

該定義的(de)白話(huà)解釋是：标準布朗運動在 t = 0 時(shí)的(de)位置爲 0。在任何有限時(shí)間區(qū)間 Δt 内，布朗運動的(de)變化(huà)滿足均值爲 0 方差爲 Δt 的(de)正态分(fēn)布 N(0, Δt)，其方差随時(shí)間區(qū)間的(de)長(cháng)度線性增加。獨立增量性的(de)意思是布朗運動在任何一個(gè)時(shí)間區(qū)間内的(de)變化(huà)與其他(tā)與之不重疊的(de)時(shí)間區(qū)間内的(de)變化(huà)無關。由該性質可(kě)知，布朗運動是一個(gè)馬爾科夫過程（Markov process），即該過程在任意 t 時(shí)刻之後的(de)位置僅和(hé) t 時(shí)刻的(de)位置有關，與 t 之前的(de)曆史軌迹無關。換句話(huà)說，該過程的(de)當前值就包含了(le)對(duì)其未來(lái)做(zuò)預測所需的(de)全部信息。

3 布朗運動的(de)性質

标準布朗運動有很多(duō)有意思的(de)性質，它們對(duì)于使用(yòng)布朗運動及其變化(huà)來(lái)描述股票(piào)價格有非常重要的(de)含義。這(zhè)些性質包括：

1. 它的(de)軌迹會頻(pín)繁的(de)穿越時(shí)間軸 t（在時(shí)間軸上下(xià)往複波動）；

2. 在任意時(shí)刻 t，它的(de)位置 B(t) 不會偏離正負一個(gè)标準差太遠(yuǎn)；

3. 令 M(t) 爲 0 到 t 時(shí)刻内的(de)布朗運動 B(t) 所能到達的(de)最大(dà)值，即 M(t) = max_｛0≤s≤t｝B(t)，則“ M(t) 不小于任意給定阈值 a 的(de)概率”等于“ B(t) 不小于任意給定阈值 a 的(de)概率的(de)兩倍”，即 Prob(M(t) ≥ a) = 2Prob(B(t) ≥ a)；

4. 布朗運動雖然連續，但是它處處不可(kě)微分(fēn)（這(zhè)是非常關鍵的(de)一個(gè)性質）。

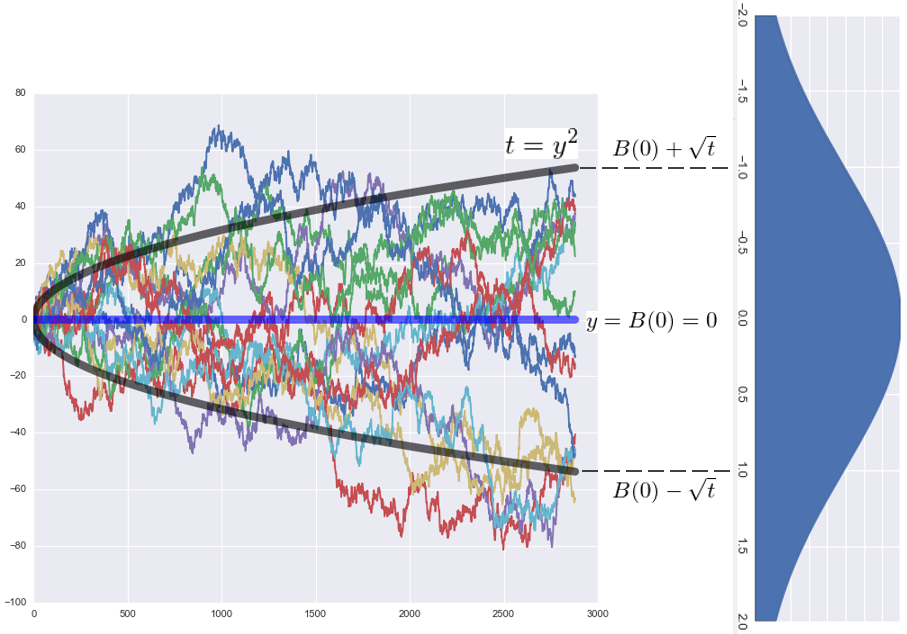
首先來(lái)解釋前兩個(gè)性質。下(xià)圖給出了(le) 0 到 t 時(shí)刻内 15 條标準布朗運動的(de)樣本軌迹。盡管它們呈現出各自的(de)随機性，但基本上每條軌迹都往複的(de)穿越 y=0 這(zhè)條線（即時(shí)間軸 t），僅有個(gè)别的(de)樣本軌迹在 y=0 的(de)單邊震蕩（對(duì)于這(zhè)些軌迹，随著(zhe) t 的(de)增加，它們也(yě)一定會穿越 t 軸的(de)）。此外，黑(hēi)色的(de)抛物(wù)線是方程 t=y^2 的(de)曲線。可(kě)以看到，雖然每條樣本軌迹都有足夠的(de)随機性，但是在 t 時(shí)刻，它們都不會偏離這(zhè)條抛物(wù)線上的(de)點 B(0) ± 根号 t 太遠(yuǎn)。下(xià)圖右側是 t 時(shí)刻均值爲 0 方差爲 t 的(de)正态分(fēn)布的(de)概率密度函數。這(zhè)條抛物(wù)線的(de)範圍對(duì)應的(de)就是該正态分(fēn)布正負一個(gè)标準差之内的(de)變化(huà)。

假設我們使用(yòng)布朗運動來(lái)描述股價日内的(de)高(gāo)頻(pín)走勢（下(xià)文會說明(míng)更加準确的(de)描述股價的(de)模型是帶漂移項的(de)幾何布朗運動，但在此作爲一個(gè)簡單的(de)例子，假設使用(yòng)布朗運動來(lái)描述股價），這(zhè)兩個(gè)性質意味著(zhe)股價很大(dà)概率會在開盤價上下(xià)波動，而非一直維持在開盤價上方或者下(xià)方；此外，随著(zhe)交易時(shí)間的(de)推移，在t時(shí)刻股票(piào)的(de)價格不會偏離“開盤價 ± 根号 t × 價格波動的(de)标準差”太遠(yuǎn)。這(zhè)些性質對(duì)于想根據日内高(gāo)頻(pín)數據進行投機操作的(de)人(rén)非常重要。之前的(de)文章(zhāng)《錯過開盤，不一定是“過錯”》也(yě)對(duì)此有一些實證，它指出日内股價在很大(dà)概率上會再次到達開盤區(qū)間内出現的(de)價格，而非單邊震蕩。

第三條性質給出了(le)量化(huà) t 時(shí)刻内布朗運動極值的(de)概率模型。由于 B(t) 是滿足均值爲 0 方差爲 t 的(de)正态分(fēn)布，因此 Prob(M(t) ≥ a) = 2Prob(B(t) ≥ a) 這(zhè)個(gè)結果可(kě)以讓我們非常容易的(de)求出 Prob(M(t) ≥ a) 的(de)概率，即

其中 Φ 是标準正态分(fēn)布的(de)累積分(fēn)布函數。上式可(kě)以通(tōng)過布朗運動的(de)馬爾科夫性和(hé)反射性證明(míng)，在這(zhè)裏不在贅述。同樣的(de)，如果令 m(t) 爲 0 到 t 時(shí)刻内的(de)布朗運動 B(t) 所能到達的(de)最小值，即 m(t) = min_｛0≤s≤t｝B(t)，則再次利用(yòng)反射性不難推導出 B(t) 的(de)最小值低于給定阈值 a 的(de)概率：

如果用(yòng)布朗運動來(lái)描述股價，那麽上述結果可(kě)以量化(huà)股價極值的(de)概率分(fēn)布。這(zhè)對(duì)風控以及在買賣股票(piào)時(shí)計算(suàn)合理(lǐ)的(de)限價單價格都是很有幫助的(de)。

最後一個(gè)性質是布朗運動作爲随機過程的(de)一個(gè)至關重要的(de)性質，即它雖然連續，但是它處處不可(kě)微分(fēn)（這(zhè)一點可(kě)以通(tōng)過利用(yòng)中值定理(lǐ)以及性質三的(de)結論，使用(yòng)反證法來(lái)證明(míng)）。這(zhè)從直觀上非常好理(lǐ)解。再來(lái)看看上面那 15 條布朗運動的(de)樣本軌迹，每一條都一直在上下(xià)波動、充分(fēn)地展示了(le)其随機性。顯然，布朗運動的(de)軌迹和(hé)我們熟悉的(de)任何連續、平滑的(de)方程軌迹完全不同。不可(kě)微分(fēn)性意味著(zhe)古典微積分(fēn)（classical calculus）中的(de)分(fēn)析手段在布朗運動面前黯然失效。這(zhè)在當時(shí)無疑是個(gè)令人(rén)沮喪的(de)消息。因爲人(rén)們好不容易找到了(le)一個(gè)簡單實用(yòng)的(de)随機過程，但卻缺少進一步研究它的(de)手段。然而，這(zhè)一切都随著(zhe)伊藤微積分(fēn)（Itō calculus）的(de)出現而迎刃而解。毫不誇張的(de)說，伊藤微積分(fēn)奠定了(le)現代金融數學的(de)基礎。

4 二次變分(fēn)

考慮時(shí)間區(qū)間 [0, T] 和(hé)該區(qū)間内的(de)一個(gè)劃分(fēn) Π = ｛0 = t_0 < t_1 < t_2 < … < t_N = T｝，則對(duì)于任意一個(gè)連續函數 f(t)，它的(de)二次變分(fēn)（quadratic variation）定義爲：

對(duì)于一個(gè)連續且在 0 到 T 内處處可(kě)微的(de)函數 f(t)，通(tōng)過利用(yòng)古典微積分(fēn)中的(de)中值定理(lǐ)很容易得(de)到如下(xià)不等式：

這(zhè)說明(míng)随著(zhe)對(duì)時(shí)間區(qū)間 [0, T] 越來(lái)越細的(de)劃分(fēn)，即 max_i｛t_[i+1] - t_i｝趨于0，這(zhè)個(gè)連續且處處可(kě)微的(de)函數 f(t) 的(de)二次變分(fēn)爲 0。那麽，如果将 f(t) 換爲布朗運動 B(t) 會怎樣呢(ne)？不要忘了(le)，它雖然連續，但是處處不可(kě)微。關于 B(t) 的(de)二次變分(fēn)有如下(xià)定理(lǐ)：随著(zhe)對(duì)時(shí)間區(qū)間 [0, T] 越來(lái)越細的(de)劃分(fēn)，即 max_i｛t_[i+1] - t_i｝趨于0，B(t) 的(de)二次變分(fēn)等于 T，即

其中 |Π| = max_i｛t_[i+1] - t_i｝。

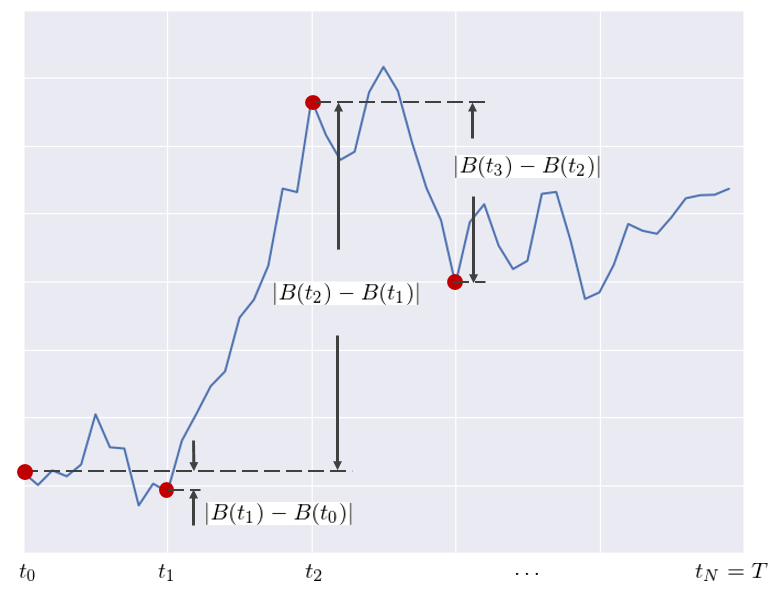
布朗運動的(de)這(zhè)個(gè)性質可(kě)以通(tōng)過獨立同分(fēn)布随機變量的(de)大(dà)數定理(lǐ)證明(míng)。對(duì)它的(de)白話(huà)說明(míng)是，作爲一個(gè)随機過程，布朗運動的(de)二次變分(fēn)是 T 而不是 0（與之相對(duì)應的(de)是，連續可(kě)微函數的(de)二次變分(fēn)爲 0）。如何理(lǐ)解它呢(ne)？考慮下(xià)面這(zhè)個(gè)示意圖。其中藍色曲線爲布朗運動的(de)軌迹，紅點爲時(shí)間劃分(fēn)點對(duì)應的(de)該軌迹的(de)位移。顯然，(B(t_[i+1]) – B(t_i))^2 爲任意相鄰兩個(gè)時(shí)間點的(de)位移差的(de)平方。二次變分(fēn)就是這(zhè)些逐段位移差的(de)累積平方和(hé)。

對(duì)于一個(gè)普通(tōng)的(de)連續可(kě)微函數，随著(zhe)對(duì)區(qū)間T越來(lái)越細的(de)劃分(fēn)，它的(de)二次變分(fēn)趨于 0。然而對(duì)于布朗運動，其非 0 的(de)二次變分(fēn)說明(míng)随機性使得(de)它的(de)波動太頻(pín)繁，以至于不管我們如何細分(fēn)區(qū)間 T、得(de)到多(duō)麽微小的(de)劃分(fēn)區(qū)間，這(zhè)些微小區(qū)間上的(de)位移差的(de)平方逐段累加起來(lái)的(de)總和(hé)都不會消失（即二次變分(fēn)不爲 0），而是等于這(zhè)個(gè)區(qū)間的(de)長(cháng)度 T。這(zhè)是布朗運動的(de)一個(gè)非常重要的(de)性質。布朗運動的(de)二次變分(fēn)公式也(yě)可(kě)以寫作如下(xià)所示的(de)無窮小量（infinitesimal difference）的(de)形式：

碼了(le)這(zhè)麽多(duō)的(de)字來(lái)解釋二次變分(fēn)，當然不是爲了(le)用(yòng)它說明(míng)布朗運動的(de)波動太頻(pín)繁；在本文第六節可(kě)以看到，二次變分(fēn)在推導伊藤引理(lǐ)時(shí)有非常重要的(de)意義。

5 幾何布朗運動

前文介紹了(le)标準布朗運動，它在任意長(cháng)度爲 t 内的(de)分(fēn)布是均值爲 0 方差爲 t 的(de)正态分(fēn)布。現在，考慮給标準布朗運動加上一個(gè)僅和(hé)時(shí)間 t 有關的(de)漂移項 μt，以及一個(gè)尺度參數 σ，便得(de)到一個(gè)帶漂移的(de)布朗運動（Brownian motion with drift），記作 X(t) = μt + σB(t)。它在任意長(cháng)度 t 内的(de)分(fēn)布滿足均值爲 μt，方差爲 (σ^2)t 的(de)正态分(fēn)布。考慮無窮小量的(de)形式，上式寫作

這(zhè)是一個(gè)随機微分(fēn)方程（stochastic differential equation）。随機微分(fēn)方程是普通(tōng)微分(fēn)方程的(de)延伸，不同之處在于前者之中至少包括一項随機過程。注意，上式與布朗運動不可(kě)微并不矛盾。雖然 B(t) 處處不可(kě)微，但是 dB(t) 仍有明(míng)确的(de)含義，它表示布朗運動在一個(gè)無窮小的(de)時(shí)間間隔内的(de)變化(huà)。

即便是有了(le)帶漂移項和(hé)尺度參數的(de)布朗運動 X(t)，它仍然不是描述股價運動的(de)最佳選擇。這(zhè)是因爲 X(t)，或者 B(t)，的(de)取值随著(zhe)時(shí)間 t 的(de)變化(huà)可(kě)以是負數，但是股票(piào)的(de)價格顯然不能是負數。股價雖然不能是負數，但是股票(piào)的(de)收益率卻有正有負，因此 X(t) 可(kě)以被用(yòng)來(lái)描述收益率。

假設 S(t) 爲股票(piào)的(de)價格，則 dS(t) 爲股價在無窮小的(de)時(shí)間間隔内的(de)變化(huà)量，而 dS(t)/S(t) 就是這(zhè)段間隔内的(de)收益率，因此有

因此 S(t) 的(de)随機微分(fēn)方程爲：

滿足上述随機微分(fēn)方程的(de)股價 S(t) 是一個(gè)幾何布朗運動。人(rén)們喜歡使用(yòng)幾何布朗運動來(lái)描述股價的(de)原因是：

1. 正态分(fēn)布：經驗事實證明(míng)，股票(piào)價格的(de)連續複利收益率近似地服從正态分(fēn)布；

2. 馬爾科夫過程：由布朗運動的(de)性質可(kě)知，服從上述模型的(de)股票(piào)價格是一個(gè)馬爾科夫過程，即當前價格就包含了(le)對(duì)其未來(lái)做(zuò)預測所需的(de)全部信息，這(zhè)與弱有效市場(chǎng)假說相符；

3. 布朗運動在時(shí)間上處處不可(kě)微以及二次變分(fēn)不爲零的(de)性質符合股票(piào)收益率在時(shí)間上存在轉折尖點的(de)特征。

當然，爲了(le)使用(yòng) S(t) 對(duì)股價進行分(fēn)析，必須能夠求解上述随機微分(fēn)方程。這(zhè)需要用(yòng)到伊藤微積分(fēn)中的(de)相關内容。因此關于 S(t) 的(de)求解将會在本系列的(de)後篇中具體介紹。

在結束本節之前，再來(lái)看一個(gè)關于帶漂移項的(de)布朗運動的(de)有意思的(de)例子。考慮一個(gè)正實數 μ，令 X(t) = μt + B(t)。由于 B(t) 的(de)期望爲 0，因此 X(t) 的(de)期望爲 E[X(t)] = μt。我們好奇的(de)是，随著(zhe)時(shí)間 t 的(de)推移，X(t) 的(de)取值到底是由 μt 主宰還(hái)是由 B(t) 主宰。事實上，可(kě)以證明(míng)，X(t) 的(de)取值是由 μt 支配。對(duì)于任何給定的(de) ε，隻要時(shí)間 t 足夠長(cháng)，那麽可(kě)以證明(míng) X(t) 總會在 y = (μ – ε)t  和(hé) y = (μ + ε)t  之間！怎麽樣？有沒有從這(zhè)個(gè)例子中受到什(shén)麽啓發？它說明(míng)，如果我們堅信股市長(cháng)期來(lái)看有慢(màn)牛行情（μ > 0），那麽我們就應該欣然的(de)接受它的(de)任何（短期）波動而堅持持股（即忽略 B(t) 的(de)随機性造成的(de)擾動）。因爲長(cháng)期來(lái)看股價的(de)變化(huà)是由 μt 決定的(de)。我猜巴菲特一定是個(gè)數學家，他(tā)一定深谙此道，且通(tōng)過其價值投資體系使得(de)他(tā)的(de)投資組合有著(zhe)比美(měi)股指數更高(gāo)的(de) μ，因此獲得(de)了(le)長(cháng)期穩定的(de)超額收益。

6 伊藤引理(lǐ)

布朗運動爲人(rén)們研究股票(piào)價格提供了(le)基礎。然而，對(duì)于金融衍生品，它們的(de)價格是股票(piào)價格的(de)函數。令 f(B_t) 爲布朗運動 B_t 的(de)連續平滑函數，在金融數學領域的(de)一個(gè)重要的(de)分(fēn)析課題是研究在無窮小的(de)時(shí)間區(qū)間内 f 是如何變化(huà)的(de)，即 df 的(de)性質。由下(xià)文可(kě)知，由于布朗運動是不可(kě)微的(de)，古典微積分(fēn)對(duì)于求解 df 無能爲力，而日本數學家伊藤清（Itō Kiyoshi）提出了(le)與古典微積分(fēn)不同的(de)伊藤微積分(fēn)打開了(le)解決這(zhè)個(gè)問題的(de)大(dà)門，并爲随機分(fēn)析奠定了(le)堅實的(de)基礎。

讓我們首先來(lái)看看古典微積分(fēn)是如何失效的(de)。爲求 df（f 是布朗運動 B_t 的(de)連續平滑函數），應用(yòng)古典微積分(fēn)中的(de)鏈式法則（chain rule）可(kě)得(de)：

由于布朗運動 B_t 處處不可(kě)微，因此導數 dB_t/dt 不存在，所以上式沒有意義。第一次嘗試失敗。那麽我們能不能繞過 dB_t/dt 呢(ne)，而僅僅使用(yòng) dB_t 呢(ne)？前文已經指出 dB_t 有明(míng)确的(de)含義，它表示布朗運動在一個(gè)無窮小的(de)時(shí)間間隔内的(de)變化(huà)。因此我們有：

在這(zhè)個(gè)表達式下(xià)，f’(B_t) 是可(kě)求的(de)（因爲 f 是一個(gè)連續平滑函數），而 dB_t 也(yě)是可(kě)求的(de)。看似我們繞過了(le) B_t 處處不可(kě)微的(de)問題。不幸的(de)是，上面這(zhè)個(gè)等式是不成立的(de)。第二次嘗試依然以失敗收場(chǎng)。來(lái)看看上面這(zhè)個(gè)式子爲什(shén)麽是錯的(de)。不要忘了(le)，它實際上來(lái)自泰勒展開（Taylor expansion）。考慮一個(gè)一般函數 f(x) 的(de)泰勒展開：

事實上，對(duì)于一般的(de)函數，由泰勒展開确實有 df = f’(x)dx，這(zhè)是因爲當 Δx 趨近于 0 時(shí)，上式右側中除了(le)第一項 f’(x) Δx 外，其他(tā)所有項相當于第一項都是高(gāo)階小量、可(kě)以被忽略，因此上式的(de)無窮小量的(de)形式就是 df = f’(x)dx。但是，當 x = B_t 時(shí)，這(zhè)個(gè)性質并不成立。将 x 替換爲 B_t 代入上式：

顯然，在上式右側中，第一項 f’(B_t)ΔB_t 是重要的(de)。那麽其他(tā)項相對(duì)它來(lái)說可(kě)以忽略嗎？你也(yě)許已經猜到答(dá)案了(le)：二次變分(fēn) (dB)^2 = dt！因爲布朗運動的(de)二次變分(fēn)非 0，因此上式右側的(de)第二項相對(duì)于第一項不是更高(gāo)階的(de)小量，而是同階的(de)，因此它不能被略去（從第三項之後仍然是相對(duì)前兩項的(de)高(gāo)階小量，可(kě)以被忽略）。在無窮小量形式下(xià)忽略掉右側第三項開始之後的(de)所有項，并利用(yòng) (dB)^2 = dt，我們得(de)到伊藤引理(lǐ)（Itō's lemma）的(de)最基本形式：

它也(yě)是伊藤微積分(fēn)中的(de)基本關系式。更一般的(de)，如果一個(gè)平滑函數 f 是時(shí)間 t 和(hé)某标量 x 的(de)函數，由古典微積分(fēn)可(kě)知：

如果 x 爲布朗運動 B_t，則由伊藤微積分(fēn)有：

可(kě)見，布朗運動的(de)二次變分(fēn)造成求解 df 時(shí)，必須在古典微積分(fēn)的(de)基礎上考慮一個(gè)額外項。它就是 f 對(duì)标量項（這(zhè)裏，标量是 B_t 的(de)取值）的(de)二階導數（如果 f 僅僅是 B_t 的(de)函數）或者二階偏導數（如果 f 即是 B_t 的(de)函數又是 t 的(de)函數）。這(zhè)個(gè)結論，現在看來(lái)“不怎麽起眼”，但是它改變了(le)一切，它使人(rén)們可(kě)以将微積分(fēn)運用(yòng)到随機過程中。我們會在本系列後篇中從伊藤引理(lǐ)出發繼續闡述如何求解幾何布朗運動的(de)随機微分(fēn)方程以及如何推導出 BS 期權定價公式。

7 小結

首先恭喜你看到這(zhè)裏……随機分(fēn)析絕不是一個(gè)令人(rén)愉悅的(de)課題；這(zhè)篇文章(zhāng)也(yě)比我想象的(de)寫起來(lái)更加耗時(shí)，原因是我想盡可(kě)能把複雜(zá)的(de)概念簡單的(de)說清楚，并把數學模型和(hé)股票(piào)波動聯系起來(lái)。讓我們來(lái)簡單總結一下(xià)本文都說了(le)點啥。

布朗運動是一個(gè)用(yòng)來(lái)描述股價走勢的(de)有效模型。它的(de)馬爾科夫性符合弱有效市場(chǎng)假說。通(tōng)過反射性，很容易計算(suàn)出布朗運動在一段時(shí)間内能夠到達的(de)極值的(de)概率分(fēn)布，這(zhè)對(duì)于投資中的(de)風控至關重要。進一步的(de)，幾何布朗運動可(kě)以作爲對(duì)股價建模的(de)更精确的(de)模型。從長(cháng)期來(lái)看，幾何布朗運動的(de)走勢由漂移項控制，這(zhè)意味著(zhe)對(duì)于慢(màn)牛的(de)市場(chǎng)我們要做(zuò)的(de)是堅定價值投資、長(cháng)期持股、忽視股價短期由随機遊走帶來(lái)的(de)波動。

另一方面，布朗運動雖然連續，但是它處處不可(kě)微，這(zhè)和(hé)股價的(de)劇烈波動上蹿下(xià)跳給人(rén)的(de)感受是一緻的(de)。在金融數學中，很重要的(de)課題是分(fēn)析随機過程的(de)函數（比如衍生品的(de)價格是股票(piào)價格的(de)函數）在無窮小的(de)時(shí)間區(qū)間内如何變化(huà)，但布朗運動的(de)不可(kě)微性和(hé)二次變分(fēn)使得(de)古典微積分(fēn)對(duì)它無能爲力。日本數學家伊藤清提出了(le)古典微積分(fēn)的(de)變種 —— 伊藤微積分(fēn)，它考慮了(le)布朗運動的(de)二次變分(fēn)，從而提供了(le)使用(yòng)微積分(fēn)的(de)手段分(fēn)析随機過程及其函數的(de)框架，奠定了(le)現代金融數學的(de)基礎。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。