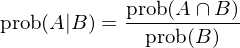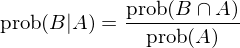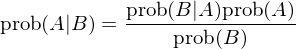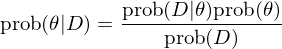貝葉斯統計
發布時(shí)間:2017-03-03 | 來(lái)源: 川總寫量化(huà)
作者:石川
摘要:貝葉斯統計在生活和(hé)量化(huà)投資中都有著(zhe)廣泛的(de)應用(yòng)。本文就爲你打開貝葉斯統計的(de)大(dà)門。
1 概率論和(hé)統計學
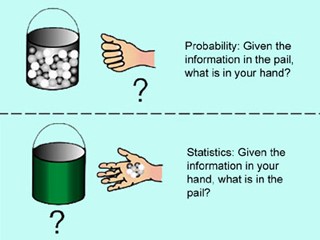
簡單來(lái)說,概率論和(hé)統計學解決的(de)問題是互逆的(de)。假設有一個(gè)具有不确定性的(de)過程(process),然後這(zhè)個(gè)過程可(kě)以随機的(de)産生不同的(de)結果(outcomes)。則概率論和(hé)統計學的(de)區(qū)别可(kě)以描述爲:
在概率論(probability theory)中,我們已知該過程的(de)概率模型,該模型的(de)不确定性由相應的(de)概率分(fēn)布來(lái)描述;概率論要回答(dá)的(de)問題是該過程産生某個(gè)結果的(de)可(kě)能性有多(duō)大(dà)這(zhè)類問題。
在統計學(statistics)中,該過程的(de)概率模型對(duì)我們來(lái)說是未知的(de),但是我們有一系列該過程産生的(de)結果的(de)觀測值;我們希望通(tōng)過這(zhè)些觀測值來(lái)推斷出這(zhè)個(gè)過程中的(de)不确定性是什(shén)麽樣的(de)。
總結來(lái)說就是:通(tōng)過已知的(de)概率模型來(lái)精确的(de)計算(suàn)各種結果的(de)可(kě)能性就是概率論;根據觀測的(de)結果來(lái)推斷模型的(de)不确定性就是統計學。
如果上面的(de)描述依然晦澀,請看下(xià)面這(zhè)個(gè)例子。假設桶裏面有 100 個(gè)小球,小球分(fēn)爲白色和(hé)黑(hēi)色。如果已知桶裏面一共有 30 個(gè)白球和(hé) 70 個(gè)黑(hēi)球,想回答(dá)随機從桶中摸出一個(gè)白球(或者黑(hēi)球)的(de)概率是多(duō)少這(zhè)樣的(de)問題,這(zhè)就屬于概率論的(de)範疇。而如果已知通(tōng)過有放回的(de)采樣抽出了(le) 10 個(gè)球并且其中 4 個(gè)白球 6 個(gè)黑(hēi)球,想要推斷的(de)是小桶裏面白球(或者黑(hēi)球)的(de)百分(fēn)比(這(zhè)些對(duì)我們來(lái)說是未知的(de)),這(zhè)就是統計學的(de)範疇。
對(duì)于概率論來(lái)說,每一個(gè)問題都有唯一的(de)答(dá)案。通(tōng)過相關計算(suàn),總可(kě)以計算(suàn)出我們關心的(de)結果發生的(de)概率。反觀統計學,它更像是一門藝術。因爲要推斷的(de)模型是未知的(de),因此很難說哪種推斷方法就優于另一種方法,或者哪種推斷結果就比其他(tā)結果更加正确。就拿上面的(de)例子來(lái)說,雖然觀測到的(de) 10 個(gè)球中有 4 個(gè)白球和(hé) 6 個(gè)黑(hēi)球,但我們仍不能斷言桶裏白球占 40% 的(de)推斷就一定比桶裏白球占 50% 或者 30% 的(de)推斷更加準确。
2 古典統計學和(hé)貝葉斯統計學
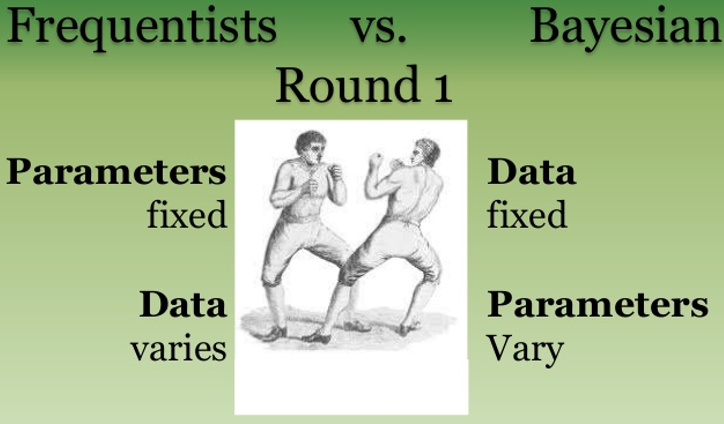
統計學領域中有兩大(dà)學派:古典統計學(classical)和(hé)貝葉斯統計學(Bayesian,以英國數學家托馬斯•貝葉斯命名)。古典統計學又稱爲頻(pín)率論(frequentist)。關于這(zhè)倆大(dà)學派孰優孰劣已有一個(gè)世紀的(de)争論。它們的(de)本質區(qū)别在于對(duì)待未知模型或者參的(de)方法是不同的(de):
古典統計學認爲,未知的(de)模型或者參數是确定的(de),隻不過我們不知道它确切的(de)形式或者取值。
貝葉斯統計學認爲,未知的(de)模型或者參數變量是不确定的(de),但是這(zhè)種不确定性可(kě)以由一個(gè)概率分(fēn)布來(lái)描述。
古典統計學通(tōng)過進行大(dà)量重複實驗并統計某個(gè)特定結果出現的(de)頻(pín)率作爲對(duì)未知參數的(de)估計。以猜桶中白球的(de)比例爲例,頻(pín)率論者會進行大(dà)量的(de)帶放回的(de)獨立抽取實驗(實驗可(kě)以做(zuò)到天荒地老海枯石爛),然後計算(suàn)所有結果中白球出現的(de)頻(pín)率,以此作爲對(duì)小球中白球比例的(de)推斷。古典統計學的(de)核心在于通(tōng)過大(dà)量的(de)實驗來(lái)消除模型或者參數估計中的(de)不确定性(因爲它假設未知模型或者參數是确定的(de))。
貝葉斯統計學則截然不同。貝葉斯統計學“使用(yòng)概率的(de)方法來(lái)解決統計學問題”。如前所述,貝葉斯統計學認爲未知的(de)模型或者參數是不确定的(de)、符合某個(gè)概率分(fēn)布。特别的(de),我們會首先根據主觀判斷或者過去的(de)經驗,對(duì)這(zhè)個(gè)概率分(fēn)布有一個(gè)猜測,稱爲先驗分(fēn)布(prior distribution);然後根據越來(lái)越多(duō)的(de)觀測值(new data 或者 new evidence)來(lái)修正對(duì)該概率分(fēn)布的(de)猜測,最後得(de)到的(de)概率分(fēn)布稱爲後驗分(fēn)布(posterior distribution)。貝葉斯統計學中的(de)“概率”的(de)概念可(kě)以被解釋爲我們對(duì)未知變量不同取值的(de)信心程度的(de)測度(measure of confidence)。貝葉斯統計不消除未知變量的(de)不确定性,而是通(tōng)過越來(lái)越多(duō)的(de)新的(de)觀測點來(lái)持續更新我們對(duì)于該未知變量不确定性的(de)認知,提高(gāo)我們對(duì)不确定性的(de)判斷的(de)信心。
對(duì)于上面這(zhè)個(gè)例子,假設在觀測值出現之前,我們猜測桶中有 50% 的(de)白球和(hé) 50% 的(de)黑(hēi)球。因此 50% 是我們對(duì)白球比例的(de)先驗信仰(prior belief)。随著(zhe)不斷進行抽取實驗,我們會根據得(de)到的(de)觀測值更新我們的(de)信仰。假設 10 次抽取後得(de)到 4 個(gè)白球和(hé) 6 個(gè)黑(hēi)球,那麽此時(shí)我們對(duì)白球比例的(de)信仰就會從最初的(de) 50% 減少一些,這(zhè)是因爲我們結合新的(de)證據(即觀測的(de) 10 個(gè)球中僅有 40% 是白球)更新了(le)猜測。假設 100 次抽取後得(de)到了(le) 35 個(gè)白球和(hé) 65 個(gè)黑(hēi)球,那麽此時(shí)我們對(duì)白球比例的(de)信仰又會繼續更新。随著(zhe)越來(lái)越多(duō)的(de)觀測值,我們會持續更新猜測,并且對(duì)該猜測的(de)信心程度也(yě)會越來(lái)越高(gāo),即未知變量(在這(zhè)裏是白球比例)後驗分(fēn)布的(de)标準差會越來(lái)越小(後面會通(tōng)過一個(gè)扔硬币的(de)例子說明(míng))。
貝葉斯統計學派被古典統計學派诟病的(de)核心問題是對(duì)于未知變量的(de)先驗分(fēn)布是非常主觀的(de)。顯然,哪怕是一個(gè)最簡單的(de)問題,不同的(de)人(rén)也(yě)會有不同的(de)考慮。比如桶中白球比例這(zhè)個(gè)例子。一個(gè)普通(tōng)人(rén)會同意 50% 是一個(gè)合理(lǐ)的(de)先驗猜測。但是,極端的(de)人(rén)也(yě)許會使用(yòng) 0% 或者 100% 白球作爲他(tā)的(de)先驗猜測。不過,盡管不同人(rén)可(kě)以有不同的(de)先驗分(fēn)布,但是随著(zhe)他(tā)們結合新的(de)觀測點來(lái)更新自己的(de)信仰,我們會發現他(tā)們最終得(de)到的(de)後驗分(fēn)布是會逐漸收斂的(de)。此外,對(duì)很多(duō)生活中的(de)實際問題,使用(yòng)一個(gè)合理(lǐ)的(de)猜測(educated guess)作爲先驗是很有好處的(de)。
3 爲什(shén)麽要學習(xí)貝葉斯統計學
貝葉斯統計在生活以及量化(huà)投資中有著(zhe)廣泛的(de)應用(yòng)。從下(xià)面兩個(gè)意義上說,相對(duì)古典統計,貝葉斯統計有明(míng)顯的(de)優勢:
1. 雖然在上面抽小球的(de)例子中我們進行大(dà)量重複性的(de)實驗并計算(suàn)白球的(de)頻(pín)率(古典統計學手段),但對(duì)于是在生活中的(de)很多(duō)實際問題,大(dà)量重複實驗是不現實的(de)。比如我們想推斷川普當選美(měi)國總統的(de)概率。顯然,我們沒法讓美(měi)國人(rén)進行成千上萬次不同的(de)投票(piào)選舉,然後計算(suàn)川普獲勝的(de)頻(pín)率。即便是通(tōng)過民意調查的(de)方式,進行成千上萬次也(yě)是不切實際的(de)(簡單從成本的(de)角度考慮就不可(kě)能)。因此,對(duì)于這(zhè)個(gè)問題我們隻能有非常有限的(de)幾次民意調查結果。我們當然可(kě)以隻通(tōng)過這(zhè)些有限的(de)結果利用(yòng)古典統計學對(duì)川普獲勝的(de)概率做(zuò)出估計,但是可(kě)以想象的(de)是這(zhè)個(gè)估計的(de)誤差會非常大(dà)。而貝葉斯統計則提供了(le)新的(de)視角。
2. 合理(lǐ)的(de)先驗分(fēn)布對(duì)未知量的(de)估計是非常有益的(de)。對(duì)生活中很多(duō)實際問題的(de)判斷都和(hé)人(rén)們的(de)學識、經驗、見識有關。在這(zhè)種情況下(xià),如果我們把有限和(hé)觀測數據和(hé)根據知識和(hé)經驗得(de)到的(de)先驗結合起來(lái),會得(de)到對(duì)未知量更好的(de)推斷。就拿對(duì)股票(piào)收益率的(de)預測這(zhè)件事來(lái)說,我們之前的(de)文章(zhāng)《收益率預測的(de)貝葉斯收縮》中提到了(le)使用(yòng)貝葉斯統計可(kě)以得(de)到更小的(de)估計誤差。而高(gāo)盛著名的(de) Black–Litterman 收益率模型就是将從市場(chǎng)均衡假設推出的(de)資産收益率作爲先驗,将基金經理(lǐ)的(de)主觀判斷作爲觀測值,通(tōng)過把它們兩者結合來(lái)得(de)到後驗判斷。它的(de)本質也(yě)是貝葉斯統計。
可(kě)見,掌握貝葉斯統計并且使用(yòng)它做(zuò)推斷,即貝葉斯推斷(Bayesian inference),十分(fēn)重要。貝葉斯統計框架的(de)核心無疑就是貝葉斯定理(lǐ)(Bayes’ rule)。
4 貝葉斯定理(lǐ)
本節簡要介紹貝葉斯定理(lǐ),它是貝葉斯推斷的(de)核心。貝葉斯定理(lǐ)的(de)推導始于條件概率。條件概率可(kě)以定義爲:在事件 B 發生的(de)前提下(xià),事件 A 發生的(de)概率。數學上用(yòng) P(A|B) 來(lái)表示這(zhè)個(gè)條件概率。生活中條件概率屢見不鮮。比如在沒有趕上 8 點這(zhè)趟地鐵,上班遲到的(de)概率是多(duō)少?
條件概率 P(A|B) 的(de)數學定義爲:
這(zhè)個(gè)公式的(de)白話(huà)解釋爲:“當 B 發生前提下(xià) A 發生的(de)概率”等于“A 和(hé) B 同時(shí)發生的(de)概率”除以“B 發生的(de)概率”。用(yòng)我們的(de)例子來(lái)說,那就是“在沒有趕上 8 點這(zhè)趟地鐵的(de)前提下(xià),上班遲到的(de)概率”等于“沒趕上 8 點這(zhè)趟地鐵且上班遲到的(de)概率”除以“沒趕上 8 點這(zhè)趟地鐵的(de)概率”。将這(zhè)個(gè)式子左右兩邊同時(shí)乘以 P(B) 得(de)到 P(B)P(A|B) = P(A∩B)。
類似的(de),我們也(yě)可(kě)以求出 P(B|A),即在 A 發生的(de)前提下(xià),B 發生的(de)概率是多(duō)少。在上面例子中,這(zhè)對(duì)應著(zhe)“在上班遲到的(de)前提下(xià),沒有趕上 8 點這(zhè)趟地鐵的(de)概率是多(duō)少”?(上班遲到的(de)原因可(kě)能很多(duō),比如沒趕上這(zhè)趟地鐵是一個(gè),又比如趕上地鐵了(le)但是下(xià)地鐵後去辦公樓咖啡館裏耽擱了(le) 10 分(fēn)鐘(zhōng)也(yě)是一個(gè),或者因爲早上發燒先去醫院了(le)等等。)根據定義:
同樣,兩邊同時(shí)乘以 P(A) (并且由 P(A∩B) = P(B∩A))得(de)到 P(A)P(B|A) = P(A∩B)。由此可(kě)知 P(B)P(A|B) = P(A)P(B|A)。這(zhè)個(gè)結果也(yě)可(kě)以寫作如下(xià)形式,即大(dà)名鼎鼎的(de)貝葉斯定理(lǐ):
5 貝葉斯推斷
由貝葉斯定理(lǐ)可(kě)以順其自然得(de)到貝葉斯推斷。前文提到,貝葉斯統計的(de)核心是通(tōng)過新的(de)觀測數據(或者新的(de)證據)來(lái)不斷的(de)更新我們對(duì)未知量的(de)認知。
考慮一個(gè)假想的(de)例子。假設我們的(de)先驗認知是明(míng)天太陽不會升起(即明(míng)天太陽不會升起的(de)概率爲 1)。然而,實際觀測到的(de)證據是每天太陽都照(zhào)常升起。由此,我們會不斷的(de)修正之前那個(gè)先驗,由此得(de)到的(de)後驗認知是下(xià)一天太陽不會升起的(de)概率越來(lái)越低。通(tōng)過新證據或者數據來(lái)更新認知的(de)過程就是貝葉斯推斷。下(xià)面我們來(lái)正式的(de)描述它。
假設我們有一個(gè)需要估計的(de)未知量 θ,并且針對(duì)該變量有一個(gè)先驗分(fēn)布 P(θ)。令 D 爲一系列觀測值或者證據。我們希望通(tōng)過 D 來(lái)修正對(duì) θ 的(de)分(fēn)布的(de)認知,即 P(θ|D) 是我們感興趣的(de)。由貝葉斯定理(lǐ)可(kě)得(de):
在貝葉斯推斷的(de)框架下(xià),上面公式中的(de)這(zhè)些概率量都有約定俗成的(de)名字:
P(θ):θ 的(de)先驗分(fēn)布(prior)。它表示在沒有任何觀測值序列 D 時(shí)我們對(duì)于 θ 的(de)不确定性的(de)認知。
P(θ|D):θ 的(de)後驗分(fēn)布(posterior)。它表示在考慮了(le)觀測值序列 D 後,我們對(duì)于θ 的(de)不确定性的(de)改進的(de)認知。
P(D|θ):似然函數(likelihood)。它是當未知變量服從 θ 的(de)前提下(xià),我們觀察到序列 D 的(de)條件概率。
P(D):觀測值或證據(evidence)。這(zhè)是在考慮所有可(kě)能的(de) θ 的(de)分(fēn)布下(xià),所能觀測到序列 D 的(de)非條件概率。
可(kě)見,通(tōng)過使用(yòng)貝葉斯推斷,我們可(kě)以合理(lǐ)的(de)将先驗認知和(hé)實際證據結合在一起,得(de)到一個(gè)更新的(de)後驗認知。此外,貝葉斯推斷框架的(de)強大(dà)之處在于我們可(kě)以叠代的(de)看問題,即在每次有新觀測數據後我們可(kě)以得(de)到一個(gè)新的(de)後驗分(fēn)布,然後把它作爲下(xià)個(gè)新數據出現前的(de)(新的(de))先驗分(fēn)布。換句話(huà)說,在這(zhè)個(gè)過程中我們通(tōng)過反複叠代使用(yòng)貝葉斯定理(lǐ),持續更新對(duì)未知量的(de)分(fēn)布的(de)認知。
6 一個(gè)例子
下(xià)面通(tōng)過一個(gè)具體的(de)例子來(lái)說明(míng)貝葉斯推斷的(de)過程。假設我們有一枚硬币,并且想要推斷出扔硬币時(shí)得(de)到頭像(正面,heads)的(de)概率 P(H) 是多(duō)少。用(yòng) θ 來(lái)表示這(zhè)個(gè)概率。通(tōng)過反複扔這(zhè)枚硬币便可(kě)以得(de)到一個(gè)由正面和(hé)(或)反面結果組成的(de)觀測序列,這(zhè)就是觀測序列 D。
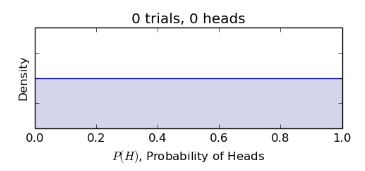
假設在開始扔硬币前,我們對(duì) θ 的(de)分(fēn)布 P(θ) 有如下(xià)先驗猜想:θ 可(kě)以是 0 到 1 範圍内的(de)任何取值,并且均勻分(fēn)布(比如 θ 等于 0 說明(míng)該硬币兩面都不是頭像;θ 等于 1 說明(míng)該硬币兩面都是頭像;θ 等于 0.5 意味著(zhe)該硬币一面頭像一面非頭像,且質地均勻等)。在這(zhè)個(gè)假設下(xià),θ 的(de)先驗概率密度函數爲 0 到 1 之間的(de)一條水(shuǐ)平線(下(xià)圖)。
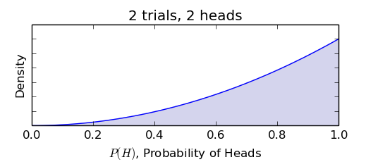
下(xià)面我們開始扔硬币。假設扔了(le)兩次後,得(de)到了(le)兩次頭像。根據貝葉斯推斷(具體數學計算(suàn)略去,下(xià)同),我們得(de)到關于 θ 的(de)更新後的(de)(後驗)概率密度函數如下(xià)圖所示。可(kě)見由于連續看到兩次頭像面的(de)結果,我們開始傾向于認爲 θ 的(de)取值是越接近 1 越有可(kě)能。
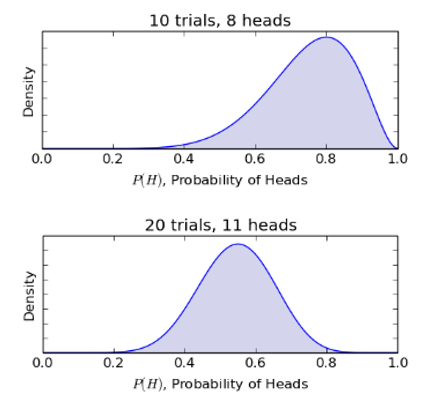
讓我們繼續實驗。假如我們扔了(le) 10 次後得(de)到 8 次正面,而扔了(le) 20 次後得(de)到了(le) 11 次正面。根據這(zhè)些結果,我們不斷更新 θ 的(de)後驗分(fēn)布(下(xià)圖)。 當 10 次中有 8 次正面時(shí),我們會認爲這(zhè)個(gè)硬币很有可(kě)能是不公平的(de),即正面和(hé)反面出現的(de)概率不同。而當 20 次中出現 11 次正面時(shí),我們的(de)認知會再次根據新的(de)結果得(de)到修正,我們開始認爲這(zhè)個(gè)硬币可(kě)能是公平的(de)了(le)。
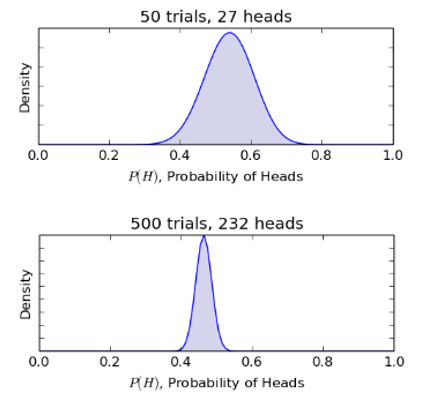
最後,下(xià)面兩張圖是經過了(le) 50 次(27 次正面)和(hé) 500 次(232 次正面)實驗後的(de) θ 的(de)後驗分(fēn)布。
随著(zhe)越來(lái)越多(duō)的(de)新結果的(de)出現,我們對(duì)于 θ 的(de)不确定性的(de)認知越來(lái)越清晰;對(duì)于 θ 的(de)不同取值的(de)信心越來(lái)越高(gāo)。特别的(de),我們越來(lái)越有把握的(de)說 θ 最有可(kě)能的(de)取值是 0.5 附近。這(zhè)體現在 500 次實驗後,θ 的(de)後驗分(fēn)布 P(θ|D) 已經非常狹窄(換句話(huà)說,θ 的(de)取值的(de)标準差越來(lái)越小),且集中在 0.46 附近。假如這(zhè)枚硬币确實是一枚公平的(de)硬币,那麽如果再進行 500 此實驗,會發現 P(θ|D) 會更加狹窄且 θ 的(de)取值一定會集中在 0.5 附近。
這(zhè)個(gè)例子完美(měi)的(de)展示了(le)貝葉斯推斷的(de)強大(dà)。我們一開始對(duì)未知量 θ 的(de)猜測有非常大(dà)的(de)不确定性(先驗是 0 到 1 的(de)均勻分(fēn)布)。随著(zhe)越來(lái)越多(duō)的(de)觀測值(500 個(gè)實驗結果)的(de)出現,通(tōng)過叠代使用(yòng)貝葉斯定理(lǐ),逐步細化(huà)、完善我們對(duì) θ 的(de)不确定性的(de)認知,最終得(de)到了(le)關于 θ 的(de)不确定性的(de)非常自信的(de)後驗分(fēn)布(即 θ 的(de)分(fēn)布以 0.5 爲中心,标準差非常小,它最有可(kě)能的(de)取值就是 0.5)。
無疑,貝葉斯統計是一個(gè)強大(dà)的(de)工具。當然,不熟悉它的(de)人(rén)卻對(duì)其敬而遠(yuǎn)之。下(xià)面是網上關于貝葉斯統計的(de)一個(gè)笑(xiào)話(huà)。它雖然透著(zhe)作者的(de)“無知”,但可(kě)能卻代表著(zhe)很多(duō)吃(chī)瓜群衆對(duì)貝葉斯統計的(de)看法,以及貝葉斯統計學派的(de)自嘲:
A Bayesian is one who, vaguely expecting a horse, and catching a glimpse of a donkey, strongly believes he has seen a mule.
免責聲明(míng):入市有風險,投資需謹慎。在任何情況下(xià),本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外,文中圖表均直接或間接來(lái)自于相應論文,僅爲介紹之用(yòng),版權歸原作者和(hé)期刊所有。