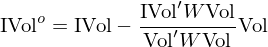特質性波動率能否提供增量定價信息？

作者：石川

摘要：本文以中證 500 爲例對(duì)特質性波動率進行了(le)實證研究，觀察到低特質性波動率異象；在控制了(le)其他(tā)常見因子後，特質性波動率依然能夠提供定價信息。

1 引言

特質性波動率（Idiosyncratic Volatility）是特質性風險的(de)一個(gè)代理(lǐ)變量。與系統性的(de)市場(chǎng)風險不同，特質性風險被認爲是上市公司面對(duì)的(de)特有風險、是可(kě)以被分(fēn)散化(huà)的(de)。長(cháng)久以來(lái)，大(dà)量的(de)研究試圖搞清楚特質性波動率和(hé)股票(piào)預期收益率之間是否存在某種關系。從實證分(fēn)析來(lái)看，上述問題并無定論。早期的(de)發現傾向認爲特質性波動率和(hé)預期收益率之間存在正相關。然而在 2006 年，Ang et al. (2006) 在 Journal of Finance 上發表了(le)一篇影(yǐng)響深遠(yuǎn)的(de)文章(zhāng)，指出了(le)特質性波動率和(hé)預期收益率之間的(de)負相關 —— 即當其他(tā)條件相同時(shí)，特質性波動率低的(de)股票(piào)未來(lái)可(kě)能獲得(de)更高(gāo)的(de)收益。

時(shí)至今日，Ang et al. (2006) 的(de)引用(yòng)已經超過 3000 次，足見其影(yǐng)響力。它也(yě)同時(shí)掀起了(le)學術界對(duì)特質性波動率的(de)極大(dà)興緻，而這(zhè)其中也(yě)不乏反對(duì)之聲。Fu (2009) 在 Journal of Financial Economics 上撰文說 Ang et al. (2006) 發現的(de)負相關源于一小撮高(gāo)特質性波動率股票(piào)收益率的(de)反轉；Fu (2009) 使用(yòng) GARCH 模型對(duì)特質性波動率建模分(fēn)析發現，它和(hé)預期收益率之間依然存在正相關。來(lái)自 Berkeley 的(de) Anderson, Bianchi, and Goldberg (2012) 指出，Ang et al. (2006) 中結果受到了(le)數據中一個(gè)極端 outlier 的(de)影(yǐng)響（1987 年 10 月(yuè)），排除該點後，Ang et al. (2006) 發現的(de)關系不再顯著。

面對(duì)質疑，Ang et al. (2009) 在 Journal of Financial Economics 上再次發文，通(tōng)過來(lái)自美(měi)國和(hé)全球的(de)更多(duō)實證結果說明(míng)特質性波動率和(hé)預期收益率之間的(de)負相關性。然而，也(yě)有研究表明(míng)，特質性波動率和(hé)預期收益率之間到底是何種關系受到實證分(fēn)析中很多(duō)因素的(de)影(yǐng)響，因此難有定論（Bali and Cakici 2008）。

面對(duì)大(dà)量難以統一的(de)實證結果，Stambaugh, Yu, and Yuan (2015) 從不對(duì)稱套利的(de)角度對(duì)（低）特質性波動率之謎進行了(le)解釋（針對(duì)美(měi)股）。他(tā)們指出，對(duì)于 overpriced 股票(piào)，特質性波動率和(hé)收益率呈現負相關；反之，對(duì)于 underpriced 股票(piào)，二者呈現正相關。由于做(zuò)空的(de)限制造成對(duì) overpriced 股票(piào)套利不充分(fēn)，因此 overpriced 股票(piào)上的(de)這(zhè)種負相關比 underpriced 股票(piào)上的(de)正相關更難被消除，綜合的(de)結果就是在整個(gè)截面上觀察到負相關，即低特質性波動率異象。

本文以中證 500 指數成分(fēn)股爲例，對(duì)特質性波動率進行實證研究。和(hé)其他(tā)針對(duì) A 股的(de)相關研究報告發現的(de)結果相似，我們觀察到特質性波動率和(hé)預期收益率之間的(de)負相關性；依照(zhào)低特質性波動率來(lái)構建投資組合可(kě)以獲得(de)傳統因子模型無法解釋的(de)超額收益。此外，Fama-MacBeth regression 分(fēn)析表明(míng)，特質性波動率能夠解釋個(gè)股預期收益率的(de)差異。

2 構建因子

本文借鑒 Ang et al. (2009) 的(de)方法構建特質性波動率因子 —— 将個(gè)股的(de)收益率相對(duì)某給定多(duō)因子模型殘差的(de)标準差作爲特質性波動率因子。按照(zhào)上述定義需要明(míng)确兩個(gè)問題：（1）多(duō)因子模型；（2）回歸獲得(de)殘差以及計算(suàn)殘差标準差的(de)時(shí)間窗(chuāng)口。在多(duō)因子模型方面，實證中選擇 Fama and French (2015) 五因子模型：

按上述定義構建這(zhè)些因子的(de)日頻(pín)收益率序列；構建風格因子的(de)多(duō)空組合時(shí)，排除停牌股票(piào)并按等權配置（本文第五節會給出按市值加權配置的(de)實證結果）。有了(le)多(duō)因子模型的(de)日頻(pín)收益率就可(kě)以進而計算(suàn)個(gè)股的(de)特質性波動率。具體來(lái)說，在每月(yuè)最後一個(gè)交易日，使用(yòng)之前 n 個(gè)交易日的(de)個(gè)股收益率和(hé)上述因子收益率進行時(shí)序回歸得(de)到個(gè)股的(de)殘差收益率，然後計算(suàn)殘差收益率的(de)标準差作爲其特質性波動率。如何選擇 n 呢(ne)？

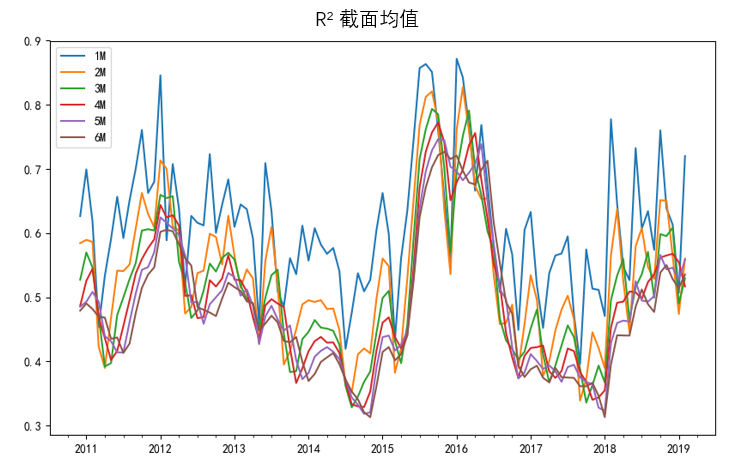
爲了(le)研究特質性波動率，我們希望上述五因子模型能夠盡可(kě)能解釋個(gè)股收益率在時(shí)序上的(de)波動，即時(shí)序回歸的(de) R² 不能太小，否則研究的(de)就不是特質性波動率而是波動率了(le)。下(xià)圖顯示了(le) n 取過去 1 至 6 個(gè)月(yuè)内的(de)交易日時(shí)，五因子模型對(duì)個(gè)股回歸的(de) R² 在截面上的(de)均值随時(shí)間的(de)變化(huà)。

使用(yòng)過去 1 到 6 個(gè)月(yuè)的(de)日頻(pín)收益率回歸，五因子模型均能較好的(de)解釋個(gè)股收益率。當然，回歸窗(chuāng)口越長(cháng)樣本點就越多(duō)，從而造成五因子模型的(de)解釋力度降低，這(zhè)也(yě)符合預期。因此不能僅以 R² 高(gāo)低作爲選擇窗(chuāng)口的(de)依據。最終，我們選擇使用(yòng)最近一個(gè)月(yuè)的(de)日頻(pín)收益率數據計算(suàn)個(gè)股的(de)特質性波動率。這(zhè)種做(zuò)法和(hé) Ang et al. (2009) 一緻。在計算(suàn)中，如果某支個(gè)股因停牌導緻其交易日少于當月(yuè)交易日的(de) 80%，則将其剔除在外。依照(zhào)上述說明(míng)，在每月(yuè)末構建特質性波動率因子（記爲 IVol）的(de)方法如下(xià)：

實證期爲 2011 年 1 月(yuè)至 2019 年 3 月(yuè)。下(xià)面來(lái)看結果。

3 實證結果

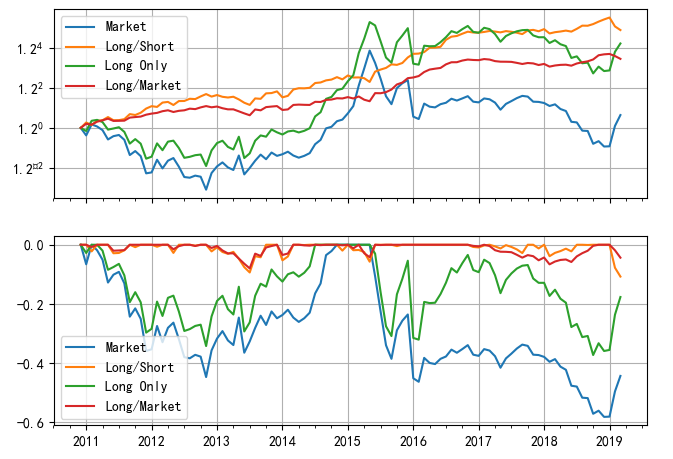
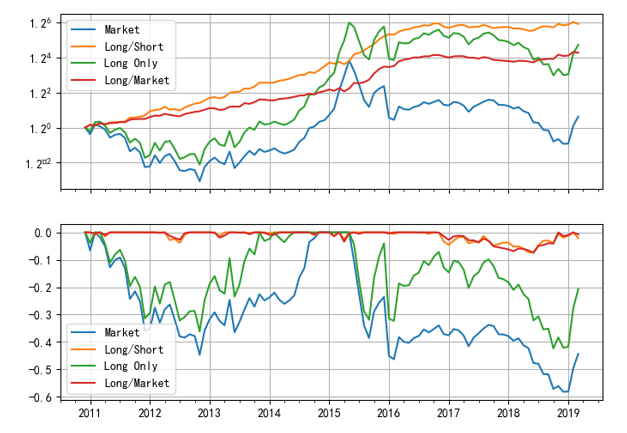
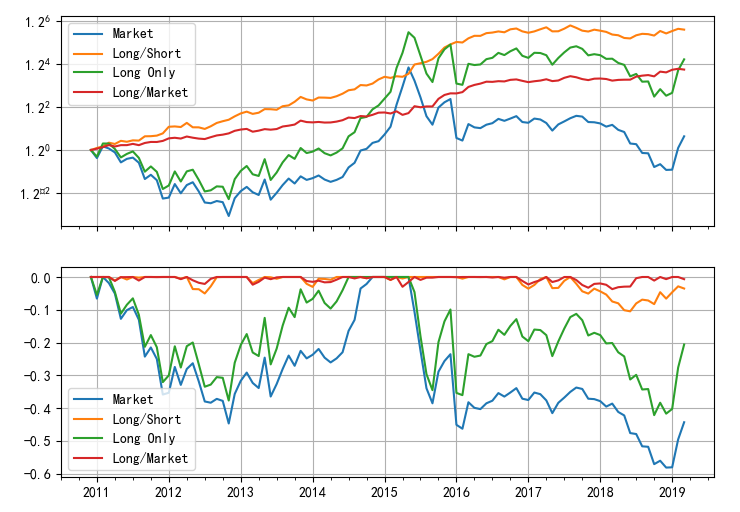
下(xià)圖顯示了(le)四個(gè)投資組合在回測期内的(de)淨值曲線。其中藍色的(de) Market 代表中證 500 指數；黃(huáng)色 Long/Short 爲多(duō)空對(duì)沖的(de)組合，它便是 IVol 因子的(de)投資組合；綠色 Long Only 代表 IVol 中的(de)多(duō)頭組合（做(zuò)多(duō) 150 支 IVol 最低的(de)股票(piào)）；最後紅色 Long/Market 代表 IVol 多(duō)頭組合相對(duì)市場(chǎng)的(de)超額收益。

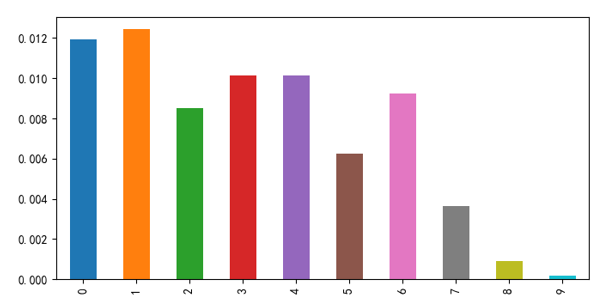
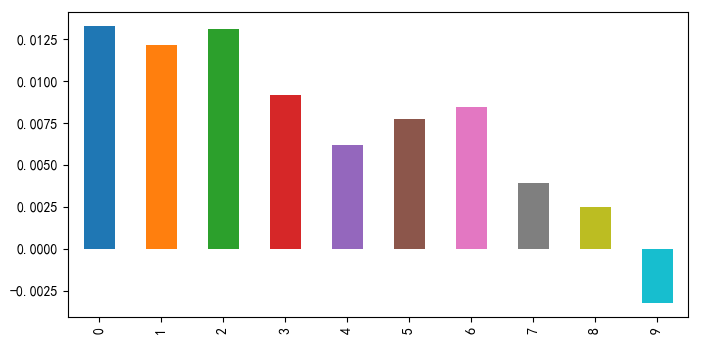
使用(yòng)低特質性波動率戰勝了(le)市場(chǎng)：IVol 多(duō)空組合的(de)年化(huà)收益率爲 11.37%（夏普率 1.24）、純多(duō)頭組合的(de)年化(huà)收益率爲 9.74%（夏普率 0.47）；同期中證 500 指數的(de)年化(huà)收益率僅爲 1.42%。不過從上圖中也(yě)能看到，從 2017 年以來(lái)，IVol 的(de)純多(duō)頭組合并沒有戰勝指數。如果在每個(gè)月(yuè)把股票(piào)池根據 IVol 的(de)大(dà)小分(fēn)成 10 檔（0 代表 IVol 最低檔、9 代表 IVol 最高(gāo)檔），則這(zhè) 10 檔投資組合的(de)月(yuè)頻(pín)收益率均值如下(xià)圖所示，呈現出較好的(de)單調性。

接下(xià)來(lái)，我們看看 IVol 因子能否獲得(de)其他(tā)因子無法解釋的(de)超額收益。由于它和(hé)波動率息息相關，因此在 Fama-French 五因子的(de)基礎上加入波動率因子 Vol。計算(suàn) Vol 時(shí)直接使用(yòng)個(gè)股日頻(pín)收益率最近一個(gè)月(yuè)的(de)标準差、将其從低到高(gāo)排序，其他(tā)步驟和(hé) IVol 類似。

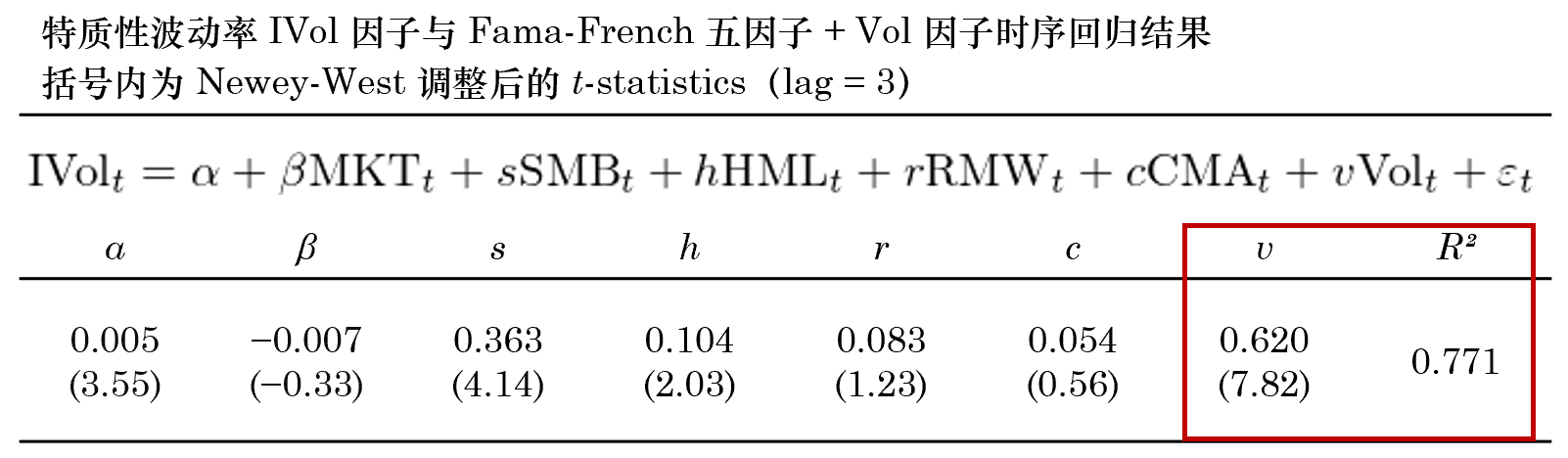
将 IVol 因子收益率和(hé) Fama-French 五因子 + Vol 因子收益率進行時(shí)序回歸，得(de)到如下(xià)結果。結果顯示，IVol 因子在 Vol 因子上有很高(gāo)的(de)暴露（v = 0.62、其 t-statistic 高(gāo)達 7.82），這(zhè)也(yě)導緻時(shí)序回歸的(de) R² 高(gāo)達 0.771（在一般學術論文中因子對(duì)異象的(de)時(shí)序回歸中往往見不到這(zhè)麽高(gāo)的(de) R²）。盡管如此，IVol 依然能獲得(de)這(zhè)六個(gè)因子無法解釋的(de)顯著 α 收益率（每月(yuè)平均 0.51%、t-statistic 3.55）。

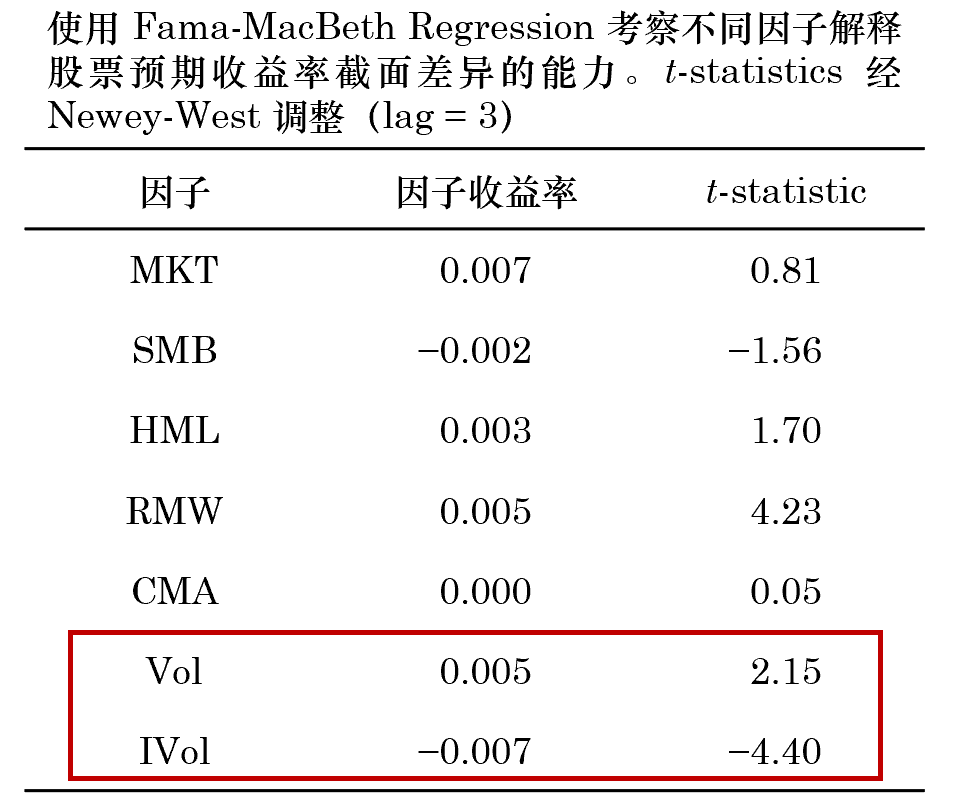
雖然 IVol 能夠獲得(de) α，但是其和(hé) Vol 的(de)高(gāo)相關性仍然讓人(rén)不爽。我們自然想看看它能能否解釋個(gè)股預期收益率的(de)截面差異，即回答(dá)本文标題中的(de)問題 —— 特質性波動率能否提供增量定價信息。爲此，使用(yòng) Fama and MacBeth (1973) Regression 對(duì)包括 IVol 在内的(de)上述七個(gè)因子同時(shí)進行分(fēn)析。将個(gè)股在每個(gè)因子上的(de)當期暴露和(hé)個(gè)股下(xià)期的(de)收益率進行截面回歸，從而得(de)到這(zhè)些因子在時(shí)序上的(de)收益率序列，以此考察每個(gè)因子。在計算(suàn)因子暴露時(shí)，對(duì)每個(gè)因子在截面上取值的(de) 1% 和(hé) 99% 分(fēn)位數之外的(de)樣本進行窗(chuāng)化(huà)，之後再進行标準化(huà)處理(lǐ)。Fama-MacBeth Regression 的(de)結果如下(xià)。

結果顯示，IVol 具有很強的(de)解釋截面預期收益率的(de)能力。它的(de)月(yuè)均收益率爲 -0.71%（t-statistic = -4.40），說明(míng)高(gāo) IVol 的(de)股票(piào)較低 IVol 的(de)股票(piào)有更低的(de)收益。然而，結果中 Vol 的(de)預期收益率爲 0.45%（t-statistic = 2.15），說明(míng)高(gāo) Vol 的(de)股票(piào)比低 Vol 的(de)股票(piào)有更高(gāo)的(de)收益，這(zhè)和(hé)我們熟悉的(de)低波動異象相左。如果把 IVol 和(hé) Vol 的(de)結果放在一起則更加令人(rén)困惑 —— 波動率高(gāo)、但特質性波動率低的(de)股票(piào)較其對(duì)立面能獲得(de)更高(gāo)的(de)收益。這(zhè)樣的(de)結果與 IVol 和(hé) Vol 之間的(de)高(gāo)相關性密不可(kě)分(fēn)。在 Fama-MacBeth Regression 中，我們希望因子之間是近似獨立的(de)，而 IVol 和(hé) Vol 這(zhè)兩個(gè)因子之間的(de)高(gāo)相關性會對(duì)分(fēn)析結果造成幹擾。爲了(le)更好的(de)考察 IVol（以及 Vol）能否解釋預期收益率截面差異，下(xià)一節将對(duì) IVol 進行正交化(huà)處理(lǐ)。

4 因子正交化(huà)

爲了(le)排除 Vol 對(duì) IVol 的(de)影(yǐng)響，使用(yòng)前者對(duì)後者進行正交化(huà)處理(lǐ)。正交化(huà)時(shí)可(kě)采用(yòng)最小二乘法（OLS）或廣義最小二乘法（GLS）。使用(yòng) OLS直接在每期截面上将股票(piào)在 IVol 上的(de)暴露作爲被解釋變量，将它們在 Vol 上的(de)暴露作爲解釋變量，回歸得(de)到的(de)殘差作爲正交化(huà)後的(de) IVol 暴露，并按照(zhào)正交化(huà)後 IVol 暴露從低到高(gāo)排序構建 IVol 因子。正交化(huà)後，IVol 因子的(de)表現如下(xià)圖所示。其多(duō)、空對(duì)沖組合的(de)年化(huà)收益率較未進行正交化(huà)提升至 14.01%、純多(duō)頭收益率提升至 11.04%。不過稍後就會看到，更高(gāo)的(de) on paper 收益率的(de)代價是更高(gāo)的(de)換手率。因此正交化(huà)在實踐中能否提升該因子的(de)效果依然需要進一步研究。

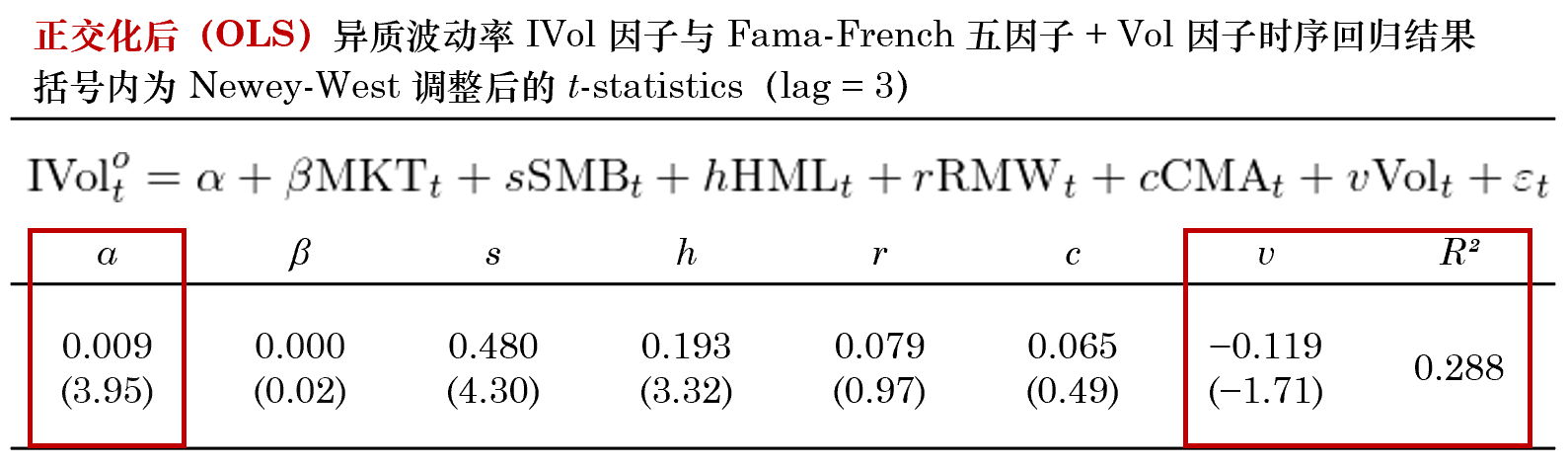
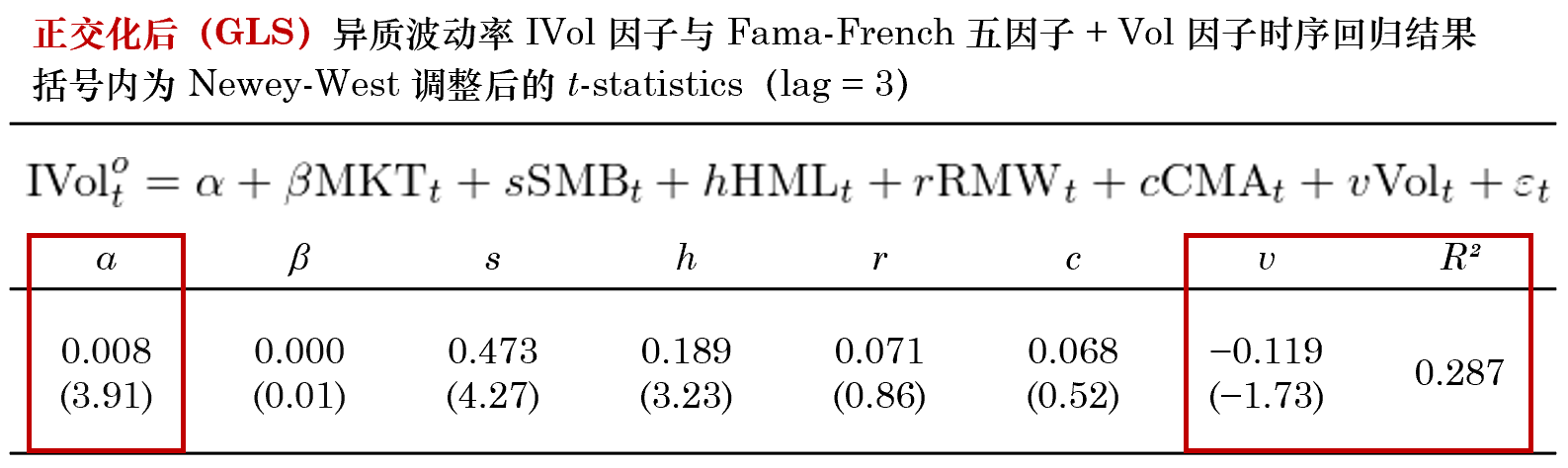
再來(lái)看看 Fama-French 五因子 + Vol 因子能否解釋正交化(huà)後的(de) IVol 因子。時(shí)序回歸顯示，正交化(huà)後的(de) IVol 因子在 Vol 因子上的(de)暴露不再顯著，而這(zhè)六個(gè)因子解釋 IVol 時(shí)的(de) R² 也(yě)下(xià)降至 0.288（屬于學術論文中常見的(de)數值範圍）。與未進行正交化(huà)相比，正交後的(de) IVol 的(de) α 收益率更加顯著。

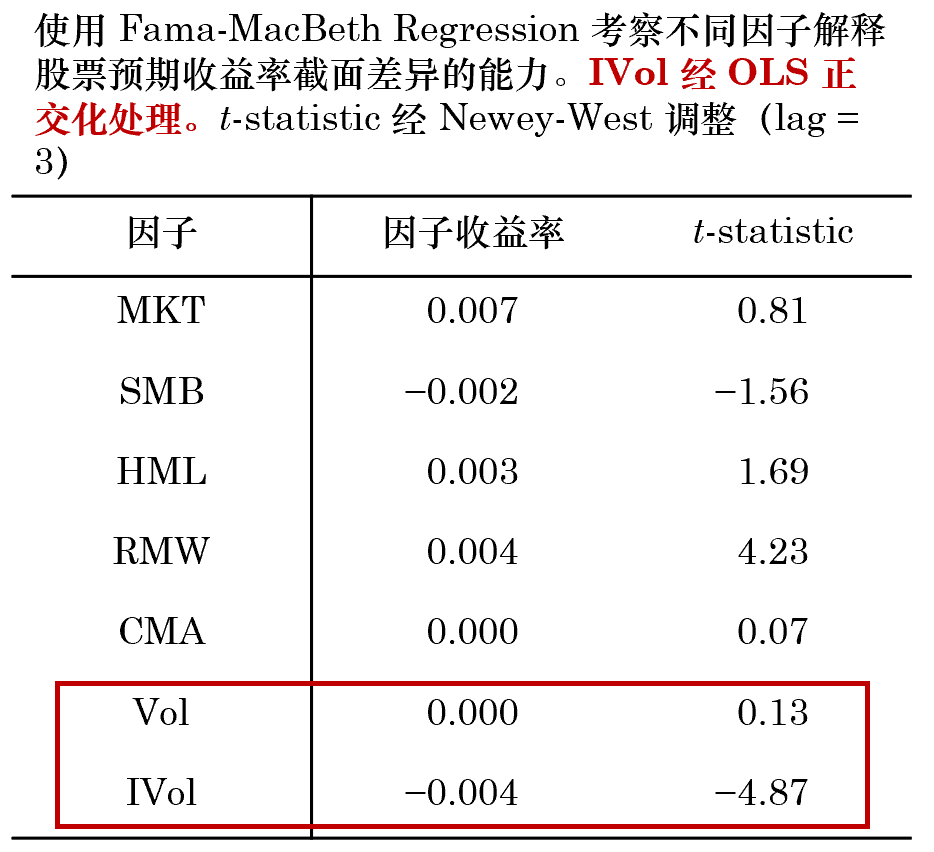
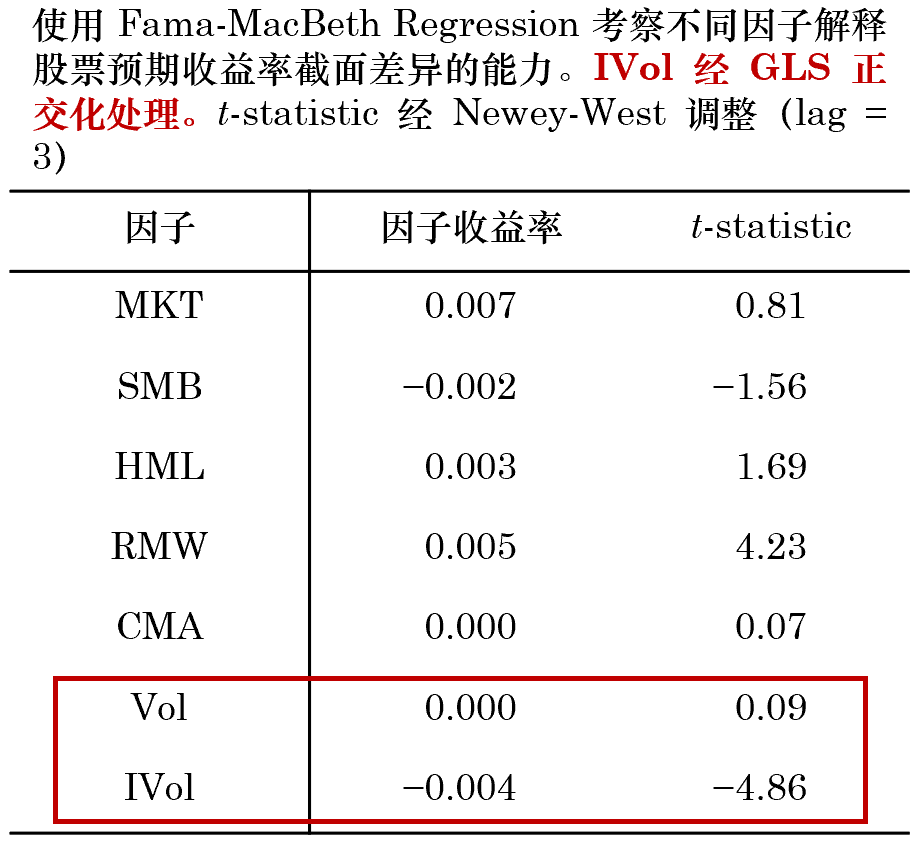
在排除了(le) Vol 對(duì) IVol 的(de)影(yǐng)響之後，Fama-MacBeth Regression 給出了(le)“期待中”的(de)結果：Vol 對(duì)股票(piào)預期收益率的(de)解釋能力驟然消失，而 IVol 因子的(de)解釋能力則變得(de)更加顯著。這(zhè)個(gè)結果說明(míng)，相比起波動率，我們更應該關注特質性波動率，而低特質性波動率異象存在于實證中的(de)中證 500 指數。

第二種正交化(huà)的(de)方法參考 Menchero (2010)，在正交化(huà)時(shí)考慮個(gè)股市值對(duì)殘差的(de)影(yǐng)響，采用(yòng) GLS：

上式中 W 是對(duì)角陣，對(duì)角線上的(de)第 i 個(gè)元素爲股票(piào) i 的(de)權重（正比于流通(tōng)市值）。這(zhè)種處理(lǐ)方法被廣泛應用(yòng)在 Barra 的(de)模型中，感興趣的(de)小夥伴可(kě)以進一步參閱相關資料。實證結果顯示，GLS 和(hé) OLS 的(de)差異很小。正交化(huà)後 IVol 因子多(duō)空組合的(de)年化(huà)收益率爲 13.76%、純多(duō)頭的(de)年化(huà)收益率爲 10.88%。下(xià)面兩張圖分(fēn)别給出了(le) GLS 正交化(huà)方法下(xià)時(shí)序回歸和(hé) Fama-MacBeth Regression 的(de)結果。

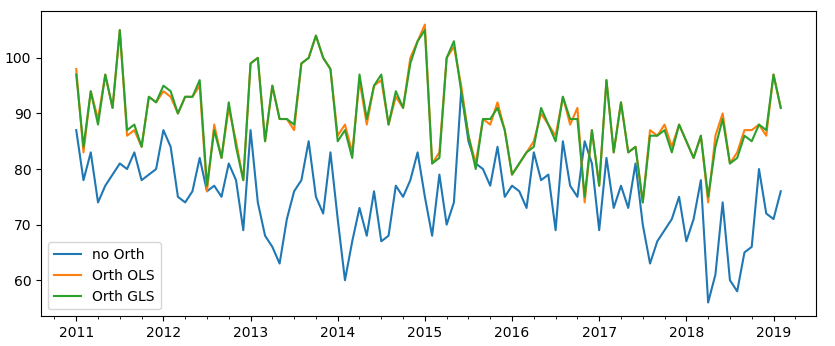
在結束本小節之前，再來(lái)回應一下(xià)之前提到的(de)高(gāo)換手率的(de)問題。下(xià)圖顯示了(le)非正交化(huà) IVol 因子和(hé)兩種正交化(huà) IVol 因子的(de)多(duō)頭組合每個(gè)月(yuè)相較于前一個(gè)月(yuè)股票(piào)變化(huà)的(de)數量（每個(gè)月(yuè)多(duō)頭一共 150 支）。正交化(huà)操作明(míng)顯的(de)提高(gāo)了(le)股票(piào)變化(huà)的(de)數量，這(zhè)在實際中會造成更高(gāo)的(de)換手率和(hé)交易成本，是必須考慮的(de)問題。

5 按市值加權

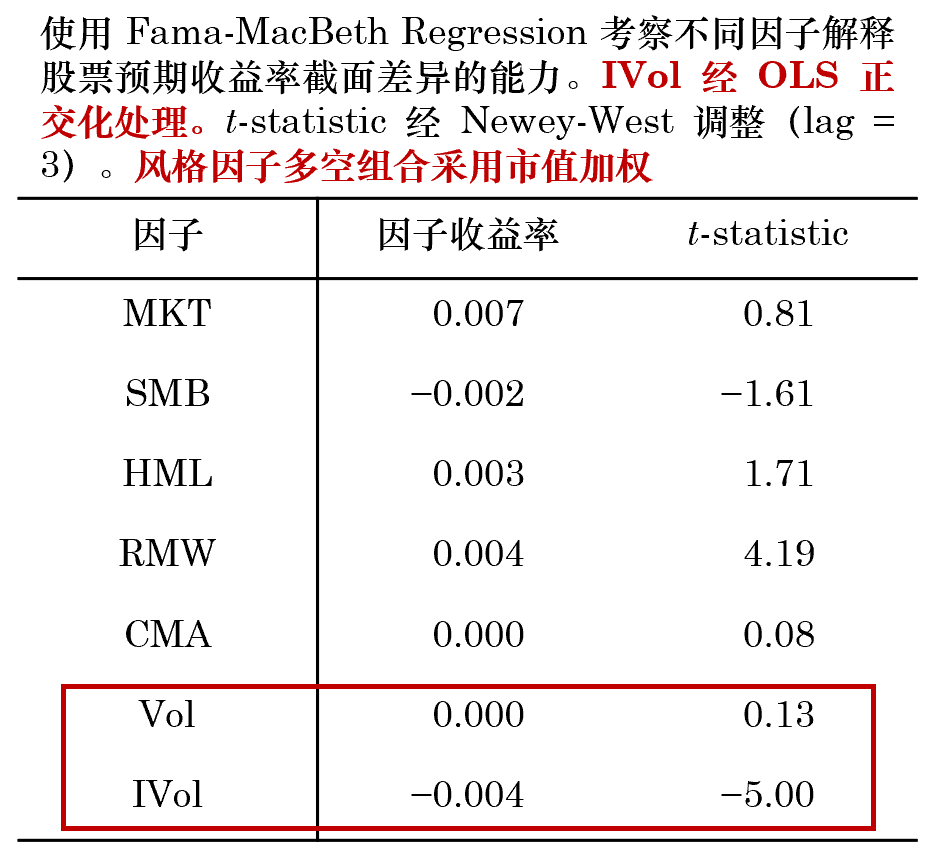
在前述的(de)實證結果中，所有風格因子的(de)多(duō)空投資組合均等權配置選出的(de)股票(piào)。作爲 robustness check，本小節給出按市值加權的(de)結果。在所有的(de)多(duō)空組合中 —— 包括計算(suàn)特質性波動率時(shí)的(de)日頻(pín)風格因子收益率，以及分(fēn)析 IVol 時(shí)的(de)月(yuè)頻(pín)因子投資組合 —— 均采用(yòng)市值加權的(de)方式構建。用(yòng)一句話(huà)總結來(lái)說：按市值加權和(hé)等權配置獲得(de)了(le)非常接近的(de)結果：特質性波動率和(hé)預期收益率呈負相關，且能顯著的(de)解釋個(gè)股預期收益率的(de)截面差異。考慮到篇幅問題，本小節僅列出按 OLS 正交化(huà)方法的(de)實證結果。下(xià)圖爲 IVol 因子組合的(de)累積淨值。IVol 因子多(duō)空投資組合的(de)年化(huà)收益率爲 13.21%（夏普率 1.76）、純多(duō)頭組合的(de)年化(huà)收益率爲 9.80%（夏普率 0.46）。

将股票(piào)池根據 IVol 的(de)大(dà)小分(fēn)成 10 檔（0 檔爲特質性波動率最低、9 檔爲特質性波動率最高(gāo)），則這(zhè) 10 檔投資組合的(de)月(yuè)頻(pín)收益率均值如下(xià)圖所示，依然呈現出較好的(de)單調性。

時(shí)序回歸結果顯示，按市值加權的(de) IVol 因子（正交化(huà)）能獲得(de)更高(gāo)的(de) α 收益率。Fama-MacBeth Regression 顯示 IVol 因子的(de)預期收益率非常顯著；與之成鮮明(míng)對(duì)比的(de)是，Vol 因子不具備解釋截面預期收益率差異的(de)能力。

6 結語

本文以中證 500 爲例對(duì)特質性波動率進行了(le)實證研究。類似的(de)方法可(kě)以推廣到全 A 股。雖然能夠觀察到低特質性波動率異象，但需要指出的(de)是上述實證區(qū)間的(de)長(cháng)度并不令人(rén)滿意，所以即便顯著的(de)結果也(yě)要打點折扣。關于低特質性波動率和(hé)低波動率異象，除了(le)本文借鑒的(de) Ang et al. (2009) 外，學術界和(hé)業界還(hái)有很多(duō)其他(tā)構件因子的(de)方法。在這(zhè)方面，感興趣的(de)小夥伴可(kě)參考《“茴”字有三種寫法，低風險異象因子呢(ne)？》，它詳盡介紹和(hé)描述了(le)不同因子的(de)構建方法，極具參考價值。最後，Herskovic et al. (2016) 指出個(gè)股的(de)特質性波動率之間也(yě)存在顯著的(de) co-movement，因此提出了(le)一個(gè) factor structure 來(lái)解釋特質性波動率。這(zhè)個(gè)發現對(duì)于 empirical asset pricing 也(yě)有一定的(de)啓示，且他(tā)們的(de)結果也(yě)反映了(le)特質性波動率和(hé)預期收益率之間的(de)負相關性。感興趣的(de)小夥伴不妨一讀。

參考文獻

Anderson, R. M., S. W. Bianchi, and L. R. Goldberg (2012). A comment on “The cross-section of volatility and expected returns”: the statistical significance of FVIX is driven by a single outlier. Working paper, Coleman Fung Risk Management Research Center, University of California Berkeley.

Ang, A., R. J. Hodrick, Y. Xing, and X. Zhang (2006). The cross-section of volatility and expected returns. Journal of Finance 61(1), 259 – 299.

Ang, A., R. J. Hodrick, Y. Xing, and X. Zhang (2009). High idiosyncratic volatility and low returns: international and further U.S. evidence. Journal of Financial Economics 91(1), 1 – 23.

Bali, T. G. and N. Cakici (2008). Idiosyncratic volatility and the cross section of expected returns. Journal of Financial and Quantitative Analysis 43(1), 29 – 58.

Chen, L. H., G. Jiang, D. Xu, and T. Yao (2012). Dissecting the Idiosyncratic Volatility Anomaly. Working paper, available at SSRN: https://ssrn.com/abstract=2023883.

Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.

Fama, E. F. and J. D. MacBeth (1973). Risk, return, and equilibrium: Empirical tests. Journal of Political Economy 81(3), 607 – 636.

Fu, F. (2009). Idiosyncratic risk and the cross-section of expected stock returns. Journal of Financial Economics 91(1), 24 – 37.

Herskovic, B., B. Kelly, H. Lustig, and S. V. Nieuwerburgh (2016). The common factor in idiosyncratic volatility: Quantitative asset pricing implications. Journal of Financial Economics 119(2), 249 – 283.

Menchero, J. (2010). Characteristics of factor portfolios. Research note, Barra.

Newey, W. K. and K. D. West (1987). A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 55(3), 703 – 708.

Stambaugh, R. F., J. Yu, and Y. Yuan (2015). Arbitrage asymmetry and the idiosyncratic volatility puzzle. Journal of Finance 70(5), 1903 – 1948.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。