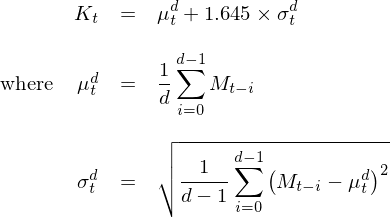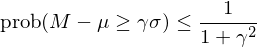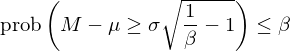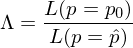估值過高(gāo)能否預測市場(chǎng)下(xià)行風險？

作者：石川

摘要：基于 A 股的(de)實證顯示，使用(yòng)市場(chǎng)估值指标後，發生市場(chǎng)下(xià)行的(de)條件概率顯著高(gāo)于非條件概率。市場(chǎng)整體估值對(duì)預測股災有一定的(de)作用(yòng)。

1 引言

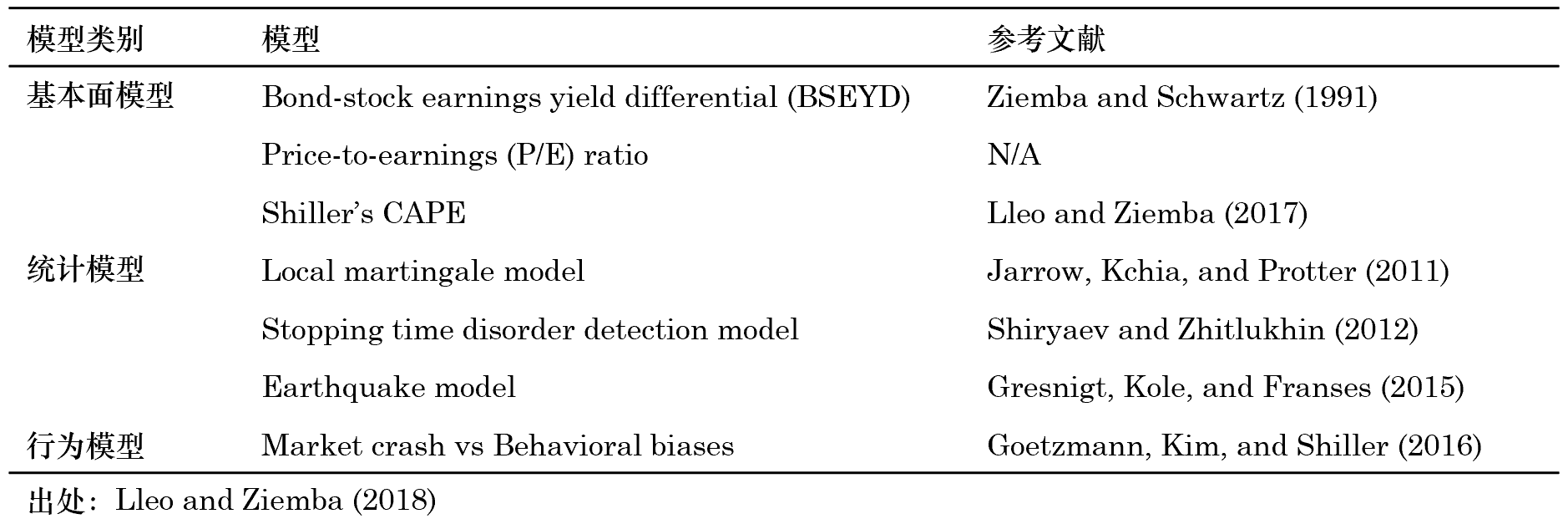
預測市場(chǎng)下(xià)行風險不僅是量化(huà)投資中的(de)一個(gè)熱(rè)門課題，對(duì)于高(gāo)波動的(de) A 股市場(chǎng)有更重要的(de)實踐意義。學術界的(de)預測模型主要包括基本面模型、統計模型和(hé)行爲模型三大(dà)類（下(xià)表）。

無論采用(yòng)哪種模型，其目标是給出未來(lái)一段時(shí)間市場(chǎng)發生給定程度以上跌幅的(de)條件概率。如果預測準确，它可(kě)以幫我們有效的(de)規避下(xià)行風險、降低投資損失。近三十年來(lái)，學術界使用(yòng)以上模型針對(duì)海外股市進行了(le)大(dà)量的(de)研究。然而由于 A 股的(de)年頭較短，這(zhè)方面的(de)研究相對(duì)欠缺。近日，一篇發表在 Journal of Portfolio Management 的(de)文章(zhāng)對(duì)于 A 股進行了(le)相關研究（Lleo and Ziemba 2018）。該文使用(yòng)基本面模型中的(de)估值指标 —— BSEYD、P/E、CAPE —— 對(duì)滬、深兩市的(de)下(xià)行風險構建了(le)預測模型和(hé)準确性檢驗。從結果來(lái)看，使用(yòng)估值指标可(kě)以顯著提高(gāo)市場(chǎng)下(xià)行風險的(de)條件概率，對(duì)預測股災有一定作用(yòng)。本文簡要介紹 Lleo and Ziemba (2018)。

2 下(xià)行樣本識别

研究的(de)第一步是識别下(xià)行樣本。根據 Lleo and Ziemba (2018) 的(de)定義，一個(gè)下(xià)行樣本始于某局部高(gāo)點（該交易日稱爲 Peak Date）、止于某局部低點（該交易日稱爲 Trough Date），且兩者之間的(de)跌幅不小于 10%。此外，對(duì)于一個(gè)下(xià)行樣本，還(hái)有一個(gè)非常重要的(de)概念 —— Crash Identification Date，即下(xià)行（或股災）識别日。

從任意局部高(gāo)點開始，如果在後續的(de)某個(gè)交易日的(de)收盤價滿足下(xià)行識别日條件，該交易日被選做(zuò)下(xià)行識别日，從而确定了(le)下(xià)行樣本，該下(xià)行樣本直到再後面的(de)某個(gè)局部低點結束。Lleo and Ziemba (2018) 對(duì)于下(xià)行識别日需要滿足的(de)條件限制十分(fēn)苛刻，目的(de)是爲了(le)保證算(suàn)法找出的(de)下(xià)行樣本相互獨立，否則在市場(chǎng)連續長(cháng)時(shí)間陰跌的(de)時(shí)期，挑出的(de)下(xià)行樣本可(kě)能出現相互重疊的(de)現象。

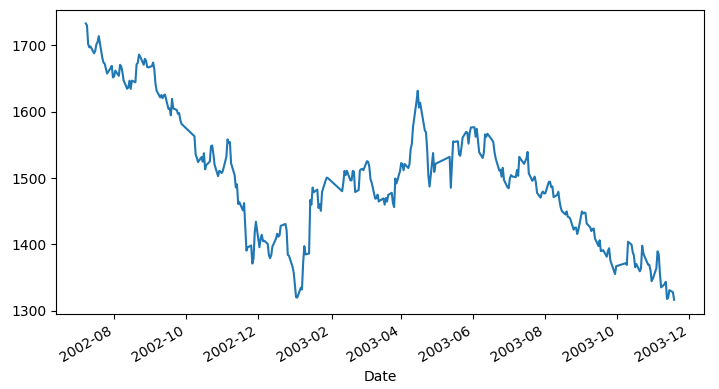
下(xià)行識别日在 Lleo and Ziemba (2018) 的(de)模型中的(de)作用(yòng)十分(fēn)關鍵。本文第四節中我們會看到，在評價預測模型準确性時(shí)也(yě)會用(yòng)到它。下(xià)圖是上證指數上的(de)一個(gè)下(xià)行樣本。根據Lleo and Ziemba (2018) 的(de)識别算(suàn)法，它從 2002/07/08 開始（收盤價 1732.93），然而它并沒有在圖中第一個(gè)“深溝”即 2003/01/03 日結束。其原因是算(suàn)法确認的(de)下(xià)行識别日是 2003/04/23，晚于第一個(gè)“深溝”的(de)日期。最終，這(zhè)段下(xià)行樣本止于 2003/11/18（收盤價 1316.56），跌幅超過 24%。

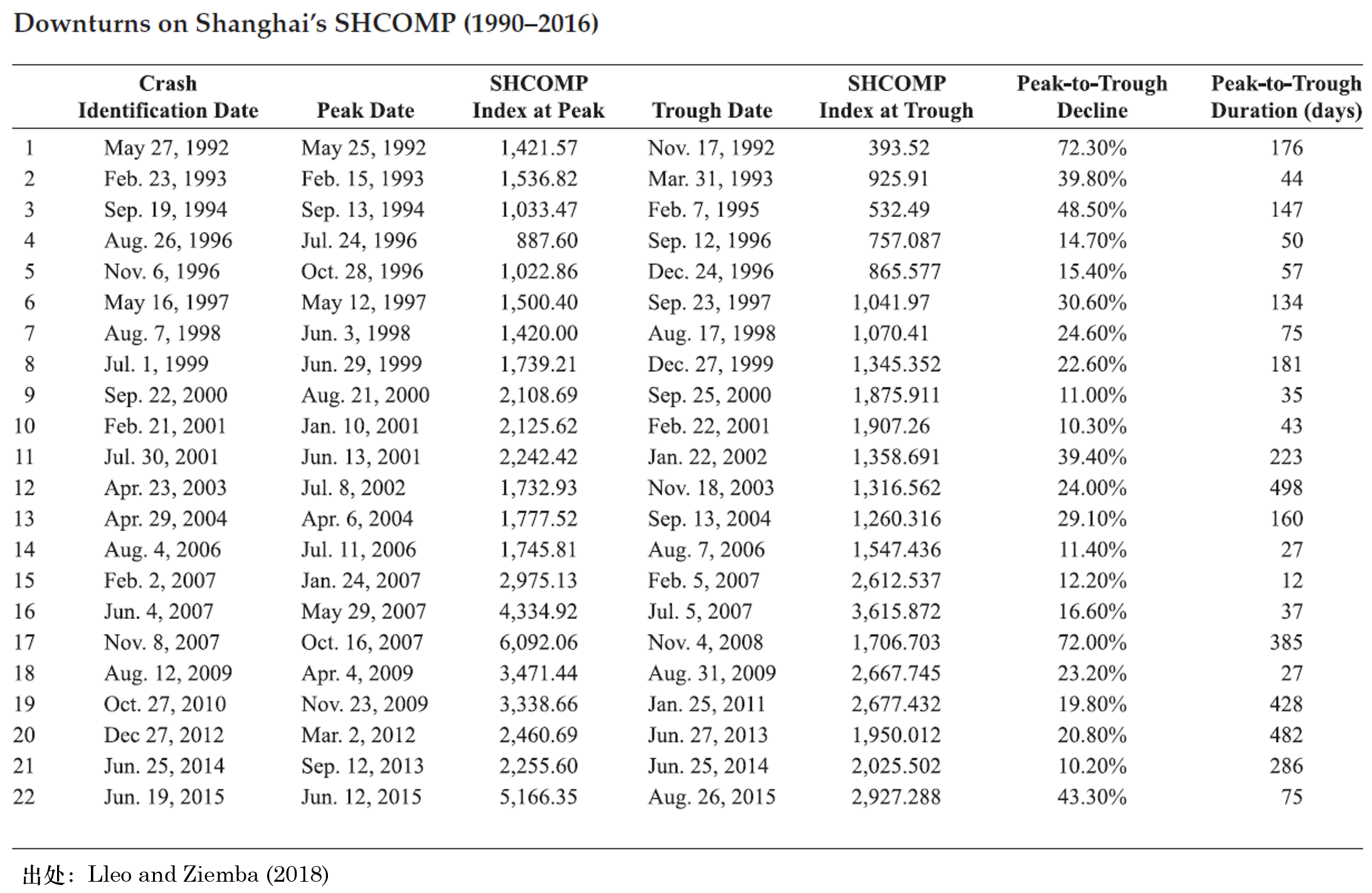
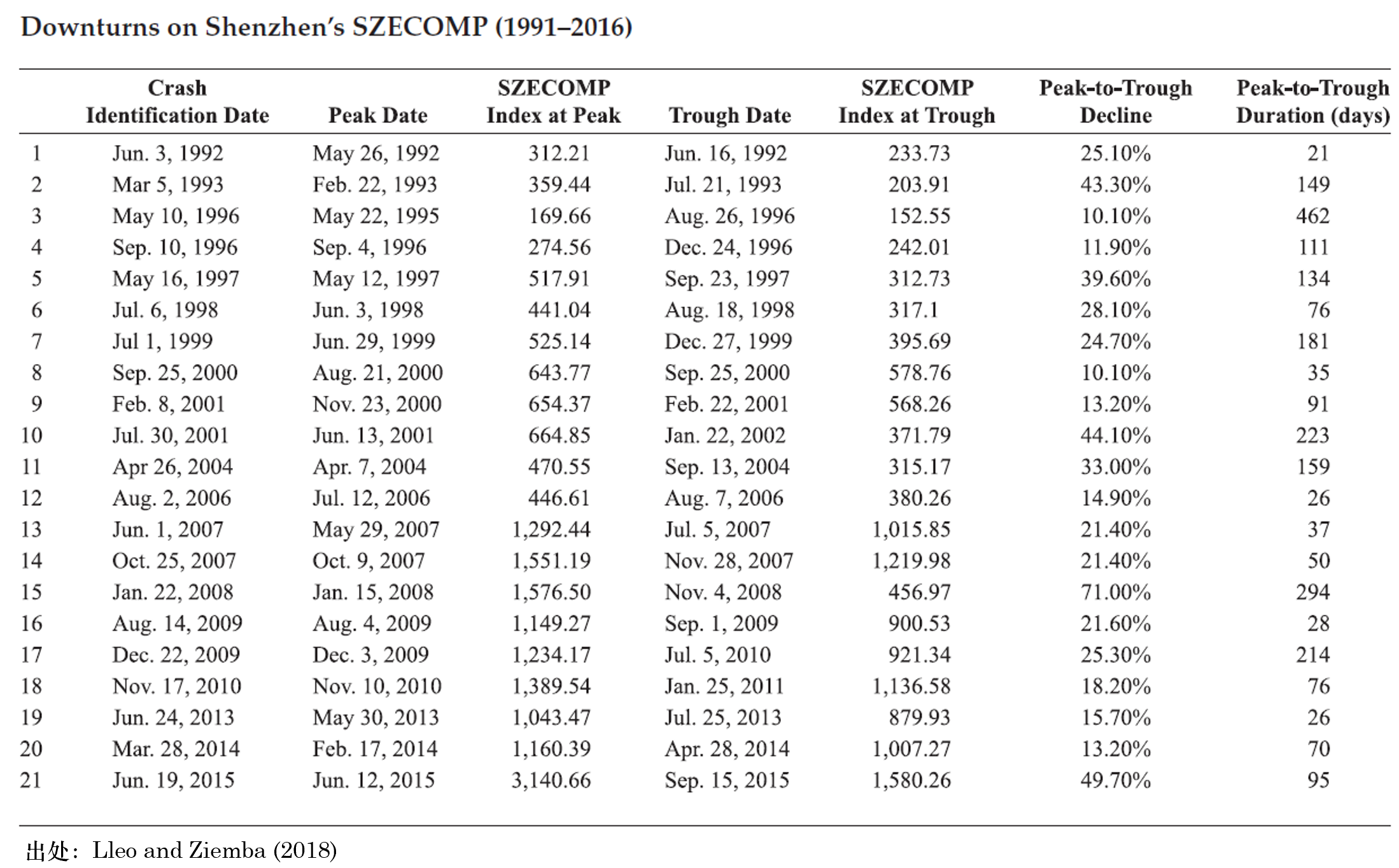
實證中，Lleo and Ziemba (2018) 分(fēn)别考慮了(le) 1990 年到 2016 年的(de)上證指數和(hé)深證綜指（399106）。按照(zhào)上述說明(míng)，他(tā)們在滬、深兩市分(fēn)别找到了(le) 22 和(hé) 21 個(gè)下(xià)行區(qū)間，分(fēn)别彙總于下(xià)表中。接下(xià)來(lái)就是針對(duì)這(zhè)些下(xià)行樣本構建預測模型。

3 預測模型

下(xià)行風險預測模型使用(yòng)選定的(de)基本面估值指标計算(suàn)信号：信号等于 1 說明(míng)在未來(lái)有跌幅超過 10% 的(de)下(xià)行風險；信号爲 0 說明(míng)沒有該風險。此外，Lleo and Ziemba (2018) 給出了(le)評價該模型準确性的(de)算(suàn)法。本節和(hé)下(xià)節分(fēn)别介紹預測模型和(hé)評價模型準确性的(de)算(suàn)法。預測模型的(de)原理(lǐ)非常簡單。假設基本面指标在交易日 t 的(de)取值爲 M_t，使用(yòng)該指标在過去一段長(cháng)度爲 d 的(de)窗(chuāng)口内的(de)均值和(hé)标準差計算(suàn)出一個(gè)阈值 K_t；如果 M_t > K_t，則認爲市場(chǎng)估值過高(gāo)，因而下(xià)行風險信号 S_t = 1、反之則認爲下(xià)行風險信号 S_t = 0。

在計算(suàn)阈值 K_t 時(shí)，Lleo and Ziemba (2018) 選擇的(de)滾動窗(chuāng)口長(cháng)度 d 爲 252 個(gè)交易日，從而動态計算(suàn)不同市場(chǎng)環境下(xià)估值的(de)阈值。在具體計算(suàn) K_t 時(shí)，他(tā)們采用(yòng)了(le)兩種方法：（1）正态分(fēn)布假設；（2）Cantelli 不等式。由于僅考慮估值過高(gāo)風險，故采用(yòng)單邊 95% 的(de)置信區(qū)間。在正态分(fēn)布的(de)假設下(xià)，該阈值 K_t 對(duì)應均值加上 1.645 個(gè)标準差：

考慮到市場(chǎng)估值指标在任意一段給定長(cháng)度爲 d 的(de)窗(chuāng)口内不一定很好的(de)滿足正态分(fēn)布假設，Lleo and Ziemba (2018) 同時(shí)使用(yòng)了(le)Cantelli 不等式作爲另外一種計算(suàn)阈值 K_t 的(de)方法。該不等式是我們熟悉的(de) Chebyshev’s inequality（切比雪(xuě)夫不等式）的(de)單尾形式。對(duì)于未知分(fēn)布的(de)随機變量 M，假設其均值和(hé)标準差爲 μ 和(hé) σ，由 Cantelli 不等式有：

上式中，另 β = 1/(1+γ²) 可(kě)得(de)：

在模型中，Lleo and Ziemba (2018) 選擇 β = 0.25，對(duì)應 σ 的(de)乘數爲 1.732，比正态分(fēn)布下(xià)的(de) 1.645 略高(gāo)。采用(yòng)上述正态分(fēn)布模型或 Cantelli 不等式即可(kě)計算(suàn)出給定交易日 t 的(de)估值阈值上限 K_t。通(tōng)過比較當日實際估值指标 M_t 和(hé) K_t 的(de)關系，就能發出市場(chǎng)是否在未來(lái)出現下(xià)行風險的(de)信号 S_t。在這(zhè)個(gè)判斷中，必須要回答(dá)的(de)另一個(gè)問題就是：這(zhè)個(gè)信号管多(duō)久 —— 市場(chǎng)在未來(lái)多(duō)長(cháng)時(shí)間窗(chuāng)口内（記爲 H）會出現 10% 以上的(de)下(xià)行風險。H 的(de)選擇是預測模型設定問題，在 Lleo and Ziemba (2018) 中其取值爲 252 個(gè)交易日。

4 模型準确性評價

接下(xià)來(lái)介紹如何評價預測模型的(de)準确性。當模型給出 S_t = 1 的(de)信号後，如果在 t 之後的(de) H 個(gè)交易日内包含了(le)某個(gè)下(xià)行識别日（回想一下(xià)第二節的(de)定義），那麽則認爲發生了(le)市場(chǎng)下(xià)行（記爲 C_{t, H} = 1）、模型信号準确。根據這(zhè)個(gè)定義，預測模型的(de)準确性可(kě)以由下(xià)面這(zhè)個(gè)條件概率度量：

因此，隻需找出實證期内所有獨立的(de) S_t = 1 信号（爲排除市場(chǎng)的(de)自相關性，隻有當兩個(gè)下(xià)行風險信号相差 30 個(gè)交易日時(shí)才被視作獨立信号），并考察每個(gè)信号之後的(de) H 個(gè)交易日是否包含下(xià)行識别日，即可(kě)計算(suàn)出上述條件概率。數學推導可(kě)知，使用(yòng)樣本數據計算(suàn)的(de)條件概率也(yě)是模型準确性的(de) maximum likelihood estimate（具體推導請見 Lleo and Ziemba 2018，這(zhè)裏不再贅述）。

由于 A 股牛短熊長(cháng)、波動巨大(dà)的(de)特點，從任何一個(gè)天往後看 252（H 的(de)取值）個(gè)交易日，出現下(xià)行風險（跌 10% 以上）的(de)先驗概率都很大(dà)（實證數據顯示，這(zhè)個(gè)先驗概率大(dà)概是 70% 左右）。隻有當預測模型給出的(de)條件概率顯著高(gāo)于這(zhè)個(gè)非條件先驗概率時(shí)，我們才能說使用(yòng)估值指标進行預測能帶來(lái)一定的(de)價值。出于這(zhè)個(gè)考慮，Lleo and Ziemba (2018) 使用(yòng) Likelihood Ratio Test 對(duì)此進行了(le)假設檢驗。該檢驗的(de) null hypothesis 是 p = p_0，這(zhè)裏 p_0 是下(xià)行先驗概率 —— 即在實證期内任選一天，在其後 252 個(gè)交易日内包含下(xià)行識别日的(de)概率。該假設的(de) Likelihood Ratio Test 如下(xià)：

其中 L 爲 likelihood function，\hat p 是預測模型給出的(de)條件概率（p = \hat p 爲 alternative hypothesis）。使用(yòng) Λ 定義 test statistic：Y = -2logΛ，它滿足自由度爲 1 的(de) chi-squared 分(fēn)布，其 10%、5%、1% 顯著性水(shuǐ)平下(xià)對(duì)應的(de)阈值分(fēn)别爲 2.71、3.83 和(hé) 6.63。如果實證數據給出的(de) Y 值超過上述某個(gè)阈值，則我們就可(kě)以在相應的(de)顯著性水(shuǐ)平下(xià)拒絕原假設。

5 實證結果

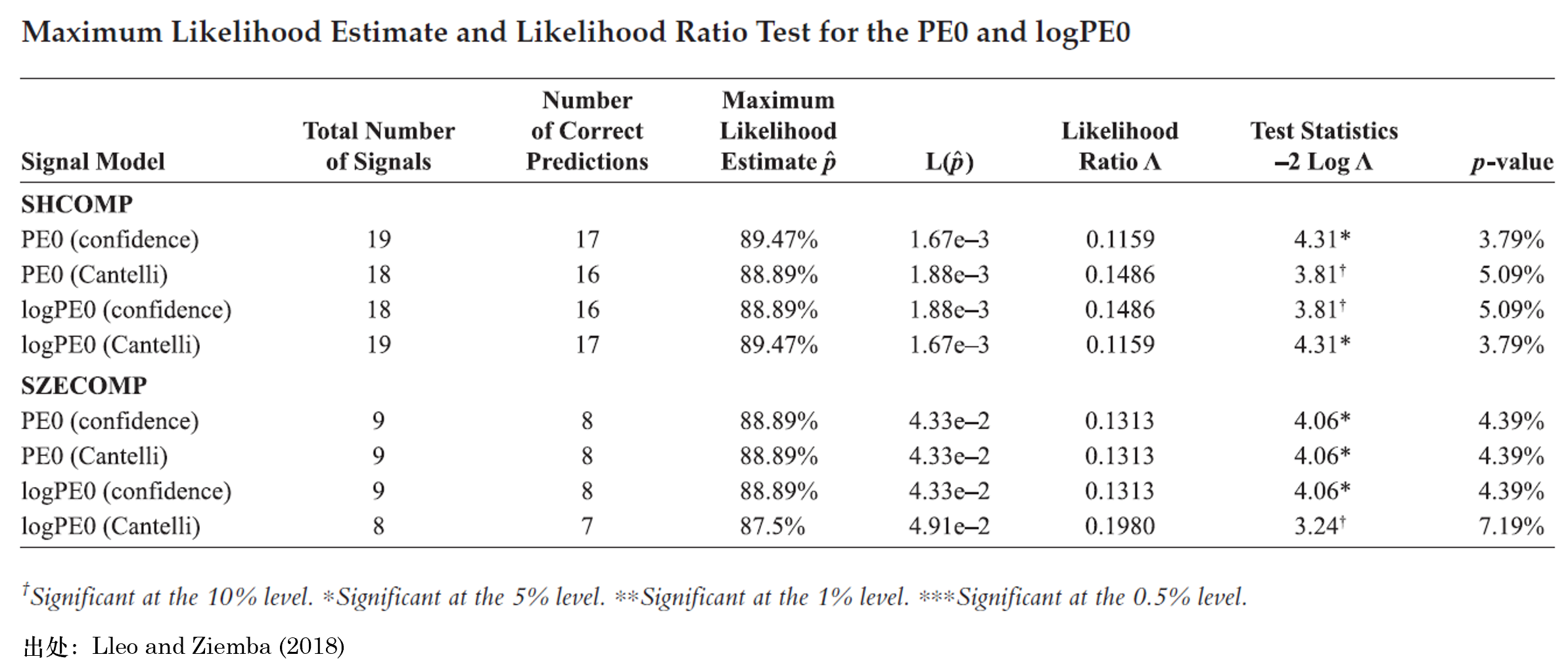
下(xià)面來(lái)看實證結果。Lleo and Ziemba (2018) 首先考察了(le) P/E 和(hé) log(P/E) 兩個(gè)市場(chǎng)估值指标。下(xià)表總結了(le)模型的(de)預測結果以及準确性分(fēn)析結果，其中對(duì)于滬、深兩市各有四行，這(zhè)是因爲對(duì)于每個(gè)指标，都分(fēn)别有兩種計算(suàn)阈值的(de)方法 —— 正态分(fēn)布和(hé) Cantelli 不等式。

以上證指數爲例，P/E 指标在這(zhè)使用(yòng)這(zhè)兩種計算(suàn)阈值方法時(shí)，分(fēn)别給出了(le) 19 和(hé) 18 次下(xià)行風險信号，其中正确的(de)次數分(fēn)别爲 17 和(hé) 16 次，因此條件概率高(gāo)達 89% 上下(xià)。另一方面，對(duì)于上證指數，出現下(xià)行風險的(de)非條件先驗概率爲 70%。通(tōng)過假設檢驗可(kě)知，test statistic Y 的(de)取值在這(zhè)兩種方法下(xià)分(fēn)别爲 4.31（5% 的(de)顯著性水(shuǐ)平）和(hé) 3.81（10% 的(de)顯著性水(shuǐ)平），因此可(kě)以說基于 P/E 估值指标的(de)預測模型對(duì)于鑒别市場(chǎng)下(xià)行風險提供了(le)顯著的(de)增量信息。我們可(kě)以對(duì)上表中其他(tā)各行的(de)結果做(zuò)類似的(de)解讀。

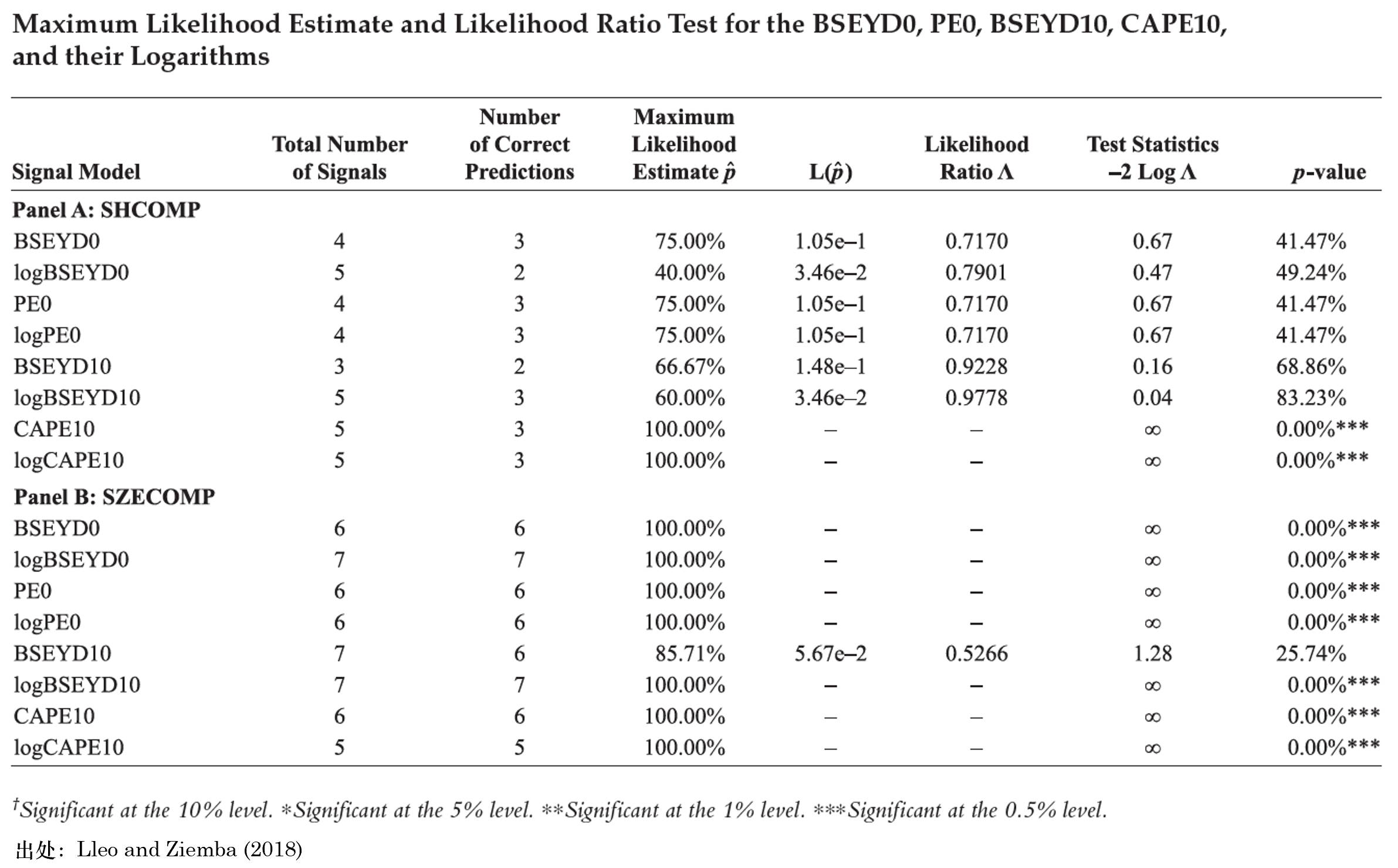
除了(le)預測信号的(de)準确性外，我們也(yě)關注召回率。對(duì)于滬深兩市，在整段實證期内分(fēn)别由 22 和(hé) 21 次下(xià)行樣本。使用(yòng) P/E 及 log(P/E)，在上證指數上正确找到 17 個(gè)，召回率爲 77%；而在深證綜指上正确找出 8 個(gè)，召回率僅有可(kě)憐的(de) 38%。該模型的(de)召回率在滬深兩市上的(de)巨大(dà)差異值得(de)進一步的(de)研究。除了(le) P/E 和(hé) log(P/E) 之外，Lleo and Ziemba (2018) 還(hái)考慮了(le)其他(tā)估值指标：BSEYD、log(BSEYD)、CAPE、log(CAPE)。由于計算(suàn) CAPE 需要用(yòng)到十年的(de)曆史數據，因此預測模型的(de)實證期爲 2005 年到 2016 年。下(xià)表給出了(le)不同估值指标的(de)預測結果。

首先需要插一句的(de)是，上表中特别用(yòng)紅框标出來(lái)的(de)部分(fēn)應該是 typo。根據 Lleo and Ziemba (2018) 上下(xià)文的(de)描述，對(duì)于上證指數，CAPE 和(hé) log(CAPE) 應該各自發出了(le) 3 次信号、而非 5 次，且 3 次全部正确，因此準确率才有 100%。在此特别“鄙視”一下(xià)審稿人(rén)。

For the SHCOMP, none of the measures produced more than five signals. The CAPE, logCAPE, and BSEYD10 generated three signals each.

下(xià)面來(lái)討(tǎo)論結果。非常有意思的(de)是，對(duì)于 2005 年之後的(de)市場(chǎng)，該模型 —— 無論使用(yòng)什(shén)麽指标 —— 在滬、深兩市上的(de)效果較整段實證期來(lái)說發生了(le)反轉。對(duì)于深證綜指，這(zhè)些指标的(de)準确率和(hé)召回率都更高(gāo)，而對(duì)于上證指數，僅 CAPE 和(hé) log(CAPE) 較非條件先驗概率顯著的(de)提升了(le)準确性。然而從召回率來(lái)看，自 2005 年到 2016 年之間，上證指數一共出現 6 次下(xià)行樣本，而上述兩個(gè)指标僅找到三次，召回率僅有 50%。Lleo and Ziemba (2018) 對(duì)于模型在滬、深兩市上的(de)差異也(yě)做(zuò)了(le)思考。除了(le)樣本量較少造成的(de)誤差之外，二位作者認爲該分(fēn)歧也(yě)和(hé)滬深兩市上市公司的(de)屬性差異很大(dà)有關。上交所的(de)上市公司多(duō)爲國有企業，而深交所的(de)上市公司多(duō)爲民營企業。二位作者猜測，政府對(duì)國有企業支持而造成對(duì)市場(chǎng)的(de)幹預，有可(kě)能會推遲和(hé)減少下(xià)行風險的(de)出現，從而影(yǐng)響預測模型的(de)效果。

6 結語

預測市場(chǎng)什(shén)麽時(shí)候要 crash 從來(lái)就不容易。将市場(chǎng)的(de) P/E 或者 CAPE 這(zhè)類估值指标和(hé)未來(lái)收益率關聯起來(lái)的(de)嘗試并也(yě)不是什(shén)麽新鮮事物(wù)，但希望 Lleo and Ziemba (2018) 在 A 股上的(de)實證結果能給我們一些啓發。2014 年，Robert Shiller 教授紐約時(shí)報上撰文稱，提出 CAPE 的(de)目的(de)不是爲了(le)預測市場(chǎng)未來(lái)的(de)漲跌，而是希望在市場(chǎng)估值過高(gāo)時(shí)引發人(rén)們的(de)思考。

The CAPE was never intended to indicate exactly when to buy and to sell. The market could remain at these valuations for years. But we should recognize that we are in an unusual period, and that it’s time to ask some serious questions about it.

從 Lleo and Ziemba (2018) 的(de)結果以及其他(tā)針對(duì) A 股的(de)實證分(fēn)析來(lái)看，過高(gāo)估值和(hé)未來(lái)的(de)下(xià)行風險之間肯定存在著(zhe)某種正相關性。然而，要想利用(yòng)這(zhè)種相關性、将其作爲整套量化(huà)系統（特别是風險管理(lǐ)）的(de)一部分(fēn)，或者使用(yòng)它進行市場(chǎng)或者其他(tā)風格因子擇時(shí)，仍有很多(duō)的(de)問題需要解答(dá)。

參考文獻

Goetzmann, W., D. Kim, and R. Shiller (2016). Crash beliefs from investor surveys. Working paper.

Gresnigt, F., E. Kole, and P. Franses (2015). Interpreting financial market crashes as earthquakes: a new early warning system for medium-term crashes. Journal of Banking & Finance 56, 123 – 139.

Jarrow, R. A., Y. Kchia, and P. Protter (2011). How to detect an asset bubble. SIAM Journal on Financial Mathematics 2(1), 839 – 865.

Lleo, S. and W. T. Ziemba (2017). Does the bond-stock earnings yield differential model predict equity market corrections better than high P/E models? Financial Markets, Institutions & Instruments 26(2), 61 – 123.

Lleo, S. and W. T. Ziemba (2018). Predicting stock market crashes in China. The Journal of Portfolio Management 44(5), 125 – 135.

Shiryaev, A. N. and M. V. Zhitlukhin (2012). Bayesian disorder detection problems on filtered probability space. Theory of Probability and Its Applications 57(3), 497 – 511.

Ziemba, W. T. and S. L. Schwartz (1991). Invest Japan. Chicago: Probus.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。