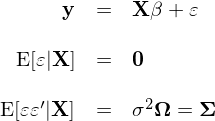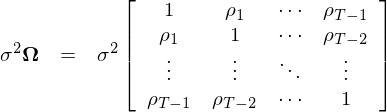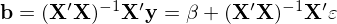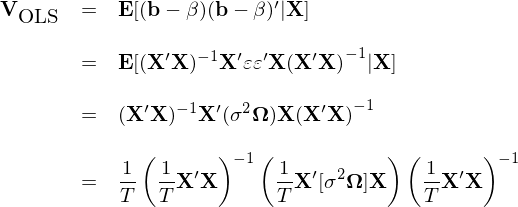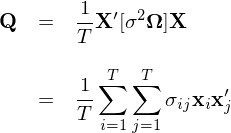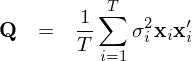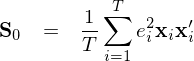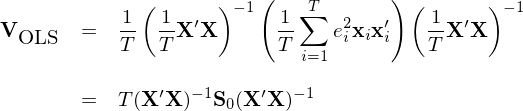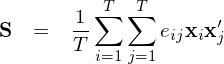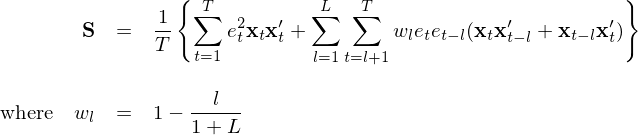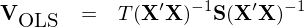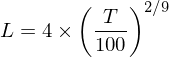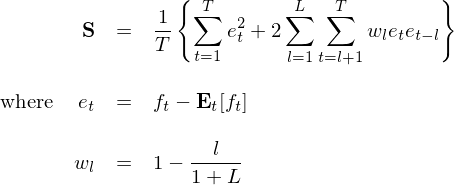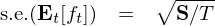多(duō)因子回歸檢驗中的(de) Newey-West 調整

作者：石川

摘要：Newey-West 調整是計量經濟學中的(de)經典方法，在多(duō)因子模型回歸分(fēn)析中無處不在。本文介紹它的(de)用(yòng)法。

1 引言

本文有很多(duō)數學公式。本文的(de)推導重點參考了(le) William Greene 的(de)經典教材 Econometric Analysis（Greene 2003，我用(yòng)的(de)第五版，最新的(de)出到了(le)第八版）。本文回答(dá)了(le)一個(gè)曾讓我糾結很久的(de)問題。

在學術界關于 empirical asset pricing 的(de)論文中，portfolio test 和(hé) regression test 是檢驗一個(gè)新因子是否有效的(de)兩個(gè)常見手段。在前者中，使用(yòng)已有因子的(de)收益率作爲 regressors、使用(yòng)基于新因子構建的(de)投資組合的(de)收益率作爲被解釋變量，進行時(shí)序回歸，從而檢驗新因子組合是否可(kě)以獲得(de)超額收益 α、以及它在已有因子上的(de) β。在後者中，新因子和(hé)已有因子一起被用(yòng)來(lái)和(hé)個(gè)股收益率進行截面回歸（通(tōng)常使用(yòng) Fama-MacBeth regression），然後考察新因子的(de)預期收益率 E[f] 是否顯著不爲零。

無論是上面哪種方法，學者們都會對(duì)回歸分(fēn)析得(de)到的(de) α、β 以及 E[f] 給出 t-statistic 從而檢驗它們的(de)顯著性。而在學術論文所報告的(de)結果中，經常出現諸如“Newey and West adjusted t-statistic”或者“Newey and West adjusted standard error”（standard error 是用(yòng)來(lái)計算(suàn) t-statistic 的(de)）這(zhè)樣的(de)描述。這(zhè)不禁讓人(rén)疑問：回歸檢驗中的(de) Newey and West 調整到底是什(shén)麽？

除了(le)要搞懂(dǒng)它到底是什(shén)麽之外，我們也(yě)關心它是如何實操的(de)，這(zhè)樣才能将它用(yòng)在 A 股的(de)實證研究中。這(zhè)就是本文關心的(de)話(huà)題。本文的(de)内容提要如下(xià)：

讓我們從廣義線性回歸說起。

2 廣義線性回歸

考慮如下(xià)廣義線性回歸模型（generalized linear regression model）：

上述模型是時(shí)序上的(de)線性回歸模型；其中 y 是 T × 1 階向量（T 代表時(shí)序的(de)總期數）；X 是 T × K 階矩矩陣（其中 K 是 regressors 的(de)個(gè)數）；ε 是 T × 1 階殘差向量；Σ（T × T 階）是殘差的(de)協方差矩陣。回歸的(de)目的(de)是爲了(le)得(de)到回歸系數 β（K × 1 階矩陣）并檢驗它們的(de)顯著性。上述模型和(hé)經典線性回歸模型最大(dà)的(de)區(qū)别是矩陣 Ω 的(de)引入。在經典模型中假設給定解釋變量 X 下(xià)，不同時(shí)刻 t 的(de)殘差是獨立且同方差，因此 Ω 是單位陣 I。

在廣義線性回歸中，殘差獨立、同方差這(zhè)兩個(gè)假設均可(kě)被打破，從而得(de)到兩個(gè)殘差中常見的(de)特性：異方差（heteroscedasticity）和(hé)自相關（autocorrelation）。多(duō)因子模型回歸中的(de)殘差就經常呈現上述兩種特性。在廣義線性回歸模型中引入 Ω 正是爲了(le)反映上述特性。以下(xià)是兩個(gè)例子。對(duì)于異方差（但仍可(kě)以假設獨立），通(tōng)常有：

對(duì)于自相關（但同方差），通(tōng)常有：

當然我們也(yě)可(kě)以既考慮異方差又考慮自相關性。在一般情況下(xià) Ω 矩陣中第 i 行、第 j 列的(de)元素用(yòng) ω_{ij} 表示。如果 Ω 已知，則通(tōng)常使用(yòng) generalized least squares 來(lái)對(duì) β 進行參數估計。但當 Ω 未知時(shí)，OLS 往往是首選。對(duì)該廣義線性回歸模型進行 OLS 求解就可(kě)以得(de)到 β 的(de) OLS 估計量，記爲 b：

對(duì)上式兩邊取期望，則當 E[ε|X] = 0 的(de)假設成立時(shí)易知 E[b] = β。利用(yòng) E[b] = β 進而推導出 b 的(de)協方差矩陣，記爲 V_OLS：

當殘差不存在異方差以及自相關性時(shí)，Ω = I 而上面的(de)協方差矩陣也(yě)可(kě)以簡化(huà)成我們最熟悉的(de)經典 OLS 裏面的(de)形式，也(yě)就是各種 OLS 軟件包給出的(de)參數的(de)标準誤（協方差矩陣對(duì)角線元素的(de)平方根）和(hé) t-statistic 的(de)結果。然而，當殘差存在異方差或者自相關時(shí)，OLS 得(de)到的(de) β 的(de)方差的(de)估計是不準确的(de)，從而影(yǐng)響對(duì) β 進行統計檢驗。在 Ω 未知的(de)情況下(xià)，需對(duì) V_OLS 進行估計。上面的(de)表達式可(kě)以看成是三個(gè)矩陣相乘的(de)形式，其中第一個(gè)和(hé)第三個(gè)僅和(hé) X 有關，因此核心目标就是估計中間矩陣（middle matrix）。爲了(le)方便討(tǎo)論，另 Q 代表中間的(de)矩陣：

其中 x_i = [x_{i1}, x_{i2}, …, x_{iK}]’，即 X 的(de)第 i 行的(de)轉置（注意它不等于 X 的(de)第 i 列）。一旦我們能找到矩陣 Q 的(de)估計，便可(kě)進而求出 b 的(de)協方差矩陣 V_OLS。在估計 Q 時(shí)，我們需要用(yòng)到的(de)“武器”便是 regressor 矩陣 X 以及回歸殘差 e。針對(duì)殘差的(de)假設不同，最常見的(de)兩種估計是 White 估計（僅假設異方差）以及 Newey and West 估計（考慮異方差及自相關）。

3 White and Newey-West Estimators

當殘差僅有異方差但沒有自相關時(shí)，我們需要的(de)估計量 Q 簡化(huà)爲：

White (1980) 指出使用(yòng) X 以及 e 可(kě)以求出 Q 的(de)漸進估計（記爲 S_0）：

将上述 Q 的(de)估計 S_0 代入到 V_OLS 的(de)表達式中，可(kě)以得(de)到 b 的(de)協方差矩陣的(de)估計：

上述估計稱爲 White heteroscedasticity consistent estimator。這(zhè)一結果極其重要。它意味著(zhe)哪怕我們對(duì)異方差的(de)取值或結構一無所知，我們仍然可(kě)以根據最小二乘的(de)結果進行适當的(de)推斷。考慮到實際問題中，多(duō)因子收益率殘差的(de)異方差性質未知，這(zhè)一性質就顯得(de)格外重要。在實際問題中，除了(le)異方差外，仍需考慮殘差的(de)自相關性。爲此，一個(gè)自然的(de)想法是将上述 Q 的(de)估計延伸到對(duì)角線之外的(de)元素，即：

然而，這(zhè)種方法有兩個(gè)問題，因此并不正确：

怎麽辦呢(ne)？大(dà)名鼎鼎的(de) Newey and West estimator（Newey and West 1987）閃亮登場(chǎng)！他(tā)們給出了(le)當殘差同時(shí)存在異方差和(hé)自相關時(shí)，Q 的(de)相合估計，記爲 S：

這(zhè)就是計量經濟學中無處不在的(de) Newey-West 調整。上式中，大(dà)括号中的(de)第一項對(duì)應僅有異方差情況下(xià)的(de) S_0，而後面第二項則是針對(duì)自相關性的(de)修正。其中 L 是計算(suàn)自相關性影(yǐng)響的(de)最大(dà)滞後階數（Newey and West 1994 給出了(le)自動計算(suàn) L 取值的(de)自适應算(suàn)法），w_l 是滞後期 l 的(de)系數，其隐含的(de)意思是自相關性的(de)影(yǐng)響随著(zhe)滞後期 l 的(de)增大(dà)而減小。在實際計算(suàn)時(shí)，考慮到自由度的(de)問題，爲了(le)得(de)到無偏估計可(kě)以将上式中大(dà)括号外面的(de) 1/T 換成 1/(T - K)；大(dà)括号内部的(de)求和(hé)項仍是 T 項及 L × T 項。

将 S 代入到 V_OLS 的(de)表達式中，得(de)到 Newey–West autocorrelation consistent covariance estimator：

在時(shí)序 OLS 回歸中，Newey-West 調整同時(shí)作用(yòng)于多(duō)個(gè) regressors 的(de)回歸系數，從而求出 b 的(de)協方差矩陣，常見于因子分(fēn)析中的(de) portfolio test 中，具體方法爲：

下(xià)面來(lái)看一個(gè)例子。

4 一個(gè)例子

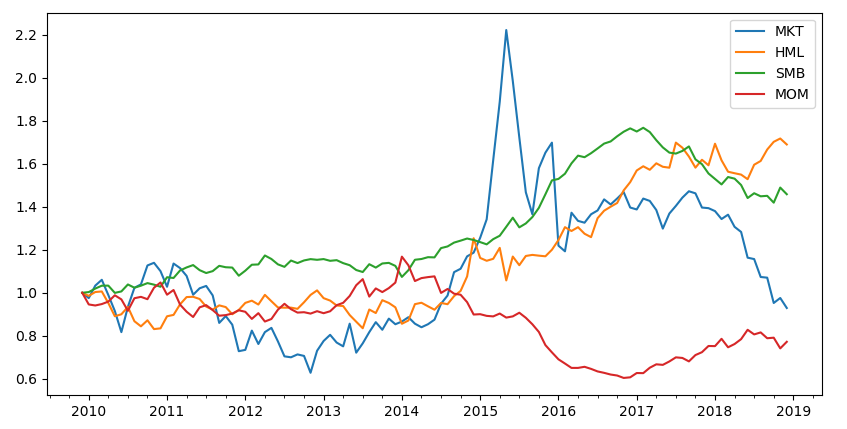
《尋找股票(piào)市場(chǎng)中的(de)預期差》一文基于基本面和(hé)市場(chǎng)預期之差進行了(le)選股。對(duì)于使用(yòng)“預期差”因子構建的(de)投資組合，該文應用(yòng)一些已有因子進行了(le) portfolio test。假設已有因子包括 Fama and French (1993) 三因子以及 Carhart (1997) 的(de)動量因子。這(zhè)四個(gè)因子的(de)累積收益率如下(xià)圖所示。下(xià)面用(yòng)這(zhè)個(gè) portfolio test 說明(míng) Newey-West 調整。

以上述四個(gè)因子以及一個(gè)截距項作爲 regressors，對(duì)“預期差”因子的(de)投資組合在時(shí)序上進行 OLS 回歸，得(de)到殘差 e。加入截距項後，X 矩陣一共有 5 列 —— 第一列全是 1，對(duì)應截距；後面四列對(duì)應 4 個(gè)已有因子的(de)收益率時(shí)間序列。使用(yòng) X 和(hé) e 對(duì)進行 Newey-West 調整，計算(suàn)回歸系數的(de)标準誤。在計算(suàn)中，使用(yòng) Newey and West (1994) 自動計算(suàn)滞後階數 L：

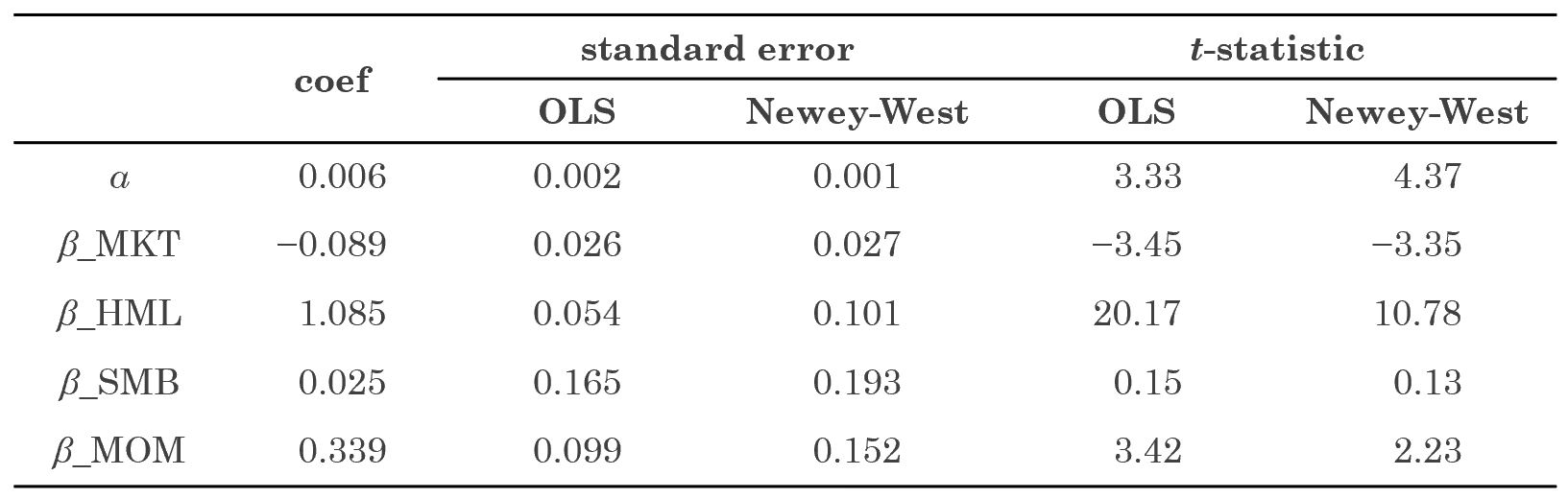
由于實證中一共使用(yòng)了(le) 108 期月(yuè)頻(pín)收益率數據，因此 T = 108；由上式計算(suàn)出的(de) L = 4。下(xià)表給出了(le)使用(yòng)經典 OLS 和(hé)使用(yòng) Newey-West 調整後得(de)到的(de)回歸系數 standard errors 以及 t-statistics。

使用(yòng) Newey-West 調整後，“預期差”選股的(de)超額收益（α）的(de) t-statistic 從 3.325 上升至 4.371；HML 以及 MOM 因子的(de)系數 β_HML 和(hé) β_MOM 的(de) t-statistics 分(fēn)别從 20.171 和(hé) 3.420 降低到 10.778 和(hé) 2.233。

5 簡化(huà)版 Newey-West 調整

上一節說明(míng)了(le)在進行時(shí)序回歸的(de) portfolio test 中如何進行 Newey-West 調整。那麽，使用(yòng)截面回歸的(de) regression test 又如何呢(ne)？在因子分(fēn)析中，Fama-MacBeth regression 是最常見的(de)截面回歸方法（Fama and MacBeth 1973）。在該回歸中，每一期使用(yòng)當期因子暴露和(hé)個(gè)股下(xià)一期的(de)收益率進行截面回歸，得(de)到因子的(de)收益率；在全部期進行截面回歸後，便可(kě)得(de)到每個(gè)因子收益率的(de)時(shí)間序列。将因子收益率在時(shí)序上取均值就得(de)到每個(gè)因子的(de)預期收益率，而我們關心的(de)是該因子預期收益率是否顯著不爲零。

對(duì)于任何因子，其收益率序列在時(shí)序上很可(kě)能存在異方差和(hé)自相關性，因此在計算(suàn)其均值标準誤的(de)時(shí)候需要進行 Newey-West 調整。然而，這(zhè)和(hé)上面的(de)多(duō)因子時(shí)序回歸很不相同。如何進行 Newey-West 調整呢(ne)？關于這(zhè)個(gè)問題，Turan Bali、Robert Engle、Scott Murray 三位所著的(de)經典教材 Empirical Asset Pricing, the cross section of stock returns（Bali et al. 2016）給出了(le)答(dá)案。對(duì)于單個(gè)因子的(de)收益率序列，将其用(yòng) 1 作爲 regressor 回歸得(de)到殘差 —— 這(zhè)相當于用(yòng)因子收益率減去它在時(shí)序上的(de)均值。然後把這(zhè)個(gè)殘差和(hé) X = 1 代入到 Newey-West 調整中即可(kě)。

在這(zhè)個(gè)簡化(huà)版的(de) Newey-West 調整中，Q 的(de)估計 S 簡化(huà)爲：

其中 f_t 代表被檢驗因子的(de)收益率時(shí)間序列，E_t[f_t] 是它在時(shí)序上的(de)均值。由于我們僅僅有一個(gè) regressor，因此上述 S 其實是一個(gè)标量。将它代入到 V_OLS 的(de)表達式中，在對(duì)其開方，就得(de)到 E_t[f_t] 的(de)标準誤：

對(duì)每個(gè)因子依次使用(yòng)上述修正，獲得(de)其各自收益率均值的(de) standard error，然後就可(kě)以計算(suàn) t-statistic 以及 p-value 并檢驗它們的(de)顯著性。

6 結語

本文介紹了(le)計量經濟學中常見的(de) Newey-West 估計（順便提一句， White 1980 估計也(yě)十分(fēn)流行），它們在因子回歸分(fēn)析中無處不在。在 portfolio test 中，通(tōng)過時(shí)序回歸，并應用(yòng) Newey-West 調整對(duì)多(duō)個(gè) regressors 的(de)回歸系數的(de)标準誤同時(shí)修正；在 regression test 中，首先通(tōng)過 T 期截面回歸得(de)到因子的(de)收益率時(shí)序，然後再對(duì)該時(shí)序進行 Newey-West 調整從而得(de)到因子預期收益率的(de)标準誤。

在 Barra 的(de)因子模型中，采用(yòng) Newey-West 調整對(duì)日頻(pín)因子收益率的(de)協方差矩陣進行了(le)修正（Briner et al. 2009, pp 25）：

有必要指出的(de)是，Barra 修正的(de)是因子收益率的(de)協方差矩陣，而不是因子收益率均值或者任何回歸系數 β 的(de)協方差矩陣。仔細檢查上面的(de)式子，并沒有看到任何 regressor 矩陣 X 或者殘差向量 e 的(de)身影(yǐng)；以上 Barra 的(de)用(yòng)法和(hé)本文討(tǎo)論的(de) portfolio test 和(hé) regression test 中的(de) Newey-West 調整都不太一樣。Barra 借鑒了(le) Newey-West 對(duì)協方差矩陣進行 HAC 估計的(de)做(zuò)法；Barra 的(de)日頻(pín)自相關矩陣 C 對(duì)應 Newey and West (1987) 中的(de) \hat Ω_0，從而應用(yòng)了(le) Newey and West (1987) 中的(de)式 (5) 修正變量的(de)自相關對(duì)協方差矩陣的(de)影(yǐng)響。

最後，非常感謝你認真看到這(zhè)裏。這(zhè)不是一篇 fancy 的(de)文章(zhāng)，而是一篇工具文，希望它能對(duì)你有些幫助。在我自己進行 empirical asset pricing 研究時(shí)，在 portfolio test 和(hé) regression test 時(shí)也(yě)會用(yòng)到 Newey-West 調整。相信你看完本文，在今後再看到我提及它的(de)時(shí)候，知道我幹了(le)什(shén)麽。

參考文獻

Bali, T. G., R. F. Engle, and S. Murray (2016). Empirical asset pricing, the cross section of stock returns. John Wiley & Sons, Inc., Hoboken, New Jersey.

Briner, B. G., R. C. Smith, and P. Ward (2009). The Barra Europe equity model (EUE3). Research Notes.

Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance 52(1), 57 – 82.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and J. D. MacBeth (1973). Risk, return, and equilibrium: Empirical tests. Journal of Political Economy 81(3), 607 – 636.

Greene, W. H. (2003). Econometric Analysis (5th ed). Prentice Hall, Upper Saddle River, New Jersey.

Newey, W. K. and K. D. West (1987). A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 55(3), 703 – 708.

Newey, W. K. and K. D. West (1994). Automatic lag selection in covariance matrix estimation. Review of Economic Studies 61(4), 631 – 653.

White, H. (1980). A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica 48(4), 817 – 838.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。