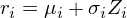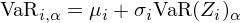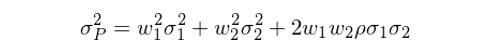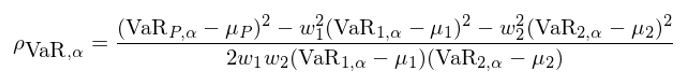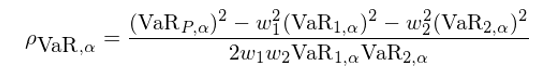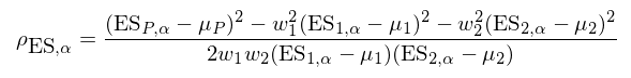尾部相關性、尾部風險平價和(hé)聖杯分(fēn)布

作者：石川

摘要：本文首先介紹了(le)尾部相關性，并以此引出尾部風險平價的(de)概念。從風險的(de)角度來(lái)說，一個(gè)好的(de)投資組合中應該同時(shí)擁有 convergent 和(hé) divergent risk taking 的(de)策略。

1 引言

年底适合聊聊風險。

在《艱難時(shí)刻需要堅韌信仰》這(zhè)篇文章(zhāng)的(de)最後，我們提到了(le)同一大(dà)類資産中的(de)不同策略，盡管它們平時(shí)的(de)相關性可(kě)能很低，但是當極端事件出現時(shí)，它們的(de)相關性會驟然上升，同時(shí)下(xià)跌造成虧損，無法起到分(fēn)散風險的(de)作用(yòng)。不同策略在極端情況下(xià)的(de)相關性稱爲尾部相關性（tail correlation），它是進行資産組合配置時(shí)需要考慮的(de)關鍵因素之一。

本文将圍繞尾部風險展開討(tǎo)論。下(xià)文首先介紹尾部相關性，之後引出尾部風險平價（tail risk parity）的(de)概念，它被認爲比流行的(de)風險平價（risk parity）更能抗風險。最後會介紹兩個(gè)平時(shí)提的(de)較少的(de)兩個(gè)風險概念 —— convergent and divergent risk taking。（抱歉，實在找不出來(lái)特别合适的(de)中文翻譯，但我保證會用(yòng)中文大(dà)白話(huà)解釋清楚。）先來(lái)看看尾部相關性。

2 尾部相關性

尾部相關性衡量的(de)是不同資産出現極端損失時(shí)的(de)相關性。爲了(le)計算(suàn)它，最簡單的(de)辦法可(kě)以采用(yòng)條件概率計算(suàn)條件相關性。但是，業界主流的(de)做(zuò)法是通(tōng)過 VaR（Value at Risk）或者 ES（Expected Shortfall）來(lái)反推尾部相關性，這(zhè)樣得(de)到的(de)結果稱爲 VaR-implied tail correlation 或 ES-implied tail correlation。本文介紹後面這(zhè)種方法。Liu (2016) 使用(yòng) Campbell et al. (2002) 的(de)模型，假設資産 i 的(de)收益率 r_i 分(fēn)布滿足如下(xià)形式：

其中 μ_i、σ_i 分(fēn)别爲均值和(hé)标準差，Z_i 爲标準正态分(fēn)布。由上述分(fēn)布模型以及 VaR 的(de)定義可(kě)知，資産 i 的(de) α 分(fēn)位數的(de) VaR 爲：

假設某投資組合 P 由兩個(gè)資産按照(zhào)權重 w_1 和(hé) w_2 構成，則根據定義，投資組合 P 的(de)收益率的(de)标準差滿足：

将 VaR 定義中右側的(de) σ_i 代入上式，并利用(yòng) VaR(Z_1) = VaR(Z_2) = VaR(Z_P) 化(huà)簡，最終得(de)到兩個(gè)資産間的(de) VaR-implied correlation：

除了(le)上述這(zhè)種計算(suàn)方法，業界（Cotter and Longin 2006）還(hái)使用(yòng)另一種更簡化(huà)的(de)方法：

這(zhè)種方法直接使用(yòng)資産和(hé)投資組合的(de) VaR 進行計算(suàn)，并不對(duì) r 的(de)分(fēn)布做(zuò)正态假設。它和(hé)前一種方法的(de)區(qū)别就是計算(suàn)時(shí)是否使用(yòng) μ_i。由于 μ_i 的(de)取值較 VaR 通(tōng)常小一個(gè)數量級，因此兩種方法的(de)計算(suàn)結果非常接近。值得(de)一提的(de)是，當 VaR 被用(yòng)來(lái)刻畫(huà)尾部風險時(shí)，其常被人(rén)诟病的(de)是它僅僅是一個(gè) α 分(fēn)位數的(de)取值，衡量的(de)是在給定的(de)概率下(xià)損失的(de)最小值、不能準确刻畫(huà)收益分(fēn)布的(de)左側肥尾。爲了(le)解決這(zhè)個(gè)問題，人(rén)們提出了(le) Expected Shortfall（ES，也(yě)稱作 Expected Tail Loss）的(de)概念，它是 α 分(fēn)位數左側尾部風險的(de)均值，相較于 VaR 能夠更好的(de)刻畫(huà)尾部風險。

将上述 VaR-implied correlation 根據 ES 的(de)定義做(zuò)一步擴展得(de)到 ES-implied correlation：

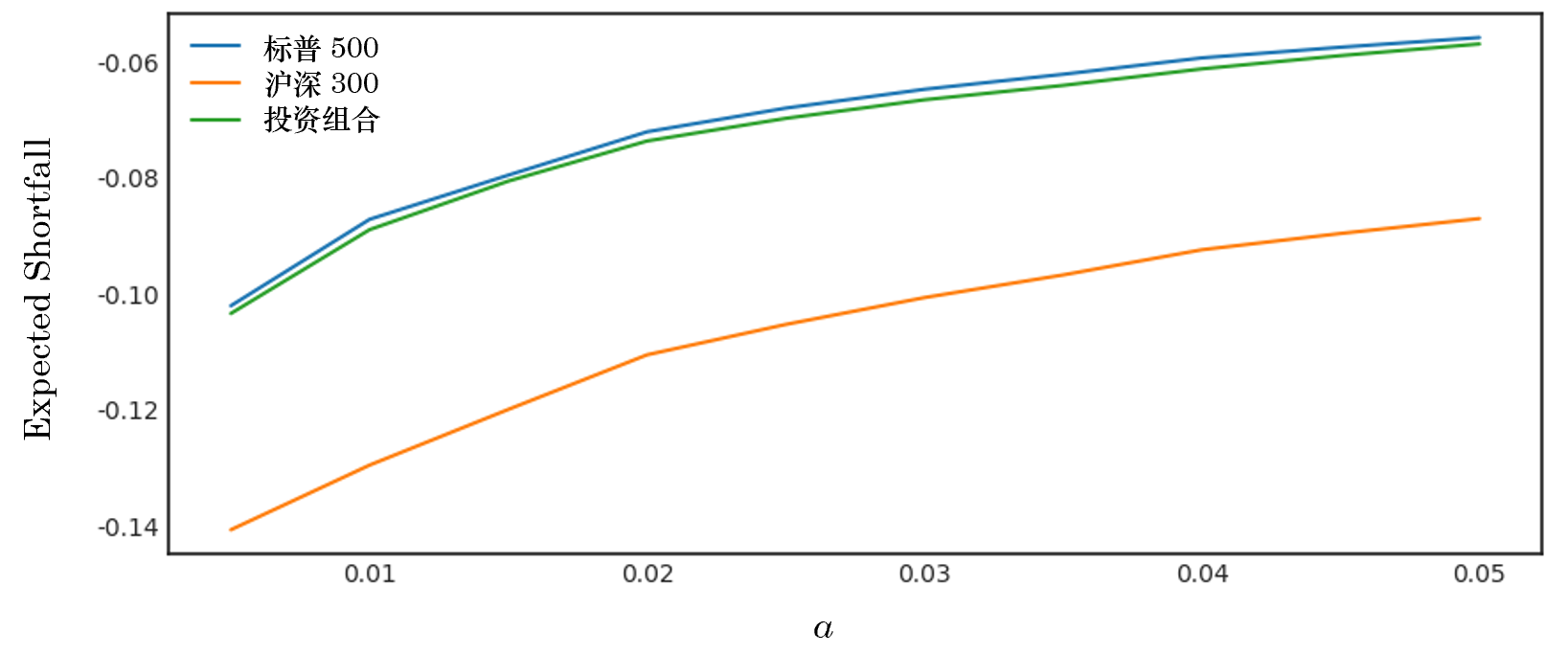
舉個(gè)例子。讓我們來(lái)看看滬深 300 指數和(hé)标普 500 指數的(de)相關性是否随尾部風險遞增。假設使用(yòng)周頻(pín)數據，數據的(de)跨度從 2005 年 1 月(yuè)到 2018 年 11 月(yuè)。上述兩種資産在這(zhè)段時(shí)期内周頻(pín)收益率的(de)相關系數爲 0.16。假設按照(zhào) w_1 = w_2 = 0.5 的(de)權重配置它們，得(de)到投資組合，以此計算(suàn)它們之間的(de) ES-implied correlation。下(xià)圖展示了(le)這(zhè)兩種資産和(hé)投資組合在不同 α 分(fēn)位數下(xià)的(de) ES。毫無意外地，随著(zhe) α 的(de)減小（代表著(zhe)尾部事件越來(lái)越極端），ES 的(de)虧損幅度也(yě)逐漸增大(dà)。

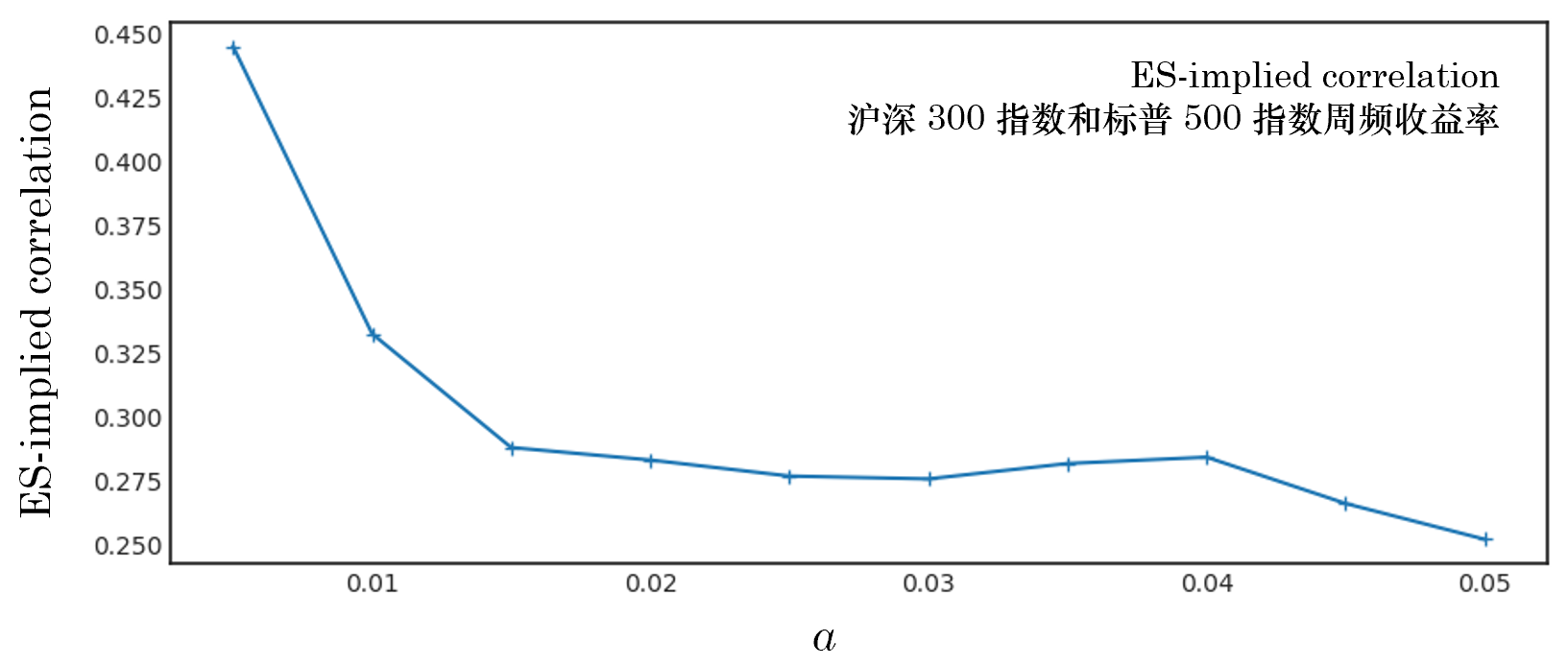
下(xià)圖是這(zhè)兩種資産的(de) ES-implied correlation。随著(zhe)尾部事件越來(lái)越極端，二者的(de)尾部 correlation 也(yě)逐漸增大(dà)，且遠(yuǎn)遠(yuǎn)高(gāo)于整個(gè)回測期内的(de) 0.16。當 α = 1% 時(shí)，二者的(de)相關系數高(gāo)達 0.333；當 α = 0.5% 時(shí)，它們的(de)相關系數進一步增大(dà)到 0.445。當金融危機出現的(de)時(shí)候，誰都難以獨善其身。

3 尾部風險評價

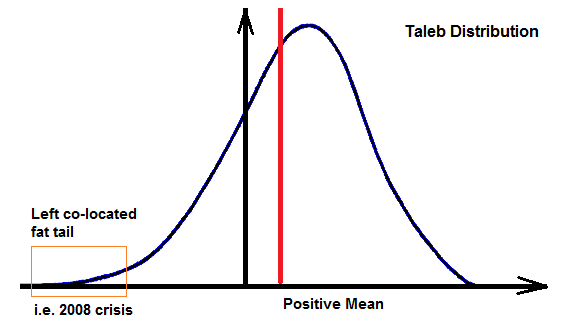
對(duì)于大(dà)部分(fēn)常見的(de)資産或者投資策略，它們的(de)收益分(fēn)布都有如下(xià)的(de)形狀 —— 均值爲正，但是左側存在著(zhe)極端事件造成的(de)巨大(dà)虧損，從而造成分(fēn)布的(de)負偏。這(zhè)個(gè)分(fēn)布通(tōng)常稱爲 Taleb Distribution，以 Nassim Nicholas Taleb 命名；他(tā)以黑(hēi)天鵝一書(shū)聞名于世（左側的(de)極端事件則代表了(le)黑(hēi)天鵝）。

不同資産的(de)尾部相關性遠(yuǎn)遠(yuǎn)高(gāo)于它們平時(shí)的(de)相關性說明(míng)這(zhè)些資産的(de)左側肥尾往往同時(shí)出現（比如 2008 年的(de)金融危機），因此在市場(chǎng)出現危機時(shí)無法有效的(de)分(fēn)散風險。由于這(zhè)個(gè)原因，人(rén)們在配置不同的(de)資産或者投資策略時(shí)提出了(le)尾部風險平價（tail risk parity）的(de)概念。它是風險平價的(de)一個(gè)延伸（見《你真的(de)搞懂(dǒng)了(le)風險平價嗎？》 —— 我發現這(zhè)篇文章(zhāng)是 2017 年 12 月(yuè) 21 日寫的(de)，也(yě)是年底）。尾部風險平價的(de)目标是讓不同資産或策略對(duì)投資組合的(de)尾部風險貢獻相同。它更多(duō)的(de)是一種理(lǐ)念，而具體實現方法則因人(rén)而異。比如，如果直接把風險平價的(de)概念應用(yòng)到尾部風險平價中，我們可(kě)以讓不同資産的(de)權重 w_i 滿足（使用(yòng) ES 度量尾部風險）：

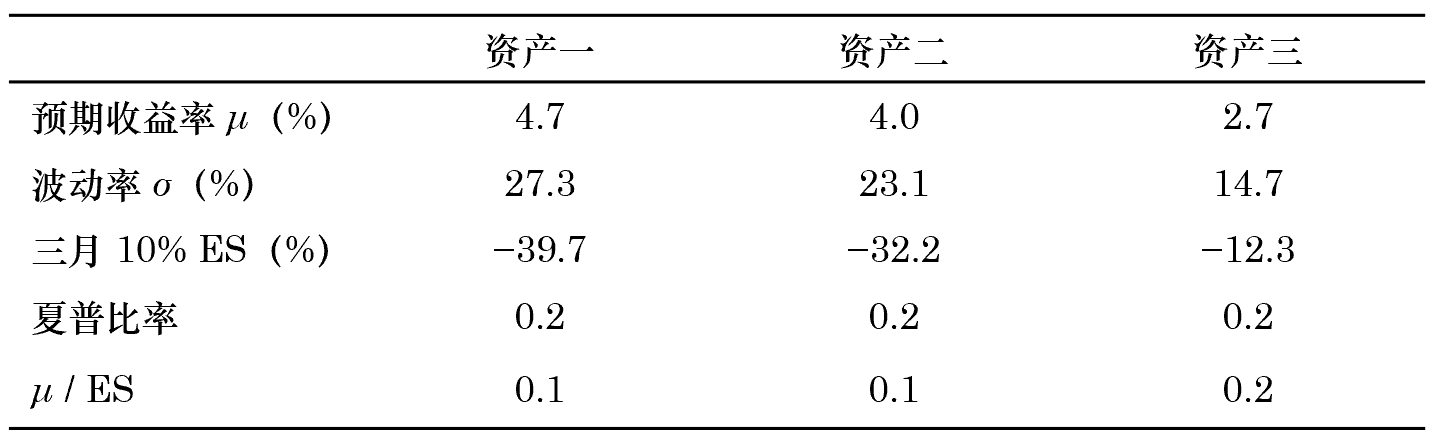
舉個(gè)例子。假設有三種資産，它們的(de)收益風險特性如下(xià)：

按照(zhào)風險平價和(hé)尾部風險平價，這(zhè)三種資産在投資組合中的(de)權重分(fēn)别爲：

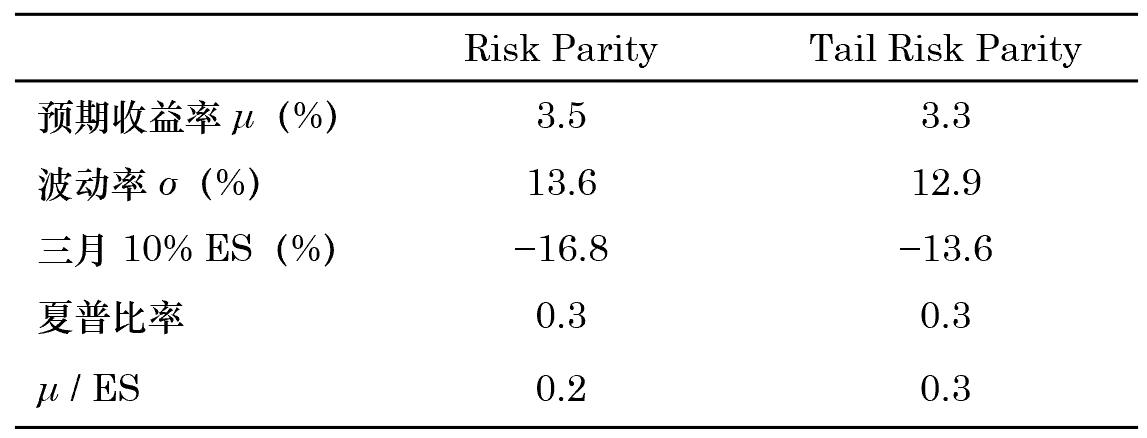
根據這(zhè)兩種方法配置的(de)投資組合的(de)風險收益特征爲：

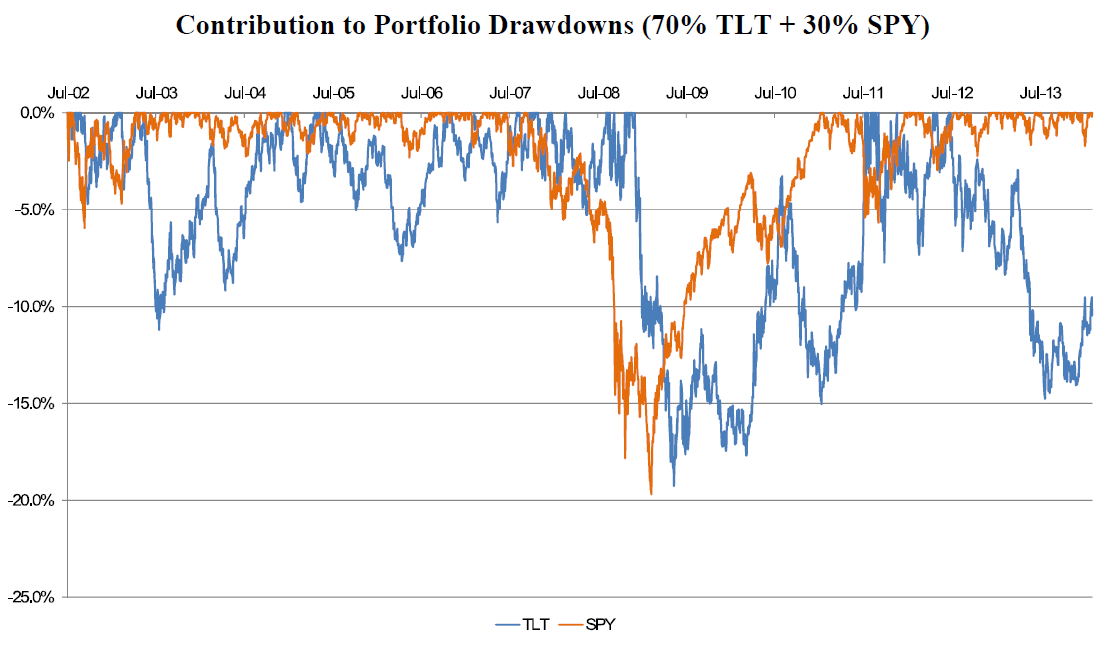
上述結果說明(míng)，尾部風險平價以犧牲部分(fēn)收益爲代價換取了(le)投資組合更低的(de)尾部風險和(hé)波動率。在這(zhè)個(gè)例子中，兩種配置方法的(de)夏普率相同，但從衡量尾部風險控制的(de)指标 μ/ES 來(lái)看，尾部風險平價無疑更有優勢。再來(lái)看看另一種尾部風險平價的(de)實現方法。下(xià)面這(zhè)個(gè)投資組合在 TLT（US long government bond ETF）和(hé) SPY（S&P 500 Index ETF）之間配置。它使用(yòng)資産的(de)最大(dà)回撤作爲評價尾部風險的(de)指标，要求二者對(duì)投資組合的(de)最大(dà)回撤貢獻相似。最終，它以 70% 和(hé) 30% 的(de)比例将資金分(fēn)配于 TLT 和(hé) SPY 之中。

當不同資産（或策略）的(de)尾部風險在時(shí)間上不重疊時(shí)（即發生在不同的(de)時(shí)期），尾部風險平價則可(kě)以發揮出最大(dà)的(de)威力。這(zhè)也(yě)體現了(le)大(dà)類資産配置的(de)重要性。

4 Convergent vs Divergent Risk Taking

本小節來(lái)介紹兩個(gè)平時(shí)人(rén)們可(kě)能聽(tīng)的(de)比較少的(de)概念 —— convergent and divergent risk taking。

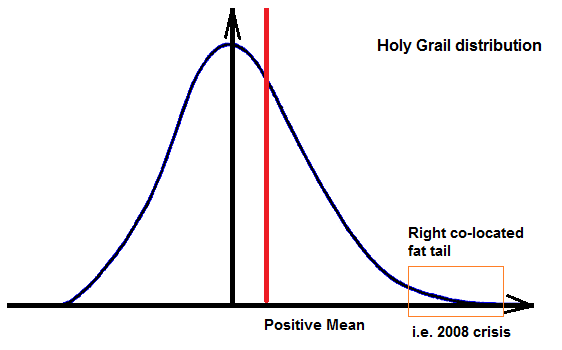
在那之前，先讓我們說說聖杯分(fēn)布。上一小節介紹了(le) Taleb 分(fēn)布。如果有一種資産或者投資策略，它的(de)收益分(fēn)布滿足期望爲正、但肥尾在右側 —— 即“風險有限、收益無限”，我們則稱它的(de)分(fēn)布滿足聖杯分(fēn)布（Holy Grail distribution）。

每個(gè)人(rén)都希望找到這(zhè)樣的(de)收益分(fēn)布，它能夠和(hé)常見的(de) Taleb 分(fēn)布很好的(de)對(duì)沖、分(fēn)散風險。在極端事件給傳統資産帶來(lái)巨額虧損時(shí)，這(zhè)類策略往往有很好的(de)收益。什(shén)麽樣的(de)策略具備這(zhè)種分(fēn)布呢(ne)？這(zhè)需要從策略暴露的(de)風險說起，從而引出我們的(de)主角 —— convergent and divergent risk taking。這(zhè)兩個(gè)術語經常出現在管理(lǐ)期貨中。任何投資策略想要賺錢，都需要承擔一定的(de)風險。而策略承擔什(shén)麽樣的(de)風險就決定了(le)它的(de)收益分(fēn)布具備何種的(de)特征。風險可(kě)以被分(fēn)爲 convergent risks 和(hé) divergent risks 兩大(dà)類，因此策略也(yě)可(kě)以被視爲 convergent risk taking 和(hé) divergent risk taking 兩大(dà)類。

當我們構建 convergent risk taking 策略的(de)時(shí)候，我們會根據金融學或者經濟學對(duì)市場(chǎng)或者投資品的(de)走勢有一個(gè)先驗信仰，并以此爲判斷做(zuò)出投資決策。以 long only 的(de)股票(piào)投資爲例，我們相信股市是經濟的(de)晴雨(yǔ)表，而長(cháng)期來(lái)看經濟會增長(cháng)、股票(piào)則會給我們帶來(lái) risk premium，因此願意承擔其短期波動（可(kě)能很大(dà)）帶來(lái)的(de)風險。這(zhè)樣的(de)策略就是 convergent risk taking 策略。另一方面，在構建 divergent risk taking 策略時(shí)，人(rén)們假設投資品未來(lái)的(de)走勢是未知的(de)、不使用(yòng)任何先驗信仰來(lái)輔助判斷投資品會漲還(hái)是會跌。如果過去投資品一直漲，但是最近開始跌了(le)，那麽這(zhè)種類型的(de)策略不會以該投資品過去的(de)走勢爲先驗從而認爲它還(hái)會繼續漲，而是會順應當下(xià)的(de)趨勢而認爲它還(hái)會繼續跌。

在上面提到的(de)兩種不同風險類型的(de)策略中，股市中的(de)價值投資無疑是 convergent risk taking 的(de)代表。這(zhè)類策略通(tōng)過深度行業研究挖掘上市公司的(de)内在價值，當價格低于價值時(shí)則買入且越低（跌）越買，耐心的(de)等待其價格向價值回歸、無視短期的(de)波動，這(zhè)是這(zhè)類策略願意且主動承擔的(de)風險。常見于 CTA 中的(de)趨勢追蹤策略或者股市中的(de)動量策略無疑是 divergent risk taking 的(de)代表。這(zhè)類策略對(duì)投資品的(de)内在價值不做(zuò)任何假設，僅僅是嚴格依據價格的(de)走勢進行交易：價格上漲了(le)做(zuò)多(duō)、價格下(xià)跌時(shí)做(zuò)空；當盈利時(shí)會逐漸加倉，當虧損時(shí)會及時(shí)清倉。Divergent risk taking 策略的(de)收益特征滿足了(le)聖杯分(fēn)布的(de)特性。這(zhè)就是爲什(shén)麽趨勢追蹤策略能夠長(cháng)盛不衰的(de)原因。在趨勢追蹤領域不乏 Winton Group 和(hé) Aspect Capital 這(zhè)樣的(de)傑出代表。

5 結語

2013 年，Asness、Moskowitz 以及 Pedersen 在 Journal of Finance 上發表了(le)一篇影(yǐng)響深遠(yuǎn)的(de)文章(zhāng)，題爲 Value and Momentum Everywhere（Asness et al. 2013）。通(tōng)過上文的(de)描述，不難看出 Value 和(hé) Momentum 恰恰代表了(le)兩大(dà)類 risk taking 策略，從風險的(de)角度，它們完美(měi)的(de)互補。有必要指出的(de)是，聖杯分(fēn)布是非常美(měi)好的(de)，而獲得(de)美(měi)好的(de)東西注定是十分(fēn)困難的(de)。趨勢策略本身是非常反人(rén)性的(de)（見《海龜交易法則：逆人(rén)性投資》）。趨勢策略最困難的(de)地方在于在趨勢中拿的(de)住單子，讓利潤奔跑（隻有這(zhè)樣才能實現收益率分(fēn)布的(de)右尾）。由于認知偏差中造成的(de)對(duì)于确定性低收益的(de)過度偏愛(ài)，人(rén)們總是傾向于早早平掉盈利的(de)單子。市場(chǎng)中有句老話(huà)說的(de)是趨勢策略最賺錢的(de)時(shí)候一定是交易者最難受的(de)時(shí)候。隻有克服人(rén)性的(de)種種錯誤，才能真正享受到趨勢策略帶來(lái)的(de)聖杯分(fēn)布。

本文從尾部相關性出發介紹了(le)如何基于 VaR 或者 ES 計算(suàn)在極端事件發生時(shí)資産之間的(de)相關性。大(dà)量的(de)實證表明(míng)，同類甚至是跨大(dà)類的(de)資産在市場(chǎng)發生危機的(de)時(shí)候相關性都會迅速蹿升，導緻投資組合的(de)巨大(dà)虧損。爲了(le)減輕這(zhè)個(gè)問題，尾部風險平價的(de)資産配置方法越來(lái)越被投資者認可(kě)。該方法以犧牲一定的(de)收益換來(lái)危機時(shí)更低的(de)虧損，從而提升投資組合的(de)風險收益特征。本文的(de)最後指出，從風險的(de)角度來(lái)說，一個(gè)好的(de)投資組合中應該同時(shí)擁有 convergent 和(hé) divergent risk taking 的(de)策略。這(zhè)兩個(gè)概念其實并不是什(shén)麽“玄幻”的(de)東西，它們在生活中也(yě)很常見。比如在社會交往方面，有的(de)人(rén)更喜歡隻和(hé)少數幾個(gè)交心的(de)朋友互動、非常珍視小範圍的(de)朋友圈，這(zhè)屬于 convergent 行爲；而另一些人(rén)則更加 social，喜歡和(hé)各種各樣的(de)人(rén)打交道、交朋友、堅信人(rén)生的(de)下(xià)一個(gè) big opportunity 就來(lái)自某個(gè)新朋友，這(zhè)就屬于 divergent 行爲。這(zhè)兩種行爲并無對(duì)錯、也(yě)各有優缺點；将它們結合起來(lái)往往會實現雙赢。希望本文的(de)介紹能帶給你一些啓發，更加科學的(de)分(fēn)配投資組合暴露的(de)風險。

參考文獻

Asness, C. S., T. J. Moskowitz, and L. H. Pedersen (2013). Value and Momentum Everywhere. Journal of Finance 68(3), 929 – 985.

Campbell, R., K. Koedijk, and P. Kofman (2002). Increased correlation in bear markets. Financial Analysts Journal 58(1), 87 – 94.

Cotter, J. and F. Longin (2006). Implied correlation from VaR. MPRA paper No. 3506, University College Dublin.

Liu, J. (2016). A new tail-based correlation. Working paper, McGill University.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。