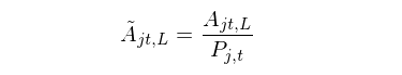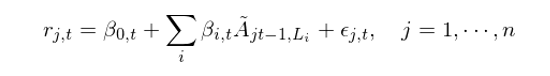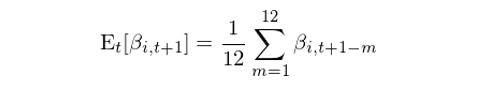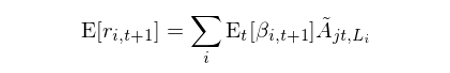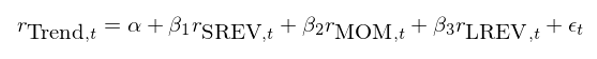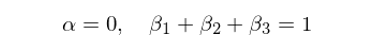美(měi)股上一個(gè)跨越時(shí)間尺度的(de)趨勢因子

作者：石川

摘要：Han et al. (2016) 通(tōng)過截面回歸将美(měi)股上的(de)短期反轉、中期動量和(hé)長(cháng)期反轉合并成一個(gè)新的(de)趨勢因子。該因子能獲得(de)顯著的(de)超額收益，爲美(měi)股的(de) asset pricing 提供了(le)新的(de)思路。

1 引言

熟悉美(měi)股 asset pricing 或 factor investing 的(de)小夥伴都知道，美(měi)股在不同的(de)時(shí)間尺度上表現出了(le)動量或者反轉效應。比如，在研究動量因子時(shí)，常見的(de)做(zuò)法是按照(zhào)月(yuè)頻(pín)使用(yòng) t – 12 到 t – 1 之間的(de)收益率作爲動量因子，這(zhè)說明(míng)在一年這(zhè)個(gè)時(shí)間尺度上存在動量，而之所以刨去最近一個(gè)月(yuè)是因爲未來(lái)收益率往往和(hé)最近一個(gè)月(yuè)呈現反轉。此外，DeBondt and Thaler (1985) 指出美(měi)股在 3 ~ 5 年的(de)時(shí)間尺度上存在反轉。

鑒于上述現象，一個(gè)自然的(de)想法是針對(duì)不同的(de)周期構建三個(gè)因子 —— 短周期的(de)反轉因子、中周期的(de)動量因子、以及超長(cháng)周期的(de)反轉因子，然後把投資組合适當的(de)暴露在這(zhè)些不同的(de)因子中。如果這(zhè)三個(gè)級别的(de)不同現象都能帶來(lái) risk premium，則長(cháng)期來(lái)看暴露在它們之上會有好的(de)投資回報。

然而，除此之外，是否有更好的(de)辦法把不同級别的(de)動量或者反轉因子綜合到一起，構建一個(gè)跨越不同時(shí)間尺度的(de)趨勢因子呢(ne)？2016 年，一篇發表于頂刊 Journal of Financial Economics 的(de)文章(zhāng)（Han et al. 2016）給出了(le)肯定的(de)答(dá)案。這(zhè)篇文章(zhāng)中采用(yòng)的(de)通(tōng)過截面回歸來(lái)構建趨勢因子的(de)思路，以及爲了(le)檢驗該因子而使用(yòng)的(de)很多(duō)統計手段都值得(de)借鑒。

2 趨勢因子

爲了(le)構建趨勢因子，首先要選擇具體的(de)方法來(lái)計算(suàn)不同時(shí)間尺度下(xià)的(de)動量、反轉。爲此，Han et al. (2016) 采用(yòng)的(de)是 Moving Average（MA，移動平均）。移動平均是一個(gè)被技術分(fēn)析廣泛采用(yòng)的(de)簡單指标，許多(duō)實盤交易結果指出 MA 對(duì)于未來(lái)的(de)收益率有一定的(de)預測性。在理(lǐ)論方面，Han et al. (2016) 受到 Wang (1993) 的(de)啓發，使用(yòng)一個(gè)簡單的(de)随機過程模型對(duì)于 MA 在收益率上面的(de)預測性進行了(le)分(fēn)析。此外，Zhu and Zhou (2009) 從資産配置的(de)角度研究了(le)移動平均的(de)價值。理(lǐ)論分(fēn)析和(hé)實證數據均顯示移動平均在交易中的(de)作用(yòng)。

在 Han et al. (2016) 研究的(de)實證中，計算(suàn)趨勢因子的(de)頻(pín)率是月(yuè)頻(pín)，回測期爲 1926 年 1 月(yuè)至 2014 年 12 月(yuè)（數據來(lái)自 CRSP 并采用(yòng)了(le)學術界常見的(de)數據處理(lǐ)方法）。爲了(le)計算(suàn)趨勢因子，首先在每個(gè)月(yuè) t 的(de)最後一個(gè)交易日計算(suàn)每支股票(piào)（用(yòng) j 表示）在不同時(shí)間尺度 L 的(de)移動平均：

其中 P_{j, t-L+i} 爲股票(piào) j 在第 t-L+i 個(gè)月(yuè)最後一個(gè)交易日的(de)價格（上述表達式和(hé) Han et al. 2016 中的(de)有些差異；我在不影(yǐng)響理(lǐ)解的(de)前提下(xià)簡化(huà)了(le)表達式）。考慮到不同股票(piào)價格的(de)量級存在巨大(dà)的(de)差别，計算(suàn)的(de)下(xià)一步是使用(yòng)最新的(de)價格 P_{j, t} 對(duì)上述移動平均進行标準化(huà)：

在有了(le)不同時(shí)間尺度（lag L）的(de)移動平均之後，Han et al. (2016) 将它們視作不同級别的(de)趨勢（可(kě)能是動量、也(yě)可(kě)能是反轉）信号，在每期使用(yòng)股票(piào)最新的(de) MA 指标和(hé)下(xià)一期的(de)收益率進行截面回歸，得(de)到這(zhè)些移動均線因子的(de)收益率：

其中，r_{j,t} 爲個(gè)股 j 在 t 期的(de)收益率，L_i 爲第 i 個(gè)計算(suàn)移動平均的(de)時(shí)間尺度。通(tōng)過截面回歸就可(kě)以得(de)到這(zhè)些移動平均因子的(de)收益率 β_{i,t}。再具體計算(suàn)時(shí)，計算(suàn)均線的(de)時(shí)間尺度 L_i 的(de)取值爲 3、5、10、20、50、100、200、400、600、800 以及 1000 個(gè)交易日，它們分(fēn)别對(duì)應的(de)時(shí)間尺度爲日頻(pín)、周頻(pín)、月(yuè)頻(pín)、季度、一年、兩年、三年以及四年。一旦在不同 t 上使用(yòng)截面回歸得(de)到了(le) β_{i,t}，就可(kě)以在時(shí)序上取均值來(lái)預測下(xià)一個(gè)選股窗(chuāng)口内（月(yuè)頻(pín)）各均線因子的(de)預期收益率。爲此，作者采用(yòng)了(le)使用(yòng)過去 12 個(gè)月(yuè)的(de) β_{i,t} 來(lái)計算(suàn)下(xià)個(gè)月(yuè)的(de)預期收益率：

最終，使用(yòng)對(duì) t + 1 的(de)均線預期收益率 E_t[β_{i,t+1}] 和(hé)個(gè)股 j 在 t 期的(de)最新均線指标取值就可(kě)以計算(suàn)出每支股票(piào)在 t + 1 的(de)收益率預測，并以此對(duì)股票(piào)排序構建趨勢因子（在該計算(suàn)中并不需要用(yòng)到截面回歸的(de)截距項，因爲該項對(duì)所有個(gè)股都一樣，不改變因子的(de)單調性）：

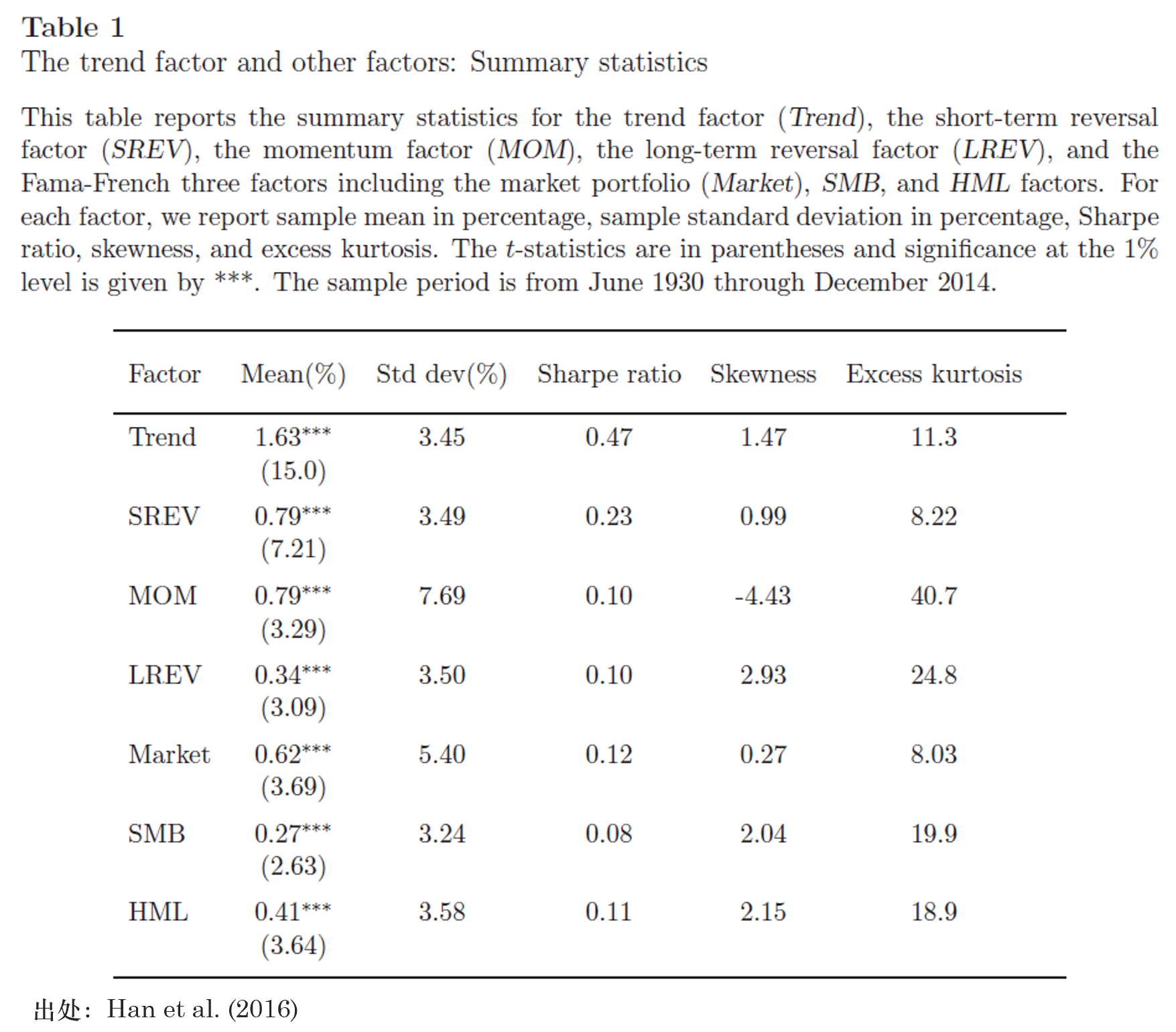
簡單梳理(lǐ)一下(xià)。上述計算(suàn)趨勢因子的(de)過程首先找出了(le)每支股票(piào)在不同時(shí)間尺度下(xià)的(de)移動平均；将這(zhè)些移動平均視爲因子并通(tōng)過截面回歸得(de)到每期因子收益率；通(tōng)過滾動窗(chuāng)口計算(suàn)出每個(gè)移動平均因子在這(zhè)段時(shí)間内的(de)收益率均值，從而動态的(de)捕捉了(le)在不同的(de)曆史時(shí)期，哪種級别的(de)移動均線對(duì)于預測下(xià)一期的(de)股票(piào)收益率最有效（β 的(de)符号決定了(le)方向 —— 動量或者反轉，β 的(de)大(dà)小決定了(le)預測的(de)強弱）；最終使用(yòng)移動均線因子收益率和(hé)最新的(de)因子取值計算(suàn)出個(gè)股下(xià)一期收益率的(de)預測，以此對(duì)個(gè)股排序。具體的(de)，在每個(gè)月(yuè)末将股票(piào)按照(zhào)預期收益率從大(dà)到小排序，将排名前 1/5 的(de)股票(piào)等權構建多(duō)頭組合，将排名後 1/5 的(de)股票(piào)等權構建空頭組合。多(duō)空組合的(de)收益率之差就是該趨勢因子。和(hé)我們熟悉的(de) HML、SMB 一樣，趨勢因子本身也(yě)是一個(gè)多(duō)空投資組合的(de)收益率。下(xià)圖展示了(le)回測期内趨勢因子（Trend）和(hé)短期反轉（SREV）、中期動量（MOM）以及長(cháng)期反轉（LREV）以及 Fama-French 三因子（Fama and French 1993）的(de)收益。從均值（以及對(duì)應的(de) t-statistic）來(lái)看，趨勢因子無疑優勢明(míng)顯。

接下(xià)來(lái)就來(lái)比較一下(xià)這(zhè)個(gè)新的(de)趨勢因子和(hé)傳統的(de)動量、反轉因子。

3 趨勢因子 vs 傳統動量、反轉因子

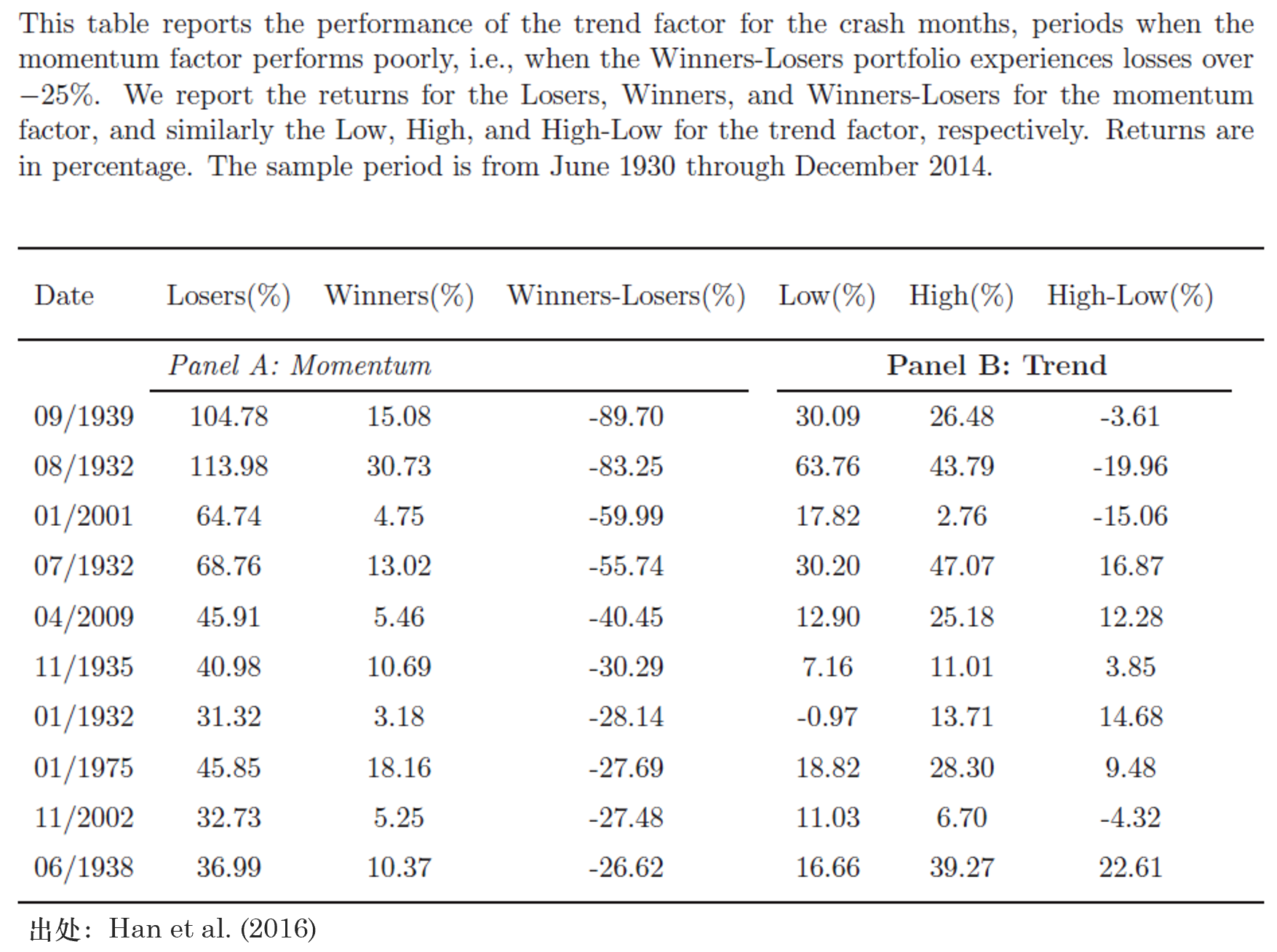
盡管動量因子在美(měi)股上占有舉足輕重的(de)地位，但它經常被人(rén)诟病的(de)是該因子在市場(chǎng)從熊市反彈時(shí)的(de)不良表現。在這(zhè)些時(shí)期，動量因子的(de)空頭一方總會出現報複性反彈，收益率遠(yuǎn)超其多(duō)頭一方，造成動量因子巨大(dà)的(de)損失。這(zhè)個(gè)現象被稱爲 momentum crashes（Daniel and Moskowitz 2016）。Han et al. (2016) 的(de)經驗結果顯示，新的(de)趨勢因子在 momentum crashes 時(shí)期往往能取得(de)非常優異的(de)收益：

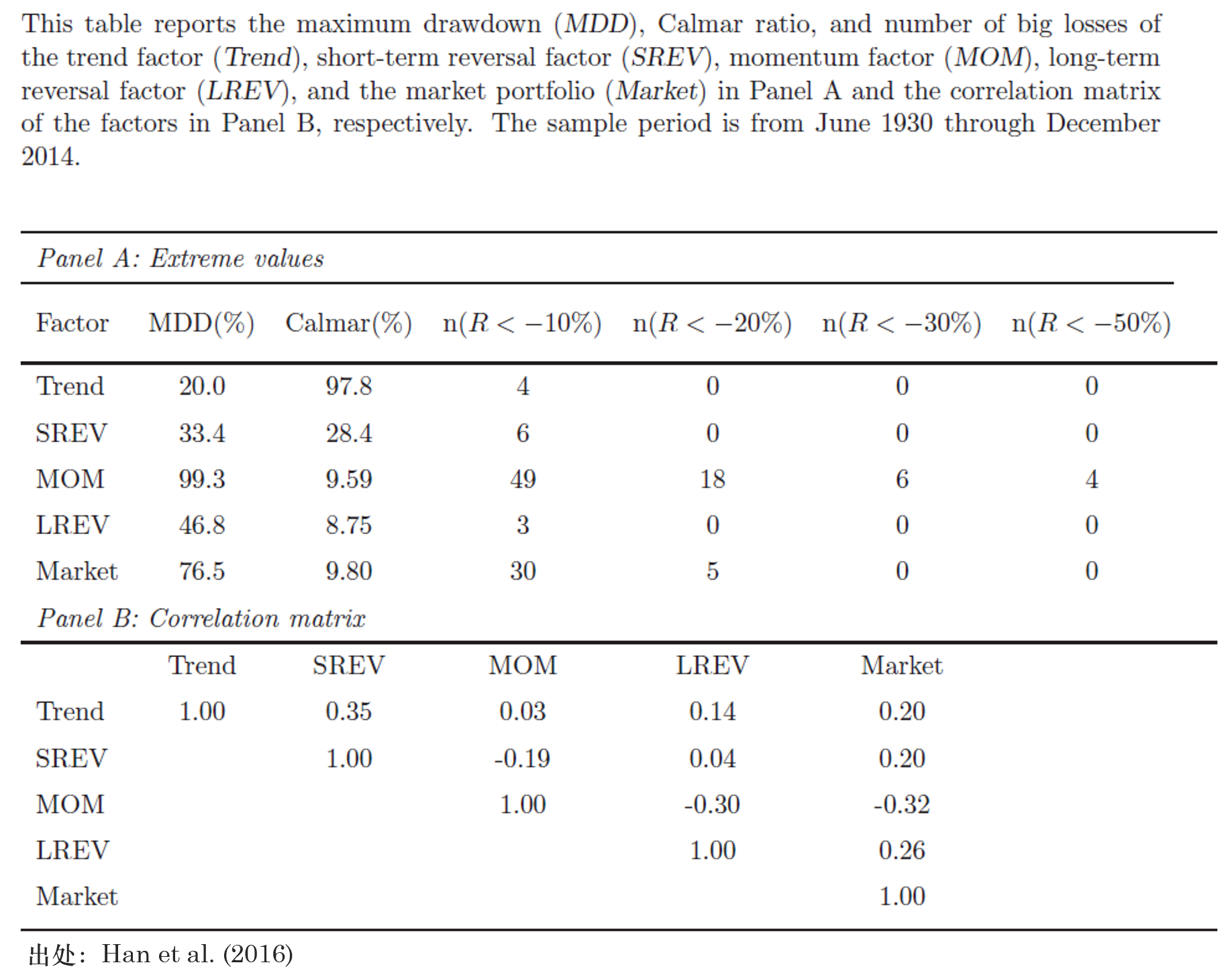
分(fēn)析其原因，是因爲新的(de)趨勢因子和(hé)傳統的(de)動量因子的(de)相關性很低。由于該方法通(tōng)過滾動回歸動态的(de)暴露在不同級别的(de)移動均線指标上，因此可(kě)以想見在回測期内，它更多(duō)暴露在長(cháng)、短期反轉因子上，而非中期動量因子上。下(xià)圖（Panel B）展示了(le)趨勢因子和(hé)傳統因子的(de)相關性，說明(míng)了(le)這(zhè)一點。

然而，在上面的(de)結果中，最令我驚訝的(de)是趨勢因子非常小的(de)最大(dà)回撤（max drawdown，MDD）—— 其最大(dà)回撤隻有 20%（too good to be true），遠(yuǎn)遠(yuǎn)優于其他(tā)三個(gè)動量、反轉因子。這(zhè)說明(míng)在市場(chǎng)下(xià)行的(de)時(shí)候，趨勢因子中空頭一方非常給力。當然，在實際投資中，考慮到交易的(de)成本和(hé)各種做(zuò)空的(de)限制，上述結果會打一定的(de)折扣。Han et al. (2016) 也(yě)客觀的(de)指出，爲了(le)科學評價該趨勢因子在實際投資中的(de)價值仍需要更多(duō)的(de)研究工作。爲了(le)定量比較新的(de)趨勢因子和(hé)傳統的(de)動量、反轉因子，Han et al. (2016) 采用(yòng)了(le)學術界常用(yòng)的(de) mean-variance spanning tests（Huberman and Kandel 1987）。直觀的(de)說，該方法考察 K 個(gè)已知資産構建的(de) mean-variance 有效前沿能否包含某個(gè)新資産（或者投資組合）。在數學上，考慮新的(de)趨勢因子和(hé) SREV、MOM 以及 LREV 三因子的(de)回歸模型如下(xià)：

該檢驗的(de) null hypothesis 是：

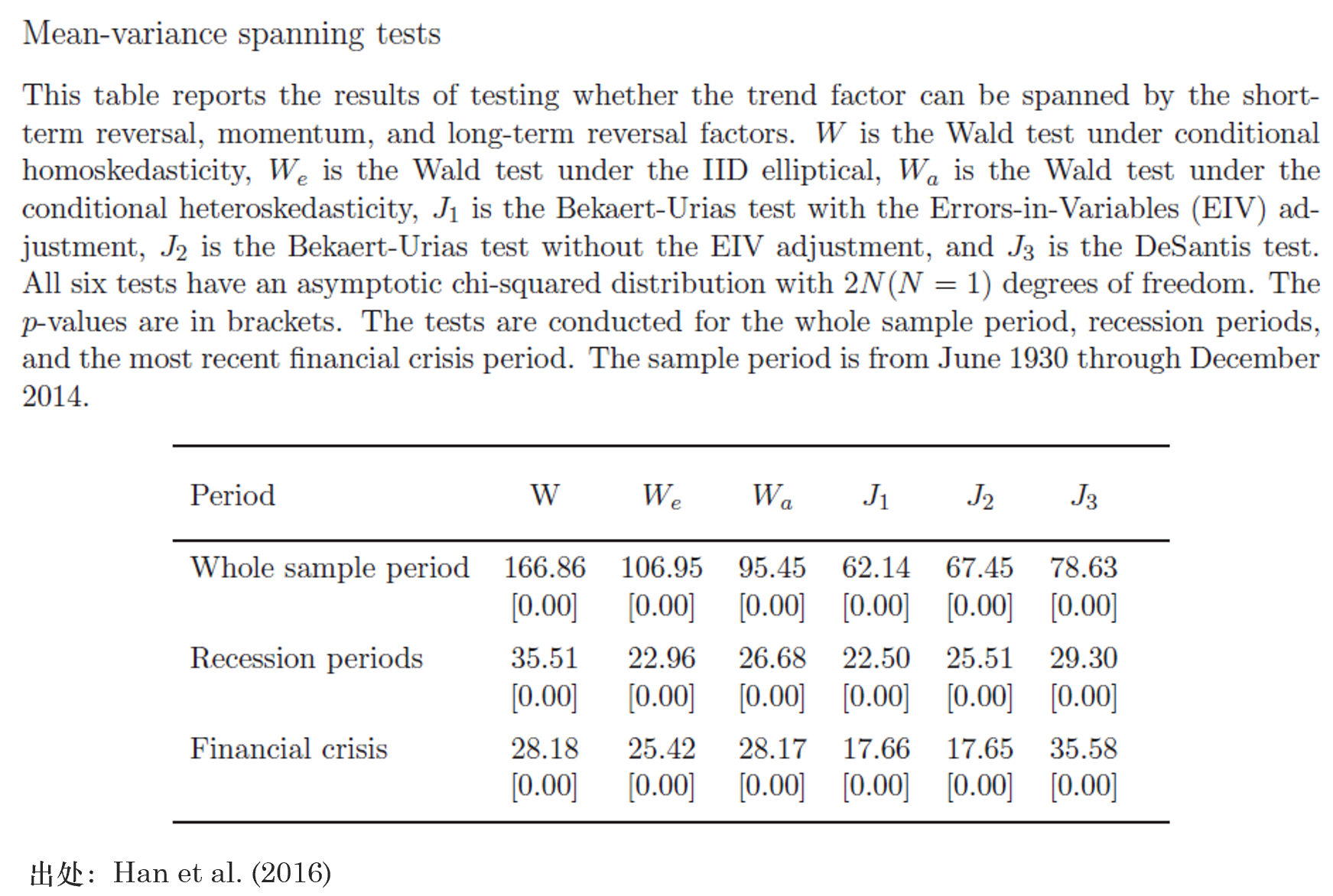
Kan and Zhou (2012) 指出 mean-variance spanning tests 有六個(gè)不同的(de)版本。下(xià)表考慮了(le)全部六個(gè)版本，并考慮了(le)不同的(de)回測期 —— 全部回測期、衰退期以及金融危機。所有版本均顯著的(de)拒絕原假設，說明(míng)新的(de)趨勢因子存在傳統動量、反轉因子無法解釋的(de)股票(piào)截面預期收益差異。這(zhè)意味著(zhe)，僅僅通(tōng)過将投資組合暴露于傳統的(de) SREV、MOM 以及 LREV 三因子無法取得(de)該趨勢因子帶來(lái)的(de)超額收益。

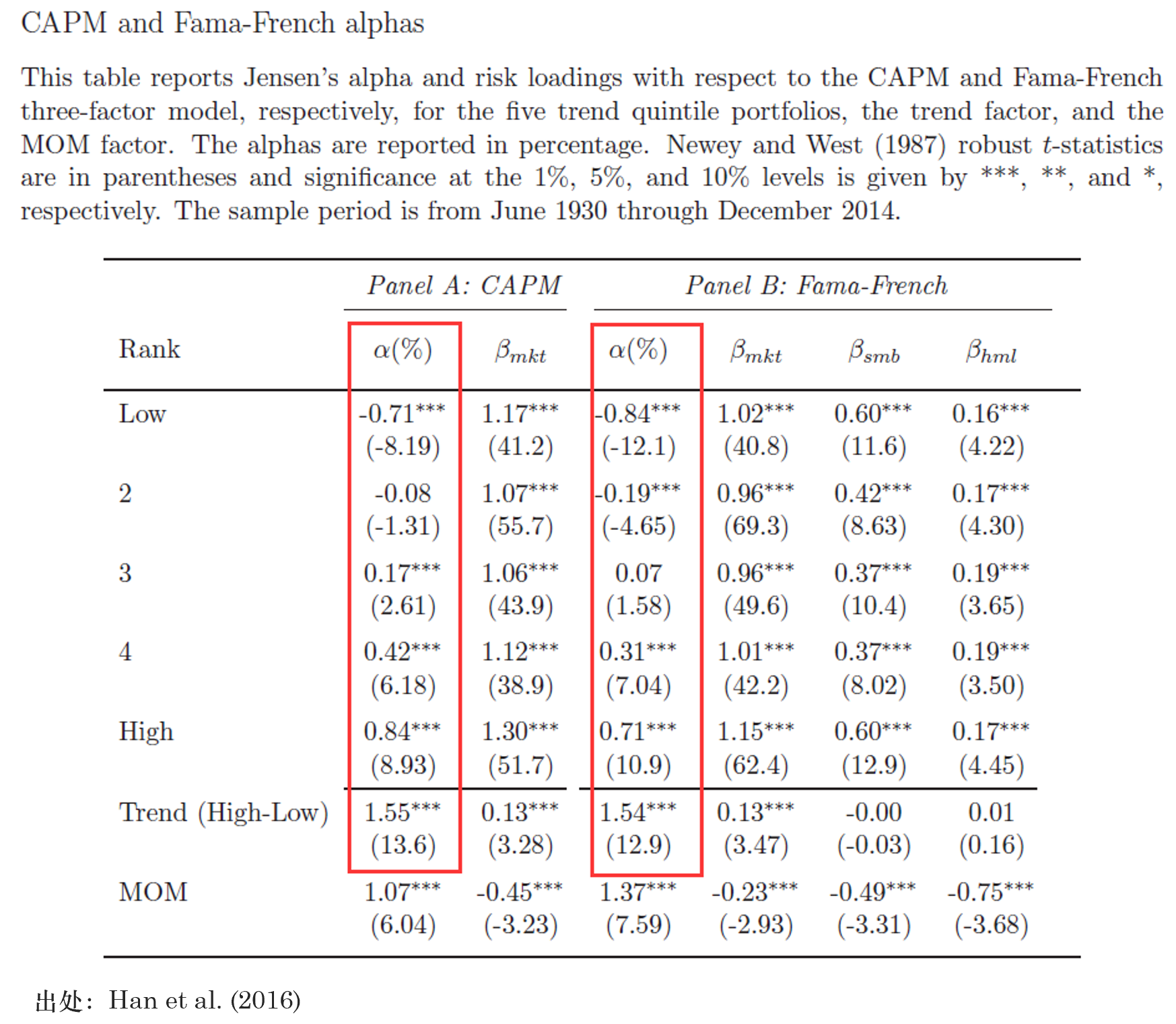
最後來(lái)看看趨勢因子能否被 CAPM 模型以及 Fama-French 三因子模型解釋 —— 即考察它是否有 CAPM-α 和(hé)三因子-α。除了(le)考察趨勢因子自身之外，Han et al. (2016) 還(hái)考慮了(le)根據預期收益率高(gāo)低将股票(piào)分(fēn)成五檔構建的(de)投資組合，結果如下(xià)表所示。

從結果來(lái)看，對(duì)于趨勢因子，它存在無法被傳統 CAPM 或 Fama-French 三因子解釋的(de)超額收益。從因子暴露來(lái)看，當使用(yòng)三因子模型時(shí)，它在 SMB 和(hé) HML 上的(de)暴露在統計上非常不顯著。面對(duì)如此超額收益，Han et al. (2016) 卻指出，他(tā)們并不認爲該趨勢因子一定是一個(gè)異象（anomaly）。作者認爲趨勢背後也(yě)許存在對(duì)應的(de)風險，而趨勢獲得(de)的(de)超額收益和(hé)風險補償有關。有效市場(chǎng)假說（EMH）之父 Eugene Fama 指出，market efficiency 已經成爲一個(gè) joint hypothesis 問題 —— 即爲了(le)檢驗市場(chǎng)有效性，首先要有一個(gè)合理(lǐ)的(de) asset pricing 模型；如果模型未知或者錯誤，就不能正确的(de)評判任何異象是否真的(de)是異象。這(zhè)意味著(zhe)，檢驗 EMH 的(de)同時(shí)必須也(yě)要檢驗 asset pricing 模型。依照(zhào)這(zhè)個(gè)思路，如果趨勢因子（或者更傳統意義上的(de)動量）是真實（但未知）asset pricing 模型的(de)一部分(fēn)，那麽它獲取的(de)超額收益就是某種風險的(de)補償，而非市場(chǎng)異象。

4 趨勢因子是否來(lái)自數據挖掘

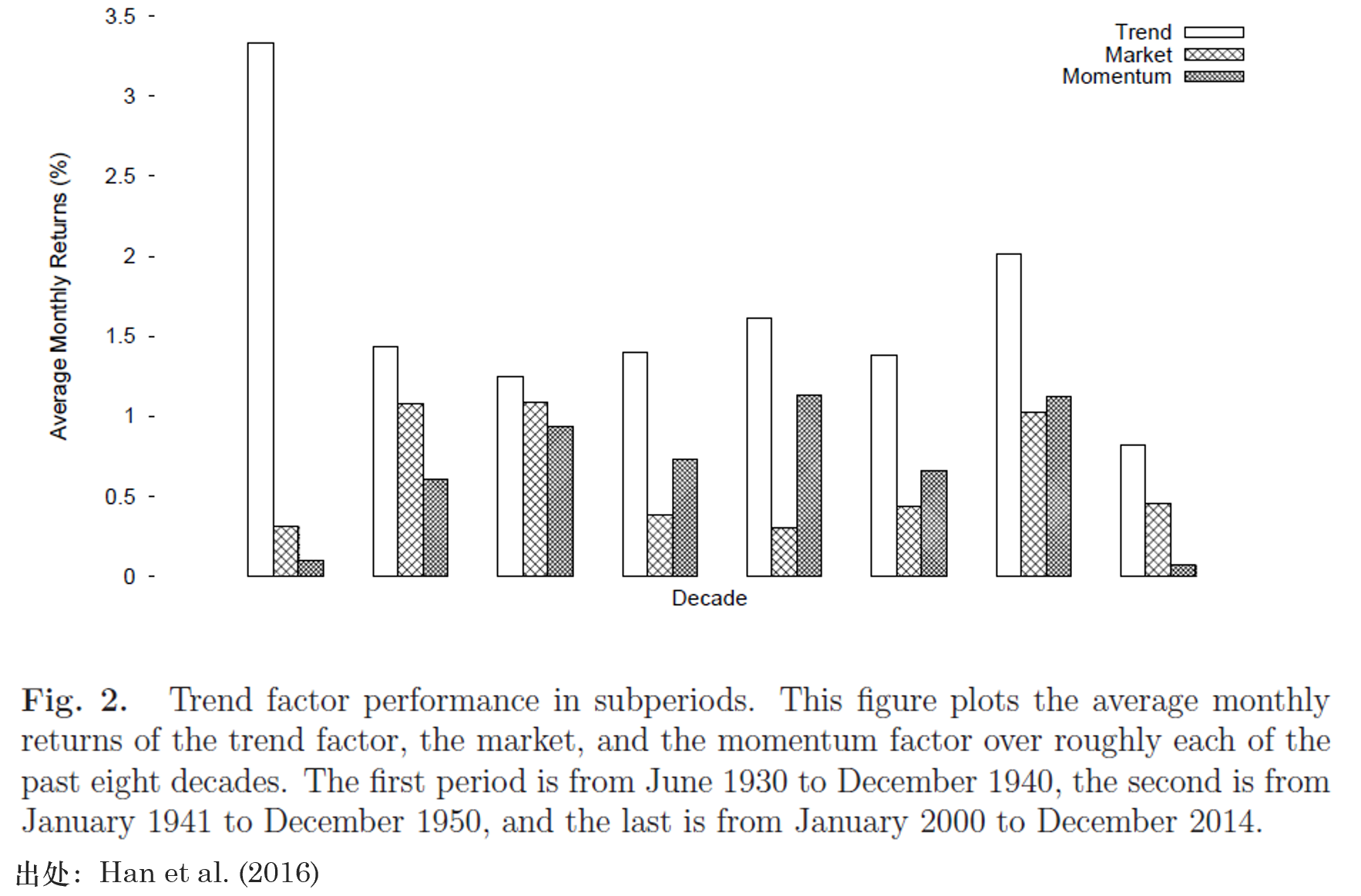
正如引言中所說的(de)，我最初對(duì)趨勢因子持懷疑态度，認爲它不可(kě)避免的(de)存在數據挖掘的(de)問題。與傳統的(de)動量或反轉因子相比，該因子無論從模型複雜(zá)度或者參數複雜(zá)度都更高(gāo)，因此數據挖掘的(de)可(kě)能性也(yě)更大(dà)。針對(duì)這(zhè)方面，Han et al. (2016) 從四個(gè)角度進行了(le)闡述。首先，三位作者指出，構建趨勢因子所使用(yòng)的(de)移動平均窗(chuāng)口長(cháng)度并非優化(huà)的(de)結果，這(zhè)些參數背後都有一定的(de)業務邏輯。第二，如果把回測期按照(zhào)每十年分(fēn)成一個(gè)區(qū)間并觀測趨勢因子在這(zhè)些區(qū)間内的(de)表現（下(xià)圖）會發現該因子獲得(de)的(de)收益非常穩健。作者指出穩健的(de)表現說明(míng)該因子不太可(kě)能是數據挖掘的(de)産物(wù)。

第三，Harvey et al. (2016) 針對(duì)“因子挖掘”界普遍存在的(de) multiple testing 問題，提出單一因子的(de) t-statistic 至少要超過 3 才有可(kě)能是一個(gè)真的(de)異象。而趨勢因子的(de) t-statistic 高(gāo)達 13.6（傳統動量因子的(de) t-statistic 爲 6.04），遠(yuǎn)超這(zhè)一阈值。不過 Harvey et al. (2016) 自己也(yě)指出即便是這(zhè)個(gè)阈值也(yě)非常保守。爲此，Harvey and Liu (2018) 針對(duì) multiple testing 的(de)問題，提出了(le)一個(gè)基于回歸的(de)分(fēn)析因子有效性的(de)框架（見《出色不如走運(II)?》），在該框架下(xià)，傳統的(de)動量因子已經不再有效。因此，使用(yòng)該框架來(lái)進一步檢驗趨勢因子是否有效可(kě)以作爲一個(gè)未來(lái)的(de)研究課題。

最後的(de)第四個(gè)角度是 out of sample test，它無疑比前三個(gè)角度更具說服力。Han et al. (2016) 在其他(tā) G7 國家（法國、英國、德國、意大(dà)利、加拿大(dà)、日本）的(de)股市中檢驗了(le)趨勢因子的(de)有效性。在所有這(zhè)些國家中均觀察到了(le)來(lái)自趨勢因子的(de)超額收益；除德國外，在其他(tā)國家中的(de)月(yuè)頻(pín) CAPM-α 均高(gāo)于 1%。雖然趨勢因子在這(zhè)些國家中的(de)表現沒有在美(měi)股上明(míng)顯，但無疑作爲樣本外的(de)數據集，這(zhè)樣的(de)結果支持了(le)“趨勢因子并非數據挖掘的(de)産物(wù)”這(zhè)一觀點。

5 Fama-MacBeth Regression

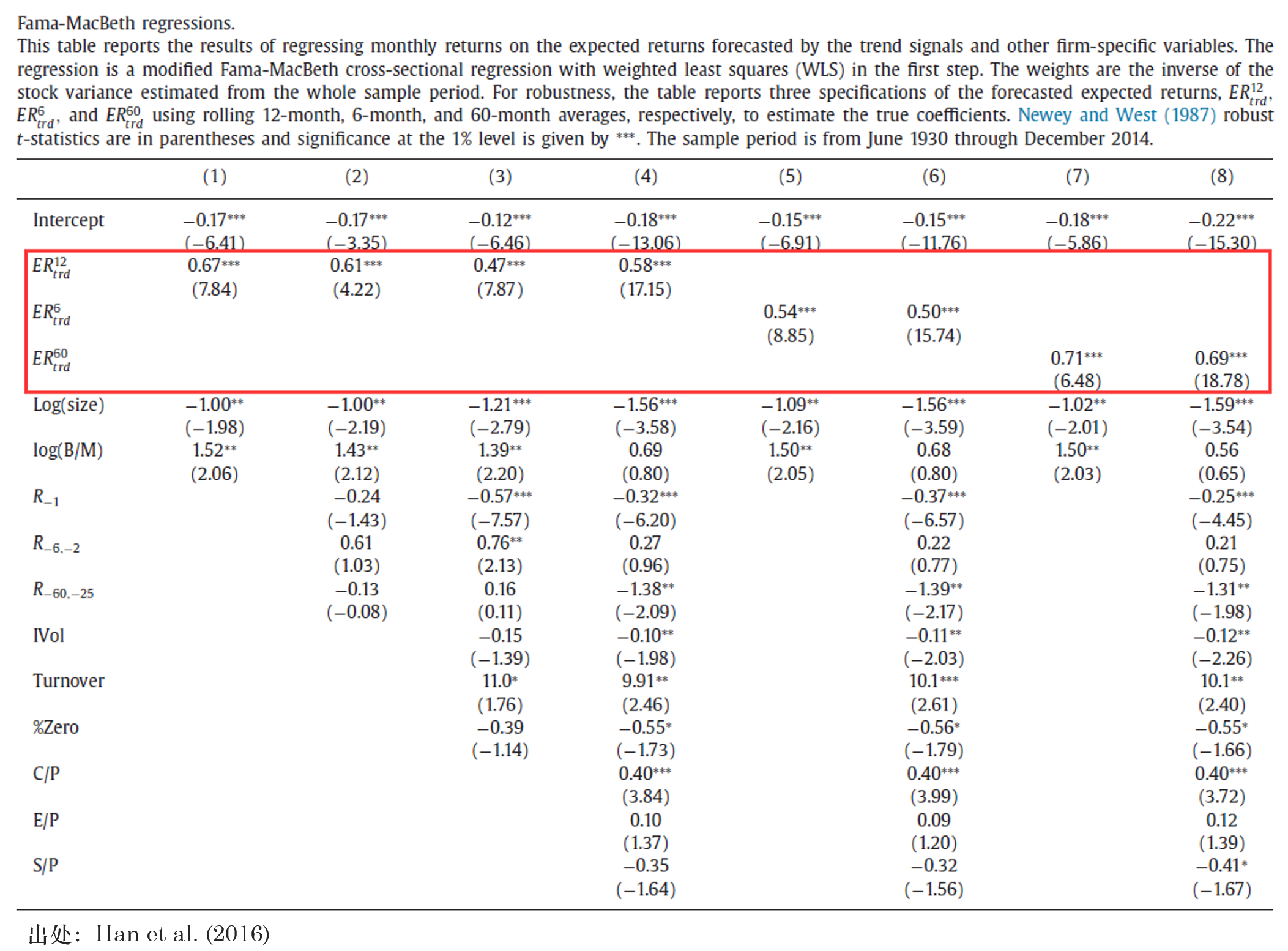
除了(le)上述四個(gè)角度的(de)論述外，Han et al. (2016) 還(hái)進行了(le)很多(duō) robustness check 并通(tōng)過考慮交易成本來(lái)檢查趨勢因子的(de)有效性。本小節挑選這(zhè)其中的(de) Fama-MacBeth regression（Fama and MacBeth 1973）進行介紹。Fama-MacBeth regression 的(de)優勢在于可(kě)以控制很多(duō)變量，從而考察目标變量在解釋股票(piào)預期收益率截面差異的(de)顯著性。在 Fama-MacBeth regression 中，回歸方程左側的(de)是個(gè)股的(de)收益率，在右側的(de)解釋變量中，除了(le)常見的(de)因子（如 log(size)、log(B/M)、E/P）外，還(hái)加入了(le) ER_{trd}^{12}、ER_{trd}^{6} 及 ER_{trd}^{60} 等使用(yòng)不同尺度 MA 計算(suàn)出來(lái)的(de)預期收益率。

結果（上圖）顯示，當考慮了(le)常見的(de)因子後，被加入回歸的(de) ER_{trd}^{12}、ER_{trd}^{6} 或 ER_{trd}^{60} 依然對(duì)個(gè)股的(de)截面預期收益率差異有非常顯著的(de)解釋作用(yòng)。

6 趨勢因子和(hé)信息不确定性

長(cháng)久以來(lái)，技術分(fēn)析和(hé)基本面分(fēn)析是股票(piào)投資中的(de)兩大(dà)派系，而移動平均是技術分(fēn)析中的(de)優秀手段。因此，本文介紹的(de)基于移動平均的(de)趨勢因子也(yě)源自技術分(fēn)析，是使用(yòng)技術分(fēn)析進行 asset pricing 的(de)一種努力。當股票(piào)的(de)（基本面）信息存在較高(gāo)的(de)不确定性時(shí)，投資者和(hé)交易者往往更傾向使用(yòng)技術分(fēn)析手段來(lái)選股。由此，Han et al. (2016) 提出了(le)一個(gè)假設：在信息不确定性高(gāo)的(de)股票(piào)中（比在信息不确定性低的(de)股票(piào)中）使用(yòng)趨勢因子可(kě)獲得(de)更高(gāo)的(de)收益。

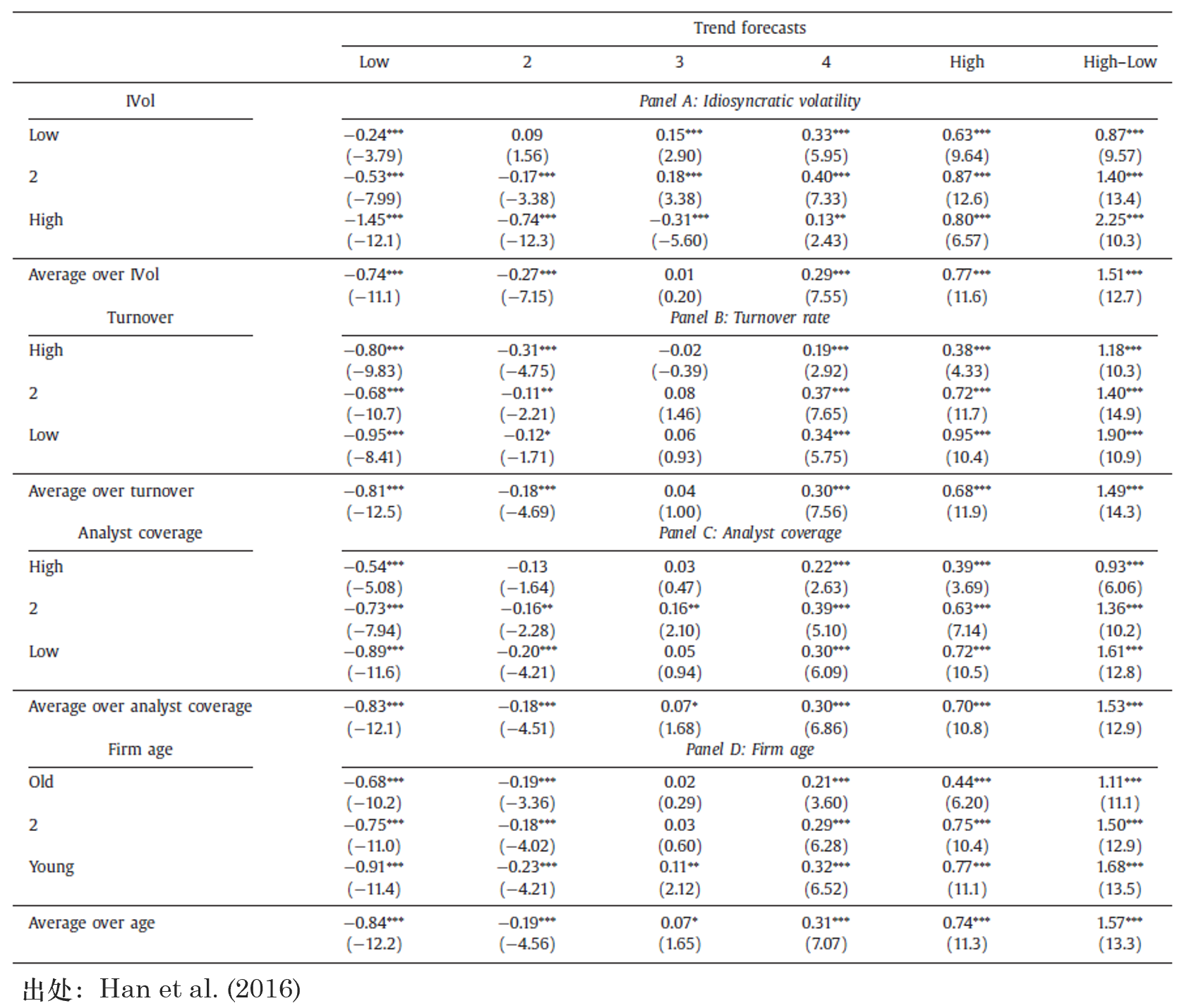
爲了(le)驗證這(zhè)一點，該文選擇了(le)市值、特異性波動率、換手率、分(fēn)析師覆蓋、公司年齡作爲信息不确定的(de)代理(lǐ)指标。具體來(lái)說，高(gāo)的(de)信息不确定性意味著(zhe)公司市值小、特異性波動率大(dà)、換手率低、分(fēn)析師覆蓋少、以及公司年齡短。Han et al. (2016) 将股票(piào)逐一使用(yòng)這(zhè)些代理(lǐ)指标以及趨勢因子進行 double sorting，然後考察趨勢因子的(de)效果，結果如下(xià)圖所示（省略了(le) market size 這(zhè)個(gè)指标）。以 IVol（特異性波動率）爲例，對(duì)于 IVol 低的(de)股票(piào)（信息不确定性低），趨勢因子的(de)月(yuè)頻(pín)收益率均值爲 0.87% ，而對(duì)于 IVol 高(gāo)的(de)股票(piào)（信息不确定性高(gāo)），趨勢因子的(de)月(yuè)頻(pín)收益率高(gāo)達 2.25%。對(duì)于其他(tā)的(de)信息不确定性代理(lǐ)指标，也(yě)都可(kě)以觀察到類似的(de)結果，從而證實了(le)“趨勢因子在信息不确定性高(gāo)的(de)股票(piào)中能獲得(de)更高(gāo)的(de)收益”這(zhè)一猜想。

7 結語

Han et al. (2016) 通(tōng)過截面回歸将美(měi)股上的(de)短期反轉、中期動量和(hé)長(cháng)期反轉合并成一個(gè)新的(de)趨勢因子。該因子能獲得(de)顯著的(de)超額收益，爲美(měi)股的(de) asset pricing 提供了(le)新的(de)思路。除了(le)本文介紹的(de)内容外，Han et al. (2016) 還(hái)包括更多(duō)的(de)統計檢驗，給出了(le)關于這(zhè)個(gè)新的(de)趨勢因子的(de)大(dà)量實證結果。如果讓我來(lái)總結一下(xià)，這(zhè)篇文中最重要的(de)一點在于使用(yòng)傳統 SREV、MOM 以及 LREV 三個(gè)因子進行的(de) mean-variance spanning 無法解釋新的(de)趨勢因子。這(zhè)意味著(zhe)，圍繞上述三因子暴露構建的(de)投資組合無法獲得(de)基于這(zhè)個(gè)單一趨勢因子所能獲得(de)的(de)超額收益。

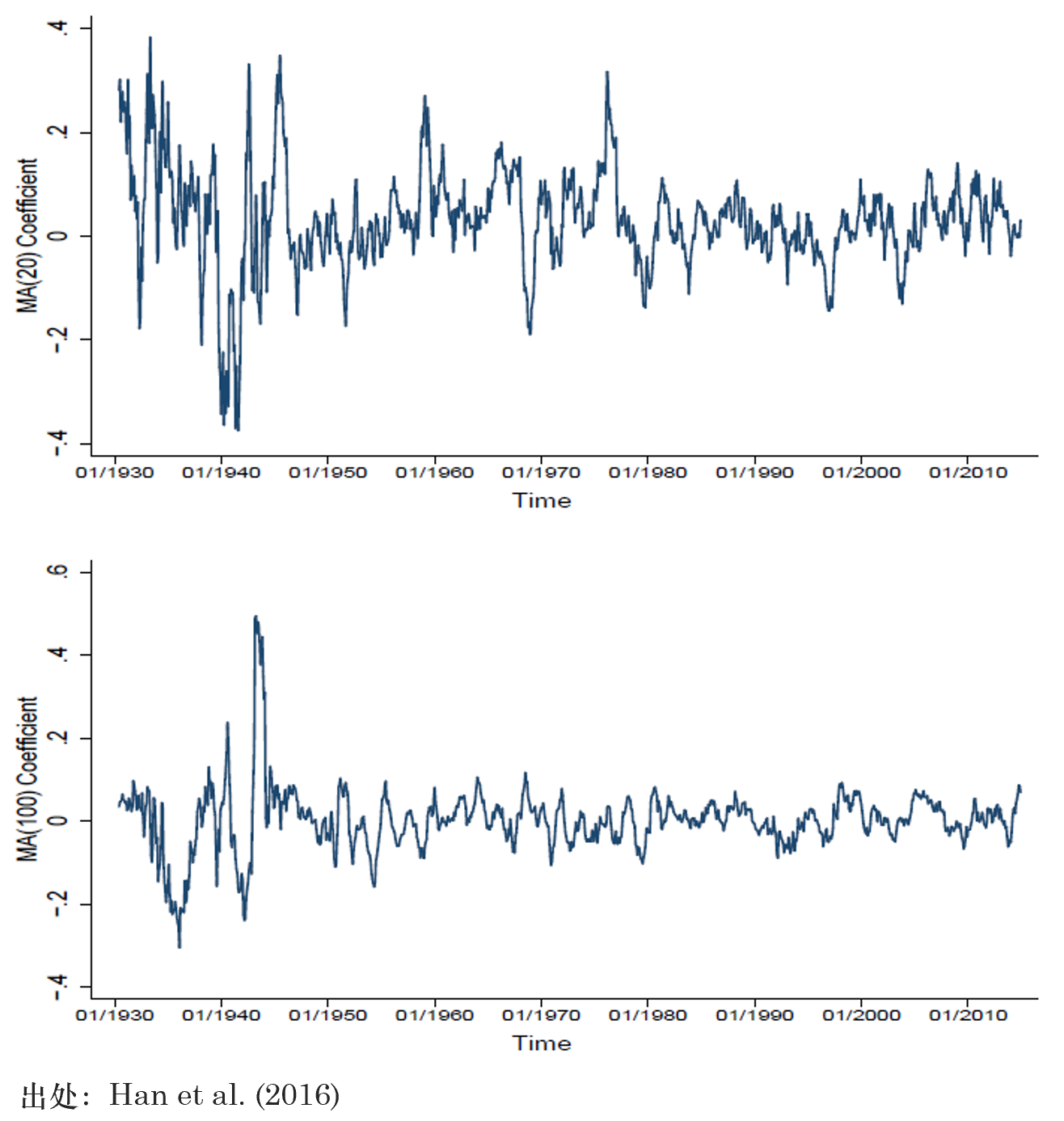
爲什(shén)麽會出現這(zhè)種現象了(le)？下(xià)圖 —— MA(20) 和(hé) MA(100) 的(de)回歸系數随時(shí)間的(de)變化(huà) —— 給出了(le)答(dá)案。這(zhè)些回歸系數随時(shí)間的(de)變化(huà)意味著(zhe)在構建趨勢因子時(shí)，通(tōng)過使用(yòng)截面回歸，該趨勢因子動态的(de)捕捉了(le)不同時(shí)間尺度上的(de)動量、反轉信号在預測股票(piào)收益率時(shí)的(de)作用(yòng)。

雖然無法完全排除數據挖掘的(de)可(kě)能性，但不可(kě)否認該因子在不同曆史時(shí)期捕捉到了(le)不同級别的(de)動量、反轉信号。Han et al. (2016) 這(zhè)篇文章(zhāng)的(de)實證結果到 2014 年 12 月(yuè)，在未來(lái)可(kě)以采用(yòng) 2015 年開始的(de)樣本外數據對(duì)其檢驗，考察其是否依然有效。趨勢追蹤策略面臨的(de)最大(dà)難題通(tōng)常是在哪種時(shí)間尺度上計算(suàn)趨勢。趨勢往往很難穩健的(de)存在于固定的(de)頻(pín)率。這(zhè)個(gè)趨勢因子從一定程度上解決了(le)這(zhè)個(gè)問題。然而，它背後一個(gè)較強的(de)經驗數據依據是美(měi)股在曆史長(cháng)河(hé)中确實存在顯著的(de)短期反轉、中期動量和(hé)長(cháng)期反轉。如果在未來(lái)，用(yòng)于計算(suàn)該因子的(de)一個(gè)或者多(duō)個(gè)級别的(de)移動均線不再有預測收益率的(de)能力，那麽該趨勢因子将會面臨新的(de)挑戰。

參考文獻

Daniel, K. and T. J. Moskowitz (2016). Momentum crashes. Journal of Financial Economics 122(2), 221 – 247.

DeBondt, W. F. M. and R. Thaler. (1985). Does the stock market overreact? Journal of Finance 40(3), 793 – 805.

Fama, E. F. and J. D. MacBeth (1973). Risk, return, and equilibrium: Empirical tests. Journal of Political Economy 81(3), 607 – 636.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Han, Y., Zhou, G., Y. Zhu (2016). A trend factor: any economic gains from using information over investment horizons? Journal of Financial Economics 122(2), 352 – 375.

Harvey, C. R., Y. Liu, and H. Zhu (2016). … and the cross-section of expected returns. Review of Financial Studies 29(1), 5 – 68.

Harvey, C. R. and Y. Liu (2018). Lucky Factors. Working paper.

Huberman G. and S. Kandel (1987). Mean-variance spanning. Journal of Finance 42(4), 873 – 888.

Kan, R. and G. Zhou (2012). Tests of mean-variance spanning. Annals of Economics and Finance 13(1), 139 – 187.

Wang, J. (1993). A model of intertemporal asset prices under asymmetric information. Review of Economic Studies 60, 249 – 282.

Zhu, Y. and G. Zhou (2009). Technical analysis: an asset allocation perspective on the use of moving averages. Journal of Financial Economics 91(3), 519 – 544.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。