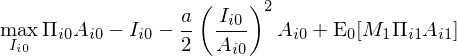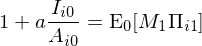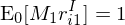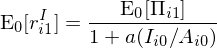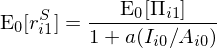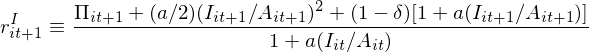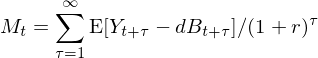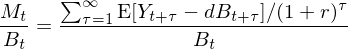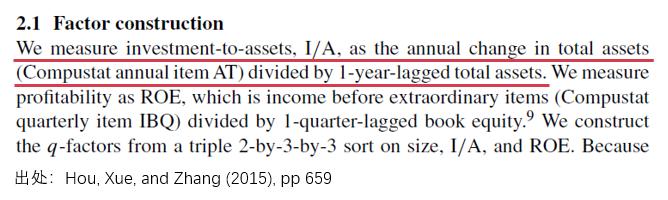從 Factor Zoo 到 Factor War，實證資産定價走向何方？

作者：石川

摘要：近年來(lái)，實證資産定價研究已經從 factor zoo 逐漸演變成 factor war，然而在這(zhè)種愈演愈烈的(de)“競争”下(xià)，我們對(duì)市場(chǎng)的(de)理(lǐ)解又增加了(le)多(duō)少？

1 引言

這(zhè)一切都源于 Hou et al. (2019a) 怼了(le) Fama and French (2015) 五因子模型。近年來(lái)，侯恪惟、薛辰以及張橹三位教授在實證資産定價領域掀起了(le)一股華人(rén)旋風。如果你對(duì)這(zhè)三個(gè)中文名字沒什(shén)麽印象，那麽對(duì)他(tā)們 Last Names 的(de)首字母組成的(de)三個(gè)字母縮寫 —— HXZ —— 一定不陌生。幾年前，這(zhè)三位教授在一篇題爲 Replicating Anomalies 的(de)文章(zhāng)中驚人(rén)的(de)複現了(le)學術界的(de) 447 個(gè)選股異象（anomalies），并指出在排除微小市值公司、考慮了(le) multiple testing 以及使用(yòng)了(le)“适當”的(de)定價模型之後，絕大(dà)部分(fēn)異象都不再顯著。這(zhè)篇最初的(de) working paper 長(cháng)達 146 頁，而如今它也(yě)終于即将被發表于頂刊 Review of Financial Studies（Hou, Xue, and Zhang 2018，下(xià)圖），其期刊編輯後的(de)版本也(yě)長(cháng)達 115 頁。我不知道這(zhè)是不是 RFS 曆史上最長(cháng)的(de)一篇，但至少是最長(cháng)之一。

HXZ 對(duì)于實證資産定價的(de)貢獻遠(yuǎn)不止于上面這(zhè)篇 Replicating Anomalies。在資産定價領域有著(zhe)不同的(de)方法論，比如人(rén)們熟悉的(de) consumption-based CAPM、以 Eugene Fama 和(hé) Ken French 爲代表的(de) empirical multi-factor asset pricing、以及最近流行的(de)基于 behavioral finance 的(de) asset pricing（Stambaugh and Yuan 2017；Daniel, Hirshleifer, and Sun 2019）。而在方法論上，HXZ 三位倡導的(de)則是 Investment-based CAPM。

在這(zhè)方面，HXZ 的(de)代表作是 Hou, Xue, and Zhang (2015) 這(zhè)篇同樣發表于 Review of Financial Studies 上的(de)文章(zhāng)，題爲 Digesting anomalies: an investment approach。他(tā)們從公司投資視角出發提出 q-factor asset pricing model（學術界簡稱 q-factor model）。以 The first principle of investment 爲依據，q-factor model 在市場(chǎng)和(hé) SMB 的(de)基礎上加入了(le) profitability 和(hé) investment 兩個(gè)維度，構建了(le)四因子模型。張橹教授也(yě)在其個(gè)人(rén)主頁上強調了(le) investment CAPM 對(duì)于資産定價理(lǐ)論的(de)貢獻：

My unique, big-picture perspective of asset pricing, which differs drastically from both the consumption CAPM and behavioral finance, is elaborated in my article titled The investment CAPM published in 2017 at European Financial Management (Zhang 2017).

Hou, Xue, and Zhang (2015) 這(zhè)篇文章(zhāng)在發表時(shí)曾被作爲 editor's choice 以及 lead article，足見其影(yǐng)響力。而 RFS 的(de)出版商，牛津大(dà)學出版社也(yě)曾以 A new benchmark model for estimating expected stock returns 爲題撰文爲其造勢。截至今日，Hou, Xue, and Zhang (2015) 已被引用(yòng)超過 890 次，是 2015 年以來(lái)發表于 RFS 上的(de)所有文章(zhāng)中引用(yòng)量最高(gāo)的(de)一篇。顯然，這(zhè)三位教授在 Investment CAPM 的(de)道路上遠(yuǎn)沒有止步于此。最近兩年，沿著(zhe) q-factor 的(de)思路，他(tā)們（以及合作者 Haitao Mo）可(kě)謂相當高(gāo)産，最新論文包括：

由于 q-factor model 和(hé) Fama and French (2015) 五因子模型中都包括投資因子，Hou et al. (2019a) 這(zhè)篇文章(zhāng)在比較多(duō)個(gè)因子模型之外，還(hái)用(yòng)了(le)相當多(duō)的(de)筆墨怼了(le) Fama and French (2015) 中的(de)投資因子。終于和(hé)本文開篇第一句呼應上了(le)。當我第一次看到 Hou et al. (2019a) 對(duì) Fama and French (2015) 的(de)抨擊時(shí)，著(zhe)實懵逼了(le)好長(cháng)時(shí)間 —— 雖然出發點不同，但兩個(gè)因子模型都有投資因子、且指标的(de)選取一模一樣（都是過去一個(gè)财年 total assets 的(de)增長(cháng)率）；爲什(shén)麽 Hou et al. (2019a) 要怼 Fama and French (2015)？爲了(le)搞清楚這(zhè)個(gè)問題，我又系統的(de)沿著(zhe) Hou, Xue, and Zhang (2015)、Hou et al. (2018, 2019a, 2019b) 一路讀下(xià)來(lái)，加深了(le)對(duì) investment CAPM 的(de)理(lǐ)解。不過在這(zhè)個(gè)過程中，也(yě)多(duō)少感到了(le)近年來(lái)學術界因子模型之争（factor model war，簡稱 factor war）的(de)硝煙(yān)。

本文就以梳理(lǐ) investment CAPM 的(de)發展脈絡爲契機，映射學術界最近在 factor war 上面愈演愈烈的(de)趨勢，以此表達一些對(duì)實質資産定價研究的(de)擔憂。最後需要強調的(de)是，在多(duō)家因子流派“千帆競發、百舸争流”之下(xià)，factor war 是一個(gè)普遍的(de)現象；因此本文雖然是透過 investment CAPM 的(de)鏡頭一窺這(zhè)一現象，并不意味著(zhe)該流派是 factor war 的(de)衆矢之的(de)。下(xià)面先來(lái)看 q-factor model。

2 q-Factor Model 的(de)經濟學原理(lǐ)

Hou, Xue, and Zhang (2015) 提出的(de) q-factor model 是受到 Cochrane (1991) 的(de) production-based asset pricing 所啓發，從公司投資的(de)經濟學原理(lǐ)出發。張橹教授曾在清華金融評論上撰文介紹過這(zhè)個(gè) q-factor model 的(de)來(lái)龍去脈（Zhang 2016）。我在接下(xià)來(lái)兩段的(de)介紹中不妨直接引用(yòng)一下(xià) Zhang (2016) 的(de)闡述。

根據 Zhang (2016)，q-factor model 是基于實體投資經濟學理(lǐ)論，又稱 q-theory（這(zhè)也(yě)是該模型被稱爲 q-factor model 的(de)原因）。它體現了(le)公司金融學中的(de)淨現值原則（NPV rule）：如果項目現值大(dà)于投資成本，則應當投資該項目；如果項目現值小于投資成本，則不應當投資。起初，公司會有很多(duō)投資項目，此時(shí)應優先投資折現率低、盈利率高(gāo)、因此現值最高(gāo)的(de)項目。随著(zhe)被投資的(de)項目越來(lái)越多(duō)，投資成本會慢(màn)慢(màn)變高(gāo)，盈利率會越來(lái)越低。投資的(de)最後一個(gè)項目應該是淨現值爲零（淨現值原則）：投資成本 = 項目現值 = 盈利率 / 折現率。

上面這(zhè)個(gè)淨現值原則說的(de)是：一家公司應該持續投資，直到投資的(de)邊際效益（被折現到今天）等于投資的(de)邊際成本。這(zhè)就是對(duì) Hou, Xue, and Zhang (2015) 所依托的(de)經濟學原理(lǐ)的(de)核心概括。Zhang (2016) 繼續介紹說：q-factor model 最富想象力和(hé)創造力的(de)是把公司金融原則當作資産定價模型。傳統資産定價理(lǐ)論從投資者最優證券組合角度出發，和(hé)公司變量沒有直接關系。但是那一老套做(zuò)了(le)近半個(gè)世紀，結果隻是大(dà)量異象現象。q-factor model 開辟了(le)一個(gè)新的(de)途徑。我對(duì)以上這(zhè)段如此之高(gāo)的(de)自我評價持保留态度。

将淨現值原則變化(huà)一下(xià)得(de)出：折現率 = 盈利率 / 投資成本。從這(zhè)個(gè)式子出發，我們可(kě)以得(de)到兩個(gè)關于折現率的(de)條件預期結論：當盈利率給定時(shí)，投資越多(duō)的(de)公司（因此投資成本越高(gāo)），折現率越低，股票(piào)預期收益率也(yě)越低；當投資給定時(shí)，盈利率越高(gāo)的(de)公司，折現率越高(gāo)，股票(piào)預期收益率也(yě)越高(gāo)。由此可(kě)知，股票(piào)收益率和(hé)投資成反比；和(hé)盈利率成正比。這(zhè)就是 q-factor model 中加入 profitability 和(hé) investment 兩個(gè)維度的(de)原因。不過我想“杠精”一下(xià)。盡管提出者對(duì) q-factor model 有著(zhe)很高(gāo)的(de)自我評價；但我們卻無法從淨現值原則中推導出市場(chǎng)和(hé) SMB 兩個(gè)因子。爲什(shén)麽最後 q-factor model 是四個(gè)因子而非兩個(gè)呢(ne)？退一步說，加入市場(chǎng)因子無可(kě)厚非，但爲什(shén)麽 q-factor model 中不是三因子，而是偏偏加入了(le) SMB 湊出四個(gè)因子呢(ne)？

事實上，第一版的(de) q-factor model 并不是我們在 Hou, Xue, and Zhang (2015) 看到的(de)那樣。它出現在 Chen and Zhang (2007) 這(zhè)篇題爲 Neoclassical Factors（新古典因子）的(de) NBER 報告中，僅包含市場(chǎng)、盈利以及投資三個(gè)因子。這(zhè)篇文章(zhāng)後被投到 Journal of Finance 卻在幾經修改之後還(hái)是被 rej 了(le)。之後，Zhang 教授聯手 Hou 和(hé) Xue，最終提出了(le)我們看到的(de)四因子版本的(de) q-factor model，它經過兩年的(de)審稿和(hé)修改，終于在 2015 年被發表在 RFS 上。反觀 Fama and French (2015)，他(tā)們從 discount cash flow（DCF）出發 promote 五因子模型（下(xià)文稱 FF5）中新加入的(de) profitability 和(hé) investment 兩個(gè)因子；而如果從 DCF 的(de)表達式來(lái)看，也(yě)是可(kě)以推出收益率和(hé) SMB 及 HML 之間的(de)關聯（後文會說明(míng)）。從這(zhè)個(gè)意義上說，FF5 更自洽一些。

那麽，Hou, Xue, and Zhang (2015) 用(yòng)了(le)哪些指标作爲盈利率和(hé)投資的(de) proxy 來(lái)構建因子呢(ne)？爲此下(xià)面一小節将簡單介紹 q-factor model 的(de)數學模型。從之前的(de)中文描述中我們已經搞清楚了(le)該模型背後的(de)核心經濟學原理(lǐ)。因此在介紹數學表達時(shí)會力求言簡意赅。了(le)解 q-factor model 的(de)數學模型也(yě)會幫助我們在本文第四節更好的(de)理(lǐ)解 q5 model —— 它在數學上是 q-factor model 的(de)一步拓展。

3 q-Factor Model 的(de)數學模型

q-factor model 背後的(de)數學模型十分(fēn)簡單；它假設一個(gè)兩期（date 0 和(hé) date 1）的(de)公司投資決策模型。假設在 date 0，某公司 i 的(de)資産爲 A_i0、利潤率是 Π_i0（假設已知）。在 date 1，該公司的(de)利潤率是 Π_i1，它是一個(gè)随機變量。對(duì)于 date 0 和(hé) 1，公司的(de) cash flow 爲每一時(shí)刻的(de)資産乘以利潤率：Π_itA_it，t = 0, 1。在這(zhè)個(gè)兩期模型中，公司的(de)決策變量是 date 0 的(de)投資額 I_i0。該模型假設公司 date 0 的(de)資産 A_i0 在 t = 1 時(shí)全部折舊(jiù)完，因此該公司在 date 1 的(de)資産正是其在 date 0 的(de)投資：A_i1 = I_i0。除此之外，伴随 I_i0 而來(lái)的(de)還(hái)包括一個(gè)調整費用(yòng)（adjustment cost）：(a/2)(I_i0/A_i0)2A_i0。有了(le)上述設定，我們就來(lái)看看最優化(huà)的(de)目标函數是什(shén)麽。

對(duì)于該公司，date 0 對(duì)于股東的(de)回報是 cash flow 減去投資額以及投資的(de)調整費用(yòng)，即 Π_i0A_i0 – I_i0 - (a/2)(I_i0/A_i0)2A_i0；而對(duì)于 date 1，由于不再有投資，因此其在 0 時(shí)刻的(de)預期回報可(kě)以表達爲 E_0[M_1Π_i1A_i1]，其中 M_1 是 stochastic discount factor、Π_i1A_i1 是 date 1 的(de) cash flow、而求期望符号 E 的(de)下(xià)标 0 代表 date 0 時(shí)的(de)預期。這(zhè)兩期的(de)回報相加就是最優化(huà)的(de)目标函數：

該目标函數的(de)最優解 I_i0 應滿足：

上式的(de)左側爲投資的(de)邊際成本（第二項爲 marginal adjustment cost）；右邊爲邊際效益預期被折現到 date 0。這(zhè)個(gè)關系是也(yě)說明(míng)了(le)上一小節提到的(de)淨現值原則。此外，由 the first principle of investment 可(kě)知，投資收益率 r^I（上标 I 表示投資收益率；爲了(le)區(qū)分(fēn)股票(piào)收益率）應滿足：

比較上面兩個(gè)式子就可(kě)以得(de)到投資收益率和(hé)邊際成本以及邊際效益的(de)關系：

根據 Cochrane (1991) 和(hé) Liu, Whited, and Zhang (2009) 的(de)研究，在上述模型（以及更 general 的(de)模型）設定下(xià)，公司的(de)投資收益率等于其股票(piào)收益率（記爲 r^S），因此最終可(kě)以把股票(piào)收益率和(hé)上述從公司投資角度出發的(de)經濟學理(lǐ)論聯系起來(lái)：

上式就和(hé)本文第二節的(de)文字解釋一緻了(le)：當預期盈利 E_0[Π_i1] 給定時(shí)，股票(piào)收益率和(hé)投資 I_i0/A_i0 成反比；當投資給定時(shí)，股票(piào)收益率和(hé)預期盈利成正比。注意，在這(zhè)個(gè)關系式中，投資 I_i0/A_i0 是 date 0 的(de)，因此是曆史投資，而非未來(lái)的(de)預期投資（expected investment）。q-factor model 背後的(de)理(lǐ)論用(yòng)的(de)是 past investment，而非 expected investment，這(zhè)是它和(hé) FF5 在投資因子上最大(dà)的(de)差異（FF5 從 DCF 模型出發 promote 出來(lái)的(de) expected investment）。之所以強調這(zhè)個(gè)，因爲它是搞清楚 Hou et al. (2019a) 怼 FF5 的(de)關鍵。

在實證研究中，Hou, Xue, and Zhang (2015) 使用(yòng) ROE 和(hé) Total Assets 的(de)增長(cháng)率作爲代表盈利和(hé)投資的(de)指标。在構建因子時(shí)，爲了(le)體現上述條件預期收益率的(de)關系，他(tā)們特意選擇了(le)通(tōng)過 size、I/A 以及 ROE 将股票(piào)池獨立進行 2 × 3 × 3 的(de) triple sort（使用(yòng) ROE 和(hé) I/A 将股票(piào)分(fēn)成三組時(shí)使用(yòng)學術界常用(yòng)的(de) 30% 和(hé) 70% 分(fēn)位數，中間的(de) 40% 爲 Middle 組），一共得(de)到 18 個(gè)投資組合（每個(gè)投資組合中的(de)股票(piào)都是按市值加權）。最終三個(gè)風格因子的(de)定義爲：

以上三個(gè)因子，再結合市場(chǎng)因子，就構成了(le) q-factor model。至于它和(hé)其他(tā)主流因子模型相比效果如何？我們留在本文的(de)第七節 factor war 見分(fēn)曉。有了(le)對(duì) q-factor model 數學模型的(de)理(lǐ)解，将它進行一步擴展，就得(de)到 q5。

4 q5

Hou et al. (2018) 這(zhè)篇文章(zhāng)雖然目前仍然隻是 working paper，但 q5 這(zhè)個(gè)題目絕對(duì)标新立異。q5 在 q-factor model 的(de)四因子基礎上加入了(le)第五個(gè)代表 expected investment growth 的(de)因子，得(de)到一個(gè)五因子模型。在數學上，它是 q-factor model 的(de)直接延伸。而我更關注的(de)是這(zhè)第五個(gè)因子被加入的(de)動機。Hou et al. (2018) 一開篇就以 Cochrane (1991) 來(lái) motivate 出這(zhè)第五個(gè)因子：

Cochrane (1991) shows that in a multiperiod investment framework, firms with high expected investment growth should earn higher expected returns than firms with low expected investment growth, holding current investment and expected profitability constant.

顯然，這(zhè)句話(huà)引入了(le) expected investment growth，同時(shí)它也(yě)指出了(le)這(zhè)是在 multiperiod investment framework 之下(xià)。由于 Hou, Xue, and Zhang (2015) 僅使用(yòng)了(le)簡單的(de)二期模型（因爲 date 1 不再投資，因此它實際上是一個(gè) one period investment framework），所以 q-factor model 中是沒有投資增長(cháng)的(de)。因此，在 q5 這(zhè)篇文章(zhāng)中，Hou et al. (2018) 把投資模型擴展到了(le)多(duō)期。上面這(zhè)個(gè)理(lǐ)論上的(de)延展看來(lái)是把 q 升級到 q5 背後的(de)主要動機。不過有意思的(de)是，Zhang 教授和(hé)另外兩位 co-authors 早在 Liu, Whited, and Zhang (2009) 一文（發表于經濟學頂刊 Journal of Political Economy）中就研究過多(duō)期投資模型。雖然該文的(de)重點不是 empirical asset pricing，但 expected investment growth 這(zhè)個(gè)維度早就出現過（Liu, Whited, and Zhang 2009, pp 1126, eq. 10）。所以……

我無從得(de)知爲什(shén)麽 Hou, Xue, and Zhang (2015) 在 q-factor model 裏沒有加入 expected investment growth；而是等到 q5 這(zhè)篇才加入。也(yě)許在 q-factor model 被提出時(shí)，它已經能解釋很多(duō)當時(shí)已有因子不能解釋的(de)異象了(le)。而這(zhè)幾年一些新的(de)因子模型有在效果上超過了(le) q-factor model，所以需要一個(gè)升級版。這(zhè)當然純屬我的(de)“陰謀論”，不過 Hou et al. (2018) 中的(de)下(xià)面這(zhè)句話(huà)也(yě)十分(fēn)耐人(rén)尋味：

Improving on the q-factor model substantially, the q5 model is the best preforming model among all the factor models.

OK，八卦結束，讓我們從數學上看看這(zhè)個(gè) q5 模型。Hou et al. (2018) 在 Hou, Xue, and Zhang (2015) 的(de)基礎上考慮無限期的(de)模型。由于是多(duō)期模型，因此他(tā)們假設資産從 t 到 t + 1 期的(de)折舊(jiù)率爲 δ（在 q-factor model 中，資産從 date 0 到 date 1 折舊(jiù)完，因此在該模型中 δ = 1）。投資決策是每一期的(de)投資 {I_it+s}, s = 0, 1, …。在任何時(shí)點 t，目标函數是最大(dà)化(huà)股東權益的(de)現值。根據 the first principle of investment 可(kě)知從 t 到 t + 1 期的(de)邊際投資成本應該等于邊際效益折現到 t，因此 t 到 t + 1 的(de)投資收益滿足：

對(duì)于 Hou, Xue, and Zhang (2015) 考慮的(de)兩期模型，由于折舊(jiù)率 δ = 1 且 date 1 的(de)投資 I_i1 = 0，因此上式分(fēn)子中僅有第一項，而上式也(yě)就變成了(le)本文第三節介紹的(de) q-factor model 的(de)情況。對(duì)于多(duō)期模型，Hou et al. (2018) 如法炮制，指出股票(piào)收益率等于投資收益率。由此，從上式我們可(kě)以找到股票(piào)收益率和(hé)投資以及盈利的(de)關系。上式中第一項近似對(duì)應“dividends”，第二項平方項與邊際調整費用(yòng)有關（由于是高(gāo)階小量故忽略），第三項近似對(duì)應“capital gain”，即 expected investment-to-asset growth（expected I/A growth）。從多(duō)期模型出發，股票(piào)收益率除了(le)和(hé) q-factor model 中已經考慮的(de) ROE 以及 I/A （條件）相關，也(yě)和(hé) expected I/A growth 正相關。因此，該因子作爲第五個(gè)因子被補充到 q-factor model 中，最終得(de)到了(le) q5。

在實際構造 expected I/A growth 因子時(shí)，Hou et al. (2018) 使用(yòng)了(le) predictive regression 外推的(de)方法。即這(zhè)個(gè)因子和(hé)我們了(le)解的(de)直接利用(yòng)曆史财務數據的(de)因子均不同，它是使用(yòng)曆史數據構建了(le)一個(gè)截面回歸預測模型，然後使用(yòng)最新的(de)财務數據預測下(xià)一期 expected I/A growth。從數學複雜(zá)度上來(lái)說，我個(gè)人(rén)對(duì)這(zhè)種構建因子的(de)方法不是很感冒。因爲這(zhè)裏面有模型設定以及參數估計誤差等太多(duō)的(de)問題。Hou et al. (2018) 自然意識到了(le)這(zhè)些問題；在文中他(tā)們也(yě)特别提到：

Our goal is a conceptually motivated yet empirically validated specification for the expected investment-to-assets changes. To this end, we turn to the investment literature in macroeconomics and corporate finance for guidance.

然而不可(kě)否認的(de)是，在構造 expected I/A growth 因子時(shí)，由于可(kě)挖的(de)數據太多(duō)，因此 data snooping 的(de)風險也(yě)很高(gāo)。本文不再贅述該因子的(de)具體構造方法，感興趣的(de)小夥伴可(kě)以查看 Hou et al. (2018)。最後想要強調的(de)是，我在上面提及這(zhè)第五個(gè)因子時(shí)，不厭其煩的(de)使用(yòng)了(le) expected 這(zhè)個(gè)詞。這(zhè)是因爲從 q-theory 出發，該因子是（未來(lái)）預期投資增長(cháng)率，而非過去的(de)投資增長(cháng)率。是否帶有 expected 一詞，含義截然不同。

5 FF5

說說 FF5 吧；它被 q-factor model 當成靶子打。從 DCF 出發并利用(yòng) Miller and Modigliani (1961) 的(de)結果可(kě)知 t 時(shí)刻公司市值 M_t 滿足如下(xià)關系：

上式中，Y_t+τ 是 t+τ 期的(de) total earnings，dB_t+τ 是未來(lái) t+τ 時(shí)刻相對(duì)其前一期的(de) total book value 的(de)變化(huà)，r 是 IRR。将上式兩邊同時(shí)處以 t 時(shí)刻公司的(de) book value B_t 可(kě)得(de)：

Fama and French (2015) 通(tōng)過上式 motivate 出 FF5：

在實證中如何圍繞預期盈利和(hé)預期投資構建因子呢(ne)？這(zhè)方面的(de)研究可(kě)以追溯到 Fama and French (2006)。2006 年，Fama 和(hé) French 在 Journal of Financial Economics 上發表了(le)一篇題爲 Profitability, investment and average returns 的(de)文章(zhāng)，專門檢驗了(le)預期盈利和(hé)預期投資這(zhè)兩個(gè)維度和(hé) expected return 的(de)關系：

Given B/M and expected profitability, higher expected rates of investment imply lower expected returns. But controlling for the other two variables, more profitable firms have higher expected returns, as do firms with higher B/M. These predictions are confirmed in our tests.

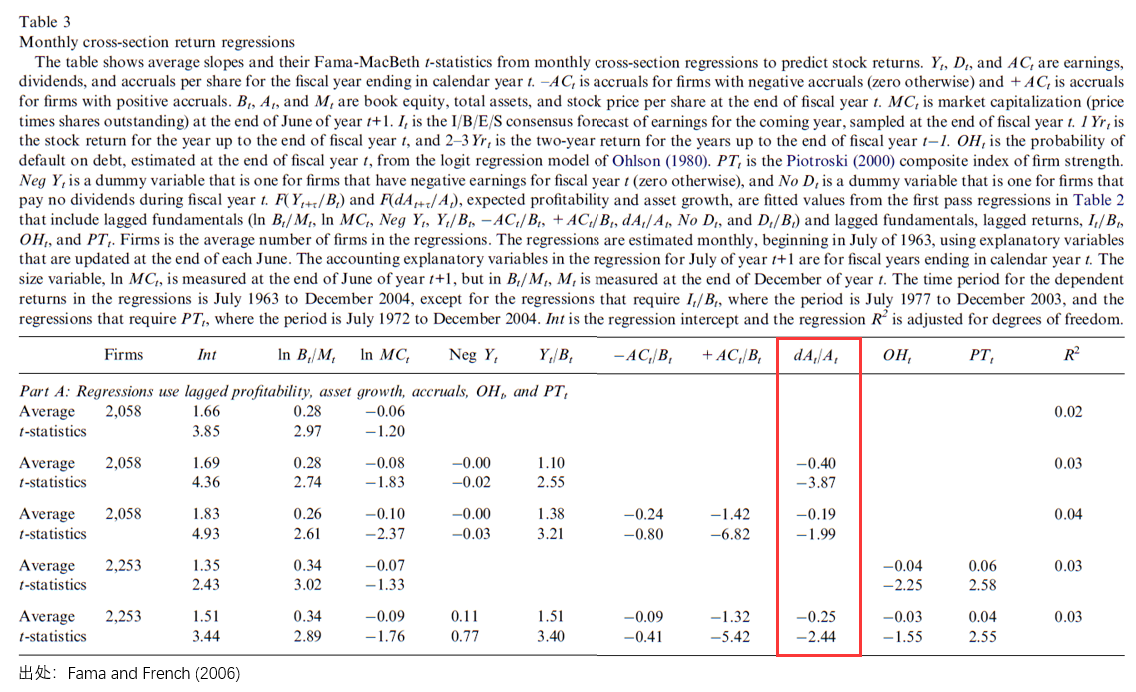
與 FF5 一樣，Fama and French (2006) 也(yě)是從 DCF 出發。它在檢驗預期盈利和(hé)預期投資時(shí)，既檢驗了(le)使用(yòng)曆史數據作爲預期的(de) naïve estimate，又考慮了(le)使用(yòng) predictive regression 構建因子。以預期投資爲例，在使用(yòng)曆史數據直接外推時(shí)，該文使用(yòng) dA/A —— total asset 的(de)變化(huà)率 —— 作爲 expected investment。截面回歸結果（下(xià)圖）顯示出它和(hé)收益率之間顯著的(de)負相關性。

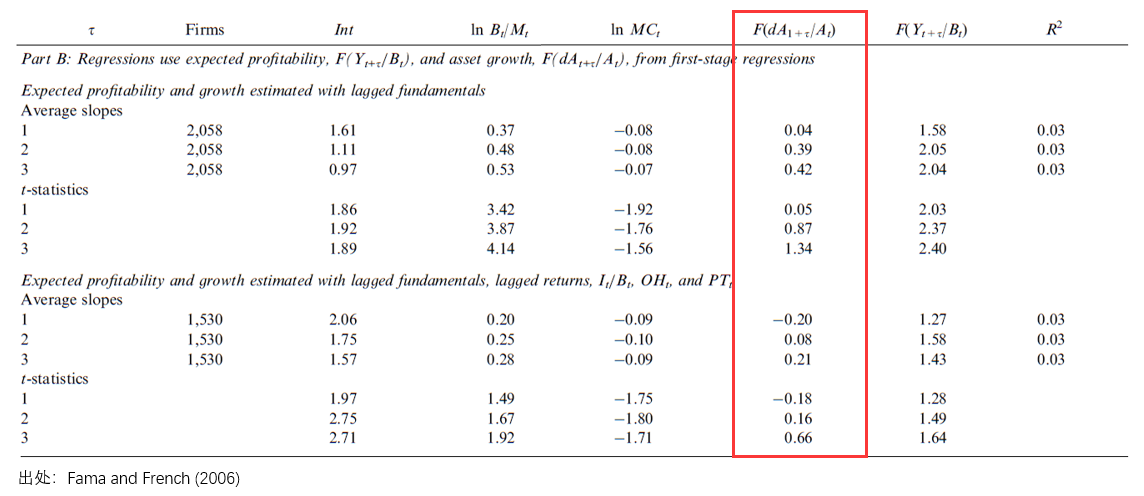
而當 Fama and French (2006) 采用(yòng) predictive regression 計算(suàn) expected investment 時(shí)，卻并沒有獲得(de)統計上顯著的(de)關系（下(xià)圖中 F(dA_t+τ/A_t)）：

上面的(de)結果顯示，預測的(de) F(dA_t+τ/A_t) 與收益率的(de)相關系數爲正（而這(zhè)和(hé)從 DCF 推出的(de) expected investment 和(hé)收益率之間的(de)負相關性是相左的(de)！），但統計上非常不顯著。以預測未來(lái)一年的(de) F(dA_t+1/A_t) 爲例，它的(de)回歸系數僅爲 0.04，t-statistic 爲 0.05。對(duì)于這(zhè)兩種方法的(de)差異，Fama and French (2006) 從計量經濟學的(de)角度進行了(le)大(dà)量的(de)探討(tǎo)，并最終選擇了(le)使用(yòng)曆史數據進行 naïve estimate 的(de)方法計算(suàn)預期投資（對(duì)于預期盈利，使用(yòng)曆史數據和(hé) predictive regression 的(de)差異很小，故也(yě)采用(yòng)曆史數據）。上述處理(lǐ)方法也(yě)最終被保留到了(le) FF5 中。

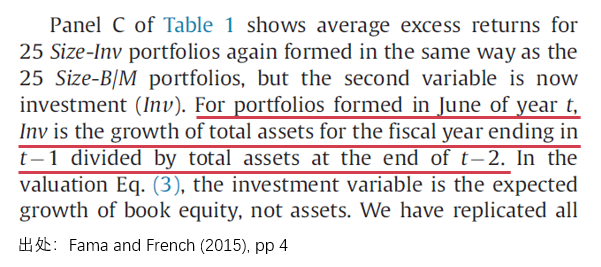
值得(de)一提的(de)是，按照(zhào)上述 DCF 模型，代表投資的(de)變量應該是 dB_t+τ/B_t，即 book value 的(de)預期變化(huà)，而非 total asset。Fama and French (2015) 坦言他(tā)們比較了(le)使用(yòng) book value 和(hé) total asset 兩種方法，發現使用(yòng)後者排序的(de)話(huà)，股票(piào)收益率在截面上的(de)差異更大(dà)，因此選擇了(le) total asset 的(de)變化(huà)。以上就是 FF5 背後的(de)來(lái)龍去脈。下(xià)面就來(lái)看看 Hou et al. (2019a) 是怎麽怼 FF5 的(de)。

6 q vs FF5

Hou et al. (2019a) 這(zhè)篇文章(zhāng)使用(yòng) spanning test 比較了(le)他(tā)們提出的(de) q 和(hé) q5 以及其他(tā)幾個(gè)主流的(de)多(duō)因子模型，包括：

結論自然不出意外，q 和(hé) q5 完勝。不過，除了(le) empirical test 之外，這(zhè)篇文章(zhāng)還(hái)從 valuation theory 的(de)角度狠狠的(de)怼了(le) FF5，而我一切的(de)困惑和(hé)寫作本文的(de)動機皆源于此。下(xià)面開始解惑之旅。如果我們仔細查看 q-factor model 和(hé) FF5 中構建投資因子的(de)指标，會發現這(zhè)兩個(gè)指标完全一緻（下(xià)圖 1 來(lái)自 Hou, Xue, and Zhang 2015；圖 2 來(lái)自 Fama and French 2015）。

雖然指标一緻，但背後的(de)出發點截然不同：

Hou et al. (2019a) 怼 FF5 的(de)兩個(gè)核心觀點是：

結合上述兩點，FF5 使用(yòng) past investment 構建的(de) CMA 因子（且該因子有效）其實是陰差陽錯的(de)利用(yòng)了(le) past investment 和(hé)收益率之間的(de)負相關（q-theory）；而非他(tā)們從 DCF 推出的(de) expected investment 和(hé)收益率之間的(de)負相關性。這(zhè)無疑直接撼動了(le) FF5 中投資因子的(de)根基，也(yě)質疑了(le) FF5 在學術界的(de)地位。

因子大(dà)戰，硝煙(yān)彌漫。

對(duì)于上面第一點，Hou et al. (2019a) 的(de)論述如下(xià)，感興趣的(de)小夥伴可(kě)以看看。

客觀的(de)說，關于 expected investment 和(hé) expected return 的(de)關系，我也(yě)認爲 Hou et al. (2019a) 比 FF5 更合理(lǐ)。但上面這(zhè)種“競賽”還(hái)是讓人(rén)感到不安。它似乎傳遞出一個(gè)信号：我們總能使用(yòng)不同的(de)金融學或經濟學模型，推導出截然相反的(de)關聯 —— 上面的(de)模型較 DCF 模型，通(tōng)過把 IRR 換成單期收益率，巧妙的(de)幹掉了(le) dB 前面的(de)負号，因此把“負相關”逆轉爲“正相關”。從實證結果出發總能講出最适合的(de)故事，但對(duì)著(zhe)曆史數據講故事真的(de)讓我們離真相更進一步了(le)嗎？

OK，抛開理(lǐ)論上的(de)差異不說，從實證結果來(lái)看，雖然 FF5 和(hé) q-factor model 使用(yòng)了(le)同樣的(de)曆史 total asset 增長(cháng)率構建投資因子，但由于構建方法不同，q-factor model 中投資因子的(de)溢價也(yě)完勝 FF5。從 q-theory 出發，投資和(hé)收益率的(de)負相關是在控制了(le) ROE 之後的(de)。因此，q-factor model 在構建投資因子時(shí)利用(yòng) size，ROE 和(hé) total assets 增長(cháng)率三個(gè)指标使用(yòng) 2 × 3 × 3 triple sort，從而更好的(de)反映了(le)在控制 ROE 之後，投資和(hé)收益率的(de)關系。反觀 FF5，它僅使用(yòng) size 和(hé) total asset 增長(cháng)率做(zuò)了(le) 2 × 3 double sort，沒有考慮控制 ROE 的(de)影(yǐng)響，效果不如 q-factor model。這(zhè)似乎佐證了(le) q-factor model 背後的(de) q-theory 能更好的(de)解釋 past investment 和(hé) expected return 之間的(de)關系。解惑之旅結束。

7 Factor War

讓我們最後來(lái)看看近幾年學術界的(de) Factor War。以下(xià)先後順序使用(yòng)論文的(de)發表時(shí)間爲基準。在 Hou, Xue, and Zhang (2015) 提出 q-factor model 時(shí)，他(tā)們使用(yòng)了(le) 80 個(gè)異象（那篇寫 Replicating Anomalies 花的(de)功夫絕對(duì)不會被浪費）比較了(le) q-factor model 和(hé) Fama and French (1993) 三因子模型和(hé) Carhart (1997) 四因子模型。結論自然是 q-factor model 戰勝了(le)它們。由于當時(shí) FF5 還(hái)沒有發表，因此并沒有被拿來(lái)比較。

頗有意思的(de)是，關于 q-factor model 和(hé) FF5 寫作背後的(de)時(shí)間先後也(yě)拿來(lái)被當作 factor war 的(de)炮彈。Zhang (2016) 介紹了(le)兩篇文章(zhāng)寫作的(de)背景（下(xià)圖），指出 Fama 和(hé) French 在 2013 年 6 月(yuè)首先加入了(le)盈利因子，然後才又加入了(le)投資因子、構建了(le) FF5，而這(zhè)個(gè) timeline 遠(yuǎn)遠(yuǎn)晚于 q-factor model 的(de)發展曆程（見本文第二節），因此巨人(rén) Fama 是站在了(le)他(tā)們的(de)肩膀上。不過 Zhang (2016) 似乎忘記了(le) Fama and French (2006) 這(zhè)篇早就對(duì)盈利和(hé)投資進行檢驗的(de)文章(zhāng) —— 雖然 Hou et al. (2019a) 怼 FF5 的(de)時(shí)候想起了(le)它。

2017 年，Stambaugh 和(hé) Yuan 在 Review of Financial Studies 上提出了(le)兩個(gè) mispricing factors（Stambaugh and Yuan 2017），并結合市場(chǎng)和(hé) SMB 構建了(le)四因子模型。新的(de)模型也(yě)少不了(le)和(hé)已有的(de)做(zuò)一番對(duì)比，而結論也(yě)自不必說：

2018 年，Barillas 和(hé) Shanken 在 Journal of Finance 上發表了(le)題爲 Comparing asset pricing models 的(de)文章(zhāng)。該文提出了(le)一個(gè) Bayesian asset pricing test 檢驗不同的(de)定價模型（Barillas and Shanken 2018）。通(tōng)過對(duì)比，q-factor model 和(hé) FF5 都敗下(xià)陣來(lái)，而 Barillas and Shanken (2018) 也(yě)根據他(tā)們的(de)結果提出了(le)一個(gè)六因子模型，包括：市場(chǎng)因子、FF5 的(de) SMB、q-factor model 的(de) ROE 和(hé) I/A，Asness and Frazzini (2013) 提出的(de)按月(yuè)更新的(de) HML，以及 UMD。

同年，在美(měi)國金融協會年會上，Daniel, Hirshleifer, and Sun (2019) —— 這(zhè)裏引用(yòng)使用(yòng)了(le)即将發表于 RFS 的(de)版本 —— 提出了(le)基于行爲金融學的(de)兩個(gè)因子，并結合市場(chǎng)因子構建了(le)一個(gè)複合三因子模型（見《一個(gè)加入行爲因子的(de)複合模型》）。在 AFA 年會的(de)報告中，Daniel, Hirshleifer, and Sun (2019) 将該模型和(hé)主流模型進行了(le)對(duì)比，除了(le)考察因子模型解釋異象及其他(tā)因子的(de)能力，也(yě)特别從模型複雜(zá)度角度進行了(le)對(duì)比（見《Anomalies, Factors, and Multi-Factor Models》）。在 AFA 年會報告的(de)討(tǎo)論環節，Stambaugh 質疑 Daniel, Hirshleifer, and Sun (2019) 的(de)三因子模型無法解釋 SMB 因子，但他(tā)們卻沒有加入這(zhè)個(gè)因子。我現在來(lái)看，這(zhè)反而是 Daniel, Hirshleifer, and Sun (2019) 的(de)一個(gè)優點。該模型從行爲金融學的(de)理(lǐ)論 promote 出長(cháng)、短兩個(gè)周期的(de)行爲因子；而從行爲金融學的(de)理(lǐ)論是無法引出 SMB 的(de)因子的(de)。所以該模型僅使用(yòng)三個(gè)因子無可(kě)厚非；如果生硬的(de)加入了(le) SMB，反而更有 data mining 之嫌。

自 2015 年 q-factor 被提出後，由于其理(lǐ)論上的(de)創新和(hé)實證方面的(de)優秀表現，獲得(de)了(le)學術界的(de)廣泛關注。但是，随著(zhe)新的(de)模型被發表，它又被别人(rén)比了(le)下(xià)去。在這(zhè)種背（yin）景（mou）之（lun）下(xià)，q5 橫空出世。Hou et al. (2019a) 的(de)實證結果顯示，q5 戰勝了(le)上述全部 candidates。

從現有的(de)實證結果來(lái)看，出自 investment CAPM 的(de) q5 的(de)五因子模型是當下(xià)“最強”的(de)實證資産定價模型。當然，在不遠(yuǎn)的(de)将來(lái)，學術界一定會搞出新的(de) factor model 來(lái)打敗它。近年來(lái)，随著(zhe) John Cochrane 所提的(de) factor zoo 越來(lái)越深入人(rén)心，學術界對(duì)挖異象的(de)熱(rè)潮似乎有所減退，轉而把研究重點放到了(le) factor war。然而，如果僅以各種 test 的(de)結果或者誰解釋的(de)異象更多(duō)爲标準，非要在衆多(duō)模型中分(fēn)出高(gāo)下(xià)，又有多(duō)少意義？如果僅以“打赢” factor war 、而非推動人(rén)們對(duì)市場(chǎng)的(de)理(lǐ)解爲目标，而使用(yòng)不同的(de)金融學或經濟學理(lǐ)論 promote 出一個(gè)“更好使”的(de)因子或者互相“怼”，這(zhè)又有多(duō)少意義？

因子大(dà)戰，烽鼓不息。

8 結語

在上一節介紹 factor war 時(shí)，我特意保留了(le)一篇，它就是 Fama and French (2018) 這(zhè)篇題爲 Choose Factors 的(de)文章(zhāng)，發表于 Journal of Financial Economics。這(zhè)篇文章(zhāng)拓展了(le) Gibbons, Ross, and Shanken (1989) test，提出使用(yòng)模型所包含因子能夠構成的(de) max squared Sharpe ratio 來(lái)比較不同的(de)模型。之所以保留這(zhè)篇文章(zhāng)是因爲它沒有和(hé)别人(rén)比，而是“自己和(hé)自己比”。該文比較了(le) CAPM，Fama and French (1993) 三因子、Fama and French (2015) 五因子以及 Fama and French (2018) 六因子模型。除了(le)方法論之外，Eugene Fama 在這(zhè)篇文章(zhāng)中表達出來(lái)的(de)對(duì) factor war 的(de)擔憂深深引起了(le)共鳴。

Fama and French (2018) 認爲，雖然 CAPM 以及 consumption-based CAPM 被 empirical data 拒絕了(le)，但是這(zhè)些理(lǐ)論模型在收益和(hé)風險之間建立了(le)有效的(de)聯系。而另一方面，實證資産定價中的(de) factor models 是來(lái)自對(duì)曆史平均收益率中某種模式的(de)發掘。因此，factor model 背後必須有理(lǐ)論支撐。一旦缺乏理(lǐ)論，那麽因子模型就會退化(huà)成以提升事後 mean-variance-efficient（MVE）tangency portfolio 爲目标對(duì)著(zhe)曆史數據進行挖掘：

There is an obvious danger that, in the absence of discipline from theory, factor models degenerate into long lists of factors that come close to spanning the ex post MVE tangency portfolio of a particular period.

出于這(zhè)個(gè)原因，Fama and French (2018) 在 FF5 加入動量因子的(de)時(shí)候顯得(de)異常小心謹慎：

We include momentum factors (somewhat reluctantly) now to satisfy insistent popular demand. We worry, however, that opening the game to factors that seem empirically robust but lack theoretical motivation has a destructive downside — the end of discipline that produces parsimonious models and the beginning of dark age of data dredging that produces a long list of factors with little hope of sifting through them in a statistically reliable way.

對(duì)于一個(gè)因子模型來(lái)說，它是爲了(le)解釋股票(piào)收益率如何共同運動的(de)，因此必須和(hé)個(gè)股的(de)協方差矩陣密切相關（Pukthuanthong, Roll, and Subrahmanyam 2019）。僅靠因子模型之間相互 spanning tests，或者用(yòng)一籮筐其實相關性都不低的(de)異象（全都是投資組合；連個(gè)股都沒有用(yòng)）來(lái)檢驗因子模型，恐怕和(hé)前面的(de)目标還(hái)有一定的(de)距離。如此 factor war 意義十分(fēn)有限。最後，我想用(yòng) Fama and French (2018) 裏的(de)一段話(huà)作爲本文的(de)結尾。他(tā)們二位呼籲高(gāo)質量和(hé)有意義的(de)因子模型比較。此外，對(duì)于 factor modeling，必須要有理(lǐ)論依據，避免建模本身成爲對(duì)著(zhe)曆史數據進行數據挖掘。然而，實現這(zhè)一切需要我們對(duì)市場(chǎng)更深的(de)理(lǐ)解。

In general, if inference is to have content, the list of models considered in a study must be relatively short. Moreover, if factor modeling is not to degenerate into meaningless dredging for the ex post MVE portfolio, the number of factors in models must also be limited. Establishing ground rules, however, awaits more experience.

參考文獻

Asness, C. and A. Frazzini (2013). The devil in HML's details. The Journal of Portfolio Management 39(4), 49 – 68.

Barillas, F. and J. Shanken (2018). Comparing asset pricing models. Journal of Finance 73(2), 715 – 754.

Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance 52(1), 57 – 82.

Chen, L. and L. Zhang (2007). Neoclassical factors. NBER Working Paper, No. 13282.

Cochrane, J. H. (1991). Production-based asset pricing and the link between stock returns and economic fluctuations. Journal of Finance 46(1), 209 – 237.

Daniel, K., D. Hirshleifer, and L. Sun (2019). Short- and long-horizon behavioral factors. Review of Financial Studies forthcoming.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K. R. French (2006). Profitability, investment and average returns. Journal of Financial Economics 82(3), 491 – 518.

Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.

Fama, E. F. and K. R. French (2018). Choosing factors. Journal of Financial Economics 128(2), 234 – 252.

Gibbons, M. R., S. A. Ross, and J. Shanken (1989). A test of the efficiency of a given portfolio. Econometrica 57(5), 1121 – 1152.

Hou, K., H. Mo, C. Xue, and L. Zhang (2018). q5. Charles A. Dice Center Working Paper No. 2018-10; Fisher College of Business Working Paper No. 2018-03-010.

Hou, K., H. Mo, C. Xue, and L. Zhang (2019a). Which factors? Review of Finance 23(1), 1 – 35.

Hou, K., H. Mo, C. Xue, and L. Zhang (2019b). Security analysis: An investment perspective. Working paper.

Hou, K., C. Xue, L. Zhang (2015). Digesting anomalies: An investment approach. Review of Financial Studies 28(3), 650 – 705.

Hou, K., C. Xue, and L. Zhang (2018). Replicating anomalies. Review of Financial Studies forthcoming.

Liu, L. X., T. M. Whited, and L. Zhang (2009). Investment-based expected stock returns. Journal of Political Economy 117(6), 1105 – 1139.

Miller, M. H. and F. Modigliani (1961). Dividend policy, growth, and the valuation of shares. Journal of Business 34(4), 411 – 433.

Pukthuanthong, K., R. Roll, and A. Subrahmanyam (2019). A protocol for factor identification. Review of Financial Studies 32(4), 1573 – 1607.

Stambaugh, R. F. and Y. Yuan (2017). Mispricing factors. Review of Financial Studies 30(4), 1270 – 1315.

Zhang, L. (2016). Factors war. Tsinghua Financial Review 37, 101 – 104, in Chinese.

Zhang, L. (2017). The investment CAPM. European Financial Management 23(4), 545 – 603.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。