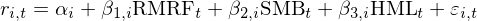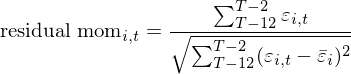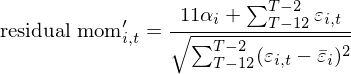殘差動量 —— 有理(lǐ)有據還(hái)是數據挖掘？

作者：BetaPlus 小組（石川，劉洋溢，刀(dāo)疤連）

摘要：與傳統動量不同，殘差動量在 A 股效果顯著。但這(zhè)背後是有理(lǐ)有據還(hái)是數據挖掘？

1 引言

動量，更确切地說是 Jegadeesh and Titman (1993) 提出的(de)截面相對(duì)強弱，一直以來(lái)是美(měi)股生命力最旺盛的(de)異象之一。無論是 Fama and French (1993) 三因子模型還(hái)是 Fama and French (2015) 五因子模型均無法解釋動量策略（Blitz et al. 2018），因此 Eugene Fama 也(yě)不得(de)不承認它是最顯著的(de)異象。

在美(měi)股上，動量策略雖然長(cháng)期來(lái)看很不錯，但這(zhè)種做(zuò)多(duō)前期 Winner 做(zuò)空前期 Loser 的(de)對(duì)沖組合卻時(shí)不時(shí)會來(lái)個(gè) crash，俗稱動量崩潰（momentum crash），即動量策略會遭遇不多(duō)但持續時(shí)間長(cháng)、幅度大(dà)的(de)下(xià)跌。學術界的(de)研究認爲這(zhè)和(hé)該組合的(de)動态風險敞口有關。Geczy and Samonov (2013) 基于超長(cháng)的(de)美(měi)國股市數據指出，動量效應對(duì)于市場(chǎng)組合有著(zhe)動态的(de)暴露，具體敞口則取決于市場(chǎng)狀态。當市場(chǎng)從一種狀态轉換到另一種狀态的(de)初期，動量組合對(duì)于最新市場(chǎng)狀态有著(zhe)負的(de)暴露，從而導緻市場(chǎng)轉換期的(de)大(dà)幅損失。Daniel and Moskowitz (2016) 發現動量崩潰與該策略的(de)尾部風險有關。崩潰往往發生在市場(chǎng)恐慌時(shí)，此時(shí)資産價格大(dà)跌而波動率大(dà)幅上升，這(zhè)與 Geczy and Samonov (2013) 的(de)發現一緻。

爲了(le)改善動量策略的(de)極端表現，2011 年來(lái)自 Robeco 的(de) David Blitz 領銜發表了(le) Blitz, Huij, and Martens (2011) 一文，提出了(le)殘差動量（residual momentum）策略。該策略使用(yòng)股票(piào)相對(duì)于 Fama and French (1993) 三因子模型的(de)殘差收益率，經殘差波動率調整後計算(suàn)了(le)殘差動量（因此也(yě)被稱爲異質動量，idiosyncratic momentum）。Blitz, Huij, and Martens (2011) 的(de)實證結果顯示，該策略比傳統動量策略能夠獲得(de)更高(gāo)的(de)風險收益比。除此之外，Hanauer and Windmueller (2019) 指出殘差動量在傳動動量 crash 的(de)時(shí)期表現更好，能夠極大(dà)降低虧損。

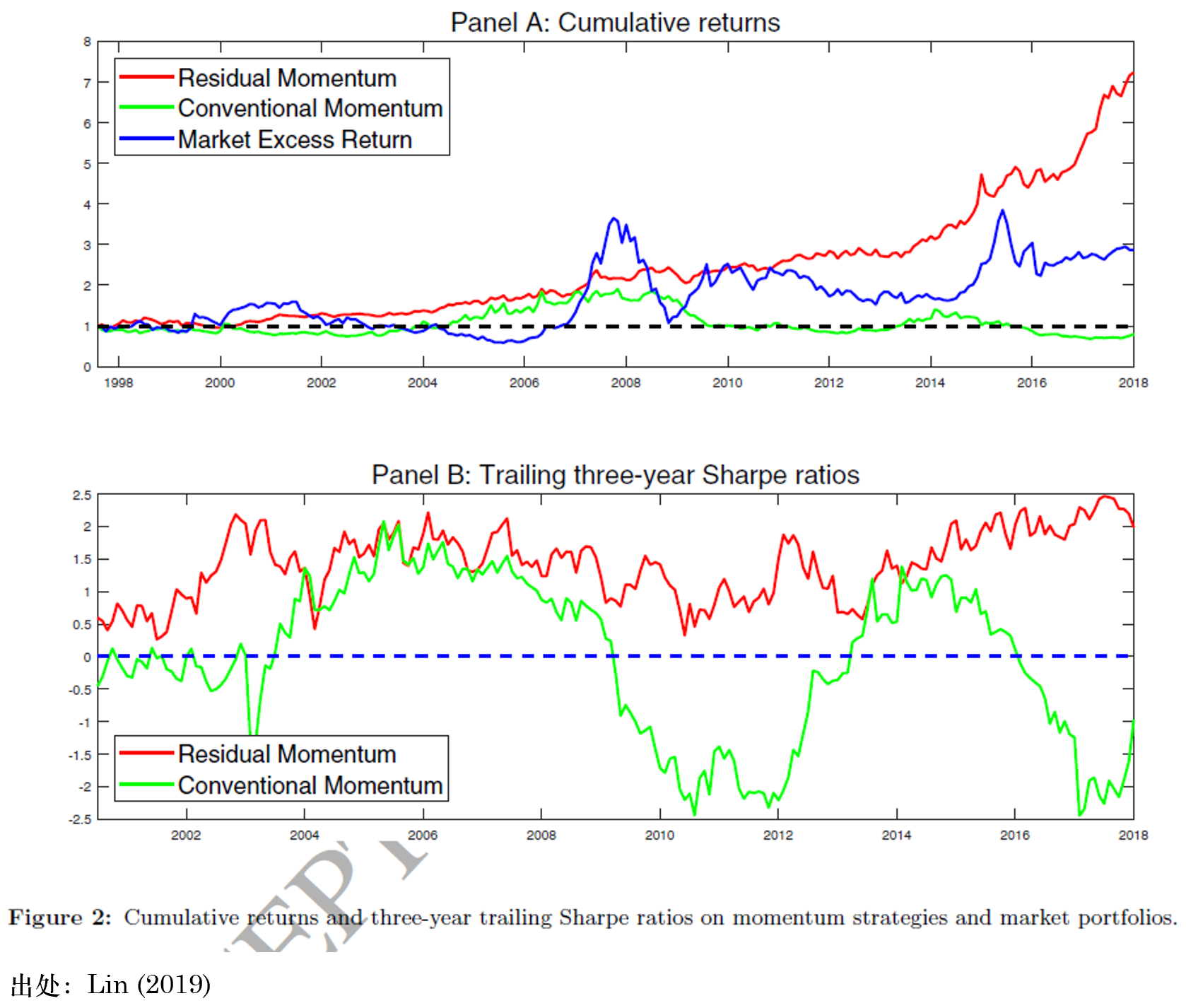
盡管動量策略在美(měi)股呼風喚雨(yǔ)，但是它到了(le) A 股中似乎畫(huà)風一變、難有作爲。那麽，殘差動量又如何呢(ne)？Lin (2019) 一文使用(yòng) Blitz, Huij, and Martens (2011) 的(de)思路在 A 股上實證了(le)殘差動量策略，得(de)出了(le)驚人(rén)的(de)效果（下(xià)圖）。

怎麽樣？多(duō)、空對(duì)沖得(de)到的(de)殘差動量（紅線）累積收益率穩健上行（Panel A），滾動三年窗(chuāng)口的(de)夏普率（Panel B）在整個(gè)實證窗(chuāng)口内均爲正，且在很高(gāo)的(de)比例下(xià)在 1.0 以上，這(zhè)種表現讓多(duō)少風格因子汗顔？

坦白說，我們第一眼看到這(zhè)個(gè)結果是不信的(de)。再加上 Finance Research Letters 這(zhè)個(gè)期刊的(de)口碑也(yě)不是太過硬，更令人(rén)增加了(le)幾分(fēn)懷疑。殘差動量的(de)計算(suàn)方法是否合理(lǐ)，即其背後到底代表了(le)什(shén)麽原因？A 股市場(chǎng)上的(de)殘差動量是否真的(de)有如此驚人(rén)的(de)表現？帶著(zhe)這(zhè)些問題，本期 BetaPlus 小組就來(lái)對(duì)殘差動量進行深度實證。

先來(lái)看看 Blitz, Huij, and Martens (2011) 提出的(de)殘差動量計算(suàn)方法。

2 有理(lǐ)有據？

Blitz, Huij, and Martens (2011) 使用(yòng) Fama and French (1993) 三因子模型爲基準，使用(yòng)股票(piào)月(yuè)頻(pín)超額收益和(hé)三因子月(yuè)頻(pín)收益率數據構建時(shí)序回歸模型：

上式中，r_{i, t} 爲股票(piào) i 在第 t 月(yuè)相對(duì)無風險利率的(de)超額收益，α_i 表示三因子模型無法解釋的(de) abnormal return，ε_{i, t} 表示殘差。在每個(gè) T 月(yuè)初，Blitz, Huij, and Martens (2011) 構建殘差動量的(de)方法包括以下(xià)幾步：

有意思的(de)是，Blitz, Huij, and Martens (2011) 一文僅是使用(yòng)文字描述了(le)殘差動量的(de)計算(suàn)方法，但并沒有給出任何一目了(le)然的(de)公式。不過最近的(de) Blitz, Hanauer, and Vidojevic (2018) 一文給出了(le)明(míng)确的(de)公式：

值得(de)一提的(de)是，該公式的(de)分(fēn)母中，根号内的(de)部分(fēn)較常見的(de)方差公式差 1/11 這(zhè)個(gè)系數。但由于它不改變殘差動量排名的(de)單調性，因此上式等價于殘差總收益被殘差波動率進行标準化(huà)。BetaPlus 小組就計算(suàn)殘差動量的(de)三個(gè)步驟有以下(xià)四點疑問。

首先，在時(shí)序回歸時(shí)，Blitz, Huij, and Martens (2011) 考慮了(le)截距項 α_i，但是并沒有把它作爲異質動量的(de)一部分(fēn)。如果僅從“殘差”動量這(zhè)個(gè)名字來(lái)看，似乎使用(yòng)回歸方程的(de)殘差計算(suàn)無可(kě)厚非；但如果抛開新的(de)動量因子叫什(shén)麽，α_i 毫無疑問屬于收益率中無法被三因子模型解釋的(de)部分(fēn)。Blitz, Huij, and Martens (2011) 給出的(de)理(lǐ)由是，α_i 的(de)作用(yòng)是控制模型設定偏誤，這(zhè)個(gè)解釋似乎是合理(lǐ)的(de)。

其次，在 Blitz, Huij, and Martens (2011) 的(de)方法中，用(yòng)來(lái)計算(suàn)每個(gè) T 時(shí)刻殘差動量的(de)殘差來(lái)自同一個(gè)時(shí)序回歸：使用(yòng) 36 期月(yuè)頻(pín)收益率回歸，但隻選擇了(le) T – 12 到 T – 2 這(zhè) 11 個(gè)點計算(suàn)非标準化(huà)之前的(de)殘差動量。從 OLS 回歸隐含的(de)假設來(lái)說，殘差時(shí)間序列應該滿足平穩性，且由于回歸中考慮了(le)截距項，因此這(zhè) 36 個(gè)殘差項的(de)均值嚴格等于零。因此，從數學上說這(zhè) 36 個(gè)殘差項是一個(gè)均值爲零的(de)平穩序列，而 T – 12 到 T – 2 中間的(de) 11 個(gè)點僅僅是這(zhè)個(gè)平穩序列中的(de)一部分(fēn)。無論這(zhè)部分(fēn)的(de)均值是否大(dà)于零，它的(de)大(dà)小爲什(shén)麽會和(hé)該股票(piào)未來(lái)收益率正相關，而非僅僅是個(gè)随機擾動呢(ne)（它們僅是一個(gè)均值爲零的(de)平穩序列中的(de)一部分(fēn)）？此外，爲什(shén)麽不同股票(piào)中，不同平穩殘差序列在同一段時(shí)期的(de)殘差和(hé)大(dà)小能夠預示它們未來(lái)預期收益率的(de)差異呢(ne)？Blitz, Huij, and Martens (2011) 一文對(duì)這(zhè)些問題并未給出太多(duō)的(de)討(tǎo)論。

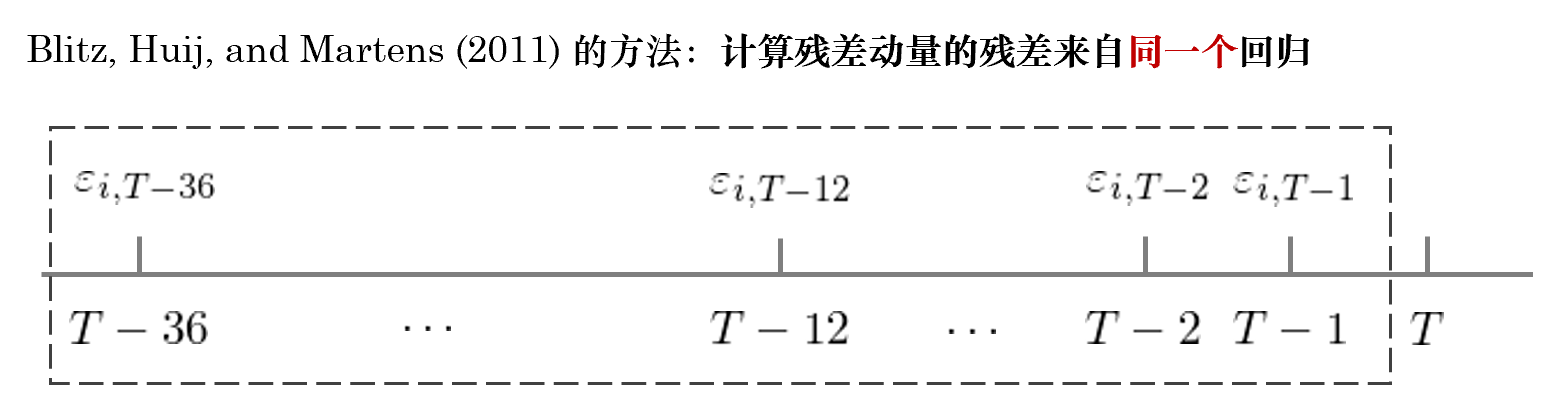
從上面的(de)說明(míng)中可(kě)以引出第三點疑問。如前所述，Blitz, Huij, and Martens (2011) 在每個(gè)月(yuè)初 T 使用(yòng)最近 36 個(gè)月(yuè)進行一次回歸得(de)到 36 個(gè)殘差，并使用(yòng)其中的(de) 11 個(gè)計算(suàn)殘差動量，因此這(zhè) 11 個(gè)殘差來(lái)自同一個(gè)回歸（如下(xià)圖）。

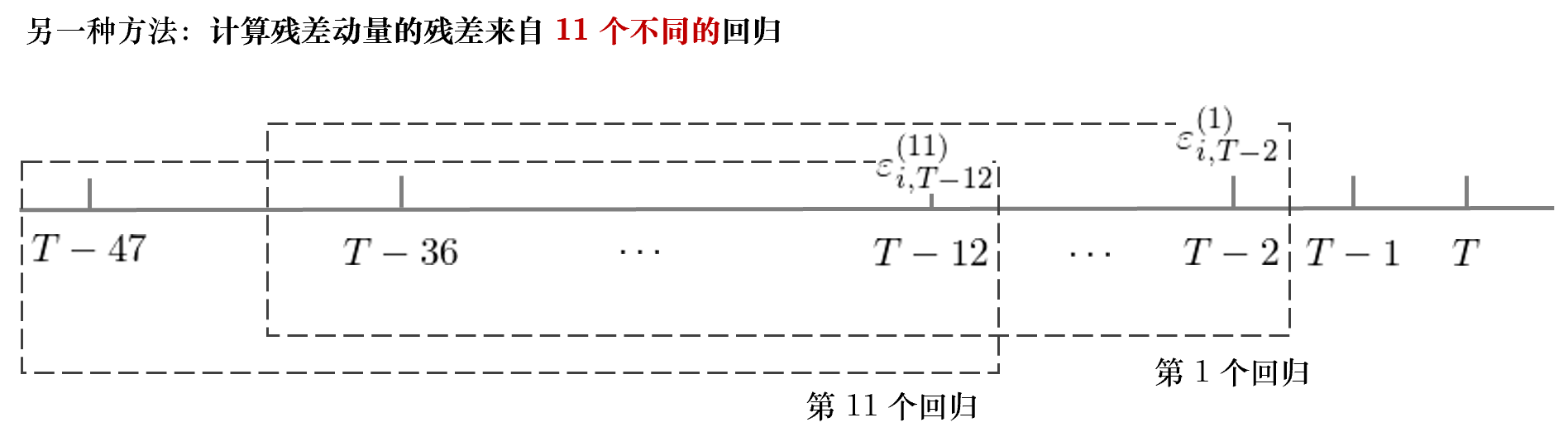
與上述方法相對(duì)應的(de)，可(kě)以考慮計算(suàn)殘差動量的(de)殘差來(lái)自 11 個(gè)不同的(de)回歸。比如，對(duì)于 T 期，使用(yòng) T – 37 到 T – 2 這(zhè) 36 個(gè)月(yuè)的(de)數據回歸，并僅記錄 T – 2 的(de)殘差，記爲 ε_{i, T-2}^(1)，上标 (1) 代表第 1 次回歸；然後使用(yòng) T – 38 到 T – 3 這(zhè) 36 個(gè)月(yuè)的(de)數據回歸，并僅記錄 T – 3 的(de)殘差 ε_{i, T-3}^(2)；以此類推，最終使用(yòng) T – 47 到 T – 12 這(zhè) 36 個(gè)月(yuè)的(de)數據回歸，并僅記錄 T – 12 的(de)殘差 ε_{i, T-12}^(11)。使用(yòng)上述來(lái)自 11 個(gè)回歸的(de)殘差計算(suàn)殘差收益率。

雖然第二種方法聽(tīng)上去有些怪怪的(de)，也(yě)不如 Blitz, Huij, and Martens (2011) 的(de)方法易于理(lǐ)解，但學術界對(duì)它也(yě)有一定的(de)研究。比如 Gutierrez and Prinsky (2007) 就使用(yòng)這(zhè)種方法研究了(le)異質動量。因此，單一回歸和(hé)多(duō)個(gè)回歸計算(suàn)殘差動量有什(shén)麽區(qū)别就是我們的(de)第三個(gè)疑問。本文的(de)實證中将會考慮這(zhè)兩種方法。

最後一點疑問是在計算(suàn)殘差動量時(shí)，是否有必要使用(yòng)殘差标準差作爲分(fēn)母，對(duì)殘差動量進行标準化(huà)。對(duì)于這(zhè)個(gè)操作，Blitz, Huij, and Martens (2011) 引用(yòng) Gutierrez and Prinsky (2007) 的(de)研究指出上述标準化(huà)可(kě)以降低殘差的(de)噪聲，得(de)到更加純淨的(de)異質動量，提高(gāo)殘差動量的(de)效果。Blitz, Hanauer, and Vidojevic (2018) 的(de)後續研究強調說無論是否标準化(huà)，殘差動量本身都可(kě)以獲得(de)顯著的(de)超額收益率。

關于這(zhè)一點，BetaPlus 小組關注的(de)重點是這(zhè)波操作在 A 股上是否會“誇大(dà)”殘差動量的(de)效果。上述标準化(huà)将殘差标準差作爲分(fēn)母，這(zhè)意味著(zhe)當分(fēn)子上的(de)殘差動量相同的(de)情況下(xià)，标準化(huà)可(kě)以起到高(gāo)配低異質波動、低配高(gāo)異質波動的(de)情況。BetaPlus 小組之前的(de)研究《異質波動率之謎》指出，低異質波動率現象确實存在于 A 股市場(chǎng)，說明(míng)如此标準化(huà)肯定有助于加強殘差動量。因此，如果按照(zhào) Blitz, Huij, and Martens (2011) 的(de)方法計算(suàn)的(de)殘差動量在 A 股上有效，那麽它到底因爲分(fēn)子的(de)部分(fēn)、分(fēn)母的(de)部分(fēn)、還(hái)是兩部分(fēn)均有貢獻？這(zhè)就成爲必須回答(dá)的(de)問題。在接下(xià)來(lái)的(de)實證中也(yě)将會把這(zhè)兩部分(fēn)拆開來(lái)看。

3 實證

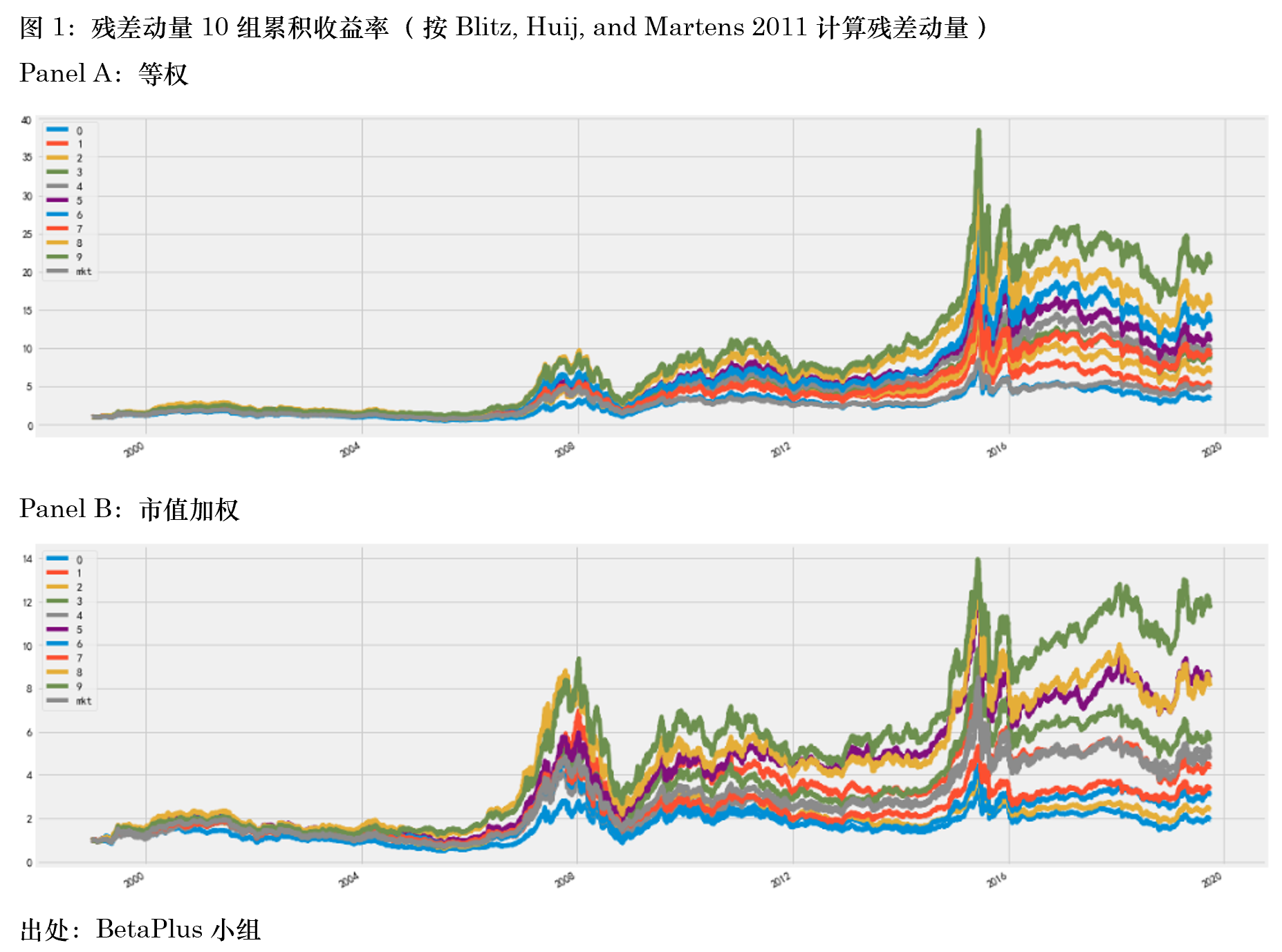
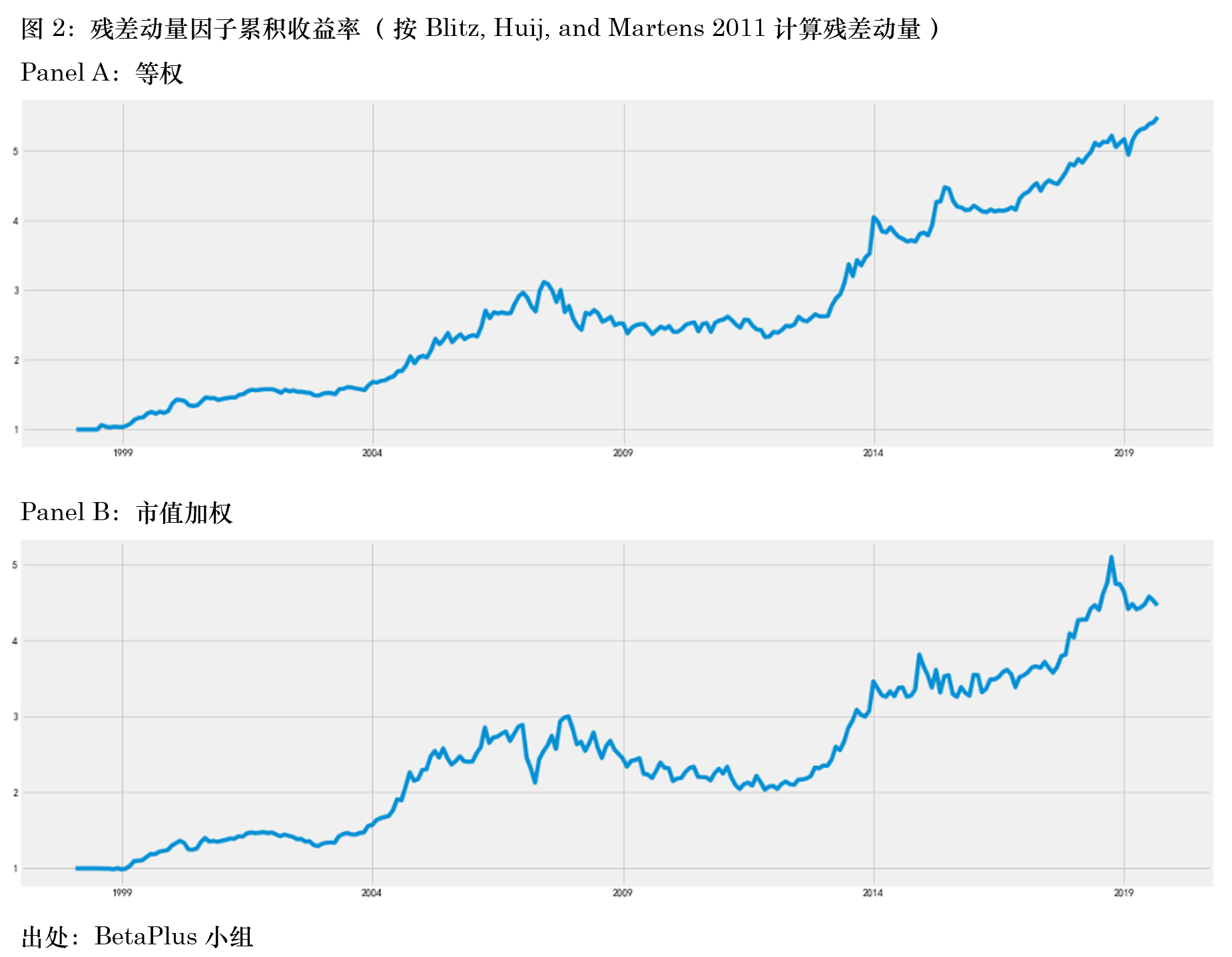
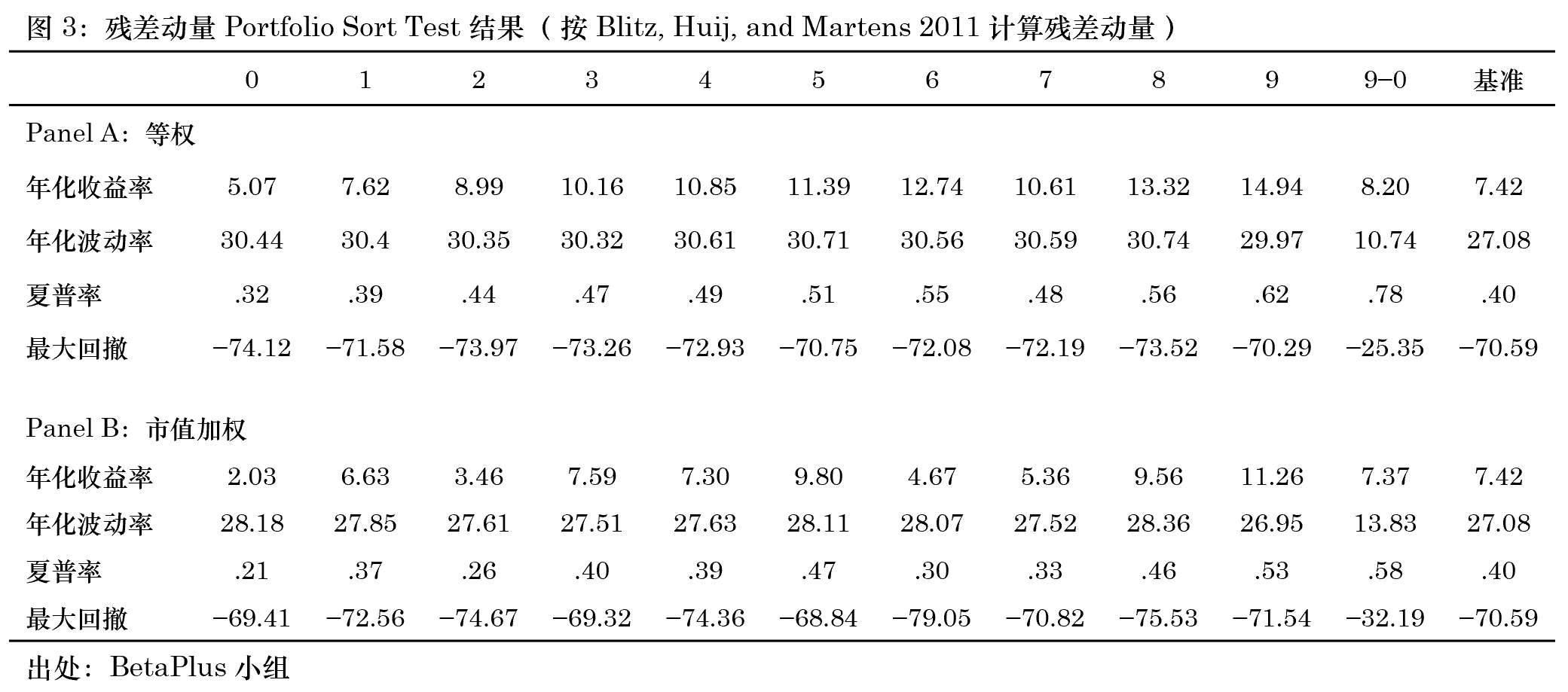
本節和(hé)下(xià)一節針對(duì) A 股進行實證分(fēn)析。本節的(de)重點是比較單一回歸（Blitz, Huij, and Martens 2011 的(de)方法）和(hé)多(duō)次回歸計算(suàn)殘差動量這(zhè)兩種方法。下(xià)一節将會把殘差波動率的(de)影(yǐng)響剝離開分(fēn)析。在以下(xià)的(de)分(fēn)析中，實證期爲 1999 年 1 月(yuè) 1 日至 2019 年 9 月(yuè) 30 日；在每月(yuè)末構建投資組合的(de)時(shí)候剔除掉次新股、停牌股、風險警示股、一字漲跌停股；同時(shí)考慮等權和(hé)市值加權兩種情況。在計算(suàn)殘差收益率時(shí)，采用(yòng) BetaPlus 小組維護的(de)以月(yuè)頻(pín)進行再平衡靈活版 Fama and French (1993) 三因子模型。首先來(lái)看按照(zhào) Blitz, Huij, and Martens (2011) 的(de)方法計算(suàn)殘差動量的(de)結果；結果以 portfolio test result 的(de)方式呈現。下(xià)圖 1 — 3 顯示了(le)這(zhè) 10 組（第 0 組爲殘差動量最低；第 9 組爲殘差動量最高(gāo)組）以及殘差動量因子（即第 9 組減去第 0 組）的(de)累積收益率和(hé)風險收益特征，其中 Panel A 爲等權、Panel B 爲市值加權。

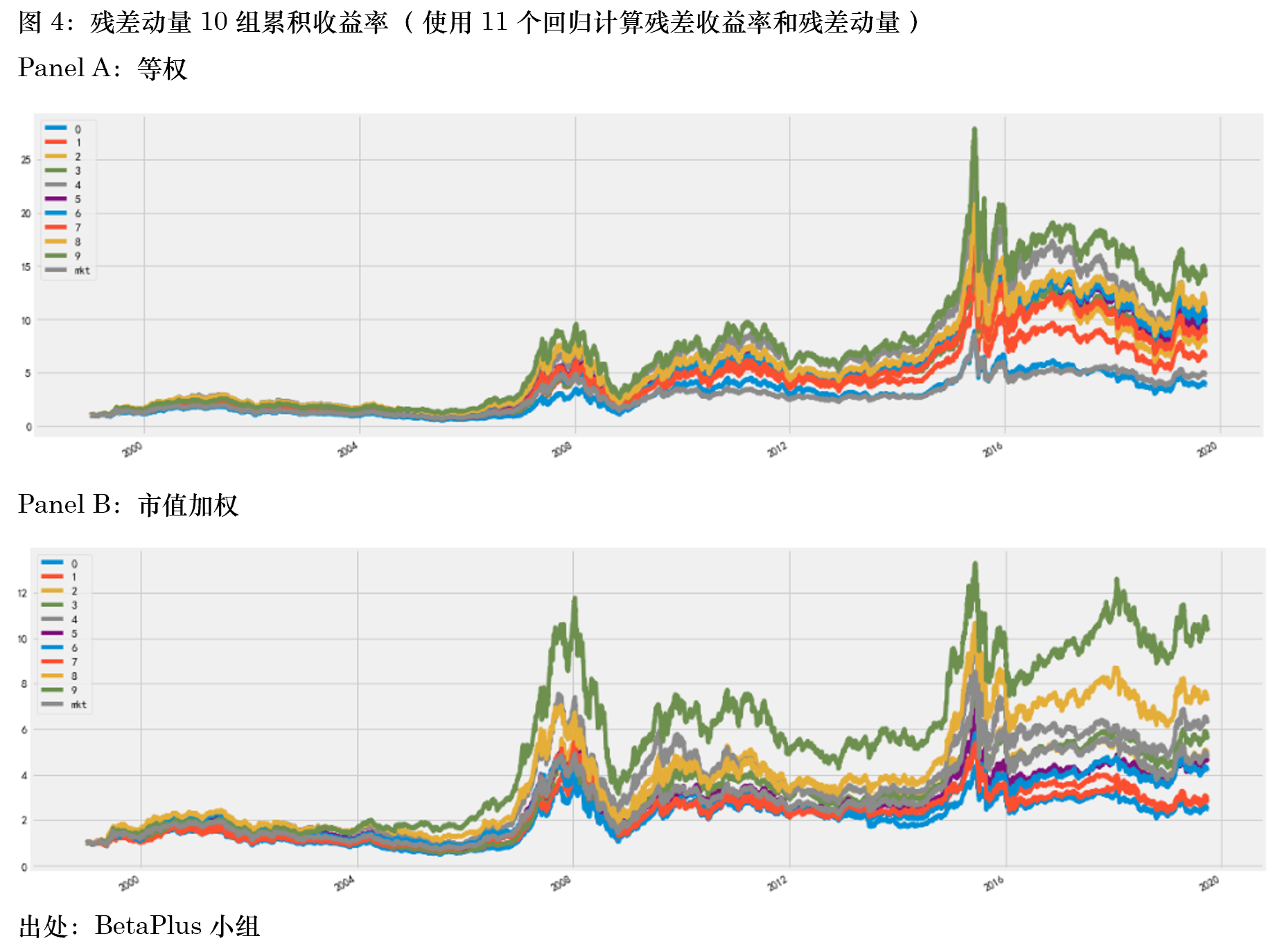
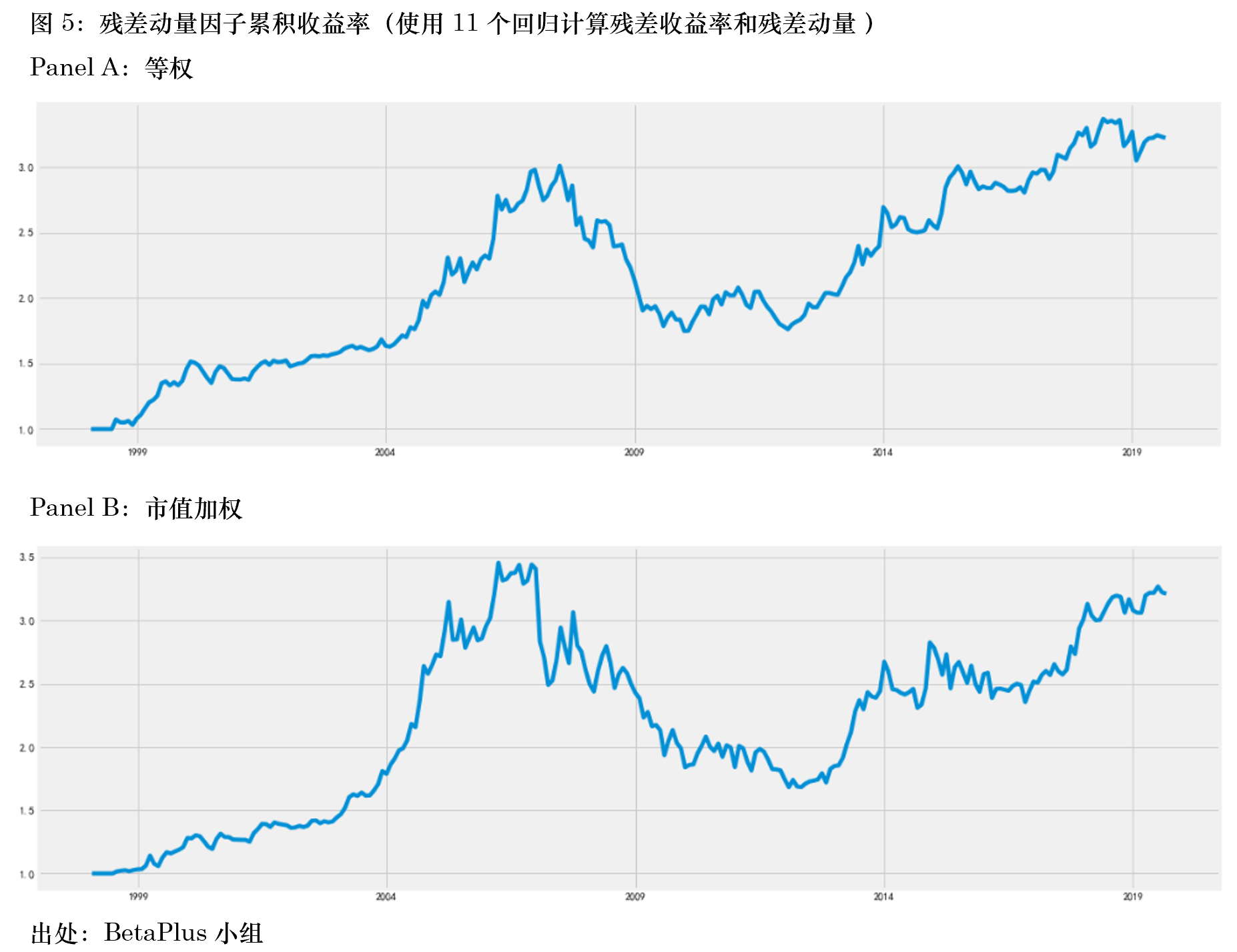
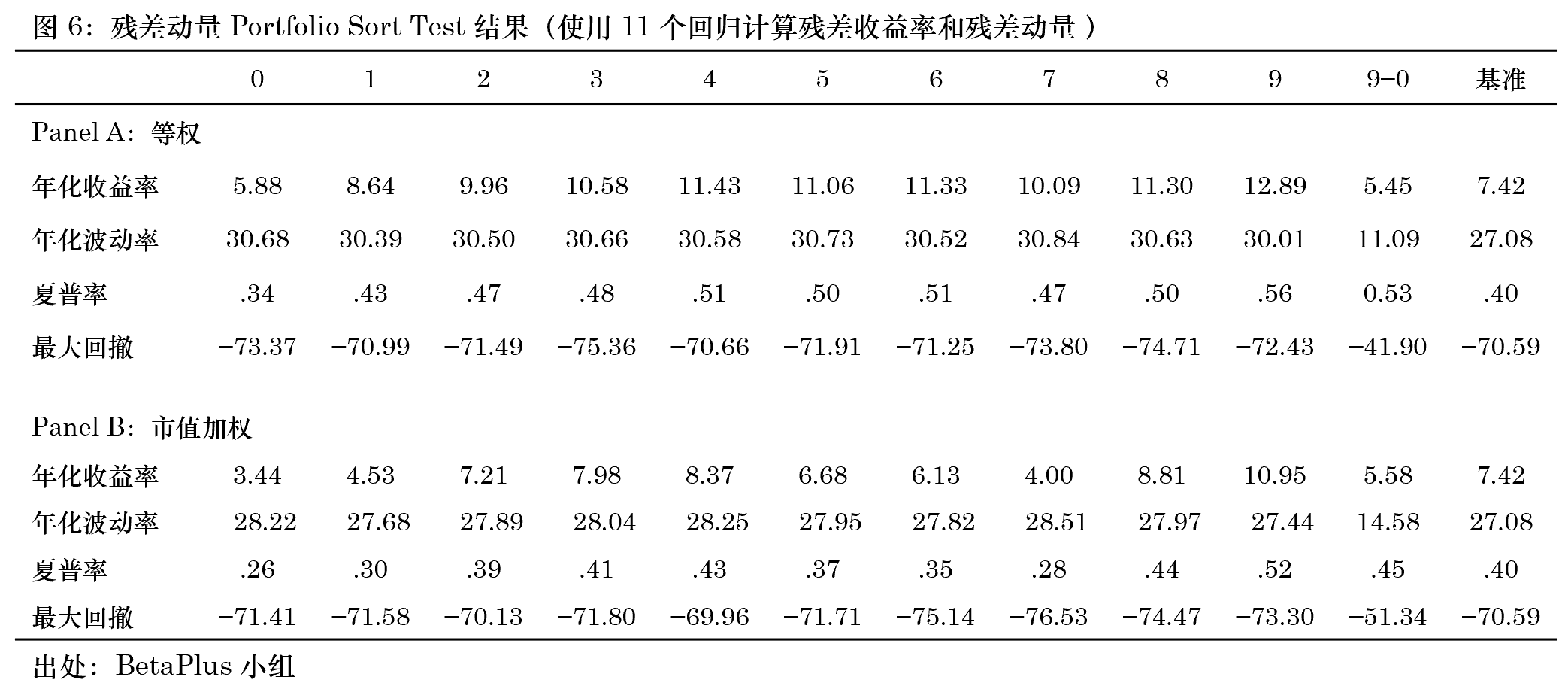
上述結果顯示，無論是等權還(hái)是市值加權，在 A 股上均可(kě)以觀察到顯著的(de)殘差動量效應（雖然本文的(de)實證結果并沒有 Lin 2019 中的(de)驚豔，該文僅考慮了(le)等權的(de)情況）。在等權下(xià)，殘差動量因子的(de)夏普率高(gāo)達 0.78，其最大(dà)回撤爲 -25.35%，有效抵禦了(le) momentum crash 風險。當采用(yòng)市值加權時(shí)，殘差動量效果有所減弱，但依然顯著。這(zhè)樣的(de)結果和(hé)傳統截面動量因子在 A 股上的(de)效果截然不同。當然，面對(duì)這(zhè)樣的(de)結果，我們仍然不知道到底是作爲分(fēn)母的(de)殘差波動率貢獻了(le)多(duō)少，該問題将在第四節研究。下(xià)面再來(lái)看看第二種方法，即采用(yòng) 11 個(gè)回歸計算(suàn)殘差收益率、再計算(suàn)殘差動量的(de)結果。下(xià)圖 4 — 6 顯示了(le)相應的(de) portfolio sort test 結果。

當采用(yòng) 11 個(gè)不同的(de)回歸時(shí)，殘差動量的(de)效果較前一種方法變差。無論是等權還(hái)是市值加權，殘差動量因子在 2007 到 2009 年間都經曆了(le)長(cháng)時(shí)間且大(dà)幅度的(de)回撤。除此之外，這(zhè)十個(gè) portfolios 的(de)單調性也(yě)變差。我們對(duì)此的(de)猜想是，使用(yòng) 11 個(gè)不同的(de)回歸計算(suàn)殘差收益率這(zhè)種方法額外引入了(le)不必要的(de)不對(duì)稱性，即不同時(shí)期的(de)殘差來(lái)自不同的(de)分(fēn)布。由于殘差動量的(de)計算(suàn)高(gāo)度依賴參數估計的(de)準确性，長(cháng)期來(lái)看這(zhè)種方法的(de)不穩定性更高(gāo)。

需要強調的(de)是，雖然第二種方法不如 Blitz, Huij, and Martens (2011) 的(de)方法，但這(zhè)種結果上的(de)差異仍然沒有回答(dá)上一節關于殘差動量計算(suàn)方法的(de)兩個(gè)問題：（1）爲什(shén)麽均值爲零的(de)平穩序列中的(de)一部分(fēn)和(hé)未來(lái)收益率正相關；（2）爲什(shén)麽這(zhè)部分(fēn)殘差能夠解釋預期收益率的(de)截面差異。

4 進一步實證

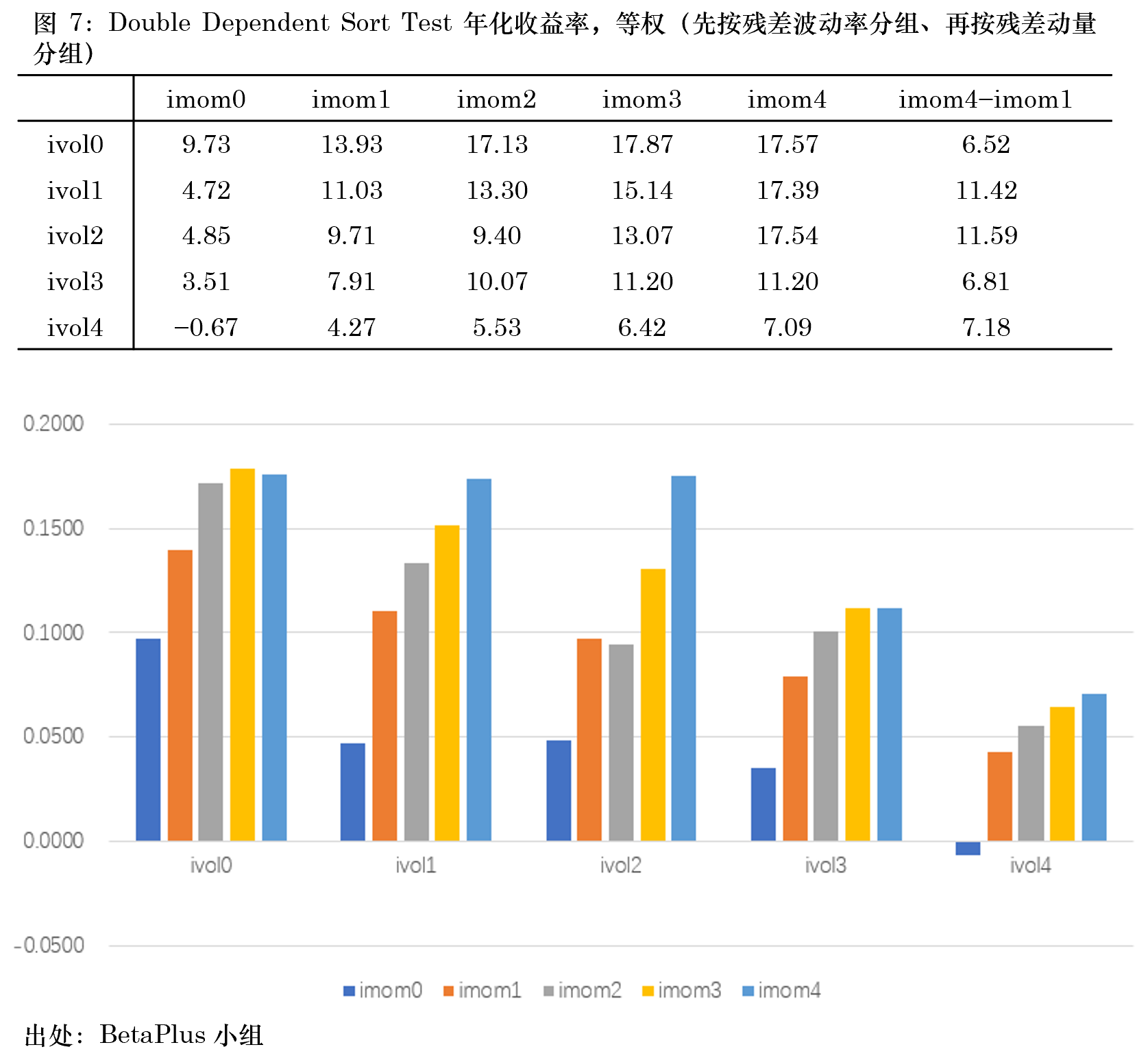
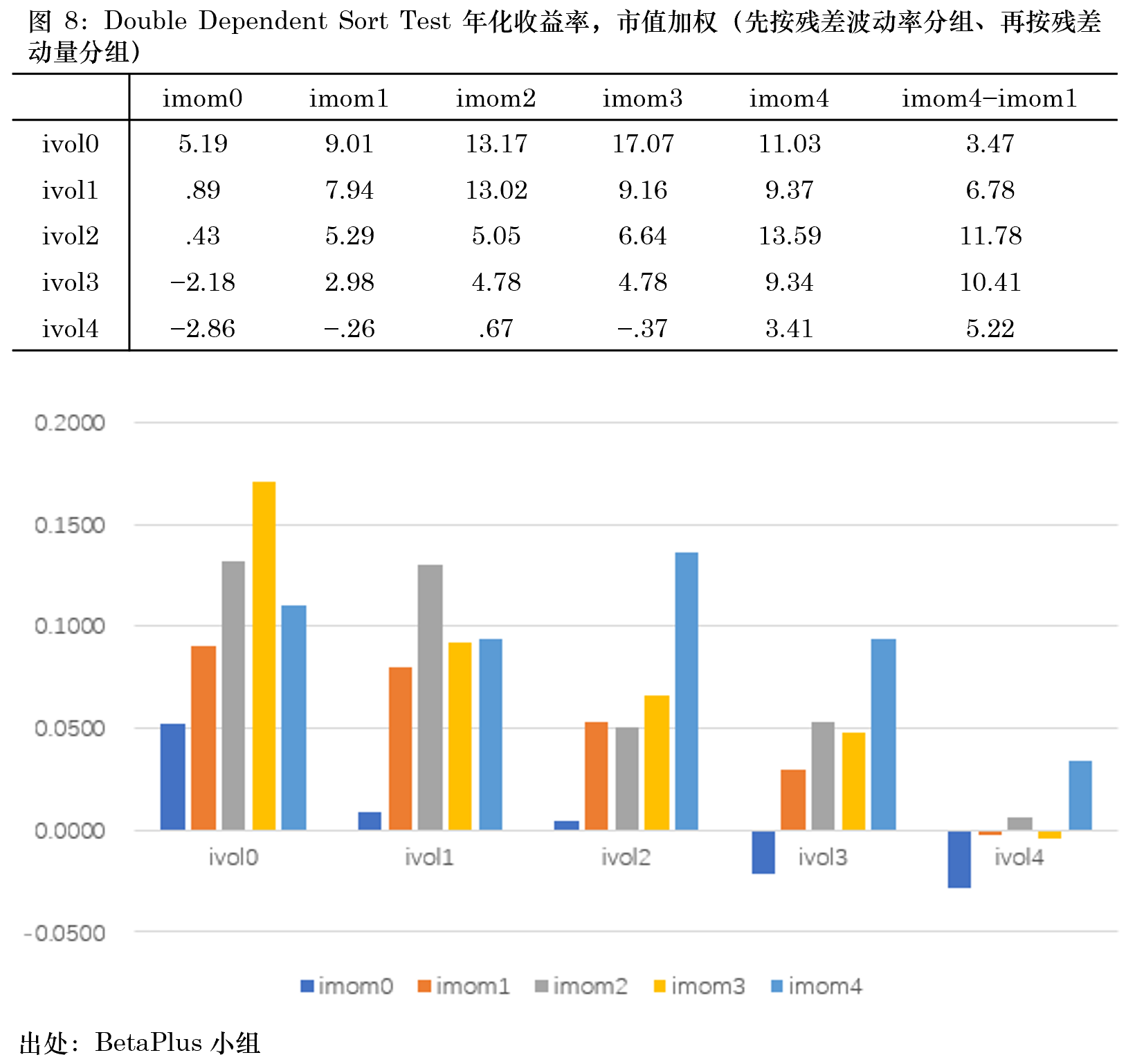
第三節的(de)實證結果顯示經标準化(huà)後的(de)殘差動量在 A 股是有效的(de)。本小節的(de)實證就來(lái)回答(dá)第二個(gè)問題：殘差波動率在這(zhè)方面是否起到了(le)顯著的(de)作用(yòng)？爲了(le)控制殘差波動率（即作爲分(fēn)母的(de)殘差标準差）的(de)影(yǐng)響，本文采用(yòng) double dependent sort 進行分(fēn)析。首先按照(zhào)殘差波動率（記爲 ivol）從低到高(gāo)把所有股票(piào)分(fēn)成五組，然後再把每組内的(de)股票(piào)按照(zhào)原始殘差動量（記爲 imom）高(gāo)低分(fēn)成五組。這(zhè)樣一共得(de)到 25 個(gè)投資組合，以考察每個(gè) ivol 組内原始殘差動量是否能夠解釋股票(piào)的(de)預期收益率差異。圖 7、8 分(fēn)别顯示了(le)等權和(hé)市值加權下(xià)，這(zhè) 25 個(gè)投資組合的(de)年化(huà)收益率。

從圖 7、8 的(de)結果中可(kě)以觀察到以下(xià)幾點：

經過以上的(de)分(fēn)析，我們可(kě)以說基于 Blitz, Huij, and Martens (2011) 定義的(de)殘差動量在 A 股有效，并非依靠了(le)低異質波動率的(de)原因，作爲分(fēn)子的(de)原始殘差動量在沒有被标準化(huà)的(de)情況下(xià)依然能獲得(de)顯著的(de)超額收益。事實上，作爲 robustness check，我們也(yě)僅使用(yòng)原始殘差動量（即未經殘差波動率标準化(huà)）構建了(le)殘差動量因子，實證結果顯示它在 A 股上的(de)效果甚至超過了(le)經标準化(huà)的(de)版本（等權時(shí)，未經标準化(huà)的(de)殘差動量因子夏普率爲 .82，高(gāo)于經标準化(huà)後的(de) .78；市值加權時(shí)，前者的(de)夏普率爲 .59，高(gāo)于後者的(de) .58）。這(zhè)樣的(de)結果似乎足以令人(rén)興奮了(le)。但是，我們還(hái)想抛出一個(gè)問号，并以此總結全文。

5 結語：問題比發現更多(duō)

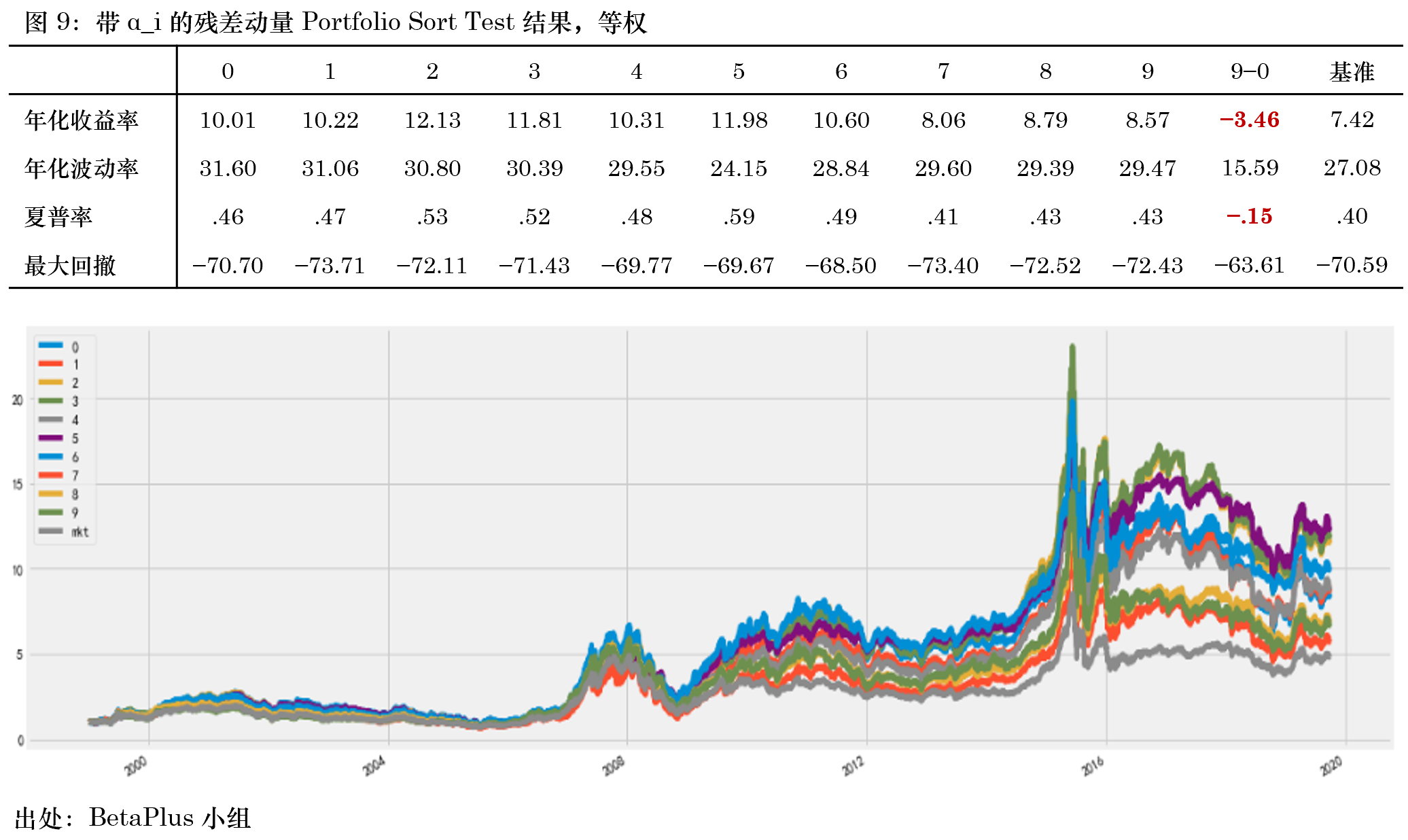
毫無疑問，殘差動量 —— 無論其背後的(de)“故事”是什(shén)麽 —— 其有效的(de)必要條件是有一個(gè)靠譜的(de)定價模型。雖然美(měi)股上已經有很多(duō)主流的(de)多(duō)因子模型，但是針對(duì) A 股卻并沒有廣泛被認可(kě)的(de)定價模型。這(zhè)讓任何研究殘差收益率的(de)實證結果都面臨挑戰。在計算(suàn)殘差動量的(de)時(shí)候，Blitz, Huij, and Martens (2011) 以控制模型設定偏誤爲由舍去了(le)回歸中的(de) α_i。面對(duì)這(zhè)種處理(lǐ)，我們仍然很好奇，如果帶上 α_i 又會怎樣？從 A 股上的(de)實證結果來(lái)看，帶上 α_i 之後，殘差動量翻車了(le)……仍然以 Blitz, Huij, and Martens (2011) 的(de)方法獲得(de)殘差收益率，在計算(suàn)殘差動量時(shí)，使用(yòng) T – 12 到 T – 2 期之間的(de) α_i 和(hé)殘差總收益之和(hé)作爲分(fēn)子：

以等權爲例，在上述定義下(xià)，殘差動量變成了(le)殘差反轉（圖 9）。除此之外，我們也(yě)嘗試了(le)在時(shí)序回歸計算(suàn)殘差收益率時(shí)不加入截距項，也(yě)得(de)到了(le)殘差反轉的(de)結果。

作爲開放性的(de)問題，本文并不試圖對(duì)上述看起來(lái)十分(fēn)矛盾的(de)結果進行更深入的(de)討(tǎo)論。隻是希望通(tōng)過它們說明(míng)，在使用(yòng)殘差收益率構建因子的(de)時(shí)候，模型怎麽設定、參數如何估計都會直接影(yǐng)響因子的(de)計算(suàn)，且有時(shí)甚至産生完全相反的(de)效果，因此必須要搞清楚每一步的(de)原因是什(shén)麽，以免陷入數據挖掘。

前文《給你的(de)動量策略加點“料”》曾指出，傳統動量策略之所以有效和(hé)人(rén)們的(de)有限注意力（limited attention）有關，并以此作爲一個(gè)維度改進了(le)傳統動量。由于大(dà)腦(nǎo)中的(de)資源有限，一系列頻(pín)繁但微小的(de)變化(huà)對(duì)于人(rén)的(de)吸引力遠(yuǎn)不如少數卻顯著的(de)變化(huà)；因此投資者對(duì)于連續信息造成的(de)股價變化(huà)反應不足。随著(zhe)時(shí)間的(de)推移，這(zhè)些信息緩慢(màn)的(de)被吸收并反映到價格中，從而導緻了(le)動量。而對(duì)于殘差動量，Blitz, Huij, and Martens (2011) 認爲也(yě)可(kě)以從 gradual-information-diffusion 假說解釋：信息在投資者之間的(de)擴散是緩慢(màn)的(de)，而且相比于影(yǐng)響所有公司的(de)公共事件，投資者對(duì)于那些針對(duì)公司的(de)特定事件的(de)反應則更加遲緩，這(zhè)就形成了(le)殘差動量。

從投資者的(de)反應不足來(lái)解釋動量和(hé)殘差動量似乎是站的(de)住腳的(de)。而對(duì)于美(měi)股市場(chǎng)，動量和(hé)殘差動量雙雙有效，且殘差動量的(de)效果優于傳統動量這(zhè)個(gè)結果也(yě)是可(kě)以支持上述假說的(de)。但是 A 股……在動量如此不好使的(de)前提下(xià)，僅僅使用(yòng)了(le)一個(gè)同樣對(duì)于 A 股也(yě)不那麽完美(měi)的(de)定價模型計算(suàn)出殘差，就得(de)到了(le)如此好使的(de)殘差動量。這(zhè)背後的(de)原因恐怕比殘差動量這(zhè)個(gè)簡單的(de)公式要複雜(zá)得(de)多(duō)。

參考文獻

Blitz, D., M. X. Hanauer, and M. Vidojevic (2018). The idiosyncratic momentum anomaly. SSRN 2947044.

Blitz, D., M. X. Hanauer, M. Vidojevic, and P. van Vliet (2018). Five concerns with the five-factor model. The Journal of Portfolio Management 44(4), 71 – 78.

Blitz, D., J. Huij, and M. Martens (2011). Residual momentum. Journal of Empirical Finance 18(3), 506 – 521.

Daniel, K. and T. J. Moskowitz (2016). Momentum crashes. Journal of Financial Economics 122(2), 221 – 247.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.

Geczy, C. and M. Samonov (2016). Two centuries of price-return momentum. Financial Analysts Journal 72(5), 32 – 56.

Gutierrez, R. C. and C. A. Prinsky (2007). Momentum, reversal, and the trading behaviors of institutions. Journal of Financial Markets 10(1), 48 – 75.

Hanauer, M. X. and S. Windmueller (2019). Enhanced momentum strategies. SSRN 2427919.

Jegadeesh, N. and S. Titman (1993). Returns to Buying Winners and Selling Losers: Implications for Stock Market Efficiency. Journal of Finance 48(1), 65 – 91.

Lin, Q. (2019). Residual momentum and the cross-section of stock returns: Chinese evidence. Finance Research Letters 29, 206 – 215.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。