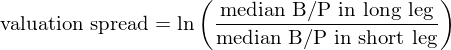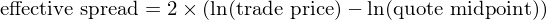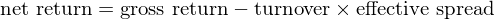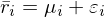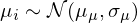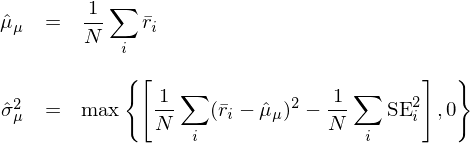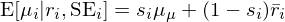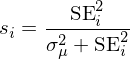因子樣本外表現爲什(shén)麽變差？

作者：石川

摘要：摘要：曝光(guāng)導緻錯誤定價減弱、因子擁擠和(hé)交易成本是因子樣本外變差的(de)三大(dà)原因。

0 引言

因子樣本外的(de)表現較樣本内變差是人(rén)們的(de)共識。這(zhè)裏的(de)因子包括異象（anomalies）和(hé)傳統意義上的(de)風格 beta 因子，在下(xià)文不做(zuò)區(qū)分(fēn)，統稱爲因子。造成因子樣本内、外表現差異的(de)最主要原因自然是樣本内的(de) data snooping（即因子本來(lái)就是假的(de)），但如果因子确實是真實的(de)，那麽它們在樣本外變差的(de)原因是什(shén)麽呢(ne)？學術界和(hé)業界的(de)主要觀點包括以下(xià)三種：

在 2019 年 9 月(yuè)剛剛結束的(de) Wharton 商學院 Jacobs Levy Center 年會中，一共深入討(tǎo)論了(le)四篇論文，其中兩篇就和(hé)因子樣本外表現有關，它們分(fēn)别是 Bowles et al. (2019) 以及 Chen and Velikov (2019)，足見這(zhè)個(gè)話(huà)題的(de)重要性。具體來(lái)說，Bowles et al. (2019) 以 Anomaly Time 爲題從“曝光(guāng)導緻錯誤定價減弱”的(de)角度談論了(le)因子的(de)表現；而 Chen and Velikov (2019) 則從“交易成本”的(de)角度指出，在考慮了(le)非常合理(lǐ)的(de)費用(yòng)之後，絕大(dà)多(duō)數因子在樣本外根本無法賺錢。本文就來(lái)簡要探討(tǎo)一下(xià)因子樣本外表現變差的(de)三個(gè)原因。

1 曝光(guāng)導緻錯誤定價減弱

因子代表著(zhe)市場(chǎng)某方面的(de)非有效性、代表了(le)某種 mispricing（錯誤定價）。隻要套利限制不是過大(dà)，那麽聰明(míng)的(de)投資者一定會先人(rén)一步去交易這(zhè)個(gè)因子，導緻錯誤定價收窄，這(zhè)就解釋了(le)爲什(shén)麽當因子被發表後，它的(de)收益往往也(yě)跟著(zhe)顯著下(xià)降。在這(zhè)方面，McLean and Pontiff (2016)  的(de)研究頗具代表性。該文研究了(le) 97 個(gè)因子，發現因子樣本外的(de)表現比樣本内的(de)表現下(xià)降了(le) 26%、而發表後（post-publication）的(de)表現較樣本内則下(xià)降了(le) 58%。McLean and Pontiff (2016)  考慮樣本内外差異是爲了(le)控制過拟合的(de)影(yǐng)響。上述結果表明(míng)，58% 與 26% 之差 —— 即 32% —— 就是發表本身造成因子效果的(de)減弱。McLean and Pontiff (2016)  把它稱作 publication-informed trading。這(zhè)背後的(de)邏輯鏈是：因子被發表導緻它被公布于衆 --> 越來(lái)越多(duō)的(de)人(rén)交易該因子從而減弱了(le)錯誤定價 --> 最終導緻因子收益率降低。

如果說 McLean and Pontiff (2016)  檢驗了(le)因子的(de)平均收益，Bowles et al. (2019) 則是從時(shí)效性的(de)角度展示了(le)因子背後的(de)信息越來(lái)越快(kuài)的(de)被 priced in。長(cháng)久以來(lái)，由于 Fama and French (1993) 的(de)影(yǐng)響太過深遠(yuǎn)，學術界在研究因子的(de)時(shí)候爲了(le)避免未來(lái)數據，通(tōng)常采用(yòng)每年再平衡的(de)方法（量價相關的(de)指标通(tōng)常是月(yuè)頻(pín)再平衡），導緻構建因子的(de)指标數據嚴重滞後。這(zhè)其中最著名的(de)例子要數 Eugene Fama 的(de)弟(dì)子 Cliff Asness 使用(yòng)月(yuè)頻(pín)價格對(duì) HML 的(de)改造（Asness and Frazzini 2013）。使用(yòng)了(le)月(yuè)頻(pín)價格數據後的(de) HML 較 Fama and French (1993) 三因子的(de) HML 表現更好，說明(míng)了(le)數據時(shí)效性的(de)重要性。

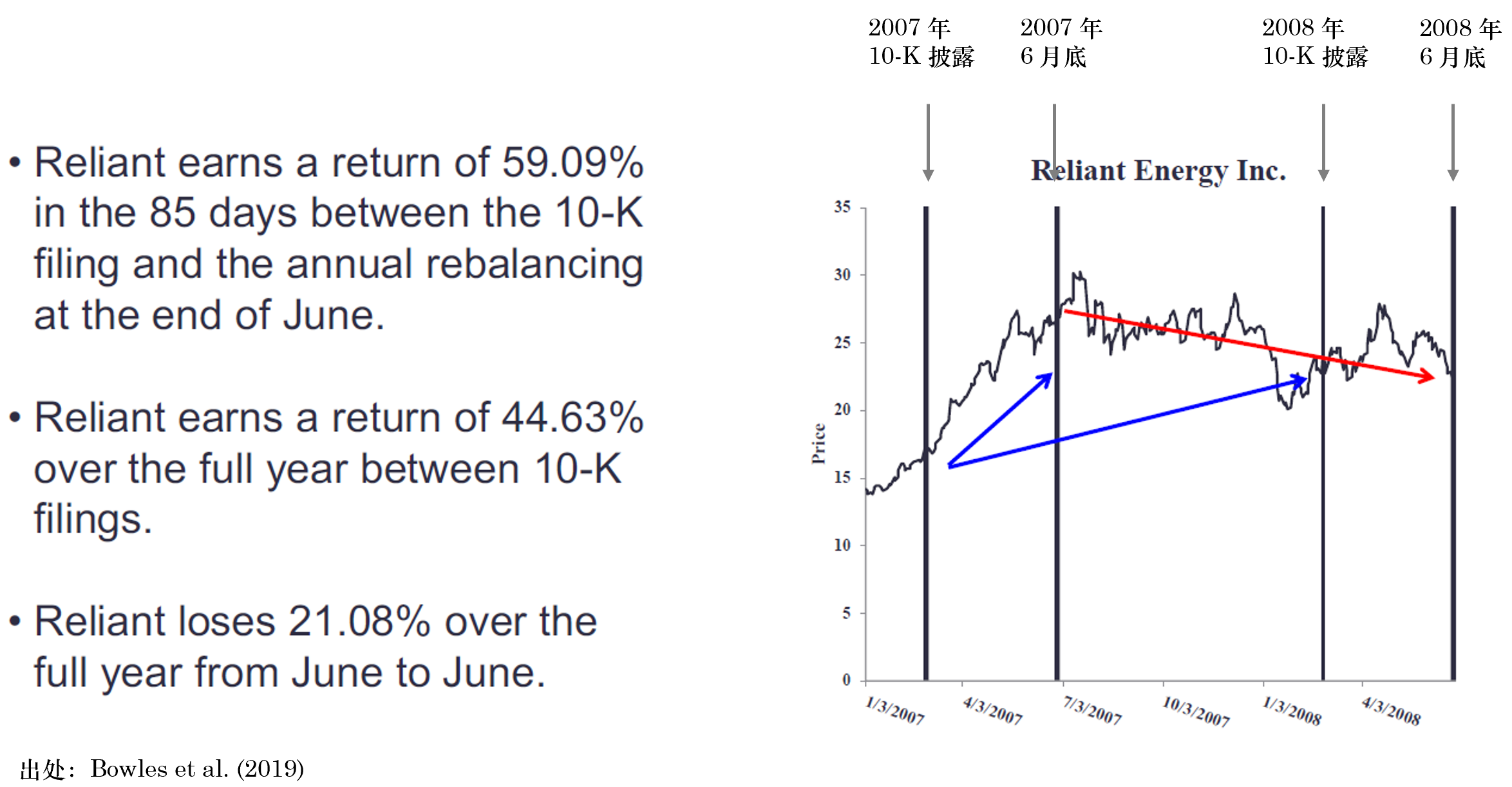
再來(lái)看個(gè)更顯著的(de)例子。下(xià)圖顯示了(le) Reliant Energy Inc. 這(zhè)家公司 2007 和(hé) 2008 兩年 10-K filing 的(de)時(shí)間，以及按學術界傳統每年 6 月(yuè)底再平衡時(shí)該公司的(de)股價變化(huà)。在 2007 年 10-K filing 到 6 月(yuè)底這(zhè) 85 天内，因最新的(de)财報數據，該公司股價上漲 59.09%。如果按照(zhào)兩個(gè) 10-K filing 之間來(lái)調倉選入該股票(piào)，那麽在兩個(gè)披露期之間可(kě)以獲利 44.63%；而在傳統研究框架下(xià)，如果在兩個(gè) 6 月(yuè)底調倉，選入該股票(piào)卻虧損 21.08%。

對(duì)于使用(yòng)财務指标構造的(de)因子，學術界之所以使用(yòng)每年再平衡是因爲學術界的(de)重心畢竟是 empirical asset pricing。爲了(le)研究成果的(de)可(kě)複制性和(hé)可(kě)比性，大(dà)家用(yòng)的(de)都是同樣的(de)數據庫、采用(yòng)同樣的(de)再平衡周期，因此也(yě)就沒有想過要用(yòng)粒度更細的(de)數據。Bowles et al. (2019) 一文則另辟蹊徑，使用(yòng) Compustat Snapshot 數據庫對(duì)因子時(shí)效進行了(le)分(fēn)析。用(yòng) Bowles et al. (2019) 自己的(de)話(huà)說，Snapshot 在學術界用(yòng)的(de)很少，但它卻是有著(zhe)粒度最細的(de)數據 —— 細到記錄财報中每個(gè)單一變量更新的(de)時(shí)間：

For each financial statement variable, Snapshot identifies the first date on which each variable was reported.

以美(měi)股爲例，通(tōng)常上市公司先有 earnings announcement 然後才有 10-Q 和(hé) 10-K filing。而在 earnings announcement 上往往隻會公布 total revenue 和(hé) net income 等少許指标，而在正式的(de) filing 中才披露全部财報内容。在這(zhè)種情況下(xià)，Snapshot 數據庫會在 earnings announcement 當日更新 total revenue 和(hé) net income 數據，而等到實際 filing 之後再更新其他(tā)數據。因此，使用(yòng) Snapshot 數據可(kě)以保證在用(yòng)來(lái)計算(suàn)因子的(de)指标被更新後，第一時(shí)間更新因子、進行投資組合的(de)再平衡。

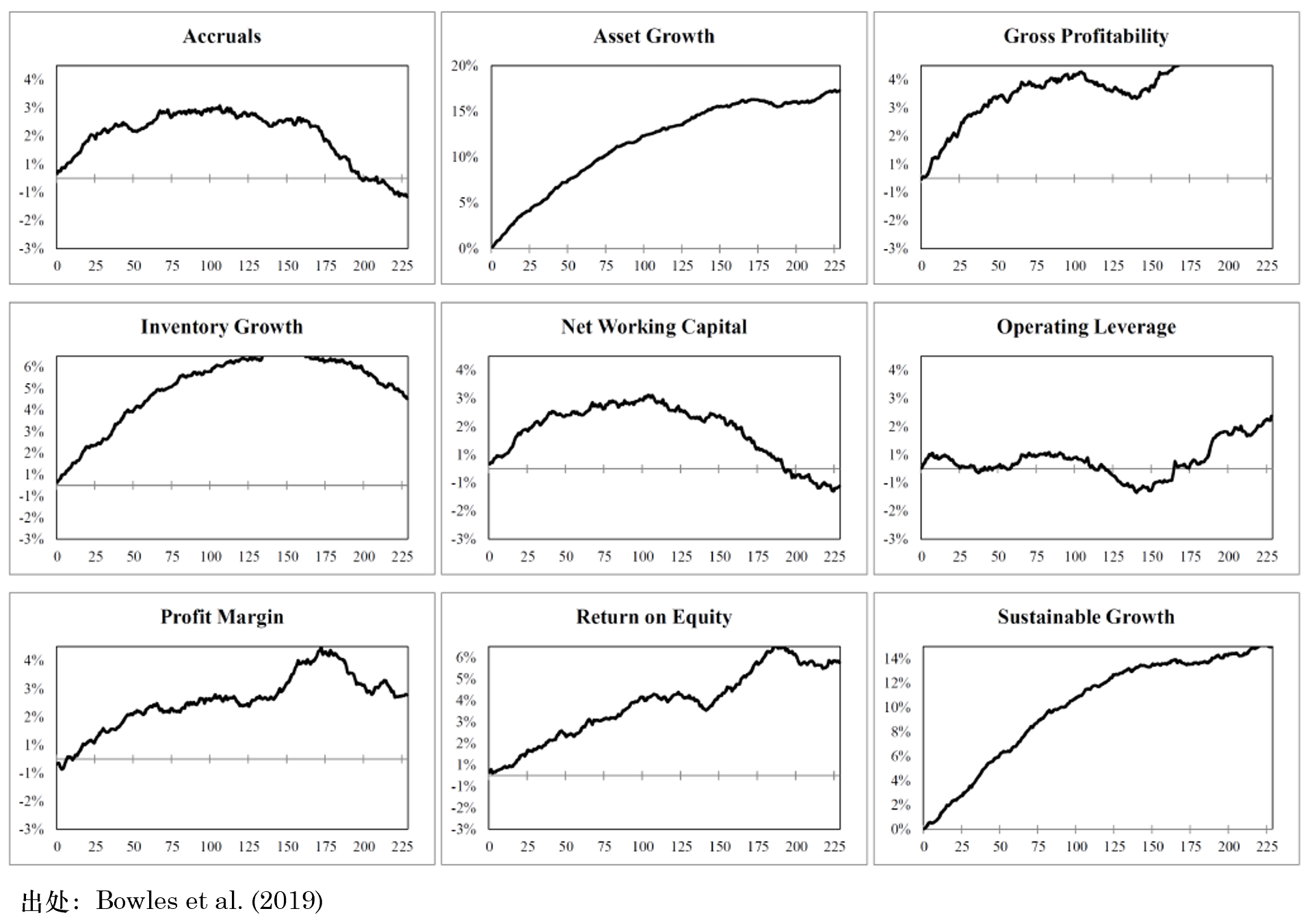
利用(yòng) Snapshot 數據，Bowles et al. (2019) 研究了(le)一些常見的(de)源自财務數據的(de)因子，發現絕大(dà)多(duō)數因子在最新數據更新後的(de) 120 天之内（特别是最初的(de) 30 天内）能夠獲得(de)顯著的(de)超額收益。而在 120 天之後，超額收益消失（下(xià)圖）。不過，Bowles et al. (2019) 也(yě)指出，最近幾年的(de)實證結果顯示，因子的(de)超額收益消失的(de)更快(kuài)。基于這(zhè)些發現，Bowles et al. (2019) 認爲因子是真實的(de)（而非 data snooping 出來(lái)的(de)），但很快(kuài)就會因套利交易而消失。

Bowles et al. (2019) 針對(duì)美(měi)股的(de)研究和(hé)前不久天風證券的(de)一篇《和(hé)時(shí)間賽跑 —— 利用(yòng)實時(shí)财務信息增強組合收益》針對(duì) A 股的(de)報告異曲同工。該研究顯示，利用(yòng)業績預告和(hé)快(kuài)報能夠提升财務信息的(de)時(shí)效性，提高(gāo)财務因子的(de)表現。

2 因子擁擠

造成因子樣本外變差的(de)第二個(gè)原因是因子擁擠（factor crowding）。通(tōng)常來(lái)說，因子都有周期性。當某類因子好使的(de)時(shí)候，就會造成更多(duō)的(de)資金引入，從而出現因子擁擠，并降低該因子未來(lái)的(de)預期收益率。而 rule-based （使用(yòng)相似的(de)指标排序、接近的(de)調倉頻(pín)率）的(de)因子投資無疑加劇了(le)這(zhè)種負面影(yǐng)響。由于因子擁擠度和(hé)因子未來(lái)收益率呈現負相關，如何定量計算(suàn)因子擁擠度就成爲人(rén)們關注的(de)問題。在這(zhè)方面，MSCI 整理(lǐ)了(le)相關研究，提出五個(gè)描述因子擁擠度的(de)代理(lǐ)指标（Bayraktar et al. 2015，Bonne et al. 2018）。這(zhè)五個(gè)指标是：valuation spread、short Interest spread、pairwise correlation、factor volatility 以及 factor reversal。考慮到由于制度問題，short interest spread 在 A 股上并不适用(yòng)，下(xià)面對(duì)其他(tā)四個(gè)指标做(zuò)簡要介紹。海通(tōng)證券的(de)報告《因子失效預警：因子擁擠》針對(duì) A 股對(duì)上述四個(gè)指标進行了(le)分(fēn)析。

2.1 Valuation Spread

顧名思義，valuation spread（估值價差）考慮的(de)正是因子的(de)估值。關于因子估值在 A 股上的(de)實證，感興趣的(de)小夥伴請參考《你家因子便宜嗎？——基于value spread的(de)因子擇時(shí)研究》。這(zhè)背後的(de)邏輯是，當更多(duō)資金湧入某個(gè)因子時(shí)（特别是多(duō)頭時(shí)），會造成受波及股票(piào)的(de)價格上漲，使它們的(de)估值變高(gāo)。因此，因子估值和(hé)因子擁擠度成正相關，是一個(gè)不錯代理(lǐ)指标。估值價差的(de)計算(suàn)方法十分(fēn)直觀。首先選擇一個(gè)合适的(de)股票(piào)估值指标，比如 B/P，然後分(fēn)别計算(suàn)因子多(duō)空兩頭組合中該估值指标的(de)中位數，以此作爲多(duō)空兩頭的(de)估值，最後這(zhè)兩個(gè)估值差就是因子的(de)估值價差。以 B/P 爲例，Bonne et al. (2018) 使用(yòng)的(de)計算(suàn)公式爲：

2.2 Pairwise Correlation

第二個(gè)指标是 Pairwise Correlation（配對(duì)相關性）。它是爲了(le)從因子投資組合内股票(piào)收益率的(de)相關程度來(lái)試圖揭示資金持倉的(de)集中程度，并以此來(lái)評價因子的(de)擁擠程度。爲了(le)計算(suàn)該指标，Bonne et al. (2018) 采用(yòng)了(le)如下(xià)步驟：

2.3 Factor Volatility

由于資金的(de)流入會加劇因子收益率的(de)波動，因此 Bonne et al. (2018) 從這(zhè)個(gè)角度提出了(le)衡量因子擁擠度的(de)第三個(gè)指标：Factor Volatility（因子波動率）。值得(de)一提的(de)是，Bonne et al. (2018) 使用(yòng)的(de)是預測的(de)未來(lái)因子波動率相對(duì)未來(lái)市場(chǎng)波動率的(de)比值來(lái)計算(suàn)該指标。他(tā)們認爲這(zhè)麽做(zuò)可(kě)以有效的(de)控制市場(chǎng)波動率變化(huà)造成的(de)影(yǐng)響。在實際操作中，一個(gè)簡化(huà)的(de)處理(lǐ)方法是使用(yòng)因子的(de)曆史波動率。

2.4 Factor Reversal

最後一個(gè)指标是 Factor Reversal（因子反轉）。De Bondt and Thaler (1985) 這(zhè)篇著名的(de)論文表明(míng)美(měi)股在 3 到 5 年的(de)中長(cháng)期尺度上存在反轉。由于因子是股票(piào)構成的(de)投資組合，因此我們可(kě)以自然的(de)從股票(piào)的(de)反轉延伸出因子的(de)反轉。Bonne et al. (2018) 使用(yòng)因子過去三年的(de)累積收益率計算(suàn)該指标。

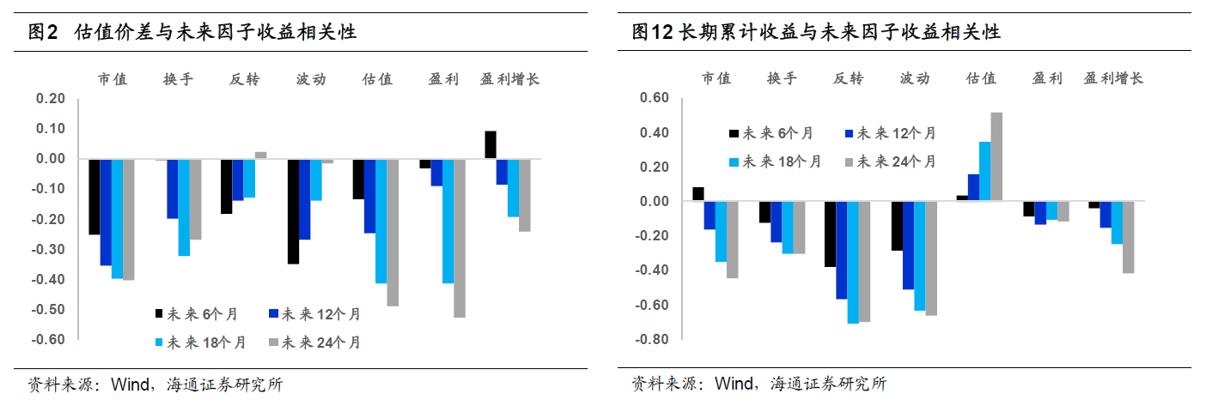
以前文提到的(de)《因子失效預警：因子擁擠》研究結果爲例，下(xià)圖展示了(le)估值價差和(hé)因子反轉兩個(gè)因子擁擠度指标和(hé) A 股上一些常見因子未來(lái)收益率的(de)關系（之所以沒有放另外兩個(gè)指标的(de)結果是因爲報告中的(de)計算(suàn)方法和(hé) Bonne et al. 2018 的(de)方法差異較大(dà)；方法并無優劣之分(fēn)，但因實證結果并不直接對(duì)應前文介紹的(de)方法，故略去）。圖中結果顯示，對(duì)其中大(dà)部分(fēn)因子，這(zhè)兩個(gè)指标和(hé)因子未來(lái)收益率成負相關，說明(míng)該因子擁擠會造成因子表現變差。

最後，因子擁擠也(yě)會引發流動性沖擊。一旦市場(chǎng)中發生沖擊因子的(de)事件後，持有相似頭寸的(de)管理(lǐ)人(rén)會競相賣出手中的(de)股票(piào)，由此産生的(de)流動性危機會造成很大(dà)的(de)虧損。2007 年 8 月(yuè)，美(měi)股市場(chǎng)上一些非常優秀的(de)量化(huà)對(duì)沖基金在短時(shí)間内錄得(de)了(le)巨大(dà)的(de)虧損。Khandani and Lo (2011) 對(duì)此進行了(le)研究并發現，很多(duō)基金經理(lǐ)在短時(shí)間内清理(lǐ)了(le)相似的(de)頭寸，巨大(dà)的(de)抛壓對(duì)流動性造成了(le)巨大(dà)的(de)打擊、使得(de)這(zhè)些股票(piào)的(de)價格在短時(shí)間内大(dà)幅下(xià)跌。

3 交易成本

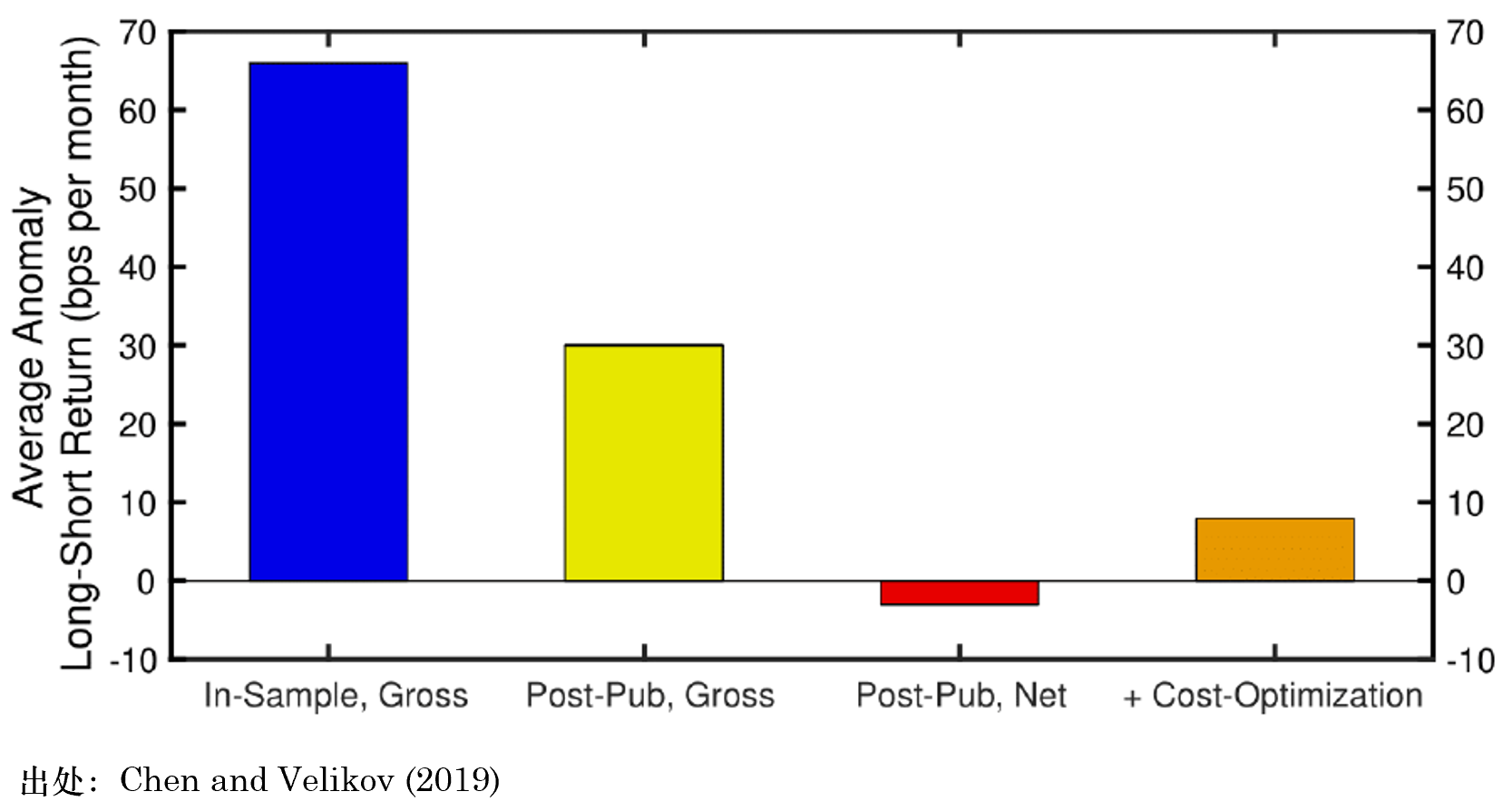
交易成本是因子在樣本外的(de)效果較樣本内顯著變差的(de)第三個(gè)原因。學術論文通(tōng)常不會對(duì)交易費用(yòng)給予充分(fēn)的(de)考慮，這(zhè)會造成對(duì)因子收益率的(de)高(gāo)估。此外，由于因子投資組合一般都是多(duō)、空對(duì)沖的(de)組合，如果不合理(lǐ)考慮做(zuò)空限制，也(yě)會高(gāo)估因子的(de)收益。Novy-Marx and Velikov (2015) 研究了(le)交易費用(yòng)對(duì)因子效果的(de)影(yǐng)響，并提出三個(gè)思路降低交易成本：（1）僅使用(yòng)交易費用(yòng)低的(de)股票(piào)構建因子組合；（2）降低因子組合再平衡的(de)頻(pín)率；（3）在交易時(shí)考慮更嚴格的(de)買賣價差約束。在 Chen and Velikov (2019) 一文中，二位作者使用(yòng) effective spread（有效價差）的(de)概念代替傳統的(de) bid-ask spread，對(duì)多(duō)達 120 種因子進行了(le)研究。他(tā)們的(de)研究發現 …… 哎，先上圖吧。

上圖中，藍色的(de) bar 代表著(zhe) 120 個(gè)因子樣本内的(de)平均 gross 收益率（不考慮任何交易成本）；黃(huáng)色 bar 爲這(zhè)些因子在發表後的(de)平均 gross 收益率；紅色 bar 爲考慮了(le)交易成本後，這(zhè)些因子的(de)平均收益率 —— 負的(de)。來(lái)看下(xià)具體研究方法。Chen and Velikov (2019) 對(duì) effective spread 的(de)定義爲：

爲了(le)考慮交易成本，他(tā)們假設每次調倉時(shí)的(de)交易費用(yòng)爲上述 effective spread 的(de)一半。從上述定義不難看出，因子的(de)費後 net return 和(hé)換手率以及換倉時(shí)的(de) effective spread 息息相關：

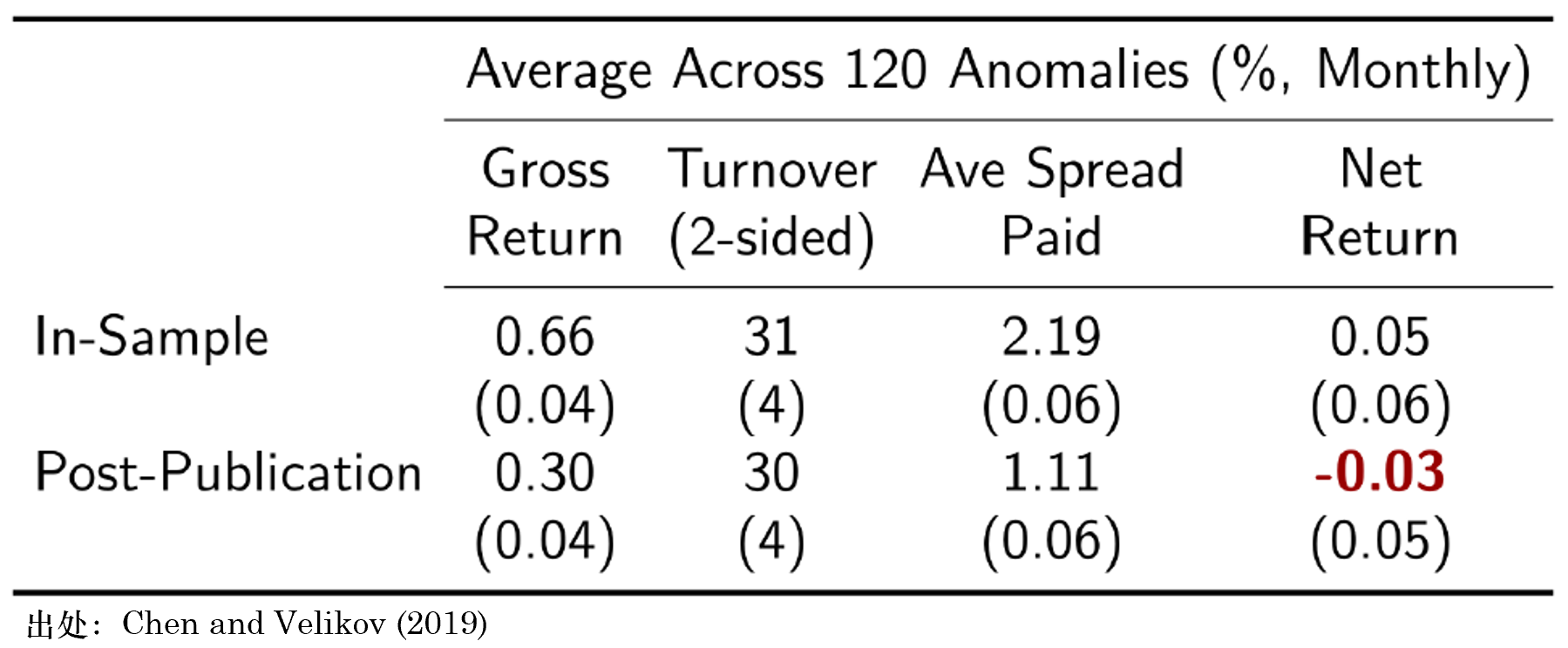
有必要指出的(de)是，Chen and Velikov (2019) 的(de)研究僅考慮交易費用(yòng)，并不考慮任何沖擊成本。這(zhè)意味著(zhe)考慮了(le)沖擊成本後，因子樣本外的(de) net return 隻能更慘。下(xià)表顯示了(le)在考慮了(le)成本後，120 個(gè)因子在樣本内、外的(de)收益情況（括号中爲标準差）。結果顯示，考慮成本後，即便是樣本内，這(zhè)些因子的(de)月(yuè)均收益僅有 0.05%，而樣本外的(de)收益更是小于零。

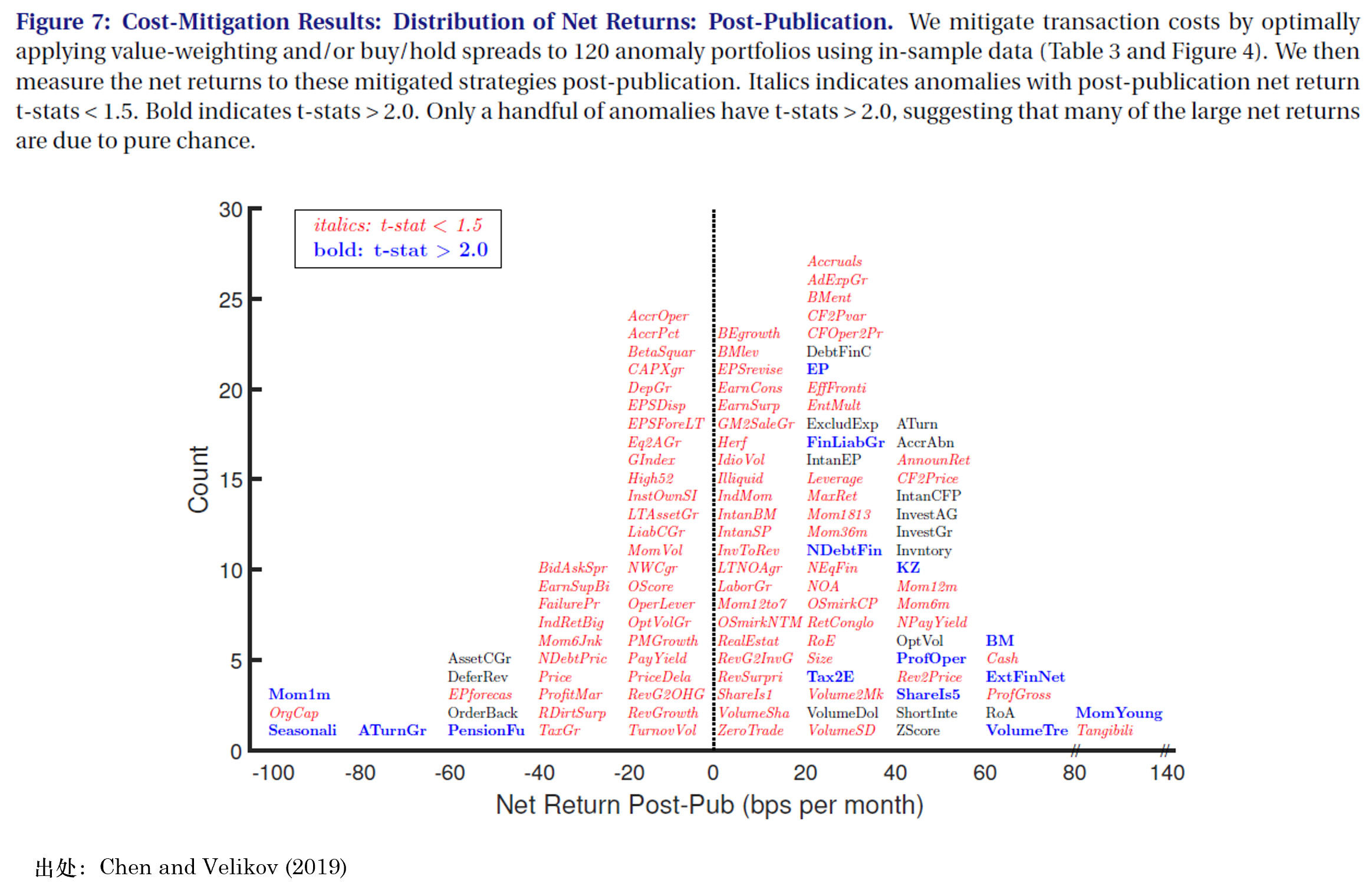
下(xià)圖展示了(le)樣本外，這(zhè) 120 個(gè)因子的(de) net returns 的(de)分(fēn)布。這(zhè)些 net returns 經過了(le)一定的(de)交易優化(huà)處理(lǐ)，有效降低了(le)換手率和(hé)交易成本，因此整體來(lái)看所有因子的(de) net return 均值是大(dà)于零的(de)，而非上表中 -0.03% 那麽慘。

這(zhè)個(gè)分(fēn)布看上去像是一個(gè)均值接近零的(de)正态分(fēn)布，和(hé)随機因子的(de)表現并無太大(dà)差異（即如果我們使用(yòng)完全随機生成的(de) 120 個(gè)因子，其中也(yě)總會有一些是“顯著”的(de)）。由于發表的(de)因子都多(duō)少存在 selection bias，因此面對(duì)上述結果，Chen and Velikov (2019) 不禁發問：排除運氣後，還(hái)有多(duō)少因子是顯著的(de)？爲了(le)回答(dá)上述問題，他(tā)們采用(yòng)了(le) empirical Bayes 方法對(duì) selection bias 進行修正。Chen and Velikov (2019) 假設因子 i 在被發表後的(de)樣本平均收益率 \bar r_i 由真實 μ_i 和(hé)噪音(yīn) ε_i 決定：

其中 ε_i 滿足正态分(fēn)布 N(0, SE_i)，這(zhè)裏 SE_i 是 \bar r_i 的(de) standard error。Chen and Velikov (2019) 進一步假設所有因子 net return 的(de)真實均值 μ_i 都滿足如下(xià)正态分(fēn)布：

Chen and Velikov (2019) 采用(yòng) method of moments 對(duì)參數 μ_μ 和(hé) σ_μ 進行估計：

上式說明(míng) \hat μ_μ 是所有因子平均收益率的(de)截面均值。看到這(zhè)裏，似乎還(hái)沒見 Bayes 的(de)影(yǐng)子。别著(zhe)急，有了(le) \bar r_i 和(hé) μ_μ 的(de)估計，接下(xià)來(lái)馬上就要貝葉斯收縮（Bayes shrinkage）了(le)：

上式中 s_i 是收縮系數，它由 \bar r_i 的(de) standard error（SE_i）和(hé) μ_μ 的(de)标準差 σ_μ 的(de)相對(duì)大(dà)小決定：

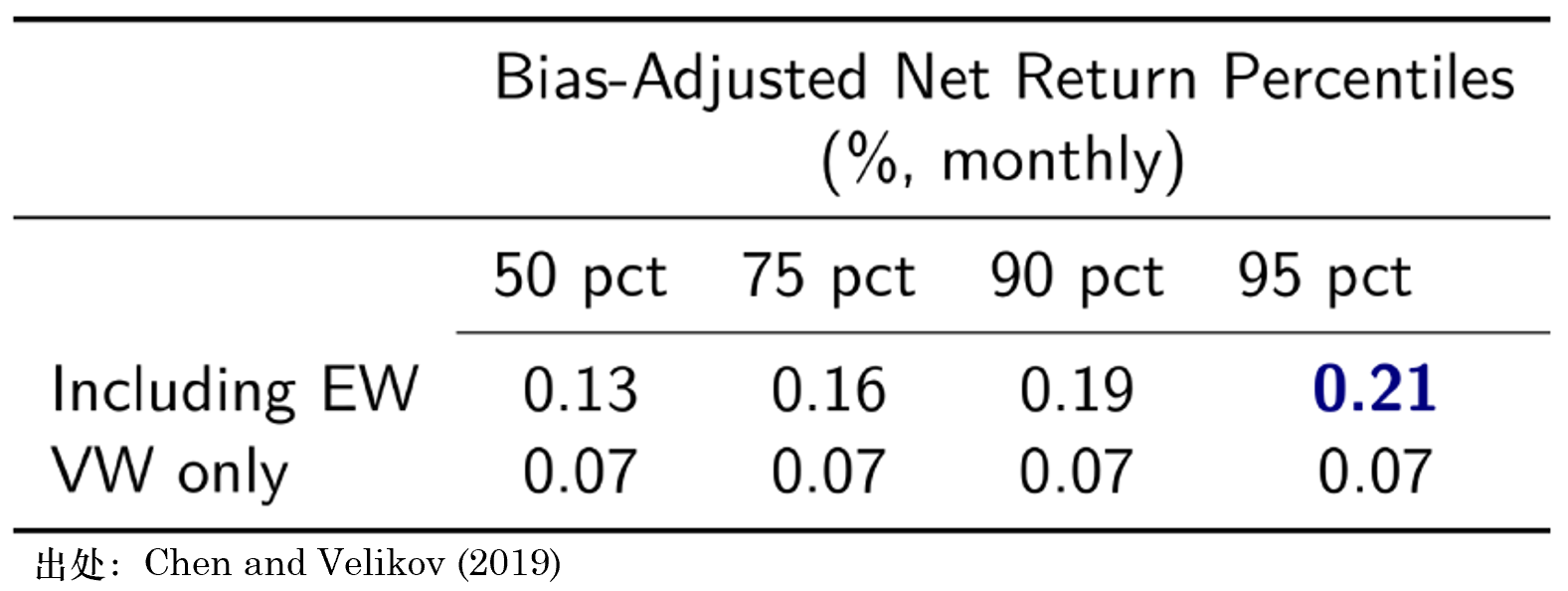
結合 s_i 的(de)定義不難看出，如果 SE_i 小說明(míng) \bar r_i 可(kě)信，則收縮後的(de)因子 i 的(de)收益率由其主宰；如果 SE_i 相對(duì) σ_μ 很大(dà)就說明(míng) \bar r_i 不靠譜，則因子 i 的(de)收益率由全部 120 個(gè)因子的(de)截面均值主宰。經如此調整後，Chen and Velikov (2019) 得(de)到了(le)如下(xià)結果。

排除 selection bias 之後，即便是最好的(de)因子（top 5%），被發表後月(yuè)均 net return 僅有 0.21% —— 這(zhè)還(hái)是在允許等權構建因子的(de)前提下(xià)。當使用(yòng)市值加權時(shí)，該數值降低至 0.07%。基于以上結果，Chen and Velikov (2019) 認爲考慮了(le)合理(lǐ)的(de)交易成本後，絕大(dà)多(duō)數因子在樣本外都無法獲利。不要忘記，以上結果還(hái)是基于對(duì)交易進行了(le)優化(huà)後的(de)結果。

Average investors should expect only tiny profits from selected, cost-mitigated anomaly strategies.

4 結語

由于曝光(guāng)導緻錯誤定價減弱、因子擁擠以及交易成本等原因，因子樣本外表現變差是因子投資中必須面對(duì)的(de)問題。這(zhè)也(yě)催生了(le)業界對(duì)因子擇時(shí)的(de)極大(dà)興趣，并嘗試使用(yòng)各種手段持續挖新的(de)因子（新的(de)因子意味著(zhe)曝光(guāng)少、擁擠度低）。Arnott et al. (2019) 一文也(yě)嚴肅討(tǎo)論了(le)投資人(rén)在因子投資中常犯的(de)三大(dà)錯誤，第一條就是對(duì)樣本内的(de)表現非理(lǐ)性外推，造成對(duì)因子樣本外的(de)表現缺乏理(lǐ)性預期。另外，當因子表現變差時(shí)，人(rén)們由此想到的(de)另一個(gè)問題是因子是否會失效。對(duì)此，我們認爲如果因子背後的(de)原因是風險補償或者錯誤定價，那麽還(hái)是有理(lǐ)由相信因子長(cháng)期來(lái)看會有效的(de)。在這(zhè)方面，Asness (2015) 有過精彩的(de)討(tǎo)論。該文認爲諸如 value、momentum、carry 等因子在長(cháng)期來(lái)看會持續有效。這(zhè)背後的(de)原因主要包括：

最後，還(hái)有一個(gè)事實也(yě)不得(de)不提：很多(duō)人(rén)知道了(le)一個(gè)因子，并不代表他(tā)會利用(yòng)這(zhè)個(gè)因子，也(yě)并不代表他(tā)無條件的(de)信任這(zhè)個(gè)因子，更不代表他(tā)會堅定不移的(de)使用(yòng)這(zhè)個(gè)因子。知道并不意味著(zhe)懂(dǒng)，懂(dǒng)并不意味著(zhe)會用(yòng)，會用(yòng)也(yě)并不意味著(zhe)始終如一。因此，有充分(fēn)先驗依據的(de)因子的(de)長(cháng)期表現依然值得(de)期待。

參考文獻

Arnott, R., C. R. Harvey, V. Kalesnik, and J. Linnainmaa (2019). Alice's adventures in factorland: Three blunders that plague factor investing. The Journal of Portfolio Management 45(4), 18 – 36.

Asness, C. S. (2015). How can a strategy still work if everyone knows about it? AQR Research Insight.

Asness, C. S. and A. Frazzini (2013). The devil in HML's details. The Journal of Portfolio Management 39(4), 49 – 68.

Bayraktar, M., S. Doole, A. Kassam, and S. Radchenko (2015). Lost in the crowd? Identifying and measuring crowded strategies and trades. MSCI Research Insight.

Bonne, G., L. Roisenberg, R. Kouzmenko, and P. Zangari (2018). MSCI integrated factor crowding model. MSCI Research Insight.

Bowles, B., A. V. Reed, M. Ringgenberg, and J. R. Thornock (2019). Anomaly time. SSRN Working Paper.

Chen, A. Y. and M. Velikov (2019). Accounting for anomaly zoo: A trading cost perspective. SSRN Working Paper.

De Bondt, W. M. and R. H. Thaler (1985). Does the stock market overreact? Journal of Finance 40(3), 793 – 805.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Khandani, A. E. and A. W. Lo (2011). What happened to the quants in August 2007? Evidence from factors and transactions data. Journal of Financial Markets 14(1), 1 – 46.

McLean, R.D. and J. Pontiff (2016). Does academic research destroy stock return predictability? Journal of Finance 71(1), 5 – 32.

Novy-Marx, R. and M. Velikov (2015). A taxonomy of anomalies and their trading costs. Review of Financial Studies 29(1), 104 – 147.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。