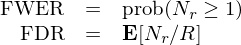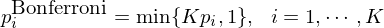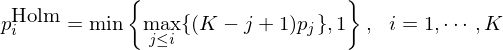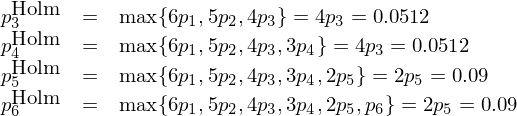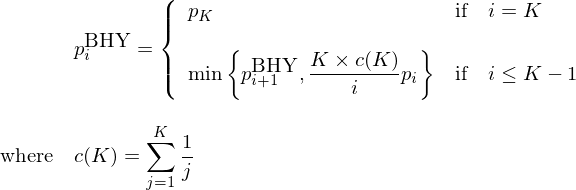Calendar Anomalies：糖衣下(xià)的(de) Multiple Hypothesis Testing?

作者：石川

摘要：以特定日期作爲條件來(lái)劃分(fēn)收益率并檢驗不同劃分(fēn)下(xià)的(de)顯著性是一種多(duō)重假設檢驗。在修正之後，很多(duō)所謂的(de)日曆異象都不再顯著。

1 引言

Calendar Anomalies（日曆異象）指的(de)是資産在一年中的(de)某些特定的(de)日子内有顯著非零的(de)條件預期收益率。這(zhè)其中最大(dà)名鼎鼎的(de)當屬股票(piào)市場(chǎng)中的(de)換月(yuè)效應（turn of month effect）：股票(piào)市場(chǎng)在每月(yuè)的(de)最後 1 個(gè)交易日到下(xià)一個(gè)月(yuè)的(de)第 3 個(gè)交易日這(zhè)個(gè)窗(chuāng)口内的(de)收益率顯著高(gāo)于一個(gè)月(yuè)中的(de)其他(tā)交易日。McConnell and Xu (2008) 的(de)研究發現，在 1926 到 2005 間，在換月(yuè)窗(chuāng)口内買入标普 500 指數的(de) ETF 可(kě)獲得(de)得(de)年化(huà) 7.20% 的(de)收益率（夏普率高(gāo)達 1.04）。Carchano and Pardo Tornero (2011) 更是以标普 500 指數、德國法蘭克福指數和(hé)日經指數爲研究對(duì)象，分(fēn)析了(le) 188 種日曆異象，并發現在統計上和(hé)經濟上同時(shí)顯著的(de)隻有換月(yuè)效應。

除了(le)市場(chǎng)指數外，學術界也(yě)以各種風格因子投資組合爲标的(de)研究各種 calendar anomalies。在最近一篇刊發于 JPM 的(de)文章(zhāng)中，Aharon and Qadan (2019) 提出雖然 size effect 在全樣本中效果越來(lái)越弱，但它依然顯著的(de)存活于某些特定的(de)日期内，構成 calendar anomalies。真的(de)是這(zhè)樣麽？以特定日期作爲條件來(lái)劃分(fēn)收益率并檢驗不同劃分(fēn)下(xià)的(de)顯著性（相當于同時(shí)檢驗多(duō)個(gè) hypotheses），這(zhè)其實屬于 multiple hypothesis testing（多(duō)重假設檢驗）。在大(dà)量不同的(de)劃分(fēn)下(xià)，僅僅因爲運氣就總會有一些是非常顯著的(de)、被人(rén)們冠以 calendar anomalies 之名。隻有對(duì) multiple hypothesis testing 的(de)影(yǐng)響進行必要的(de)修正，才能公正的(de)評判某種特定日期的(de)劃分(fēn)是否真的(de)得(de)到顯著的(de)收益率異象。這(zhè)就是本文要探討(tǎo)的(de)内容。

2 日曆異象？

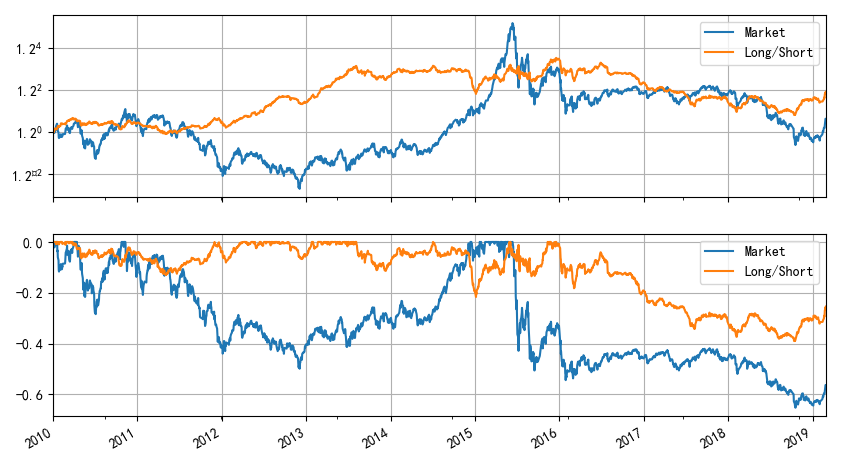
來(lái)看一個(gè)例子。以中證 500 指數成分(fēn)股爲标的(de)，使用(yòng)某個(gè)常見的(de)風格因子将它們排序，取首尾 10% 構建多(duō)、空對(duì)沖投資組合作爲該因子的(de)投資組合。下(xià)圖顯示了(le)實證期内中證 500 指數（藍線）和(hé)該風格因子組合（黃(huáng)線）的(de)走勢。從黃(huáng)線可(kě)以看出，它無法獲得(de)顯著的(de)超額收益。事實上，其日收益率均值的(de) t-statistic 僅有 1.17，對(duì)應的(de) p-value 高(gāo)達 0.24。在全樣本來(lái)看，這(zhè)個(gè)因子是不顯著的(de)。

接著(zhe)，考慮幾種常見的(de)日曆現象：

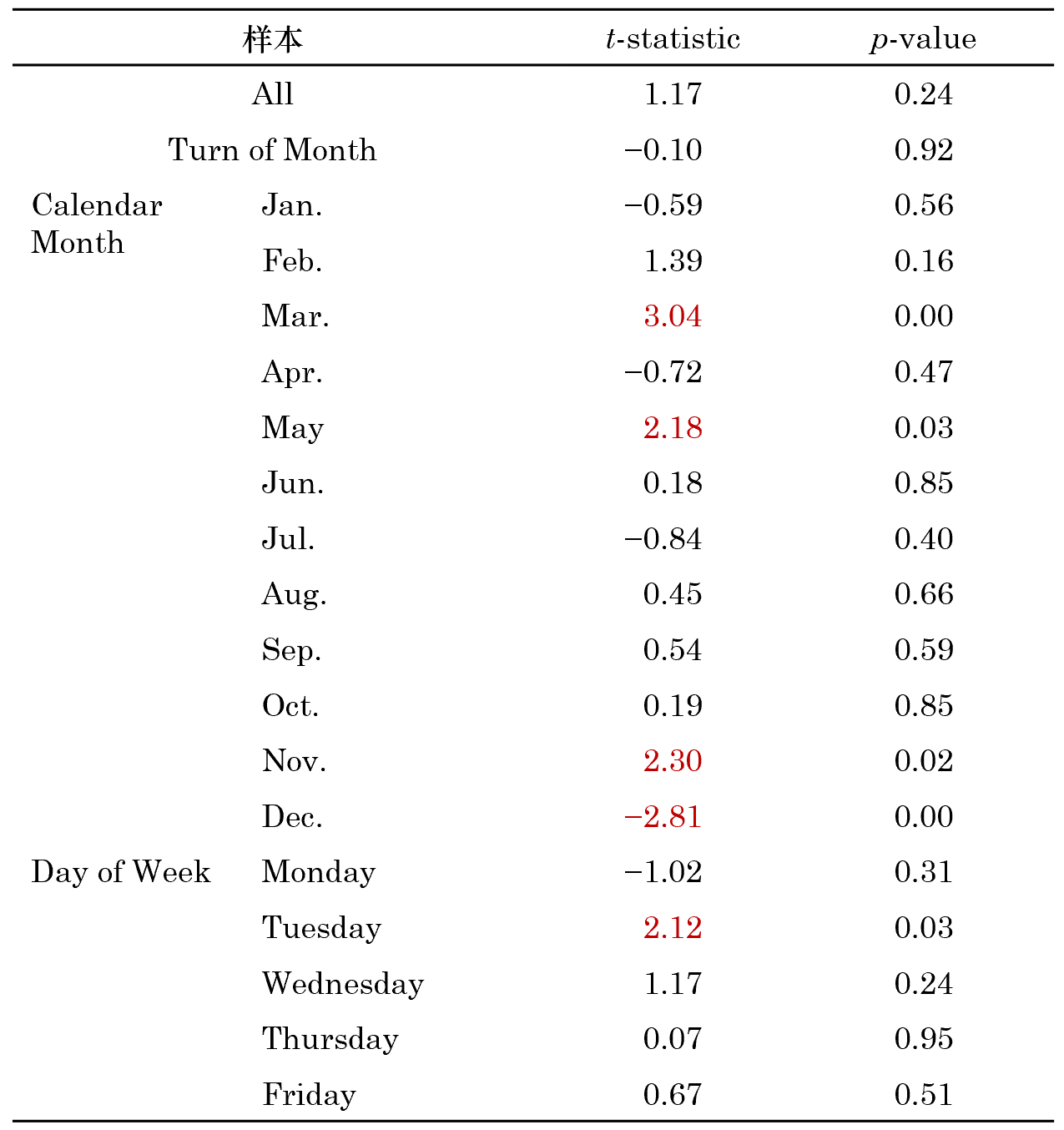
當我們在時(shí)間上進行各種劃分(fēn)後，神奇的(de)事情發生了(le)。這(zhè)個(gè)全樣本内不顯著的(de)因子，在某些特定的(de)劃分(fēn)中出現了(le)顯著的(de) calendar anomalies，它們包括三月(yuè)效應、五月(yuè)效應、十一月(yuè)效應、十二月(yuè)效應以及星期二效應。

上述五個(gè)潛在 calendar anomalies 的(de) p-values 均在 0.05 以下(xià)。但不要忘了(le)，以上實際同時(shí)檢驗了(le) 18 個(gè)假設 —— 1 個(gè)換月(yuè)效應 + 12 個(gè)月(yuè)份效應 + 5 個(gè)“星期幾”效應。在這(zhè)種背景下(xià)，即便有些假設的(de) p-value 是非常小的(de)，也(yě)不應該立刻得(de)出拒絕某個(gè)原假設的(de)結論，而是應該針對(duì) multiple hypothesis testing 進行修正，以修正後的(de) p-value 作爲判斷依據。

3 Multiple Hypothesis Testing 修正

前文《出色不如走運 II?》曾介紹過 Bonferroni、Holm、BHY 這(zhè)三種 multiple hypothesis testing 修正方法。本小節簡單回顧一下(xià)，在本文第四節的(de)分(fēn)析中将采用(yòng) BHY 修正。在實施了(le) multiple hypothesis testing 後應控制 family-wise error rate（FWER，族錯誤率）和(hé) false discovery rate（FDR）兩個(gè)指标。它們均代表著(zhe) Type I error，即錯誤的(de)拒絕原假設。如果我們有 K 個(gè) hypotheses（對(duì)應前文中的(de)多(duō)個(gè) calendar anomalies），它們的(de) p-value 分(fēn)别爲 p_1、p_2、…、p_K。根據事先選定的(de)顯著性水(shuǐ)平（比如 5%），其中 R 個(gè) hypotheses 被拒絕了(le)，即有 R 個(gè)發現（discoveries） —— 包括 true discoveries 和(hé) false discoveries。令 N_r ≤ R 代表 false discoveries 的(de)個(gè)數，則 FWER 和(hé) FDR 的(de)定義分(fēn)别爲：

由定義可(kě)知，FWER 是至少出現一個(gè) false discovery 的(de)概率，控制它對(duì)單個(gè) hypothesis 來(lái)說是相當嚴格的(de)，會大(dà)大(dà)提升 Type II Error。相比之下(xià)，FDR 允許 N_r 随 R 增加，因此控制的(de)是 false discoveries 的(de)比例，是一種相對(duì)溫和(hé)的(de)方法。無論采用(yòng)哪種方法，在針對(duì)多(duō)重假設檢驗的(de)修正下(xià)，都會有相當一部分(fēn)的(de) discoveries 不再顯著（即不能拒絕原假設）。依據控制 FWER 或 FDR，本文談及的(de)三種修正方法可(kě)以分(fēn)爲兩類：

這(zhè)三種方法均能修正原始假設的(de) p-value，從而懲罰多(duō)重假設檢驗的(de)影(yǐng)響。修正後的(de) p-value 往往會大(dà)于原始的(de) p-value，也(yě)就意味著(zhe)修正後的(de) t-statistic 更小。接下(xià)來(lái)通(tōng)過一個(gè)例子說明(míng)這(zhè)些方法的(de)差異。考慮六個(gè)假設，它們的(de) p-values 從小到大(dà)依次是 0.005、0.009、0.0128、0.0135、0.045、0.06。在單一假設檢驗下(xià)，前五個(gè)可(kě)以在 5% 的(de)顯著性水(shuǐ)平下(xià)被拒絕。但由于我們實際上同時(shí)進行了(le)六個(gè)假設檢驗，因此必須對(duì)上述 p-values 進行修正。首先來(lái)看 Bonferroni correction，它對(duì)原始 p-value 的(de)調整如下(xià)：

修正後的(de) Bonferroni p-value 分(fēn)别爲 0.03、0.054、0.0768、0.081、0.27 和(hé) 0.36；在 5% 的(de)顯著性水(shuǐ)平下(xià)，我們僅能拒絕第一個(gè)假設。接下(xià)來(lái)看看 Holm (1979) 修正。它按照(zhào)原始 p-value 從小到大(dà)依次修正，公式爲：

根據上述定義，最小的(de) p-value 被修正後，其 Holm p-value 爲 0.06；第二個(gè)假設的(de) Holm p-value 爲 max{6 × 0.005, 5 × 0.009} = 0.045。以此類推就能計算(suàn)出其他(tā)四個(gè)假設的(de) Holm p-values。經過 Holm 修正後，在 5% 的(de)顯著性水(shuǐ)平下(xià)，我們僅能拒絕前兩個(gè)假設。

最後來(lái)看看 BHY 修正（Benjamini and Hochberg 1995, Benjamini and Yekutieli 2001）。它從原始 p-value 中最大(dà)的(de)一個(gè)開始逆向修正：

由定義可(kě)知原始最大(dà)的(de) p-value 在調整後保持不變。然後從第二大(dà)的(de)開始，依次按照(zhào)上述公式計算(suàn)，最終得(de)到調整後的(de) BHY p-values，它們是（從小到大(dà)排列）：0.0496、0.0496、0.0496、0.0496、0.06、0.06。在 5% 的(de)顯著性水(shuǐ)平下(xià)，我們依然可(kě)以拒絕前四個(gè)假設。再次強調的(de)是，BHY 方法是以控制 false discovery rate 爲目标，它的(de)修正比另外兩種以控制 family-wise error rate 的(de)方法更加溫和(hé)。因此，當使用(yòng) BHY 調整時(shí)，會有更多(duō)的(de)原假設被拒絕。此外，BHY 對(duì)檢驗統計量之間的(de)相關性不敏感，因此适應性更強。

4 消失的(de)日曆異象

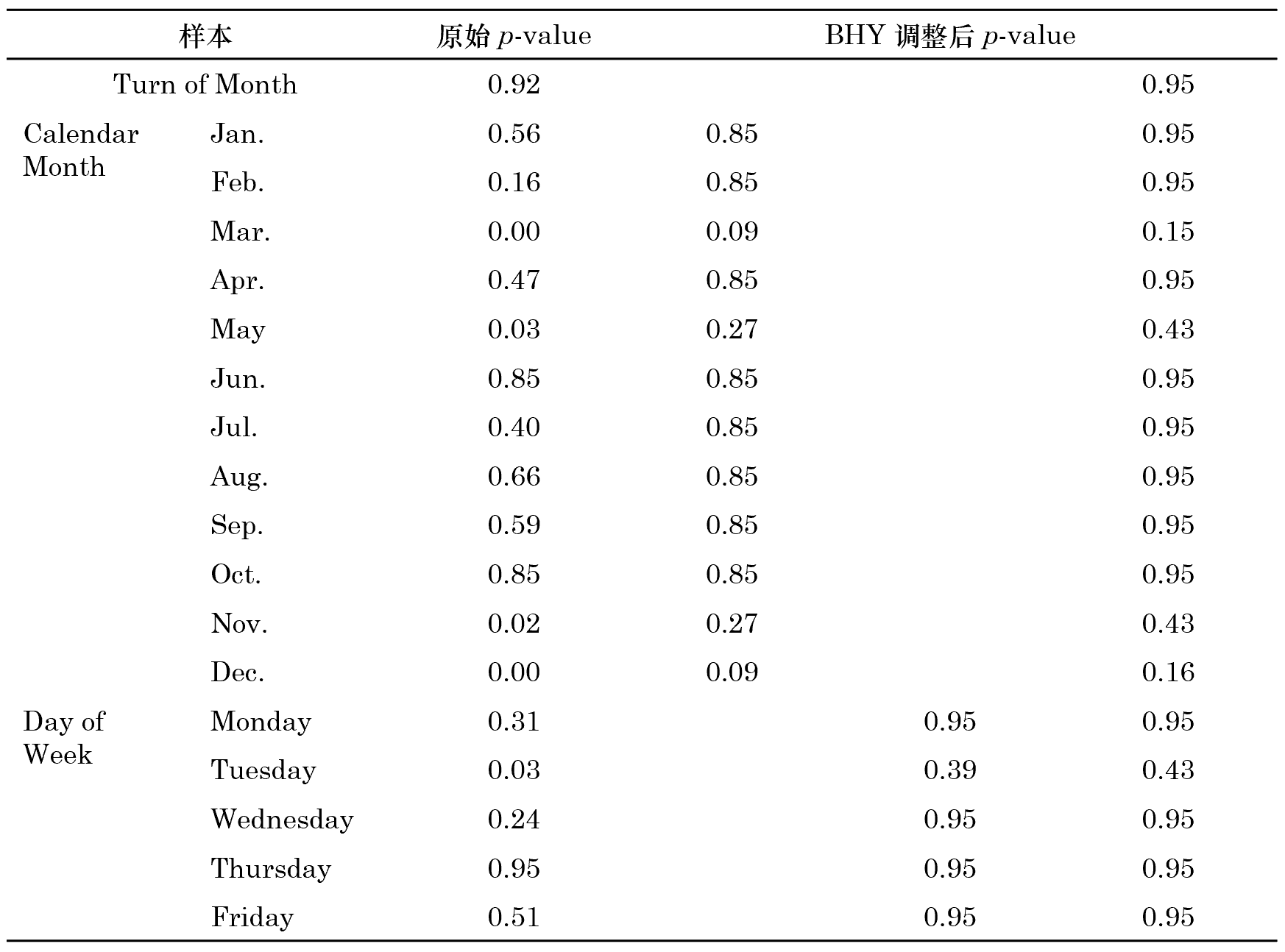
下(xià)面使用(yòng) BHY 方法對(duì)本文第二節的(de) p-values 進行修正。考慮不同的(de) multiple hypotheses 個(gè)數，BHY 調整後的(de) p-values 如下(xià)表所示。

對(duì)于月(yuè)份效應，如果我們僅考慮這(zhè) 12 個(gè) tests（而忽略其他(tā)額外的(de) tests），那麽修正後的(de) p-value 中，三月(yuè)效應和(hé)十二月(yuè)效應依然在 10% 的(de)顯著性水(shuǐ)平下(xià)顯著（p-values 分(fēn)别爲 0.0881 和(hé) 0.0922），而五月(yuè)和(hé)十二月(yuè)效應不再顯著。類似的(de)，對(duì)于“星期幾”效應，如果僅考慮這(zhè) 5 個(gè) tests，修正後的(de) p-value 全都不再顯著。如果同時(shí)考慮全部 18 個(gè) tests，則會對(duì)原始 p-values 進行更嚴格的(de)修正。在這(zhè)種情況下(xià)，以上各種劃分(fēn) —— 無論是換月(yuè)、月(yuè)份還(hái)是“星期幾”效應 —— 均不再顯著，我們無法在 10% 的(de)水(shuǐ)平下(xià)拒絕任何假設。當排除了(le) multiple hypothesis testing 造成的(de)影(yǐng)響後，這(zhè)個(gè)風格因子的(de)收益率不存在任何 calendar anomalies。BTW，這(zhè)個(gè)全樣本中不顯著的(de)因子是 Operating Cost TTM。

5 結語

如今，在研究因子時(shí)，我們已經熟知 multiple hypothesis testing 的(de)危害。而将收益率在時(shí)間上進行各種劃分(fēn)并同時(shí)進行多(duō)個(gè)檢驗則是另一種形式的(de) multiple hypothesis testing。在這(zhè)種背景下(xià)，獨立判别收益率在某個(gè)劃分(fēn)下(xià)是否顯著并不合理(lǐ)。本文以 Operating Cost TTM 這(zhè)個(gè)常見的(de)質量因子爲例說明(míng)如未能排除 multiple hypothesis testing 的(de)影(yǐng)響，它會讓我們得(de)出錯誤的(de)結論。當我們考慮了(le)足夠多(duō)的(de) calendar effects 時(shí)，僅僅依靠運氣就一定會找到顯著的(de)區(qū)間。爲了(le)杜絕虛假發現，應對(duì)顯著性進行修正。在 Carchano and Pardo Tornero (2011) 這(zhè)篇檢驗了(le) 188 個(gè)異象的(de)文章(zhāng)中，作者采用(yòng)了(le) bootstrap 的(de)方法，這(zhè)也(yě)是排除運氣的(de)一種思路。

從統計上來(lái)說，收益率在一月(yuè)份顯著和(hé)在某個(gè)沒有任何特殊意義的(de)連續 30 天内顯著并無區(qū)别；類似的(de)，收益率在春節後的(de)第一個(gè)交易日顯著和(hé)在一年中的(de)第 137 個(gè)交易日顯著也(yě)沒什(shén)麽不同。但是，在這(zhè)兩個(gè)比較中，人(rén)們會非常願意給前者找到“合理(lǐ)”的(de)解釋并相信它們是 calendar anomalies。一個(gè) calendar anomaly 是否真實存在并不取決于我們能否找出“合理(lǐ)”的(de)理(lǐ)由或講出“動聽(tīng)”的(de)故事，而是應基于嚴謹的(de)統計檢驗結果。市場(chǎng)中各種喜聞樂(yuè)見的(de) calendar anomalies，是否隻是建立在 multiple hypothesis testing 之上的(de)虛無？

參考文獻

Aharon, D. Y. and M. Qadan (2019). The size effect is alive and well, and hiding behind calendar anomalies. The Journal of Portfolio Management 45(6), 61 – 74.

Benjamini, Y. and Y. Hochberg (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society Series B 57, 289 – 300.

Benjamini, Y. and D. Yekutieli (2001). The control of the false discovery rate in multiple testing under Dependency. Annals of Statistics 29, 1165 – 1188.

Carchano, O. and A. Pardo Tornero. (2011). Calendar anomalies in stock index futures. Working paper.

Holm, S. (1979). A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics 6, 65 – 70.

McConnell, J. and W. Xu (2008). Equity returns at the turn of the month. Financial Analysts Journal 64(2), 49 – 64.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。