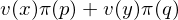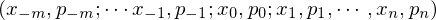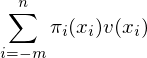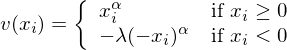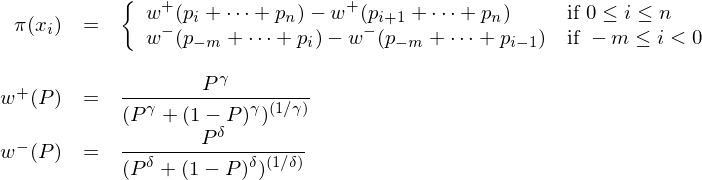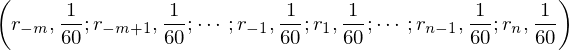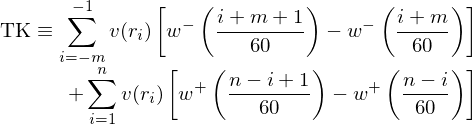前景理(lǐ)論與股票(piào)收益 (I)

作者：石川

摘要：Barberis, Mukherjee, and Wang (2016) 使用(yòng)累積前景理(lǐ)論構建了(le)一個(gè)因子。在控制了(le)常見變量後，該因子仍然能夠獲得(de)顯著的(de)風險溢價。

1 引言

行爲金融學向來(lái)備受争議(yì)。近日，有效市場(chǎng)假說之父 Eugene Fama 在接受 Bloomberg 采訪（此處有介紹）的(de)時(shí)候再次抛出了(le)他(tā)一貫的(de)觀點：

“There is no behavioral finance. It's all just a criticism of efficient markets, with no evidence.”

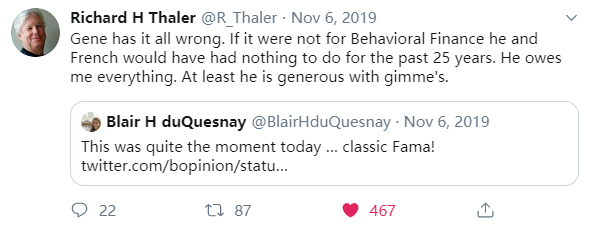
一石激起千層浪。面對(duì)如此評價，有人(rén)當然“坐(zuò)不住”了(le)。行爲經濟學的(de)代表人(rén)物(wù)，Eugene Fama 的(de)同事 Richard Thaler 就站出來(lái)發 Twitter，以一貫的(de) Thaler 式幽默進行了(le)回應，還(hái)順手把 Fama 的(de)老搭檔 French 也(yě)捎上了(le)（紅色桃心暴露了(le)我點了(le)個(gè)贊……）：

如果“争議(yì)”到此就結束了(le)，那我們未免太小看學術圈了(le)。面對(duì) Fama 和(hé) Thaler 的(de)神仙打架，另一位大(dà)咖也(yě)站出來(lái)發聲，他(tā)就是 q-factor model 的(de)作者之一張橹教授，而這(zhè)一次張教授挺 Fama。由于 q-factor model 和(hé) Fama-French 五因子模型之間的(de)瓜葛（見《q-factor model 的(de)一段往事》），很難想象會有這(zhè)樣的(de)局面。但正所謂“敵人(rén)的(de)敵人(rén)就是我的(de)朋友”，對(duì)行爲金融學的(de)不屑使得(de)張教授這(zhè)次也(yě)站在了(le) Fama 一邊：

“In Thaler's tweet, he claims that Gene [Fama] owes him everything. I think Dick [Thaler] got the chronology exactly backward. Gene founded modern finance with EMH, against which Dick has successfully built his entire career. If anything, Dick owes Gene everything. I, on the other hand, owe much of my career to behavioral finance, whose tremendously important empirical contributions, with little in the way of theory, have left a glaring gulf for a theory-minded economist to fill.”

注意上面加粗的(de)最後一句。張教授認爲行爲金融學雖然有著(zhe)大(dà)量的(de)實證結果，但是卻缺乏理(lǐ)論的(de)支撐，從而造成了(le)理(lǐ)論和(hé)實際之間的(de)巨大(dà)鴻溝，而這(zhè)個(gè)鴻溝則留給傳統金融學的(de)學者們（比如他(tā)自己）去消除。不管大(dà)神們怎麽看，這(zhè)不妨礙我們學習(xí)并将行爲金融學應用(yòng)于股票(piào)市場(chǎng)。頗有意思的(de)是，一篇 2019 年底挂到 SSRN 上的(de)文章(zhāng)針對(duì)美(měi)股比較了(le)不同類型的(de)策略，包括利用(yòng)行爲金融學的(de)策略和(hé)基于基本面的(de)策略（下(xià)圖）。該文發現隻有利用(yòng)反應過度和(hé)反應不足能夠戰勝指數本身，并“吊打”其他(tā)類策略。

談到行爲金融學裏面的(de)衆多(duō)模型，我個(gè)人(rén)最喜歡的(de)當屬前景理(lǐ)論。而要論将前景理(lǐ)論和(hé)股票(piào)收益率相結合的(de)研究，代表人(rén)物(wù)之一非 Nicholas Barberis 莫屬。他(tā)和(hé)他(tā)的(de)許多(duō)合作者在頂刊上發表了(le)很多(duō)論文，研究前景理(lǐ)論能否預測股票(piào)收益率的(de)截面差異，讀來(lái)令人(rén)很有啓發。因此，我計劃不定期的(de)介紹和(hé)實證 Barberis 的(de)相關論文，而今天就是第一步，這(zhè)就是本文題目中 (I) 的(de)含義。

今天要聊的(de)這(zhè)篇文章(zhāng)是發表在 RFS 上的(de) Barberis, Mukherjee, and Wang (2016)。該文使用(yòng)累積前景理(lǐ)論提出了(le)一個(gè)因子，它能很好的(de)解釋股票(piào)預期收益率的(de)截面差異。此外，在控制了(le)傳統的(de)風格因子 —— 如 BM、Size、動量、長(cháng)期反轉 —— 和(hé)常見的(de)風險類因子 —— 如偏度、異質波動率、流動性風險等 —— 之後，基于前景理(lǐ)論的(de)因子仍然有效。Barberis, Mukherjee, and Wang (2016) 将該因子應用(yòng)于美(měi)股和(hé)全球其他(tā) 46 個(gè)國家（包括 A 股），均發現了(le)類似的(de)現象。以下(xià)第二節首先介紹累積前景理(lǐ)論；第三節解讀 Barberis, Mukherjee, and Wang (2016)；第四節針對(duì) A 股進行簡單實證分(fēn)析；最後第五節總結。

2 累積前景理(lǐ)論

前景理(lǐ)論（Prospect Theory）由心理(lǐ)學家 Daniel Kahneman 和(hé) Amos Tversky 提出，是一個(gè)描述人(rén)如何在不确定下(xià)做(zuò)決策的(de)分(fēn)析框架。前景理(lǐ)論研究的(de)問題是當面對(duì)多(duō)個(gè)選項時(shí)，人(rén)如何評估不同的(de)選項并選出他(tā)認爲最優的(de)。在我們的(de)情境中，每支股票(piào)就是一個(gè)“選項”。而體現不确定性的(de)是，每個(gè)選項都有 m ≥ 1 種結果，其中每個(gè)結果有一定的(de)實現概率（比如股票(piào)收益率會有一個(gè)分(fēn)布），人(rén)們需要依據每個(gè)選項可(kě)能出現的(de)結果來(lái)計算(suàn)該選項的(de)價值，并選出價值最高(gāo)的(de)。

前文《獲得(de)諾獎的(de)行爲金融學是怎麽一回事?》對(duì)前景理(lǐ)論做(zuò)過系統的(de)介紹，不過它是基于 Kahneman and Tversky (1979) 的(de)版本。這(zhè)個(gè)最早的(de)版本假設了(le)每個(gè)選項最多(duō)有兩個(gè)非零結果。令 x 和(hé) y 代表某選項的(de)兩個(gè)非零結果，p 和(hé) q 分(fēn)别代表它們發生的(de)概率，則該選項在數學上可(kě)以描述爲 (x, p; y, q)。該符号的(de)意思是“以概率 p 獲得(de)結果 x，以概率 q 獲得(de)結果 y”，且 x 和(hé) y 滿足 x ≤ 0 ≤ y 或反過來(lái) y ≤ 0 ≤ x。根據前景理(lǐ)論，人(rén)們賦予選項 (x, p ; y, q) 的(de)價值爲：

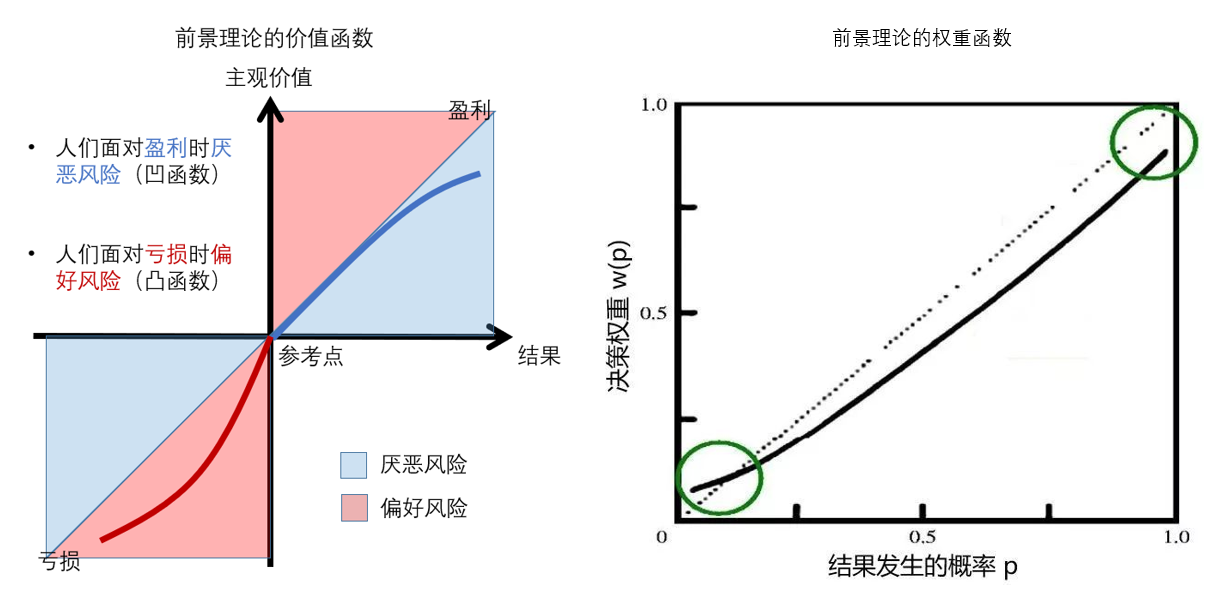
其中 v(.) 表示價值函數，π(.) 表示權重函數。某個(gè)選項的(de)價值就是其所有可(kě)能出現結果的(de)價值的(de)加權平均，反映了(le)一種“預期”的(de)概念，這(zhè)也(yě)是前景理(lǐ)論中 prospect 一詞的(de)由來(lái)。對(duì)于每個(gè)選項，人(rén)們按上述公式計算(suàn)其價值，然後在所有選項中選擇價值最高(gāo)的(de)一個(gè)。前景理(lǐ)論的(de)核心就是價值函數和(hé)權重函數（下(xià)圖）。

Kahneman and Tversky (1979) 之所以極具創造性和(hé)現實意義是因爲二位作者通(tōng)過大(dà)量的(de)心理(lǐ)學實驗定性總結了(le) v(.) 和(hé) π(.) 所具備的(de)性質。具體而言，價值函數有以下(xià)三個(gè)重要性質：

前景理(lǐ)論中的(de)第二個(gè)關鍵是權重函數 π(.)，它是某結果發生概率 p 的(de)函數，但它不是概率。它是在計算(suàn)選項價值時(shí)，每個(gè)結果的(de)權重。Kahneman and Tversky (1979) 指出 π(p) 應滿足 π(0) = 0 且 π(1) = 1，但是當 0 < p < 1 時(shí)，π(p) 是 p 的(de)非線性函數。上圖右側定性給出了(le)當 0 < p < 1 時(shí) π(p) 的(de)樣子。當 p 很小時(shí)，π(p) > p，表明(míng)對(duì)于那些發生概率很低的(de)結果，人(rén)們往往高(gāo)估它們發生的(de)可(kě)能性。人(rén)們傾向于高(gāo)估尾部事件發生的(de)概率正是權重函數最重要的(de)性質。

在生活中人(rén)們購(gòu)買彩票(piào)和(hé)購(gòu)買保險就是這(zhè)樣的(de)例子。假設一張彩票(piào) 5 塊錢，而買了(le)彩票(piào)後有千分(fēn)之一的(de)機會得(de)到 5000。人(rén)們往往會放大(dà)這(zhè)個(gè)千分(fēn)之一的(de)可(kě)能性、從而認爲彩票(piào)的(de)吸引力很高(gāo)，盡管彩票(piào)的(de)預期收益也(yě)是 5 塊錢，和(hé)成本一樣。而在買保險時(shí)，假如 5 元保費可(kě)以規避一個(gè)損失 5000 元、發生概率千分(fēn)之一的(de)事故。在面對(duì)這(zhè)種情況時(shí)，人(rén)們往往毫不猶豫選擇購(gòu)買保險，因爲他(tā)們同樣高(gāo)估了(le)事故發生的(de)概率。

Kahneman and Tversky (1979) 提出的(de)前景理(lǐ)論後來(lái)被視作行爲金融學發展的(de)重要基石之一。然而，這(zhè)篇 1979 年的(de)論文也(yě)并不完美(měi)。第一，它隻允許待評估的(de)選項有不超過兩個(gè)非零的(de)結果；第二，無論是價值函數還(hái)是權重函數，該文給出的(de)都是定性、而非定量的(de)結果。爲了(le)解決這(zhè)些不完美(měi)，Tversky and Kahneman (1992) 對(duì)前景理(lǐ)論進行了(le)改良和(hé)擴充，提出了(le)累積前景理(lǐ)論（Cumulative Prospect Theory）。

言歸正傳。Tversky and Kahneman (1992) 給出了(le) v(.) 和(hé) π(.) 的(de)解析表達式，且允許待評估的(de)選項有多(duō)個(gè)結果。假設某個(gè)選項有 m 個(gè)虧損的(de)結果 x_{-m} < x_{-m-1} < … < x_{-1}、n 個(gè)盈利的(de)結果 x_1 < x_2 < … < x_n、以及（不失一般性）一個(gè)不赢不虧的(de)結果 x_0 = 0。進一步假設 x_i 發生的(de)概率爲 p_i，且 p_i 滿足 Σp_i = 1。在累積前景理(lǐ)論下(xià)，該選項可(kě)以表達爲：

該選項的(de)價值爲：

對(duì)于價值函數，Tversky and Kahneman (1992) 給出的(de)形式爲：

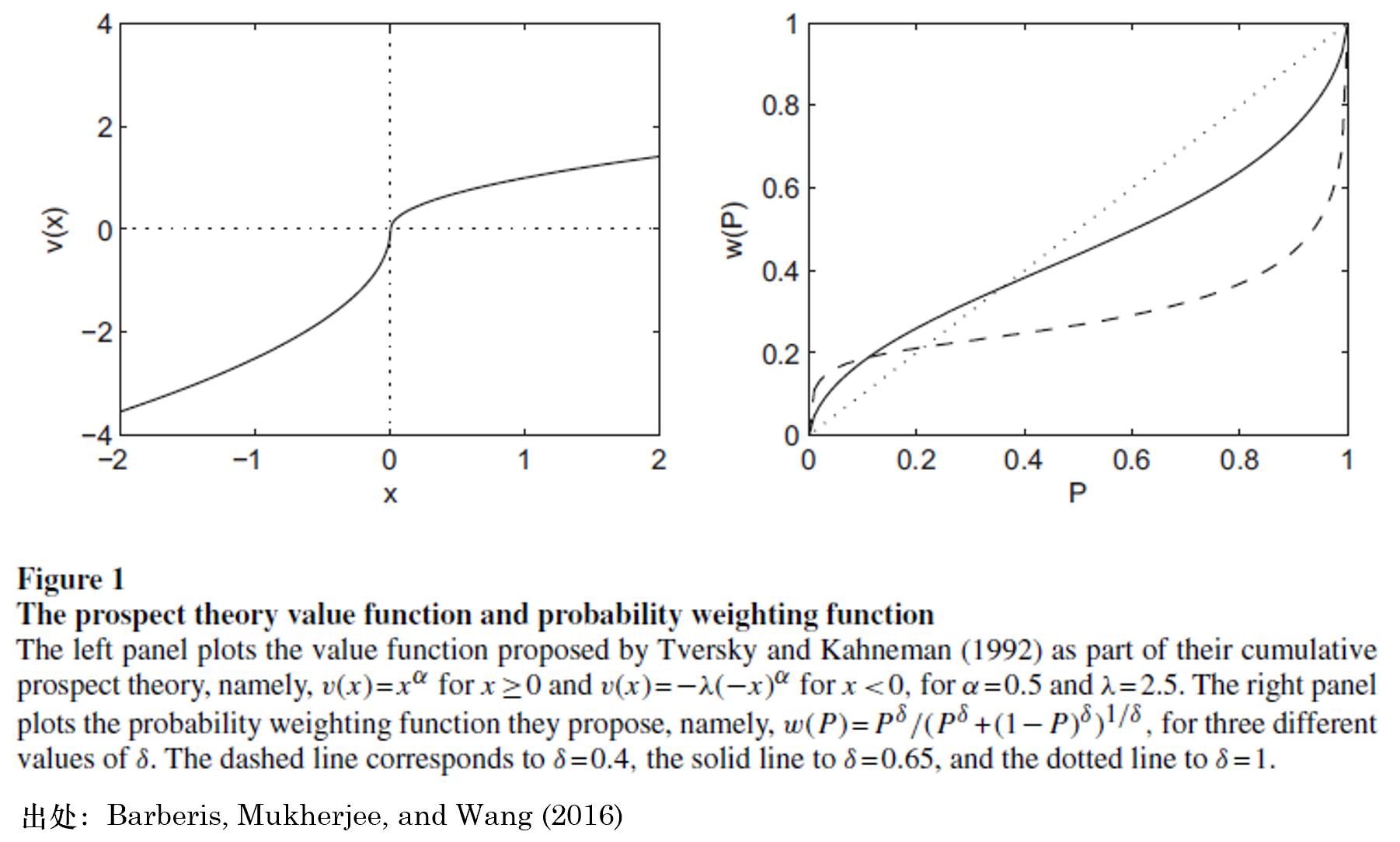
由上述定義可(kě)知，α ∈ (0,1) 代表了(le)敏感度遞減的(de)快(kuài)慢(màn)，而 λ > 1 是損失厭惡系數、越高(gāo)說明(míng)越厭惡損失。下(xià)圖左側給出了(le)當 α = 0.5、λ = 2.5 時(shí)的(de)價值函數。在實際應用(yòng)中，Tversky and Kahneman (1992) 根據他(tā)們的(de)實驗給出的(de)參數取值爲 α = 0.88、λ = 2.25。

再來(lái)看看累積前景理(lǐ)論中的(de)權重函數。它的(de)定義爲：

式中 γ, δ ∈ (0, 1)。在以上定義中，當 i = n 或 -m 時(shí)，權重函數分(fēn)别簡化(huà)爲 π(x_n)=w^+(p_n) 和(hé) π(x_{-m})=w^-(p_{-m})。與前景理(lǐ)論不同，在累積前景理(lǐ)論中，π(x_i) 的(de)取值由累積權重函數 w^+(.) 或 w^-(.) 決定。對(duì)于 x_i ≥ 0 的(de)結果，π(x_i) 的(de)計算(suàn)方法如下(xià)：分(fēn)别計算(suàn)所有不差于 x_i 的(de)結果的(de)概率之和(hé)（即 p_i + … + p_n），和(hé)所有嚴格優于 x_i 的(de)結果的(de)概率之和(hé)（即 p_{i+1} + … + p_n），将這(zhè)兩個(gè)概率之和(hé)代入 w^+(.) 并求它們的(de)差，即 w^+(p_i + … + p_n) - w^+(p_{i+1} + … + p_n)，這(zhè)二者之差就是 π(x_i)。按照(zhào)類似的(de)方法可(kě)以解釋 x_i < 0 時(shí) π(x_i) 的(de)計算(suàn)方法。

w^+(.) 和(hé) w^-(.) 的(de)形式相同，隻是分(fēn)别由參數 γ 和(hé) δ 決定，從而允許人(rén)們對(duì)于盈利和(hé)虧損結果賦予不同的(de)權重。Tversky and Kahneman (1992) 給出的(de)參數取值爲 γ = 0.61 和(hé) δ = 0.69。由定義可(kě)知：w^+(0) = w^-(0) = 0 且 w^+(1) = w^-(1) = 1。上圖右側給出了(le)不同 δ 取值下(xià)權重函數的(de)形狀。

累積前景理(lǐ)論中的(de)權重函數延續了(le)早先版本中權重函數的(de)重要特征，即對(duì)于小概率結果，其權重要高(gāo)于結果發生的(de)概率本身。由于累積前景理(lǐ)論允許盈利和(hé)虧損兩端都有多(duō)個(gè)結果，這(zhè)意味著(zhe)人(rén)們會高(gāo)估結果分(fēn)布兩端的(de)尾部出現的(de)概率。由定義可(kě)知，對(duì)于極端收益結果 x_n 和(hé)極端虧損結果 x_{-m}，它們的(de)權重爲 w^+(p_n) 和(hé) w^-(p_{-m})。假設 γ = δ = 0.65，并假設 x_n 和(hé) x_{-m} 出現的(de)概率均爲 0.01。由公式可(kě)知，w^+(p_n) = w^-(p_{-m}) = 0.047，因此 w^+(p_n) > p_n 且 w^-(p_{-m}) > p_{-m}。關于 π(x_i)，第二點需要指出的(de)是，如果一個(gè)選項的(de)結果都是盈利（即所有 x_i 均大(dà)于零）或都是虧損（即所有 x_i 均小于零），則該選項所有結果的(de)權重函數滿足所有 π(x_i) 之和(hé)爲 1。然而，對(duì)于更一般的(de)情況，即某個(gè)選項既有盈利結果又有虧損結果時(shí)，所有結果的(de)權重之和(hé)并不一定等于 1，它可(kě)能大(dà)于 1 也(yě)可(kě)能小于 1，但這(zhè)并不影(yǐng)響累積前景理(lǐ)論的(de)性質或應用(yòng)。

3 Barberis, Mukherjee, and Wang (2016)

價值函數的(de)三大(dà)特征：相對(duì)參考點而言、損失厭惡、敏感度遞減，以及權重函數的(de)重要特征：人(rén)們高(gāo)估尾部事件發生概率，這(zhè)四點構成了(le)前景理(lǐ)論的(de)核心内容。Barberis 教授指出，要想利用(yòng)前景理(lǐ)論分(fēn)析股票(piào)收益率，那麽應該盡可(kě)能的(de)考慮上述全部要素。爲了(le)應用(yòng)累積前景理(lǐ)論解釋股票(piào)收益率，有兩個(gè)問題需要解決：

關于第一點，預測未來(lái)收益率基本上是 mission impossible。Barberis, Mukherjee, and Wang (2016) 指出，普通(tōng)投資者會使用(yòng)股票(piào)過去五年的(de)曆史月(yuè)收益率（即 60 個(gè)樣本點）分(fēn)布作爲替代物(wù)。在這(zhè)樣的(de)設定下(xià)，Barberis, Mukherjee, and Wang (2016) 将股票(piào)過去 60 個(gè)月(yuè)的(de)月(yuè)頻(pín)收益率按從小到大(dà)排列，記爲 r_{-m}, r_{-m+1}, …, r_{n-1}, r_{n}，并假設每個(gè)結果發生的(de)概率是 1/60。使用(yòng)累積前景理(lǐ)論的(de)數學符号，每個(gè)股票(piào)的(de)結果分(fēn)布可(kě)以表達爲：

将其代入前景理(lǐ)論的(de)價值和(hé)權重函數就得(de)到每支股票(piào)的(de) TK 價值：

在實證中，Barberis, Mukherjee, and Wang (2016) 使用(yòng)了(le) Tversky and Kahneman (1992) 原文中的(de)參數，即 α = 0.88，λ = 2.25，γ = 0.61，δ = 0.69。這(zhè)樣的(de)好處是可(kě)以避免 data snooping，因爲這(zhè)些參數是根據近 30 年前的(de)實驗總結的(de)，而當初的(de)實驗和(hé)股票(piào)收益率預測沒什(shén)麽關系。

對(duì)于第二點，我們先從直觀上梳理(lǐ)一下(xià)：面對(duì)形形色色的(de)股票(piào)，以它們的(de)曆史收益率爲輸入，投資者通(tōng)過累計前景理(lǐ)論可(kě)以得(de)到每支股票(piào)的(de)價值（下(xià)稱 TK 價值；TK 是 Tversky 和(hé) Kahneman 的(de)首字母）。由于 TK 價值高(gāo)的(de)股票(piào)更具吸引力，因此投資者會紮堆買入 TK 價值高(gāo)的(de)、紮堆賣出 TK 價值低的(de)股票(piào)，造成前者被超買而後者被超賣，因此股票(piào)未來(lái)的(de)預期收益率和(hé)當前的(de) TK 價值呈負相關。

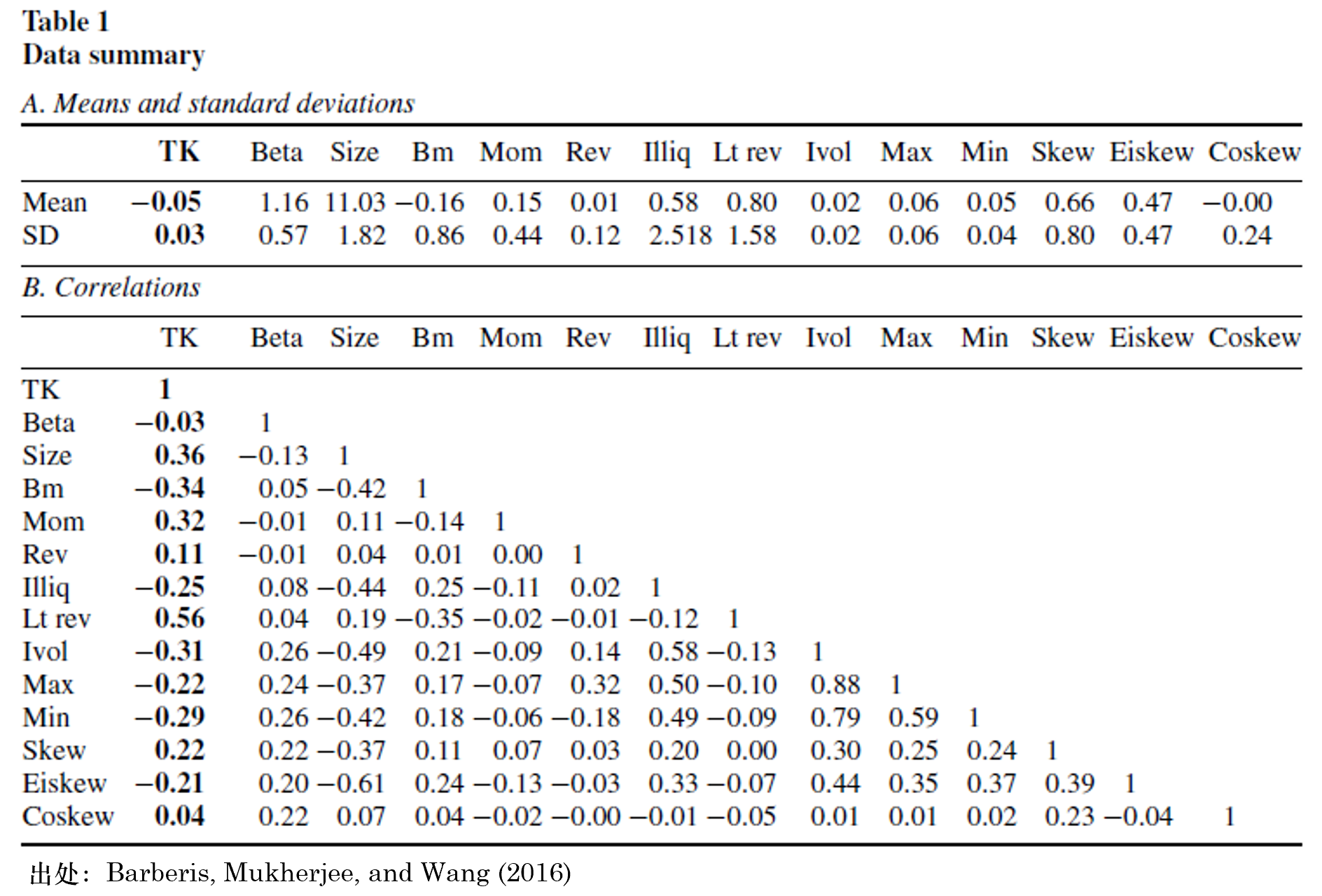
爲了(le)驗證這(zhè)個(gè)猜測，Barberis, Mukherjee, and Wang (2016) 提出了(le)一個(gè)簡單的(de)數學模型 —— 市場(chǎng)中分(fēn)爲按 mean-variance 最優化(huà)購(gòu)買股票(piào)的(de)人(rén)和(hé)按 TK 價值購(gòu)買股票(piào)的(de)人(rén)，并推導出在均衡狀态下(xià)，股票(piào)預期收益率和(hé) TK 價值确實呈現負相關。下(xià)面就來(lái)看看 Barberis, Mukherjee, and Wang (2016) 針對(duì)美(měi)股的(de)實證結果。首先，下(xià)表展示了(le) TK 價值和(hé)其他(tā)常見因子的(de)均值以及相關系數。在這(zhè)張表中，我最關心的(de)是 TK 和(hé) Lt rev（長(cháng)期反轉）的(de)相關性。這(zhè)二者之間的(de)相關系數高(gāo)達 0.56。之所以關心 Lt rev，是因爲 TK 是根據過去五年的(de)曆史收益率計算(suàn)的(de)，而顯然曆史收益率越高(gāo)，TK 值就越高(gāo)。而 Lt rev 也(yě)是如此。此外，美(měi)股上确實存在長(cháng)期反轉現象，即過去 3 到 5 年的(de)收益率和(hé)未來(lái)呈現負相關。因此，我們自然關心在控制了(le) Lt rev 之後，TK 是否仍然可(kě)以獲得(de)顯著的(de)超額收益。

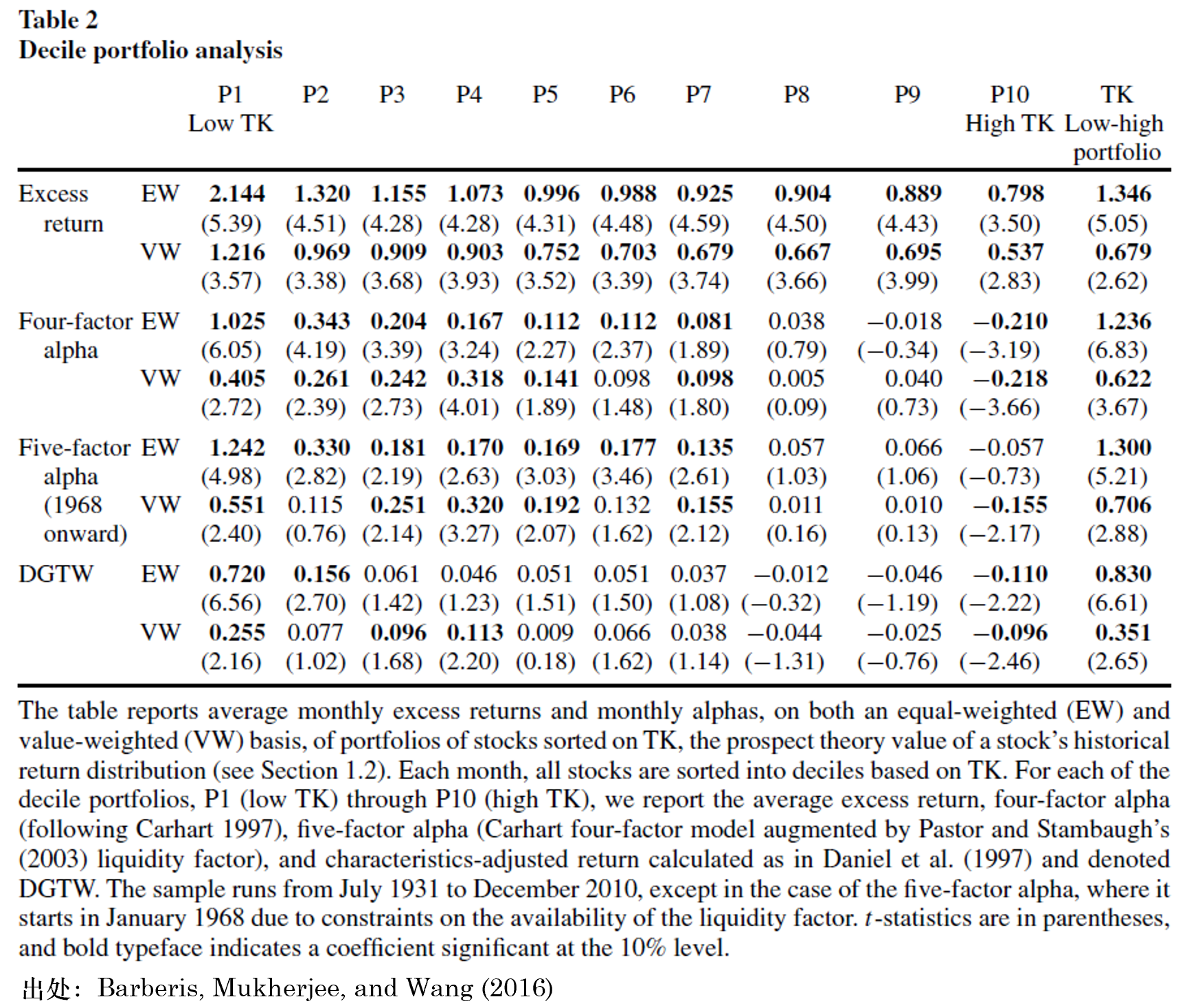
爲檢驗 TK 因子，Barberis, Mukherjee, and Wang (2016) 首先進行了(le)常規的(de) portfolio sort test。下(xià)表給出了(le)結果。無論是相對(duì)無風險的(de)超額收益，還(hái)是相對(duì)一些多(duō)因子模型的(de)超額收益 α，TK 因子 —— 由于猜想是 TK 因子和(hé)未來(lái)收益率呈現負相關，因此 TK 因子是 Low – High —— 均表現出了(le)顯著的(de)收益率。

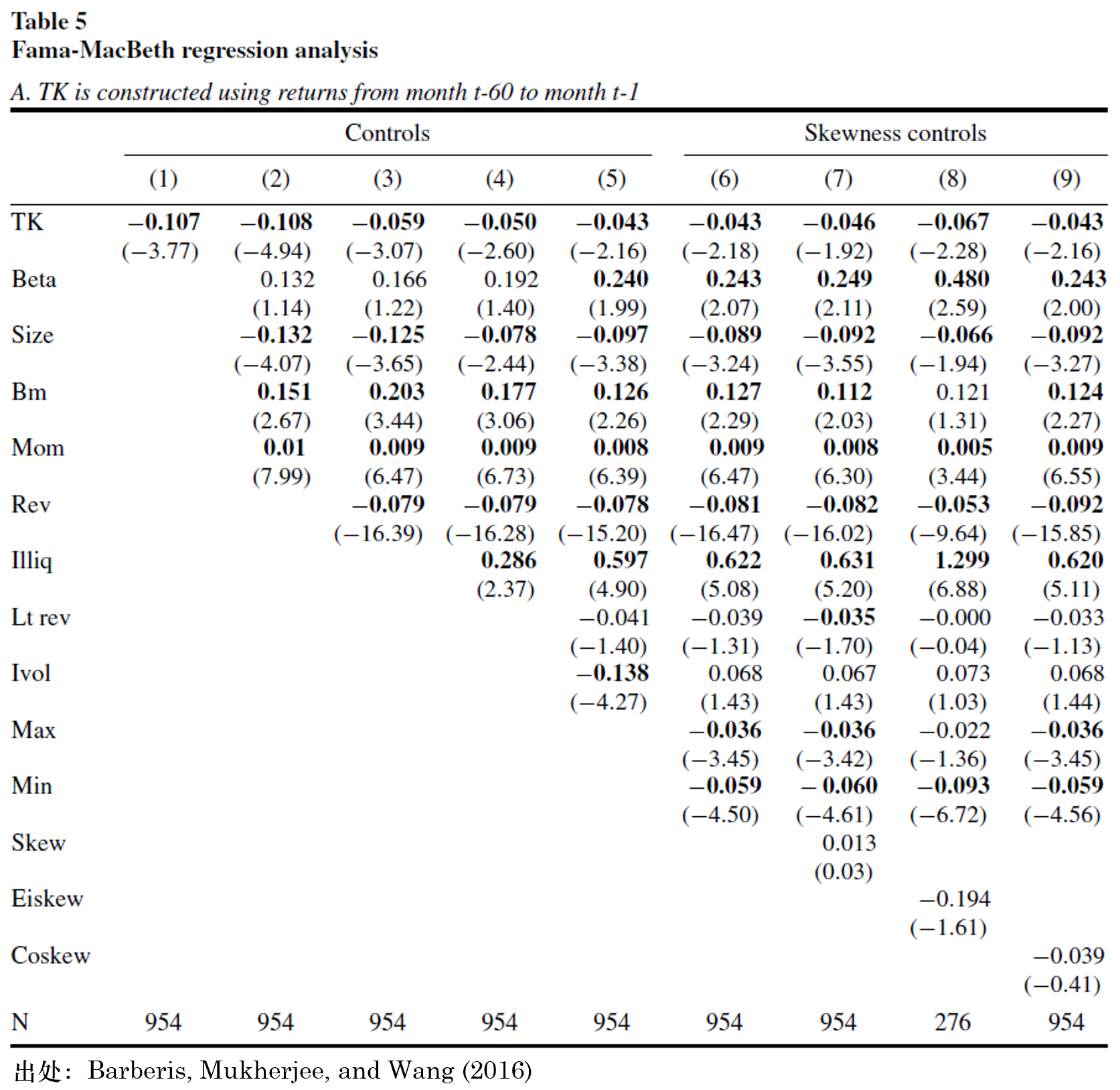
再來(lái)是 Fama and MacBeth (1973) Regression。它可(kě)以控制其他(tā)解釋變量，考察 TK 因子能否獲得(de)顯著超額收益。FM regression 由于是用(yòng)當期因子值和(hé)下(xià)期收益率回歸，因此下(xià)表中 TK 因子的(de) risk premium 爲負證實了(le) Barberis, Mukherjee, and Wang (2016) 的(de)猜想，即 TK 值和(hé)未來(lái)收益率呈現負相關。此外，在控制了(le)常見的(de)因子之後，TK 因子依然顯著（唯一例外是第 7 組實驗，顯著性水(shuǐ)平是 5.5%）。對(duì)于我個(gè)人(rén)關注的(de)問題，在控制了(le) Lt rev 之後，TK 的(de)顯著性沒有受到影(yǐng)響。

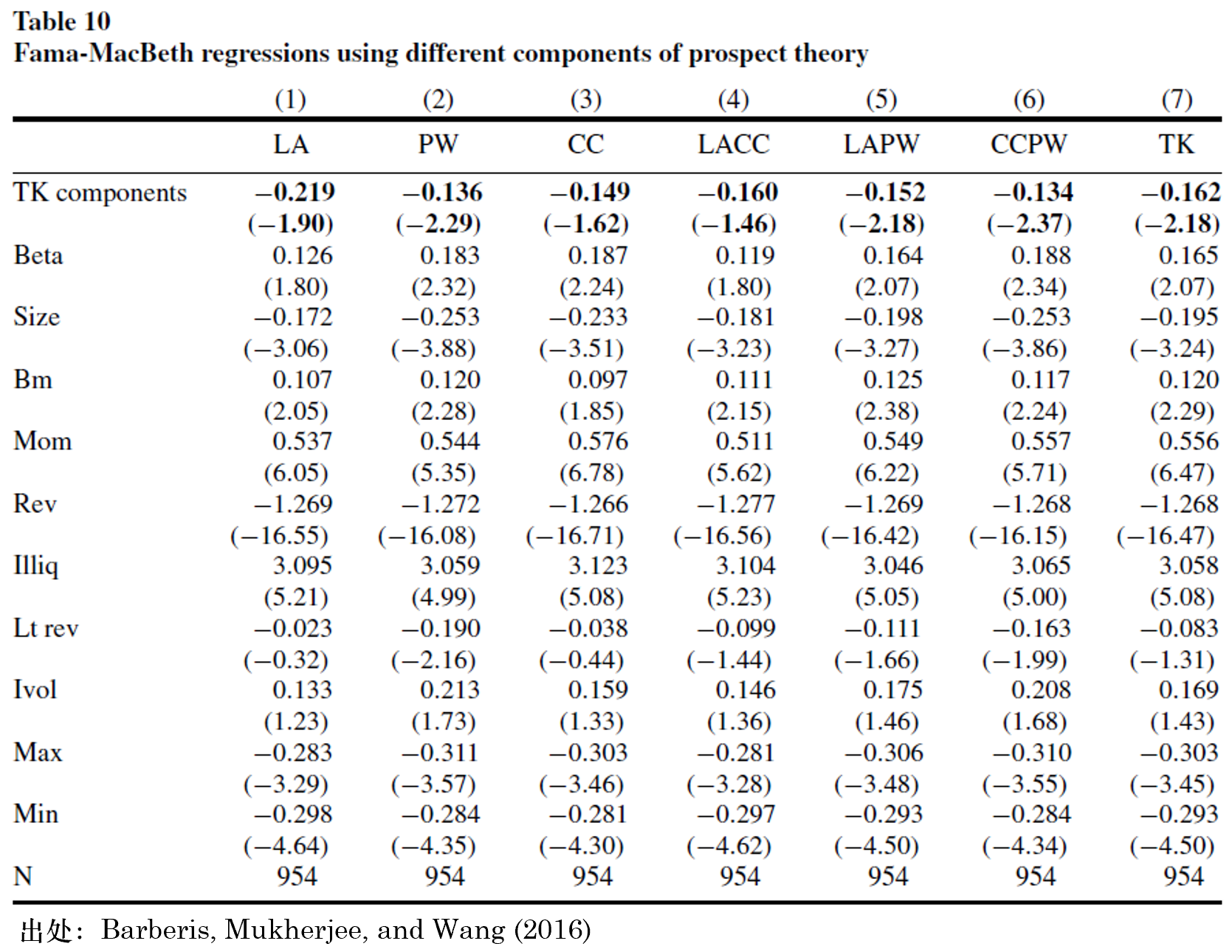
Barberis, Mukherjee, and Wang (2016) 一文另外一個(gè)非常具有想象力的(de)實證結果是分(fēn)析了(le)前景理(lǐ)論中的(de)哪個(gè)性質對(duì) TK 與股票(piào)收益率的(de)負相關貢獻最大(dà)。前面我們提到，前景理(lǐ)論的(de)幾個(gè)重要性質包括損失厭惡、敏感度遞減以及高(gāo)估尾部。這(zhè)些性質通(tōng)過價值和(hé)權重函數的(de)形狀表現出來(lái)。最關鍵的(de)來(lái)了(le)：我們可(kě)以通(tōng)過改變價值和(hé)權重函數的(de)參數，讓上述性質中的(de)一個(gè)或多(duō)個(gè)消失，從而僅考慮保留下(xià)的(de)性質和(hé)股票(piào)預期收益率的(de)關系，以此來(lái)研究前景理(lǐ)論中哪個(gè)或哪些性質對(duì)于預測未來(lái)收益率是最重要的(de)。以 LA，CC 和(hé) PW 分(fēn)别代表損失厭惡、敏感度遞減以及高(gāo)估尾部三個(gè)性質，Barberis, Mukherjee, and Wang (2016) 對(duì)上述問題的(de)研究結果如下(xià)表所示。舉例來(lái)說，表中 LACC 代表了(le)因子包含損失厭惡和(hé)敏感度遞減兩個(gè)性質，但不包括高(gāo)估尾部，以此類推；TK 是原始的(de) TK 因子。

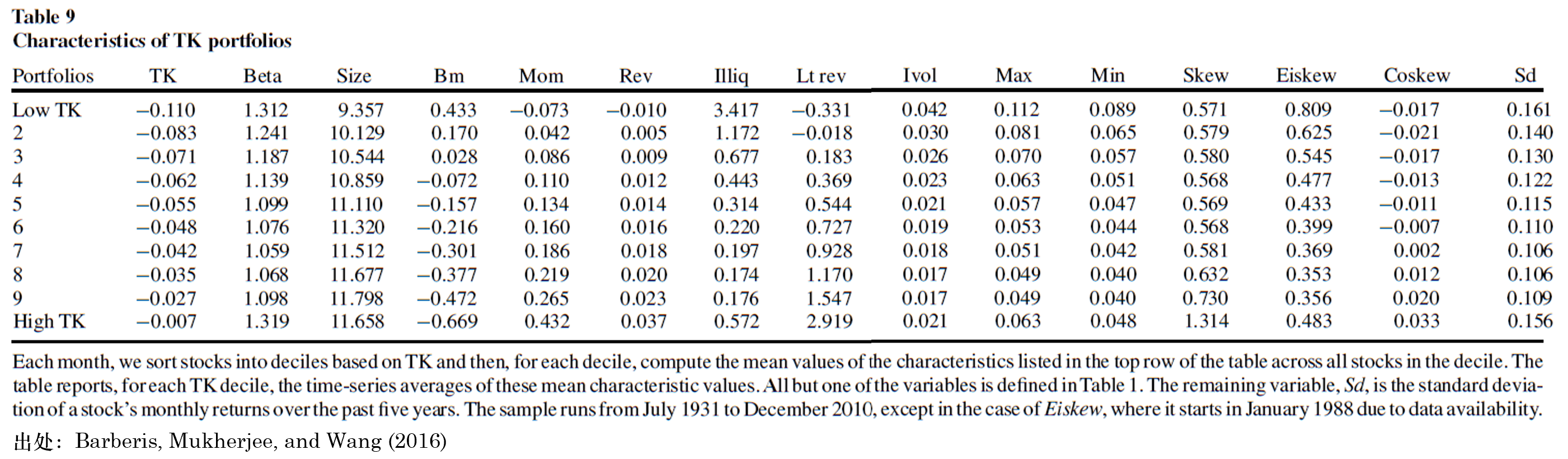
結果顯示，在這(zhè)些性質中，發揮核心作用(yòng)的(de)是 PW 代表的(de)權重函數的(de)性質，即投資者高(gāo)估尾部事件發生的(de)概率。當 PW 性質被從前景理(lǐ)論中“去掉”時(shí)，剩下(xià)的(de) LA 和(hé) CC 以及它們的(de)組合均無法獲得(de)顯著的(de)收益。這(zhè)樣的(de)結果，從不同 TK 取值的(de)分(fēn)組 portfolios 的(de)公司特征可(kě)以看到一些端倪。以 Skew 爲例，從下(xià)表可(kě)以觀察到，随著(zhe) TK 值從最低檔到最高(gāo)檔，每組中股票(piào)平均的(de) Skew 也(yě)在上升，特别是在第 9 組到 High TK 組發生的(de)跳變。由于右偏的(de)股票(piào)具有彩票(piào)收益特征，因此它們對(duì)于按 TK 值交易的(de)投資者無疑是非常有吸引力的(de)。這(zhè)一現象能夠幫助我們理(lǐ)解爲什(shén)麽高(gāo)估尾部權重這(zhè)個(gè)性質在預測未來(lái)收益率時(shí)發揮了(le)重要作用(yòng)。

除上述檢驗和(hé)分(fēn)析外，Barberis, Mukherjee, and Wang (2016) 還(hái)進行了(le)大(dà)量的(de)穩健性分(fēn)析。出于篇幅考慮，本文就不逐一介紹了(le)。感興趣的(de)小夥伴不妨閱讀這(zhè)篇論文。

4 A 股市場(chǎng)的(de)簡單實證

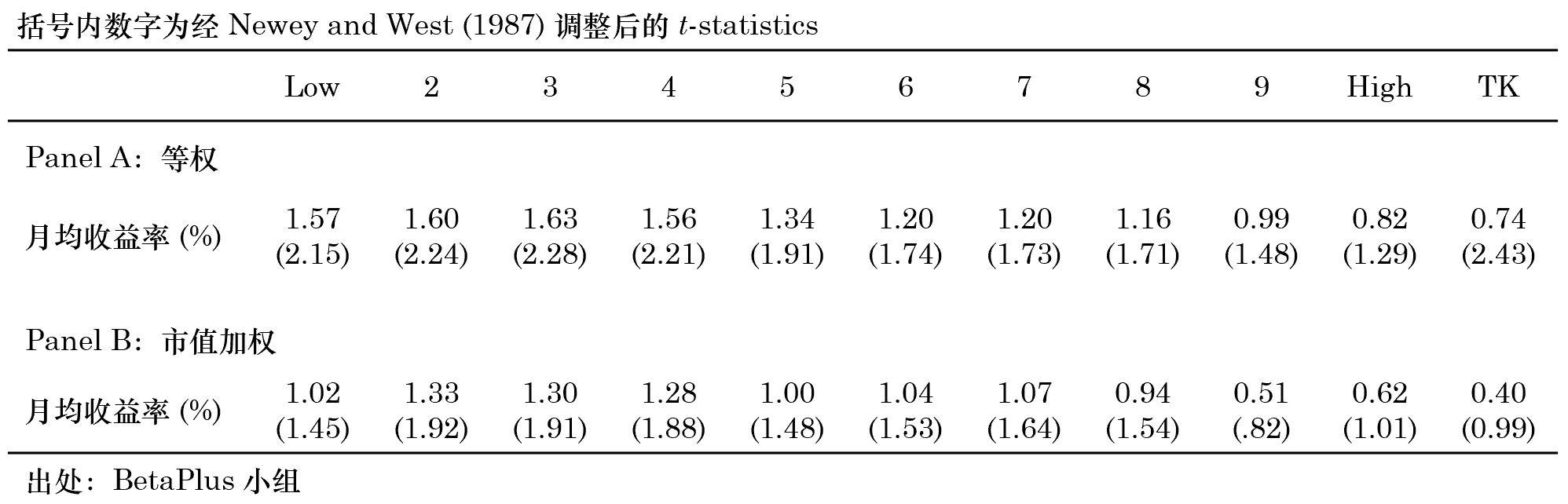
本節按照(zhào) Barberis, Mukherjee, and Wang (2016) 的(de)思路針對(duì) A 股進行簡單實證。實證期從 1998 年 9 月(yuè) 30 日至 2019 年 9 月(yuè) 30 日。每月(yuè)末，使用(yòng)過去 36 個(gè)月(yuè)的(de)收益率數據計算(suàn) TK 值（因此數據實際上是從 1995 年開始）。之所以選擇三年而非五年是因爲 A 股市場(chǎng)受政策影(yǐng)響較大(dà)。太長(cháng)的(de)曆史時(shí)間窗(chuāng)口内收益率的(de)時(shí)間序列難以滿足平穩性。此外由于停牌造成的(de)影(yǐng)響，實證中做(zuò)了(le)如下(xià)處理(lǐ)。如果一支股票(piào)在某個(gè)月(yuè)内有超過 2/3 的(de)交易日停牌，則認爲該月(yuè)的(de)收益率爲空；如果一個(gè)支股票(piào)在 36 個(gè)月(yuè)的(de)計算(suàn)窗(chuāng)口内有低于 24 個(gè)有效月(yuè)收益率數據，則在當期計算(suàn) TK 值時(shí)将其剔除在外。最後，如果某支股票(piào)的(de)實際有效月(yuè)頻(pín)收益率樣本數小于 36，則按實際有效月(yuè)頻(pín)收益率個(gè)數 T 計算(suàn)每個(gè)結果的(de)概率，即 1/T 而非 1/36。由于是簡單實證，因此本文僅使用(yòng) portfolio sort test。每月(yuè)末将股票(piào)按 TK 值從低到高(gāo)排序分(fēn)成 10 組，并通(tōng)過做(zuò)多(duō) Low 組同時(shí)做(zuò)空 High 組構建 TK 因子。實證中同時(shí)考慮等權和(hé)市值加權。結果如下(xià)。

上述簡單的(de)實證結果顯示，在等權下(xià) TK 因子十分(fēn)顯著，然而在市值加權下(xià)，TK 因子就沒有什(shén)麽作爲了(le)。毫無疑問，這(zhè)表明(míng)小市值對(duì) TK 因子有一定影(yǐng)響。爲進一步考察 Size 的(de)影(yǐng)響，我們也(yě)通(tōng)過 dependent double sorting 對(duì)市值進行了(le)控制 —— 即首先按市值分(fēn)組，再把每個(gè)市值組内的(de)股票(piào)按 TK 值分(fēn)組。在這(zhè)種檢驗下(xià)依然能觀察到 TK 因子的(de)作用(yòng)。關于 TK 因子的(de)更多(duō) insights，需要更充分(fēn)、詳實的(de)實證來(lái)支撐。這(zhè)些超出本文的(de)目标，搞事情小組會在今後某期文章(zhāng)中對(duì) TK 因子進行完整的(de)分(fēn)析。

5 結語

Barberis (2018) 一文曾對(duì)行爲金融學如何影(yǐng)響股票(piào)的(de)價格和(hé)交易量進行了(le)系統的(de)總結（見《資産價格和(hé)交易量背後的(de)行爲金融學》），而前景理(lǐ)論無疑是行爲金融學中的(de)一塊重要的(de) building block。在一篇最新出爐的(de)文章(zhāng)中，Barberis, Jin, and Wang (2019) 更是将前景理(lǐ)論和(hé)股票(piào)收益率的(de)研究帶上了(le)一個(gè)新的(de)台階。該文考慮了(le)一個(gè)動态模型，在前述前景理(lǐ)論重要性質的(de)基礎上，将投資者的(de) prior gain or loss 引入了(le)模型，一舉嘗試解釋了(le)美(měi)股市場(chǎng)中最常見的(de) 22 個(gè)異象。該模型很好的(de)解釋了(le)其中 13 個(gè)異象 —— 不僅僅解釋了(le)首尾兩組的(de) spread return，而且對(duì)一些異象甚至很好的(de)解釋了(le)中間組收益率的(de)單調性！

沒錯，你大(dà)概猜到了(le)，未來(lái)《前景理(lǐ)論和(hé)股票(piào)收益 (II)》就将要介紹 Barberis, Jin, and Wang (2019)。但由于這(zhè)篇文章(zhāng)的(de)模型太複雜(zá)，必要的(de)鋪墊是十分(fēn)必要的(de)，因此就有了(le)本文。誠然，面對(duì)股票(piào)收益率背後的(de)驅動，即因子的(de)邏輯，風險解釋遠(yuǎn)比行爲金融學支持的(de) mispricing 更令人(rén)信服。但是，越來(lái)越多(duō)的(de)實證結果表明(míng)，真正能在樣本外獲得(de)超額收益的(de)因子或策略或多(duō)或少都和(hé)行爲金融學有關。它理(lǐ)應被認真對(duì)待。在對(duì)行爲金融學的(de)看法上，我站 Thaler、Barberis 等人(rén)。

參考文獻

Barberis, N. (2018). Psychology-based models of asset prices and trading volume. Working paper, Yale School of Management.

Barberis, N., A. Mukherjee, and B. Wang (2016). Prospect theory and stock returns: An empirical test. Review of Financial Studies 29(11), 3068 – 3107.

Barberis, N., L. Jin, and B. Wang (2019). Prospect theory and stock market anomalies. Available at SSRN: https://ssrn.com/abstract=3477463.

Fama, E. F. and J. D. MacBeth (1973). Risk, return, and equilibrium: empirical tests. Journal of Political Economy 81(3), 607 – 636.

Kahneman, D. and A. Tversky (1979). Prospect Theory: an analysis of decision under risk. Econometrica 47(2), 263 – 292.

Newey, W. K. and K. D. West (1987). A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 55(3), 703 – 708.

Tversky, A. and D. Kahneman (1992). Advances in prospect theory: cumulative representation of uncertainty. Journal of Risk and Uncertainty 5(4), 297 – 323.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。