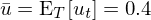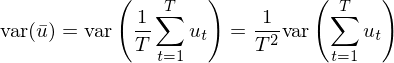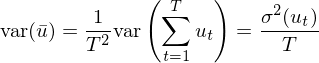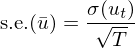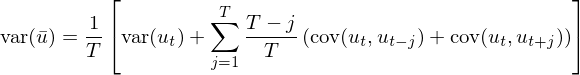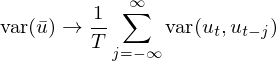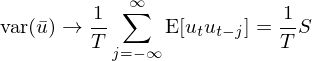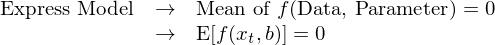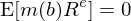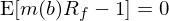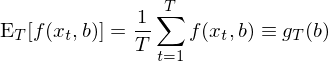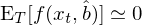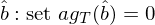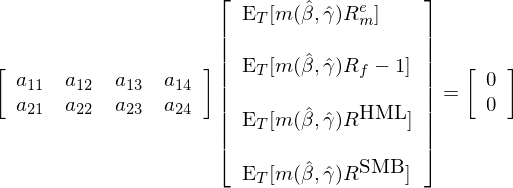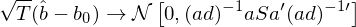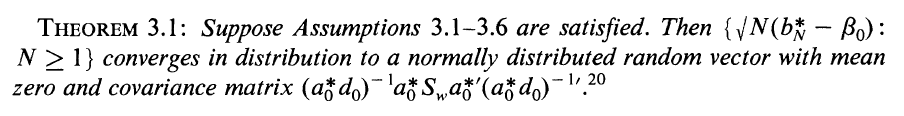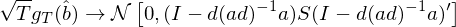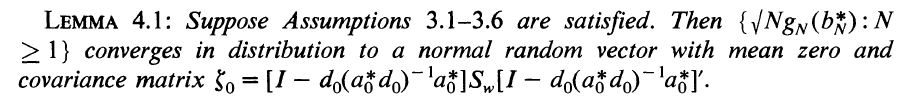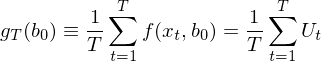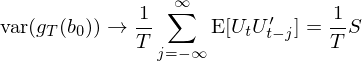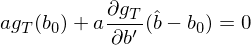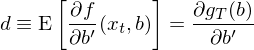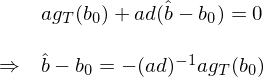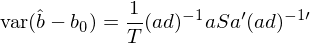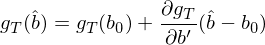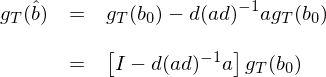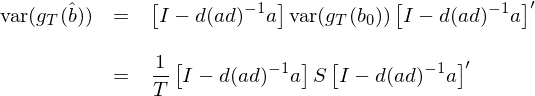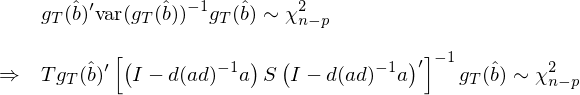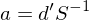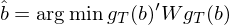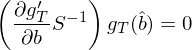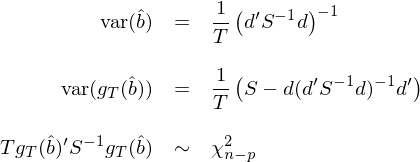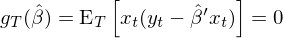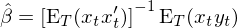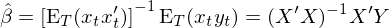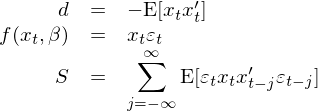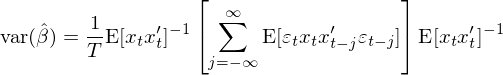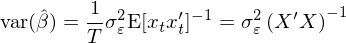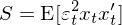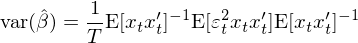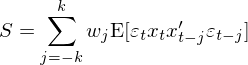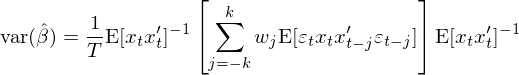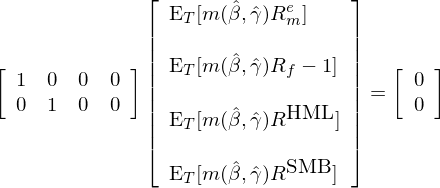Generalized Method of Moments

作者：石川

摘要：GMM 是研究 asset pricing 時(shí)繞不過的(de)工具。本文介紹 GMM 框架的(de)強大(dà)之處，并闡述其背後的(de)數學之美(měi)。

1 引言

前文《理(lǐ)解資産價格》已經提到，Hansen (1982) 提出的(de) GMM 在 empirical asset pricing 研究的(de)曆史上起到了(le)舉足輕重的(de)作用(yòng)，而如今無論是在經濟學領域還(hái)是金融學領域，GMM 因其數學上的(de)優雅和(hé)特性上的(de)強大(dà)都被廣泛的(de)運用(yòng)。今天這(zhè)篇文章(zhāng)算(suàn)是我自己關于 GMM 的(de)一個(gè)學習(xí)筆記，而我的(de)學習(xí)資料（公衆号的(de)老朋友一定猜到了(le)）正是 John Cochrane 教授的(de)神書(shū) Asset Pricing（Cochrane 2005）以及他(tā)在 UChicago 時(shí)做(zuò)的(de) Online 課程中對(duì) GMM 的(de)介紹。Cochrane 教授講的(de)實在是太清楚、到位了(le)，本文是我做(zuò)對(duì)他(tā)所講的(de)内容的(de)消化(huà)、梳理(lǐ)和(hé)再串聯。

本文的(de)目标是試圖從 intuition 出發揭示 GMM 蘊含數學之美(měi)；試圖把公式掰開揉碎講清楚從而幫助感興趣的(de)朋友理(lǐ)解大(dà)公式背後的(de)本質。Cochrane 教授說，學習(xí) GMM 時(shí)最大(dà)的(de)障礙就是它的(de) notation（數學符号）繁多(duō)；隻要搞清楚 notation，其實 GMM 背後的(de)數學精髓是非常簡單的(de)，因爲 GMM 的(de)核心最終能夠歸結爲計算(suàn) the variance of the sample mean。希望本文能夠帶給你這(zhè)種恍然大(dà)悟之感。先來(lái)劇透一下(xià)，本文希望傳達以下(xià)三方面内容：

以我一貫的(de)風格，行文中會“死磕”數學公式，因此這(zhè)注定是一篇十分(fēn) technical 的(de)文章(zhāng)。本文的(de)技術性遠(yuǎn)超《股票(piào)多(duō)因子模型的(de)回歸檢驗》，因此同樣建議(yì)在一個(gè)能靜下(xià)心來(lái)思考的(de)心境下(xià)和(hé)環境中閱讀。對(duì)于不關心數學、僅想快(kuài)速了(le)解 GMM 是什(shén)麽的(de)讀者來(lái)說，我強烈推薦慧航大(dà)神在知乎上關于 GMM 的(de)回答(dá)（參考文獻中最後一條）。那篇回答(dá)對(duì)讀者非常友好，涉及到的(de)數學恰到好處，深入淺出的(de)介紹了(le) GMM 的(de)原理(lǐ)。

如果本文能對(duì)你理(lǐ)解 GMM 起到一點幫助，那完全是 Cochrane 教授的(de)功勞；如果你看完後依然困惑，那一定也(yě)必須是怪我沒寫好……鑒于寫作本文耗時(shí)較長(cháng)（消耗腦(nǎo)細胞過多(duō)），接下(xià)來(lái)公衆号将會暫停一段時(shí)間。Cochrane 教授說 GMM 的(de)核心最終能夠歸結爲計算(suàn) the variance of the sample mean；讓我們就從 the variance of the sample mean 說起。

2 Variance of the Sample Mean

考慮某随機變量 u_t。假設它在某個(gè)樣本内的(de)取值爲 0，-1，3，3，-3。我們可(kě)以很容易的(de)算(suàn)出樣本均值：

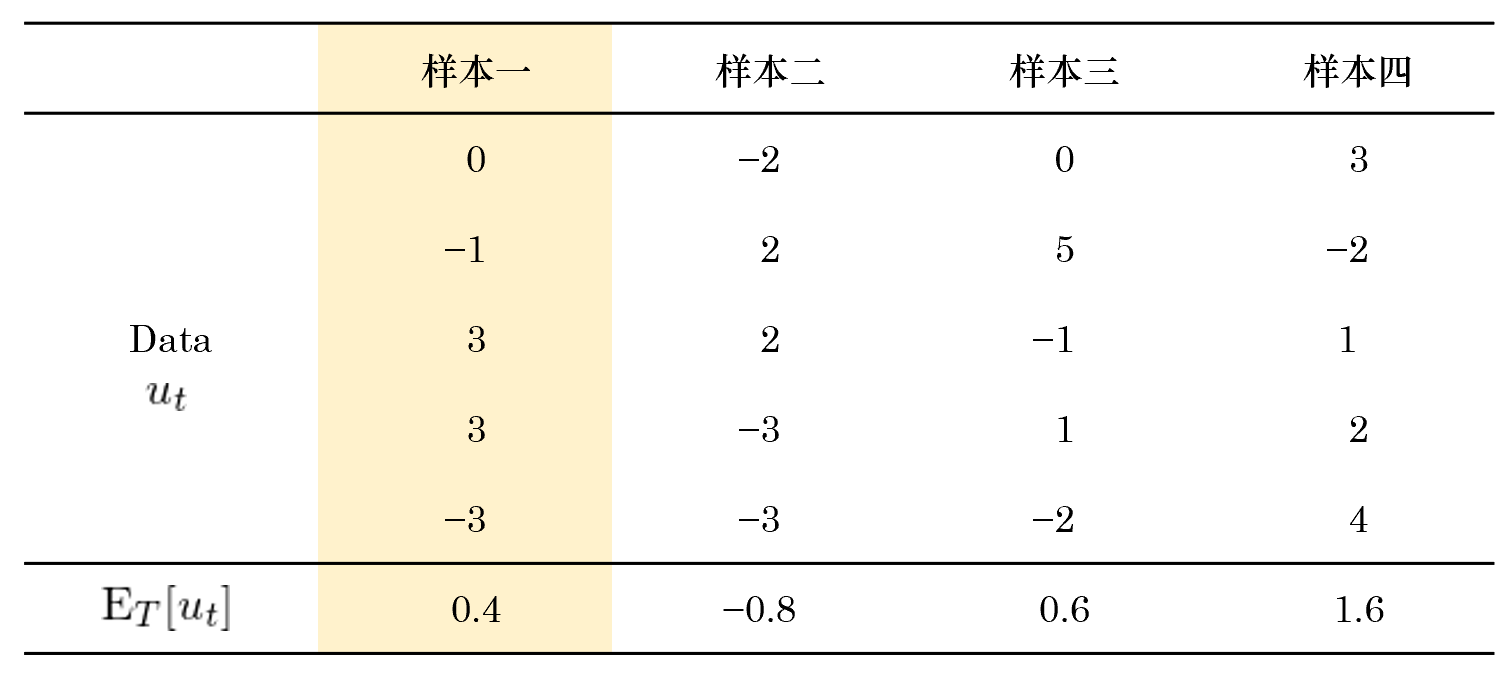
上式中，E_T = (1/T)Σ(.) 表示對(duì)樣本數據求平均，\bar u 表示 u_t 的(de)樣本均值。由于 u_t 是一個(gè)随機變量，因此其樣本均值本身（即 \bar u_t）也(yě)是一個(gè)随機變量。雖然它在我們這(zhè)個(gè)樣本中的(de)取值爲 0.4，但如果我們能夠乘坐(zuò)時(shí)光(guāng)機回到過去“重寫曆史”，得(de)到不同的(de)樣本，那麽在不同樣本中，樣本均值的(de)取值也(yě)會有所變化(huà)。比如在下(xià)面這(zhè)個(gè)表中，假設除樣本一（就是上面這(zhè)個(gè)樣本）之外，還(hái)有三個(gè)樣本，而它們的(de)樣本均值 \bar u 的(de)取值分(fēn)别爲 -0.8，0.6 和(hé) 1.6。

既然樣本均值本身也(yě)是一個(gè)随機變量，那麽一個(gè)很自然的(de)問題就是樣本均值在不同的(de)樣本中是如何變化(huà)的(de)，即 variance of the sample mean。從 variance 的(de)定義出發可(kě)得(de)：

在最簡單的(de)情況中，假設 u_t 序列滿足 i.i.d.，則上式可(kě)以簡化(huà)成：

把兩邊開方就得(de)到樣本均值的(de) standard error：

這(zhè)大(dà)概是我們在統計課中學到的(de)印象最深的(de)一個(gè)式子（假設 u_t 滿足 i.i.d. 條件下(xià)樣本均值的(de) standard error）。在更一般的(de)情況中 —— 尤其是在金融數據（比如收益率）數據中 —— u_t 序列是前後是有非零的(de)自相關的(de)，即 cov(u_t, u_{t-j}) ≠ 0，因此需要得(de)到更一般下(xià)樣本均值 \bar u 的(de) variance：

當 T 趨于無窮大(dà)時(shí)（即 sample size 越來(lái)越大(dà)），(T – j)/T 趨于 1，就可(kě)以求出 var(\bar u) 的(de)漸進（asymptotic）形式：

下(xià)面再假設一個(gè)特殊的(de)情況，即随機變量 u_t 的(de)總體均值 E[u_t] = 0，并利用(yòng)協方差的(de)定義 cov(X, Y) = E[XY] – E[X]E[Y] 可(kě)得(de)：

上式最後一項中的(de) S 代表了(le)中間項中那一大(dà)坨求和(hé)項。在 GMM 的(de)術語中，S 被稱作 spectral density matrix at frequency zero of u_t。

OK！整理(lǐ)一下(xià)。本小節從我們熟悉的(de)樣本均值出發指出樣本均值本身也(yě)是一個(gè)随機變量，并推導出當 sample size（T）趨于無窮且假設 E[u_t] = 0 時(shí)，variance of the sample mean 漸進趨于 S/T，其中 S 是無窮級數求和(hé) ΣE[u_tu_{t-j}]。千萬不要小看這(zhè)個(gè) var(\bar u) --> S/T 這(zhè)個(gè)式子，它在下(xià)文 GMM 的(de)數學推導中起著(zhe)至關重要的(de)作用(yòng)。用(yòng) Cochrane 的(de)話(huà)說，GMM 中大(dà)絕大(dà)部分(fēn)計量學均可(kě)歸結到這(zhè)個(gè)式子（most econometrics boils down to this）！

3 GMM 框架

回顧了(le) variance of the sample mean 之後，本小節就來(lái)直觀的(de)看看 GMM 到底是怎麽回事兒(ér)。GMM 的(de)作用(yòng)是爲了(le)檢驗模型。模型到底對(duì)不對(duì)？模型的(de)參數如何估計？誤差是來(lái)自運氣還(hái)是因爲模型有誤？GMM 提供了(le)一個(gè)優雅而強大(dà)的(de)計量學框架來(lái)回答(dá)這(zhè)些問題。一般來(lái)說，GMM 框架分(fēn)爲以下(xià)三個(gè)部分(fēn)：

所以概括來(lái)說就是 GMM 就是用(yòng) sample moments 代替 population moments 然後對(duì) population moments 進行統計檢驗。

3.1 GMM 第一部分(fēn)

我們用(yòng) x_t 代表 data，b 代表參數（這(zhè)些都是 vectors），且存在一系列關于 x_t 和(hé) b 的(de)函數 f(x_t, b)。f(x_t, b) 的(de) expected value 即 E[f(x_t, b)] 就是 population moments。在 GMM 中，我們要求 population moments 滿足 E[f(x_t, b)] = 0 的(de)約束，這(zhè)一系列 E[f(x_t, b)] = 0 約束就是 GMM 中的(de) population moment conditions（矩條件）。這(zhè)些 moment conditions 是我們關于真實模型（true model）的(de)猜測。

GMM 的(de)第一部分(fēn)是把待研究的(de)問題轉化(huà)成數據 x_t 和(hé)參數 b 的(de)一系列方程 f、且假設在 true model 下(xià)這(zhè)些方程的(de) moments 滿足 E[f(x_t, b)] = 0。

仍然晦澀？馬上來(lái)看一些 asset pricing 中的(de)例子。從最基礎的(de) p = E[mx] 出發（詳見《理(lǐ)解資産價格》），其中 m 是 stochastic discount factor（由某些未知參數 b 決定）、x 是回報、p 是價格。如果把 x 換成超額收益（用(yòng) R^e 表示）則有：

如果把 x 換成 gross risk-free rate R_f（即 t 投入 1，t + 1 得(de)到 R_f）則有：

這(zhè)些都是 asset pricing 中常見的(de) moment conditions。

3.2 GMM 第二部分(fēn)

第一部分(fēn)雖然把問題描述清楚了(le)，但它們都是 population moment conditions，隻是我們對(duì)于真實模型的(de)猜想，我們有的(de)隻是樣本數據。GMM 的(de)第二部分(fēn)就是用(yòng) sample moments 來(lái)代替 population moments，從而建立起模型和(hé)數據之間的(de)聯系，以進行參數估計。和(hé)本文第二節一樣，用(yòng) E_T 代表對(duì)樣本數據求平均，則 sample moments 可(kě)以寫成：

上式中最後引入符号 g_T 僅僅是爲了(le)下(xià)文中簡化(huà)公式。怎麽樣？看著(zhe)這(zhè)個(gè)式子有沒有什(shén)麽感想？無論研究的(de)具體問題是什(shén)麽（我們研究的(de)是 asset pricing，而别人(rén)也(yě)可(kě)以研究經濟學或金融學中其他(tā)的(de)問題），不管 f 到底長(cháng)什(shén)麽樣子或數據 x_t 和(hé)參數 b 向量都是什(shén)麽，上面的(de) sample moment 實際上隻是 f(x_t, b) 在樣本内取平均，因此也(yě)是一種 sample mean！從 sample moments 出發就可(kě)以進行參數估計。來(lái)自總體的(de) moment conditions 要求 E[f(x_t, b)] = 0；使用(yòng)樣本數據，GMM estimator 的(de)核心是找到 b 的(de)估計 —— 記爲 \hat b —— 使得(de)所有 sample moments 都盡可(kě)能的(de)等于零：

上式中之所以用(yòng)了(le)約等于而非等于，是因爲在實際問題中，sample moments 的(de)個(gè)數往往超過參數的(de)個(gè)數（這(zhè)也(yě)被稱爲 overidentification）。假設一共有 n 個(gè) moments（即 g_T 是 n × 1 階 vector），p 個(gè)參數（即 b 是 p × 1 階 vector）。當 n > p 時(shí)，我們無法讓所有的(de) sample moments 都等于零，而是選擇讓這(zhè)其中的(de) p 個(gè) sample moments 或者這(zhè)些 sample moments 的(de) p 個(gè)線性組合等于 0。這(zhè)就是 GMM estimator：

上式中，a 是 p × n 階矩陣，每一行都代表一個(gè) sample moments 的(de)線性組合。在具體問題中，根據 g_T 的(de)具體形式，上式可(kě)能有解析解或數值解。求解上式就可(kě)以獲得(de) \hat b。不過有的(de)小夥伴可(kě)能會說：等一下(xià)，你還(hái)沒說矩條件的(de)線性組合矩陣 a 是什(shén)麽！不同的(de) a 顯然會得(de)到不同的(de)參數估計。沒錯，在 GMM 的(de)框架下(xià)，我們可(kě)以自由選擇 a。然而，純從計量學的(de)角度，有一個(gè)特殊的(de)矩陣 a 會讓 GMM estimator 成爲 efficient estimator。下(xià)文第 3.3 節和(hé)第 5 節将會就 efficiency 進行說明(míng)。

爲了(le)加深理(lǐ)解，仍然用(yòng) asset pricing 來(lái)舉例子。假設 consumption-based CAPM（CCAPM）是真正的(de)模型，因此随機折現因子 m 由兩個(gè)參數 β 和(hé) γ 決定（CCAPM 的(de)介紹請見《理(lǐ)解資産價格》），即 b = [β, γ]'；進一步假設我們有四個(gè)資産來(lái)檢驗 CCAPM，它們是 risk-free、市場(chǎng)組合以及 Fama and French (1993) 中的(de) HML 和(hé) SMB。在這(zhè)個(gè)例子中，n = 4 而 p = 2，因此 a 是一個(gè) 2 × 4 階矩陣，而 GMM estimator 可(kě)以寫成：

根據上式就可(kě)以使用(yòng) sample moments 求出參數估計 \hat b。

3.3 GMM 第三部分(fēn)

使用(yòng) GMM estimator 得(de)到的(de) \hat b 僅僅是真實但未知參數 b_0 的(de)一個(gè)估計。從統計學的(de)角度，我們自然關心估計的(de)誤差，即 var(\hat b)。馬上來(lái)回答(dá)上面遺留的(de)矩陣 a 的(de)選擇的(de)問題。對(duì)于給定的(de) moments g_T，從計量學的(de)角度有一個(gè)特殊的(de)矩陣 a 使得(de) var(\hat b) 最小，這(zhè)就是 efficient 的(de)含義。Hansen (1982) 給出了(le)這(zhè)個(gè) a 的(de)形式。關于 a 的(de)進一步討(tǎo)論将放在本文第五節。

Var(\hat b) 的(de)大(dà)小僅僅告訴我們參數估計是否準确，而對(duì)于研究的(de)問題來(lái)說，我們更加關注的(de)是當給定 \hat b 時(shí)，sample moments 的(de) variance var(g_T(\hat b)) 的(de)大(dà)小。在一般的(de) overidentification 問題下(xià)（moments 個(gè)數多(duō)于參數個(gè)數），sample moments 不可(kě)能都是零（如果 moments 個(gè)數 n 等于參數個(gè)數 p，我們可(kě)以令每個(gè) moment 都等于零從而求出全部 p 個(gè)參數），因此我們關心 sample moments 聯合起來(lái)相對(duì)于零的(de)偏離的(de)大(dà)小是多(duō)少。

我們必須搞清楚 g_T(\hat b) 聯合起來(lái)相對(duì)于零的(de)偏離是因爲運氣成分(fēn)還(hái)是因爲選擇的(de) population moment condition 就是錯的(de)。如果僅僅因爲運氣（即偏離的(de)很小），那可(kě)以接受 population moment conditions —— 比如接受一個(gè)選擇的(de) asset pricing 模型；如果不是因爲運氣（即偏離很大(dà)），那就隻能拒絕 population moment conditions —— 即 reject 一個(gè) asset pricing 模型。這(zhè)就是 statistical test。唯有有了(le) var(g_T(\hat b))，才能夠進行 statistical test。計算(suàn) sample moments 的(de) variance 并進行 statistical test 就是 GMM 的(de)第三部分(fēn)。

值得(de)一提的(de)是，由于 \hat b 和(hé) g_T(\hat b) 都是向量，因此 var(\hat b) 和(hé) var(g_T(\hat b)) 事實上都代表了(le)它們各自的(de) variance-covariance matrix，其中 var(\hat b) 是 p × p 階矩陣（共有 p 個(gè)參數），而 var(g_T(\hat b)) 是 n × n 階矩陣（共有 n 個(gè) moments）。有了(le) var(\hat b) 和(hé) var(g_T(\hat b)) 就可(kě)以寫出 \hat b 和(hé) g_T(\hat b) 的(de)分(fēn)布。當 sample size T 趨于無窮時(shí)，\hat b 的(de)滿足以下(xià)漸進正态性：

上式中，-1 表示求逆，’ 表示轉置，所以 (ad)^{-1}’ 表示先求 ad 的(de)逆矩陣再轉置。這(zhè)個(gè)式子正是 Hansen (1982) 中的(de) Theorem 3.1。Hansen (1982) 給出了(le)漸進分(fēn)布成立需要滿足的(de)一系列假設。在實際應用(yòng)中，我們需要記住的(de)是數據 x_t 需要滿足弱平穩性，這(zhè)是因爲 GMM 的(de)基礎是随著(zhe) T 的(de)增大(dà)，sample mean 向 population mean 收斂。

此外，g_T(\hat b) 滿足如下(xià)漸進正态性：

上式中，I 是 n × n 階單位陣。這(zhè)個(gè)式子正是 Hansen (1982) 中的(de) Lemma 4.1。

看到這(zhè)裏，你大(dà)概在想：What the hell?! 這(zhè)又 a 又 d 又 S 又求逆又轉置，這(zhè)都是什(shén)麽“牛鬼蛇神”？有一種“每個(gè)字都認識、但是放在一起就看不懂(dǒng)了(le)”的(de)既視感。這(zhè)裏的(de) a 就是上面 sample moments 的(de)線性組合矩陣，但是 d 和(hé) S 還(hái)沒有介紹。别著(zhe)急，第四節将會把這(zhè)些式子掰開了(le)、揉碎了(le)說清楚的(de)。

看到 S 你是否想到什(shén)麽？沒錯，本文第二節講 the variance of the sample mean 的(de)時(shí)候提到了(le) S。而上面 var(\hat b) 和(hé) var(g_T(\hat b)) 看似無比複雜(zá)，但它們的(de)本質也(yě)都離不開 the variance of the sample mean！在有了(le) g_T(\hat b) 的(de)分(fēn)布後，就可(kě)以對(duì) GMM 第一部分(fēn)中選擇的(de)模型進行檢驗，從而決定是接受還(hái)是拒絕它。以 asset pricing 爲例，這(zhè)些 moments 代表了(le)給定定價模型下(xià)不同資産或投資組合的(de) pricing errors。我們關心 pricing errors 是否聯合起來(lái)顯著不爲零，這(zhè)時(shí)可(kě)以用(yòng) g_T(\hat b) 的(de)分(fēn)布構建 chi-squared statistic 來(lái)檢驗。如果 test statistic 超過給定顯著性水(shuǐ)平的(de)阈值，那麽我們就可(kě)以拒絕該 asset pricing 模型。

總結一下(xià)，本小節介紹了(le) GMM 的(de)三部分(fēn)：

下(xià)一節就來(lái)看看 statistical test 背後的(de)數學基礎。

4 數學基礎

Let's do the math!

本節的(de)目标是解釋 var(\hat b) 和(hé) var(g_T(\hat b)) 裏面的(de)那些 a、d、S、求逆以及轉置。我會力争把所有涉及到的(de)公式都講清楚。了(le)解本節的(de)内容無疑會更好的(de)理(lǐ)解 GMM 背後的(de)數學之美(měi)（汗），但是從閱讀的(de)角度，跳過本小節也(yě)不影(yǐng)響對(duì)後文的(de)理(lǐ)解。先說 S，這(zhè)是一切的(de)核心。從下(xià)式出發來(lái)解釋 S：

上式中第一個(gè)等價符号是 g_T 的(de)定義（參考 3.2 節），第二個(gè)等号是使用(yòng) U_t 來(lái)代表 f(x_t, b_0)。需要強調的(de)是，上式中 g_T 的(de)參數是真實（但未知）的(de)參數 b_0。而 g_T(b_0) 的(de)方差 var(g_T(b_0)) 就表示 sample moments g_T 在真實參數 b_0 下(xià)的(de) sampling variance。無論 f 長(cháng)什(shén)麽樣子，sample moments 的(de)數學形式都僅僅取平均，因此 var(g_T(b_0)) 正是 the variance of the sample mean！（這(zhè)就是本文第二節的(de)價值所在。）上面之所以用(yòng)了(le) U_t，一是爲了(le)簡化(huà)表達式，二是爲了(le)和(hé)本文第二節中的(de)小寫 u_t 呼應起來(lái)：這(zhè)裏的(de) U_t 對(duì)應第二節的(de) u_t、g_T(b_0) 就是第二節的(de) \bar u，因此馬上得(de)到（當 T 趨于無窮）：

這(zhè)正是 S 的(de)定義（實際中，它可(kě)以用(yòng)樣本數據來(lái)估計）。上面的(de)計算(suàn)中之所以能把方差和(hé)協方差寫成 E[XY] 的(de)形式是因爲我們假設真實模型滿足 E[f(x_t, b_0)] = E[U_t] = 0。（預期符号 E 沒有下(xià)标 T，表示 population expectation。）重要的(de)事情說三遍：

當然，我們最終關心的(de)是當 b = \hat b 時(shí) g_T 的(de)方差，即 var(g_T(\hat b))。然而，一旦有了(le) var(g_T(b_0)) = S/T，計算(suàn) var(\hat b) 以及 var(g_T(\hat b)) 就變得(de)迎刃而解。這(zhè)就是爲什(shén)麽 Cochrane 教授說一切都可(kě)以歸結爲計算(suàn) the variance of the sample mean。接下(xià)來(lái)就看看 var(\hat b) 如何計算(suàn)。由 GMM estimator 可(kě)知，ag_T(\hat b) = 0。将該式在真實參數 b_0 進行一階泰勒展開有：

細心的(de)小夥伴可(kě)能注意到了(le)一階偏導數 ∂g_T/∂b’ 的(de)分(fēn)母中 b 右上角有個(gè)十分(fēn)詭異的(de)轉置符号。在計算(suàn)偏導數時(shí)，g_T 是一個(gè) n × 1 階向量（n 個(gè) moments），而 b 是一個(gè) p × 1 階向量（p 個(gè)參數），因此偏導數其實是一個(gè)矩陣（要麽 n × p 階、要麽 p × n 階），而這(zhè)類運算(suàn)屬于 matrix calculus。當轉置符号出現在分(fēn)母時(shí)，得(de)到的(de)矩陣是 n × p 階，即每一行代表一個(gè) moment，這(zhè)種排列方式稱作 numerator layout，也(yě)稱作 Jacobian formulation。而這(zhè)個(gè)一階偏導數矩陣也(yě)正是我們的(de) d：

嚴格來(lái)說，d 應該由 population moments 的(de)一階導數計算(suàn)（上面的(de)第一個(gè)等價條件）；但在應用(yòng)中，d 的(de)取值用(yòng) sample moments 和(hé) b = \hat b 來(lái)估計（上面的(de)第二的(de)等式）。用(yòng) d 替換 ∂g_T/∂b’ 并代入上面的(de)泰勒展開，進行簡單的(de)代數運算(suàn)可(kě)得(de)：

上式兩邊直接求 variance 就得(de)到 var(\hat b)。值得(de)一提的(de)是，上式右側的(de) (ad)^{-1}a 是系數矩陣而 g_T(b_0) 的(de) variance 我們之前已經求出來(lái)了(le) —— 沒錯正是 S/T。因此有：

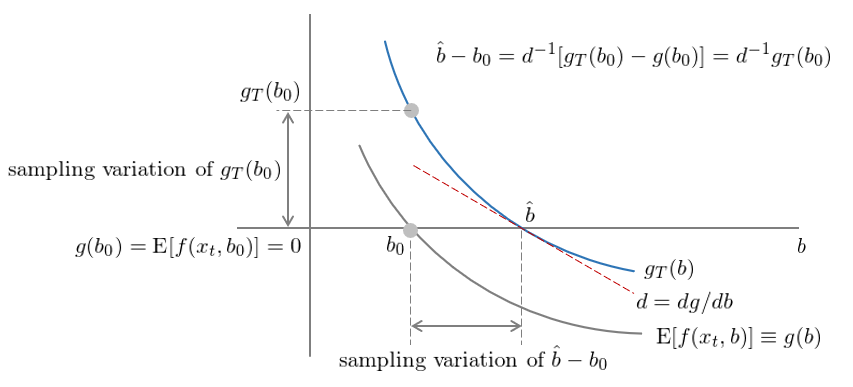
數學上雖然通(tōng)過泰勒展開順理(lǐ)成章(zhāng)的(de)從 var(g_T(b_0)) 得(de)到了(le) var(\hat b - b_0)，但我們仍然希望從直覺上了(le)解上面一頓操作猛如虎到底幹了(le)什(shén)麽。考慮最簡單的(de)情況，即一個(gè) moment 和(hé)一個(gè)參數（因此 a 是一個(gè)标量，令 a = 1），我們可(kě)以畫(huà)出 var(g_T(b_0)) 和(hé) var(\hat b - b_0) 的(de)關系。

圖中，灰色曲線表示不同參數 b 時(shí)的(de) population moment，用(yòng) g(b) 表示。對(duì)于真實參數 b_0，由假設有 g(b_0) = E[f(x_t, b_0)] = 0，因此在圖上，灰色曲線經過 (b_0, 0) 這(zhè)個(gè)點；藍色曲線表示不同參數 b 時(shí)的(de) sample moment，用(yòng) g_T(b) 表示。圖中 g_T(b_0) 和(hé) g(b_0) = 0 之間的(de)距離就是 g_T(b_0) 的(de) sampling variation，即我們的(de)樣本可(kě)能由于 luck 或者 unluck，以至于 g_T(b_0) ≠ 0 而是較 0 有一定的(de)偏離，在統計上它就是 var(g_T(b_0))。

接下(xià)來(lái)，對(duì)于 sample moment g_T，我們令其等于 0 求出的(de)參數估計爲 \hat b，因此藍色曲線 g_T 經過 (\hat b, 0) 這(zhè)個(gè)點。下(xià)面在藍線上的(de) \hat b 點計算(suàn)其切線（紅色）并計算(suàn)切線的(de)斜率 d = dg/db。通(tōng)過 d 我們就可(kě)以把 g_T(b_0) 和(hé) g(b_0) = 0 之間的(de) sampling variation 轉換成 \hat b 和(hé) b_0 之間的(de) sampling variation，即 var(\hat b – b_0)。這(zhè)正是 var(g_T(b_0)) 和(hé) var(\hat b - b_0) 關系的(de)幾何含義。

下(xià)面我們如法炮制，利用(yòng)一階泰勒展開從 var(g_T(b_0)) 求解 var(g_T(\hat b))：

由于 \hat b – b_0 已經在之前求出了(le)，因此隻需把它代入到上式就可(kě)得(de)到：

兩邊同時(shí)求 variance（确切的(de)說是 variance-covariance matrix）有：

上式中的(de)第二個(gè)等式用(yòng)到了(le)我們的(de)老朋友：var(g_T(b_0)) = S/T —— variance of sample mean！關于 var(g_T(\hat b)) 和(hé) var(g_T(b_0)) 的(de)關系也(yě)可(kě)以從直覺上解釋兩句。不難看出，var(g_T(\hat b)) 是 var(g_T(b_0)) 乘以一個(gè)系數矩陣，這(zhè)個(gè)系數矩陣是單位陣 I 減去這(zhè)一大(dà)坨 d(ad)^{-1}a。因此從直覺上說，g_T 在 b = \hat b 時(shí)的(de)方差 var(g_T(\hat b)) 會比 g_T 在 b = b_0 時(shí)的(de)方差 var(g_T(b_0)) 要小一些。這(zhè)是因爲在 GMM 估計時(shí)，我們要求 g_T 的(de) p 個(gè)線性組合等于零 —— ag_T(\hat b) = 0 —— 從而求出 \hat b，因此求解 \hat b 的(de)過程用(yòng)掉了(le) sample moments 的(de)一些 variation，所以當 b = \hat b 時(shí) g_T 的(de)方差小于當 b = b_0 時(shí) g_T 的(de)方差。

無論是 var(\hat b) 還(hái)是 var(g_T(\hat b))，上面一頓泰勒展開操作雖然非常熱(rè)鬧，但它們其實都僅是用(yòng)了(le)統計學中的(de) delta method。所以，其實我們隻是用(yòng)了(le) variance of the sample mean（S/T）+ delta method 就求出了(le)我們關心的(de) var(\hat b) 和(hé) var(g_T(\hat b))。就是這(zhè)麽簡單。有了(le) var(g_T(\hat b))，就可(kě)以得(de)到 g_T(\hat b) 的(de)漸近分(fēn)布（3.3 節介紹過），使用(yòng)它的(de)分(fēn)布就可(kě)以構建 chi-squared statistic 來(lái)對(duì)模型進行檢驗：

上式的(de)第二步是把 var(g_T(\hat b)) 的(de)表達式代入并求逆；chi-squared statistic 的(de)自由度是 moments 的(de)個(gè)數減去參數的(de)個(gè)數，即 n – p。由于估計 \hat b 的(de)時(shí)候用(yòng)掉了(le) p 個(gè)自由度，所以 g_T(\hat b) 的(de) variance-covariance matrix 不是滿秩的(de)（這(zhè)也(yě)體現在了(le) chi-squared statistic 的(de)自由度 n – p 上），因此上式中對(duì) var(g_T(\hat b)) 求逆實際上是 pseudo-inverse。

如果你在 Wikipedia 或者其他(tā)書(shū)籍上查閱 GMM 的(de)資料，也(yě)許看到的(de) chi-squared statistic 的(de)表達式遠(yuǎn)沒有上面這(zhè)個(gè)複雜(zá)。上述表達式是最 general 的(de)情況，因爲我們尚未討(tǎo)論那個(gè)使 GMM estimator 變得(de) efficient 的(de)特殊的(de)矩陣 a。在那個(gè) a 下(xià)，var(g_T(\hat b)) 矩陣以及 chi-squared statistic 表達式将被大(dà)大(dà)的(de)簡化(huà)。Efficient GMM 就是下(xià)一節的(de)内容。

總結一下(xià)本小節。上面用(yòng)了(le)大(dà)量的(de)文字和(hé)推導把 var(\hat b) 和(hé) var(g_T(\hat b)) 背後的(de)數學含義呈現給各位，是希望這(zhè)個(gè)過程能幫助小夥伴們加深對(duì) GMM 的(de)理(lǐ)解。站在 notation 的(de)角度來(lái)說，雖然這(zhè)些公式看上去很複雜(zá)（又是轉置、又是求逆的(de)），但我們隻需給 GMM 框架提供它需要的(de) a、g_T、d 和(hé) S，剩下(xià)的(de)“無腦(nǎo)”交給 GMM 就可(kě)以計算(suàn)出各種想要的(de)統計量并進行 test，非常方便。

5 Efficient GMM

本文的(de) 3.2 小節給出的(de) GMM estimator 如下(xià)：

其中 a 是一個(gè) p × n 階矩陣，每一行都代表一個(gè) sample moments 的(de)線性組合。本節關心的(de)問題是，如何選取矩陣 a？回答(dá)這(zhè)個(gè)問題可(kě)以從業務上和(hé)統計上兩方面思考 —— 永遠(yuǎn)不要忘記業務層面的(de)思考！從經濟學或金融學原理(lǐ)出發，尤其是針對(duì) asset pricing 的(de)問題，我們可(kě)以選擇一些最 economically important 的(de) moments，讓它們或它們的(de)線性組合等于零。我們不應讓 GMM 成爲一個(gè) statistical 黑(hēi)箱，代替我們的(de)思考。第七節将會進一步說明(míng)。

再來(lái)從統計上說，Hansen (1982) 指出了(le)一個(gè)特殊的(de) a 矩陣，它能确保得(de)到 efficient GMM estimator，即在給定的(de) moments g_T 下(xià)，該矩陣 a 使得(de) var(\hat b) 最小。這(zhè)個(gè)特殊的(de) a 矩陣爲：

看到這(zhè)兒(ér)可(kě)能又有小夥伴會問：d 見過、S 見過、轉置明(míng)白、求逆矩陣清楚，但是這(zhè)四個(gè)符号組合在一起得(de)到的(de) d'S^{-1} 是個(gè)什(shén)麽鬼？？這(zhè)個(gè) a 到底有沒有什(shén)麽更直觀的(de)含義？别急，先來(lái)看看 a 的(de)階數。本文的(de) 3.2 節已經指出 a 是一個(gè) p × n 階矩陣，下(xià)面我們來(lái)驗證一下(xià)。

前面首次提到 d 的(de)時(shí)候說過了(le)，它是一階偏導數 ∂g_T/∂b'。但由于 g_T（n × 1 階）和(hé) b（p × 1 階）都是 vectors，因此 d 是一個(gè)遵照(zhào) numerator layout（也(yě)稱作 Jacobian formulation）排列的(de) n × p 階矩陣。因此矩陣 d 的(de)轉置 d’ 就是 p × n 的(de)矩陣，它同樣也(yě)是一個(gè)一階偏導數 ∂g_T'/∂b —— 這(zhè)次轉置在 g_T 上，遵循的(de)是 denominator layout（也(yě)稱 Hessian formulation），通(tōng)常表示求梯度（gradient）。最後，由于 S 是 n × n 階，因此 a 确實是 p × n 階。

下(xià)面我們就來(lái)看看 d'S^{-1} 到底是個(gè)什(shén)麽鬼。其實它有著(zhe)非常清晰的(de)含義。爲了(le)解釋 a 就不得(de)不提 GMM estimator 的(de)另一種表達式，這(zhè)可(kě)能也(yě)是之前接觸過 GMM 的(de)小夥伴更熟悉的(de)一種表達式：

上式中 W 是權重矩陣（weighting matrix），它是一個(gè)半正定矩陣。這(zhè)個(gè)式子的(de)含義是，在 overidentification 問題中，既然我們無法讓所有的(de) g_T 都等于零，那麽就讓所有 n 個(gè) g_T 的(de)範數的(de)加權之和(hé)盡可(kě)能的(de)接近零，以此來(lái)确定 \hat b。正如在本文的(de)第一種 GMM estimator 表達中我們可(kě)以随意選擇矩陣 a 一樣，在上面的(de)第二種 GMM estimator 表達中我們可(kě)以随意選擇權重矩陣 W。但是從 efficiency 的(de)角度，最優的(de)權重矩陣 W 滿足：

這(zhè)從統計上非常好理(lǐ)解：我們有一組 moments g_T，我們希望它們（非負）加權之和(hé)最接近零。使用(yòng) W = S^{-1} 即 S 的(de)逆矩陣（别忘了(le) S/T 是 var(g_T(b_0))）相當于給那些 sampling variation 大(dà)的(de) g_T 更低的(de)權重、給那些 sampling variation 小的(de) g_T 更高(gāo)的(de)權重（inverse 的(de)意義）。換句話(huà)說，我們更願意相信那些誤差小的(de) moments 并使用(yòng)它們來(lái)得(de)到盡可(kě)能準确的(de)參數估計 \hat b，從而使 var(\hat b) 最低，這(zhè)也(yě)就是 efficient 的(de)含義。将 W = S^{-1} 代入上面第二個(gè) GMM estimator 并求其 first order condition 有：

怎麽樣，看著(zhe)眼熟不？括号裏的(de)第一項正是 d 的(de)轉置 d'，第二項是 S^{-1}，這(zhè)兩個(gè)放一起 d'S^{-1} 正是第一種 GMM estimator 下(xià)最優的(de)矩陣 a = d'S^{-1}：

這(zhè)就是最優矩陣 a = d'S^{-1} 的(de)含義。從上面的(de)推導也(yě)不難看出這(zhè)兩種 GMM estimator 表達式是等價的(de)：無論我們取何種 W 權重矩陣，都有一個(gè)與之對(duì)應的(de) a = d'W 矩陣。當矩陣 a 或權重矩陣 W 取統計上最優時(shí)，var(\hat b)、var(g_T(\hat b)) 以及 chi-squared test statistic 的(de)表達式均可(kě)以大(dà)大(dà)化(huà)簡。Hansen (1982) 給出了(le)它們的(de)形式：

需要強調的(de)是，以上的(de)這(zhè)些大(dà)大(dà)簡化(huà)了(le)的(de)表達式隻有當 a = d'S^{-1}（或 W = S^{-1}）時(shí)才成立！如果 a 或 W 取别的(de)值，則應該使用(yòng)本文第 4 節中介紹的(de)更 general 的(de)形式。很多(duō)關于 GMM 的(de)材料中默認 W = S^{-1} 而給出了(le)這(zhè)些統計量的(de)簡化(huà)形式，使用(yòng)時(shí)應搞清楚前提條件。在實際估計中，因爲必須先有 \hat b 才能估計 S，并計算(suàn) W = S^{-1}（或最優的(de) a）；但另一方面隻有使用(yòng) S^{-1} 才能得(de)到最優的(de) \hat b。這(zhè)似乎是一個(gè)雞生蛋、蛋生雞的(de)問題。因此，實際中往往采用(yòng) two-stage estimates：

當然，如果願意，也(yě)可(kě)以把上面的(de)第二步叠代多(duō)次，得(de)到最終的(de) \hat b。以上就完成了(le)關于 GMM 的(de)全部介紹。

6 GMM does OLS

GMM 之所以如此強大(dà)，是因爲它自帶的(de)“estimate、variance、test”三部曲能夠幹很多(duō)事兒(ér)！對(duì)于很多(duō)需要研究的(de)問題，隻要把它的(de)模型塞進 GMM 的(de)框架，就可(kě)以得(de)到想要的(de)分(fēn)析結果。本節就把我們熟悉的(de) OLS 放在 GMM 的(de)框架下(xià)看看後者的(de)強大(dà)之處。由于參數個(gè)數和(hé) moments 個(gè)數相同，因此 OLS 不存在 overidentification 的(de)問題，我們沒有什(shén)麽可(kě)以檢驗的(de)。但是 GMM 仍然可(kě)以輕松的(de)計算(suàn)出參數的(de) variance（即完成 estimate 和(hé) variance 兩步），無論 OLS 的(de)殘差是否存在自相關或異方差。

想要使用(yòng) GMM 框架，隻需要把 OLS 表述成 moment conditions。考慮 OLS 問題（截距被視作一個(gè)解釋變量，不做(zuò)區(qū)分(fēn)；假設一共有 k 個(gè)解釋變量，因此 x_t 表示 k × 1 階向量）如下(xià)：

由 OLS 的(de)性質可(kě)知，其解釋變量和(hé)殘差正交，因此 OLS 的(de) moment conditions 爲：

由于 moments 個(gè)數和(hé)參數個(gè)數相同，因此我們隻需要令所有 sample moments 都等于零即可(kě)，這(zhè)意味著(zhe)矩陣 a 是單位陣 I，因此在上式的(de) GMM estimator 中省略了(le) a。求解上述 sample moment conditions 就可(kě)以得(de)到參數的(de)估計：

如果令 X = [x_1 x_2 … x_t]' 表示 data matrix，則有 (1/T)X'X = E_T[x_tx_t']，因此上式又可(kě)以寫成：

這(zhè)正是我們熟悉的(de) OLS estimator。GMM 的(de)強大(dà)之處在于輕松的(de)計算(suàn) var(\hat β)。爲此，我們需要給 GMM 框架提供它所需要的(de) d 和(hé) S（已經有了(le) a 和(hé) g_T）。根據 d 和(hé) S 的(de)定義可(kě)得(de)：

有了(le) a、g_T、d、S，直接利用(yòng) GMM 中的(de)公式就可(kě)以求出 var(\hat β)：

這(zhè)正是廣義 OLS 下(xià) var(\hat β) 的(de)表達式（請參考《多(duō)因子回歸檢驗中的(de) Newey-West 調整》對(duì)比）。

We are done!

下(xià)面考察幾種情況。首先如果殘差滿足 i.i.d.，var(\hat β) 就可(kě)以簡化(huà)成我們最熟悉的(de)樣子：

通(tōng)常來(lái)說，殘差中可(kě)能存在異方差、自相關或者兩者皆有。在 GMM 的(de)框架下(xià)，爲了(le)計算(suàn) var(\hat β) 僅需要在 S 矩陣中考慮異方差和(hé)自相關造成的(de)影(yǐng)響。當殘差僅存在異方差時(shí)，S 的(de)表達式爲：

因此 var(\hat β) 的(de)表達式變成：

這(zhè)正是大(dà)名鼎鼎的(de) White (1980) heteroscedasticity consistent estimator。當殘差即存在異方差又存在自相關時(shí)，S 可(kě)以寫作：

而 var(\hat β) 的(de)表達式變成：

這(zhè)正是大(dà)名鼎鼎的(de) Newey and West (1987) autocorrelation consistent covariance estimator（見《多(duō)因子回歸檢驗中的(de) Newey-West 調整》）。無論殘差具有什(shén)麽特性，整個(gè) OLS 的(de)求解過程都可(kě)以很好的(de)裝到 GMM 的(de)框架中。而當使用(yòng) GMM 框架時(shí)，隻需按照(zhào)它的(de)要求來(lái)定義 a、g_T、d 以及 S，就可(kě)以“無腦(nǎo)”的(de)利用(yòng) GMM 給出的(de)結果。這(zhè)正是 GMM 的(de)強大(dà)之處。

7 不應成爲黑(hēi)箱

在結束本文之前，再花一小節討(tǎo)論一個(gè)很重要的(de)問題：GMM 不應該成爲計量學黑(hēi)箱。這(zhè)是我聽(tīng)完 Cochrane 教授的(de)講解後印象非常深刻的(de)一點。GMM 如此強大(dà)再加上現在各種編程語言（R、Stata 等）都能方便的(de)計算(suàn)，這(zhè)種便捷性似乎把人(rén)們都慣壞了(le)；人(rén)們習(xí)慣于把問題描述成 moment conditions 然後一股腦(nǎo)塞進 GMM 并純從統計的(de)角度使用(yòng) efficient estimator（即 W = S^{-1}）。Cochrane 教授警告說這(zhè)麽做(zuò)十分(fēn)危險。

GMM 的(de)強大(dà)之處在于它不僅僅是一個(gè)計量學工具來(lái)做(zuò) test，而是它足夠 flexible 從而可(kě)以讓我們研究我們真正關心的(de)經濟學或金融學問題，這(zhè)體現在我們可(kě)以從“先驗”出發去定義最适合待研究問題的(de)矩陣 a（或權重矩陣 W），而非無腦(nǎo)的(de)選擇 W = S^{-1}。

以 3.2 節中 asset pricing 的(de)例子來(lái)說，我們有四個(gè) moments，兩個(gè)參數。這(zhè)四個(gè) moments 來(lái)自四個(gè)資産：risk-free、市場(chǎng)組合以及 HML 和(hé) SMB，我們假設待檢驗的(de)模型是 CCAPM。從經濟學業務出發，我們可(kě)以選擇如下(xià)的(de) ag_T(\hat b) = 0：

在這(zhè)個(gè)矩陣 a 中，我們令市場(chǎng)超額收益和(hé) R_f 完美(měi)滿足兩個(gè) sample moment conditions，并由此進行 CCAPM 的(de)參數估計，求出兩個(gè)參數，然後使用(yòng)另外兩個(gè)資産 HML 和(hé) SMB 來(lái)檢驗 CCAPM。由 GMM 框架可(kě)知，最終的(de) chi-squared test statistic 的(de)自由度爲 2（因爲一共 4 個(gè)資産，2 個(gè)被用(yòng)來(lái)估計參數），因此聯合檢驗的(de)實際上正是 HML 和(hé) SMB 在 CCAPM 這(zhè)個(gè)定價模型下(xià)的(de) pricing errors。如果 pricing errors 聯合顯著不爲零，那麽就可(kě)以拒絕 CCAPM。這(zhè)個(gè)例子說明(míng)，從經濟學原理(lǐ)出發選擇合适的(de) a 或 W 能讓我們回答(dá)最感興趣的(de)經濟學問題。GMM 的(de)強大(dà)之處正在于此。

純從統計學的(de)角度來(lái)說，W = S^{-1} 确實能夠得(de)到 efficient GMM。但不要忘記，這(zhè)個(gè) efficient 的(de)是以給定的(de) moments 爲前提的(de) —— 如果換了(le)或者添加了(le)更多(duō)的(de) moments，參數的(de) efficient 估計也(yě)會發生變化(huà)。在金融市場(chǎng)中，有無數的(de)資産，包括股票(piào)、債券、外彙、商品等，還(hái)有無數的(de)投資組合，這(zhè)些資産可(kě)以構成無數的(de) moments。爲了(le) efficiency，我們應該把這(zhè)成千上萬資産的(de) moments 都塞進 GMM 才能得(de)到 efficient 的(de)估計。但從業務的(de)角度來(lái)說這(zhè)毫無意義。在研究資産定價的(de)時(shí)候，我們應該使用(yòng)最“clever”的(de)資産，比如 HML、SMB 這(zhè)些投資組合。它們才是我們真正關心的(de)問題。

The quest for efficiency doesn't really drive us as much as the quest for something that is robust and that expresses what the model is supposed to do. —— John Cochrane

GMM 非常好使，但在 asset pricing 的(de)研究中，我們不應追求使用(yòng) GMM 進行一個(gè)僅在統計上正式但模型卻缺乏含義的(de) statistical test。GMM 的(de)強大(dà)在于它讓我們從經濟學和(hé)金融學原理(lǐ)出發，去 measure 和(hé) estimate 最合理(lǐ)的(de)模型、并同時(shí)對(duì) sampling error 保持足夠的(de)認識。不要讓 GMM 成爲計量學的(de)黑(hēi)箱。

8 結語

呼！終于寫完了(le)！感謝你看到最後！作爲感謝，上點硬貨 —— GMM 的(de) formula sheet（出自 Cochrane 2005）。它總結了(le)前文解讀的(de)每一個(gè)公式。網上能找到的(de) Asset Pricing 的(de)電子版還(hái)是 2000 年 6 月(yuè)的(de)版本，有不少 Typo。這(zhè)張截圖是來(lái)自 2005 年的(de)修訂版。怎麽樣？GMM 其實并不複雜(zá)，我們隻需要提供并計算(suàn) a，g_T，d 和(hé) S；有了(le)它們，GMM 框架 takes care of everything else！

最後對(duì)全文簡要總結如下(xià)：

寫完本文，我的(de)感受和(hé)寫完《股票(piào)多(duō)因子模型的(de)回歸檢驗》是一模一樣的(de)，對(duì) Cochrane 教授崇拜的(de)五體投地。關于 GMM 的(de)内容，Cochrane 教授在其 UChicago 的(de)課程中介紹的(de)非常生動、到位，聽(tīng)完再結合他(tā)的(de)書(shū)仔細體會，那收獲就一個(gè)字 —— 爽！

最後，我想用(yòng)和(hé)《股票(piào)多(duō)因子模型的(de)回歸檢驗》一文同樣的(de)結語作爲本文的(de)收尾。在介紹 Asset Pricing 這(zhè)門課的(de)時(shí)候，Cochrane 教授談到：

The math in real, academic, finance is not actually that hard. Understanding how to use the equations, and see what they really mean about the world... that's hard, and that's what I hope will be uniquely rewarding about this class.

再一次的(de)，我也(yě)真心希望本文在你理(lǐ)解 GMM 以及應用(yòng)它研究 asset pricing 的(de)道路上起到一點點幫助。

參考文獻

Cochrane, J. H (2005). Asset Pricing (revised edition). Princeton University Press.

Fama, E. F. and K. R. French (1993). Common Risk Factors in the Returns on Stocks and Bonds. Journal of Financial Economics 33(1), 3 – 56.

Hansen, L. P. (1982). Large sample properties of generalized method of moments estimators. Econometrica 50(4), 1029 – 1054.

Newey, W. K. and K. D. West (1987). A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 55(3), 703 – 708.

White, H. (1980). A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica 48(4), 817 – 838.

https://www.zhihu.com/question/41312883/answer/91484566?

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。