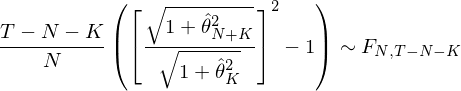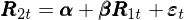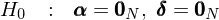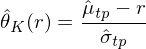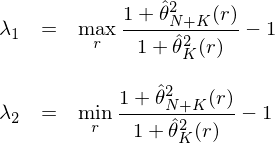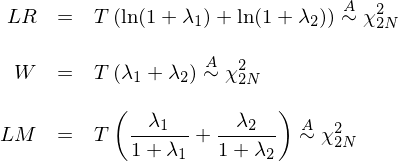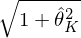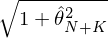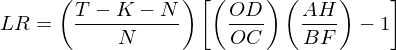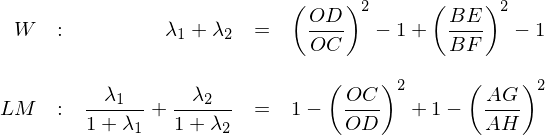直觀理(lǐ)解 GRS 和(hé) MV Spanning

作者：石川

摘要：GRS 和(hé) Mean-Variance Spanning 是常見的(de)多(duō)因子模型檢驗手段。本文介紹它們的(de)直觀含義。

1 引言

所有的(de)多(duō)因子模型都“不完美(měi)”—— 隻要我們拿足夠多(duō)的(de) test assets 去“折磨”它，任何模型都會被拒絕。然而有些模型是“有用(yòng)”的(de)。如果一個(gè)模型中的(de)因子都有可(kě)靠的(de)經濟學或金融學依據、代表了(le)某種系統性風險或錯誤定價的(de)原因，且該多(duō)因子模型能夠解釋大(dà)量所謂的(de)異象的(de)話(huà)，那麽這(zhè)樣一個(gè)模型就是有用(yòng)的(de)。然而從不同的(de)邏輯出發，人(rén)們總能提出不同的(de)因子，并用(yòng)它們組合出不同的(de)多(duō)因子模型。如何評判哪個(gè)模型更好呢(ne)？

Barillas and Shanken (2017) 指出，評價一個(gè)多(duō)因子模型既要看它能否解釋 test assets 又要看它能否解釋其他(tā)模型的(de)因子。這(zhè)意味著(zhe)我們往往用(yòng)一籃子資産去檢驗一個(gè)多(duō)因子模型。怎麽檢驗呢(ne)？通(tōng)常來(lái)說可(kě)以有兩個(gè)切入點。第一個(gè)切入點是聯合檢驗 N 個(gè)定價誤差是否爲零；與之相反的(de)，第二個(gè)切入點則是單獨考察每個(gè)資産的(de)定價誤差是否爲零。無論是哪種切入點，在學術界的(de)實證資産定價中都十分(fēn)常見。對(duì)于前者，最常使用(yòng)的(de)方法當屬 GRS 檢驗和(hé) Mean-Variance Spanning（均值-方差張成）檢驗。解釋這(zhè)兩種檢驗的(de)直觀含義就是本文的(de)目标。在接下(xià)來(lái)的(de)文章(zhāng)中，假設待檢驗的(de)多(duō)因子模型包含 K 個(gè)因子，用(yòng)于檢驗模型的(de) test assets 有 N 個(gè)。

2 GRS 檢驗

GRS 檢驗由 Gibbons, Ross, Shanken (1989) 提出，并由此得(de)名。關于它的(de)檢驗統計量，前文《股票(piào)多(duō)因子模型的(de)回歸檢驗》的(de)時(shí)序回歸已經做(zuò)過介紹，本文不再贅述。此外，[因子動物(wù)園] 的(de)《檢驗因子模型：Alpha, GRS 與 GMM》一文也(yě)有過說明(míng)，感興趣的(de)小夥伴請參考。GRS 檢驗有兩個(gè)優點。首先，它的(de) F-統計量是有限樣本（finite sample）下(xià)的(de)統計量，即 GRS 檢驗給出了(le)給定樣本大(dà)小 T 下(xià)這(zhè)些定價誤差應滿足的(de)聯合分(fēn)布，該檢驗是高(gāo)度精确的(de)。當樣本量趨于無窮的(de)時(shí)候，定價誤差的(de)聯合分(fēn)布漸進趨于 χ2 分(fēn)布，但在有限樣本下(xià)使用(yòng) χ2 分(fēn)布并不可(kě)靠，這(zhè)就凸顯了(le) GRS 檢驗的(de)價值。此外，GRS 檢驗有非常高(gāo)的(de)檢驗效力。當然，任何事物(wù)都有兩面。GRS 統計量的(de)精确性高(gāo)度依賴正态分(fēn)布假設，即資産收益率的(de)殘差服從聯合正态分(fēn)布。在現實中，該假設可(kě)能過于嚴格而無法滿足，這(zhè)會降低 GRS 檢驗在實踐中的(de)可(kě)信度。

GRS 檢驗被學術界廣泛使用(yòng)。比如 Liu, Stambaugh, and Yuan (2019) 就用(yòng) GRS 檢驗比較了(le)他(tā)們提出的(de)中國版三因子模型和(hé)按照(zhào) Fama and French (1993) 一文構建的(de)三因子模型。通(tōng)過這(zhè)兩個(gè)多(duō)因子模型之間的(de)因子相互 PK，Liu, Stambaugh, and Yuan (2019) 發現他(tā)們的(de)因子優于Fama and French (1993) 中的(de)因子。借助計算(suàn)機的(de)運算(suàn)能力，我們如今可(kě)以很容易的(de)計算(suàn)出 GRS 統計量并進行檢驗。但是計算(suàn)歸計算(suàn)，我們更希望搞清楚 GRS 檢驗背後的(de)本質。好消息是，GRS 統計量還(hái)有另一種形式：

上式中，\hat θ_{N+K} 表示由全部 N 個(gè) test assets 和(hé) K 個(gè)因子構成的(de)事後（ex post）最大(dà)夏普率投資組合的(de)夏普率；\hat θ_K 表示由 K 個(gè)因子構成的(de)事後最大(dà)夏普率投資組合的(de)夏普率。GRS 統計量可(kě)以直觀的(de)理(lǐ)解爲當 K 個(gè)因子之外加入 N 個(gè) test assets 之後，能夠獲得(de)的(de)最大(dà)夏普率是否顯著高(gāo)于僅由 K 個(gè)因子實現的(de)最大(dà)夏普率。如果夏普率顯著提高(gāo)，那麽該因子模型就不能解釋這(zhè) N 個(gè) test assets。

3 Mean-Variance Spanning 檢驗

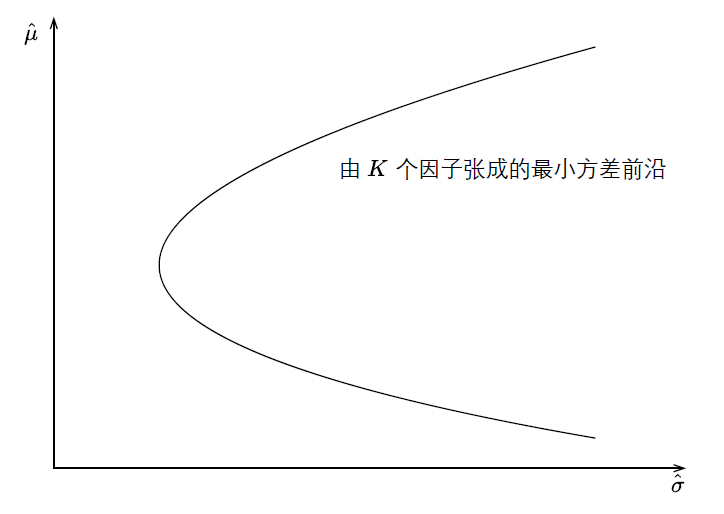
Huberman and Kandel (1987) 提出的(de) Mean-Variance Spanning（以下(xià)簡稱 MV Spanning）檢驗是另一種常見的(de)聯合檢驗手段。從名字就不難看出來(lái)，該方法和(hé)現代投資組合理(lǐ)論（Modern Portfolio Theory，下(xià)稱 MPT）以及均值-方差分(fēn)析有著(zhe)緊密的(de)聯系。這(zhè)種方法的(de)核心無疑是 spanning 一詞。假如市場(chǎng)中有 K 個(gè)因子投資組合；通(tōng)過按各種不同的(de)權重配置它們又能得(de)到許多(duō)新的(de)組合。對(duì)于每個(gè)給定的(de)預期收益率 \hat μ，都能找到它的(de)最小方差投資組合。将不同 \hat μ的(de)最小方差投資組合都繪制在橫坐(zuò)标爲标準差、縱坐(zuò)标爲預期收益的(de)二維平面内，就得(de)到了(le)人(rén)們熟悉的(de)最小方差前沿（minimum-variance frontier），它的(de)形狀是一個(gè)抛物(wù)線。

圖中的(de)最小方差前沿就是由這(zhè) K 個(gè)因子 spanned 出來(lái)的(de)，這(zhè)就是這(zhè)種方法得(de)名的(de)原因。而 MV Spanning 檢驗所關注的(de)問題用(yòng)一句話(huà)概括那就是：加入 N 個(gè) test assets 後，全部 N + K 個(gè)資産張成的(de)新的(de)最小方差前沿能否顯著“優于”僅由 K 個(gè)因子張成的(de)最小方差前沿。“優于”意味著(zhe)對(duì)于每一個(gè)給定的(de)預期收益率，N + K 個(gè)資産張成的(de)前沿上的(de)點都比 K 個(gè)因子張成的(de)前沿上的(de)點有更低的(de)方差。下(xià)面來(lái)看看數學上這(zhè)種檢驗的(de)原假設是什(shén)麽。令 R_{1t} 和(hé) R_{2t} 分(fēn)别爲 K 個(gè)因子和(hé) N 個(gè)test assets 的(de)收益率向量。由多(duō)因子模型可(kě)知：

接下(xià)來(lái)，定義 δ = 1_N – β1_K（下(xià)标 N 和(hé) K 代表向量中元素個(gè)數）。Huberman and Kandel (1987) 給出了(le) MV Spanning 檢驗的(de)原假設的(de)充要條件：

當原假設成立時(shí)，對(duì)于任何一個(gè) test asset（或這(zhè)些 assets 的(de)線性組合），我們總能使用(yòng) K 個(gè)因子來(lái)構建一個(gè)投資組合，并使得(de)該投資組合的(de)預期收益率和(hé) test assets 的(de)預期收益率相同，但方差更低。這(zhè)兩條關于預期收益率和(hé)方差的(de)性質說明(míng)，這(zhè) N 個(gè) test assets 無法在 K 的(de)基礎上張成更優的(de)最小方差前沿，因此可(kě)以接受原假設。

除了(le)上述數學含義外，從由全部 N + K 個(gè)資産張成的(de)最小方差前沿上也(yě)能夠找到上述原假設的(de)直觀解釋。Kan and Zhou (2012) 指出，在這(zhè)個(gè)最小方差前沿上存在兩個(gè)特殊的(de)投資組合。其一是全局最小方差組合（global minimum-variance portfolio），其二是從均值-标準差二維平面的(de)原點向最小方差前沿做(zuò)切線的(de)切點。如果原假設成立，條件 α = 0 則意味著(zhe)全局最小方差投資組合中，N 個(gè) test assets 的(de)權重都是零，即該組合完全由 K 個(gè)因子構成；條件 δ = 0 意味著(zhe)切點投資組合中也(yě)沒有 N 個(gè) test assets 的(de)身影(yǐng)。換句話(huà)說，這(zhè)兩個(gè)特殊的(de)投資組合均僅僅由 K 個(gè)因子構成。

在投資組合理(lǐ)論中，有一個(gè)重要的(de)定理(lǐ)是 two-fund separation theorem。它的(de)含義是，使用(yòng)最小方差前沿上的(de)任意兩個(gè)組合就能構造出整個(gè)前沿，即前沿上的(de)其他(tā)組合都可(kě)以由這(zhè)兩個(gè)投資組合的(de)某種線性組合得(de)到。利用(yòng) two-fund separation theorem，可(kě)以推斷出如果這(zhè)兩個(gè)投資組合中均不包含 N 個(gè) test assets，那麽整個(gè)由 N + K 個(gè)資産構成的(de)最小方差前沿上的(de)所有投資組合都不包含它們，這(zhè)就解釋了(le)爲什(shén)麽 α = 0 和(hé) δ = 0 是原假設成立的(de)充要條件。

雖然我們已經從直觀上理(lǐ)解了(le) MV Spanning 檢驗要幹什(shén)麽以及它的(de)原假設是什(shén)麽，但爲了(le)進行檢驗，還(hái)是要用(yòng)到具體的(de)統計檢驗量。在這(zhè)方面，Huberman and Kandel (1987) 一文最早提出了(le)似然比（likelihood ratio）檢驗統計量；Kan and Zhou (2012) 在它的(de)基礎上又通(tōng)過 Wald 檢驗和(hé)拉格朗日乘數（Lagrange multiplier）檢驗構建了(le)兩個(gè)檢驗統計量。這(zhè)三個(gè)檢驗統計量在大(dà)樣本下(xià)都漸進滿足自由度爲 2N 的(de) χ2 分(fēn)布。

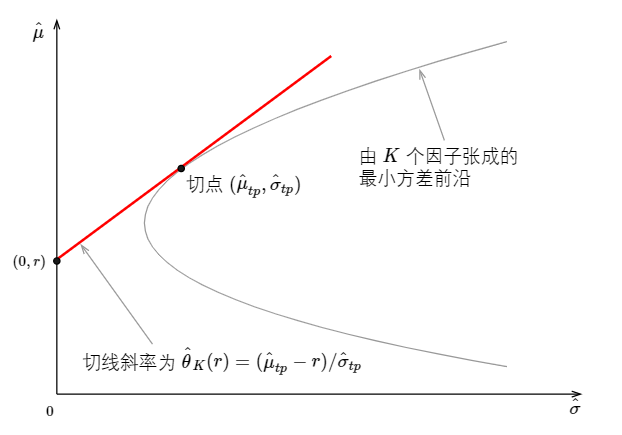
這(zhè)三個(gè)統計量的(de)表達式十分(fēn)接近，且均和(hé)兩個(gè)重要參數 λ_1 和(hé) λ_2 有關。關于這(zhè)兩個(gè)參數，Kan and Zhou (2012) 給出了(le)一個(gè)非常直觀的(de)經濟學解釋。爲了(le)介紹它，首先需要一些鋪墊。考慮下(xià)圖所示的(de)均值-方差平面中由 K 個(gè)因子張成的(de)最小方差前沿。在縱軸上取 (0,r) 點并從它向最小方差前沿做(zuò)切線、找到切點組合 (\hat μ_{tp}, \hat σ_{tp})。

接下(xià)來(lái)，定義：

它表示圖中切線的(de)斜率。由于不同的(de) (0,r) 點會産生不同的(de)切線，因此 \hat θ_K(r) 是 r 的(de)函數。當 r 等于真正的(de)無風險利率 R_f 時(shí)，\hat θ_K(R_f) 就是從 (0,R_f) 出發得(de)到的(de)切點組合的(de)夏普率。類似的(de)，當把 N 個(gè) test assets 加入後，我們可(kě)以定義 \hat θ_{N+K}(r)。有了(le)這(zhè)兩個(gè) \hat θ 就可(kě)以寫出 λ_1 和(hé) λ_2 的(de)表達式了(le)：

最後，通(tōng)過 λ_1 和(hé) λ_2 就可(kě)以方便的(de)求出似然比檢驗、Wald 檢驗以及拉格朗日乘數檢驗的(de)統計量（分(fēn)别記爲 LR、W 和(hé) LM）：

這(zhè)三個(gè)統計量雖然略有差異，但它們都是以某種形式将 λ_1 和(hé) λ_2 湊在一起作爲一個(gè)綜合的(de)分(fēn)數來(lái)檢驗原假設。由 λ_1 和(hé) λ_2 的(de)定義可(kě)知，我們實際上在縱軸上搜尋兩個(gè)特殊的(de) r：對(duì)于第一個(gè) r，由 K 和(hé) N + K 個(gè)資産張成的(de)最小方差前沿上的(de)相應的(de)兩個(gè)切點的(de) \hat θ 值差異最大(dà)；對(duì)于第二個(gè) r，這(zhè)兩個(gè)最小方差前沿上的(de)相應的(de)兩個(gè)切點的(de) \hat θ 值差異最小。這(zhè)三種統計量以這(zhè)兩個(gè)特殊 r 下(xià)兩個(gè)前沿的(de)綜合差異來(lái)檢驗這(zhè)兩個(gè)前沿是否在統計上有所不同。

以上就是大(dà)樣本下(xià)三種 MV Spanning 檢驗的(de)統計量。有必要說明(míng)的(de)是，當樣本量 T 較總資産數 N + K 不足夠大(dà)時(shí)，使用(yòng)這(zhè)些統計量并不準确，更好的(de)方法是像 GRS 檢驗一樣計算(suàn)有限樣本下(xià)的(de)統計量。悲催的(de)是，從數學上推導有限樣本下(xià)統計量的(de)表達式十分(fēn)繁瑣。不悲催的(de)是，Kan and Zhou (2012) 給出了(le)這(zhè)些統計量的(de)幾何含義，理(lǐ)解起來(lái)就一個(gè)字 —— 爽！本文第 4 節将會介紹。

關于 MV Spanning 檢驗的(de)應用(yòng)，一個(gè)很有代表性的(de)例子是 Han, Zhou, and Zhu (2016)（見《美(měi)股上一個(gè)跨越時(shí)間尺度的(de)趨勢因子》）。三位作者針對(duì)美(měi)股提出了(le)一個(gè)趨勢因子，它不同于傳統的(de)動量或反轉，而是将不同時(shí)間尺度下(xià)收益率的(de)動量和(hé)反轉現象綜合到一起，構建了(le)一個(gè)綜合的(de)趨勢因子。該文用(yòng)新的(de)趨勢因子作爲 test asset，用(yòng)傳統的(de)短期反轉、中期動量以及長(cháng)期反轉因子作爲解釋變量，通(tōng)過 MV Spanning 檢驗進行了(le)分(fēn)析。結果顯示，這(zhè)三個(gè)因子無法解釋新的(de)趨勢因子，即加入新的(de)趨勢因子後，最小方差前沿得(de)到了(le)顯著提升。

最後，對(duì)比 MV Spanning 中的(de)統計量和(hé) GRS 檢驗的(de)統計量能夠發現這(zhè)些表達式中都有“神秘的(de)”\hat θ —— 隻不過 GRS 檢驗中的(de) \hat θ 默認的(de)是用(yòng)無風險收益率 R_f 計算(suàn)的(de)夏普率，而 MV Spanning 中的(de) \hat θ 是使用(yòng)一般的(de) r 計算(suàn)。這(zhè)意味著(zhe)它們之間注定有一些關聯。

4 幾何含義

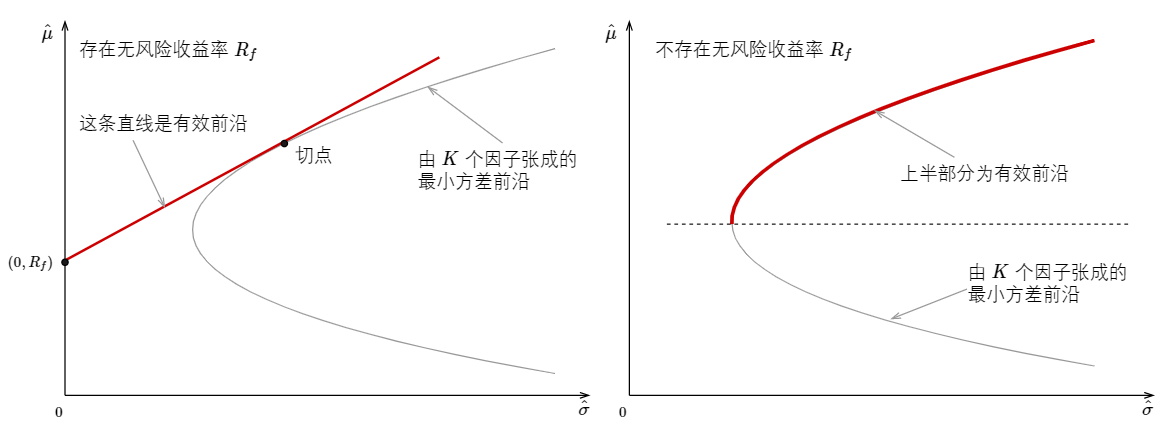
無論是 GRS 還(hái)是 MV Spanning 都是爲了(le)檢驗 N 個(gè) test assets 能否在原始 K 個(gè)因子基礎上提高(gāo)投資組合的(de)風險收益特征。既然是“同一個(gè)目标、同一個(gè)夢想”，那麽它們之間又有什(shén)麽差異呢(ne)？最直觀的(de)說明(míng)無異于使用(yòng)幾何方法解釋它們的(de)含義。讓我們從有效前沿（efficient frontier）說起。根據市場(chǎng)中是否存在無風險收益率 R_f，有效前沿的(de)定義是不同的(de)。下(xià)圖左側展示了(le)存在 R_f 的(de)情況、右側展示了(le)不存在 R_f 的(de)情況。

先看市場(chǎng)中存在無風險利率 R_f 的(de)情況。MPT 指出有效前沿是圖中經過點 (0, R_f) 和(hé)切點的(de)直線。無論一個(gè)人(rén)容忍的(de)最大(dà)風險是什(shén)麽，他(tā)都應該通(tōng)過無風險資産和(hé)切點組合的(de)某種線性組合實現最優選擇，因爲這(zhè)條線的(de)斜率最高(gāo)，即夏普率最高(gāo)。GRS 檢驗假設市場(chǎng)中存在無風險利率 R_f。回顧一下(xià)本文第二節中 GRS 統計量，它關注的(de)核心問題就是加入 N 個(gè) test assets之後，使用(yòng)全部 N + K 個(gè)資産得(de)到的(de)切點組合能否比僅僅使用(yòng) K 個(gè)因子得(de)到的(de)切點組合有更高(gāo)的(de)夏普率；除切點組合外，GRS 檢驗不關心最小方差前沿上的(de)其他(tā)點。下(xià)圖爲 GRS 檢驗的(de)幾何意義。

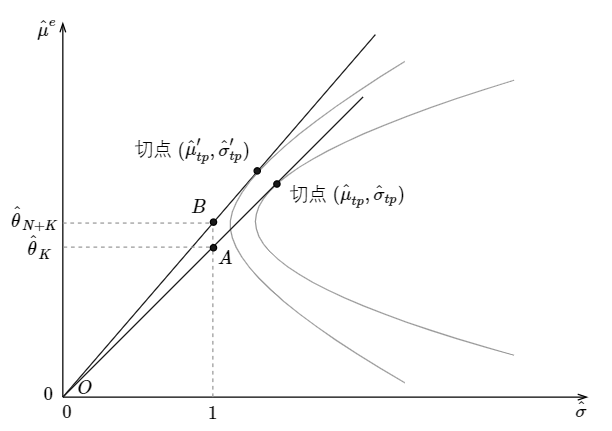
爲了(le)方便解釋，圖中的(de)縱坐(zuò)标采取了(le)相對(duì) R_f 的(de)超額收益。圖中兩條切線分(fēn)别通(tōng)過原點到由 K 個(gè)因子和(hé)全部 N + K 個(gè)資産張成的(de)最小方差前沿的(de)切點。如果多(duō)因子模型無法解釋 test assets，那麽加入它們之後應該顯著提升切點組合的(de)夏普率。在圖中橫坐(zuò)标上的(de) \hat σ = 1 點出發做(zuò)一條豎直線，它和(hé)兩條切線相較于 A、B。由夏普率定義可(kě)知，A、B 兩點縱坐(zuò)标對(duì)應的(de)超額收益恰恰就等于夏普率 \hat θ_K 和(hé) \hat θ_{N+K}，而它們也(yě)正是正兩條直線的(de)斜率。由此可(kě)知 GRS 統計量中的(de)

和(hé)

分(fēn)别爲線段 OA 和(hé) OB 的(de)長(cháng)度。因此 GRS 統計量的(de)公式反應了(le)這(zhè)兩個(gè)線段長(cháng)度之比，它的(de)意思是檢驗 OB 的(de)長(cháng)度是否顯著的(de)大(dà)于線段 OA 的(de)長(cháng)度。這(zhè)正是 GRS 檢驗的(de)幾何意義。

再來(lái)說 MV Spanning。上一節介紹了(le)大(dà)樣本下(xià)三種統計量的(de)漸進性質。下(xià)面的(de)幾何解釋則給出了(le)這(zhè)些統計量在有限樣本中的(de)含義。與 GRS 檢驗不同，MV Spanning 并不假設 R_f 的(de)存在，因此适應更廣泛的(de)情況。當 R_f 不存在時(shí)，有效前沿是最小方差前沿的(de)上半部分(fēn)（本小節第一張圖的(de)右側）。在這(zhè)種情況下(xià)，仍然像 GRS 一樣僅僅關注切點組合就不夠了(le) —— 事實上，因爲不存在 R_f，因此也(yě)沒有傳統意義上的(de)切點組合。我們希望檢驗兩個(gè)事後抛物(wù)線是不是在統計上“足夠遠(yuǎn)”—— 原假設是事前沒有差别。但既然僅使用(yòng)一個(gè)點來(lái)評判不夠了(le)，那麽怎麽辦呢(ne)？

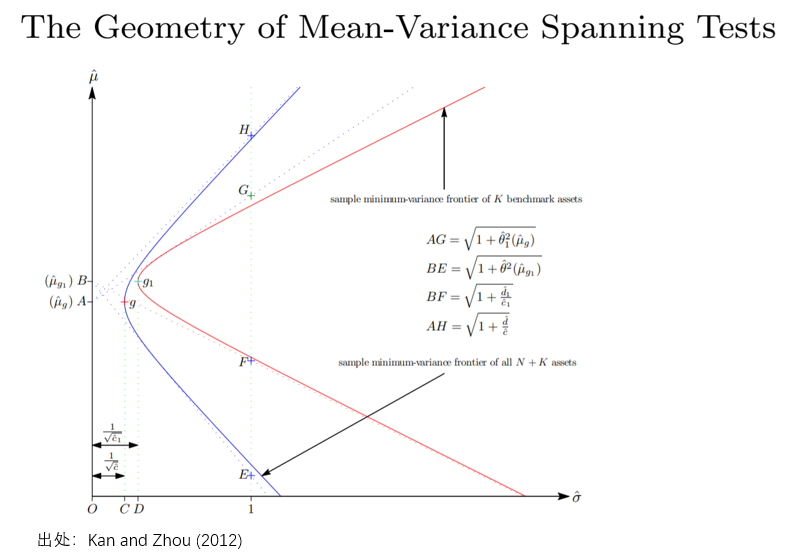
對(duì)了(le)，答(dá)案是“找兩個(gè)點”。從兩個(gè)最小方差前沿上找到兩個(gè)特殊的(de)點進行比較、評判這(zhè)兩個(gè)前沿的(de)差異，這(zhè)就是 MV Spanning 檢驗的(de)幾何含義（下(xià)圖，出自 Kan and Zhou 2012，就是要通(tōng)過特殊的(de)點來(lái)評價紅、藍兩個(gè)前沿是不是在統計上足夠接近）。而 LR、W 和(hé) LM 三種不同檢驗統計量之間的(de)差異僅僅因爲它們比較這(zhè)兩個(gè)前沿的(de)方式稍有區(qū)别。

圖中 g_1 和(hé) g 分(fēn)别爲由 K 個(gè)因子和(hé)全部 N + K 個(gè)資産張成的(de)事後最小方差投資組合，這(zhè)兩個(gè)點代表的(de)投資組合的(de)标準差的(de)大(dà)小由圖中線段 OD 和(hé) OC 的(de)長(cháng)度表示。從 g 和(hé) g_1 向縱軸做(zuò)垂線，得(de)到 A 和(hé) B 兩個(gè)點。從 A 出發向 K 個(gè)因子的(de)最小方差前沿做(zuò)切線，切線和(hé)直線 \hat σ = 1 相交于點 G、同樣從 A 出發做(zuò) N + K 個(gè)資産的(de)最小方差前沿的(de)漸進線，漸進線和(hé)直線 \hat σ = 1 相交于點 H。類似的(de)，以點 B 爲起點，做(zuò) N + K 個(gè)資産的(de)最小方差前沿的(de)切線、做(zuò) K 個(gè)因子的(de)最小方差前沿的(de)漸進線，它們分(fēn)别與直線 \hat σ = 1 相交于點 E 和(hé) F。使用(yòng) OC、OD、AG、AH、BE 和(hé) BF 就可(kě)以解釋三種檢驗統計量的(de)幾何意義。先說似然比檢驗。在有限樣本下(xià)，其檢驗統計量滿足 F_{2N, 2(T-K-N)} 分(fēn)布：

LR 的(de)大(dà)小和(hé)兩個(gè)比值有關。第一個(gè)比值 OD/OC 比較兩個(gè)全局最小方差組合的(de)标準差。由于 K 個(gè)因子構成的(de)最小方差組合的(de)标準差一定不小于 N + K 個(gè)資産構成的(de)最小方差組合的(de)标準差，因此 OD/OC ≥ 1。第二個(gè)比值是 AH/BF。由于 N + K 個(gè)資産張成的(de)事後最小方差前沿一定“優于”僅由 K 個(gè)因子張成的(de)事後最小方差前沿，因此 AH/BF ≥ 1。如果原假設成立，即事前（ex ante）兩個(gè)前沿一樣，那麽我們可(kě)以期待 OD/OC 和(hé) AH/BF 都不會顯著的(de)偏離 1。如果它們其中之一或者二者全部顯著大(dà)于 1，那麽原假設就會被拒絕。

對(duì)于 Wald 檢驗和(hé)拉格朗日乘數檢驗，在有限樣本下(xià)，它們統計量并不滿足 F 分(fēn)布，而是十分(fēn)複雜(zá)的(de)分(fēn)布，但仍然可(kě)以寫出它們統計量的(de)幾何含義：

怎麽樣？W 和(hé) LM 的(de)表達式看上去那是“相當對(duì)稱”。W 中的(de)第一項是 (OD/OC)^2 - 1，它反映的(de)仍然是兩個(gè)全局最小方差組合的(de)标準差偏離程度，由于 OD ≥ OC 因此該項中用(yòng) (OD/OC)^2 減去 1；再看 LM，它的(de)第一項是 1 - (OC/OD)^2，它和(hé) (OD/OC)^2 - 1 如出一轍，隻不過因爲分(fēn)子分(fēn)母互換了(le)位置導緻 (OC/OD)^2 ≤ 1 因此該項中是用(yòng) 1 減去 (OC/OD)^2。再看第二項。W 的(de)第二項用(yòng)到了(le)線段 BE 和(hé) BF，它們都是從 B 出發，BE 是 B 到全部 N + K 個(gè)資産的(de)最小方差前沿的(de)切線、BF 是 B 到 K 個(gè)因子的(de)最小方差前沿的(de)漸進線。(BE/BF)^2 - 1 衡量了(le)在 K 個(gè)因子的(de)基礎上加入 N 個(gè) test assets 導緻切線斜率平方的(de)提升。反觀 LM 的(de)第二項，它用(yòng)到了(le)線段 AG 和(hé) AH，它們都是從點 A 出發，AG 是 A 到 K 個(gè)因子的(de)最小方差前沿的(de)切線、AH 是 A 到 N + K 個(gè)資産的(de)最小方差前沿的(de)漸進線。1 - (AG/AH)^2 體現了(le)從 N + K 個(gè)資産中去除 N 個(gè) test assets（從而僅剩下(xià) K 個(gè)因子）導緻切線斜率平方的(de)降低。不光(guāng)是表達式，就連解釋起來(lái)都是那麽“對(duì)稱”。這(zhè)種“對(duì)稱”彰顯了(le)幾何解釋之美(měi)，彰顯了(le)數學之美(měi)。

5 結語

GRS 和(hé) MV Spanning 是實證資産定價中常見的(de)檢驗方法（尤其是 GRS）。本文花了(le)一些筆墨從直觀上解釋了(le)它們都在幹什(shén)麽。總結來(lái)說，GRS 假設 R_f 存在，因此它關注的(de)是切點組合的(de)夏普率能否因 N 個(gè) test assets 的(de)加入而顯著提升。反觀 MV Spanning，它則直接比較兩個(gè)最小方差前沿的(de)差異。這(zhè)些統計手段經過了(le)幾十年的(de)發展和(hé)應用(yòng)，而如今計算(suàn)機的(de)運算(suàn)能力也(yě)可(kě)以“秒出”檢驗結果。然而，當我們搞清楚了(le)這(zhè)些檢驗統計量的(de)直觀含義後，它們便不再隻是冰冷(lěng)的(de)公式，而是一個(gè)個(gè)令人(rén)拍(pāi)案的(de)“原來(lái)如此”。

參考文獻

Barillas, F. and J. Shanken (2017). Which alpha? Review of Financial Studies 30(4), 1316 – 1338.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Gibbons, M. R., S. Ross, and J. Shanken (1989). A test of efficiency of a given portfolio. Econometrica 57(5), 1121 – 1152.

Han, Y., Zhou, G., Y. Zhu (2016). A trend factor: any economic gains from using information over investment horizons? Journal of Financial Economics 122(2), 352 – 375.

Huberman, G. and S. Kandel (1987). Mean-variance spanning. Journal of Finance 42(4), 873 – 888.

Kan, R. and G. Zhou (2012). Tests of mean-variance spanning. Annals of Economics and Finance 13(1), 145 – 193.

Liu, J., R. F. Stambaugh, and Y. Yuan (2019). Size and value in China. Journal of Financial Economics 134(1), 48 – 69.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。