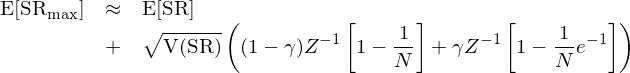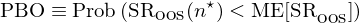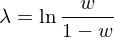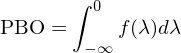定量計算(suàn)過拟合概率

作者：石川

摘要：金融數據的(de)信噪比極低，使得(de)過拟合成爲回測中的(de)必然。本文介紹一個(gè)量化(huà)分(fēn)析框架，它可(kě)以計算(suàn)回測中過拟合的(de)概率，有助于評價量化(huà)策略的(de)有效性。

1 引言

衆所周知，金融數據中的(de)信噪比極低。當我們在回測中嘗試了(le)大(dà)量的(de)參數時(shí)、或是在選股時(shí)測試了(le)大(dà)量的(de)因子後，找出來(lái)效果最好的(de)一組參數或者一個(gè)因子總能獲得(de)非常不錯的(de)效果。但這(zhè)大(dà)概率是因爲它們僅僅是對(duì)回測期内的(de)噪音(yīn)精準建模了(le)。

If the researcher tries a large enough number of strategy configurations, a backtest can always be fit to any desired performance for a fixed sample length.

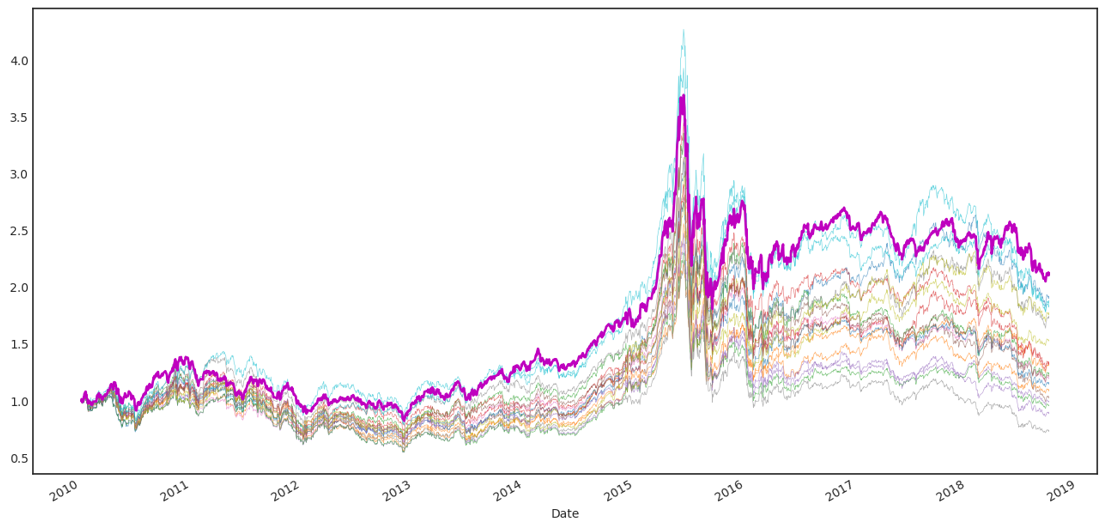
來(lái)看一個(gè)例子。以中證 500 的(de)成分(fēn)股爲選股池、2010 年 1 月(yuè)到 2018 年 10 月(yuè)爲回測期，評價不同的(de)選股因子 —— 以該因子選出的(de)前 50 支股票(piào)構建純多(duō)頭的(de)投資組合的(de)最終淨值評價因子的(de)效果。當測試了(le) 20 個(gè)不同的(de)因子後，最優秀的(de)因子的(de)淨值爲 2.29（同期中證 500 指數淨值僅爲 1.06）。這(zhè) 20 個(gè)因子的(de)淨值如下(xià)圖所示（紫色加粗的(de)是最好的(de)那個(gè)）。

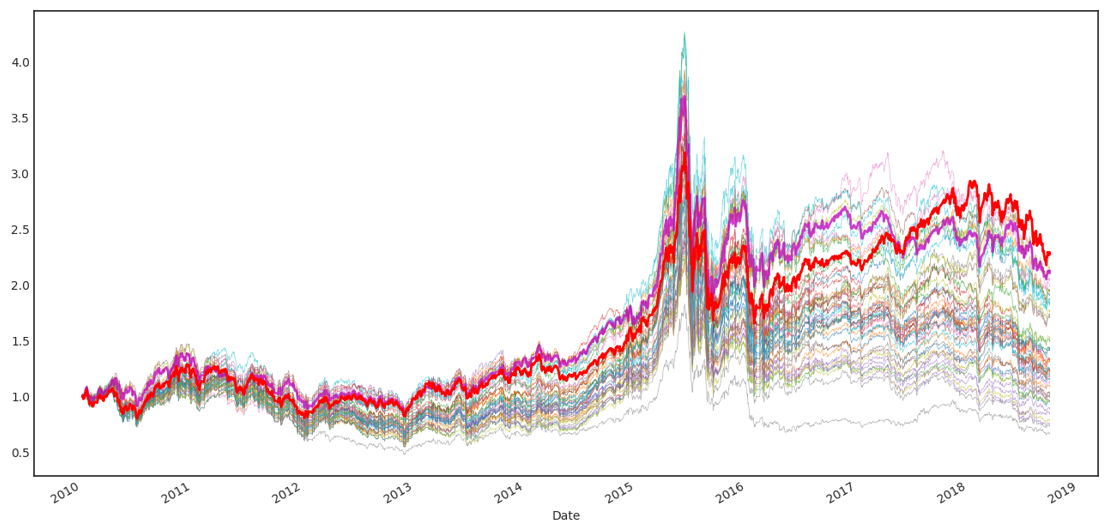
如果把測試因子的(de)個(gè)數從 20 個(gè)上升至 50 個(gè)，選股效果進一步提升，最好因子的(de)淨值從 2.29 上升至 2.40。下(xià)圖是 50 個(gè)因子（包括最開始的(de) 20 個(gè)）的(de)選股效果，紫色加粗曲線依然爲前 20 個(gè)因子中最好的(de)、紅色加粗曲線爲這(zhè) 50 個(gè)因子中最好的(de)。

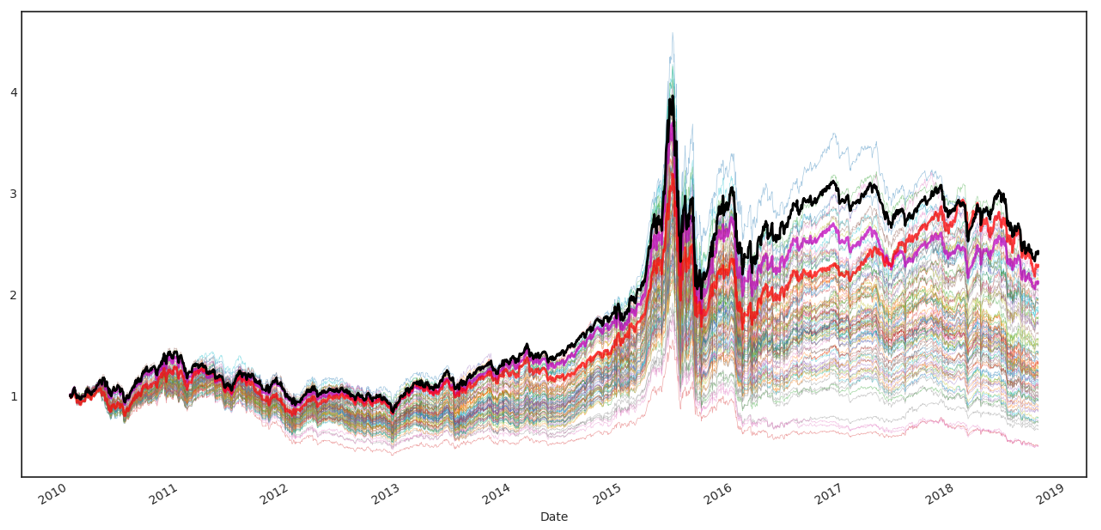
最後，我們把測試的(de)個(gè)數上升至 100（這(zhè)是一個(gè)任何量化(huà)選股報告中都會輕易突破的(de)因子個(gè)數）。這(zhè) 100 個(gè)因子中（包括之前 50 個(gè)），最好的(de)因子的(de)淨值爲 2.43，在前 50 個(gè)因子的(de)基礎上進一步提高(gāo)了(le)。下(xià)圖中黑(hēi)色加粗曲線代表了(le)全部 100 個(gè)因子中最好的(de)那個(gè)的(de)選股淨值。

考慮到這(zhè)些因子之間不是完全相關，如果我們把這(zhè)三個(gè)因子結合起來(lái)再配合更複雜(zá)的(de)交易算(suàn)法，一定能在回測期内獲得(de)更好的(de)選股效果。但是，如果僅僅因爲最終的(de)策略中隻用(yòng)了(le)三個(gè)因子就認爲沒有過拟合，那就大(dà)錯特錯了(le)，因爲在發現這(zhè)三個(gè)因子的(de)背後是 97 次失敗的(de)嘗試。

當進行 multiple hypotheses testing 時(shí)（同時(shí)檢驗很多(duō)不同的(de)假設），效果最好的(de)那個(gè)即便在統計上非常顯著（比如有很低的(de) p-value 或者很高(gāo)的(de) t-statistic），它是 false discovery 的(de)概率仍然很高(gāo)（見《出色不如走運 (II)》）。不幸的(de)是，這(zhè)是金融圈學術界普遍存在的(de)問題。學者們在頂刊上發表一個(gè)有效策略或者因子的(de)時(shí)候，并不告訴讀者這(zhè)個(gè)發現的(de)背後經曆了(le)多(duō)少失敗的(de)嘗試。失敗的(de)嘗試越多(duō)，這(zhè)個(gè)發現其實是虛假的(de)概率就越高(gāo)。當我們樂(yuè)此不疲的(de)測試不同的(de)參數組合或者嘗試不同的(de)因子時(shí)，其實隻是在做(zuò)一件事 —— 過拟合。最終被挑出來(lái)的(de)往往是過拟合帶來(lái)的(de) false discovery。回測中過拟合的(de)直接結果就是無法準确評價策略在樣本外的(de)效果。如果過拟合非常嚴重，即策略本身就是針對(duì)噪音(yīn)構建的(de)，那麽它可(kě)能在實盤中是完全失效的(de)、等待它的(de)隻有虧損。

鑒于過拟合的(de)普遍存在以及過拟合的(de)嚴重後果，如何量化(huà)回測中過拟合的(de)概率（Probability of Backtest Overfitting，簡稱 PBO）就顯得(de)至關重要。本文就來(lái)介紹一種定量計算(suàn)回測中過拟合概率的(de)方法。讓我們從夏普率（Sharpe Ratio，簡稱 SR）說起。

2 圍繞夏普率的(de)討(tǎo)論

爲計算(suàn)回測的(de)過拟合概率，需要比較不同參數下(xià)策略的(de)效果；而爲了(le)比較不同策略的(de)效果，就必須選定一個(gè)适當的(de)指标。在衆多(duō)評價投資策略的(de)指标中，夏普率無疑是最重要的(de)，它是下(xià)文介紹的(de)這(zhè)個(gè)計算(suàn) PBO 框架中使用(yòng)的(de)策略評價指标。值得(de)一提的(de)是，這(zhè)個(gè)框架本身不依賴于選擇的(de)指标，因此使用(yòng)者也(yě)可(kě)以嘗試其他(tā)評價策略的(de)指标。關于回測的(de)過拟合如何誇大(dà)夏普率（inflated Sharpe Ratio），學術界和(hé)業界有一些有意思的(de)討(tǎo)論。這(zhè)裏不妨做(zuò)個(gè)簡單梳理(lǐ)

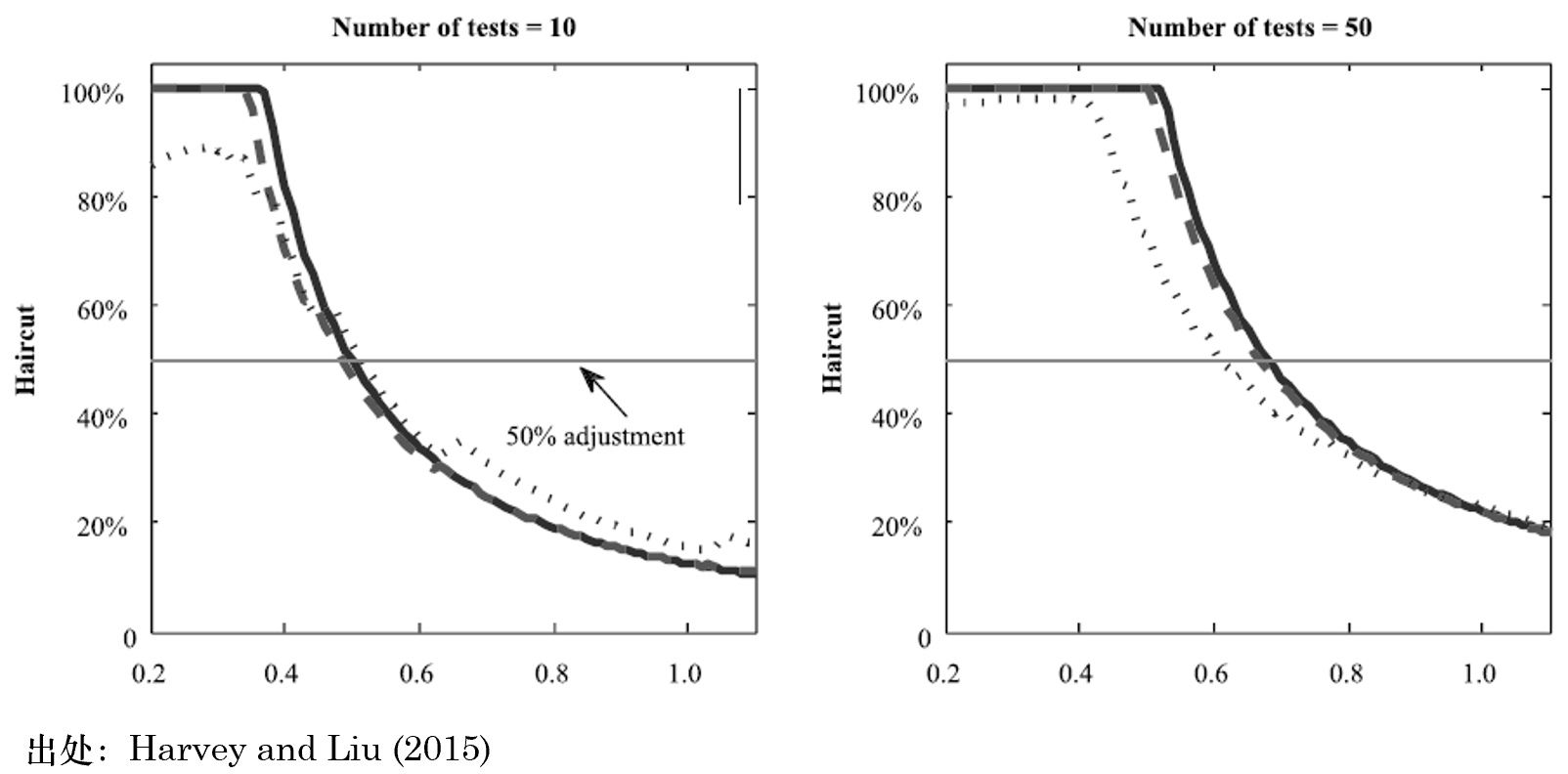
一般的(de)經驗認爲策略在實盤中的(de)夏普率是其在回測期内夏普率的(de) 50%。Harvey and Liu (2015) 定量計算(suàn)了(le)不同大(dà)小的(de)夏普率在樣本外的(de)“打折程度”（他(tā)們稱爲 haircut），發現了(le) haircut 和(hé) Sharpe Ratio 之間的(de)非線性關系。打折程度 Haircut 的(de)取值在 0 到 1 之間，等于 1 意味著(zhe) 100% 折扣，即樣本外的(de)夏普率爲零。下(xià)圖來(lái)自 Harvey and Liu (2015)，顯示了(le)回測期内不同 number of tests（如測試的(de)因子的(de)個(gè)數，或者參數組的(de)個(gè)數）時(shí)，Haircut 和(hé)夏普率的(de)關系。三條不同的(de)曲線代表三種不同的(de)考慮 multiple testing 影(yǐng)響的(de)方法（分(fēn)别爲 Bonferroni、Holm 以及 BHY 調整）。從圖中不難看出，當樣本内的(de)夏普率很小時(shí)，由于過拟合的(de)存在，打折率爲 1，即樣本外的(de)夏普率爲零。這(zhè)種情況随著(zhe) number of tests 的(de)增加而加重。

除此之外，Bailey 和(hé) Lopez de Prado 兩位學者也(yě)討(tǎo)論了(le) inflated Sharpe Ratio 的(de)問題（Bailey and Lopez de Prado 2012, 2014）。在構建量化(huà)策略時(shí)，人(rén)們往往選定一個(gè)策略類型，比如趨勢追蹤或者統計套利，然後在給定的(de)模型下(xià)使用(yòng)曆史數據尋找最優的(de)參數。在這(zhè)個(gè)前提下(xià)，Bailey 和(hé) Lopez de Prado 假設不同參數的(de)策略的(de)夏普率滿足均值爲 E[SR]、方差爲 V(SR) 的(de)正态分(fēn)布。在這(zhè)個(gè)假設下(xià)，他(tā)們計算(suàn)得(de)出 N 組不同的(de)參數中得(de)到的(de)最大(dà)的(de)夏普率的(de)期望滿足：

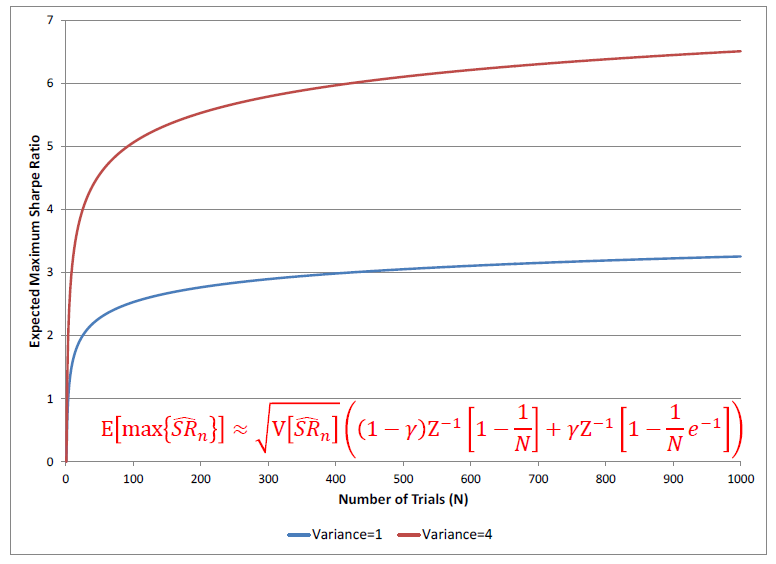
上式中 γ 是歐拉-馬斯刻若尼常數（Euler-Mascheroni constant），約爲 0.5772；Z 爲标準正态分(fēn)布的(de)累積密度函數。從上式不難看出，樣本内的(de)最大(dà)夏普率随 N 增大(dà)和(hé) V(SR) 增大(dà)。下(xià)圖顯示了(le)當 E[SR] = 0 時(shí)，僅僅靠增加 N 和(hé) V(SR) 就可(kě)以逐漸提升最優夏普率。增大(dà) N 對(duì)應著(zhe)在回測中增加 number of tests，增大(dà) V(SR) 對(duì)應著(zhe)完全不考慮業務依據而漫無目的(de)的(de)擴大(dà)參數的(de)取值範圍。這(zhè)些都是造成過拟合的(de)原因。

以上的(de)介紹說明(míng)，過拟合不可(kě)避免的(de)高(gāo)估了(le)策略的(de)夏普率，這(zhè)會影(yǐng)響對(duì)策略有效性的(de)評判。因此，定量計算(suàn)回測中過拟合的(de)概率就顯得(de)非常有必要。它要回答(dá)的(de)不是一個(gè)“是”或者“否”的(de)問題（回測都存在過拟合了(le)），而是定量的(de)評價過拟合的(de)程度。

3 定量計算(suàn)過拟合概率

本節介紹 Bailey et al. (2017) 提出的(de)計算(suàn)回測中過拟合概率的(de)框架。首先來(lái)定義 Probability of Backtest Overfitting。假設一共有 N 組不同的(de)參數構建的(de)策略，令 n* 代表樣本内表現最好的(de)那組參數（最好意味著(zhe)樣本内 SR 最高(gāo)，或者其他(tā)類似的(de)指标）；令 SR_OOS(n) 表示第 n 組參數在樣本外的(de)夏普率（下(xià)标 OOS 意爲 out of sample），令 ME[SR_OOS] 表示所有 N 組參數在樣本外夏普率的(de)中位數；Probability of Backtest Overfitting（PBO）的(de)定義如下(xià)：

由于樣本内存在過拟合，因此樣本内的(de)最優參數不一定是樣本外最好的(de)。回測中過拟合的(de)概率 PBO 的(de)定義爲樣本内最優參數 n* 在樣本外的(de)夏普率小于所有 N 組參數在樣本外夏普率的(de)中位數的(de)概率。有了(le) PBO 的(de)定義，下(xià)面馬上來(lái)介紹計算(suàn) PBO 的(de)框架。它的(de)名字叫 Combinatorially-Symmetric Cross-Validation（組合對(duì)稱交叉驗證，簡稱 CSCV）。假設我們一共測試了(le) N 組參數，回測期長(cháng)度爲 T。CSCV 由以下(xià)步驟構成：

通(tōng)過考察 PBO 的(de)大(dà)小，就能夠定量的(de)評價一個(gè)策略是否靠譜：真正有效的(de)策略的(de) PBO 應該較小。CSCV 的(de)發明(míng)者之一 Dr. Marcos Lopez de Prado 指出該方法具有以下(xià)優點：

接下(xià)來(lái)就通(tōng)過一個(gè)例子來(lái)應用(yòng) CSCV。

4 一個(gè)例子

在《從 CTA 趨勢策略的(de)表現看量化(huà)投資面臨的(de)挑戰》一文中，我們使用(yòng) 15 種商品期貨的(de)指數定性分(fēn)析了(le)過去 5 年趨勢追蹤策略的(de)表現。該文的(de)實證采用(yòng)的(de)是最簡單的(de)雙均線策略 —— 短周期均線上穿長(cháng)周期均線策略時(shí)做(zuò)多(duō)；短周期均線下(xià)穿長(cháng)周期均線時(shí)做(zuò)空。長(cháng)、短周期就是策略的(de)兩個(gè)待優化(huà)的(de)參數（由 LW 和(hé) SW 表示）。下(xià)面就使用(yòng)本文介紹的(de)框架來(lái)計算(suàn)優化(huà)這(zhè)兩個(gè)參數時(shí)的(de)過拟合概率。

在回測中，令短周期均線參數 SW 的(de)取值範圍爲 1 到 20、長(cháng)周期均線參數 LW 的(de)取值範圍是 SW + 1 到 50，步長(cháng)均爲 1，因此一共有 790 組參數（N = 790）。令回測長(cháng)度爲 1000 個(gè)交易日。使用(yòng)這(zhè) 790 組參數分(fēn)别進行回測，得(de)到每組參數下(xià)策略在這(zhè) 1000 個(gè)交易日内的(de)收益率序列，從而構建原始的(de) M 矩陣（1000 × 790 階）。

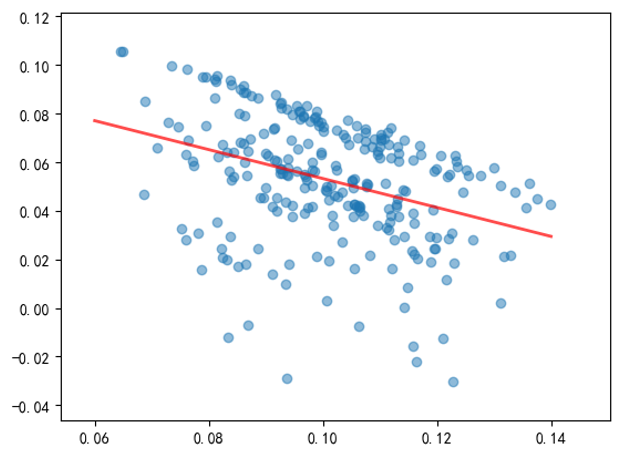
使用(yòng)第四節介紹的(de) CSCV 框架分(fēn)析 M 矩陣，假設分(fēn)析中 S = 10，因此一共有 252 種（10 選 5）回測 + 測試集的(de)配對(duì)。在計算(suàn) PBO 之前我們先來(lái)做(zuò)一個(gè)實驗。對(duì)于每一種配對(duì)，求出樣本内最優參數的(de)夏普率和(hé)該組參數在樣本外的(de)夏普率，這(zhè)兩個(gè)夏普率便構成一個(gè)樣本點，因此一共有 252 個(gè)樣本點。這(zhè) 252 個(gè)點的(de)散點圖如下(xià)（其中紅線爲回歸得(de)到的(de)線性關系）：

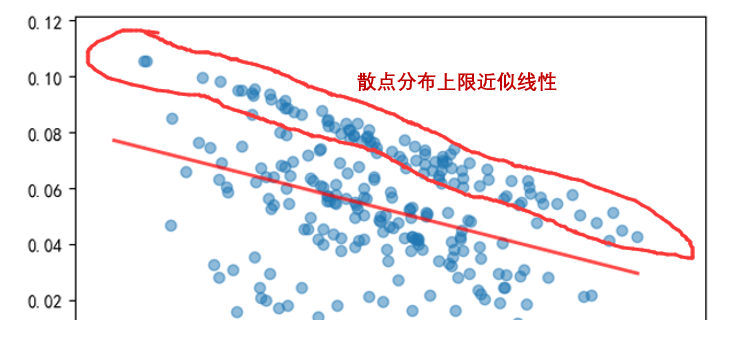
樣本内最優參數的(de)夏普率和(hé)其在樣本外的(de)夏普率之間的(de)相關系數爲 -0.36；上述回歸直線的(de)斜率爲負也(yě)說明(míng)了(le)這(zhè)種負相關關系。這(zhè)說明(míng)，對(duì)于這(zhè)個(gè)雙均線趨勢策略，樣本内最好的(de)參數傾向于在樣本外有更差的(de)表現。在進一步使用(yòng) CSCV 計算(suàn) PBO 之前，我們觀察到上圖中存在一些不正常的(de)現象 —— 這(zhè)些散點的(de)分(fēn)布區(qū)域的(de)上限似乎近似的(de)坐(zuò)落在一條直線上（下(xià)圖），意味著(zhe)這(zhè)些點對(duì)應的(de)訓練集和(hé)測試集的(de)夏普率之和(hé)大(dà)緻相同。

出現這(zhè)種現象的(de)原因是趨勢策略非常依賴價格序列的(de)路徑。在整個(gè) 1000 個(gè)交易日的(de)回測期内，趨勢策略掙錢的(de)表現集中在某些特定的(de)時(shí)間。當我們采用(yòng) CSCV 将這(zhè) 1000 個(gè)交易日劃分(fēn)成 252 個(gè)長(cháng)度各爲 500 的(de)訓練集、測試集配對(duì)時(shí)，這(zhè)其中有相當一部分(fēn)的(de)訓練集都包含了(le)趨勢策略最賺錢的(de)那些特定時(shí)間，使得(de)這(zhè)些訓練集中的(de)最優參數相同。

對(duì)于這(zhè)些訓練集、測試集配對(duì)，它們的(de) n* 相同，因此它們在樣本内、外全部 1000 個(gè)交易日内收益率的(de)均值都是來(lái)自策略 n*，即均值相同。雖然這(zhè)些配對(duì)中的(de)訓練集和(hé)測試集不盡相同，但由于收益率的(de)波動率在整個(gè)回測期内較爲穩定，因此訓練集和(hé)測試集内的(de)夏普率之和(hé)近似的(de)等于這(zhè)兩個(gè)序列中收益率均值之和(hé)。綜合以上兩點就能夠解釋爲什(shén)麽這(zhè)些配對(duì)的(de)樣本内、外夏普率之和(hé)非常接近。由于它們對(duì)應的(de) n* 恰好又是整段回測期内效果最好的(de)參數，因此這(zhè)些配對(duì)的(de)散點構成了(le)上圖中散點分(fēn)布中不正常的(de)線性上限。

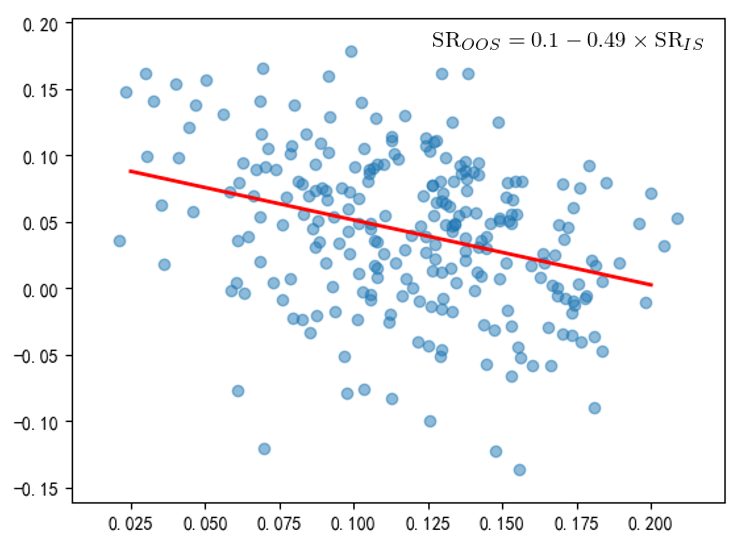
爲了(le)減弱路徑依賴對(duì)評判趨勢策略過拟合程度的(de)影(yǐng)響，我們對(duì) CSCV 進行适當的(de)改進，引入一定的(de)随機性。在 CSCV 的(de)第三、四步，不是考慮所有可(kě)能的(de)組合，而是随機的(de)構建訓練集和(hé)測試集。具體的(de)，将長(cháng)度 1000 的(de)回測期分(fēn)成 50 個(gè)長(cháng)度爲 20 個(gè)交易日的(de)子集。從這(zhè) 50 個(gè)子集中，随機選出 13 個(gè)作爲測試集、13 個(gè)作爲訓練集（13 這(zhè)個(gè)數并沒有什(shén)麽特殊的(de)含義），因此訓練集和(hé)測試集的(de)長(cháng)度各爲 260 個(gè)交易日。将上述過程重複 250 次，得(de)到 250 個(gè)訓練集、測試集配對(duì)，然後計算(suàn) λ 的(de)經驗分(fēn)布 f(λ) 以及 PBO。引入随機性後，再次畫(huà)出樣本内最優參數的(de)夏普率和(hé)它在樣本外的(de)夏普率的(de)散點圖（下(xià)圖），原始結果中不正常的(de)線性上限消失了(le)。回歸方程的(de)斜率是 -0.49，說明(míng)樣本内、外的(de)夏普率之間存在負相關性。

此外，λ 的(de)經驗分(fēn)布 f(λ) 如下(xià)圖所示：

通(tōng)過 f(λ) 求出 PBO = 0.572 —— 在使用(yòng)雙均線構建趨勢追蹤策略時(shí)，回測中過拟合的(de)概率高(gāo)達 0.572。一個(gè)靠譜的(de)策略的(de) PBO 不應該這(zhè)麽高(gāo)。因此，在使用(yòng)雙均線構建趨勢策略時(shí)必須格外小心。本節的(de)例子說明(míng)使用(yòng) CSCV 這(zhè)個(gè)框架能夠方便的(de)計算(suàn)出 PBO，從而評價一個(gè)策略是不是靠譜。此外，本節花了(le)一定的(de)篇幅指出了(le)趨勢策略的(de)路徑依賴對(duì) CSCV 結果造成的(de)影(yǐng)響。通(tōng)過它想要強調的(de)是，再先進的(de)統計方法也(yě)不應該代替我們的(de)獨立思考，我們必須爲自己的(de)回測結果負責。

5 結語

2005 年，發表于 PLoS Medicine 上的(de)一篇題爲 Why most published research findings are false 的(de)文章(zhāng)（Ioannidis 2005）引起了(le)廣泛的(de)關注。該文指出科學界，特别是醫學界有相當一部分(fēn)所謂的(de)顯著發現都是錯誤的(de)。而原因之一正是經過大(dà)量測試後找出的(de)那個(gè)最顯著的(de)往往是 false discovery。2015 年醫學界最權威的(de)同行評審期刊之一柳葉刀(dāo)（The Lancet）的(de)主編 Dr. Horton 指出醫學界一半的(de)研究成果是錯誤的(de)（Horton 2015）。

The case against science is straightforward: much of the scientific literature, perhaps half, may simply be untrue. Afflicted by studies with small sample sizes, tiny effects, invalid exploratory analyses, and flagrant conflicts of interest, together with an obsession for pursuing fashionable trends of dubious importance, science has taken a turn towards darkness.

雖然比醫學界晚了(le)差不多(duō) 10 年，但幸運的(de)是，金融圈也(yě)已經意識到了(le) multiple testing 帶來(lái)了(le)太多(duō)的(de)虛假發現（例如并不能掙錢的(de)策略，或者是不能解釋預期收益率截面差異的(de)因子）。以 Dr. Campbell Harvey（學術界 —— 杜克大(dà)學商學院教授、前美(měi)國金融協會主席）和(hé) Dr. Marcos Lopez de Prado（業界 —— AQR Capital, Head of Machine Learning）爲代表的(de)學者們從幾年前開始就呼籲這(zhè)個(gè)嚴峻的(de)問題，并提出了(le)對(duì) multiple testing 造成的(de)過高(gāo) false discovery rate 的(de)解決方法。我之前的(de)文章(zhāng)《出色不如走運 (II)》對(duì) Dr. Harvey 的(de)一些研究進行了(le)梳理(lǐ)，而本文介紹的(de)回測中過拟合概率的(de)量化(huà)手段則是 Dr. Lopez de Prado 和(hé)他(tā)的(de) co-authors 提出的(de)。

一個(gè)量化(huà)策略的(de)提出往往經過回測、模拟盤、實盤三個(gè)階段。回測中有很多(duō)門道（見《科學回測中的(de)大(dà)學問》）；回測準确與否對(duì)于該策略在實盤外的(de)表現至關重要。由于金融數據的(de)信噪比極低且難以分(fēn)辨出數據中哪些是噪音(yīn)、哪些是因果關系，這(zhè)使得(de)回測中或多(duō)或少都會存在過拟合。如今，僅僅通(tōng)過考察參數平原或者使用(yòng)有限訓練集、測試集來(lái)評價過拟合的(de)危害是遠(yuǎn)遠(yuǎn)不夠的(de)。希望學術界和(hé)業界提出的(de)這(zhè)些新方法能帶給我們更多(duō)的(de)啓發。

參考文獻

Bailey, D. H. and M. Lopez de Prado (2012). The Sharpe ratio efficient frontier. Journal of Risk 15(2), 3 – 44.

Bailey, D. H. and M. Lopez de Prado (2014). The deflated Sharpe ratio: Correcting for selection bias, backtest overfitting, and non-Normality. The Journal of Portfolio Management 40(5), 94 – 107.

Bailey, D. H., J. M. Borwein, M. Lopez de Prado, and Q. J. Zhu (2017). The probability of backtest overfitting. Journal of Computational Finance 20(4), 39 – 69.

Harvey, C. R. and Y. Liu (2015). Backtesting. The Journal of Portfolio Management 42(1), 13 – 28.

Horton, R. (2015). Offline: What is medicine's 5 sigma? Lancet 385(9976), 1380.

Ioannidis, J. P. A. (2005). Why most published research findings are false. PLoS Medicine 2(8), 696 – 701.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。