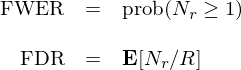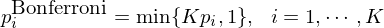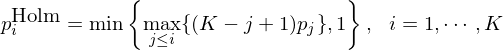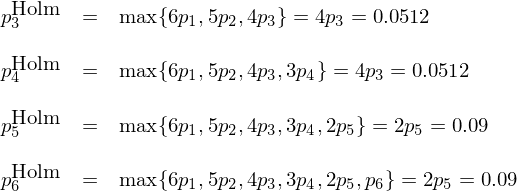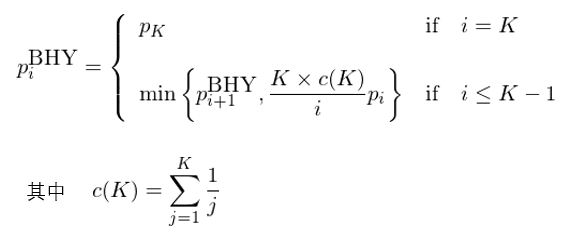出色不如走運 (II)？

作者：石川

摘要：本文指出在做(zuò)因子測試時(shí)應考慮多(duō)重假設檢驗的(de)影(yǐng)響、排除 data mining 造成的(de)運氣成分(fēn)，從而有效的(de)從大(dà)量因子中選出真正能夠解釋截面收益率的(de)好因子；該方法也(yě)可(kě)用(yòng)于基金經理(lǐ)或投資策略的(de)篩選。

1 引言

兩年前，我寫了(le)一篇《出色不如走運？》。該文使用(yòng)順序統計量（order statistics）解釋了(le)當很多(duō)投資者（或基金）使用(yòng)相同的(de)數據構建不同的(de)策略時(shí)，最好的(de)那個(gè)一定是非常優秀的(de)，但它很有可(kě)能僅僅是因爲運氣好，而非真正的(de)水(shuǐ)平高(gāo)。

如果我們直接從某個(gè)經濟學規律中找出了(le)一個(gè)解釋股票(piào)預期收益截面差異的(de)因子，并且該因子在統計上顯著，那麽它可(kě)能是真的(de)顯著；但如果我們試了(le) 500 個(gè)因子，然後找到了(le)一個(gè)最牛逼的(de)，那麽哪怕它的(de) t-statistic 非常高(gāo)，我們也(yě)不能保證它就一定是個(gè)真的(de)因子。這(zhè)就好比我們在大(dà)街(jiē)上随便抓了(le)一個(gè)人(rén)讓他(tā)猜 20 次扔硬币的(de)結果，如果他(tā)全都猜對(duì)了(le)，那麽他(tā)很可(kě)能真的(de)擁有天生神力；但是如果我們讓 3 億人(rén)同時(shí)玩猜 20 次扔硬币結果的(de)遊戲，20 輪過後全對(duì)的(de)還(hái)會有 250 人(rén)左右，但是我們會認爲這(zhè)些人(rén)僅僅是運氣好。

這(zhè)些例子背後的(de)數學邏輯是，如果有一個(gè)因變量 Y 和(hé)一個(gè)解釋變量 X，通(tōng)過回歸分(fēn)析後我們發現回歸系數的(de) t-statistic 很高(gāo)（比如 2.0，對(duì)應 5% 的(de)顯著性水(shuǐ)平），那麽從傳統的(de)單因素假設檢驗角度可(kě)以認爲 X 能夠顯著的(de)解釋 Y。然而，如果我們有很多(duō)個(gè)變量（比如 100 個(gè)）X_1、X_2、…、X_{100}，我們全都試了(le)之後發現第 55 個(gè)變量最好。這(zhè)時(shí)，如果它的(de) t-statistic 也(yě)是 2.0，我們卻不能說 X_{55} 顯著的(de)解釋 Y。這(zhè)是因爲僅僅靠運氣，這(zhè) 100 個(gè)變量（假設獨立）中最好的(de)那個(gè)的(de) t-statistic 大(dà)于 2.0 的(de)概率高(gāo)達 99%。

如何在層出不窮的(de)因子中排除靠 data mining 挖掘的(de)、而找到真正能夠解釋股票(piào)預期收益截面差異的(de)？如何在大(dà)量的(de)基金經理(lǐ)（或策略）中排除走運的(de)、而找到真正能夠戰勝市場(chǎng)的(de)？這(zhè)些已成爲非常迫切的(de)問題。在《出色不如走運》中，我們隻說了(le)僅僅憑運氣就能得(de)到非常好的(de)結果，卻沒有說應該怎樣排除運氣，找到真正的(de)好因子或者好策略。帶著(zhe)這(zhè)些問題，今天就來(lái)一篇升級版 —— 出色不如走運 (II)？最後一點提示，本文非常 technical，建議(yì)靜下(xià)心來(lái)閱讀。此外，熟悉《股票(piào)多(duō)因子模型的(de)回歸檢驗》、《爲什(shén)麽要進行因子正交化(huà)處理(lǐ)？》、以及《用(yòng) Bootstrap 進行參數估計大(dà)有可(kě)爲》對(duì)閱讀本文會有幫助。

2 理(lǐ)論依據

既然是升級版，就不能光(guāng)靠 order statistics 說事兒(ér)了(le)，咱也(yě)得(de)武裝升級一下(xià)理(lǐ)論。當學術界有大(dà)量因子來(lái)解釋同一個(gè)問題 —— 股票(piào)截面預期收益（或者有許多(duō)不同的(de)策略在同一個(gè)市場(chǎng)中交易時(shí)），僅考慮單一檢驗（single testing ，即每次檢驗一個(gè) hypothesis，比如一個(gè)單因子是否有效？）就不再适合了(le)；這(zhè)時(shí)候必須要考慮 multiple hypotheses testing（多(duō)重假設檢驗）造成的(de)影(yǐng)響。在統計上，multiple hypotheses testing 指的(de)是同時(shí)檢驗多(duō)個(gè) hypotheses。

在金融領域對(duì) multiple hypotheses testing 的(de)重視程度在最近幾年得(de)到了(le)飛(fēi)速發展。這(zhè)其中的(de)代表人(rén)物(wù)要數杜克大(dà)學的(de) Campbell Harvey 教授（曾于 2016 年任美(měi)國金融協會主席），他(tā)自 2014 年以來(lái)發表了(le)多(duō)篇文章(zhāng)、進行了(le)多(duō)個(gè)演講。其中最具代表性的(de)文章(zhāng)包括：

除上述研究外，Harvey and Liu (2015b) 提出了(le)一個(gè)全新的(de)基于 regression 的(de)檢驗框架排除 multiple testing 影(yǐng)響、解決因子挑選問題。它的(de)優勢是可(kě)以按順序逐一挑出最顯著的(de)因子、第二顯著的(de)因子，以此類推，直到再沒有顯著因子。這(zhè)麽做(zuò)的(de)好處是可(kě)以評價每個(gè)新增加的(de)因子在解釋股票(piào)截面收益率時(shí)的(de)增量貢獻。這(zhè)是傳統的(de)多(duō)重假設檢驗無法做(zuò)到的(de)。此外，該方法也(yě)可(kě)以被用(yòng)來(lái)找到真正能夠戰勝市場(chǎng)的(de)基金經理(lǐ)或投資策略。

本文的(de)主要目标是介紹 Harvey and Liu (2015b) 提出的(de)基于 regression 的(de)檢驗方法。考慮到早期的(de)多(duō)重假設檢驗修正（即 Bonferroni、Holm、BHY adjustments）也(yě)非常容易上手便捎帶著(zhe)加以說明(míng)。至于 Harvey et al. (2016) 提出的(de)方法，其技術性較強，複制起來(lái)比較困難，因此我們今後找機會再聊它（倒是可(kě)以先記住它的(de)結論，即 t-statistic 要至少大(dà)于 3 才有可(kě)能在排除了(le) multiple testing 影(yǐng)響後依然顯著）。下(xià)面首先來(lái)看容易上手的(de) Bonferroni、Holm 以及 BHY adjustments。

3 Bonferroni、Holm、BHY Adjustments

這(zhè)三種多(duō)重假設檢驗修正可(kě)以分(fēn)爲兩類：

在多(duō)重假設檢驗中，family-wise error rate（FWER）和(hé) false discovery rate（FDR）代表著(zhe) Type I error 的(de)兩個(gè)不同的(de)定義。Type I error 是錯誤的(de)拒絕原假設，也(yě)叫 false positive 或 false discovery。在我們的(de)上下(xià)文中，它意味著(zhe)錯誤的(de)發現了(le)一個(gè)其實沒用(yòng)的(de)因子。假設 K 個(gè) hypotheses 的(de) p-value 分(fēn)别爲 p_1、p_2、…、p_K。根據事先選定的(de)顯著性水(shuǐ)平，比如 0.05，其中 R 個(gè) hypotheses 被拒絕了(le)。換句話(huà)說，我們有 R 個(gè)發現（discoveries） —— 包括 true discoveries 和(hé) false discoveries。令 Nr ≤ R 代表 false discoveries 的(de)個(gè)數。由此，FWER 和(hé) FDR 的(de)定義如下(xià)：

從定義不難看出，FWER 是至少出現一個(gè) false discovery 的(de)概率，控制它對(duì)單個(gè) hypothesis 來(lái)說是相當嚴格的(de)，會大(dà)大(dà)提升 Type II Error。相比之下(xià)，FDR 控制的(de)是 false discoveries 的(de)比例，它允許 Nr 随 R 增加，是一種更溫和(hé)的(de)方法。無論采用(yòng)哪種方法，都會有相當一部分(fēn)在 single testing 中存活下(xià)來(lái)的(de)“顯著”因子被拒絕。需要說明(míng)的(de)是 Bonferroni、Holm 以及 BHY 這(zhè)三種方法都是爲了(le)修正 single testing 得(de)到的(de) p-value，修正後的(de) p-value 往往會大(dà)于原始的(de) p-value，也(yě)就意味著(zhe)修正後的(de) t-statistic 更小，即 hypotheses 不再那麽顯著。

下(xià)面通(tōng)過簡單的(de)例子（出自 Harvey and Liu 2015a）解釋這(zhè)三種方法。假設一共有六個(gè)因子，它們 single testing 的(de) p-value 從小到大(dà)依次是 0.005、0.009、0.0128、0.0135、0.045、0.06。按照(zhào) 0.05 的(de)顯著性水(shuǐ)平來(lái)看，前五個(gè)因子是顯著的(de)。首先來(lái)看 Bonferroni correction（中文稱作邦費羅尼校正），它對(duì)每個(gè)原始 p-value 的(de)調整如下(xià)：

根據定義，這(zhè)六個(gè)因子的(de) Bonferroni p-value 分(fēn)别爲 0.03、0.054、0.0768、0.081、0.27 和(hé) 0.36。經過修正後，在 0.05 的(de)顯著性水(shuǐ)平下(xià)，僅第一個(gè)因子依然顯著。接下(xià)來(lái)看看 Holm 修正（Holm 1979）。它按照(zhào)原始 p-value 從小到大(dà)依次修正，公式爲：

根據上述定義，原始 p-value 最小的(de)因子被修正後，其 Holm p-value 爲 0.06；第二個(gè)因子的(de) Holm p-value 爲 max{6×0.005, 5×0.009} = 0.045。以此類推就能計算(suàn)出其他(tā)四個(gè)因子的(de) Holm p-value：

經過 Holm 修正後，在 0.05 的(de)顯著性水(shuǐ)平下(xià)，隻有前兩個(gè)因子依然顯著。最後來(lái)看看 BHY 修正（Benjamini and Hochberg 1995, Benjamini and Yekutieli 2001）。它從原始 p-value 中最大(dà)的(de)一個(gè)開始從大(dà)到小逆向修正，公示如下(xià)：

在本例中，因爲 K = 6，因此 c(K) = 2.45。由 BHY 的(de)定義可(kě)知原始 p-value 最大(dà)的(de)因子調整後的(de) BHY p-value 就是它自己。然後從第二大(dà)的(de)開始，依次按照(zhào)上述公式計算(suàn)，最終得(de)到了(le)全部因子調整後的(de) BHY p-value，它們是（從小到大(dà)排列）：0.0496、0.0496、0.0496、0.0496、0.06、0.06。在 0.05 的(de)顯著性水(shuǐ)平下(xià)，前四個(gè)因子依然顯著。

BHY 方法是以控制 false discovery rate 爲目标，它的(de)修正比另外兩種以控制 family-wise error rate 的(de)方法更加溫和(hé)。這(zhè)體現出來(lái)的(de)結果就是在 BHY 調整下(xià)，有更多(duō)的(de)因子依然顯著。此外，BHY 方法對(duì)檢驗統計量之間的(de)相關性不敏感，它的(de)适應性很強。各位小夥伴不妨使用(yòng)上面介紹的(de)這(zhè)三種方法對(duì)因子的(de) p-value 進行修正試試。

4 基于 Regression 的(de)檢驗

本節介紹 Harvey and Liu (2015b) 提出的(de)基于 regression 的(de)檢驗方法，該方法受到了(le) Foster et al. (1997) 以及 Fama and French (2010) 的(de)啓發，在這(zhè)二者的(de)基礎上又有不少的(de)創新。它的(de)目的(de)是爲了(le)從一大(dà)堆号稱顯著的(de)因子中排除 data mining、找到真正顯著的(de)；該方法也(yě)可(kě)以被用(yòng)于從一大(dà)堆基金經理(lǐ)或策略中找出真正能夠戰勝市場(chǎng)的(de)。

當很多(duō)因子被用(yòng)來(lái)解釋截面收益時(shí)，效果最顯著（最顯著可(kě)以由最高(gāo)的(de) t-statistic、R-squared 等指标代表）的(de)因子中一定包含了(le)運氣的(de)成分(fēn)。這(zhè)個(gè)方法的(de)巧妙之處在于通(tōng)過正交化(huà)和(hé) Bootstrap 得(de)到了(le)僅靠運氣能夠得(de)到的(de)顯著性的(de)經驗分(fēn)布；如果在排除了(le)運氣帶來(lái)的(de)顯著性之後某個(gè)因子依然顯著，那它就是真正的(de)因子，而非 data mining 的(de)結果。

随著(zhe)處理(lǐ)方式略有不同，Harvey and Liu (2015b) 這(zhè)個(gè)方法可(kě)以用(yòng)于 predictive regression（考察哪個(gè) X 能預測 Y）、panel regression 以及 Fama-MacBeth regression（這(zhè)兩類回歸可(kě)以用(yòng)于挑選好因子），但它們背後的(de)邏輯完全一緻。下(xià)面高(gāo)度概括一下(xià)該方法的(de)邏輯（正交化(huà)和(hé) Bootstrap 是核心）：

接下(xià)來(lái)以 predictive regression 爲例說明(míng)這(zhè)個(gè)多(duō)重假設檢驗方法的(de)具體步驟。Harvey and Liu (2015b) 中給出了(le)使用(yòng) panel regression 和(hé) Fama-MacBeth regression 時(shí)所需的(de)改動。爲了(le)評價哪個(gè)因子有效，需要用(yòng)到 panel regression，因此下(xià)一節會介紹針對(duì) panel regression 的(de)改動。假設有因變量 Y 和(hé) 100 個(gè)解釋變量 X 的(de) 500 期樣本數據，我們想看看哪個(gè) X 能夠預測 Y。多(duō)重假設檢驗的(de)步驟爲：

第一步：用(yòng)每個(gè) X 和(hé) Y 回歸（在我們的(de)例子中就是 100 次回歸），得(de)到 100 個(gè)殘差 OX，它們和(hé) Y 正交。這(zhè)構成了(le) null hypothesis：所有 OX 對(duì) Y 沒有預測性。

第二步：以這(zhè) 500 期的(de) Y 和(hé)正交化(huà)得(de)到的(de) OX 爲原始數據（500 × 101 的(de)矩陣，每一行代表一期，第一列爲 Y，第二到第 101 列爲 100 個(gè) OX 變量），使用(yòng)帶放回的(de) Bootstrap 重采樣從這(zhè) 500 行中不斷的(de)随機抽取，構建和(hé)原始長(cháng)度一樣的(de) bootstrapped 數據（也(yě)是 500 × 101 矩陣）。整行抽取保留了(le)這(zhè) 100 個(gè)變量在截面上的(de)相關性。此外 Bootstrap 的(de)好處是不對(duì)原始數據中的(de)概率分(fēn)布做(zuò)任何假設。

第三步：使用(yòng) bootstrapped 數據，用(yòng)每個(gè) OX 和(hé) Y 回歸得(de)到一個(gè)檢驗統計量（比如是 t-statistic）；找出所有 OX 中該檢驗統計量最大(dà)的(de)那個(gè)值，稱爲 max statistic。如果我們的(de)檢驗統計量是 t-statistic，那麽這(zhè)個(gè) max statistic 就是 500 個(gè) t-statistic 中最大(dà)的(de)。

第四步：重複上述第二、第三步 10000 次，得(de)到 max statistic 的(de)經驗分(fēn)布（empirical distribution），這(zhè)是純靠運氣（因爲 null hypothesis 已經是 OX 對(duì) Y 沒有任何預測性了(le)）能夠得(de)到的(de) max statistic 的(de)分(fēn)布。

第五步：比較原始數據 Y 和(hé)每個(gè) X 回歸得(de)到的(de) max statistic 和(hé)第四步得(de)到的(de) max statistic 的(de)經驗分(fēn)布：

第六步：使用(yòng)目前爲止已被挑出來(lái)的(de)全部顯著解釋變量對(duì) Y 進行正交化(huà)，得(de)到殘差 OY。它是原始 Y 中這(zhè)些變量無法解釋的(de)部分(fēn)。

第七步：使用(yòng) OY 來(lái)正交化(huà)剩餘的(de) X（已經選出來(lái)顯著變量，比如 X_7，不再參與餘下(xià)的(de)挑選過程）。

第八步：重複上述第三步到第七步：反複使用(yòng)已挑出的(de)顯著因子來(lái)正交化(huà) Y，再用(yòng) OY 來(lái)正交化(huà)剩餘解釋變量 X；在 Bootstrap 重采樣時(shí)，使用(yòng) OY、k 個(gè)已經選出的(de) X、和(hé)剩餘 100 - k 個(gè)正交化(huà)後的(de) OX 作爲原始數據生成 bootstrapped 樣本；通(tōng)過大(dà)量的(de) Bootstrap 實驗得(de)到新的(de) max statistic 的(de)經驗分(fēn)布，并判斷剩餘解釋變量中是否仍然有顯著的(de)。

第九步：當剩餘解釋變量的(de) max statistic 無法超過 null hypothesis 下(xià) max statistic 的(de)經驗分(fēn)布阈值時(shí)，整個(gè)過程結束，剩餘的(de)解釋變量全都是不顯著的(de)。

以上以 predictive regression 爲例介紹了(le) Harvey and Liu (2015b) 提出的(de)多(duō)重假設檢驗框架。

5 用(yòng) Panel Regression 挑選好因子

在分(fēn)析因子是否能顯著的(de)解釋股票(piào)或投資組合的(de)截面預期收益率時(shí)，回歸方法是 panel / cross-sectional regression 而非前一節的(de) predictive regression。需要說明(míng)的(de)是，這(zhè)裏的(de)選股因子都是某個(gè)投資組合的(de)（超額）收益率，比如 MKT，HML，SMB 這(zhè)種。在使用(yòng) panel regression 的(de)檢驗過程中，Bootstrap 的(de)思想和(hé)上一節介紹的(de)完全一緻，但是在正交化(huà)、回歸分(fēn)析、以及 max statistic 的(de)選取有上些差異。

5.1 正交化(huà)

在挑選因子中，null hypothesis 是因子對(duì)解釋預期收益率截面差異沒有作用(yòng)。如果能夠拒絕原假設，則說明(míng)因子是有效的(de)。但是運氣的(de)成分(fēn)往往帶來(lái) false discovery，即本來(lái)這(zhè)個(gè)因子沒用(yòng)，但是 data mining （嘗試了(le)一大(dà)堆因子中找到的(de)效果最好的(de)那個(gè)）使得(de)它看起來(lái)有用(yòng)。爲此，和(hé)前一節的(de) predictive regression 一樣，多(duō)重假設檢驗的(de)第一步通(tōng)過正交化(huà)來(lái)構造出一個(gè)“純淨”的(de) null hypothesis，即因子不能解釋截面收益率。正交化(huà)的(de)方法爲：

5.2 回歸分(fēn)析

在 predictive regression 中，我們會對(duì)因變量和(hé)解釋變量都進行正交化(huà)。假設已經選出了(le) k ≥ 0 個(gè)顯著變量。在選擇第 k + 1 個(gè)時(shí)，首先将 Y 投影(yǐng)到這(zhè) k 個(gè)變量上得(de)到殘差 OY，這(zhè)就是對(duì) Y 的(de)正交化(huà)。之後，再把剩餘待檢驗的(de)解釋變量 X 逐一投影(yǐng)到 OY 上，得(de)到 OX。然後再用(yòng) OY 和(hé)每個(gè) OX 獨立回歸進行後續 Bootstrap 步驟。這(zhè)使得(de)我們可(kě)以評估新加入變量 X 在預測 Y 時(shí)的(de)增量貢獻。

進行 panel regression 時(shí)，個(gè)股或者投資組合的(de)收益率作爲因變量出現在回歸方程的(de)左側，對(duì)它們不進行正交化(huà)處理(lǐ)。在回歸方程的(de)右側，使用(yòng)已經選出的(de) k（k ≥ 0）個(gè)顯著因子和(hé)正交化(huà)後的(de)第 k + 1 個(gè)因子（正交化(huà)方法參考 5.1 節）作爲解釋變量。始終将已經選出的(de)前 k 個(gè)因子加入回歸方程的(de)右側可(kě)保證檢驗第 k + 1 個(gè)因子對(duì)解釋截面收益率的(de)增量貢獻。将因變量和(hé)解釋變量在時(shí)序上回歸，得(de)到的(de)截距項就是這(zhè)些因子無法解釋的(de) pricing error。

上面的(de)對(duì)比說明(míng)：在 predictive regression 中，回歸方程的(de)左側是 OY（用(yòng)已經選出的(de) k 個(gè) X 正交化(huà) Y），而右側隻有一個(gè) OX（每個(gè)剩餘的(de) X 正交化(huà)後依次和(hé) OY 回歸）；而在 panel regression 中，回歸方程的(de)左側是 Y（不正交化(huà)），而是把已經選出的(de) k 個(gè) X 都放在回歸方程的(de)右側，因此右側爲 k 個(gè) X 以及一個(gè)新的(de)待檢驗的(de)正交化(huà)後的(de) OX。不同的(de)方法是由于這(zhè)兩種回歸中 null hypothesis 的(de)性質不同造成的(de)。雖然這(zhè)兩種方法的(de)略有不同，但都保證了(le)考察待檢驗變量對(duì)解釋 Y 的(de)增量貢獻。

在 Harvey and Liu (2015b) 的(de)最新版本 Harvey and Liu (2018) 中對(duì)上述回歸有非常詳細的(de)說明(míng)。值得(de)一提的(de)是，雖然作者将這(zhè)個(gè)回歸稱爲 panel regression，但 Harvey and Liu (2018) 對(duì)每個(gè)投資品單獨的(de)使用(yòng)這(zhè)些因子進行時(shí)序回歸。因此對(duì)于 N 個(gè)投資品，一共得(de)到了(le) N 個(gè) pricing errors；如果直接使用(yòng) N 個(gè)投資品一起做(zuò) panel regression 并加入 fixed effects 也(yě)可(kě)以得(de)到 N 個(gè)不同的(de)截距。

5.3 “Max statistic”

在 null hypothesis 下(xià)，因子不能解釋收益率的(de)截面差異。這(zhè)意味著(zhe)回歸的(de)截距（pricing error）應該距離零越遠(yuǎn)越好。由于因子挖掘界 data mining 的(de)“優良傳統”，當很多(duō)因子被測試後，最好的(de)那個(gè)僅僅靠著(zhe)運氣的(de)成分(fēn)也(yě)可(kě)以讓 pricing error 非常接近零。爲了(le)量化(huà)并排除運氣的(de)影(yǐng)響，Bootstrap 的(de)目标就是得(de)到 null hypothesis 下(xià) pricing error 的(de)經驗分(fēn)布，即僅靠運氣能夠得(de)到的(de) pricing error 的(de)經驗分(fēn)布。

從 asset pricing 角度來(lái)說，如果一個(gè)因子能夠解釋收益率截面差異，那麽回歸截距應十分(fēn)接近零。由于一共有 N 個(gè)投資品，使用(yòng)這(zhè) N 個(gè)投資品的(de) pricing error 絕對(duì)值的(de)中位數作爲“max statistic”（實際上是希望 pricing error  的(de)絕對(duì)值越小越好，因此應稱之爲 min statistic；爲了(le)和(hé)前一節對(duì)應，故稱之爲帶了(le)引号的(de)“max statistic”）來(lái)評價因子。通(tōng)過 Bootstrap 得(de)到“max statistic”的(de)經驗分(fēn)布。如果來(lái)自真實數據的(de)最小 pricing error 絕對(duì)值的(de)中位數小于從經驗分(fēn)布中得(de)到的(de)阈值，則它對(duì)應的(de)因子就是真正有效的(de)因子。

6 一個(gè)例子

Harvey and Liu (2015b) 給出了(le)一個(gè)示例性例子說明(míng)如何應用(yòng)他(tā)們提出的(de)多(duō)重假設檢驗框架挑選真正有效的(de)因子。這(zhè)個(gè)例子考察了(le)學術界的(de) 13 個(gè)“顯著”因子。加個(gè)雙引号是因爲它們都在 single testing 中顯著，但是在新的(de)多(duō)重假設檢驗下(xià)很多(duō)就失效了(le)。這(zhè) 13 個(gè)因子爲：

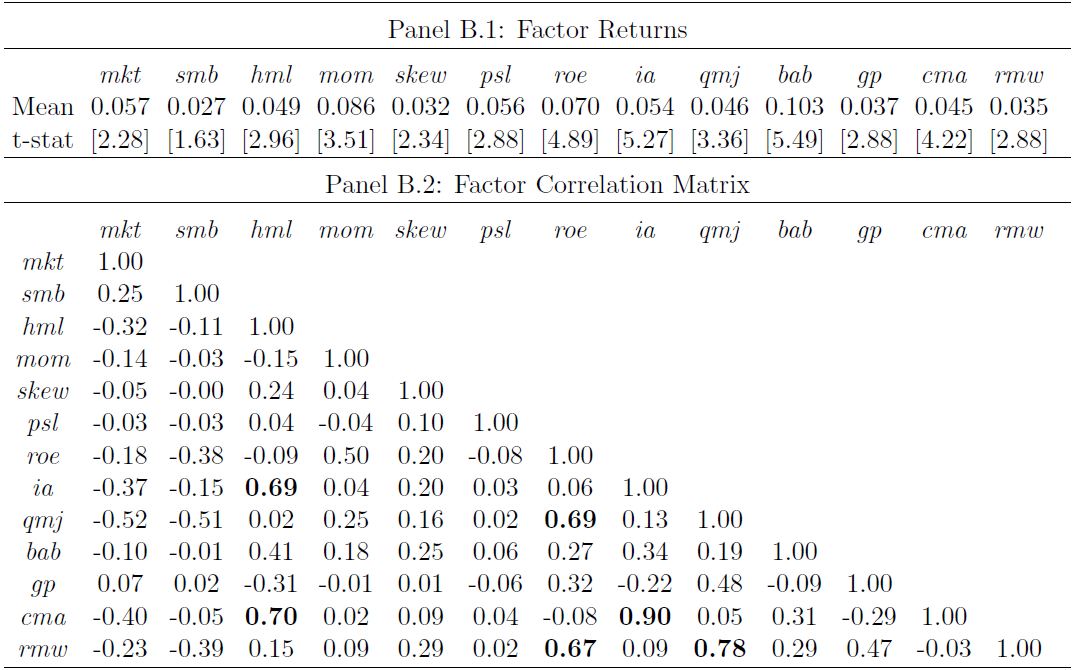
這(zhè)些因子的(de) single testing 結果（以因子收益率的(de) t-statistic 表示）以及它們之間的(de)相關性如下(xià)圖所示。從圖中不難看出：（1）除了(le) SMB 外，所有因子的(de) t-statistic 都大(dà)于 2，在 0.05 的(de)顯著性水(shuǐ)平下(xià)顯著；有些因子的(de) t-statistic 甚至超過 5！（2）這(zhè)些因子中有一些對(duì)的(de)相關性非常高(gāo)，比如 ROE 和(hé) QMJ、CMA 和(hé) IA（它們都是 investment 類的(de)因子）、CMA 和(hé) HML 等。

爲了(le)測試因子，最好的(de)因變量應該是一攬子股票(piào)，因爲我們希望考察這(zhè)些因子在解釋股票(piào)預期收益率截面差異上的(de)作用(yòng)。在 Harvey and Liu (2015b) 給出的(de)例子中，二位作者使用(yòng)的(de)是 25 個(gè)投資組合，而非個(gè)股。他(tā)們強調例子的(de)目的(de)是爲了(le)說明(míng)多(duō)重假設檢驗的(de)步驟。用(yòng)來(lái)作爲因變量的(de) 25 個(gè)投資組合來(lái)自使用(yòng) Fama-French 三因子中的(de) SMB 和(hé) HML 兩個(gè)因子各自把股池分(fēn)成 5 組并交叉配對(duì)，因此一共 5 × 5 = 25 個(gè)組合。

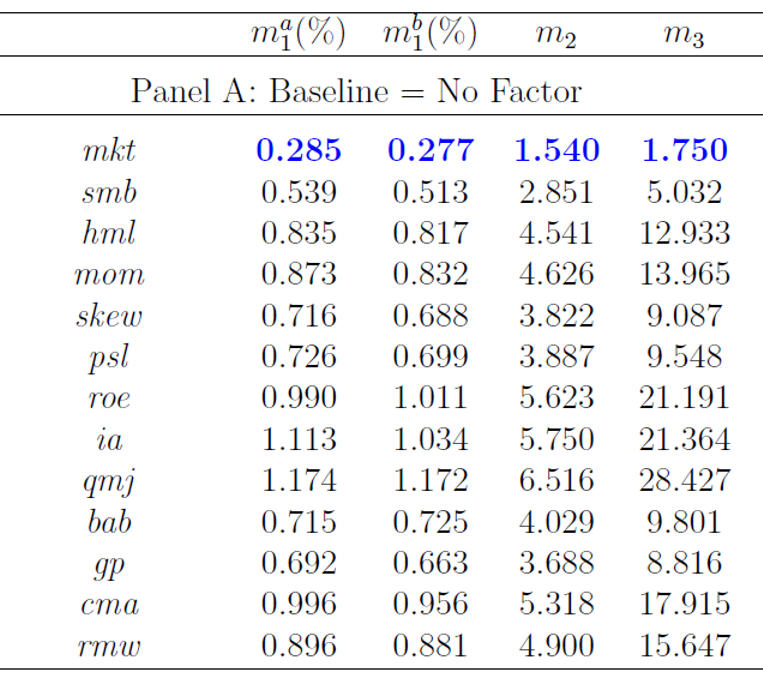
Harvey and Liu (2015b) 使用(yòng)了(le)這(zhè) 25 個(gè)組合的(de) pricing error 絕對(duì)值的(de)中位數作爲挑選因子的(de)指标（在文章(zhāng)中，這(zhè)個(gè)指标被記爲 m_1^a）。除了(le)這(zhè)個(gè)指标外還(hái)有其他(tā)三個(gè)指标，這(zhè)裏不做(zuò)討(tǎo)論。首先用(yòng)這(zhè) 13 個(gè)因子各自對(duì)這(zhè) 25 個(gè)投資組合進行回歸。每個(gè)因子 pricing error 絕對(duì)值的(de)中位數如下(xià)圖所示。從單個(gè)因子回歸結果來(lái)看，MKT（市場(chǎng)）因子是最顯著的(de)（它的(de)指标 0.285% 是所有因子中最小的(de)），但是裏面包含了(le)運氣的(de)成分(fēn)。

下(xià)面應用(yòng)多(duō)重假設檢驗來(lái)排除運氣的(de)成分(fēn)。對(duì)這(zhè) 13 個(gè)因子分(fēn)别正交化(huà)（demean），然後使用(yòng) Bootstrap 重采樣進行反複多(duō)次的(de)大(dà)量實驗。每個(gè)實驗中，單獨使用(yòng) 13 個(gè)正交化(huà)後的(de)因子和(hé) 25 個(gè)投資組合收益率回歸，得(de)到每個(gè)因子的(de) pricing error 絕對(duì)值中位數的(de)最小值（我們的(de)“max statistic”）。大(dà)量 Bootstrap 實驗便得(de)到了(le)“max statistic”的(de)經驗分(fēn)布。MKT 因子的(de)取值（0.285%）在這(zhè)個(gè)分(fēn)布下(xià)出現的(de)概率僅爲 3.9%，即 p-value = 3.9%，小于常用(yòng)的(de) 5% 的(de)阈值。因此我們說即便考慮了(le)運氣成分(fēn)後，MKT 因子依然是顯著的(de)。市場(chǎng)因子是第一個(gè)被選出來(lái)的(de)顯著因子，這(zhè)多(duō)少符合預期。

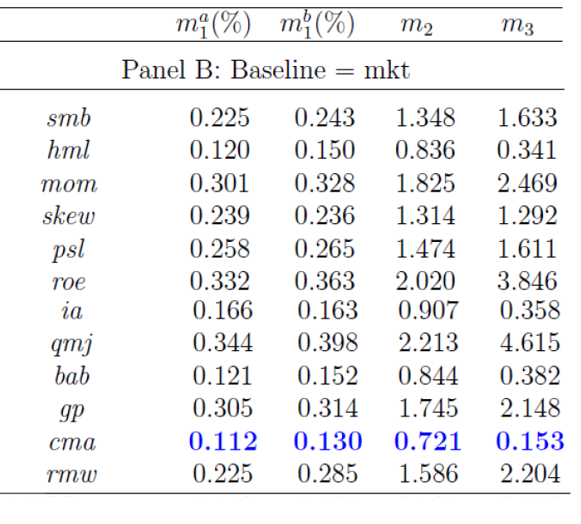
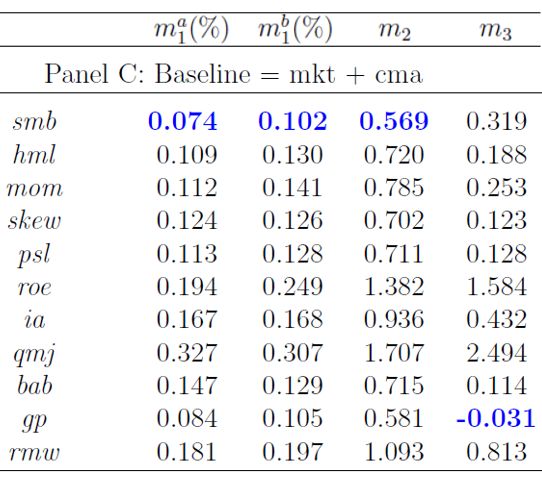
在接下(xià)來(lái)的(de)步驟中，使用(yòng) MKT 因子正交化(huà)其餘 12 個(gè)因子。然後用(yòng) MKT 因子和(hé)正交化(huà)之後的(de)每個(gè)剩餘因子獨立對(duì)這(zhè) 25 個(gè)投資組合進行回歸分(fēn)析，得(de)到考慮了(le)每個(gè)剩餘因子的(de) pricing error 絕對(duì)值的(de)中位數，如下(xià)圖所示。不難看出，在剩餘的(de) 12 個(gè)因子中，CMA 是最好的(de)（它的(de) pricing error 最低），但是 HML 和(hé) BAB 和(hé)它也(yě)難分(fēn)伯仲！因此，在真實數據中，“max statistic”的(de)取值爲 0.112%（來(lái)自 CMA）。

再一次，使用(yòng) Bootstrap 重采樣進行反複多(duō)次的(de)大(dà)量實驗得(de)到“max statistic”的(de)經驗分(fēn)布。CMA 因子的(de)取值（0.112%）在這(zhè)個(gè)分(fēn)布下(xià)出現的(de)概率僅爲 2.2%，依然小于常用(yòng)的(de) 5% 的(de)阈值。在考慮了(le)運氣以及 MKT 因子之後，CMA 因子依然是顯著的(de)。如果不選 CMA 作爲第二個(gè)，也(yě)可(kě)以選 HML 或 BAB 作爲第二個(gè)顯著的(de)因子。

如上所述，重複這(zhè)個(gè)過程就可(kě)以一直分(fēn)析下(xià)去。在找到了(le)最有效的(de)兩個(gè)因子 —— MKT 和(hé) CMA —— 之後，剩餘 11 個(gè)因子中第三個(gè)最顯著的(de)因子是 SMB，它的(de) pricing error 是 0.074%。然而，使用(yòng) Bootstrap 得(de)到“max statistic”的(de)經驗分(fēn)布後發現，SMB 因子的(de)取值（0.074%）在這(zhè)個(gè)分(fēn)布下(xià)出現的(de)概率高(gāo)達 13.9%，大(dà)于常用(yòng)的(de) 5% 的(de)阈值，因此認爲 SMB 以及其他(tā) 10 個(gè)因子在進一步解釋截面收益率差異時(shí)都不顯著。

經過修正多(duō)重假設檢驗發現，MKT 和(hé) CMA（也(yě)可(kě)以選 HML 或 BAB）是兩個(gè)顯著的(de)因子，其他(tā)因子均不顯著，均爲 data mining 的(de)産物(wù)。以上便實現了(le)從一攬子所謂顯著的(de)因子中提出運氣成分(fēn)、找到真正有效的(de)因子。這(zhè)就是這(zhè)套多(duō)重假設檢驗體系最大(dà)的(de)價值。這(zhè)套體系也(yě)可(kě)以用(yòng)于基金經理(lǐ)的(de)篩選，具體的(de)例子見 Harvey and Liu (2015b)。

7 結語

2015 年，Harvey 教授在 Jacobs Levy Center Conference 上進行了(le)題爲 Lucky Factors 的(de)演講。在演講的(de)開篇，他(tā)從生物(wù)進化(huà)的(de)角度指出人(rén)類可(kě)能有 overfitting 或者 data mining 的(de)傾向。假設一隻機警的(de)羚羊在草(cǎo)原中聽(tīng)到了(le)沙沙響聲。如果它開始奔跑，但事後發現響聲隻是由于一陣微風造成的(de)（即沒有威脅），那麽它無疑犯了(le) Type I error，爲此付出的(de)代價是消耗一定的(de)能量；但是如果它不奔跑，但事後發現響聲是因爲一隻獵豹沖向它造成的(de)，那麽它則犯了(le) Type II error，爲此則付出了(le)生命的(de)代價。可(kě)見，從 cost 的(de)角度，它必須選擇奔跑。

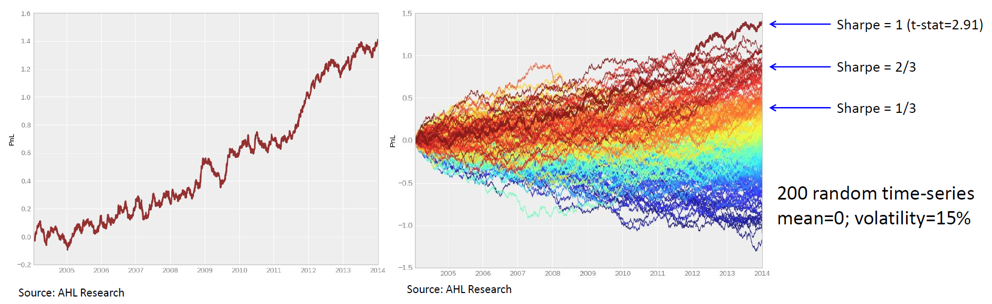
這(zhè)個(gè)故事告訴我們，動物(wù)想生存，就必須控制 Type II error，而可(kě)以允許更高(gāo)的(de) Type I error（false discovery）。這(zhè)種傾向在進化(huà)中被一代代傳下(xià)來(lái)。因此，人(rén)類在分(fēn)析問題時(shí)允許更高(gāo)的(de) Type I error、存在 overfitting 或者 data mining 的(de)傾向。下(xià)圖左側是一個(gè)假想的(de)策略淨值曲線，它持續上漲，回撤可(kě)控，Sharpe Ratio 理(lǐ)想。然而，它僅僅是下(xià)圖右側中展示的(de) 200 個(gè)使用(yòng)零均值純随機生成的(de)策略淨值中表現最好的(de)那個(gè)。換句話(huà)說，它的(de)表現完全來(lái)自運氣。出色還(hái)是走運？回答(dá)這(zhè)個(gè)問題刻不容緩。

S&P Capital IQ 有一個(gè) Alpha Factor Library（α 因子庫），非常自豪的(de)宣稱有 500 個(gè) α 因子！這(zhè)裏面有多(duō)少是運氣？有多(duō)少是真正的(de) α？本文介紹的(de)幾種方法是爲了(le)回答(dá)這(zhè)個(gè)問題所做(zuò)的(de)努力。美(měi)國統計協會（American Statistical Association）的(de) Ethical Guidelines for Statistical Practice 中，有這(zhè)樣一句話(huà)，發人(rén)深省：

Selecting the one "significant" result from a multiplicity of parallel tests poses a grave risk of an incorrect conclusion. Failure to disclose the full extent of tests and their results in such a case would be highly misleading.

參考文獻

Asness, C. S., A. Frazzini, and L. H. Pedersen (2013). Quality minus junk. AQR Capital Management working paper.

Benjamini, Y. and Y. Hochberg (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society Series B 57, 289 – 300.

Benjamini, Y. and D. Yekutieli (2001). The control of the false discovery rate in multiple testing under dependency. Annals of Statistics 29, 1165 – 1188.

Carhart, M. M. (1997). Onp persistence in mutual fund performance. Journal of Finance 52(1), 57 – 82.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K.R. French (2010). Luck versus skill in the cross-section of mutual fund returns. Journal of Finance 65(5), 1915 – 1947.

Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.

Foster, F. D., T. Smith and R. E. Whaley (1997). Assessing goodness-of-fit of asset pricing models: The distribution of the maximal R2. Journal of Finance 52(2), 591 – 607.

Harvey, C. R. and A. Siddique (2000). Conditional skewness in asset pricing tests. Journal of Finance 55(3), 1263 – 1295.

Harvey, C. R. and Y. Liu (2015a). Backtesting. The Journal of Portfolio Management 42(1), 13 – 28.

Harvey, C. R. and Y. Liu (2015b). Lucky factors. Working paper.

Harvey, C. R. and Y. Liu (2018). Lucky factors. Working paper.

Harvey, C. R., Y. Liu, and H. Zhu (2016). … and the cross-section of expected returns. Review of Financial Studies 29(1), 5 – 68.

Holm, S. (1979). A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics 6, 65 – 70.

Hou, K., C. Xue, and L. Zhang (2015). Digesting anomalies: An investment approach. Review of Financial Studies 28(3), 650 – 705.

Novy-Marx, R. (2013). The other side of value: The gross profitability premium. Journal of Financial Economics 108(1), 1 – 28.

Pastor, L. and R. F. Stambaugh (2003). Liquidity risk and expected stock returns. Journal of Political Economy 111(3), 642 – 685.

https://en.wikipedia.org/wiki/Bonferroni_correction 

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。