到底需要多(duō)少因子 ?

作者：石川

摘要：“How many of these factors are really important?” —— John Cochrane

1

2011 年，時(shí)任 AFA 主席的(de) John Cochrane 在他(tā)的(de)主席演講調侃了(le) zoo of factors，并提出了(le)铿锵三問。其中第三個(gè)問題是：

“How many of these factors are really important?”

這(zhè)個(gè)問題引發了(le)關于随機貼現因子（SDF）是否有稀疏表達（sparsity）的(de)大(dà)討(tǎo)論。由資産定價理(lǐ)論可(kě)知，SDF 可(kě)以被表示爲一系列資産的(de)線性組合（Hansen and Richard 1987）：

式中  爲随機貼現因子，  維向量  表示資産的(de)超額收益率，  維向量  表示它們在 SDF 中的(de)權重。理(lǐ)論上我們可(kě)以用(yòng)個(gè)股作爲資産來(lái)構造（span）SDF。但由于參數估計問題，常見的(de)做(zuò)法是使用(yòng)投資組合（即因子）代替個(gè)股作爲資産。因此，Cochrane 的(de)第三個(gè)問題就可(kě)以重述爲，  的(de)表達式中到底需要多(duō)少個(gè)因子。

關于這(zhè)個(gè)問題，稀疏 vs. 不稀疏兩派均有人(rén)支持：

1. 認爲 SDF 有稀疏表達的(de)研究包括使用(yòng)正則化(huà)（進行變量選擇）或者降維技術來(lái)估計低維 SDF；

2. 認爲 SDF 沒有稀疏表達的(de)研究則指出，在估計 SDF 時(shí)應該考慮盡可(kě)能多(duō)的(de)因子。

以下(xià)兩個(gè)小結分(fēn)别簡要闡述這(zhè)兩派的(de)觀點。本文最後會給出我的(de)看法。

2

首先來(lái)看稀疏 SDF 的(de)相關研究。

爲尋求低維 SDF，一個(gè)自然的(de)想法就是在模型中稀疏性約束（sparsity constraint）。這(zhè)可(kě)以通(tōng)過加入  正則化(huà)來(lái)實現。這(zhè)方面的(de)研究包括 Feng, Giglio and Xiu (2020) 和(hé) Freyberger, Neuhierl and Weber (2020)。這(zhè)二者都通(tōng)過 Lasso-style 回歸進行變量選擇，從而得(de)到了(le)稀疏的(de) SDF。

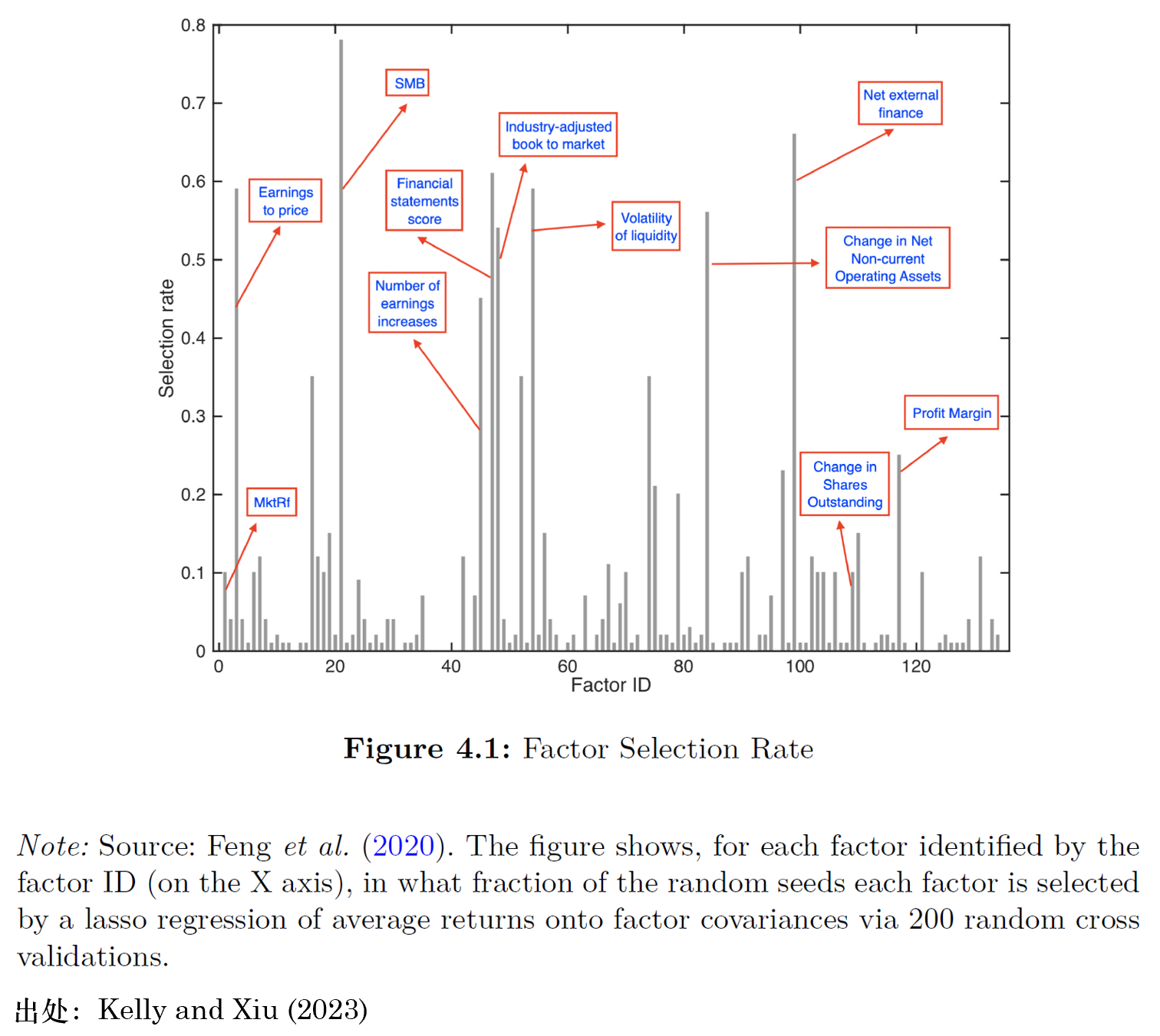
以前者爲例，下(xià)圖展示了(le)每個(gè)因子被模型選擇的(de)概率。該文的(de)實證發現顯示，在 120 多(duō)個(gè)候選因子中隻有 17 個(gè)因子是有用(yòng)的(de)，而其他(tā)大(dà)多(duō)數因子則是冗餘或無用(yòng)的(de)。

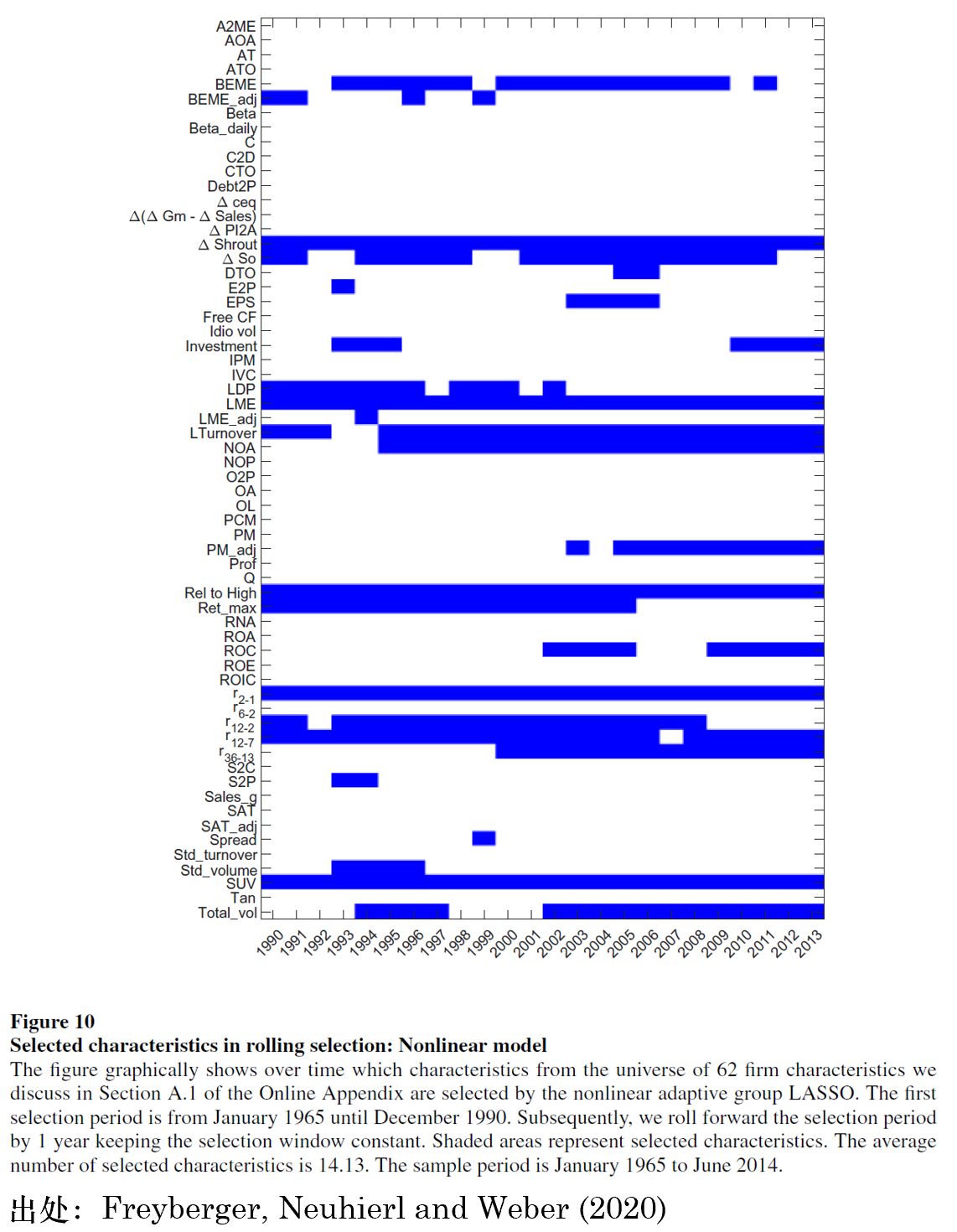
類似地，後者也(yě)給出了(le)稀疏 SDF 的(de)實證結果。下(xià)圖展示了(le)在他(tā)們的(de)實證區(qū)間内，每個(gè)因子被選中的(de)情況。圖中藍色區(qū)域标識被選中。在 1990 到 2014 年之間，被選中的(de)平均個(gè)數約爲 14，和(hé) Feng, Giglio and Xiu (2020) 在數量上十分(fēn)接近。

除了(le)變量選擇之外，另一個(gè)思路是降維（dimension reduction）。近年來(lái)諸多(duō)基于 PCA 及其變化(huà)的(de)方法已經将這(zhè)條研究線發揮的(de)淋漓盡緻。這(zhè)其中一篇代表作是 Lettau and Pelger (2020)。該文認爲傳統 PCA 方法僅僅利用(yòng)了(le)收益率的(de)二階矩信息，丢失掉了(le)原始因子和(hé)資産收益率在截面上的(de)關系，即一階矩信息。因此，它在 PCA 的(de) loss function 中加入了(le)一階矩信息，進而提出了(le) PR-PCA（risk premium PCA）估計量。

實證分(fēn)析表明(míng)，RP-PCA 在絕大(dà)多(duō)數情況下(xià)都優于 PCA，且可(kě)以将大(dà)量因子涵蓋的(de)信息聚合到 5 個(gè)低維主成分(fēn)上。其中，第一主成分(fēn)有非常高(gāo)的(de)方差和(hé)較爲顯著的(de)平均收益，表現非常類似市場(chǎng)因子；第三主成分(fēn)可(kě)視作價值因子；第五主成分(fēn)近似于短期反轉因子。而第二和(hé)第四主成分(fēn)更偏重是諸多(duō)原始因子的(de)組合。

無論是變量選擇還(hái)是降維，都可(kě)以産生 SDF 的(de)稀疏表達。然而，一個(gè)必須要面對(duì)和(hé)回答(dá)的(de)問題是，雖然不同方法給出的(de) SDF 都是低維的(de)，但它們涵蓋的(de)原始因子卻未必相同。事實上，頗有意思的(de)是，上面提到的(de) Lettau and Pelger (2020) 和(hé) Freyberger, Neuhierl and Weber (2020) 兩篇文章(zhāng)都出自 2020 年 RFS 的(de)特刊 New Methods for the Cross-Section of Returns。在特刊的(de)導讀中，兩位編輯 Karolyi and Van Nieuwerburgh (2020) 也(yě)就如何尋找低維定價模型中的(de)共性靈魂發問，激勵學術界探尋不同模型導緻不同因子這(zhè)一現象背後的(de)原因。

3

關于 SDF 的(de)非稀疏表達，一篇值得(de)一提的(de)實證研究是 Kozak, Nagel and Santosh (2020)。當然，與其說這(zhè)篇文章(zhāng)是明(míng)确立場(chǎng)，倒不如說它是在探究這(zhè)個(gè)問題。（你馬上就會知道爲啥這(zhè)麽說。）

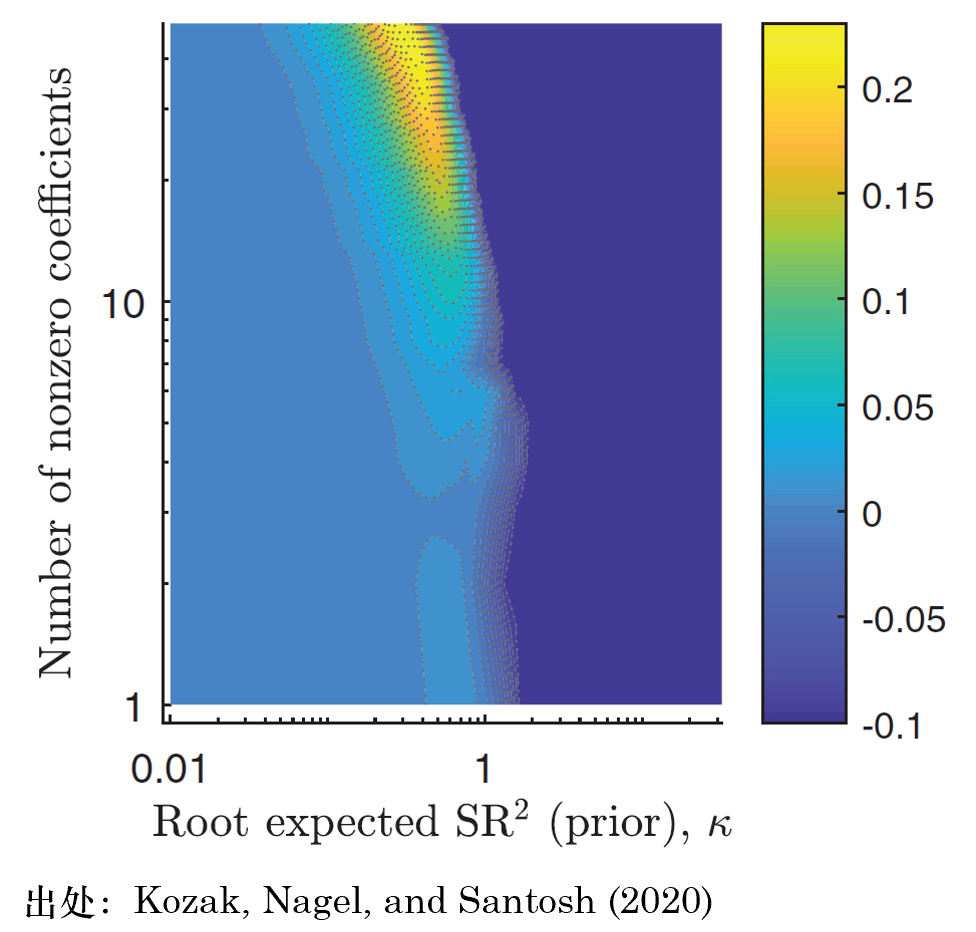
該文首先使用(yòng) 50 個(gè)基于公司特征構造的(de)因子來(lái)估計 SDF，并通(tōng)過同時(shí)加入  和(hé)  正則化(huà)挑選變量以及控制模型的(de)複雜(zá)度。在下(xià)圖所示結果中，顔色越亮（越發黃(huáng)）的(de)區(qū)域對(duì)應著(zhe)越高(gāo)的(de)樣本外預測性。圖中的(de)縱坐(zuò)标表示模型納入的(de)因子的(de)個(gè)數，橫坐(zuò)标表示  正則化(huà)的(de)強度。結果清晰地顯示出，黃(huáng)色區(qū)域聚焦于模型包含足夠多(duō)因子的(de)情況，說明(míng) SDF 并不稀疏。此外，伴随諸多(duō)因子被納入 SDF 的(de)是足夠強的(de)  正則化(huà)。二者缺一不可(kě)。

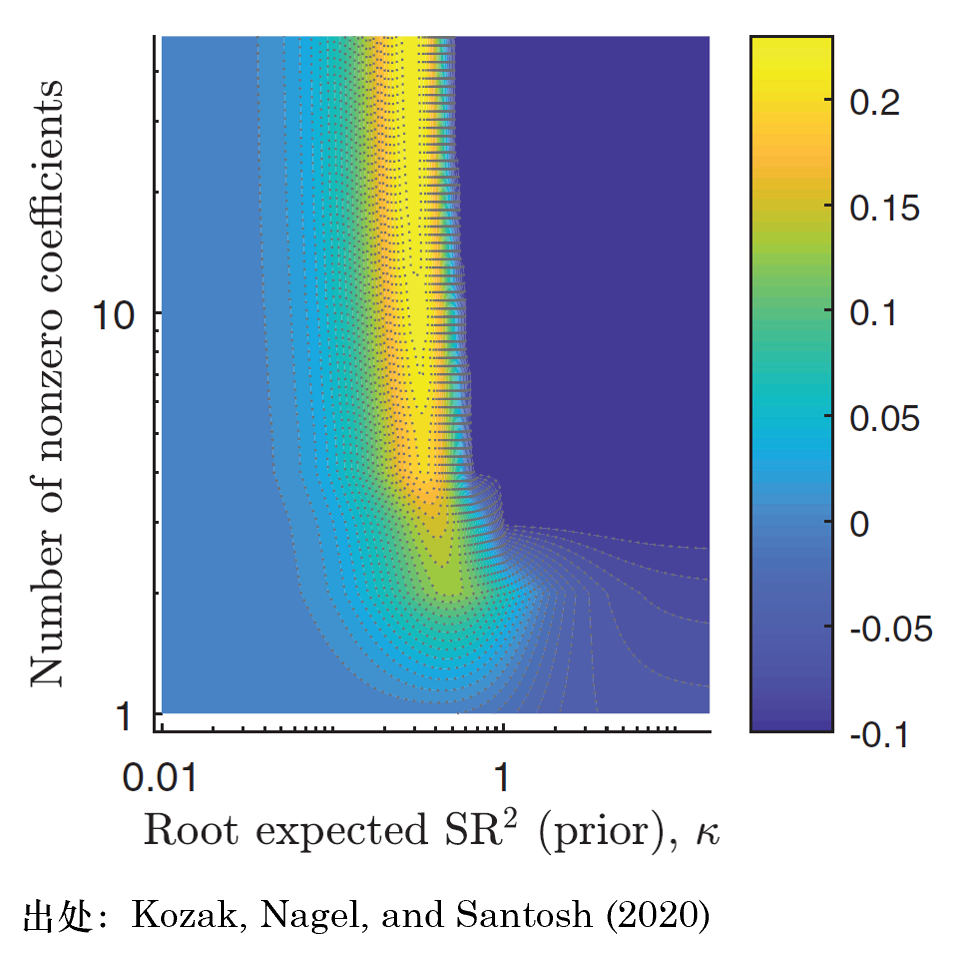
不過有意思的(de)是，該文并未放棄構造稀疏 SDF 的(de)嘗試。爲此，三位作者首先對(duì)原始的(de) 50 個(gè)因子使用(yòng) PCA，旨在通(tōng)過統計手段在不損失預測信息的(de)前提下(xià)構造簡約模型。下(xià)圖展示了(le)以 50 個(gè)主成分(fēn)作爲因子并估計 SDF 的(de)情況。和(hé)使用(yòng)原始因子相比，此時(shí)亮黃(huáng)色的(de)區(qū)域覆蓋了(le)模型隻納入少數因子的(de)情況。這(zhè)意味著(zhe)，隻需要通(tōng)過有限幾個(gè)主成分(fēn)就能夠獲得(de)足夠的(de)樣本外預測性，因而實現了(le)稀疏的(de) SDF。但盡管如此，由于每個(gè)主成分(fēn)都是所有原始因子的(de)線性組合，因此該 SDF 表達依然隐含地納入了(le)衆多(duō)因子的(de)信息。

上述結論也(yě)在 Bryzgalova, Huang and Julliard (2023) 中得(de)到了(le)進一步确認。該文以 51 個(gè)因子的(de)超過 2 千萬億種排列組合所構造的(de)模型爲分(fēn)析對(duì)象，發現不存在某個(gè)最優的(de)模型，而是存在數百種可(kě)能的(de)模型設定，給出了(le)幾乎相同的(de)資産定價實證結果。更爲重要的(de)是，盡管它們的(de)方法識别出一些對(duì)于構造 SDF 來(lái)說最重要的(de)因子，但它們并不能完全描述 SDF。反之，SDF 在可(kě)觀測的(de)因子空間中密集（dense）的(de)。它們的(de)模型能夠有效聚合不同因子所涵蓋的(de)關于 SDF 的(de)帶噪聲信息。

另外，談到非稀疏 SDF，不得(de)不提的(de)另一個(gè) research agenda 就是 Bryan Kelly 的(de)“複雜(zá)度美(měi)德”系列文章(zhāng)。在最新的(de) Didisheim et al. (2023) 中，幾位作者将複雜(zá)度美(měi)德推廣到了(le)截面定價模型。該文的(de)結果顯示，來(lái)自因子定價模型的(de)樣本外定價誤差會随著(zhe)因子數量的(de)增加而減少。無疑，這(zhè)種偏好複雜(zá)度的(de)觀點挑戰了(le)傳統的(de) APT（Ross 1976），即少量的(de)風險因子應該捕捉資産之間的(de)風險和(hé)收益率的(de)權衡。然而，用(yòng)該文自己的(de)話(huà)說，即使不存在套利且真實 SDF 存在，人(rén)們也(yě)能夠在實證中持續地挖出新的(de)、未被已有因子定價的(de)因子（或異象），而将它們加到 SDF 中會持續改善樣本外的(de)表現。

另外，鑒于 SDF 和(hé) MVE 組合的(de)等價性，該文的(de)理(lǐ)論和(hé)實證結果對(duì)業界的(de)啓發是，随著(zhe)納入投資組合的(de)因子個(gè)數的(de)增多(duō)，其樣本外的(de)風險調整後收益會提高(gāo)。也(yě)就是說，對(duì)投資者來(lái)說，最優的(de) MVE 組合是使用(yòng)大(dà)量因子，從而提高(gāo)樣本外的(de)夏普比率。此外，Kelly 他(tā)們的(de)發現對(duì)于 zoo of factors 也(yě)有新的(de)解讀。即實證中的(de)大(dà)量異象既不是令人(rén)頭疼的(de)難題，更不意味著(zhe)學術界的(de) p-hacking 風氣盛行（Jensen, Kelly and Pedersen 2023）。反之，它是在複雜(zá)的(de)資産定價環境中的(de)必然結果。

4

毫無疑問，估計 SDF 是實證資産定價中的(de)最核心問題。因爲一旦有了(le) SDF，通(tōng)過資産和(hé)它的(de)協方差就可(kě)以給資産定價。而關于這(zhè)個(gè)問題，一個(gè)人(rén)的(de)看法取決于他(tā)所持有的(de)立場(chǎng)。站在業界的(de)角度，我們關心的(de)如何最大(dà)化(huà)樣本外條件夏普比率。從這(zhè)個(gè)立場(chǎng)出發，我個(gè)人(rén)認同 SDF 是非稀疏的(de)，或者說我更傾向在估計 SDF 的(de)時(shí)候使用(yòng)更多(duō)的(de)因子。

爲了(le)給出進一步的(de)說明(míng)，仍然回到 SDF 和(hé) MVE 的(de)等價性。在數據如此豐富的(de)時(shí)代，用(yòng)于構造真實 MVE 組合的(de)因子可(kě)能會有很多(duō)，而每個(gè)低維模型都隐含了(le)對(duì) MVE（也(yě)即 SDF）所包含因子的(de)先驗。比如，最簡單的(de) FF3 使用(yòng)規模和(hé)價值兩個(gè)因子，意味著(zhe)該模型認爲這(zhè)兩個(gè)組合在 MVE 組合/SDF 中這(zhè)兩個(gè)因子的(de)權重非零。所以，我們必須客觀的(de)問自己是否有足夠充分(fēn)的(de)先驗認爲并相信 SDF 隻和(hé)少數幾個(gè)因子有關。

Baba-Yara, Boyer and Davis (2021) 從 MVE 組合夏普比率的(de)角度比較了(le)諸多(duō)使用(yòng)傳統和(hé)機器學習(xí)方法構造的(de)低維實證模型，發現這(zhè)些模型并不能解釋彼此。該文通(tōng)過貝葉斯統計發現當潛在的(de)因子數非常大(dà)時(shí)，使用(yòng)不同先驗的(de)模型（哪怕其中包含真實的(de)模型）都注定無法爲彼此定價。換句話(huà)說，在因子的(de)高(gāo)維數時(shí)代，從 pricing error 檢驗的(de)角度出發，不存在最優的(de)低維模型，所以這(zhè)種 factor war 比較似乎是徒勞的(de)（或者說 factor model "failure" 是注定的(de)）。而如果以最大(dà)化(huà)夏普比率爲目标，與其苦苦尋找低維 SDF，也(yě)許更應該想想如何利用(yòng)好衆多(duō)因子所包含的(de)信息。

參考文獻

Baba-Yara, F., B. Boyer, and C. Davis (2021). The factor model failure puzzle. Working paper.

Bryzgalova, S., J. Huang, and C. Julliard (2023). Bayesian solutions for the factor zoo: We just ran two quadrillion models. Journal of Finance 78(1), 487-557.

Didisheim, A., S. Ke, B. Kelly, and S. Malamud (2023). Complexity in factor pricing models. Tech. rep. Yale University.

Hansen, L. P. and S. F. Richard (1987). The role of conditioning information in deducing testable restrictions implied by dynamic asset pricing models. Econometrica 55(3), 587-613.

Feng, G., S. Giglio, and D. Xiu (2020). Taming the factor zoo: A test of new factors. Journal of Finance 75(3), 1327-1370.

Freyberger, J., A. Neuhierl, and M. Weber (2020). Dissecting characteristics nonparametrically. Review of Financial Studies 33(5), 2326-2377.

Jensen, T. I., B. Kelly, and L. H. Pedersen (2023). Is there a replication crisis in finance? Journal of Finance 78(5), 2465-2518.

Karolyi, G. A. and S. Van Nieuwerburgh (2020). New methods for the cross-section of returns. Review of Financial Studies 33(5), 1879-1890.

Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.

Lettau, M., and M. Pelger (2020). Factors that fit the time series and cross-section of stock returns. Review of Financial Studies 33(5), 2274-2325.

Ross, S. A. (1976). The arbitrage theory of capital asset pricing. Journal of Economic Theory 13(3), 341-360.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。