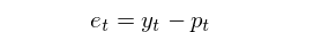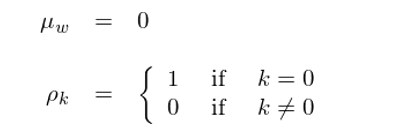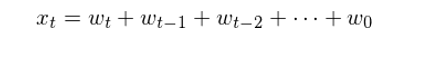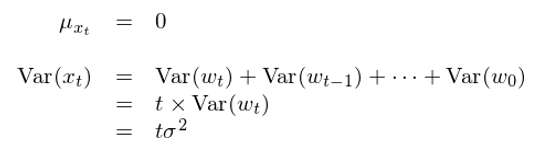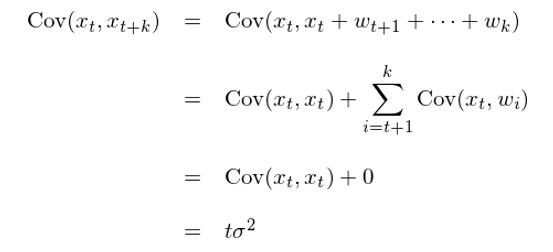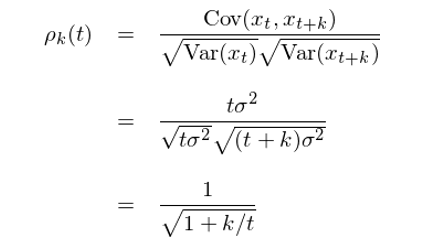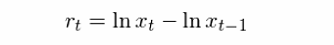寫給你的(de)金融時(shí)間序列分(fēn)析：初級篇

作者：石川

摘要：作爲系列第二篇，本文介紹了(le)時(shí)間序列的(de)最基本模型：白噪聲和(hé)随機遊走，說明(míng)白噪聲并不是描述收益率序列的(de)有效模型。

1 書(shū)接前文

前文《寫給你的(de)金融時(shí)間序列分(fēn)析：基礎篇》介紹了(le)金融時(shí)間序列的(de)核心特性：自相關性；說明(míng)金融時(shí)間序列分(fēn)析的(de)核心正是挖掘該時(shí)間序列中的(de)自相關性。一個(gè)優秀的(de)模型應該能夠有效的(de)刻畫(huà)原始時(shí)間序列中不同間隔的(de)自相關性；而衡量一個(gè)模型是否适合原始時(shí)間序列的(de)标準正是考察原始值和(hé)拟合值之間的(de)殘差序列是否近似的(de)爲白噪聲。

本篇是系列的(de)第二篇，初級篇。白噪聲正是本文的(de)内容之一，它是時(shí)間序列分(fēn)析中最基本的(de)模型。在它的(de)基礎上延伸出的(de)另一個(gè)基本模型便是随機遊走。通(tōng)常，白噪聲和(hé)随機遊走被認爲是用(yòng)來(lái)分(fēn)别描述投資品收益率和(hé)價格的(de)最簡單模型。我們稍後會看到，對(duì)于收益率來(lái)說（特别是股指的(de)收益率），白噪聲模型并不有效。

2 時(shí)間序列建模

本質上說講，時(shí)間序列模型是一個(gè)可(kě)以“解釋”時(shí)間序列中的(de)自相關性的(de)數學模型。

能夠解釋時(shí)間序列的(de)自相關性在量化(huà)投資領域意義重大(dà)：

時(shí)間序列分(fēn)析爲我們研究投資品收益率的(de)行爲提供了(le)有力的(de)統計學框架。在投資中，對(duì)收益率的(de)預測顯然是非常有用(yòng)的(de)。如果我們能夠預測投資品的(de)漲跌，那麽就能基于此構建一個(gè)交易策略；如果我們能夠預測收益率的(de)波動率，那麽就可(kě)以進行風險管理(lǐ)（因此我們對(duì)時(shí)間序列的(de)二階統計量——如方差——同樣感興趣）。假設原始時(shí)間序列爲｛y_t｝，模型拟合出來(lái)的(de)序列爲｛p_t｝，則殘差序列｛e_t｝ 定義爲原始序列和(hé)拟合序列的(de)差值：

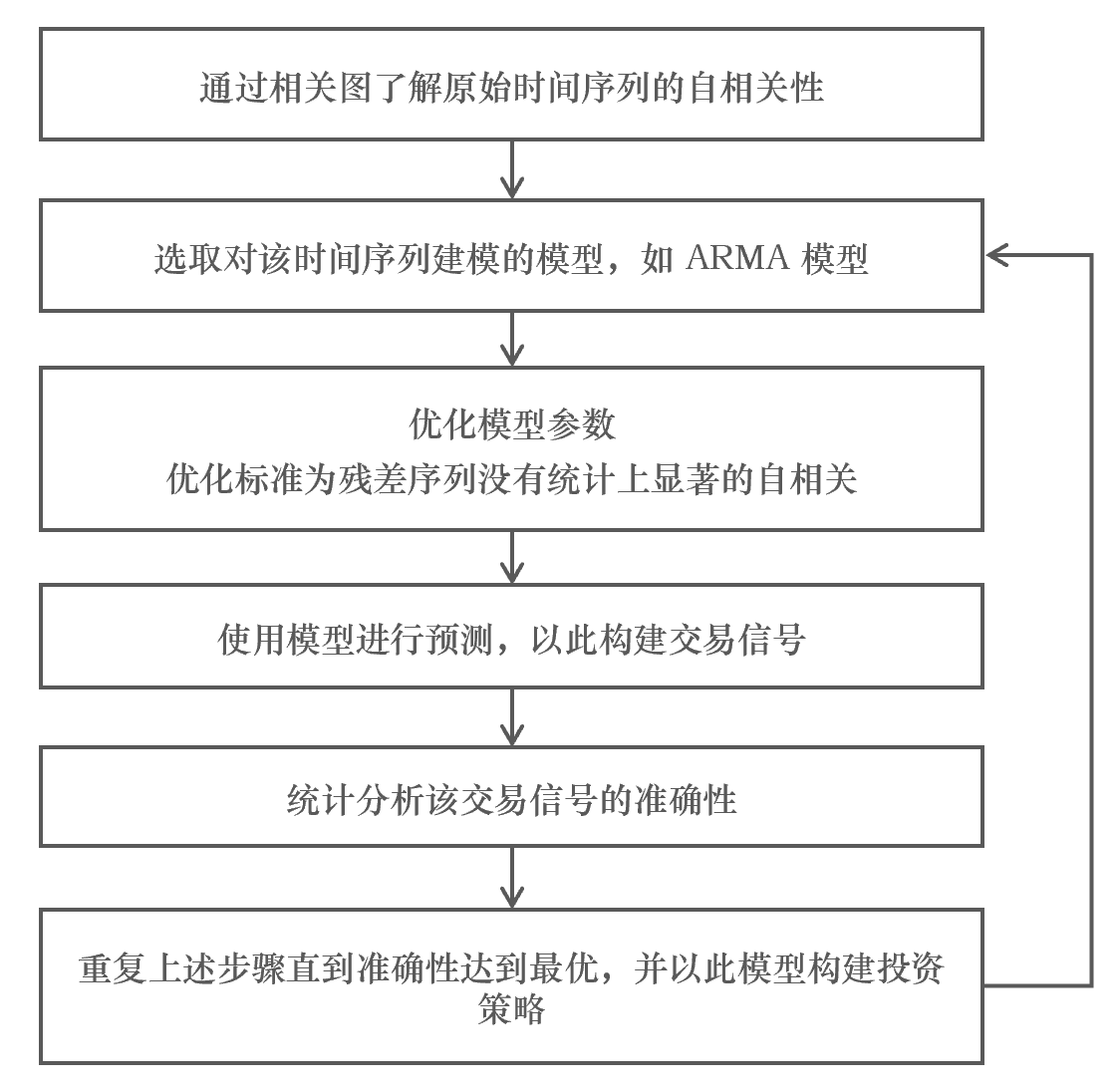
如果模型很好的(de)捕捉了(le)原始時(shí)間序列的(de)自相關性，那麽殘差序列｛e_t｝應該近似的(de)爲白噪聲，對(duì)任何非零間隔 k，該殘差序列的(de)自相關系數 ρ_k 都應該在統計意義上不顯著的(de)偏離 0。當然，這(zhè)僅僅是我們說該模型是個(gè)優秀模型的(de)充分(fēn)條件，因爲一個(gè)好模型最關鍵的(de)還(hái)是能産生賺錢的(de)交易信号。因此，模型的(de)檢驗最終還(hái)要看它在樣本外預測的(de)準确性。時(shí)間序列建模的(de)過程可(kě)以總結如下(xià)。

對(duì)于一個(gè)時(shí)間序列，我們總是希望首先畫(huà)出它的(de)相關圖來(lái)看看它存在什(shén)麽樣的(de)自相關性。基于對(duì)其自相關性的(de)認知，第二步則是選擇合适的(de)模型，比如 AR、MA 或者 ARMA 模型，甚至于更高(gāo)級對(duì)波動率建模的(de) GARCH 模型等。選定模型後，接下(xià)來(lái)便需要優化(huà)模型的(de)參數，以使其盡可(kě)能解釋時(shí)間序列的(de)自相關性。在這(zhè)一步，我們通(tōng)過對(duì)殘差進行自相關性分(fēn)析來(lái)判斷模型是否合适。在這(zhè)方面，Ljung–Box 檢驗是一個(gè)很好的(de)方法，它同時(shí)檢驗給殘差序列各間隔的(de)自相關系數是否顯著的(de)不爲 0。在選定模型參數之後，仍需定量評價該模型在樣本外預測的(de)準确性。畢竟，對(duì)于樣本内的(de)數據，錯誤的(de)過拟合總會得(de)到“優秀”的(de)模型，但它們往往對(duì)樣本外數據的(de)預測效果很差。因此，隻有樣本外預測的(de)準确性才能客觀的(de)評價模型的(de)好壞。如果模型的(de)準确性較差，這(zhè)說明(míng)該模型存在缺陷，無法充分(fēn)捕捉原序列的(de)自相關性。這(zhè)時(shí)必須考慮更換模型。這(zhè)就構成了(le)上述步驟的(de)反饋回路，直到最終找到一個(gè)既能解釋原時(shí)間序列自相關性，又能在樣本外有不錯的(de)準确性的(de)模型。之後，該模型将被用(yòng)來(lái)産生交易型号并構建量化(huà)投資策略。

接下(xià)來(lái)我們就來(lái)介紹一個(gè)最簡單的(de)時(shí)間序列模型：白噪聲。

3 白噪聲

本文第一節指出，對(duì)于收益率來(lái)說，白噪聲（white noise）并不是一個(gè)十分(fēn)有效的(de)模型。那麽爲什(shén)麽我們還(hái)要研究它呢(ne)？這(zhè)是因爲它有一個(gè)重要的(de)特性，即序列不相關：一個(gè)白噪聲序列中的(de)每一個(gè)點都獨立的(de)來(lái)自某個(gè)未知的(de)分(fēn)布，它們滿足獨立同分(fēn)布（independent and identically distributed）。一個(gè)（離散）白噪聲的(de)定義如下(xià)：

上面的(de)定義并沒有假設 w_t 來(lái)自正态分(fēn)布。事實上，白噪聲對(duì)分(fēn)布沒有要求。當 w_t 來(lái)自正态分(fēn)布時(shí)，該序列又稱爲高(gāo)斯白噪聲（Gaussian white noise）。根據白噪聲的(de)定義，一個(gè)白噪聲序列顯然滿足平穩性要求。它的(de)均值和(hé)二階統計量爲：

我們已經多(duō)次強調，當一個(gè)模型很好的(de)捕捉了(le)原始時(shí)間序列的(de)自相關性，它的(de)殘差序列就應該沒有任何（統計意義上顯著的(de)）自相關性了(le)。換句話(huà)說，一個(gè)優秀模型的(de)殘差序列應該（近似）爲一個(gè)白噪聲。因此，使用(yòng)白噪聲序列的(de)性質可(kě)以幫助我們确認我們的(de)殘差序列中沒有任何相關性了(le)，一旦殘差序列沒有相關性便意味著(zhe)模型是原始時(shí)間序列的(de)一個(gè)良好的(de)拟合。

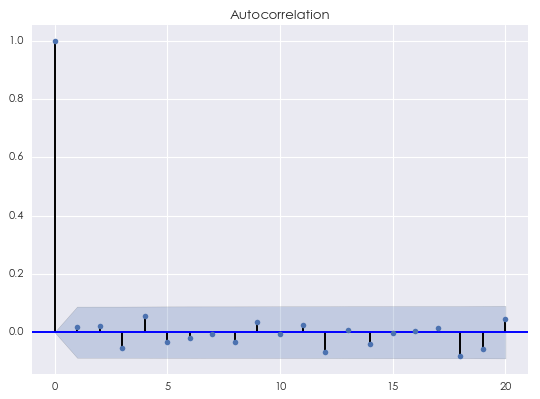
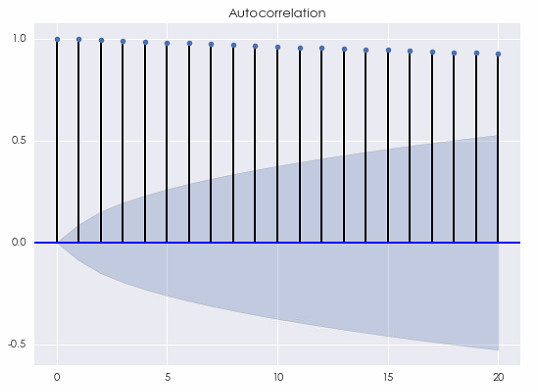
在白噪聲模型中，唯一的(de)參數就是方差 σ^2。這(zhè)個(gè)參數可(kě)以通(tōng)過曆史數據估計得(de)到。在本系列的(de)第一篇文章(zhāng)中，我們曾給出了(le)一個(gè)白噪聲序列的(de)相關圖（如下(xià)），該序列由标準正态分(fēn)布生成（因此爲高(gāo)斯白噪聲），共 500 個(gè)觀測值。可(kě)以看到，對(duì)圖中顯示的(de)間隔 k 的(de)取值，對(duì)所有 k ≥ 1 均有自相關系數在統計上等于 0。

4 随機遊走

将白噪聲模型進行一步延伸，便得(de)到随機遊走（random walk）模型，它的(de)定義如下(xià)：

由定義可(kě)知，在任意 t 時(shí)刻的(de) x_t 都是不超過 t 時(shí)刻的(de)所有曆史白噪聲序列的(de)總和(hé)，即：

随機遊走的(de)序列均值和(hé)方差爲：

雖然均值不随時(shí)間 t 改變，但是由于方差是 t 的(de)函數，因此随機遊走不滿足穩定性。随著(zhe) t 的(de)增加，x_t 的(de)方差增大(dà)，說明(míng)其波動性不斷增加。對(duì)于任意給定的(de) k，通(tōng)過以下(xià)推導給得(de)出随機遊走的(de)自協方差：

上述推導中使用(yòng)了(le)獨立随機變量的(de)方差可(kě)加性。有了(le)自協方差和(hé)方差，便可(kě)以方便的(de)求出随機遊走的(de)自相關函數：

顯然，自相關系數既是時(shí)間 t 又是間隔 k 的(de)函數。ρ 的(de)表達式說明(míng)，對(duì)于一個(gè)足夠長(cháng)的(de)随機遊走時(shí)間序列（t 很大(dà)），當考察的(de)自相關間隔 k 很小時(shí)，自相關系數近似爲 1。這(zhè)是随機遊走的(de)一個(gè)非常重要的(de)特性，不熟悉它往往容易造成不必要的(de)錯誤。

舉個(gè)例子。我們通(tōng)常假設股價的(de)對(duì)數收益率符合正态分(fēn)布，因此股價對(duì)數是一個(gè)布朗運動（随機遊走的(de)一種特殊形式）。如果當前的(de)（對(duì)數）股價是 x_t，由随機遊走的(de)特性可(kě)知，t + 1 時(shí)刻的(de)股價的(de)條件期望爲 E[x_[t+1] | x_t] = x_t，即我們對(duì)下(xià)一時(shí)點的(de)股價的(de)最好的(de)猜測就是當前的(de)價格。随機遊走是一個(gè)鞅（martingale）。

假如我們有一個(gè)預測股價的(de)模型，而該模型就是用(yòng) t 時(shí)刻的(de)股價作爲對(duì) t + 1 時(shí)刻的(de)股價的(de)預測，則該模型的(de)預測值和(hé)實際值之間的(de)相關系數就等于股價序列的(de)間隔爲 1 的(de)自相關系數。如果股價近似的(de)爲随機遊走，那麽由它的(de)性質可(kě)知，間隔爲 1 的(de)自相關系數非常接近 1。因此我們的(de)股價預測模型——用(yòng)今天的(de)價格作爲明(míng)天的(de)價格的(de)預測——的(de)預測值和(hé)實際值之間的(de)相關系數也(yě)非常接近 1。這(zhè)會給我們造成錯覺：這(zhè)個(gè)模型相當準确。不幸的(de)是，這(zhè)個(gè)模型猜測的(de)收益率在任何時(shí)刻都爲 0，因此它對(duì)于我們構建交易信号毫無作用(yòng)。

我看到過無數的(de)學術論文（大(dà)多(duō)是碩士論文）中，針對(duì)投資品價格本身構建自回歸模型。獨立變量就包括曆史價格，用(yòng)它們和(hé)其他(tā)一些基本面或宏觀經濟數據來(lái)預測下(xià)一個(gè)交易日的(de)股價。從上面的(de)分(fēn)析可(kě)知，這(zhè)樣的(de)模型将會“精準的(de)毫無用(yòng)處”，因爲回歸模型中曆史價格的(de)系數之和(hé)将會非常接近 1。

任何價格序列的(de)自回歸模型都是耍流氓。

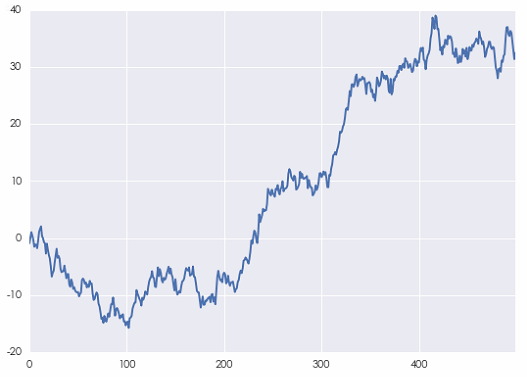
利用(yòng)本文第三節例子中的(de)白噪聲序列，便可(kě)以構建一個(gè)人(rén)工随機遊走序列的(de)例子。它的(de)軌迹如下(xià)圖所示。

不出意外，當間隔 k 相對(duì)于時(shí)間序列的(de)長(cháng)度很小時(shí)，它的(de)自相關系數（下(xià)圖）非常接近 1，這(zhè)源自随機遊走的(de)性質。不要忘了(le)，随機遊走是對(duì)股價的(de)對(duì)數建模。因此，這(zhè)種自相關性對(duì)于基于收益率預測的(de)投資策略并沒有幫助。

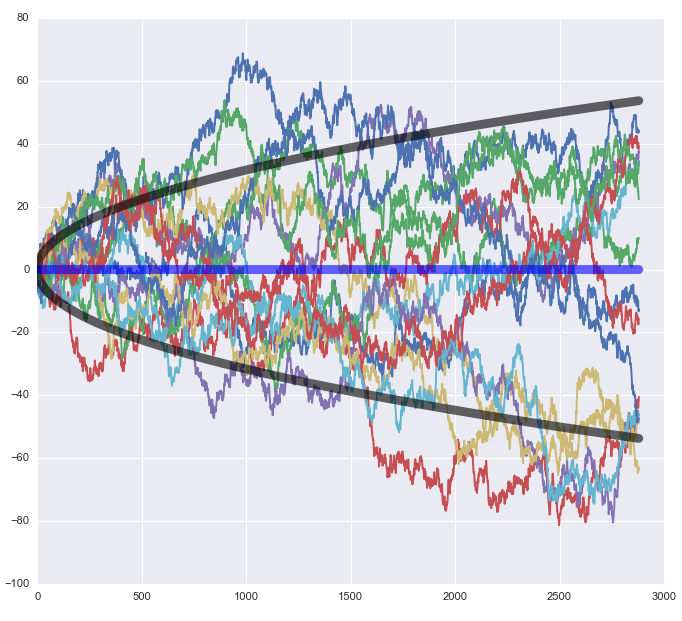
事實上，如果（對(duì)數）股價嚴格的(de)符合随機遊走，那麽該時(shí)間序列的(de)方差将會随時(shí)間線性增長(cháng)。這(zhè)說明(míng)，長(cháng)期來(lái)看它将呈現出巨大(dà)的(de)波動。下(xià)圖爲來(lái)自同一個(gè)分(fēn)布的(de) 15 條随機遊走的(de)軌迹。随著(zhe)時(shí)間的(de)推進，這(zhè)些軌迹上對(duì)應觀測值的(de)波動越來(lái)越大(dà)，充分(fēn)的(de)展現出随機性。

5 用(yòng)白噪聲對(duì)收益率建模

如果股票(piào)的(de)對(duì)數收益率爲白噪聲，那麽它的(de)自相關系數應該在任何非零的(de)間隔上都在統計意義上等于零。下(xià)面我們就來(lái)看看真實的(de)股票(piào)收益率是否滿足這(zhè)一點。爲此，考慮一支個(gè)股（萬科）和(hé)一個(gè)股指（上證指數）。以日頻(pín)爲例，通(tōng)過交易日的(de)複盤後收盤價可(kě)以算(suàn)出對(duì)數收益率：

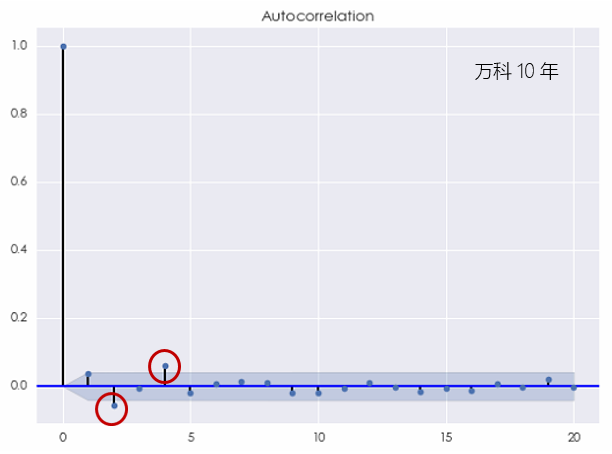
首先來(lái)看看萬科，當考察期爲過去 10 年時(shí)，萬科的(de)對(duì)數收益率的(de)相關圖爲：

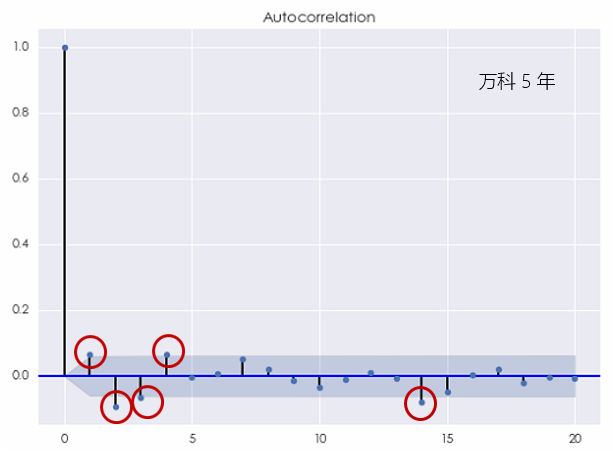
上圖指出，在間隔爲 2 和(hé) 4 時(shí)，該收益率序列表現出了(le)統計意義上顯著的(de)相關性。當然，由于圖中的(de)藍色區(qū)域僅僅是 95% 的(de)置信區(qū)間，因此僅僅根據随機性也(yě)很可(kě)能出現在一個(gè)或者兩個(gè)間隔上的(de)自相關系數處于置信區(qū)間之外的(de)情況。因此，根據上面的(de)結果，我們并不能一定就說白噪聲不是萬科收益率的(de)一個(gè)适當的(de)模型。如果我們把考察的(de)窗(chuāng)口縮短到過去 5 年，則萬科的(de)對(duì)數日收益率序列的(de)相關圖變爲：

當 k = 1，2，3，4 以及 14 的(de)時(shí)候，自相關系數都超過了(le)置信區(qū)間，即在 5% 的(de)顯著性水(shuǐ)平下(xià)不爲零。我們無法再無視這(zhè)樣的(de)結果而把它們都歸結于随機性。該相關圖清晰地說明(míng)白噪聲不能有效的(de)解釋收益率序列中的(de)自相關性。

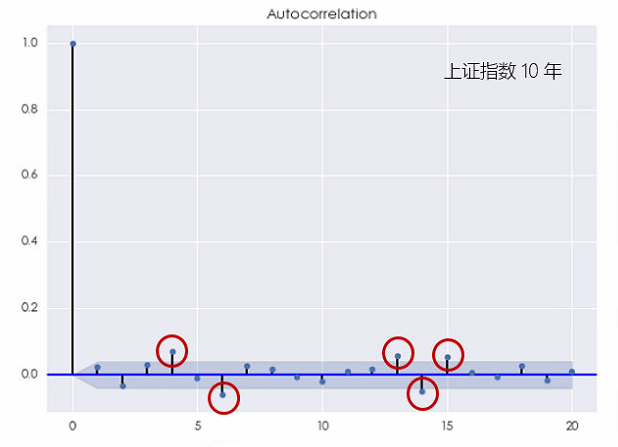
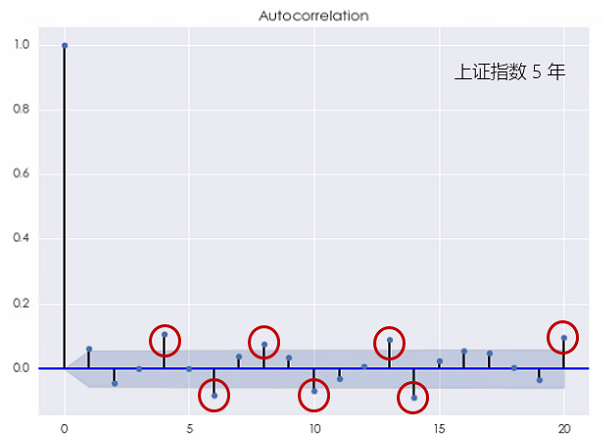
對(duì)于上證指數，這(zhè)種結論則更加明(míng)顯。無論是考察 10 年還(hái)是 5 年的(de)窗(chuāng)口，上證指數的(de)對(duì)數收益率均在不同的(de)間隔上表現出了(le)顯著的(de)自相關（下(xià)圖），且它比個(gè)股的(de)自相關性更加顯著。

這(zhè)個(gè)結果說明(míng)上證指數的(de)對(duì)數收益率序列無法用(yòng)白噪聲來(lái)建模。更有意思的(de)是，當 k 較小或者較大(dà)時(shí)，上證指數的(de)收益率均表現出了(le)自相關性，這(zhè)說明(míng)它既有短記憶又有長(cháng)記憶。

6 下(xià)文預告

本文的(de)分(fēn)析引出如下(xià)的(de)結論：

因此，我們必須考慮更加高(gāo)級的(de)時(shí)間序列模型來(lái)對(duì)自相關性建模。在這(zhè)方面，自回歸模型（AR）和(hé)移動平均模型（MA），以及它們二者的(de)組合——自回歸移動平均模型（ARMA）——都是非常有力的(de)工具。它們将是本系列下(xià)一篇的(de)内容。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。