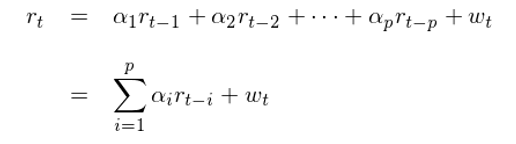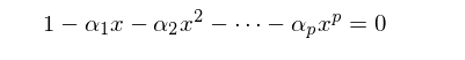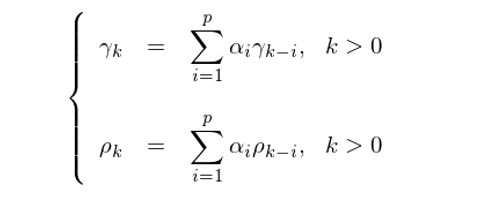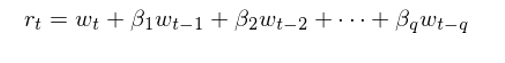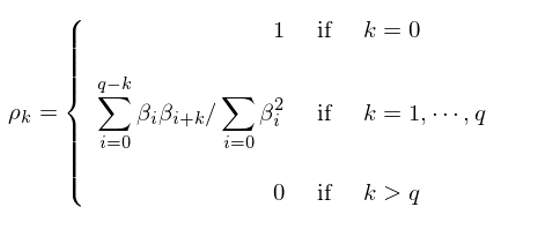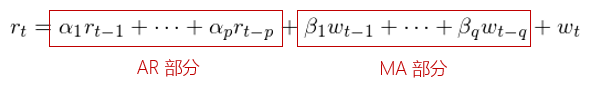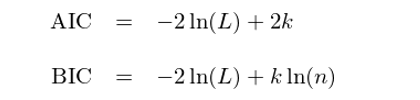寫給你的(de)金融時(shí)間序列分(fēn)析：進階篇

作者：石川

摘要：系列第三篇，介紹時(shí)間序列分(fēn)析中最常用(yòng)的(de)線性模型：自回歸模型、移動平均模型，以及二者結合的(de)自回歸移動平均模型。

1 書(shū)接前文

本系列的(de)前兩篇 —— 基礎篇和(hé)初級篇 —— 分(fēn)别介紹了(le)金融時(shí)間序列分(fēn)析的(de)核心以及時(shí)間序列建模中最簡單的(de)模型：白噪聲和(hé)随機遊走。在金融時(shí)間序列研究的(de)對(duì)象中，投資品的(de)收益率無疑是最重要的(de)一個(gè)。挖掘收益率序列的(de)自相關性是金融時(shí)間序列的(de)核心内容。無論對(duì)于個(gè)股還(hái)是指數，它們的(de)收益率序列都表現著(zhe)一定的(de)自相關性。前面的(de)文章(zhāng)說明(míng)，白噪聲模型假設了(le)時(shí)間序列各觀測點之間的(de)獨立性、無法捕捉收益率序列的(de)自相關性，因此使用(yòng)白噪聲來(lái)對(duì)投資品收益率建模是不妥的(de)。

本文爲系列的(de)第三篇——進階篇。我們将介紹時(shí)間序列分(fēn)析中最常用(yòng)的(de)線性模型：自回歸模型、移動平均模型，以及它們二者結合的(de)自回歸移動平均模型。在下(xià)文中我們将看到，自回歸和(hé)移動平均模型這(zhè)兩個(gè)模型都從某種程度上符合交易者對(duì)收益率變化(huà)的(de)理(lǐ)解，因此它們都能刻畫(huà)出收益率序列中的(de)某種自相關性。

2 自回歸模型

對(duì)于 A 股的(de)收益率，人(rén)們往往有這(zhè)樣的(de)感受：

這(zhè)些感受給我們的(de)啓發是，收益率序列的(de)前後觀測點之間往往不是獨立的(de)，而是以某種自相關性聯系在一起。因此，一個(gè)很自然的(de)問題就是：能不能用(yòng)過去的(de)收益率序列對(duì)未來(lái)的(de)收益率建模？答(dá)案是肯定的(de)。這(zhè)便引出了(le)自回歸模型（autoregressive model）。

這(zhè)是一個(gè)典型的(de)線性回歸模型。它和(hé)傳統線性回歸的(de)不同之處在于自變量是序列自身（曆史觀測值），而非其他(tā)變量，這(zhè)就是自回歸中“自”的(de)由來(lái)。另外，p 階的(de)意思是模型使用(yòng)當前時(shí)刻 t 之前的(de) p 個(gè)觀測值作爲自變量對(duì) r_t 建模。這(zhè)個(gè)模型的(de)含義是，r_t 可(kě)以表達爲 t 時(shí)刻之前的(de) p 個(gè)收益率觀測值的(de)線性組合以及一個(gè) t 時(shí)刻的(de)随機誤差 w_t。

在上面這(zhè)個(gè)定義中，我們沒有考慮截距項。如果截距項對(duì)于待研究的(de)時(shí)間序列是必要的(de)，則可(kě)以在上面的(de)公式右側加入一個(gè)常數項 c。另外需要特别說明(míng)的(de)是，自回歸模型不一定都滿足平穩性。舉一個(gè)最簡單的(de)例子，本系列初級篇介紹的(de)随機遊走模型其實就是一個(gè) 1 階自回歸模型，滿足：x_t = x_[t-1] + w_t。由于 x_t 的(de)方差是時(shí)間 t 的(de)函數，因此該序列不滿足平穩性。對(duì)于一個(gè) p 階自回歸模型，由它的(de)回歸系數 α_i 可(kě)以寫出它的(de)特征方程（characteristic equation）：

它是一個(gè) p 次多(duō)項式，有 p 個(gè)解，其中可(kě)能既包括實數解又包括複數解；這(zhè) p 個(gè)解的(de)倒數稱爲該方程的(de)特征根（characteristic roots）。自回歸模型平穩性要求模型特征方程的(de)所有特征根的(de)模都小于 1。在上面的(de)随機遊走例子中，該模型的(de)特征方程爲 1 - x = 0，它的(de)特征根爲 1。由于它不滿足模小于 1 這(zhè)個(gè)條件，因此該模型不滿足平穩性。

對(duì)于一個(gè)滿足平穩性、且假設沒有截距項的(de) p 階自回歸模型，它的(de)均值顯然爲 0（如果有截距項的(de)話(huà)，該時(shí)間序列的(de)均值就是 c）；它的(de)不同間隔 k 的(de)自協方差 γ_k 和(hé)自相關系數 ρ_k 可(kě)以表達爲如下(xià)的(de)遞歸方程，又稱爲 Yule-Walker equations：

在實際中，想要使用(yòng)自回歸模型對(duì)收益率建模，必須确定模型的(de)階數 p。這(zhè)一點将在本文的(de)第 5 節討(tǎo)論。

3 移動平均模型

移動平均（moving average）模型是另一個(gè)常見的(de)線性時(shí)間序列模型。在自回歸模型中，我們将收益率 r_t 看作是給定階數 p 下(xià)曆史收益率序列的(de)線性組合。與自回歸模型不同，移動平均模型将收益率 r_t 看作是曆史白噪聲的(de)線性組合。這(zhè)聽(tīng)起來(lái)也(yě)許有些費解。但它背後的(de)邏輯也(yě)符合人(rén)們的(de)認知。以美(měi)股指數（比如标準普爾 500 指數）爲例，它給我們的(de)印象是它的(de)收益率有一個(gè)微弱的(de)但是大(dà)于零的(de)漂移率（drift），形成一個(gè)常年慢(màn)牛的(de)走勢。除了(le)這(zhè)個(gè) drift 項之外，它的(de)收益率呈不規則的(de)波動。在這(zhè)種背景下(xià)，自回歸模型仿佛不是那麽好用(yòng)。而移動平均模型則是對(duì)漂移率之外“随機噪聲”建模，它把這(zhè)些噪聲理(lǐ)解爲不同時(shí)刻出現的(de)影(yǐng)響收益率的(de)新息或者沖擊（shocks）。通(tōng)過對(duì)“噪聲”建模來(lái)預測當前時(shí)刻 t 的(de)“噪聲”，再和(hé)漂移率結合，作爲 t 時(shí)刻的(de)收益率預測。

與自回歸模型不同，移動平均模型一定滿足平穩性。它的(de)序列均值爲 0（如果考慮截距項，則可(kě)以在上式右側加入一個(gè)常數 c 代表漂移率，這(zhè)時(shí)序列均值變爲 c）。它的(de)各間隔 k 的(de)自相關系數滿足：

其中 β_0 = 1。同樣，我們将在第 5 節中介紹如何選擇移動平均模型的(de)階數 q。

4 自回歸移動平均模型

前面兩節分(fēn)别討(tǎo)論了(le)自回歸和(hé)移動平均模型。前者用(yòng)收益率的(de)曆史對(duì)未來(lái)收益率做(zuò)預測，它背後的(de)邏輯是捕捉市場(chǎng)參與者的(de)有效性（或者非有效性）造成的(de)市場(chǎng)的(de)動量或者反轉效應；而後者對(duì)噪聲建模，其邏輯爲突發信息對(duì)收益率将會造成沖擊（比如上市公司超出預期的(de)财報或者内部交易醜聞等）。

将一個(gè) p 階的(de)自回歸模型和(hé)一個(gè) q 階的(de)移動平均模型組合在一起，便得(de)到了(le)一個(gè)階數爲 (p,q) 的(de)自回歸移動平均模型（autoregressive moving average model），它将 AR 和(hé) MA 模型的(de)優勢互補起來(lái)。由于 AR 和(hé) MA 模型都是線性模型，因此它倆的(de)線性組合，即 ARMA 模型，也(yě)是線性模型。

相比較單一的(de) AR 或者 MA 模型，ARMA 模型擁有更多(duō)的(de)參數。因此它出現過拟合的(de)危險就更高(gāo)。雖然它能夠捕捉到兩個(gè)單一模型各自所代表的(de)時(shí)間序列自回歸性，但是在确定階數 p 和(hé) q 的(de)時(shí)候，我們應時(shí)刻謹記，防止過拟合。下(xià)面就來(lái)看看如何利用(yòng)信息量準則（information criterion）和(hé)殘差自相關檢驗來(lái)确定 AR、MA 以及 ARMA 模型的(de)階數。

5 模型的(de)階數

在實際中使用(yòng) AR、MA 或 ARMA 模型對(duì)收益率建模，必須确定模型的(de)階數 p 以及 q。顯然，p 或者 q 越大(dà)，則模型的(de)參數越多(duō)，越有可(kě)能捕捉到時(shí)間序列中不同間隔 k 的(de)自相關性。但是，參數太多(duō)的(de)話(huà)容易造成過拟合。因此在選擇階數時(shí)，必須同時(shí)考慮拟合的(de)準确性和(hé)防止過拟合。

在确定模型階數時(shí)，常用(yòng)的(de)工具是使用(yòng)信息量準則，包括赤池信息量準則（Akaike information criterion，簡稱 AIC，由日本統計學家赤池弘次創立）以及貝葉斯信息量準則（Bayesian information criterion，簡稱 BIC）。這(zhè)兩個(gè)信息量準則的(de)目的(de)都是尋找可(kě)以最好地解釋數據但包含最少自由參數的(de)模型。它們均使用(yòng)模型的(de)似然函數、參數個(gè)數以及觀測點個(gè)數來(lái)構建一個(gè)标量函數，以此作爲評價模型好壞的(de)标準。它們的(de)區(qū)别是标量函數的(de)表達式有所不同。令 L、k、n 表示模型的(de)似然函數，則 AIC 和(hé) BIC 的(de)定義分(fēn)别爲：

從定義可(kě)知，AIC 和(hé) BIC 都由兩部分(fēn)組成：第一部分(fēn)衡量模型的(de)拟合度，第二部分(fēn)是對(duì)參數個(gè)數的(de)懲罰（防止過拟合）。當一個(gè)模型能夠很好的(de)解釋（樣本内）數據時(shí)，它的(de)似然函數很大(dà)，因此第一項 -2ln(L) 就會越小；如果模型的(de)參數越少，則第二項也(yě)越少。所以 AIC 和(hé) BIC 總是越小越好。

值得(de)說明(míng)的(de)是，AIC 和(hé) BIC 的(de)表達式雖然長(cháng)得(de)差不多(duō)，但是還(hái)是有細微的(de)差别。因此在實際中，有可(kě)能 AIC 對(duì)應的(de)最優階數（即使得(de) AIC 最小）和(hé) BIC 對(duì)應的(de)最優階數（即使得(de) BIC 最小）略有差别。具體選擇哪個(gè)信息量準則則取決于使用(yòng)者自身。

當我們使用(yòng) AIC 或者 BIC 确定模型的(de)最優階數之後，便可(kě)以對(duì)時(shí)間序列建模。但是，我們仍然需要檢驗該模型是否很好的(de)捕捉了(le)時(shí)間序列的(de)自相關性。在本系列反複強調過，如果一個(gè)模型和(hé)原時(shí)間序列的(de)殘差滿足白噪聲，那麽該模型就是合适的(de)。因此，我們隻需要檢驗殘差序列是否在任何間隔 k 上呈現出統計意義上顯著的(de)自相關性。在這(zhè)方面，Ljung–Box 檢驗是一個(gè)很好的(de)方法，它同時(shí)檢驗殘差序列各間隔的(de)自相關系數是否顯著的(de)不爲 0。

6 利用(yòng) AR、MA 以及 ARMA 建模

本節中，我們利用(yòng)上面介紹的(de) AR、MA 以及 ARMA 對(duì)上證指數的(de)對(duì)數收益率建模。實驗考慮 2012 年 4 月(yuè) 24 日到 2017 年 4 月(yuè) 24 日這(zhè)五年之中上證指數的(de)日收益率。在确定模型階數時(shí)，在給定的(de) p、q 參數區(qū)間内使用(yòng)不同的(de)參數取值建模，并采用(yòng) AIC 準則進行參數選擇，在建模時(shí)讓保留常數項。p 和(hé) q 的(de)區(qū)間分(fēn)别爲：

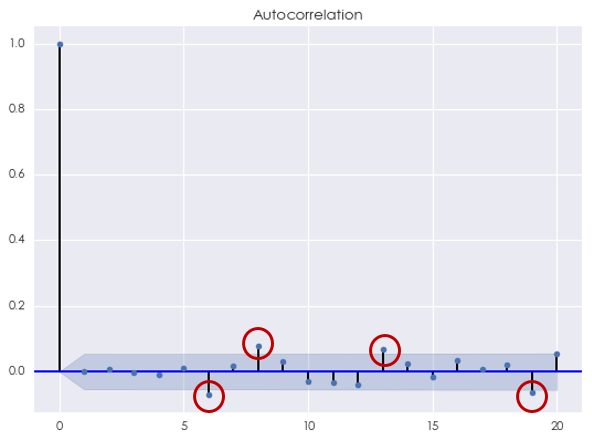
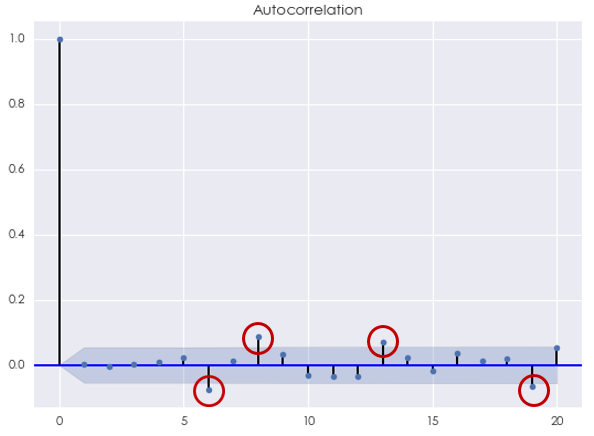
首先來(lái)看 AR 模型。根據 AIC 準則，最優的(de)階數 p* = 4，此時(shí) AIC = -7305.31。使用(yòng) Ljung-Box 檢驗原始對(duì)數收益率序列和(hé) AR(4) 模型的(de)殘差是否在 20 以内的(de)間隔上有任何自相關性，統計量的(de) p-value 爲 0.005132，說明(míng)我們可(kě)以在 1% 的(de)顯著性水(shuǐ)平下(xià)拒絕原假設。這(zhè)意味著(zhe)殘差中存在相關性。事實上，這(zhè)可(kě)以從殘差序列的(de)相關圖中看到，它說明(míng)殘差序列在間隔 k 等于 6、8、13 和(hé) 19 時(shí)仍然有 AR(4) 模型未捕捉到的(de)自相關性。

再來(lái)看看 MA 模型。根據 AIC 準則，最優的(de)階數同樣爲 q* = 4，此時(shí) AIC = -7302.70。使用(yòng) Ljung-Box 檢驗原始對(duì)數收益率序列和(hé) MA(4) 模型的(de)殘差是否在 20 以内的(de)間隔上有任何自相關性，統計量的(de) p-value 爲 0.001371。同樣，我們可(kě)以在 1% 的(de)顯著性水(shuǐ)平下(xià)拒絕原假設。從下(xià)面的(de)殘差相關圖不難發現，與 AR(4) 模型類似，MA(4) 模型的(de)殘差序列在間隔 k 等于 6、8、13 和(hé) 19 時(shí)仍然有模型未捕捉到的(de)自相關性。

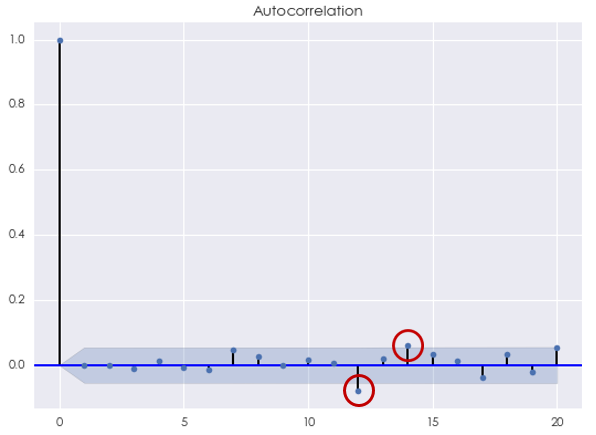
最後來(lái)看看 ARMA 模型。根據 AIC 準則，最優的(de)階數爲 p*=5，q* = 4，此時(shí) AIC = -7330.43。使用(yòng) Ljung-Box 檢驗原始對(duì)數收益率序列和(hé) ARMA(5,4) 模型的(de)殘差是否在 20 以内的(de)間隔上有任何自相關性，統計量的(de) p-value 爲 0.103462。這(zhè)說明(míng)我們不能在 10% 的(de)顯著性水(shuǐ)平下(xià)拒絕原假設。它意味著(zhe)間隔 20 以内，該模型的(de)殘差序列沒有統計上顯著的(de)自相關。從殘差序列的(de)相關圖中看到，雖然當 k = 12 和(hé) 14 時(shí)自相關系數超過了(le) 95% 置信區(qū)間，但我們無法從統計上否定它們可(kě)能是來(lái)自随機誤差。

從殘差的(de)自相關性分(fēn)析來(lái)看，ARMA 模型比 AR 和(hé) MA 模型單獨使用(yòng)更有效的(de)捕捉了(le)收益率序列中的(de)自相關性。

7 下(xià)文預告

衆所周知，投資品的(de)收益率序列具有一個(gè)屬性稱爲波動聚類（volatility clustering）。這(zhè)意味著(zhe)收益率的(de)波動率是随時(shí)間變化(huà)的(de)（它是對(duì)收益率序列的(de)二階平穩性假設的(de)直接挑戰），這(zhè)種波動率行爲的(de)術語稱爲條件異方差（conditional heteroskedasticity）。本文介紹的(de) AR，MA 和(hé) ARMA 模型均是不條件異方差模型；它們不考慮波動聚類（事實上，上一節中采用(yòng)這(zhè)些模型對(duì)過去 5 年上證指數對(duì)數收益率建模時(shí)，我們看到這(zhè)些模型無法解釋 k 較大(dà)時(shí)的(de)自相關性，這(zhè)說明(míng)收益率存在長(cháng)記憶性，這(zhè)就和(hé)波動聚類有關）。爲了(le)定量的(de)描述這(zhè)種特性，我們需要更加複雜(zá)的(de)模型。

針對(duì)波動率的(de)特性，我們實際上是對(duì)收益率的(de)平方直接建模。這(zhè)時(shí)，可(kě)以使用(yòng)自回歸條件異方差（Autoregressive Conditional Heteroskedastic，又稱 ARCH）模型和(hé)廣義自回歸條件異方差（Generalized Autoregressive Conditional Heteroskedastic，又稱 GARCH）模型。(G)ARCH 模型是定量金融中應用(yòng)廣泛，主要用(yòng)于預測風險。

下(xià)一篇文章(zhāng)将介紹如何應用(yòng) ARMA 模型對(duì)上證指數收益率進行預測，并以此産生交易信号、構建交易策略。對(duì)于收益率的(de)預測，時(shí)間序列分(fēn)析到底是紙上談兵(bīng)還(hái)是實戰利器？我們将在下(xià)篇見分(fēn)曉。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。