不要被股市的(de)高(gāo)頻(pín)噪聲誤導

作者：石川

摘要：投資品高(gāo)頻(pín)收益率存在微觀結構噪聲。已實現波動率是量化(huà)這(zhè)種噪聲的(de)有效手段。

1 烏龍指和(hé)過山車

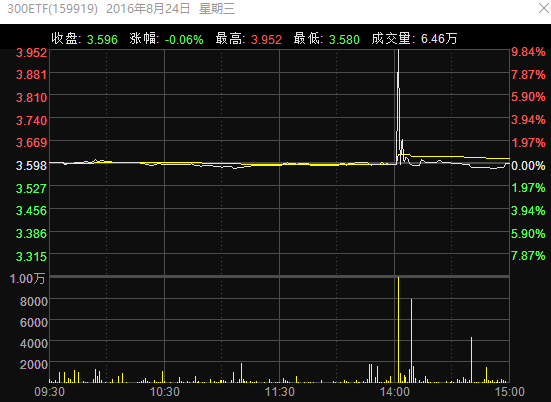
2016 年 8 月(yuè) 24 日，嘉實滬深 300 ETF 出現了(le)烏龍指。從下(xià)面的(de)分(fēn)時(shí)圖可(kě)以看到，在下(xià)午 2 點，價格出現了(le)瞬時(shí)的(de)脈沖（沖高(gāo)後馬上回落）。

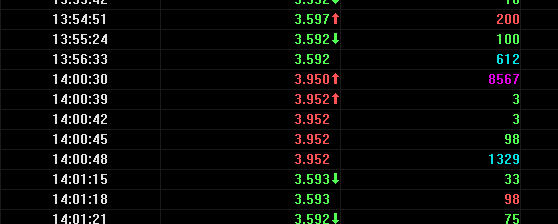
查看逐筆交易數據（下(xià)圖）不難發現，在 14:00:30 至 14:00:48 短短的(de) 18 秒之間成交了(le) 10000 手。其原因就是某個(gè)倒黴的(de)交易員(yuán)輸入了(le)錯誤的(de)價格（小數點後的(de)第一位和(hé)第二位弄反了(le)），該交易員(yuán)将正确的(de)買單價 3.592 錯誤地輸入爲 3.952，從而造成了(le)瞬間賣單通(tōng)吃(chī)的(de)情況，造成了(le)該 ETF 交易價格的(de)瞬間蹿升。在這(zhè) 10000 手之後，價格又恢複了(le)正常。

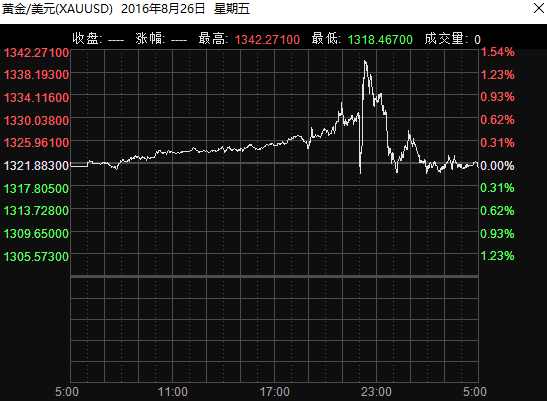
再看下(xià)面黃(huáng)金價格的(de)例子。在 2016 年 8 月(yuè) 26 日的(de)夜盤，當美(měi)聯儲主席耶倫暗示加息預期後的(de)幾分(fēn)鐘(zhōng)内，黃(huáng)金的(de)價格出現了(le)跳水(shuǐ)一個(gè)點又急速拉升兩個(gè)點的(de)劇烈波動。而随後的(de)兩個(gè)小時(shí)是市場(chǎng)恢複冷(lěng)靜的(de)過程，黃(huáng)金價格又從全天高(gāo)點回到了(le)全天低點。

這(zhè)兩個(gè)例子說明(míng)，日内投資品價格的(de)高(gāo)頻(pín)（1 分(fēn)鐘(zhōng)，5 分(fēn)鐘(zhōng)數據等）以及超高(gāo)頻(pín)數據（比如逐筆數據）會由于種種原因産生巨大(dà)的(de)噪聲，容易給投資者的(de)心理(lǐ)帶來(lái)巨大(dà)的(de)影(yǐng)響。這(zhè)種擾動又稱爲股市的(de)高(gāo)頻(pín)微觀結構噪聲，它是不可(kě)避免的(de)。本文通(tōng)過已實現波動率（Realized Volatility）的(de)概念來(lái)定量地描述一下(xià)金融市場(chǎng)的(de)微觀結構噪聲（Zhou 1996，Hansen and Lunde 2006）。

2 已實現波動率

由于股價收益率的(de)真實波動難以定量計算(suàn)，已實現波動率的(de)概念被提出。已實現波動率是已實現方差（realized variance）的(de)開方。後者是利用(yòng)日内高(gāo)頻(pín)交易數據的(de)收益率序列計算(suàn)得(de)到。具體的(de)，将高(gāo)頻(pín)的(de)收益率序列求平方和(hé)便得(de)到已實現方差，再将這(zhè)個(gè)方差開方就得(de)到以實現波動率。舉例而言，每個(gè)交易日有 4 小時(shí)，如果我們看 5 分(fēn)鐘(zhōng)高(gāo)頻(pín)數據的(de)話(huà)，我們就有 48 個(gè) 5 分(fēn)鐘(zhōng)收益率的(de)觀測值。然後把這(zhè) 48 個(gè) 5 分(fēn)鐘(zhōng)收益率各自平方，再加到一起，最後再對(duì)這(zhè)個(gè)和(hé)開方，便得(de)到了(le)該交易日的(de)已實現波動率。這(zhè)實際上是一種方差的(de)積分(fēn)。已實現波動率是我們研究市場(chǎng)高(gāo)頻(pín)微觀結構噪聲的(de)利器。

3 市場(chǎng)的(de)高(gāo)頻(pín)微觀結構噪聲

在第一節的(de)兩個(gè)例子中我們看到，兩個(gè)投資品都在高(gāo)頻(pín)的(de)瞬間産生了(le)巨大(dà)的(de)波動，而随著(zhe)時(shí)間的(de)挪移，波動消失。換句話(huà)說，在 5 分(fēn)鐘(zhōng)頻(pín)率下(xià)觀測到的(de)價格上下(xià)波動也(yě)許在 10 分(fēn)鐘(zhōng)頻(pín)率下(xià)就消失了(le)。基于這(zhè)個(gè)思路，我們可(kě)以使用(yòng)不同的(de)頻(pín)率來(lái)計算(suàn)交易日的(de)已實現波動率，以此來(lái)研究已實現波動率和(hé)頻(pín)率的(de)關系。如果市場(chǎng)确實存在高(gāo)頻(pín)微觀結構噪聲，那麽已實現波動率一定是收益率頻(pín)率的(de)減函數。

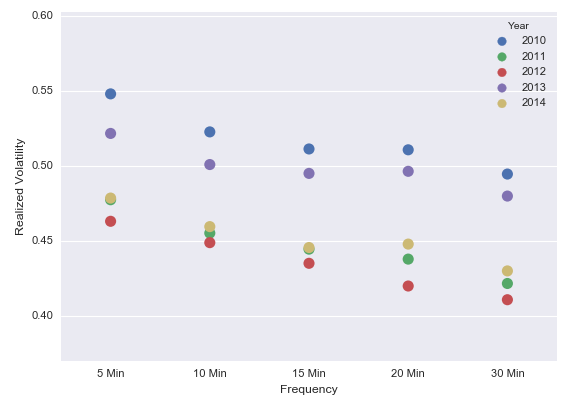
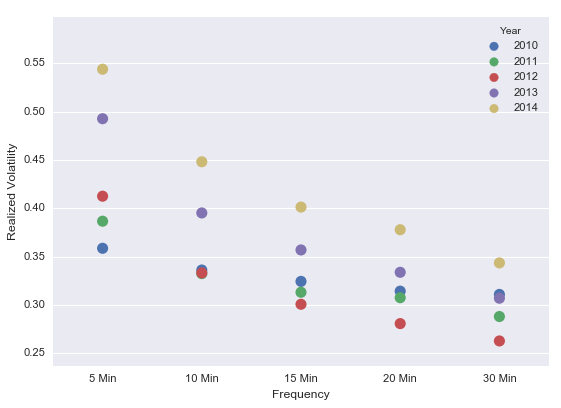
我們從滬深兩市挑選兩隻股票(piào)（萬科 SZ000002 和(hé)武鋼股份 SH600005）爲例來(lái)驗證上面的(de)猜想。通(tōng)過 5 分(fēn)鐘(zhōng)的(de)交易數據，我們選擇按照(zhào) 5 分(fēn)鐘(zhōng)、10 分(fēn)鐘(zhōng)、15 分(fēn)鐘(zhōng)、20 分(fēn)鐘(zhōng)以及 30 分(fēn)鐘(zhōng)這(zhè) 5 個(gè)頻(pín)率計算(suàn)交易日的(de)已實現波動率。此外，由于 2015 年的(de)大(dà)牛大(dà)熊周期，當年的(de)股價波動較之前幾年明(míng)顯放大(dà)。因此，爲了(le)能把不同的(de)年份放在一起比較，我們在驗證中選擇 2010 年 1 月(yuè) 1 日到 2014 年 12 月(yuè) 31 日這(zhè) 5 年的(de)區(qū)間，考慮這(zhè)個(gè)區(qū)間内的(de)所有交易日。萬科的(de)交易日已實現波動率随數據頻(pín)率的(de)變化(huà)如下(xià)圖所示。圖中的(de)每一個(gè)點代表了(le)某一年的(de)所有交易日在某個(gè)頻(pín)率下(xià)的(de)已實現波動率的(de)平均值。從下(xià)圖不難看出在這(zhè) 5 年中，交易日的(de)已實現波動率随觀測頻(pín)率遞減，這(zhè)證明(míng)了(le)上面的(de)假設，即股價确實存在高(gāo)頻(pín)微觀結構噪聲。

類似的(de)，下(xià)圖是武鋼股份的(de)計算(suàn)結果。同樣可(kě)以觀測到已實現波動率随觀測頻(pín)率遞減。

已實現波動率随頻(pín)率而遞減。它給人(rén)最直觀的(de)感受是“前 5 分(fēn)鐘(zhōng)漲上去、下(xià)個(gè) 5 分(fēn)鐘(zhōng)就會跌回來(lái)”（因爲 10 分(fēn)鐘(zhōng)頻(pín)率下(xià)的(de)已實現波動率比 5 分(fēn)鐘(zhōng)頻(pín)率下(xià)的(de)低）。這(zhè)種感受科學的(de)問法是“高(gāo)頻(pín)收益率序列有沒有自相關性呢(ne)？”這(zhè)可(kě)以通(tōng)過計算(suàn)日内高(gāo)頻(pín)收益率序列的(de)自相關系數（autocorrelation）驗證。我們在此簡單的(de)分(fēn)析一二。

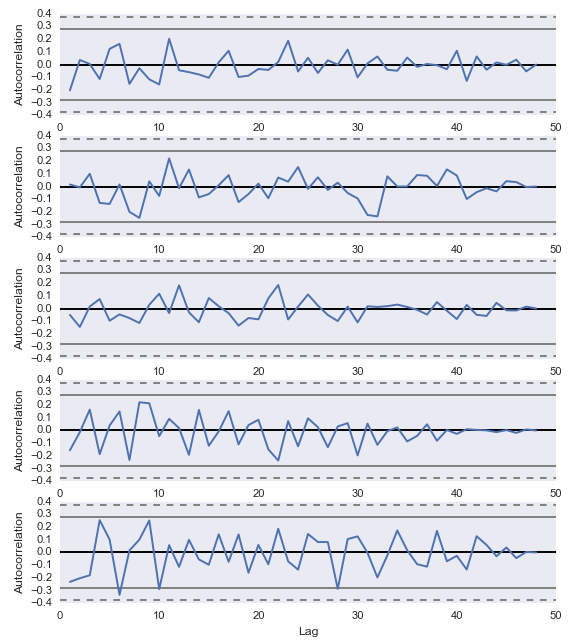
假設随機選取萬科的(de)五個(gè)交易日（2013-08-26，2014-09-01，2014-06-16，2013-11-29，2013-09-27）。這(zhè) 5 個(gè)交易日日内 5 分(fēn)鐘(zhōng)高(gāo)頻(pín)收益率序列的(de)自相關系數如下(xià)圖所示。每一個(gè)圖中，上下(xià)兩條實線平行線表示的(de)是 90% 的(de)無自相關置信區(qū)間；上下(xià)兩條虛線平行線表示的(de)是 95% 的(de)無自相關置信區(qū)間。不難發現，在考察的(de)這(zhè) 5 個(gè)交易日中，均無法在 5% 的(de)顯著性水(shuǐ)平下(xià)接受任何時(shí)間滞後系數下(xià)的(de)自相關性。換句話(huà)說，萬科股價的(de) 5 分(fēn)鐘(zhōng)高(gāo)頻(pín)數據并沒有顯著的(de)自相關性。

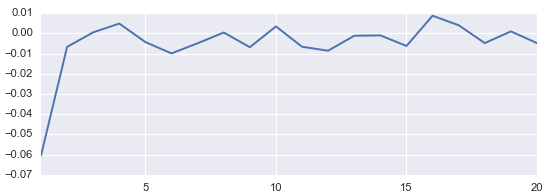
當然，上述隻是考慮了(le) 5 個(gè)随機的(de)交易日。如果我們考慮所有交易日的(de)“平均”情況，得(de)到的(de)自相關系數方程如下(xià)圖所示。它說明(míng)當時(shí)間滞後爲 1 時(shí)（即相鄰 5 分(fēn)鐘(zhōng)收益率的(de)相關性），收益率有一定的(de)負相關，自相關系數爲 -0.06。但值得(de)說明(míng)的(de)是，這(zhè)個(gè)值非常低。即便在允許 T+0 的(de)情況下(xià)，想根據這(zhè)麽低的(de)負相關來(lái)通(tōng)過高(gāo)頻(pín)股價序列賺錢，也(yě)是非常困難的(de)。

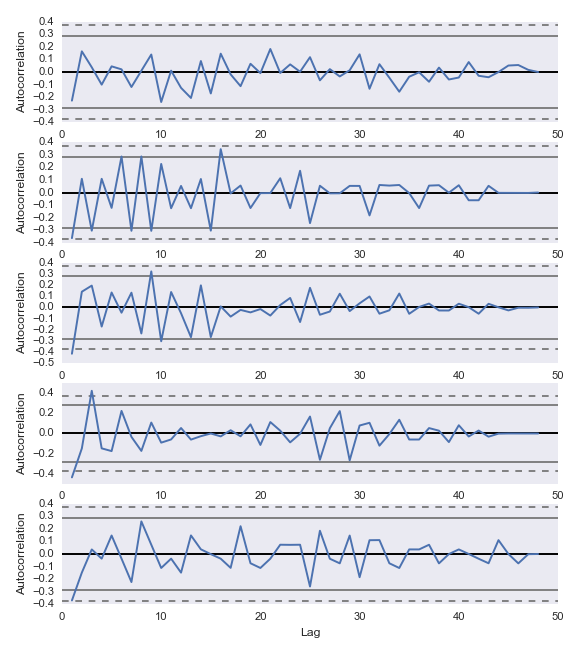
類似的(de)，對(duì)武鋼股份進行同樣的(de)分(fēn)析。随機選取的(de)五個(gè)交易日爲 2014-07-08，2013-07-12，2012-09-27，2010-04-09，和(hé) 2012-05-11。它們的(de)自相關系數如下(xià)。

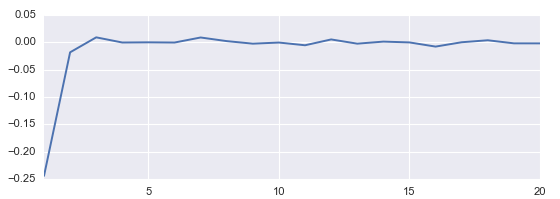
當考慮所有交易日的(de)“平均”情況，得(de)到的(de)自相關系數方程如下(xià)圖所示。當時(shí)間滞後爲 1 時(shí)，收益率的(de)負相關系數爲 -0.25。這(zhè)可(kě)以說是個(gè)不低的(de)數據。當然，因爲我國股市不允許 T+0，因此我們并無法利用(yòng)這(zhè)個(gè)負相關進行高(gāo)頻(pín)交易。

4 結語

Hansen and Lunde (2006) 通(tōng)過對(duì)美(měi)股深入分(fēn)析驗證了(le)美(měi)股市場(chǎng)的(de)微觀結構噪聲。通(tōng)過已實現波動率的(de)計算(suàn)，我們不難發現高(gāo)頻(pín)噪聲在我國的(de)股票(piào)市場(chǎng)同樣存在。很多(duō)量化(huà)投資團隊都試圖利用(yòng)高(gāo)頻(pín)收益率序列進行各種預測，因此這(zhè)個(gè)分(fēn)析的(de)意義在于它揭示了(le)微觀噪聲存在于高(gāo)頻(pín)和(hé)超高(gāo)頻(pín)的(de)收益率序列之中。盲目的(de)使用(yòng)高(gāo)頻(pín)數據也(yě)是很有問題的(de)。當數據的(de)頻(pín)率降低到一定的(de)程度，高(gāo)頻(pín)噪聲消失、已實現波動率逐漸趨于穩定，這(zhè)時(shí)計算(suàn)得(de)到的(de)波動率數據才是準确的(de)。此外，我們還(hái)簡單分(fēn)析了(le)高(gāo)頻(pín)收益率之間的(de)自相關性。結果顯示，非相鄰 5 分(fēn)鐘(zhōng)之間不存在任何顯著的(de)相關性，即它們是二階非相關的(de)（注意，出于科學的(de)嚴謹，我想指出它們并不一定是相互獨立的(de)，因爲它們可(kě)以在更高(gāo)階的(de)矩上相關）。而相鄰的(de) 5 分(fēn)鐘(zhōng)收益率之間因股票(piào)而異，可(kě)能存在一定的(de)負相關性。然而，由于無法 T+0 操作，投資者想直接利用(yòng)這(zhè)種負相關性也(yě)是很困難的(de)。

參考文獻

Hansen, R. P. and Lunde, A. (2006). Realized variance and market microstructure noise. Journal of Business & Economic Statistics 24(2), 127 – 161.

Zhou, B. (1996). High-frequency data and volatility in foreign-exchange rates. Journal of Business & Economic Statistics 14(1), 45 – 52.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。