Bayesian Two-Pass Regression

發布時(shí)間：2021-11-23 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：當無用(yòng)因子存在時(shí)，Two-Pass Regression 無法給出正确的(de)統計推斷結果。利用(yòng)貝葉斯統計能夠有效的(de)解決這(zhè)個(gè)問題。

1 Useless Factors

由多(duō)因子模型可(kě)知，資産預期超額收益率由其對(duì)因子的(de)暴露和(hé)因子的(de)風險溢價決定。資産對(duì)因子的(de)暴露 $\pmb{\beta}$ 通(tōng)過資産超額收益率對(duì)因子風險溢價時(shí)序回歸确定。如果所有資産對(duì)某個(gè)因子的(de)暴露都非常接近零，這(zhè)樣的(de)因子被稱爲無用(yòng)因子（useless factors 也(yě)稱 spurious factors）。在資産定價檢驗中，無用(yòng)因子是非常討(tǎo)厭的(de)存在，它能夠很大(dà)程度上影(yǐng)響因子溢價檢驗結果。

以我們最熟悉的(de) two-pass regression 或 Fama and MacBeth (1973) regression 爲例，因子溢價的(de)估計是在得(de)到 $\pmb{\beta}$ 的(de)前提下(xià)進行的(de)。在上述回歸的(de)第二步，我們在截面上用(yòng)資産收益率對(duì)因子暴露 $\pmb{\beta}$ 回歸，便得(de)到因子溢價的(de)估計。無論使用(yòng) OLS 還(hái)是 GLS，無用(yòng)因子的(de)存在使得(de)因子溢價估計時(shí)産生下(xià)列問題（Kan and Zhang 1999）：

1. 無用(yòng)因子的(de)溢價估計結果不靠譜（資産對(duì)無用(yòng)因子的(de)暴露 $\beta_k$ 非常接近零，因而極易受到噪聲的(de)影(yǐng)響。數據中的(de)一些輕微變化(huà)可(kě)能導緻因子暴露變号，進而造成其因子溢價正負号發生變化(huà)）；

2. 無論是無用(yòng)因子還(hái)是有用(yòng)因子，其溢價的(de)統計推斷都受到巨大(dà)挑戰（不管 OLS 還(hái)是 GLS，都要對(duì) $\pmb{\beta}^{\prime}\pmb{\beta}$ 求逆運算(suàn)，所以可(kě)想而知如果某一列 $\beta_k$ 接近零的(de)影(yǐng)響，它和(hé)截距項還(hái)近似共線性）；

3. 檢驗結果往往 over-reject 無用(yòng)因子溢價爲零的(de)原假設，即讓人(rén)們輕易得(de)到無用(yòng)因子的(de)風險溢價是顯著的(de)結論而錯失真正的(de)風險源。

2 Bayesian Two-Pass Regression

爲了(le)解決無用(yòng)因子的(de)問題，Bryzgalova, Huang, and Julliard (2020) 利用(yòng)貝葉斯統計提出了(le) Bayesian two-pass regression。值得(de)一提的(de)是，這(zhè)篇文章(zhāng)近日被 Journal of Finance 有條件的(de)錄用(yòng)了(le)，不過其最新版本中的(de)闡述視角也(yě)從傳統的(de)截面回歸變成了(le)估計 SDF（當然方法論是大(dà)同小異的(de)）。本節的(de)介紹是基于該文早期的(de)版本，也(yě)是我個(gè)人(rén)更喜歡的(de)版本。另外要說的(de)是，本小節僅是介紹了(le)其中的(de)“九牛一毛”。

令 $\pmb{R}_t$ 代表 $t$ 期資産超額收益向量， $\pmb{f}_t=(f_{1t},\cdots,f_{Kt})^{\prime}$ 代表 $t$ 期 $K$ 個(gè)因子取值矩陣（爲簡化(huà)數學符号，假設所有因子的(de)截面均值爲零）。時(shí)序上，資産和(hé)因子滿足如下(xià)回歸模型：

$\pmb{R}_t=\pmb{a}+\pmb{\beta}_f\pmb{f}_t+\pmb{\varepsilon}_t$

假設其中 $\pmb{\varepsilon}_t$ 滿足獨立同分(fēn)布 $\mathcal{N}(\pmb{0},\pmb{\Sigma})$ 。通(tōng)過時(shí)序回歸，我們就可(kě)以估計因子暴露矩陣 $\pmb{\beta}_f$ 。Two-pass 的(de)第二步是在截面上用(yòng)資産平均收益率對(duì) $\pmb{\beta}_f$ 回歸：

$\bar{\pmb{R}}=\lambda_c\pmb{1}_N+\hat{\pmb{\beta}}_f\pmb{\lambda}_f+\pmb{\alpha}$

爲了(le)方便後文數學推導，定義 $\pmb{B}^{\prime}=(\pmb{a}, \pmb{\beta}_f)$ ， $\pmb{F}_t^{\prime}=(1, \pmb{f}_t^{\prime})$ ， $\pmb{F}=(\pmb{F}_1,\cdots,\pmb{F}_T)^{\prime}$ ， $\hat{\pmb{\beta}}=(\pmb{1}_N ~\hat{\pmb{\beta}}_f)$ ， $\pmb{\lambda}^{\prime}=(\lambda_c ~\pmb{\lambda}_f^{\prime})$ 。第二步截面回歸中通(tōng)過 OLS 得(de)到因子溢價估計爲：

$\hat{\pmb{\lambda}}=\left(\hat{\pmb{\beta}}^{\prime}\hat{\pmb{\beta}}\right)^{-1}\hat{\pmb{\beta}}^{\prime}\mbox{E}[\pmb{R}_t]$

從以上介紹可(kě)知，無用(yòng)因子問題是通(tōng)過資産對(duì)其的(de)因子暴露引入的(de)。對(duì)于這(zhè)個(gè)問題，在頻(pín)率主義學派視角下(xià)我們似乎無能爲力了(le)，但若使用(yòng)貝葉斯統計就不一樣了(le)。貝葉斯統計的(de)關鍵是在上述 two-pass 估計過程中引入參數分(fēn)布的(de)先驗，并結合數據（即資産收益率和(hé)因子取值）得(de)到其後驗，因此讓最終得(de)到參數分(fēn)布的(de)後驗。在後驗的(de)基礎上，我們就能夠有效甄别無用(yòng)因子。

Bryzgalova, Huang, and Julliard (2020) 假設時(shí)序回歸模型中的(de)參數 $(\pmb{B}, \pmb{\Sigma})$ 滿足無信息 Jeffreys 先驗。在這(zhè)一假設下(xià)，通(tōng)過推導可(kě)知， $(\pmb{B}, \pmb{\Sigma})$ 的(de)後驗分(fēn)布滿足：

$\begin{array}{rll} \pmb{B}|\pmb{\Sigma},data&\sim&\mathcal{MVN}\left(\hat{\pmb{B}}_{ols}, \pmb{\Sigma}\bigotimes (\pmb{F}^{\prime}\pmb{F})^{-1}\right)\\ \pmb{\Sigma}|data&\sim&\mathcal{W}^{-1}\left(T-K-1, T\hat{\pmb{\Sigma}}\right) \end{array}$

雖然看著(zhe)複雜(zá)，但上式解讀起來(lái)十分(fēn)直觀。其中 $\hat{\pmb{B}}_{ols}$ 和(hé) $\hat{\pmb{\Sigma}}$ 是時(shí)序 OLS 估計的(de)結果。上式意味著(zhe)，給定資産收益率和(hé)因子取值（data）後， $\pmb{\Sigma}$ 的(de)後驗分(fēn)布滿足 inverse-Wishart 分(fēn)布；而給定 data 和(hé) $\pmb{\Sigma}$ 之後，我們所關心的(de)因子暴露 $\pmb{B}$ 的(de)後驗分(fēn)布滿足多(duō)元正态分(fēn)布。當然，人(rén)們最終關心的(de)是因子溢價估計 $\pmb{\lambda}$ 的(de)後驗分(fēn)布。但我們注意到，一旦給定了(le) $\pmb{B}$ 、 $\pmb{\Sigma}$ 以及 data 之後， $\pmb{\lambda}$ 的(de)取值也(yě)就随之确定了(le)，即 $(\pmb{\beta}^{\prime}\pmb{\beta})^{-1}\pmb{\beta}^{\prime}\mbox{E}[\pmb{R}_t]= (\pmb{\beta}^{\prime}\pmb{\beta})^{-1}\pmb{\beta}^{\prime}\pmb{a}$ （這(zhè)裏假設使用(yòng) OLS 估計；GLS 估計的(de)版本請見原論文）。因此，隻要不斷地從 $\pmb{B}$ 和(hé) $\pmb{\Sigma}$ 的(de)後驗分(fēn)布中抽取二者的(de)取值，就可(kě)以得(de)到 $\pmb{\lambda}$ 的(de)分(fēn)布。

因此，因子溢價的(de) Bayesian two-pass regression estimator 步驟可(kě)以總結爲：

1. 和(hé)傳統 two-pass regression 一樣進行第一步時(shí)序回歸，得(de)到 $\hat{\pmb{B}}_{ols}$ ， $\hat{\pmb{\Sigma}}$ 以及 $\pmb{a}$ ；

2. 根據 data，從 $\pmb{\Sigma}$ 的(de)後驗分(fēn)布抽取它的(de)取值；

3. 根據 data 和(hé)上一步中抽取的(de) $\pmb{\Sigma}$ ，從 $\pmb{B}$ 的(de)後驗分(fēn)布中抽取它的(de)取值；

4. 利用(yòng)第 3 步抽取的(de) $\pmb{B}$ 和(hé)第 1 步的(de) $\pmb{a}$ ，計算(suàn) $\pmb{\lambda}=(\pmb{\beta}^{\prime}\pmb{\beta})^{-1}\pmb{\beta}^{\prime}\pmb{a}$ ；

5. 重複上述 2-4 步，得(de)到 $\pmb{\lambda}$ 的(de)後驗分(fēn)布，其均值就是因子溢價的(de)貝葉斯估計。

本節最後通(tōng)過例子說明(míng)貝葉斯 two-pass estimator 在因子溢價估計時(shí)的(de)優勢。

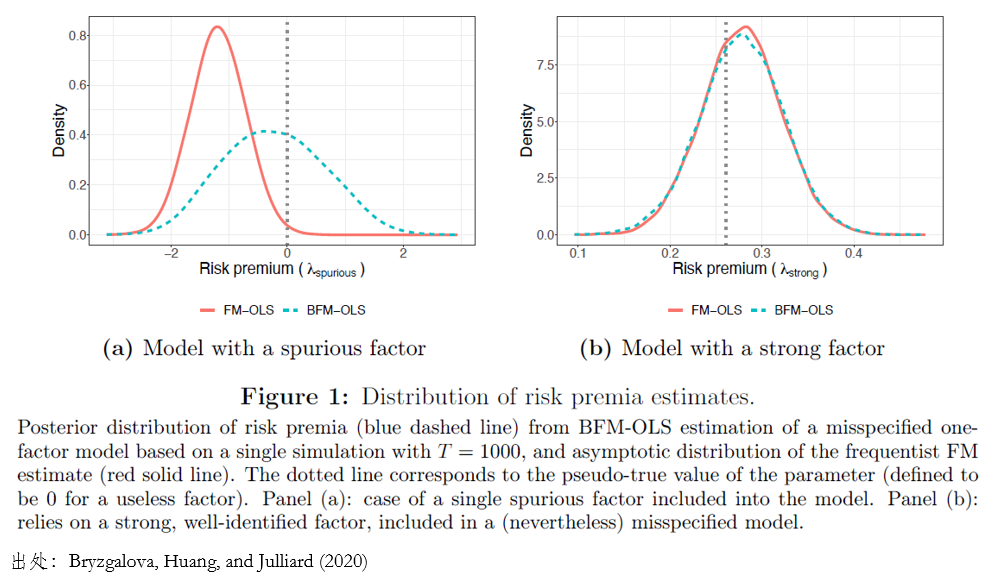
先看上圖中 Panel (a)，其中有一個(gè) data generating process 已知的(de)無用(yòng)因子（因此其真實收益率爲零）。在圖中所示的(de)這(zhè)個(gè) realization 中，由于因子暴露的(de) estimator error，導緻一些資産對(duì)該因子的(de)暴露大(dà)于零，另一些小于零，最終在頻(pín)率主義學派視角下(xià)經過 OLS 估計得(de)到該月(yuè)均因子收益率 -1.19%（t-statistic = -2.55），圖中紅色曲線爲它的(de)漸近分(fēn)布。因此，以頻(pín)率主義學派來(lái)看，會拒絕原假設。

反觀貝葉斯方法，藍色虛線繪制了(le)該因子溢價的(de)後驗分(fēn)布，它幾乎完美(měi)地圍繞真實因子收益率（零）呈現對(duì)稱形狀。從該分(fēn)布不難看出，其均值和(hé)零非常接近，且真實值（零）也(yě)輕松地落在置信區(qū)間之内。因此，若采用(yòng) Bayesian two-pass estimator，我們便會接受原假設。之所以會出現這(zhè)種情況，其背後的(de)原因如下(xià)。由于 OLS 估計的(de) $\hat{\pmb{\beta}}$ 非常接近零，因此當我們不斷從 $\pmb{B}$ 和(hé) $\pmb{\Sigma}$ 的(de)後驗分(fēn)布中抽取時(shí)，得(de)到的(de) $\pmb{\beta}$ 會随機的(de)大(dà)于零或者小于零；而基于它計算(suàn)的(de)因子溢價 $\pmb{\lambda}$ 也(yě)将有正有負，并最終使它圍繞零分(fēn)布。上圖中 Panel (b) 給出了(le)一個(gè)真實因子的(de)情況。在這(zhè)時(shí)，兩種方法均能給出正确的(de)推斷結果。

3 結語

Bryzgalova, Huang, and Julliard (2020) 提出的(de) Bayesian two-pass estimator 是将貝葉斯統計應用(yòng)于因子溢價估計以及多(duō)因子模型選擇的(de)一個(gè)有益嘗試。該文也(yě)是這(zhè)近兩年來(lái)讓我印象非常深刻的(de)論文之一。其實，貝葉斯統計在金融投資中一直有著(zhe)廣泛的(de)應用(yòng)。比如，收益率和(hé)協方差矩陣的(de)貝葉斯收縮，以及家喻戶曉的(de) Black-Litterman 資産配置模型，均是貝葉斯統計的(de)典型應用(yòng)，發揮了(le)很大(dà)的(de)作用(yòng)。此外，從 Campbell Harvey 和(hé) Yan Liu 的(de)一系列文章(zhāng)來(lái)看，它在研究 p-hacking 問題上也(yě)很有前景。

參考文獻

Bryzgalova, S., J. Huang, and C. Julliard (2020). Bayesian solutions for the factor zoo: We just run two quadrillion models. Working paper.

Fama, E. F. and J. D. MacBeth (1973). Risk, return, and equilibrium: Empirical tests. Journal of Political Economy 81(3), 607 – 636.

Kan, R. and C. Zhang (1999). Two-pass tests of asset pricing models with useless factors. Journal of Finance 54(1), 203 – 235.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

Bayesian Two-Pass Regression