你真的(de)搞懂(dǒng)了(le)風險平價嗎？

作者：石川

摘要：風險平價因橋水(shuǐ)的(de)全天候基金的(de)優異表現而名聲大(dà)噪。然而，如果不理(lǐ)解其核心邏輯就套用(yòng)數學模型，無疑是東施效颦。

1 Dalio、全天候和(hé)風險平價

在 20 世紀 90 年代初，橋水(shuǐ)基金（Bridgewater Associates）的(de)創始人(rén) Ray Dalio 和(hé)他(tā)的(de)合夥人(rén) Bob Prince 首次提出了(le)全天候（all weather）策略。該策略的(de)初衷是構建一個(gè)投資組合使其在不同的(de)經濟環境中都能夠有穩健的(de)表現。自 1996 年開始，Dalio 使用(yòng)該策略管理(lǐ)他(tā)的(de)家族基金，進而推出了(le)全天候基金。事實上，橋水(shuǐ)的(de)全天候基金在過去 20 多(duō)年内有著(zhe)非凡的(de)表現，這(zhè)其中自然也(yě)包括 2008 年次貸危機和(hé) 2010 年的(de)歐債危機。

如今，橋水(shuǐ)已經成爲世界上最大(dà)的(de)對(duì)沖基金（AUM 約 1600 億美(měi)元），而 Dalio 的(de)全天候策略也(yě)早已享譽華爾街(jiē)。雖然橋水(shuǐ)版本的(de)全天候策略的(de)實施細節我們不得(de)而知（那是人(rén)家的(de)商業機密），但全天候的(de)理(lǐ)念是完全公開的(de)，Dalio 本人(rén)也(yě)在橋水(shuǐ)的(de)每日觀察中對(duì)它進行了(le)解讀（Dalio et al. 2015）。

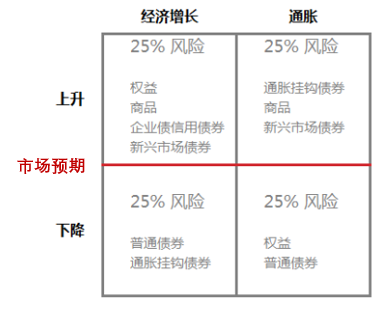
橋水(shuǐ)認爲，各類投資品（權益、債券、商品等）的(de)收益率由未來(lái)的(de)經濟情況決定，而經濟情況則主要由經濟增長(cháng)和(hé)通(tōng)脹兩大(dà)因素驅動。根據它們的(de)變動，經濟環境可(kě)分(fēn)爲四種情況 —— “經濟上升”、“經濟下(xià)降”、“通(tōng)脹上升”、“通(tōng)脹下(xià)降”，不同類投資品在不同經濟環境中表現各異。比如，權益類資産（股票(piào)）傾向于在經濟增長(cháng)時(shí)有好的(de)表現；債券類資産在經濟變弱或通(tōng)脹下(xià)降時(shí)收益更好；而商品在經濟上升或通(tōng)脹上升時(shí)投資回報更好。上述四種經濟情況下(xià)利好的(de)投資品如下(xià)面這(zhè)個(gè)四宮格所示。

當我們知道了(le)在每種經濟環境中應該投資哪種投資品之後，下(xià)面一個(gè)自然的(de)問題就是：未來(lái)一段時(shí)間屬于什(shén)麽經濟環境？對(duì)此，橋水(shuǐ)給出的(de)答(dá)案是：“不知道”也(yě)“不猜”！取而代之的(de)是，橋水(shuǐ)構建了(le)一個(gè)适應于不同經濟環境的(de)投資組合，這(zhè)便是“全天候”的(de)含義。爲此他(tā)們要求其“全天候”投資組合在這(zhè)四種經濟環境中有著(zhe)同樣的(de)風險暴露。具體的(de)，他(tā)們賦予每個(gè)經濟情況 25% 的(de)風險。可(kě)以理(lǐ)解爲橋水(shuǐ)在這(zhè)四種經濟環境中各構建一個(gè)子投資組合，每個(gè)子投資組合的(de)風險相等且各占總投資組合的(de)四分(fēn)之一。總的(de)投資組合就是這(zhè)四個(gè)子投資組合的(de)合集。

“全天候”的(de)核心是将投資組合的(de)風險平均的(de)暴露在不同的(de)經濟環境中，從而對(duì)沖市場(chǎng)環境的(de)風險，使得(de)未來(lái)無論處于哪一種經濟環境，該投資組合的(de)風險都是可(kě)控的(de)。後來(lái)業界使用(yòng)風險平價（risk parity）這(zhè)個(gè)術語來(lái)指代“将投資組合暴露于宏觀經濟環境中的(de)風險平均分(fēn)配到這(zhè)四個(gè)經濟環境中”這(zhè)個(gè)理(lǐ)念。

看到這(zhè)裏，我們也(yě)許會問全天候策略在一些經濟環境中配權益類資産而在另外的(de)環境中配債券類資産，而債券類資産比權益類資産的(de)風險低很多(duō)，那麽如何做(zuò)到風險平均分(fēn)配呢(ne)？這(zhè)個(gè)問題的(de)答(dá)案便是“全天候”的(de)另一個(gè)核心 —— 使用(yòng)杠杆。低風險、低回報的(de)資産（如債券）可(kě)以通(tōng)過加杠杆提高(gāo)風險以及回報；高(gāo)風險、高(gāo)回報的(de)資産（如股票(piào)）可(kě)以通(tōng)過去杠杆降低風險和(hé)回報。通(tōng)過使用(yòng)杠杆，使得(de)經濟四宮格中的(de)各類資産對(duì)總的(de)投資組合有相似的(de)風險貢獻。

此外，全天候策略要求這(zhè)四個(gè)經濟環境中的(de)子投資組合有著(zhe)近似的(de)收益風險比（即夏普率）。這(zhè)意味著(zhe)在平均分(fēn)配了(le)風險後，每個(gè)環境中的(de)子投資組合對(duì)總的(de)投資組合有著(zhe)相似的(de)收益貢獻。這(zhè)四個(gè)子投資組合每一個(gè)适應一種經濟環境，它們爲了(le)對(duì)沖掉宏觀經濟的(de)風險而構建，因此表現存在一定的(de)負相關。無論處于哪種經濟環境，總會有一個(gè)适應于該環境的(de)投資組合表現好，可(kě)謂“你方唱罷我登場(chǎng)”。随著(zhe)時(shí)間的(de)推移，由于存在風險溢價，“四宮格”中的(de)子投資組合都會上漲，因此總的(de)投資組合便可(kě)以穿越不同的(de)經濟環境而經久不衰。由于有效的(de)對(duì)沖了(le)風險，全天候投資組合較每個(gè)子投資組合有更小的(de)波動和(hé)更高(gāo)的(de)收益風險比，因此長(cháng)期來(lái)看它會取得(de)比這(zhè)些子組合更高(gāo)的(de)收益。

較傳統的(de)按資金分(fēn)配投資品的(de)組合，按風險分(fēn)配的(de)風險平價策略能在不同的(de)經濟環境中做(zuò)到更有效的(de)對(duì)沖。比如，傳統的(de) 60/40 投資組合将資金量的(de) 60% 分(fēn)配給股票(piào)，40% 分(fēn)配給債券。但是，考慮到股票(piào)的(de)風險是債券的(de) 3 倍，該投資組合風險的(de) 90% 事實上來(lái)自于股票(piào)。當經濟環境不利于股票(piào)時(shí)，債券的(de)收益顯然無法和(hé)股票(piào)的(de)虧損有效對(duì)沖。

2 等風險貢獻組合

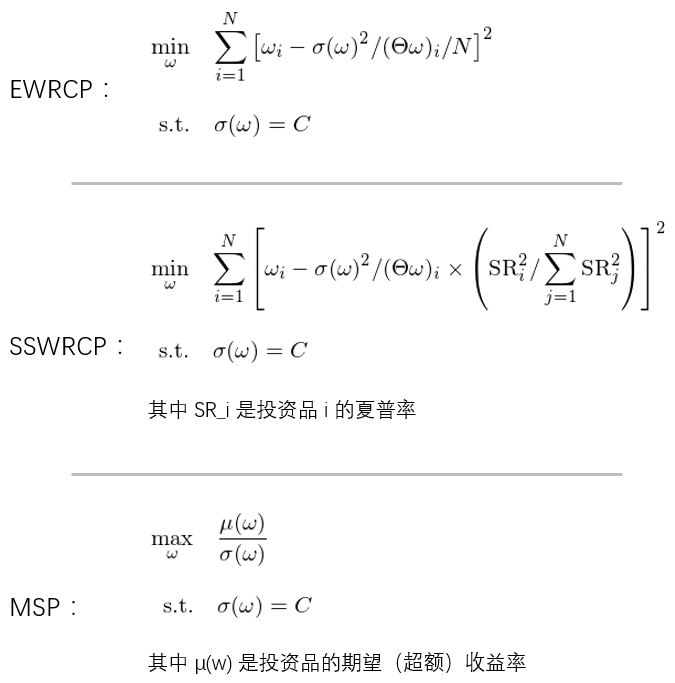
由于全天候基金的(de)大(dà)獲成功，風險平價理(lǐ)念在投資界迅速普及，被其他(tā)對(duì)沖基金競相模仿，形成了(le)很多(duō)版本。這(zhè)其中，最著名的(de)版本當屬等風險貢獻投資組合（equally-weighted risk contributions portfolio，下(xià)文簡稱 EWRCP）。它使用(yòng)投資組合（收益率）的(de)波動率作爲風險的(de)代理(lǐ)指标，該方法以每個(gè)投資品對(duì)組合的(de)波動率貢獻相同爲目标來(lái)确定最佳的(de)配置權重。該組合的(de)數學模型如下(xià)。

上述最優化(huà)問題的(de)輸入就是 N 個(gè)投資品的(de)協方差矩陣 Θ 以及給定的(de)組合風險值 C。對(duì)其求解便得(de)到最優的(de)配置 w_i，使得(de)每個(gè)投資品對(duì)該組合有著(zhe)同樣大(dà)小的(de)風險貢獻。上述模型在數學上雖然簡單，但是它背後的(de)業務含義是什(shén)麽呢(ne)？它又和(hé)我們熟悉的(de)馬科維茨均值方差最優化(huà)（MVO）問題有什(shén)麽關聯呢(ne)？不難看出（下(xià)圖），在限定了(le)投資組合的(de)波動率之後，馬科維茨的(de) MVO 問題就等價于最大(dà)化(huà)投資組合的(de)夏普率。

可(kě)以證明(míng)，當投資品的(de)夏普率相同，且收益率相互獨立時(shí)（即協方差矩陣 Θ 是一個(gè)對(duì)角陣），上述風險平價最優化(huà)問題就等價于最大(dà)化(huà)投資組合的(de)夏普率問題。這(zhè)就給等風險貢獻投資組合一個(gè)非常合理(lǐ)的(de)業務解釋 —— 它可(kě)以最大(dà)化(huà)投資組合的(de)夏普率。

然而，如果夏普率不同且（或）投資品收益率之間不獨立（即協方差矩陣 Θ 的(de)非對(duì)角線元素非零）又會怎樣呢(ne)？我們求解上述 EWRCP 模型得(de)到的(de)最優權重到底有沒有意義呢(ne)？我們必須搞懂(dǒng)這(zhè)個(gè)問題，因爲在實際投資中，不同投資品之間的(de)夏普率往往不同，且它們收益率之間存在一定的(de)正相關或負相關。如果不弄清楚 EWRCP 模型背後的(de)意義，拿來(lái)協方差矩陣就盲目的(de)一通(tōng)優化(huà)，得(de)到的(de)所謂“最優”風險平價投資組合往往一點業務含義都沒有，該組合有時(shí)甚至會造成巨大(dà)的(de)虧損。

爲了(le)研究這(zhè)個(gè)問題，在接下(xià)來(lái)的(de)分(fēn)析中，我們考察三個(gè)最優化(huà)問題。第一個(gè)便是上述 EWRCP 風險平價模型。在第二個(gè)模型中，考慮到不同投資品的(de)夏普率不同，我們不把組合的(de)風險平均的(de)分(fēn)配給這(zhè)些投資品，而是按照(zhào)每個(gè)投資品自身的(de)夏普率的(de)平方作爲權重分(fēn)配給這(zhè)些投資品。這(zhè)種方法可(kě)稱爲 Sharpe Ratio-Squared-weighted risk contributions portfolio，即 SSWRCP。在這(zhè)個(gè)組合中，風險不再平均分(fēn)配，而是正比于夏普率的(de)平方。這(zhè)是一種主動的(de)風險預算(suàn)（risk budgeting）。第三種模型是最大(dà)化(huà)投資組合夏普率組合（下(xià)稱 MSP，maximum Sharpe ratio portfolio）。除了(le)協方差矩陣外，後兩種模型還(hái)需要投資品的(de)期望收益率作爲輸入。

根據定義可(kě)知，當投資品的(de)夏普率相同時(shí)，SSWRCP 簡化(huà)爲 EWRCP 問題。這(zhè)三種模型的(de)數學表達如下(xià)：

無論采取哪種優化(huà)問題求解投資組合中資産配置的(de)權重，我們的(de)終極目标都是最大(dà)化(huà)該組合的(de)夏普率。因此，MSP 問題的(de)最優配置就是“标準答(dá)案”。我們想要看看，在什(shén)麽情況下(xià)，MSP 和(hé) EWRCP 或 SSWRCP 等價，以及當投資品夏普率不同或者投資品收益率不獨立時(shí)，EWRCP 和(hé) SSWRCP 比 MSP 的(de)夏普率差多(duō)少。

首先來(lái)看最簡單的(de)情況 —— 僅有兩種投資品。

3 兩個(gè)資産的(de)情況

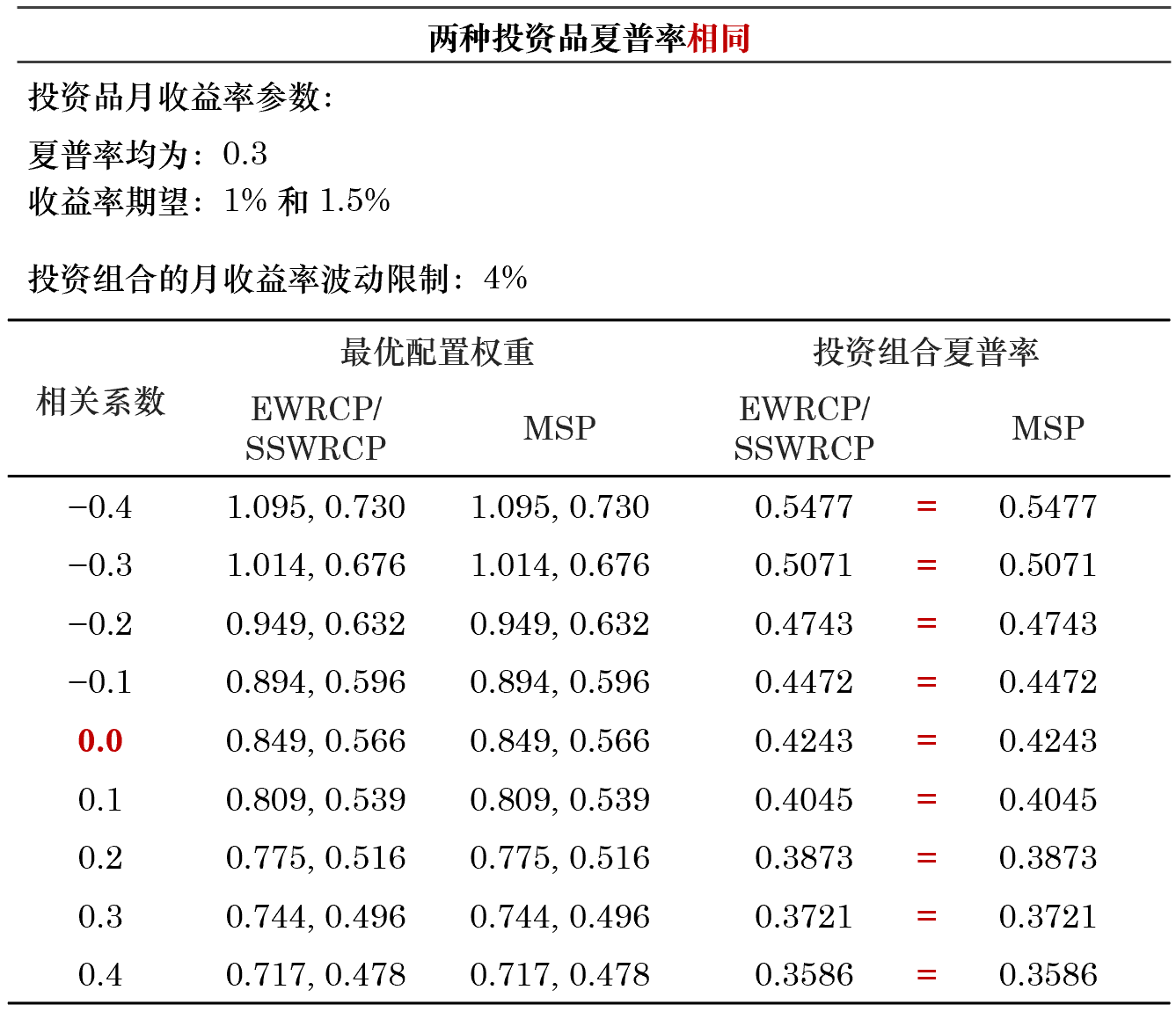
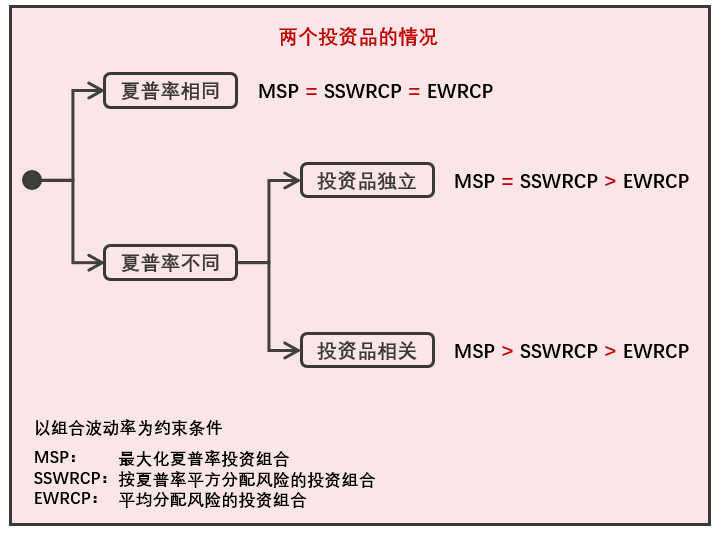
首先假設兩個(gè)投資品的(de)夏普率相同。根據它們是否獨立（相關系數是否爲零），我們進行了(le)一組實驗。對(duì)于兩個(gè)投資品，隻要它們的(de)夏普率一樣，無論它們的(de)收益率是否相關，上述三種優化(huà)方式等價（三個(gè)問題的(de)最優投資組合一緻）。

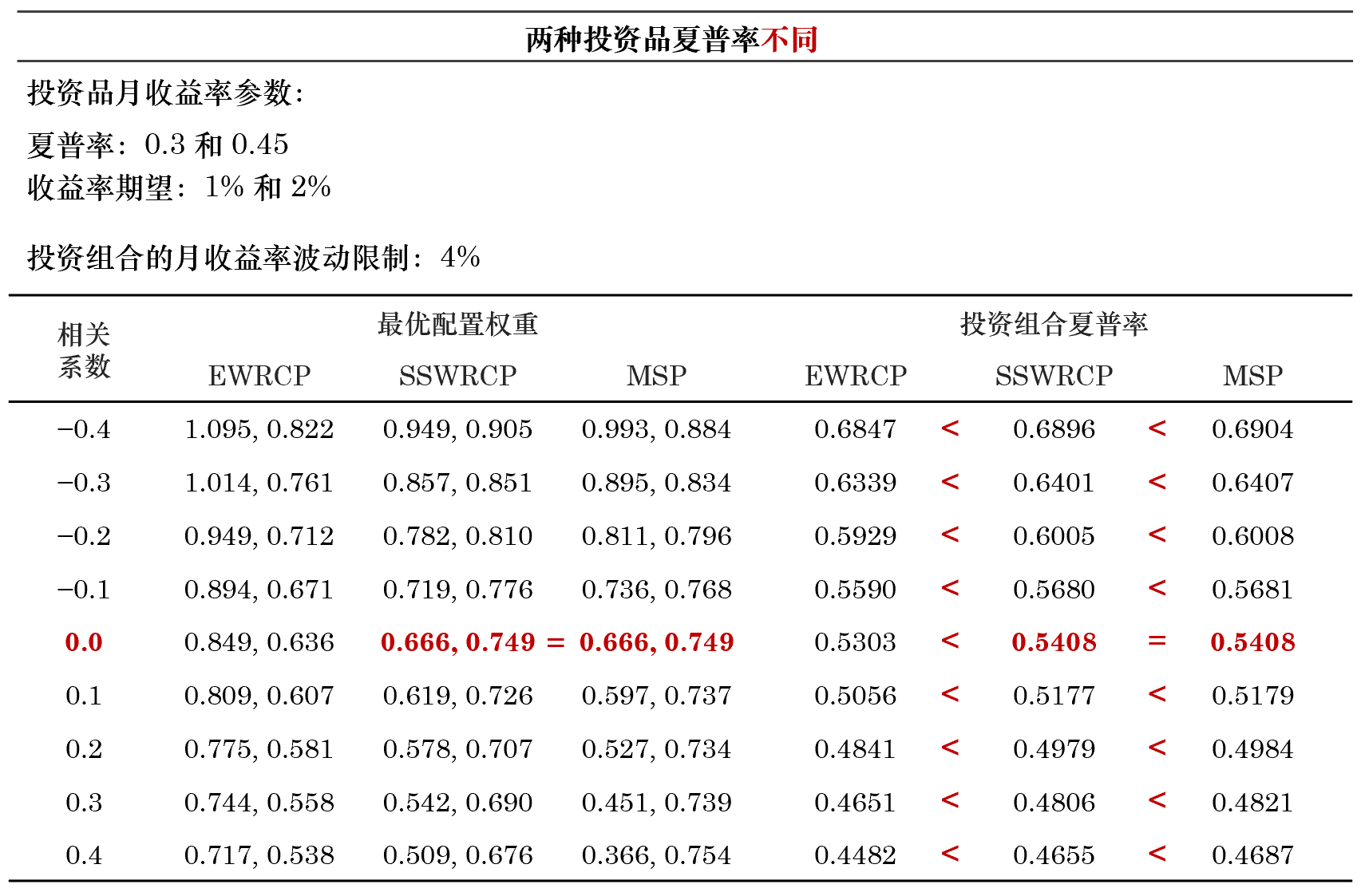
下(xià)面，假設這(zhè)兩種投資品的(de)夏普率不同，我們又進行了(le)一組實驗。當夏普率不同時(shí)，如果投資品獨立，則有 MSP 和(hé) SSWRCP 等價，且它們都優于原始的(de) EWRCP；如果這(zhè)兩個(gè)投資品相關，則 MSP 的(de)最優資産配置權重優于 SSWRCP，而 SSWRCP 則又優于 EWRCP。此外，無論夏普率是否相同，EWRCP 求解出的(de)最優資産配置權重和(hé)這(zhè)兩個(gè)投資品各自的(de)波動率成反比。

上述實驗中，MSP、SSWRCP 和(hé) EWRCP 表現總結如下(xià)。

接下(xià)來(lái)我們看看三種投資品的(de)情況，它的(de)結論也(yě)可(kě)以推廣到多(duō)種投資品。

4 三（多(duō)）個(gè)資産的(de)情況

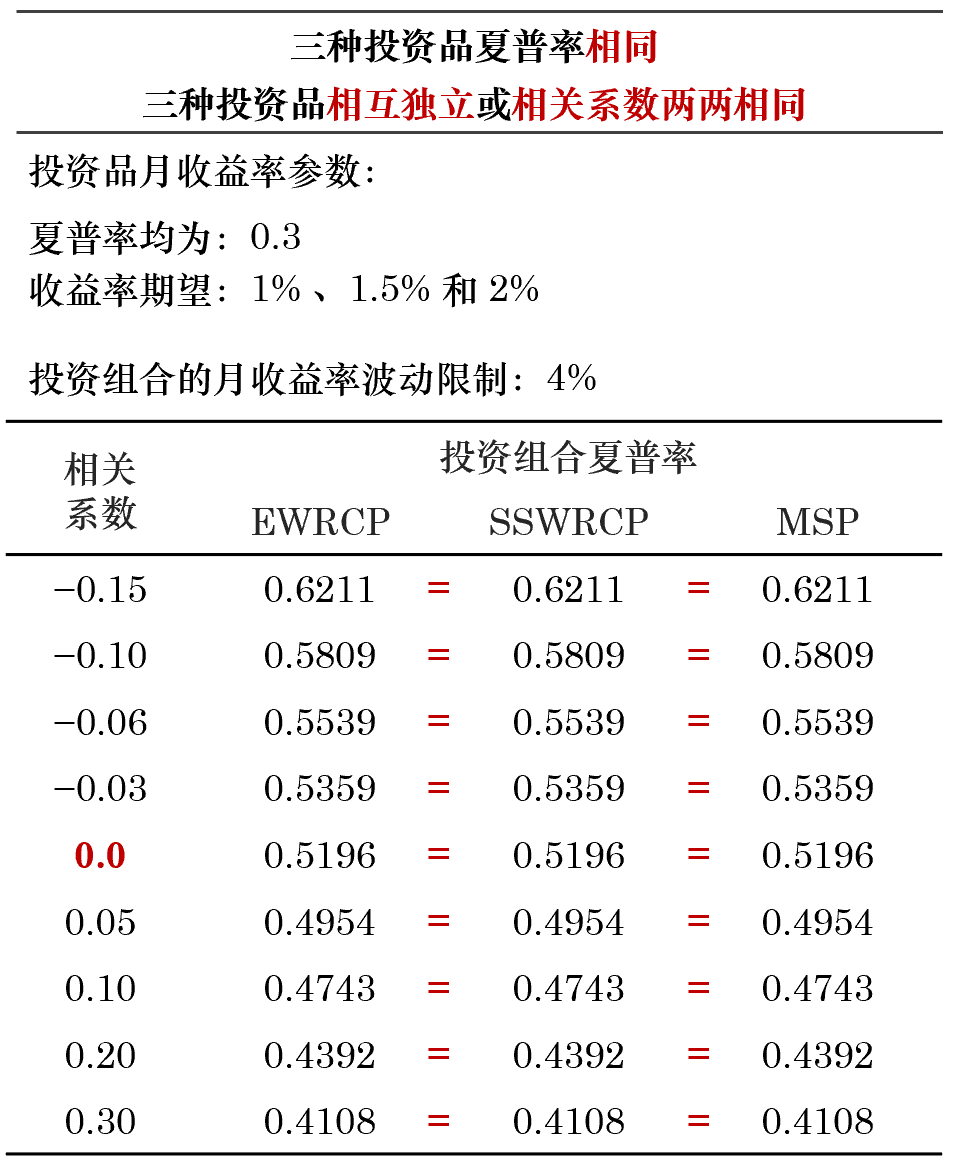
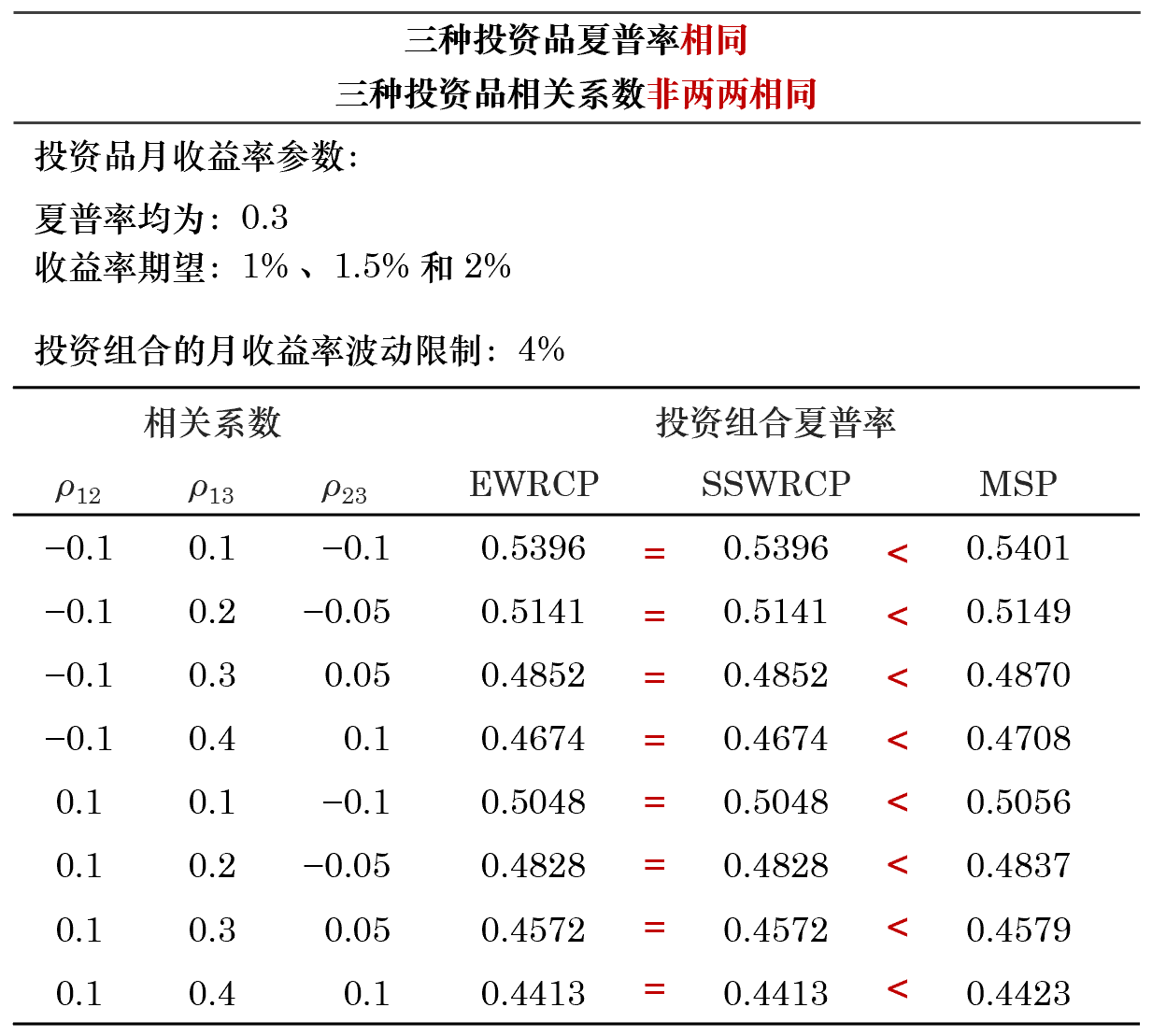
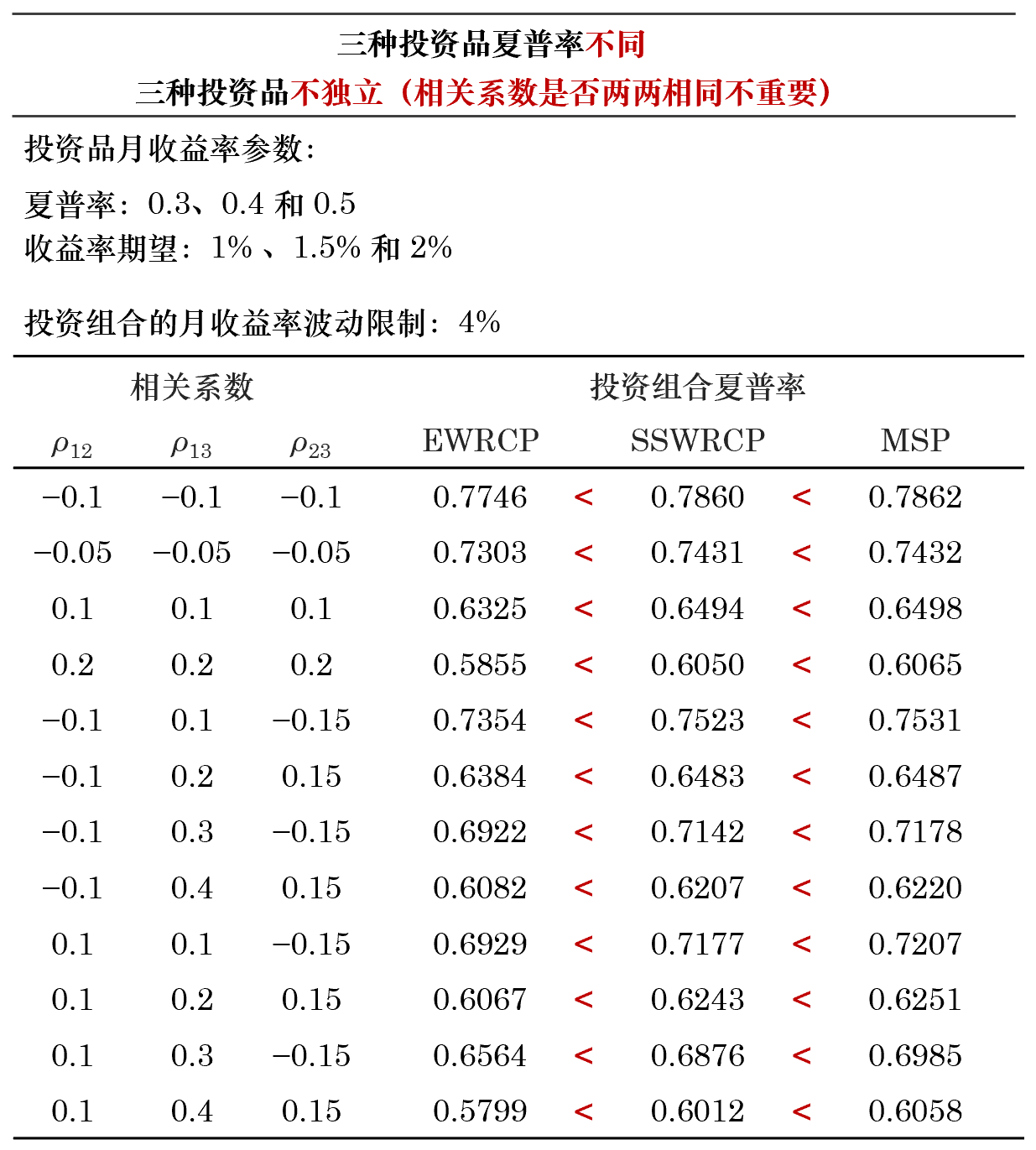
首先假設這(zhè)三個(gè)投資品的(de)夏普率相同，進行如下(xià)兩組實驗。對(duì)于三種投資品，當夏普率一樣且兩兩的(de)相關系數一樣（包括零，即獨立），上述三種優化(huà)等價；如果它們的(de)相關系數不滿足前述條件，則有 MSP 優于 SSWRCP 和(hé) EWRCP（後兩個(gè)問題等價）。

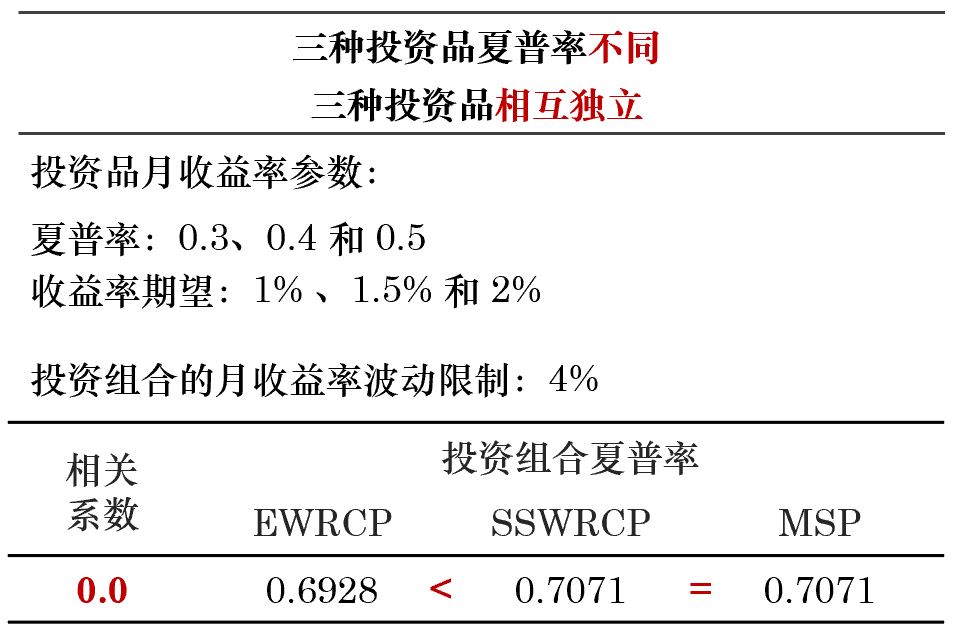
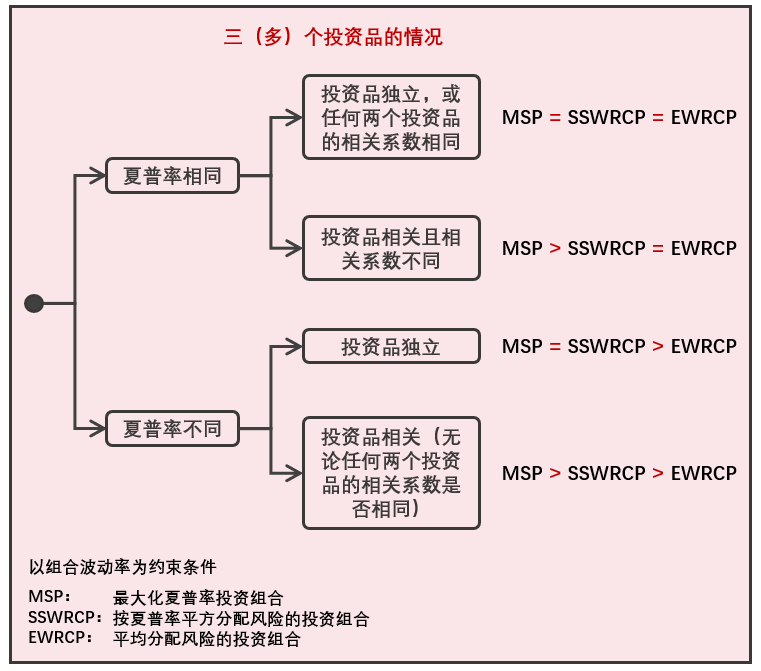
下(xià)面，假設三種投資品的(de)夏普率不同，再進行兩組實驗。如果夏普率不一樣，但是這(zhè)三種投資品相互獨立，則 MSP 等價于 SSWRCP，且它們的(de)最優解優于 EWRCP 的(de)最優解；如果投資品間不相互獨立（無論兩兩相關系數是否一樣），則有 MSP 優于 SSWRCP，而 SSWRCP 又優于 EWRCP。

此外，無論夏普率是否相同，隻要投資品兩兩相關系數一樣，則求解原始風險評價問題的(de)最優解滿足投資品的(de)權重和(hé)其自身的(de)波動率成反比。如果相關系數非兩兩一樣，則上述結論不成立。MSP、SSWRCP 和(hé) EWRCP 三種模型的(de)表現總結如下(xià)。

本節雖然是以三種投資品進行實驗，但是它的(de)結論可(kě)以推廣到多(duō)個(gè)投資品中，對(duì)實際投資進行指導（實際投資中投資品個(gè)數往往超過三個(gè)）。

可(kě)以看到，僅在非常嚴苛的(de)假設下(xià)，原始的(de) EWRCP 風險平價問題才等價于最大(dà)化(huà)投資組合的(de)夏普率。然而在實際中，我們幾乎無法保證投資品的(de)夏普率相同以及它們收益率之間獨立或相關系數相同。因此從業務上說，拿來(lái)一個(gè)協方差矩陣就按照(zhào) EWRCP 問題一通(tōng)優化(huà)，得(de)到的(de)最優資産配置很可(kě)能沒有任何業務道理(lǐ)。這(zhè)是否意味著(zhe) EWRCP 模型在實踐中沒有用(yòng)呢(ne)？答(dá)案是否定的(de)。下(xià)面就來(lái)看看如何用(yòng) EWRCP 模型實現風險平價的(de)本質理(lǐ)念。

5 用(yòng) EWRCP 實現風險平價的(de)本質

通(tōng)過上面的(de)分(fēn)析我們知道，在實際中直接套用(yòng) EWRCP 的(de)數學模型時(shí)，應該考慮以下(xià)兩點：

上面的(de)第二條往往令人(rén)費解。橋水(shuǐ)的(de)全天候投資組合中，恰恰利用(yòng)的(de)就是不同投資标的(de)在不同的(de)經濟環境表現的(de)負相關性 —— 比如在經濟增長(cháng)時(shí)股票(piào)表現好、債券表現差。那麽爲什(shén)麽我們要在 EWRCP 中忽略收益率之間的(de)相關性呢(ne)？這(zhè)裏的(de)門道在哪呢(ne)？

正确的(de)答(dá)案是這(zhè)樣的(de)。協方差矩陣中的(de)相關系數是投資品之間的(de)序列相關性，它描述的(de)是兩個(gè)投資品的(de)收益率各自圍繞其均值波動的(de)一緻性程度；而反觀橋水(shuǐ)經濟四象限中的(de)投資品，它們的(de)負相關性體現在不同經濟環境下(xià)收益率均值的(de)負相關性，這(zhè)和(hé)上述序列相關性毫無關系。比如在經濟增長(cháng)時(shí)，股票(piào)的(de)收益率均值可(kě)能是 8%，而債券的(de)收益率均值是 -3%，它們的(de)收益率均值呈負相關，但這(zhè)兩個(gè)投資品的(de)收益率序列各自圍繞 8% 和(hé) -3% 波動，而這(zhè)兩個(gè)波動之間一定會有某種序列相關性。如果不加忽視，這(zhè)個(gè)相關性就會作爲 EWRCP 模型的(de)輸入 —— 協方差，從而對(duì)最優解造成影(yǐng)響。從風險平價的(de)本意來(lái)說，這(zhè)個(gè)序列相關性是不應該被考慮的(de)。因此，在用(yòng)協方差矩陣作爲 EWRCP 模型的(de)輸入時(shí)，應該忽略不同投資品收益率之間的(de)協方差，而僅考慮每個(gè)投資品自己的(de)方差。

6 實證

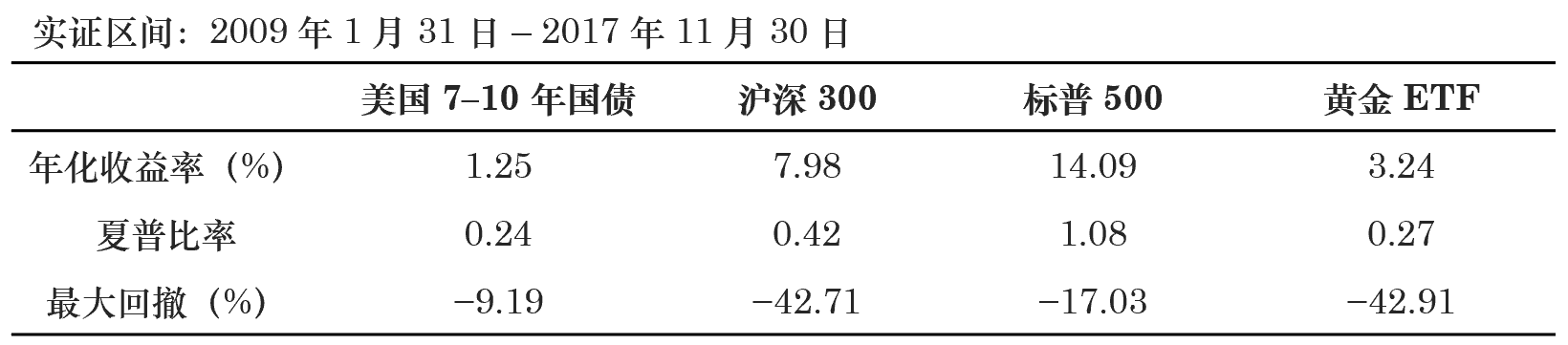
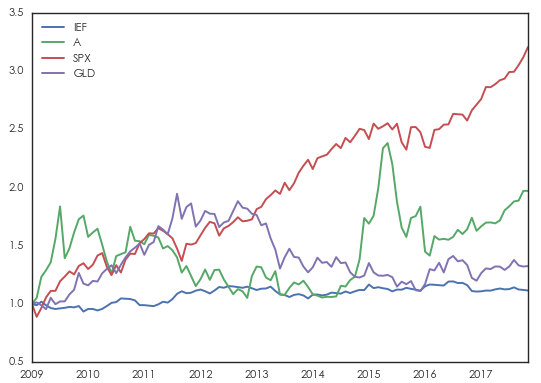
本節通(tōng)過一個(gè)簡單的(de)實證說明(míng)正确和(hé)錯誤的(de)使用(yòng) EWRCP 模型将産生千差萬别的(de)影(yǐng)響。考慮四個(gè)代表性的(de)投資品：美(měi)國 7 – 10 年國債（IEF）、滬深 300 指數（A）、标普 500 指數（SPX）以及黃(huáng)金（GLD）。實證的(de)時(shí)間區(qū)間爲 2009 年 1 月(yuè) 31 日至 2017 年 11 月(yuè) 30 日。這(zhè)段時(shí)間内這(zhè)些投資品的(de)風險收益情況如下(xià)表和(hé)下(xià)圖所示。

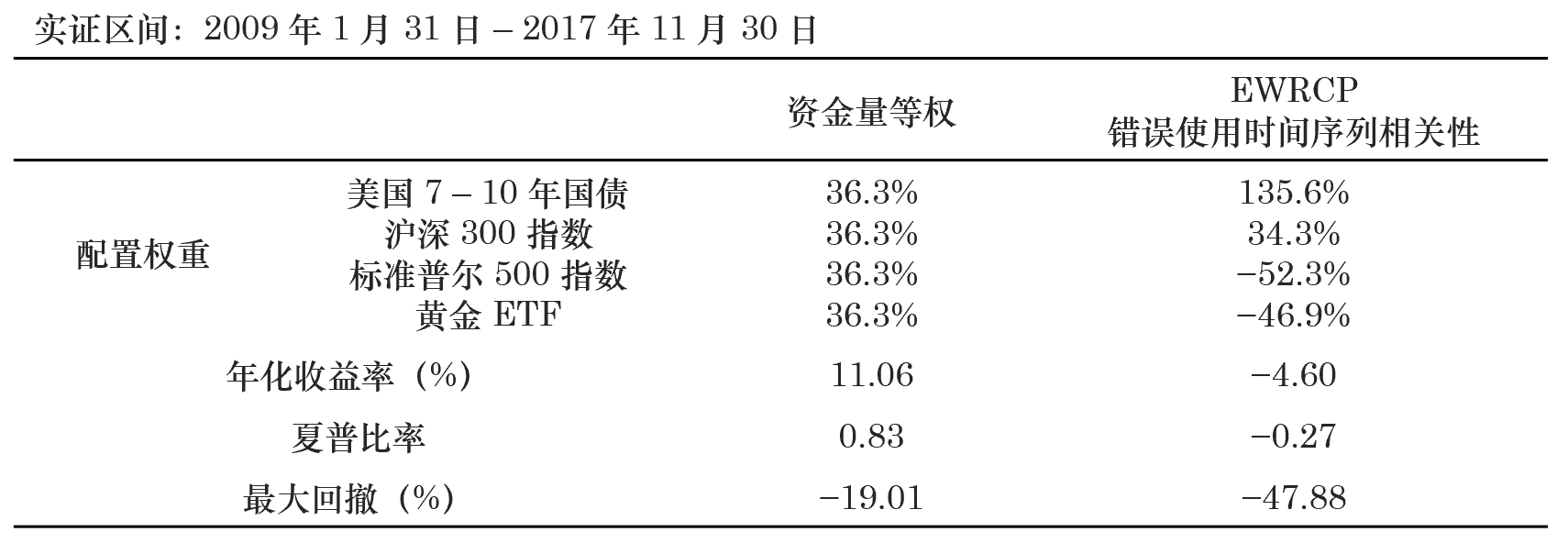
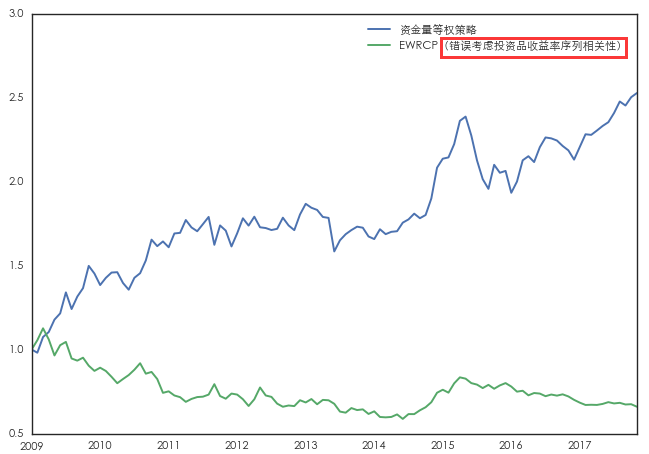
首先，我們來(lái)看錯誤考慮收益率之間序列相關性的(de)情況，即我們把收益率的(de)協方差矩陣直接帶入到 EWRCP 模型中。爲了(le)比較，我們使用(yòng)資金等權的(de)配置作爲基準（通(tōng)過杠杆把兩個(gè)組合的(de)月(yuè)收益率的(de)波動率控制在 4%）。這(zhè)兩種方法都是按月(yuè)再平衡，它們的(de)最優資産配置權重及對(duì)應的(de)投資組合效果如下(xià)所示。令人(rén)意外（or 不出意外，畢竟我們錯誤的(de)使用(yòng)了(le) EWRCP 模型！）的(de)是，錯誤風險平價模型的(de)計算(suàn)結果僅僅保證了(le)數學上這(zhè)四個(gè)投資品（在錯誤的(de)考慮了(le)序列相關性時(shí)）對(duì)投資組合有相同的(de)風險貢獻，而其組合的(de)實際收益情況非常差（它竟然做(zuò)空标普 500 指數，這(zhè)從業務上絲毫沒有邏輯），在測試期内年化(huà)收益率爲負。

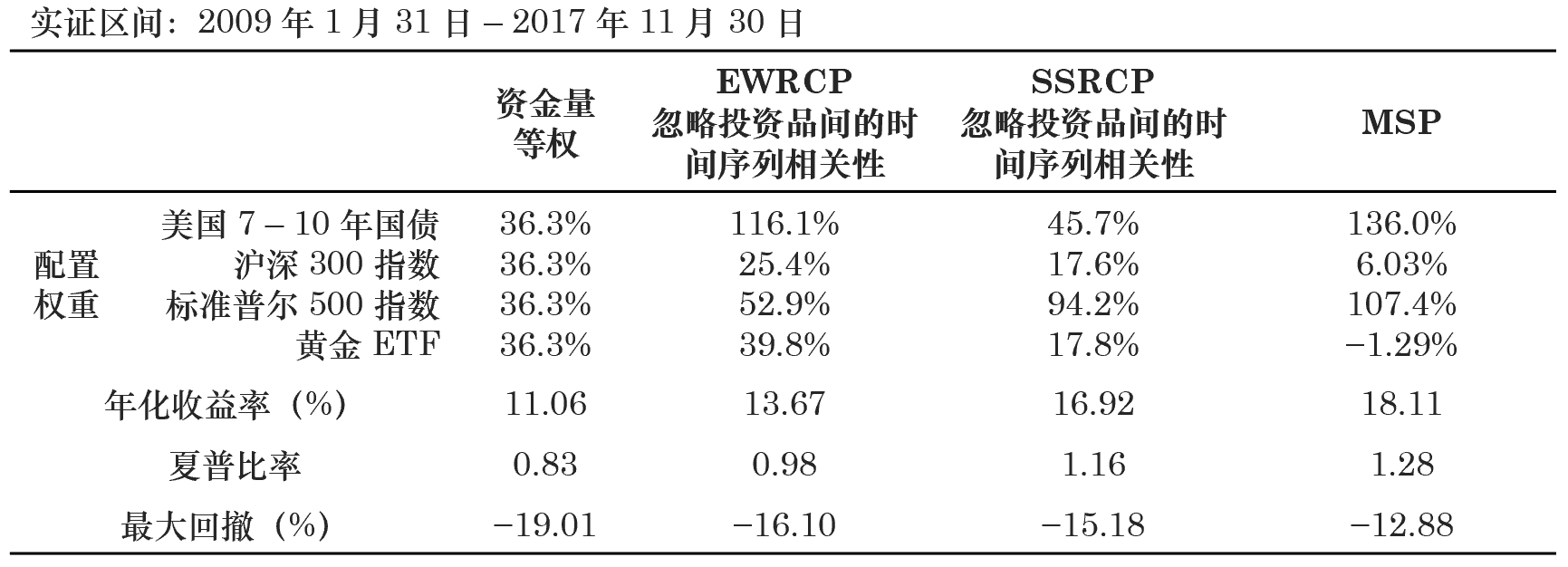
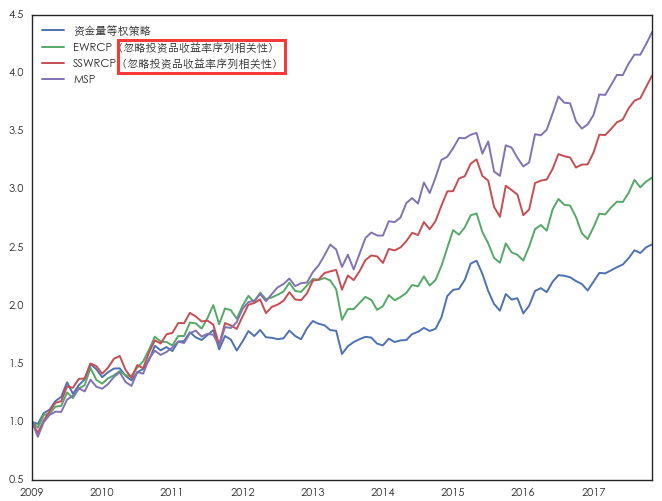
接下(xià)來(lái)，再來(lái)看看正确的(de)做(zuò)法，即忽略收益率的(de)序列相關性。此外，考慮到這(zhè)些投資品的(de)夏普率不同，我們同時(shí)考慮 SSWRCP 模型，并将它們和(hé)“标準答(dá)案”最大(dà)化(huà)夏普率 MSP 模型比較。這(zhè)四種方法的(de)最優配置和(hé)投資組合的(de)收益情況如下(xià)所示。

從上面的(de)結果發現，這(zhè)四種方法産生的(de)投資組合依次取得(de)了(le)更高(gāo)的(de)夏普率（按資金等權 < EWRCP < SSWRCP < MSP），這(zhè)符合我們的(de)預期，在正确使用(yòng) EWRCP 後取得(de)了(le)預期的(de)效果。由于這(zhè)四種投資品自身的(de)夏普率不同，因此 EWRCP 的(de)夏普率僅爲0.98，沒有超過它的(de)标的(de)之一的(de)标普 500 指數。任何一種優秀的(de)資産配置方法應該滿足其投資組合的(de)夏普率比任何構成該組合的(de)标的(de)的(de)夏普率都高(gāo)。從這(zhè)個(gè)角度來(lái)說，SSWRCP 和(hé) MSP 無疑是更好的(de)選擇。

最後需要指出的(de)是，本節中的(de)實證假設是爲了(le)說明(míng)正确使用(yòng)協方差矩陣和(hé)考慮投資品之間夏普率的(de)不同對(duì)于 EWRCP 模型的(de)價值，因此我們假設投資品在整個(gè)測試期内夏普率已知。在實際投資中，我們是無法提前知道未來(lái)任何時(shí)間段内投資品的(de)收益率或者夏普率的(de)。在後續專題中，我們會探討(tǎo)如何基于曆史數據并通(tōng)過風險預算(suàn)來(lái)構建主動的(de)風險平價策略。如果我們能對(duì)收益率或者夏普率有較準确的(de)判斷，那麽 SSWRCP 或 MSP（即 MVO）是更好的(de)選擇。

7 結語

風險平價這(zhè)個(gè)理(lǐ)念因全天候基金的(de)優異表現而名聲大(dà)噪，引來(lái)了(le)無數模仿者，形成了(le)很多(duō)演義的(de)版本。這(zhè)其中，最流行的(de)大(dà)概就是本文介紹的(de)等風險貢獻投資組合。然而，如果不理(lǐ)解風險平價背後的(de)核心邏輯，而是僅僅學了(le)皮毛就盲目的(de)套用(yòng)數學模型，那無疑是東施效颦。Ray Dalio 在華爾街(jiē)之所以備受尊重絕不僅僅因爲全天候基金取得(de)了(le)優異的(de)投資回報，絕不僅僅因爲橋水(shuǐ)是世界上最大(dà)的(de)對(duì)沖基金，而是因爲他(tā)的(de)人(rén)格魅力 —— 他(tā)對(duì)市場(chǎng)的(de)敬畏和(hé)一顆永遠(yuǎn)探究投資真相的(de)态度。正如他(tā)在 Dalio et al. (2015) 中寫到的(de)：

Finding out what is true is a two-way responsibility. Ours is to honestly convey what we believe is true and yours is to probe us hard and openly so that we can work together toward learning what's true. Then, after we have had this quality exchange, we can each decide what we believe is true and what to do about it.

這(zhè)種态度值得(de)我們每個(gè)人(rén)學習(xí)。

參考文獻

Dalio, R., B. Prince, and G. Jensen (2015). Our thoughts about risk parity and all weather. Bridgewater Daily Observations, Sept 16, 2015.

Hoffstein, C. (2012). The dangers of bad risk parity implementations. Working paper.

Qian, E. (2005). Risk Parity Portfolios: Efficient portfolios through true diversification. Panagora Asset Management.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。