機器學習(xí)與資産定價: Facts and Fictions
發布時(shí)間:2023-06-21 | 來(lái)源: 川總寫量化(huà)
作者:石川
摘要:本文從五方面闡述中低頻(pín)實證資産定價中的(de)機器學習(xí)應用(yòng)。
自 Gu, Kelly and Xiu (2020) 這(zhè)篇綜述把機器學習(xí)方法正式引入實證資産定價研究以來(lái),學術界的(de)一衆學者在這(zhè)幾年将各種(線性的(de)非線性的(de))機器學習(xí)模型都應用(yòng)到了(le)股票(piào)收益率的(de)預測之上。
這(zhè)背後的(de)契機是大(dà)數據和(hé)機器學習(xí)時(shí)代協變量的(de)激增以及協變量和(hé)未來(lái)收益率之間的(de)複雜(zá)關系。這(zhè)二者給傳統基于計量經濟學方法的(de)實證研究帶來(lái)了(le)巨大(dà)的(de)挑戰。毫無疑問,計量經濟學方法是可(kě)以被用(yòng)來(lái)分(fēn)析簡單線性關系和(hé)進行參數審定(parameter adjudication)的(de)利器,然而它并非處理(lǐ)高(gāo)維預測(prediction)問題時(shí)的(de)首選。對(duì)于後者來(lái)說,早在自然語言處理(lǐ)、圖像識别等其他(tā)領域證明(míng)了(le)自己的(de)機器學習(xí)算(suàn)法自然而然地走進了(le)人(rén)們的(de)視野。
伴随而來(lái)的(de),是學界的(de)研究從 diminishing anomalies(即提出 ad-hoc 簡約模型來(lái)消滅異象)向 increasing prominence of machine learning methods(即如何通(tōng)過機器學習(xí)算(suàn)法得(de)到更好的(de)預測)的(de)轉型,并從中形成新的(de)研究範式。研究悄然從 procedurally 轉向了(le) empirically。無論認可(kě)與否,在大(dà)勢面前,一切似乎都不可(kě)逆轉,那些将機器學習(xí)算(suàn)法用(yòng)于資産定價并發表在頂刊上的(de)實證文章(zhāng)就是最好的(de)證明(míng)。
通(tōng)讀這(zhè)些基于美(měi)股市場(chǎng)(當然,有不少已經被 copy & paste 到了(le) A 股,sorry for 吐槽)、發表在頂刊上的(de)實證文章(zhāng)其實不難發現,無論是理(lǐ)論描述還(hái)是實證結果,它們都有很多(duō)的(de)共性。深入理(lǐ)解它們,有助于加深對(duì)将機器學習(xí)算(suàn)法應用(yòng)于實證資産定價的(de)正确認知。因此,今天這(zhè)篇小文就以 Facts 和(hé) Fictions 爲題從五方面梳理(lǐ)這(zhè)類研究的(de)“是”與“非”。希望通(tōng)過此文幫你客觀了(le)解實證研究的(de)現狀。
最後想要強調的(de)是,本文的(de)闡述僅限于中低頻(pín)實證資産定價中的(de)機器學習(xí)應用(yòng)。在國内外的(de)量化(huà)投資實踐中,注定會有一些領先于學術研究的(de)内容,但它們不在本文討(tǎo)論範圍之内。另外,本文參考文獻中優先引用(yòng)已發表的(de)版本。
1
Fiction: 将數據無腦(nǎo)扔進高(gāo)級算(suàn)法,單純指望數據發聲。
金融數據低信噪比和(hé)不滿足平穩性這(zhè)兩個(gè)特點足以打消人(rén)們單純指望數據發聲的(de)良好願景。就資産定價來(lái)說,參數先驗、協變量尺度縮放、正則化(huà)罰項以及調參依據選擇等都會影(yǐng)響最終的(de)結果(Nagel 2021,我和(hé)王熙老師的(de)翻譯在此)。
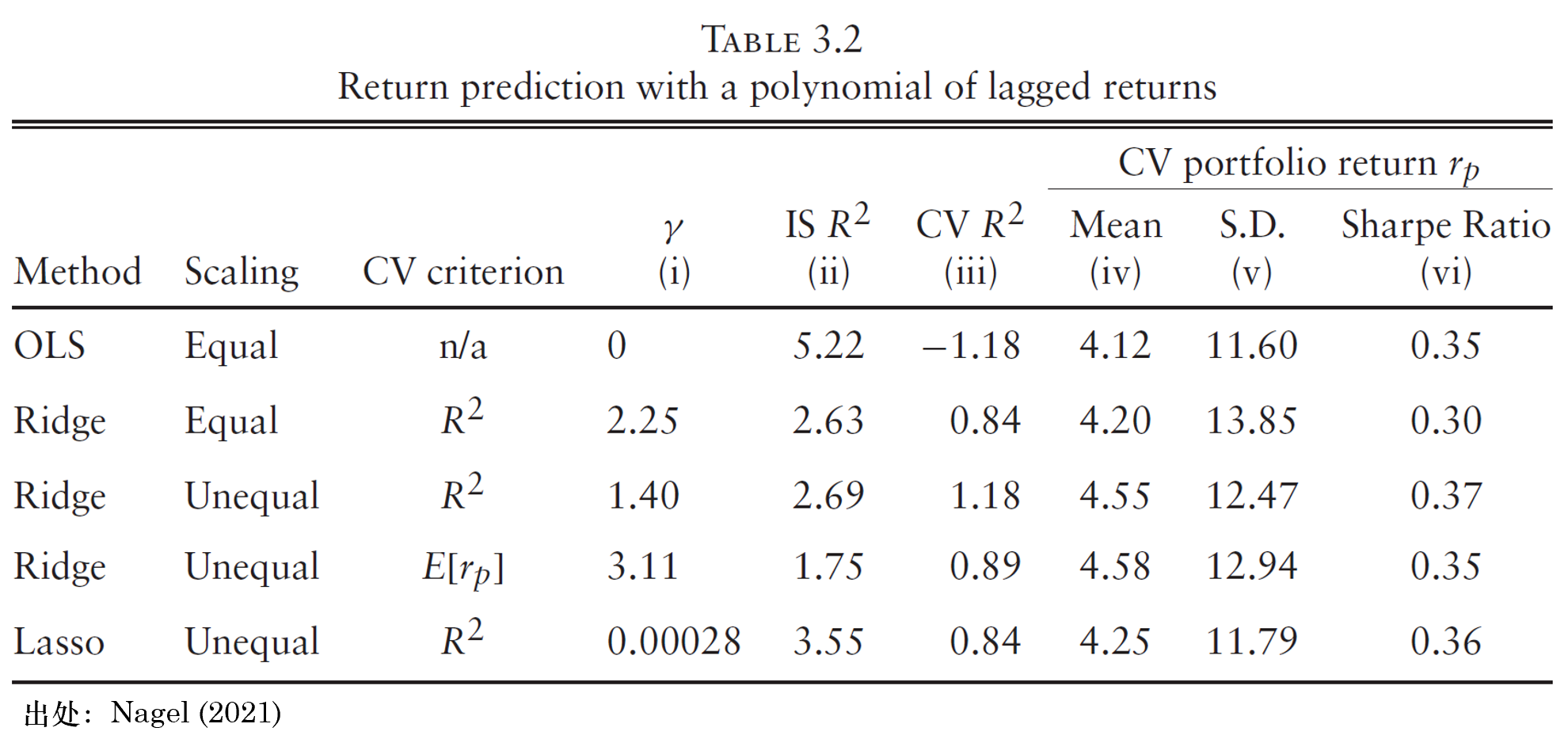
下(xià)面這(zhè)個(gè)例子來(lái)自 Nagel (2021),雖然簡單,但能清晰闡明(míng)上面的(de)問題。假設我們使用(yòng)過去 120 期的(de)曆史收益率以及它們的(de)平方和(hé)三次方作爲協變量來(lái)預測下(xià)一期收益率。下(xià)表總結了(le)不同設定下(xià)的(de)預測結果。其中 Method 一欄表明(míng)了(le)正則化(huà)的(de)罰項(OLS 表示沒有正則化(huà)),Scaling 一欄表明(míng)對(duì)協變量進行了(le)怎樣的(de)标準化(huà)處理(lǐ)(Equal 表示協變量都被标準化(huà)到均值爲 0、标準差爲 1;Unequal 表明(míng)協變量标準化(huà)之後的(de)标準差不同),CV criterion 一欄表示調參的(de)依據(例如以驗證集 R-squared 或者以投資組合在驗證集上的(de)預期收益率
表中的(de)實證結果顯示,模型設定對(duì)于會産生怎樣的(de)結果影(yǐng)響很大(dà)。然而,當我們面臨衆多(duō)選擇時(shí),不該也(yě)無法枚舉所有的(de)排列組合,而是應該充分(fēn)利用(yòng)先驗。例如,如果我們認爲模型是非稀疏的(de),那麽就會傾向 Ridge 而非 Lasso;如果我們認爲協變量在預測收益率時(shí)的(de)重要程度不同,可(kě)能就會選擇 Unequal 而非 Equal 的(de)處理(lǐ)方式;如果我們從金融問題核心出發,可(kě)能會選擇以最大(dà)化(huà)夏普比率(或最小化(huà) pricing errors)而非傳統的(de) R-squared 來(lái)進行模型調優。而這(zhè)些的(de)背後,都離不開資産定價理(lǐ)論。
Fact: 以大(dà)數據爲依托、以機器學習(xí)算(suàn)法爲工具,圍繞資産定價理(lǐ)論展開。
在實證資産定價這(zhè)個(gè)領域,從 CAPM,到 APT/ICAPM,再到 zoo of factors,層出不窮的(de)實證挑戰無疑極大(dà)推動了(le)學科的(de)發展。然而,無論範式如何演化(huà),研究都是圍繞著(zhe)實證資産定價理(lǐ)論展開的(de)。
以最近幾年火爆的(de)幾篇文章(zhāng)爲例,Bryzgalova, Pelger and Zhu (2020) 以及 Chen, Pelger and Zhu (forthcoming),雖然前者使用(yòng)了(le)決策樹而後者使用(yòng)了(le)生成對(duì)抗網絡(GAN),但它們都是在随機貼現因子(SDF)這(zhè)一框架下(xià)将不同的(de)算(suàn)法應用(yòng)于資産定價。又比如,Kelly, Pruitt and Su (2019) 的(de) IPCA 以及 Gu, Kelly and Xiu (2021) 的(de) Autoencoder 則使用(yòng)了(le)隐性多(duō)因子模型,即把
在實證方面,這(zhè)些文章(zhāng)的(de)共性是使用(yòng)了(le)大(dà)量的(de)協變量(of course 較傳統研究而言),并通(tōng)過投資組合的(de) OOS 表現來(lái)表明(míng)方法的(de)有效性。雖然它們各自嘗試了(le)不同的(de)機器學習(xí)算(suàn)法,但鑒于 SDF 和(hé)多(duō)因子模型的(de)等價性,它們都可(kě)以被放在一統的(de)框架下(xià)審視和(hé)學習(xí)。
2
Fiction: 機器學習(xí)模型是黑(hēi)箱,學術研究不關注可(kě)解釋性。
對(duì)于傳統的(de) ad-hoc 多(duō)因子模型或者異象研究而言,可(kě)解釋性是它們的(de)靈魂。比如 FF5 是基于 DDM、q-factor model 是基于 q-theory。而各種關于異象的(de)論文中也(yě)會有解釋(risk-based vs mispricing)。而一旦把研究目标轉移到通(tōng)過複雜(zá)模型構造更準确的(de)收益率預測,給人(rén)的(de)印象就是這(zhè)方面的(de)要求就被淡化(huà)了(le)。然而,事實并非如此。
對(duì)于線性模型而言,例如 Kozak, Nagel and Santosh (2018, 2020) 的(de) PCA,以及 KPS 的(de) IPCA,模型的(de)解釋是非常清晰的(de)。以前者爲例,KNS 在對(duì)通(tōng)過 size 和(hé) value 劃分(fēn)出的(de) 25 個(gè)投資組合進行 PCA 時(shí)發現前兩個(gè) PCs 完美(měi)對(duì)應著(zhe) SMB 和(hé) HML 因子;而對(duì)于後者而言,IPCA 雖然在數學上看似繁瑣,但其背後的(de)直覺解釋卻是一系列通(tōng)過 cross-section regression 構造的(de) managed portfolios 的(de)線性組合(PCs)。因此,對(duì)于線性模型而言,其解釋性恰恰植根于我們熟悉的(de) regression 以及 portfolio sort 方法中。
而對(duì)于非線性模型而言,其可(kě)解釋性雖然不如線性模型那麽直觀,但學術研究依然給予了(le)它足夠的(de)重視(見 fact 部分(fēn))。
Fact: 機器學習(xí)揭示的(de)最重要預測變量和(hé)大(dà)量實證資産定價結果吻合。
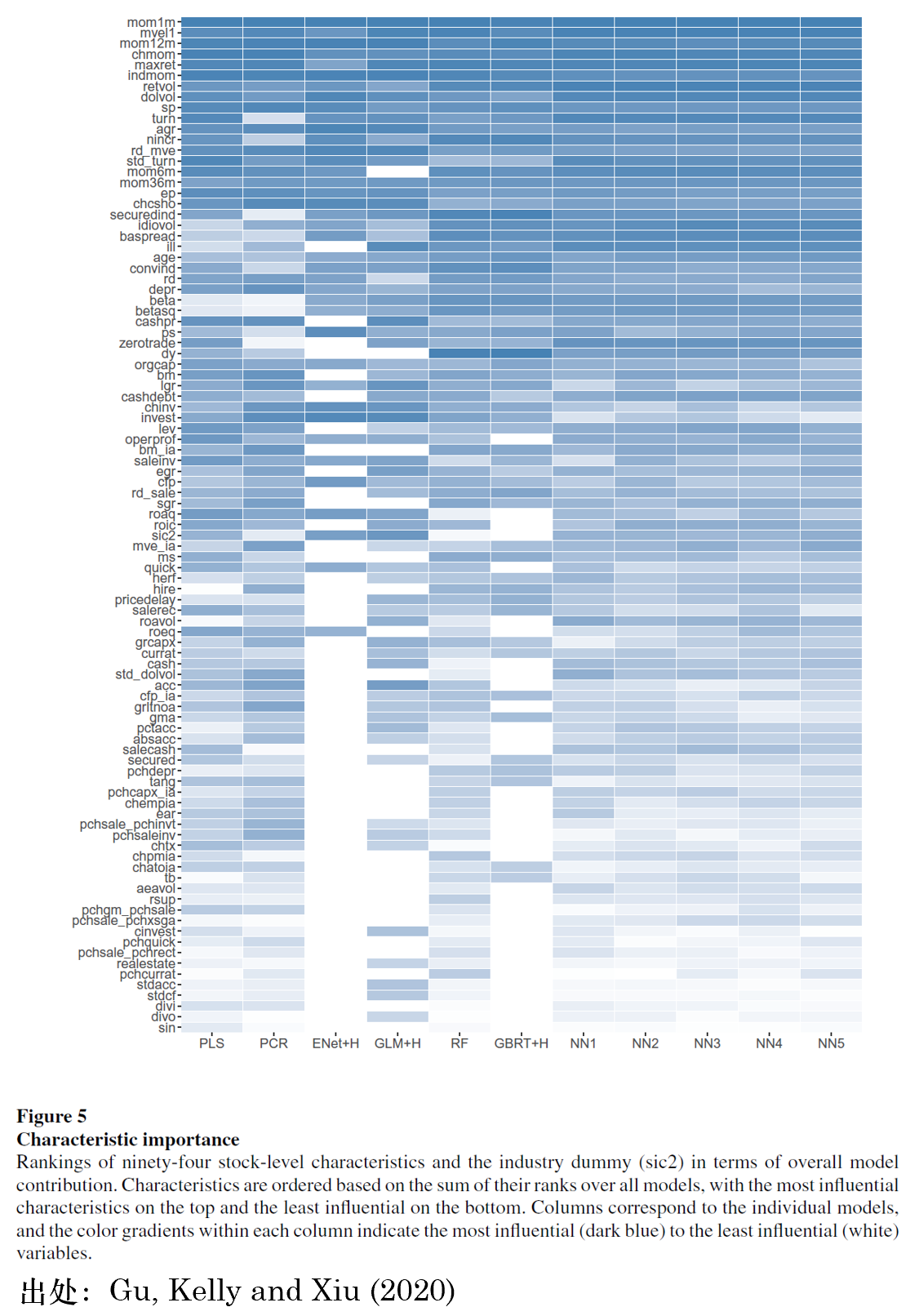
Gu, Kelly and Xiu (2020) 使用(yòng) permutation importance 揭示了(le)哪些協變量對(duì)解釋預期收益率最重要(下(xià)圖)。從中我們可(kě)以看出:(1)最重要的(de)協變量和(hé)以往實證結果相吻合,其中最重要的(de)變量大(dà)緻可(kě)以分(fēn)爲四大(dà)類,即動量/反轉,流動性相關,風險相關(比如 IVOL)以及基本面相關;(2)不同的(de)機器學習(xí)模型來(lái)說,最重要的(de)協變量也(yě)在很大(dà)程度上是相似的(de)。
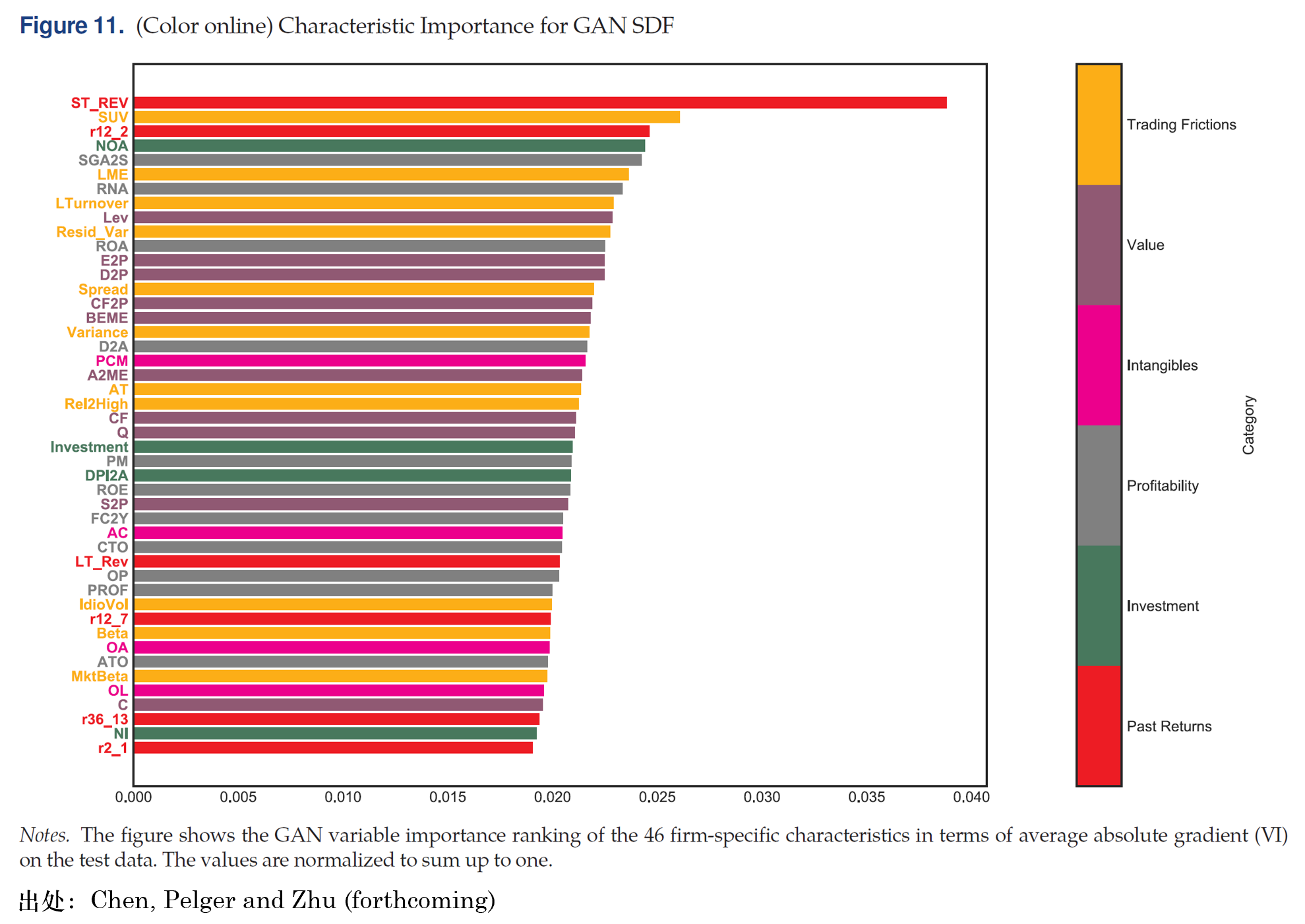
Chen, Pelger and Zhu (forthcoming) 通(tōng)過計算(suàn) SDF 權重對(duì)協變量的(de)偏導數來(lái)評價模型的(de)可(kě)解釋性。下(xià)圖顯示,在所有協變量中,最重要的(de)可(kě)以被分(fēn)爲交易摩擦、價值、無形資産、盈利、投資以及曆史收益率幾大(dà)類。
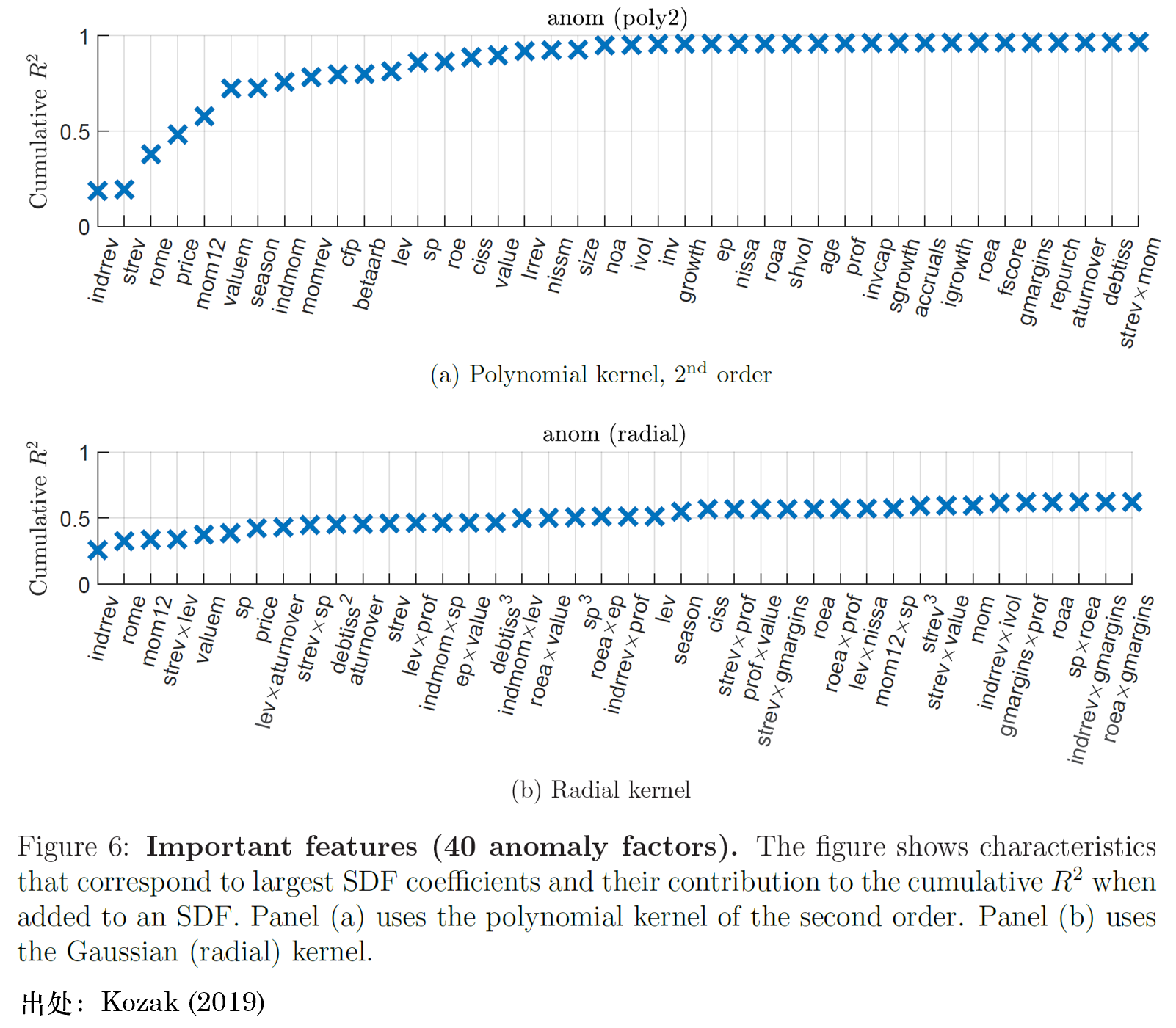
另一篇值得(de)一提的(de)文章(zhāng)是 Kozak (2019)。它利用(yòng) kernel trick 巧妙地在不增加運算(suàn)量的(de)前提下(xià)将協變量映射到高(gāo)維并對(duì)映射後的(de)協變量進行 PCA,以此來(lái)進行資産定價。在使用(yòng)了(le)非線性 kernel 後,我們無從知道映射後的(de)協變量是什(shén)麽樣子。但是,通(tōng)過将構造的(de) SDF 映射到原始協變量的(de) managed portfolios,依然能夠鑒别出最重要的(de)解釋變量。
最後,也(yě)可(kě)以通(tōng)過觀察選出股票(piào)(多(duō)頭或者多(duō)空對(duì)沖組合)在不同協變量上是否有共性來(lái)判斷哪些變量更加重要,例如 Avramov, Cheng and Metzker (2023)。
3
Fiction: 複雜(zá)模型容易樣本内過拟合,導緻樣本外預測誤差加劇。
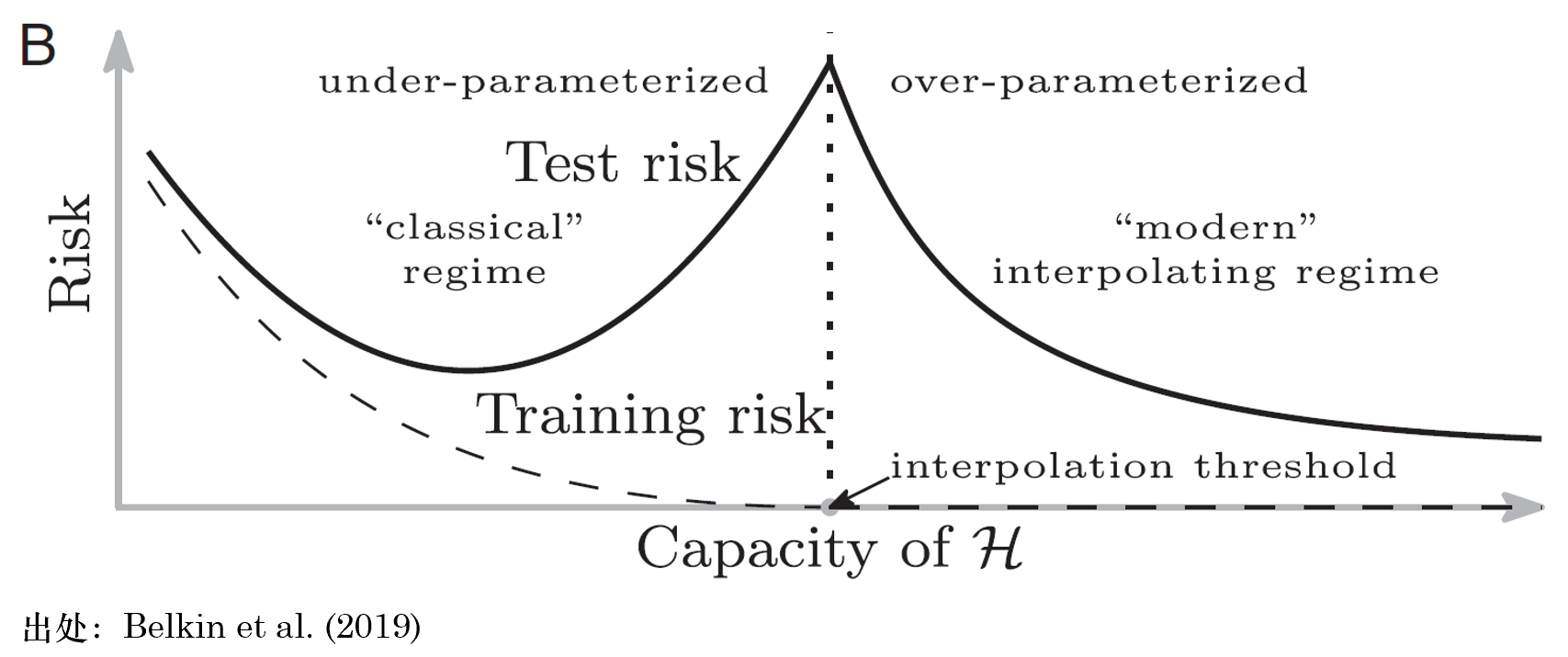
對(duì)于模型來(lái)說,其樣本外表現和(hé)模型複雜(zá)度關系密切。當模型複雜(zá)度很低時(shí),模型的(de)方差很小,但是偏差很高(gāo);當模型複雜(zá)度高(gāo)時(shí),模型的(de)方差變大(dà),但是偏差降低。二者的(de)共同作用(yòng)就是人(rén)們熟悉的(de) bias-variance trade-off,因此存在某個(gè)最優的(de)超參數,使得(de)樣本外的(de)總誤差(風險)最低。
我們還(hái)可(kě)以換個(gè)角度來(lái)理(lǐ)解 bias-variance trade-off。當模型很簡單時(shí),它能夠有效規避過拟合,但并非是真實世界的(de)很好近似;而當模型複雜(zá)時(shí),它更有可(kě)能逼近真實世界,但是也(yě)的(de)确更容易過拟合。因此 bias-variance trade-off 也(yě)可(kě)以理(lǐ)解爲 approximation-overfit trade-off。
然而,上述結論有一個(gè)人(rén)們習(xí)以爲常的(de)前提:變量個(gè)數 < 樣本個(gè)數。如果模型複雜(zá)到變量的(de)個(gè)數超過了(le)樣本的(de)個(gè)數又會怎樣呢(ne)?事實上,這(zhè)一問題并非無緣無故的(de)憑空想象。對(duì)于複雜(zá)的(de)神經網絡模型來(lái)說,模型參數的(de)個(gè)數很容易超過樣本的(de)個(gè)數。當變量個(gè)數 ≥ 樣本個(gè)數時(shí)(被稱爲 over-parameterization),模型在樣本内能夠完美(měi)的(de)拟合全部樣本(當變量個(gè)數和(hé)樣本個(gè)數相等時(shí),模型能夠完美(měi)的(de) fit 所以樣本點。這(zhè)個(gè)現象在機器學習(xí)術語中被稱爲 interpolation)。由于金融數據的(de)信噪比極低,對(duì)于這(zhè)樣一個(gè)妥妥樣本内過拟合了(le)噪聲的(de)模型,人(rén)們通(tōng)常的(de)認知是,它在樣本外的(de)預測誤差一定會“爆炸”。然而事實也(yě)許并非如此。
Fact: 複雜(zá)模型是真實 DGP 的(de)更好近似,在正則化(huà)使用(yòng)得(de)當的(de)前提下(xià),複雜(zá)模型帶來(lái)的(de)好處可(kě)能優于統計代價。
近年來(lái),機器學習(xí)領域一個(gè)令人(rén)興奮的(de)發現就是樣本外誤差随模型複雜(zá)度變化(huà)的(de) double descent 現象。Belkin et al (2019) 指出,當模型複雜(zá)度突破樣本個(gè)數這(zhè)個(gè)“禁忌之地”後,神奇的(de)事情發生了(le):樣本外總誤差并沒有“爆炸”,而是随著(zhe)複雜(zá)度的(de)提升單調下(xià)降。正因爲在樣本個(gè)數兩側都出現了(le)誤差單調下(xià)降的(de)情況,這(zhè)個(gè)現象被稱爲 double descent。
這(zhè)背後的(de)直覺解釋是:當協變量個(gè)數超過樣本個(gè)數的(de)時(shí)候,樣本内的(de)解是不唯一的(de),而最優的(de)解可(kě)以理(lǐ)解爲讓參數的(de)方差最小的(de)那個(gè)解。随著(zhe)變量越來(lái)越多(duō),最優解的(de)方差總能單調下(xià)降。再來(lái)看偏差,通(tōng)常來(lái)說,偏差确實會随著(zhe)複雜(zá)度的(de)提升而增加。但是所有模型都是真實 DGP 的(de)某個(gè) mis-specified 版本。當存在模型設定偏誤的(de)時(shí)候,可(kě)以證明(míng)當變量個(gè)數超過樣本個(gè)數時(shí),偏差也(yě)會在一定範圍内随著(zhe)複雜(zá)度而下(xià)降。因此,二者的(de)綜合結果就是模型在樣本外的(de)誤差表現會随複雜(zá)度的(de)上升而下(xià)降。對(duì)于 double descent 現象背後的(de)理(lǐ)論,感興趣的(de)小夥伴請參考 Hastie et al. (2022)。
在實證資産定價方面, Kelly, Malamud and Zhou (forthcoming) 将上述理(lǐ)念應用(yòng)到了(le)美(měi)股擇時(shí)之中,并發現了(le)類似的(de) double descent 現象:當采用(yòng)協變量個(gè)數遠(yuǎn)遠(yuǎn)超過樣本個(gè)數的(de)模型時(shí),樣本外的(de)夏普比率提升了(le)。客觀的(de)說,關于模型複雜(zá)度和(hé)樣本外表現的(de)討(tǎo)論,在資産定價領域尚處于萌芽階段,且正則化(huà)(或者 implied 正則化(huà))在這(zhè)個(gè)過程中至關重要,期待未來(lái)在這(zhè)方面有更多(duō)精彩的(de)研究成果。
4
Fiction: 非線性模型可(kě)以輕松讓夏普比率翻倍。
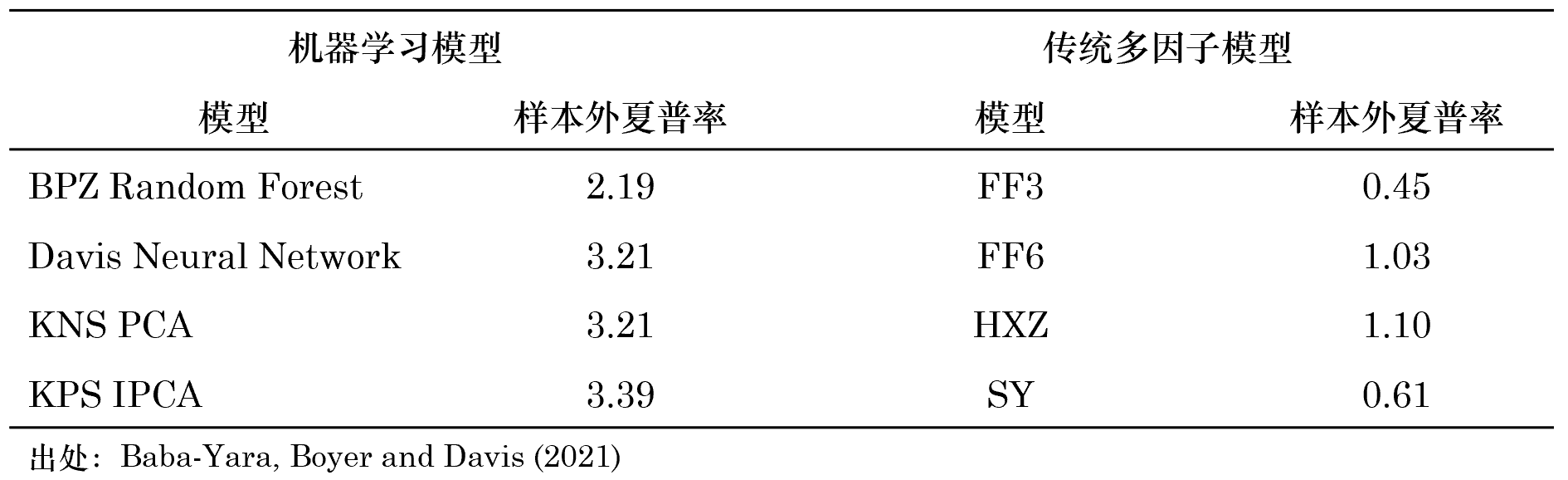
我們先看一組似乎足以推翻這(zhè)個(gè) fiction 的(de)實證結果。Baba-Yara, Boyer and Davis (2021) 複現了(le)最近幾年最重要的(de)機器學習(xí)模型,并将它們的(de)結果和(hé)傳統的(de)多(duō)因子模型進行了(le)比較。我挑選了(le)幾個(gè)有代表性的(de)彙總于下(xià)表。
上述結果清晰的(de)表明(míng),相比于傳統多(duō)因子模型,機器學習(xí)模型的(de)夏普比率确實是前者的(de)兩倍甚至是三倍。但不要忘了(le),右邊這(zhè)些都是強加了(le)特設稀疏性的(de)簡約模型(隻用(yòng)了(le)太少的(de)變量),因此這(zhè)樣的(de)比較是不公平的(de)。(另外,在本節 fact 部分(fēn)我們還(hái)會再次討(tǎo)論上述結果,相信那時(shí)候你會更加确信。)另一方面,如果你仔細觀察就不難發現,在上面的(de)結果中,KNS 的(de) PCA 以及 KPS 的(de) IPCA(這(zhè)兩個(gè)非條件和(hé)條件線性模型)的(de)夏普比率反而要高(gāo)于另外兩個(gè)分(fēn)别利用(yòng)随機森林(lín)和(hé)神經網絡的(de)模型。因此,非線性模型(至少在上述實證結果中)并沒有占得(de)便宜。
Fact: 非線性模型能捕捉協變量和(hé)預期收益率之間的(de)非線性關系,且現階段對(duì)表現隻是提供邊際增量貢獻。
事到如今,我們無需懷疑協變量和(hé)預期收益率之間存在非線性關系。哪怕是傳統的(de) double portfolio sort,也(yě)是考察控制了(le)變量 A 之後,變量 B 和(hé)預期收益率的(de)關系。由 Nagel (2021) 以及大(dà)量最新實證資産定價論文的(de)結果可(kě)知,在非線性關系中,變量的(de)交互作用(yòng)是最重要的(de)。對(duì)于傳統線性回歸模型來(lái)說,一旦協變量數目激增,枚舉考慮兩兩變量的(de)交乘項是不切實際的(de),因此這(zhè)就給了(le)善于處理(lǐ)非線性關系的(de)機器學習(xí)模型施展的(de)空間。
話(huà)雖如此,我們也(yě)應該對(duì)非線性關系對(duì)于預測收益率提供的(de)增量貢獻有正确的(de)預期。Chen, Pelger and Zhu (forthcoming) 的(de)實證結果顯示,他(tā)們的(de)生成對(duì)抗網絡在構造 SDF 時(shí)能夠捕捉到協變量之間的(de)交互作用(yòng),然而另一方面,他(tā)們也(yě)強調獨立協變量對(duì)于 SDF 的(de)影(yǐng)響幾乎是線性的(de)。
下(xià)面讓我們回到 fiction 部分(fēn)提到的(de) Baba-Yara, Boyer and Davis (2021) 一文。上面的(de)這(zhè)個(gè)表來(lái)自該文的(de)早期版本,其 OOS 實證區(qū)間是 1990 到 2020。然而,在最新的(de)版本中,其 OOS 實證區(qū)間搖身一變縮短爲 1990 到 2016。論文的(de)版本更新了(le),而實證區(qū)間卻倒退了(le),實在令人(rén)不解。而更讓人(rén)匪夷所思的(de)是,作者給出的(de)解釋竟然是作爲比較的(de) ad-hoc 模型 Stambaugh-Yuan 的(de)數據隻到 2016 年(你們在複現機器學習(xí)模型!拜托!)。既然早期工作版本中能複現到 2020 年,爲什(shén)麽在新的(de)版本中卻又以此爲借口放棄了(le)?真正的(de)動機恐怕隻有作者自己清楚。
在這(zhè)個(gè)短一些的(de)實證區(qū)間内,實證結果如下(xià)(下(xià)表中括号内數據是截至到 2020 年的(de)結果,放在這(zhè)裏方便比較)。有意思的(de)是,當實證區(qū)間的(de)終點選爲 2016 之後,四個(gè)機器學習(xí)模型都不同程度的(de)變差了(le)(BPZ 有些讓人(rén)意外),而四個(gè) ad-hoc 模型卻都提升了(le)(SY 發表在 2017,FF6 = FF5 + Carhart Mom 而 FF5 以及 HXZ 都發表在 2015,玄妙吧)。
Anyway,讓我們聚焦于機器學習(xí)模型。上述對(duì)比說明(míng),随著(zhe)實證區(qū)間的(de)不同,模型的(de)結果也(yě)會有較大(dà)的(de)波動。而另一方面,所有這(zhè)些發表在頂刊上的(de)論文,雖然它們都是使用(yòng) rolling 或者 expanding 窗(chuāng)口進行訓練和(hé)驗證,然後再預測樣本外的(de) next month、如此往複,但是這(zhè)些文章(zhāng)并沒有對(duì)調參的(de)過程以及不同參數下(xià)模型的(de)穩健性進行多(duō)少(if any!)的(de)描述。從這(zhè)個(gè)意義上說,機器學習(xí)應用(yòng)于資産定價的(de)研究生态還(hái)遠(yuǎn)談不上完善(呼籲有大(dà)佬能站出來(lái),提出學界認可(kě)的(de)研究生态)。
5
Fiction: 機器學習(xí)模型可(kě)以很容易地被應用(yòng)于實踐。
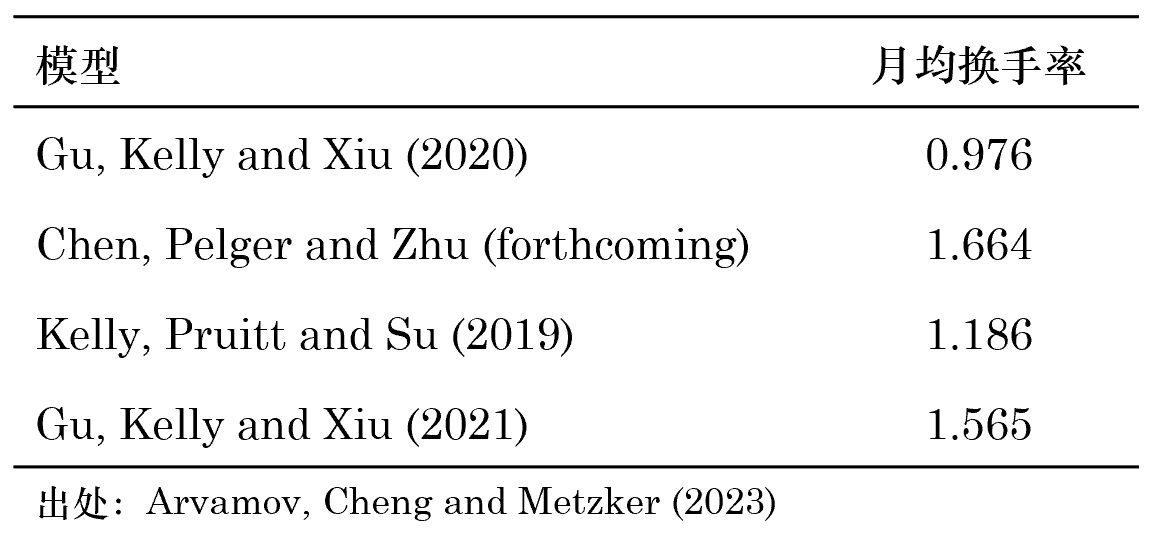
雖然機器學習(xí)模型在實證資産定價的(de)學術研究中取得(de)了(le)令人(rén)欣慰的(de)結果,但并不意味著(zhe)它們能夠被輕易的(de)用(yòng)于實踐,并獲得(de)可(kě)觀的(de)費後超額收益。這(zhè)方面一個(gè)最重要的(de)經驗事實是,機器學習(xí)模型構造的(de)投資組合都有很高(gāo)的(de)換手率。
在這(zhè)方面,Avramov, Cheng and Metzker (2023) 複現了(le) Gu, Kelly and Xiu (2020) 中的(de)神經網絡模型、CPZ 的(de) GAN、KPS 的(de) IPCA 以及 Gu, Kelly and Xiu (2021) 的(de)(Conditional)Autoencoder (CA)。這(zhè)些模型的(de)月(yuè)均換手率如下(xià)。作爲對(duì)比,像 size 和(hé) value 這(zhè)種傳統低頻(pín)風格因子的(de)月(yuè)均換手率通(tōng)常低于 10%(即 0.1)。通(tōng)過對(duì)交易成本的(de)估計,Avramov, Cheng and Metzker (2023) 指出,在如此高(gāo)的(de)換手率下(xià),對(duì)于一般投資者(average investors)來(lái)說,很難通(tōng)過機器學習(xí)模型賺取額外的(de)超額收益(當然不排除有些投資者能夠很好的(de)将這(zhè)些模型工程化(huà),并在高(gāo)換手率的(de)前提下(xià)依然獲得(de)超額收益)。
爲了(le)應對(duì)交易成本帶來(lái)的(de)挑戰,Jensen et al. (2022) 提出了(le) implementable efficient frontier 的(de)概念,即在構造策略的(de)時(shí)候直接通(tōng)過費後收益率進行評估,從而将帶有交易成本的(de)投資組合優化(huà)問題融入到機器學習(xí)的(de)框架之中,并取得(de)了(le)不錯的(de)結果。
Fact: 機器學習(xí)發現的(de)可(kě)預測性部分(fēn)集中于套利成本和(hé)交易成本高(gāo)的(de)股票(piào),對(duì)一些機構投資者價值有限。
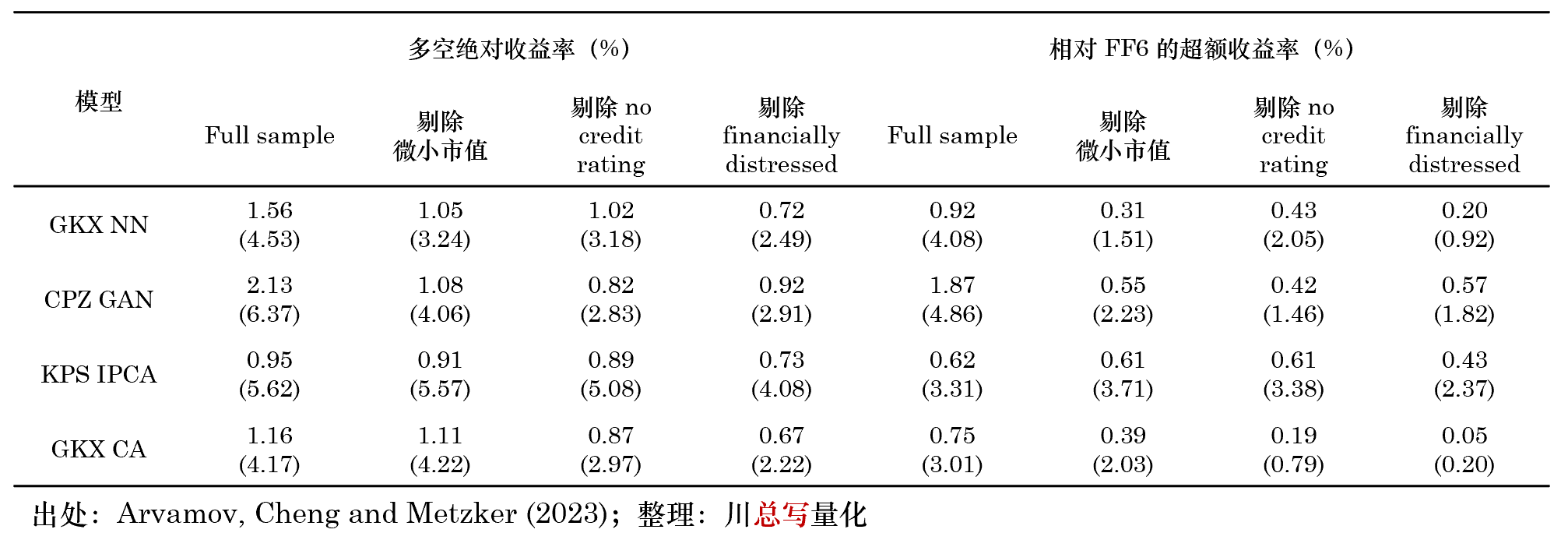
實證結果表明(míng),諸多(duō)異象的(de)超額收益主要來(lái)自空頭(Avramov et al. 2013)或者微小市值股票(piào)(Novy-Marx and Velikov 2016)。而對(duì)于機器學習(xí)模型來(lái)說,它們也(yě)善于從套利和(hé)交易成本更高(gāo)的(de)股票(piào)中挖掘可(kě)預測性,因而削弱了(le)它們的(de)實踐價值。仍以 Avramov, Cheng and Metzker (2023) 的(de)實證結果爲例。除 full sample 外,該文還(hái)分(fēn)别考察了(le)剔除微小市值、剔除無 credit rating 公司以及剔除 financially distressed 公司的(de)三個(gè)子樣本。結果(下(xià)表,表中括号内爲 t-statistics)顯示,和(hé) full sample 相比,主流機器學習(xí)模型(IPCA 除外)在這(zhè)三個(gè)子樣本中的(de)表現均有明(míng)顯的(de)下(xià)降,且一些模型較傳統 ad-hoc 多(duō)因子模型(例如 FF6)的(de)
以 GAN 爲例,其在剔除微小市值子樣本中的(de)月(yuè)均收益率和(hé) full sample 相比,降低了(le)超過 50%。在上述四個(gè)模型中,除 IPCA 之外都是非線性模型,而唯有 IPCA 的(de)結果比較穩健(在 full 和(hé)幾個(gè)子樣本中的(de)結果較爲一緻)。需要說明(míng)的(de)是,上述針對(duì)三個(gè)子樣本的(de)結果仍然是使用(yòng)基于 full sample 訓練出的(de)模型得(de)到的(de)。這(zhè)也(yě)許會讓一些讀者頗有微詞。對(duì)于此,Avramov, Cheng and Metzker (2023) 進一步使用(yòng)子樣本進行訓練和(hé)樣本外預測,但發現結果并沒有實質的(de)改變,而且在一些子樣本中 OOS 的(de)表現還(hái)下(xià)降了(le)。換句話(huà)說,原本打算(suàn)通(tōng)過約束讓模型學習(xí)目标樣本,然而結果卻是更少的(de)樣本量(子樣本 vs full)卻導緻了(le)更差的(de) OOS 表現。成功 tweak 非線性模型使其聚焦于套利和(hé)交易成本低的(de)股票(piào),将會是機器學習(xí)模型落地的(de)重要前提。
6
以上從五方面的(de) facts and fictions 梳理(lǐ)了(le)近幾年最重要的(de)機器學習(xí)資産定價實證發現。
作爲本文的(de)結尾,我想最後強調的(de)是,雖然這(zhè)些論文的(de)實證結果都是 OOS(即用(yòng)曆史數據建模和(hé)調參,然後預測下(xià)一個(gè) period),然而它們使用(yòng)的(de)協變量幾乎都是來(lái)自以往實證資産定價研究所挖出來(lái)的(de) anomaly。從這(zhè)個(gè)意義上說,我不得(de)不再抛出一直以來(lái)的(de)觀點“所有曆史數據都是樣本内”。
在協變量和(hé)收益率存在非線性關系,以及協變量都是在曆史上顯著的(de)前提下(xià),我們似乎不用(yòng)對(duì)這(zhè)些模型在 OOS 的(de)優越表現感到特别的(de)意外。然而,另一個(gè)值得(de)思考的(de)問題是,如果以 agnostic 視角出發,将機器學習(xí)模型應用(yòng)實證資産定價之中,又會有怎樣的(de)結果?在這(zhè)方面,Nagel (2021) 有過初步的(de)嘗試,發現機器學習(xí)能夠從諸多(duō)變量中識别出和(hé)預期收益率相關的(de)那些。
希望本文的(de)梳理(lǐ)能幫助你對(duì)基于機器學習(xí)模型的(de)實證資産定價研究形成正确的(de)預期,在抱有期待的(de)同時(shí)也(yě)客觀認識到研究的(de)現狀和(hé)面臨的(de)挑戰。最後,我想引用(yòng) Bryan Kelly 在某 Q&A 環節就機器學習(xí)正确預期的(de)回答(dá)總結本文。作爲學界新生代當仁不讓的(de)扛把子之一以及 AQR 的(de) Head of Machine Learning,Kelly 的(de)觀點值得(de)認真體會。
參考文獻
Avramov, D., S. Cheng, and L. Metzker (2023). Machine learning vs. economic restrictions: Evidence from stock return predictability. Management Science 69(5), 2587 – 2619.
Avramov, D., T. Chordia, G. Jostova, and A. Philipov (2013) Anomalies and financial distress. Journal of Financial Economics 108(1), 139 – 159.
Baba-Yara, F., B. Boyer, and C. Davis (2021). The factor model failure puzzle. Working paper.
Belkin, M., D. Hsu, S. Ma, and S. Mandal (2019). Reconciling modern machine-learning practice and the classical bias-variance trade-off. PNAS 116(32), 15849 – 15854.
Bryzgalova, S., M. Pelger, and J. Zhu (2020). Forest through the trees: Building cross-sections of stock returns. Working paper.
Chen, L., M. Pelger, and J. Zhu (forthcoming). Deep learning in asset pricing. Management Science.
Gu, S., B. T. Kelly, and D. Xiu (2020). Empirical asset pricing via machine learning. Review of Financial Studies 33(5), 2223 – 2273.
Gu, S., B. T. Kelly, and D. Xiu (2021). Autoencoder asset pricing models.Journal of Econometrics 222(1), 429 – 450.
Hastie, T., A. Montanari, S. Rosset, and R. J. Tibshirani (2022). Surprise in high-dimensional ridgeless least squares interpolation. Annals of Statistics 50(2), 949 – 986.
Jensen, T. I., B. T. Kelly, S. Malamud, and L. H. Pedersen (2022). Machine learning and the implementable efficient frontier. Working paper.
Kelly, B. T., S. Malamud, and K. Zhou (forthcoming). The virtue of complexity in return prediction. Journal of Finance.
Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.
Kozak, S. (2019). Kernel trick for the cross-section. Working paper.
Kozak, S., S. Nagel, and S. Santosh (2018). Interpreting factor models. Journal of Finance 73(3), 1183 – 1223.
Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.
Nagel, S. (2021). Machine Learning in Asset Pricing. Princeton University Press.
Novy-Marx, R and M. Velikov (2016). A taxonomy of anomalies and their trading costs. Review of Financial Studies 29(1), 104 – 147.
免責聲明(míng):入市有風險,投資需謹慎。在任何情況下(xià),本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外,文中圖表均直接或間接來(lái)自于相應論文,僅爲介紹之用(yòng),版權歸原作者和(hé)期刊所有。