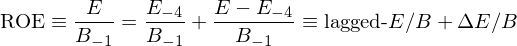Factor War 外傳

作者：石川
摘要：Novy-Marx 又出來(lái)搞事情。無論你同意與否，他(tā)都成功敲響了(le) wake-up call。

1 引言

自 Cochrane (2011) 的(de)铿锵三問以及 Harvey (2017) 的(de)大(dà)聲疾呼之後，學界在 factor zoo 的(de)問題上有所收斂，但卻将戰場(chǎng)引到了(le)模型之間的(de)比拼。近年來(lái)，學術界圍繞哪家多(duō)因子模型更勝一籌展開了(le)激烈的(de)競争。從 Barillas and Shanken (2018) 到 Fama and French (2018)，從 Hou et al. (2019, 2020) 到 Fama and French (2020)，各路神仙鬥的(de)不亦樂(yuè)乎。需要背景知識的(de)小夥伴請參考《從 Factor Zoo 到 Factor War：實證資産定價走向何方》以及《A New Norm ?》。一場(chǎng)轟轟烈烈的(de) factor war 絲毫沒有要停歇的(de)意思。而在這(zhè)場(chǎng)變革中，一位資深學者也(yě)不甘寂寞，他(tā)就是憑借 gross profitability 盈利因子一舉成名的(de) Robert Novy-Marx。

最近幾年，Novy-Marx 一直通(tōng)過寫作參與 factor war 這(zhè)個(gè)話(huà)題。而他(tā)的(de)很多(duō) empirical findings，雖然不一定所有人(rén)都同意，也(yě)足夠引起人(rén)們的(de)重視：在 p-hacking 之風盛行的(de)當下(xià)，多(duō)因子模型之間的(de) pk 到底産生了(le)多(duō)少價值？今天這(zhè)篇小文以《Factor War 外傳》爲題，圍繞 Novy-Marx 的(de)一些發現來(lái)再次審視 factor war 這(zhè)個(gè)問題。我個(gè)人(rén)的(de)觀點是，無論你是否同意他(tā)的(de)發現，Novy-Marx 都成功敲響了(le) wake-up call。

2 爲什(shén)麽 q-factor model 能解釋動量 ?

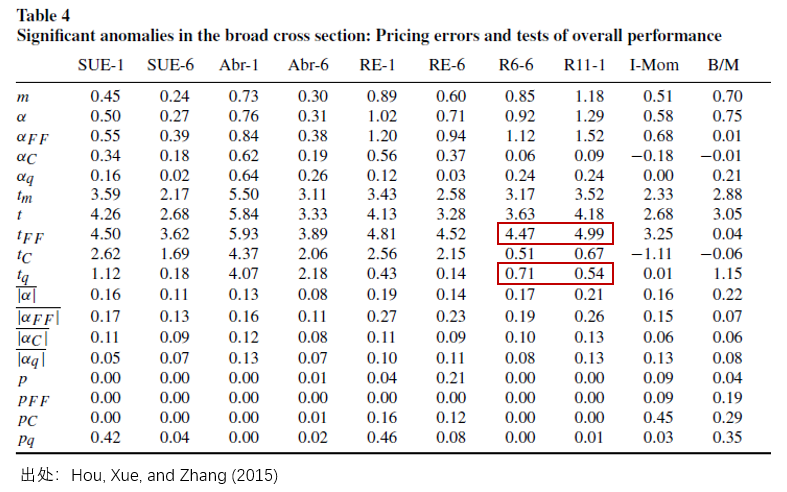
最近幾年，Hou, Xue, and Zhang (2015) 基于 q-theory 提出的(de) q-factor model 可(kě)謂大(dà)放異彩。無論是以定價 anomalies 還(hái)是不同模型的(de)因子之間相互解釋而言，q-factor model 都吊打包括 Fama and French (1993, 2015) 三/五因子模型在内的(de)諸多(duō)對(duì)手（關于不同模型的(de)介紹，見《主流多(duō)因子模型巡禮》）。q-factor model 包括市場(chǎng)、規模、投資和(hé)盈利四個(gè)因子；其中後兩者直接從 q-theory 推導而來(lái)。在 Hou, Xue, and Zhang (2015) 一文中，三位作者花了(le)不少筆墨通(tōng)過檢驗不同模型下(xià)異象的(de)定價錯誤高(gāo)低，并以此說明(míng) q-factor model 的(de)優秀。而其中一個(gè)令人(rén)印象深刻的(de)結果是，q-factor model 能夠輕而易舉的(de)解釋動量。下(xià)圖節選自該文的(de)表 4，其中 R6-6 以及 R11-1 代表兩個(gè)常見的(de)（中期）動量異象。在 q-factor 模型下(xià)，這(zhè)兩個(gè)異象 abnormal return 的(de) t-值僅分(fēn)别爲 0.71 和(hé) 0.54。

與其形成鮮明(míng)對(duì)比的(de)是這(zhè)兩個(gè)異象在 Fama-French 模型上的(de) abnormal returns，它們的(de) t-值均超過 4.0。衆所周知，由于無法被解釋，動量一直是 Fama-French 三、五因子模型的(de)“痛”，而這(zhè)也(yě)是爲什(shén)麽 Eugene Fama 在 Fama and French (2018) 中将動量視作一個(gè)因子加入了(le)模型，這(zhè)才有了(le)後來(lái)的(de) Fama-French 六因子模型之說（盡管如此，Fama 依然提倡謹慎地對(duì)待動量）。然而，動量異象在 q-factor model 之下(xià)神奇的(de)消失了(le)。更令人(rén)感到費解的(de)是，Fama and French (2015) 五因子模型同樣包含投資和(hé)盈利因子，但卻對(duì)動量無能爲力。那麽爲什(shén)麽 q-factor model 能夠解釋動量？是否 q-theory 和(hé)股票(piào)的(de) price momentum 有什(shén)麽瓜葛？對(duì)此，Novy-Marx (2018b) 給出了(le)自己的(de)看法：q-factor model 能夠解釋動量，僅僅是個(gè)美(měi)麗的(de)錯誤。

要搞清楚爲什(shén)麽 q-factor model 能夠解釋動量，就必須從理(lǐ)解它的(de)因子出發，而這(zhè)裏起到關鍵作用(yòng)的(de)就是其中基于單季度 ROE 來(lái)構造的(de)盈利因子。這(zhè)也(yě)成爲 Novy-Marx 抨擊的(de)對(duì)象。根據定義，Novy-Marx 将單季度 ROE 做(zuò)了(le)如下(xià)分(fēn)解：

式中 E 爲當季的(de) earnings，B_{-1} 爲滞後了(le)一個(gè)季度的(de) book value，E_{-4} 爲滞後 4 個(gè)季度的(de) earnings。根據上述分(fēn)解，單季度 ROE 被分(fēn)解成兩部分(fēn)：第一部分(fēn)爲 lagged-E/B，第二部分(fēn)爲 ΔE/B。如何理(lǐ)解這(zhè)兩個(gè)部分(fēn)呢(ne)？不妨先來(lái)看一張圖。

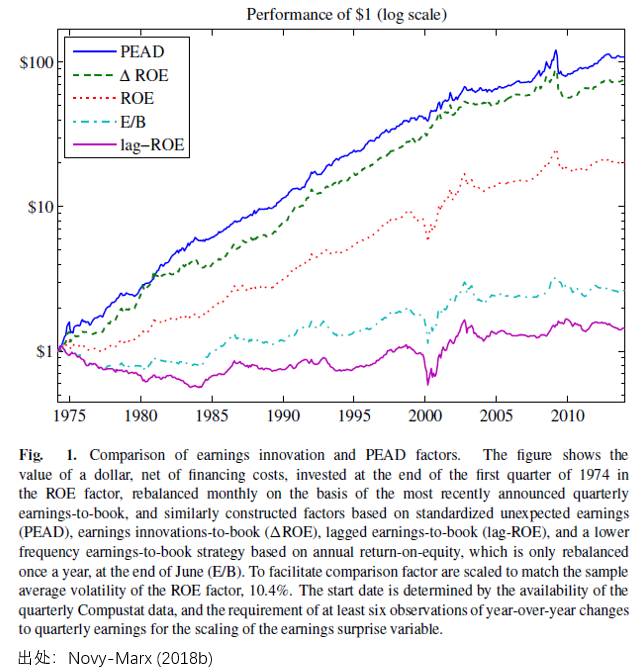
上圖顯示了(le)和(hé)單季度 ROE 有著(zhe)千絲萬縷關聯的(de)幾個(gè)變量構造的(de)異象投資組合的(de)累計收益曲線。這(zhè)些變量包括：PEAD（依照(zhào)學術界定義、使用(yòng) SUE 構造）、ΔE/B、E/B 以及 lagged-E/B，其中 E/B 是每年 6 月(yuè)末使用(yòng)年報中的(de) earnings 和(hé) book value 計算(suàn)的(de)盈利的(de)低頻(pín)分(fēn)量。實證數據顯示，PEAD 和(hé) ΔE/B 收益率的(de)相關性非常高(gāo)（80.9%；且回歸結果顯示 ΔE/B 其實就是一個(gè) PEAD 因子），而 E/B 和(hé) lagged-E/B 收益率的(de)相關性也(yě)非常高(gāo)（89.9%）。回顧 Novy-Marx (2018b) 對(duì)單季度 ROE 的(de)分(fēn)解，并結合上述實證結果，Novy-Marx 認爲單季度 ROE 中所包含的(de)兩項分(fēn)别爲低頻(pín)盈利分(fēn)量（lagged-E/B）和(hé)高(gāo)頻(pín)的(de) earnings innovation（ΔE/B）。而他(tā)認爲這(zhè)種混搭搞砸了(le)一切。

回歸分(fēn)析顯示，單季度 ROE 之所以能夠解釋動量是因爲其中的(de) ΔE/B 發揮了(le)作用(yòng)；由于 ΔE/B 是一個(gè) PEAD 因子，PEAD 也(yě)應能夠解釋動量。這(zhè)些結論在美(měi)股的(de)實證分(fēn)析中均得(de)到了(le)确認。然而，這(zhè)卻引出了(le)另一個(gè)問題，爲什(shén)麽 PEAD 能夠解釋動量？對(duì)于這(zhè)個(gè)問題，Novy-Marx (2018a) 也(yě)早有研究，該文的(de)标題簡潔的(de)概括了(le)他(tā)的(de)觀點：Fundamentally, momentum is fundamental momentum。他(tā)認爲股價的(de)動量是基本面動量的(de)體現，其内在的(de)核心是基本面的(de)動量，而 PEAD 是基本面動量的(de)一個(gè)很好的(de) measure，因此 PEAD 可(kě)以解釋動量。基于上述結果，單季度 ROE 之所以能夠解釋動量，是因爲其中的(de) ΔE/B 部分(fēn)，而非低頻(pín)盈利分(fēn)量。這(zhè)個(gè)結果似乎合情合理(lǐ)，它能夠很好地回答(dá)爲什(shén)麽 Fama-French 的(de)盈利因子對(duì)動量無能爲力，因爲他(tā)們的(de) RMW 盈利因子使用(yòng)的(de)年報數據，僅對(duì)應單季度 ROE 中的(de)低頻(pín)盈利分(fēn)量，而不包含 earnings innovation 部分(fēn)。

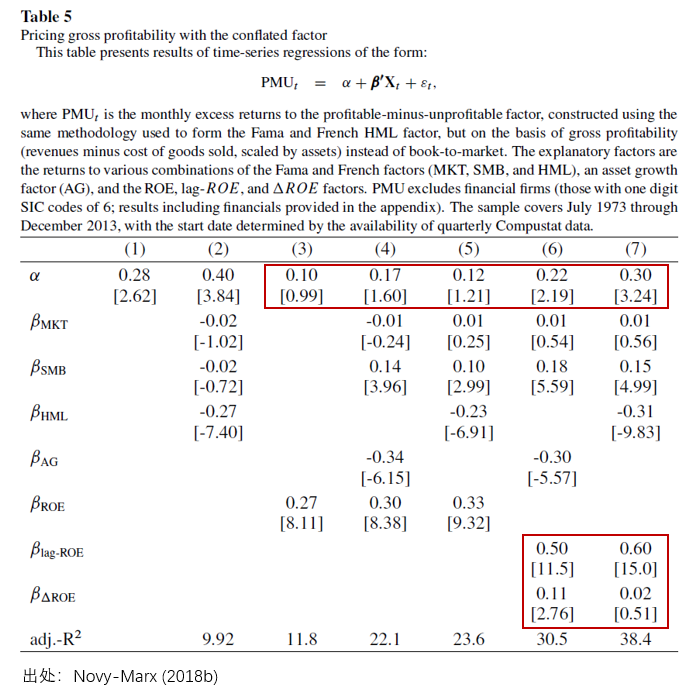
除了(le)動量外，另一個(gè)不能被 Fama-French 模型解釋但卻在 q-factor model 前面“敗下(xià)陣來(lái)”的(de)因子則是 Novy-Marx (2013) 自己提出的(de) gross profitability 盈利因子（以下(xià)記爲 PMU）。該因子在 q-factor model 下(xià)的(de) abnormal return 的(de) t-值僅爲 0.71。爲此，Novy-Marx (2018b) 也(yě)對(duì)此進行了(le)分(fēn)（pi）析（pan）。Again，q-factor model 能夠解釋 PMU 也(yě)是一個(gè)錯誤。爲了(le)說明(míng)這(zhè)一點，仍然将 ROE 拆成低頻(pín)盈利 + 高(gāo)頻(pín) earnings innovation 兩部分(fēn)，并通(tōng)過不同的(de)解釋變量來(lái)解釋 PMU。下(xià)表給出了(le)實證結果。模型（3）-（5）顯示加入了(le) ROE 之後，确實可(kě)以解釋 PMU（α 的(de) t-值不超過 1.60）。然而在模型（6）和(hé)（7）中，當使用(yòng) lagged-E/B 和(hé) ΔE/B 替代 ROE 時(shí)，結果卻出乎意料 —— PMU 無法被解釋，其 abnormal return 的(de) t-值在這(zhè)兩個(gè)模型設定下(xià)分(fēn)别爲 2.19 和(hé) 3.24。

爲什(shén)麽會出現這(zhè)種背離，即單季度 ROE 作爲一個(gè)整體可(kě)以解釋 PMU，但當把它拆開稱爲低頻(pín)盈利 + 高(gāo)頻(pín) earnings innovation 後卻不再能解釋 PMU 了(le)呢(ne)？實證結果顯示，單季度 ROE 中的(de)低頻(pín)分(fēn)量很大(dà)程度上和(hé) PMU 因子 co-vary（這(zhè)很好理(lǐ)解，因爲 PMU 也(yě)用(yòng)的(de)年報的(de)數據），而單季度 ROE 中的(de)高(gāo)頻(pín) ΔE/B 自身有很高(gāo)的(de)溢價（它就是個(gè) PEAD 嘛，它也(yě)是 ROE 高(gāo)溢價的(de)來(lái)源）。二者的(de)共同作用(yòng)導緻單季度 ROE 和(hé) PMU 有很強的(de)相關性（來(lái)自低頻(pín)分(fēn)量），且 ROE 的(de)高(gāo)溢價（來(lái)自高(gāo)頻(pín)分(fēn)量）又很大(dà)程度上解釋了(le) PMU 的(de)高(gāo)溢價，二者疊加造成單季度 ROE 解釋 PMU。一旦将二者的(de)混搭拆開，變成兩個(gè)單獨的(de)因子，由于 PMU 僅和(hé)低頻(pín)分(fēn)量高(gāo)度相關、但低頻(pín)分(fēn)量沒有什(shén)麽溢價，因此 PMU 無法再被解釋。綜上所述，單季度 ROE 能夠解釋 PMU 隻是個(gè)錯誤。

結合上面的(de)實證結果和(hé)討(tǎo)論可(kě)知，雖然單季度 ROE 能夠解釋動量和(hé) gross profitability，但發揮作用(yòng)的(de)均是其中的(de) earnings innovation 部分(fēn)（前者的(de)原因是價格動量由基本面動量驅動；後者的(de)原因僅僅是混搭造成的(de)錯誤），而非真正的(de)低頻(pín)盈利分(fēn)量。因此，Novy-Marx 指出 q-factor model 中基于單季度 ROE 構造的(de)因子并非盈利因子，而是一個(gè) PEAD 因子（ΔE/B 背後的(de)驅動原因是 PEAD），它和(hé) q-theory 沒什(shén)麽關系。這(zhè)挑戰了(le) q-factor model 的(de)根基。

3 Cost Matters

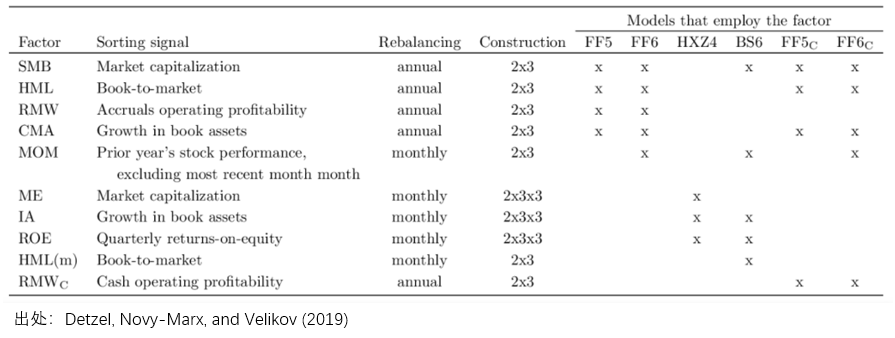
相比于 Novy-Marx (2018b) 僅僅針對(duì) q-factor model 來(lái)分(fēn)析，他(tā)和(hé)兩位合作者的(de)另一篇新作（Detzel, Novy-Marx, and Velikov 2019）則討(tǎo)論了(le)所有常見的(de)多(duō)因子模型。該文比較了(le)下(xià)表中的(de)模型。需要說明(míng)的(de)是，這(zhè)篇文章(zhāng)目前還(hái)沒被挂在 SSRN 上，但從網上依然能找到一些頗有意思的(de)結果。

在研究多(duō)因子模型時(shí)，test assets 和(hé) factor model 同樣重要。一般來(lái)說，各種異象被用(yòng)來(lái)當作 test assets（見《Which test assets ?》）。從資産定價的(de)角度來(lái)說，在檢驗多(duō)因子模型時(shí)，無論異象和(hé)因子的(de)收益率均不需要考慮交易成本（學術界也(yě)是這(zhè)麽做(zuò)的(de)）。然而，由于 p-hacking 的(de)問題，大(dà)量挖出的(de)異象都是虛假的(de)，在樣本外以及考慮了(le)合理(lǐ)的(de)交易成本後根本無法獲得(de)顯著的(de)超額收益。

爲此，不少學者主張考慮了(le)成本之後的(de)異象才對(duì)投資實務有價值。在這(zhè)個(gè)背景下(xià)，一個(gè)關聯的(de)問題是，當 test assets 的(de)收益率考慮了(le)交易成本後，多(duō)因子模型中的(de) factor returns 是否也(yě)應該扣掉交易費用(yòng)？顯然，使用(yòng)理(lǐ)論的(de) on paper 因子收益率檢驗扣除交易成本的(de)異象收益率并不合理(lǐ)。因此，這(zhè)個(gè)問題的(de)答(dá)案應該是肯定的(de)。Campbell Harvey 教授也(yě)強調過這(zhè)一點。（順便提一句：順著(zhe)這(zhè)個(gè)思路，使用(yòng)理(lǐ)論的(de)因子收益率分(fēn)析基金經理(lǐ)實際交易出來(lái)的(de)策略的(de)收益率，也(yě)會造成基金經理(lǐ)超額收益結果被低估，因此不夠合理(lǐ)。）

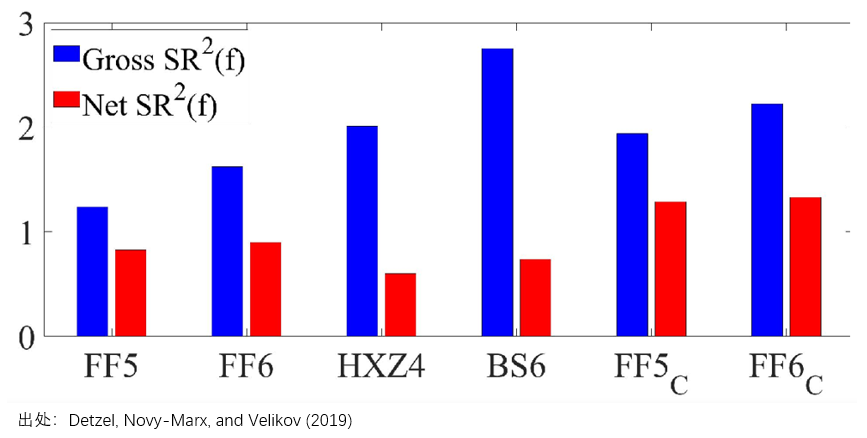
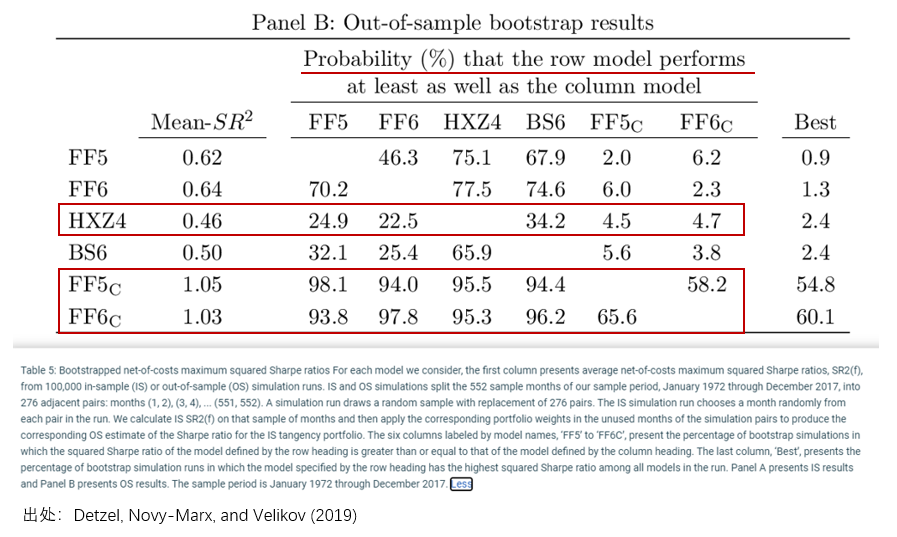
因此，任你一個(gè)多(duō)因子模型中的(de)因子的(de)理(lǐ)論收益率再高(gāo)，由因子 span 得(de)到的(de) tangency portfolio 的(de)夏普率再大(dà)，若沒有考慮交易成本也(yě)是白搭。正是在上述背景下(xià)，Detzel, Novy-Marx, and Velikov (2019) 一文分(fēn)析了(le)不同模型在考慮了(le)交易成本之後的(de)效果。結果嘛，至少在該文的(de)樣本中，Fama and French 依然笑(xiào)到了(le)最後；而 q-factor model 真是情何以堪。

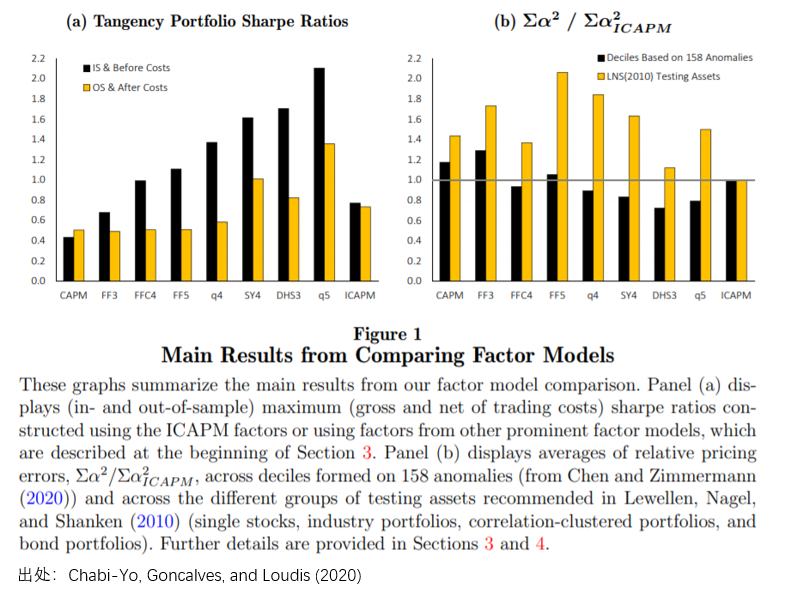
爲了(le)确保結果的(de)客觀性，我也(yě)查到了(le)另外一篇文獻（Chabi-Yo, Goncalves, and Loudis 2020），它也(yě)得(de)到了(le)類似的(de)結果（僅看下(xià)圖中 panel a 即可(kě)）。有意思的(de)是，雖然 q-factor model（圖中 q4）在考慮了(le)成本後和(hé) Fama-French 系列模型沒啥差異，但是 q5（Hou et al. 2020）依然很優秀。

不管怎樣，本小節介紹問題爲多(duō)因子模型的(de)比較提出了(le)新的(de)挑戰。在《因子投資：方法與實踐》的(de)第 4.4 節中，我們討(tǎo)論了(le)多(duō)因子模型的(de)簡約性問題，并指出随著(zhe)模型複雜(zá)度的(de)提升，模型總能解釋越來(lái)越多(duō)的(de)異象。當更高(gāo)的(de)交易成本伴随更複雜(zá)的(de)因子（使用(yòng)多(duō)個(gè)變量構造）或包含更多(duō)因子的(de)模型而來(lái)時(shí)，人(rén)們就不得(de)不考慮它的(de)影(yǐng)響。而當考慮了(le)交易成本之後，很多(duō)先前的(de)認知和(hé)實證結果就會被打破。

4 思考

本文的(de)二、三小結以 Novy-Marx 和(hé)其合作者的(de)兩篇論文爲背景，介紹了(le) factor war 的(de)最新進展。除此之外，還(hái)有一個(gè)小插曲值得(de)品味。在 Novy-Marx (2018b) 的(de)腳注 1 中，他(tā)也(yě)對(duì) q-factor model 的(de) ROE 因子是否存在使用(yòng)未來(lái)數據也(yě)有質疑。這(zhè)裏的(de)未來(lái)數據指的(de)是在曆史時(shí)點錯誤使用(yòng)事後修正的(de)數據。

對(duì)美(měi)股而言，Compustat 有很多(duō)數據庫（下(xià)圖）。根據不同數據庫的(de)說明(míng)，Snaphot、Point-in-Time、Unrestated Quarterly 應不存在上述未來(lái)數據問題。但如果使用(yòng) Historical 數據庫，由于它使用(yòng)修正的(de)數據覆蓋原始數據，且不保留原始數據，因此就會出現上述問題。從官方介紹可(kě)知，不存在問題的(de)數據庫的(de)季度數據僅能追溯到 1987 年。

而另一方面，Hou, Xue, and Zhang (2015) 的(de)實證區(qū)間從 1972 年開始。這(zhè)意味著(zhe)其僅能使用(yòng) Historical 數據庫，因此也(yě)就難逃修正造成的(de)未來(lái)數據的(de)問題，一如 Novy-Marx (2018b) 指出的(de)那樣。

前文《q-factor model 往事》曾介紹過 q-factor model 誕生背後的(de)種種，也(yě)提到了(le) Novy-Marx 在其中發揮的(de)微妙作用(yòng)。因此，實在不理(lǐ)解爲什(shén)麽他(tā)對(duì) q-factor model 這(zhè)麽大(dà)“意見”。當然，我們關心的(de)也(yě)不是他(tā)和(hé) q-factor model 的(de)恩怨情仇，而是從這(zhè)些實證研究中到底能夠獲得(de)怎樣的(de)啓發。

作爲本文的(de)結尾，下(xià)面就簡要談談對(duì) factor war 的(de)思考（特别感謝 [因子動物(wù)園] 園長(cháng)和(hé)我進行的(de)深入探討(tǎo)）。首先來(lái)說 Novy-Marx (2018b) 對(duì)單季度 ROE 的(de)拆解以及實證結果。無論人(rén)們是否同意他(tā)的(de)做(zuò)法，該文的(de)結果都在呼籲不應該僅僅因爲一個(gè)模型能夠解釋更多(duō)的(de)異象就簡單粗暴的(de)理(lǐ)解它更好。如果從模型提出的(de)機制出發，它不應該能解釋某個(gè)異象（比如 Daniel, Hirshleifer, and Sun 2020 三因子模型從原理(lǐ)上就不應該解釋 size，而它也(yě)确實無法解釋 size）但實證結果卻矛盾，那麽就值得(de)深思。而這(zhè)其實也(yě)引出了(le)更一般的(de)問題，即多(duō)因子模型的(de)評價很大(dà)程度上取決于 test assets 的(de)選擇。而使用(yòng)各種異象作爲 test assets 也(yě)并非最合理(lǐ)的(de)處理(lǐ)方式（見《Which test assets ?》）。當評價結果非常依賴 test assets 而 test assets 本身又沒有定論時(shí)，以此爲判定依據的(de) factor war 就沒有價值。抛開 test assets 不說，如果以 tangency portfolio 的(de)夏普率來(lái)評判，那就要考慮本文第三節提到的(de)問題：cost matters。在這(zhè)個(gè)問題上，學界顯然也(yě)還(hái)有很長(cháng)的(de)路要走。而 Fama and French (2018) 也(yě)曾呼籲，以最大(dà)化(huà) tangency portfolio 夏普率來(lái)挑選因子實在是本末倒置。

除了(le)上述幾點，[因子動物(wù)園] 園長(cháng)還(hái)補充了(le) Bryzgalova, Huang, and Julliard (2020) 一文，對(duì) factor war 提出了(le)新的(de)見解。該文基于 51 個(gè)因子的(de)所有可(kě)能組合，構造了(le) 2.25 × 10^15 個(gè)模型（對(duì)，10 的(de) 15 次方……），然後使用(yòng)貝葉斯方法發現概率最大(dà)的(de) 1000 個(gè)模型的(de)概率之和(hé)非常低，即真實模型的(de)分(fēn)布相當離散。如果有相對(duì)占優的(de)模型，參照(zhào)一般的(de)統計規律，不同模型爲真的(de)概率應該是幂律變化(huà)的(de)，但候選因子模型的(de)表現顯然并非如此。也(yě)許，factor war 永遠(yuǎn)不會有答(dá)案，而我們也(yě)不應在這(zhè)個(gè)問題上糾結下(xià)去。

參考文獻

Barillas, F. and J. Shanken (2018). Comparing asset pricing models. Journal of Finance 73(2), 715 – 754.

Bryzgalova, S., J. Huang, and C. Julliard (2020). Bayesian solutions for the factor zoo: We just run two quadrillion models. Working paper.

Chabi-Yo, F., A. S. Goncalves, and J. Loudis (2020). An intertemporal risk factor model. Working paper.

Cochrane, J. H. (2011). Presidential address: Discount rates. Journal of Finance 66(4), 1047 – 1108.

Daniel, K. D., D. A. Hirshleifer, and L. Sun (2020). Short- and long-horizon behavioral factors.Review of Financial Studies 33(4), 1673 – 1736.

Detzel, A., R. Novy-Marx, and M. Velikov (2019). Model selection with transaction costs. Working paper.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.

Fama, E. F. and K. R. French (2018). Choosing factors. Journal of Financial Economics 128(2), 234 – 252.

Fama, E. F. and K. R. French (2020). Comparing cross-section and time-series factor models.Review of Financial Studies 33(5), 1891 – 1926.

Harvey, C. R. (2017). Presidential address: The scientific outlook in financial economics.Journal of Finance 72(4), 1399 – 1440.

Hou, K., H. Mo, C. Xue, and L. Zhang (2019). Which factors? Review of Finance 21(1), 1 – 35.

Hou, K. H. Mo, C. Xue, and L. Zhang (2020). An augmented q-factor model with expected growth. Review of Finance forthcoming.

Hou, K., C. Xue, and L. Zhang (2015). Digesting anomalies: An investment approach. Review of Financial Studies 28(3), 650 – 705.

Novy-Marx, R. (2013). The other side of value: The gross profitability premium. Journal of Financial Economics 108(1), 1 – 28.

Novy-Marx, R. (2018a). Fundamentally, momentum is fundamental momentum. Working paper.

Novy-Marx, R. (2018b). How can a q-theoretic model price momentum? Working paper.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。