稀疏性幻覺

作者：石川

摘要：早期實證資産定價研究中存在不合理(lǐ)的(de)稀疏性假設；新時(shí)代的(de)資産定價研究需直面高(gāo)維數挑戰。

1 特設稀疏性

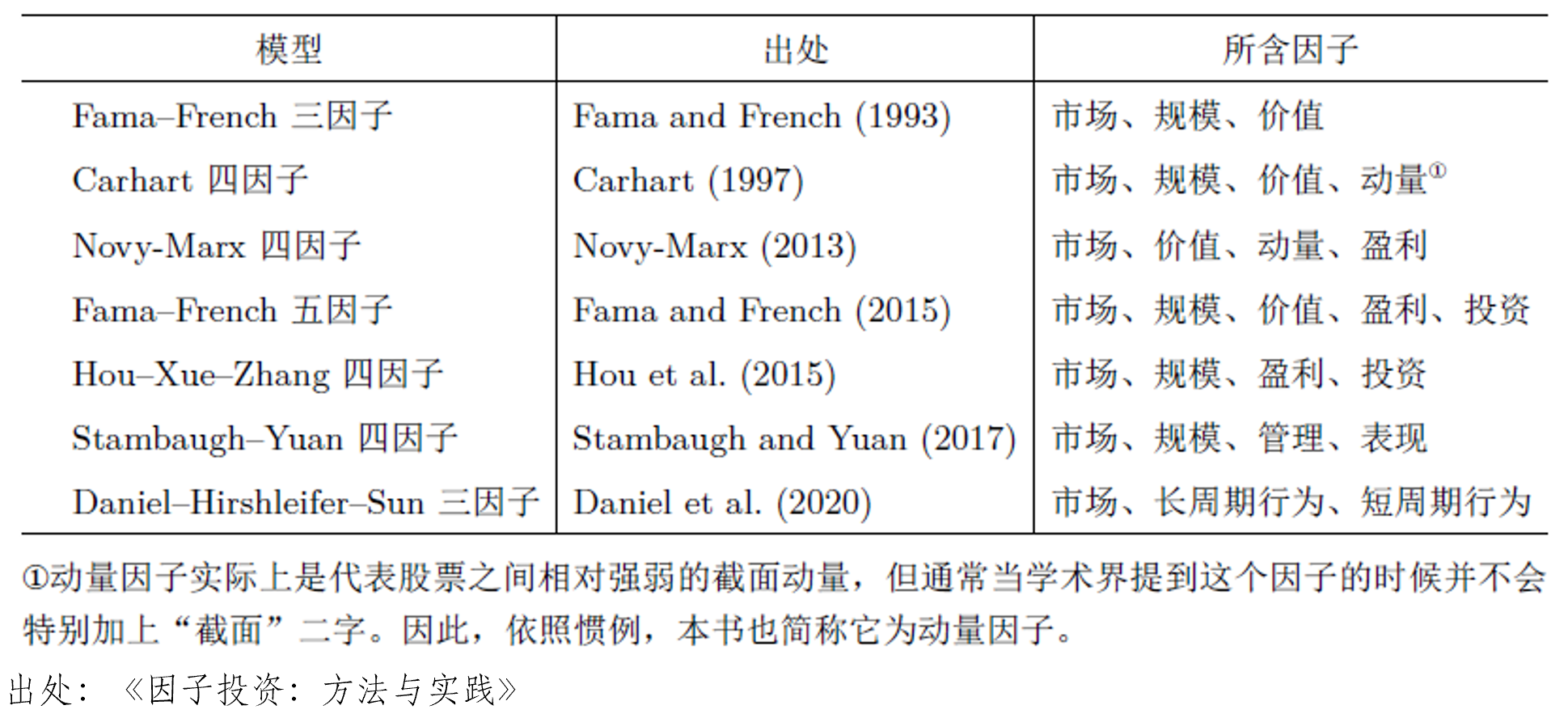
下(xià)表列出了(le)過去 30 年學術界針對(duì)股票(piào)市場(chǎng)提出的(de)主流多(duō)因子模型。讓我從它們說起。

觀察這(zhè)些模型，能夠發現它們的(de)共同之處：每個(gè)模型都僅有非常少的(de)因子（3 到 5 個(gè)）。如果把所有模型中非重複的(de)因子（不考慮計算(suàn)方法的(de)差異）都列出來(lái)，這(zhè) 7 個(gè)模型總共也(yě)就包含了(le)市場(chǎng)、規模、價值、動量、盈利、投資、管理(lǐ)、表現、長(cháng)周期行爲以及短周期行爲區(qū)區(qū) 10 個(gè)因子。它們傳遞出來(lái)的(de)觀點是：從不同的(de)動機出發，從這(zhè) 10 個(gè)因子裏選 3 到 5 個(gè)排列一下(xià)就能夠很好地解釋不同股票(piào)預期收益率的(de)截面差異。真的(de)如此嗎？

在過去 30 年中，實證資産定價的(de)研究提出了(le)成百上千個(gè)能夠預測收益率的(de)變量。比如，[量化(huà)投資與機器學習(xí)] 公衆号整理(lǐ)的(de)因子日曆介紹了(le)其中典型的(de) 300+ 個(gè)。雖然我們有理(lǐ)由對(duì) factor zoo 充滿質疑，但也(yě)無法認可(kě)區(qū)區(qū) 10 個(gè)因子（甚至更少）能夠（很好地）解釋和(hé)預測資産的(de)預期收益率。那麽，爲什(shén)麽上述主流多(duō)因子模型均隻包含了(le)不超過 5 個(gè)因子呢(ne)？要知道，每個(gè)模型背後都有一個(gè)令人(rén)信服的(de)動機（比如 DDM、行爲金融學或者 q-theory），很難想象從如此動機推出的(de)模型能夠包含太多(duō)的(de)因子，否則便難以“自圓其說”。此外，當變量太多(duō)的(de)時(shí)候，portfolio sort 難以有效構造 factor（比如 q-factor model 裏面的(de)三重排序已經是極限了(le)）。出于這(zhè)些原因，學者們紛紛在多(duō)因子模型中加入了(le) ad-hoc sparsity（特設稀疏性）。這(zhè)意味著(zhe)每個(gè)人(rén)選擇幾個(gè)因子以及哪些因子，完全是因人(rén)（動機）而異的(de)，沒有普适性可(kě)言（這(zhè)正是 ad-hoc 的(de)含義）。

然而另一方面，從模型的(de)發展曆程來(lái)看，我們也(yě)能觀察出兩點：

1. 随著(zhe)越來(lái)越多(duō)的(de) anomalies 被挖出來(lái)，多(duō)因子模型中因子個(gè)數也(yě)基本上是随時(shí)間遞增的(de)，例如 FF3 到 q-factor model 到 FF5 —— 更多(duō)的(de)因子才能解釋更多(duō)的(de) anomalies；

2. 哪怕因子的(de)個(gè)數沒有顯著增加，但用(yòng)來(lái)構造因子的(de)變量的(de)個(gè)數也(yě)得(de)到了(le)提升，例如管理(lǐ)和(hé)表現兩個(gè)因子 —— 更多(duō)的(de)變量能解釋更多(duō)的(de) anomalies。

這(zhè)兩點說明(míng)，學術界逐漸意識到越來(lái)越多(duō)的(de)（而非一隻手數得(de)過來(lái)的(de)）因子能夠幫助解釋股票(piào)預期收益率。從實證角度，我們再來(lái)看另一組佐證。Bryzgalova, Huang, and Julliard (2020) 通(tōng)過貝葉斯統計研究發現，後驗概率最高(gāo)的(de)多(duō)因子模型中均包含了(le)至少數十個(gè)因子。從後驗概率來(lái)看，上表中的(de)這(zhè)些模型離最優差了(le)“十萬八千裏”。所有實證結果都表明(míng)，在多(duō)因子模型中強加稀疏性假設，從而把定價問題變成低維問題難言合理(lǐ)。希望通(tōng)過若幹 ad-hoc 因子來(lái)解釋股票(piào)預期收益率或者 span 出更大(dà)的(de)夏普率平方，僅僅是一種稀疏性幻覺。雖然追求簡約模型本身并無不妥，但上述通(tōng)過特設稀疏性假設提出的(de)多(duō)因子模型絕非實證資産定價的(de)未來(lái)。

2 稀疏性幻覺

近日，經濟學五大(dà)頂刊之一 Econometrica 刊載了(le)一篇文章(zhāng) Giannone, Lenza, and Primiceri (2021)，研究了(le)大(dà)數據時(shí)代經濟學領域常見的(de)六大(dà)類預測問題，而股票(piào)收益率的(de) cross-section 正是其中之一。該文的(de)題目正是稀疏性幻覺（Economic predictions with big data: The illusion of sparsity）。該文通(tōng)過兩個(gè)核心變量來(lái)控制模型納入協變量的(de)概率（probability of inclusion）以及協變量參數被向先驗收縮的(de)程度（degree of shrinkage）。後面這(zhè)個(gè)很好理(lǐ)解。當變量太多(duō)以後，shrinkage 是防止過拟合的(de)有效手段。通(tōng)過貝葉斯統計，該文給出了(le)諸多(duō)非常有益的(de)定量統計推斷。

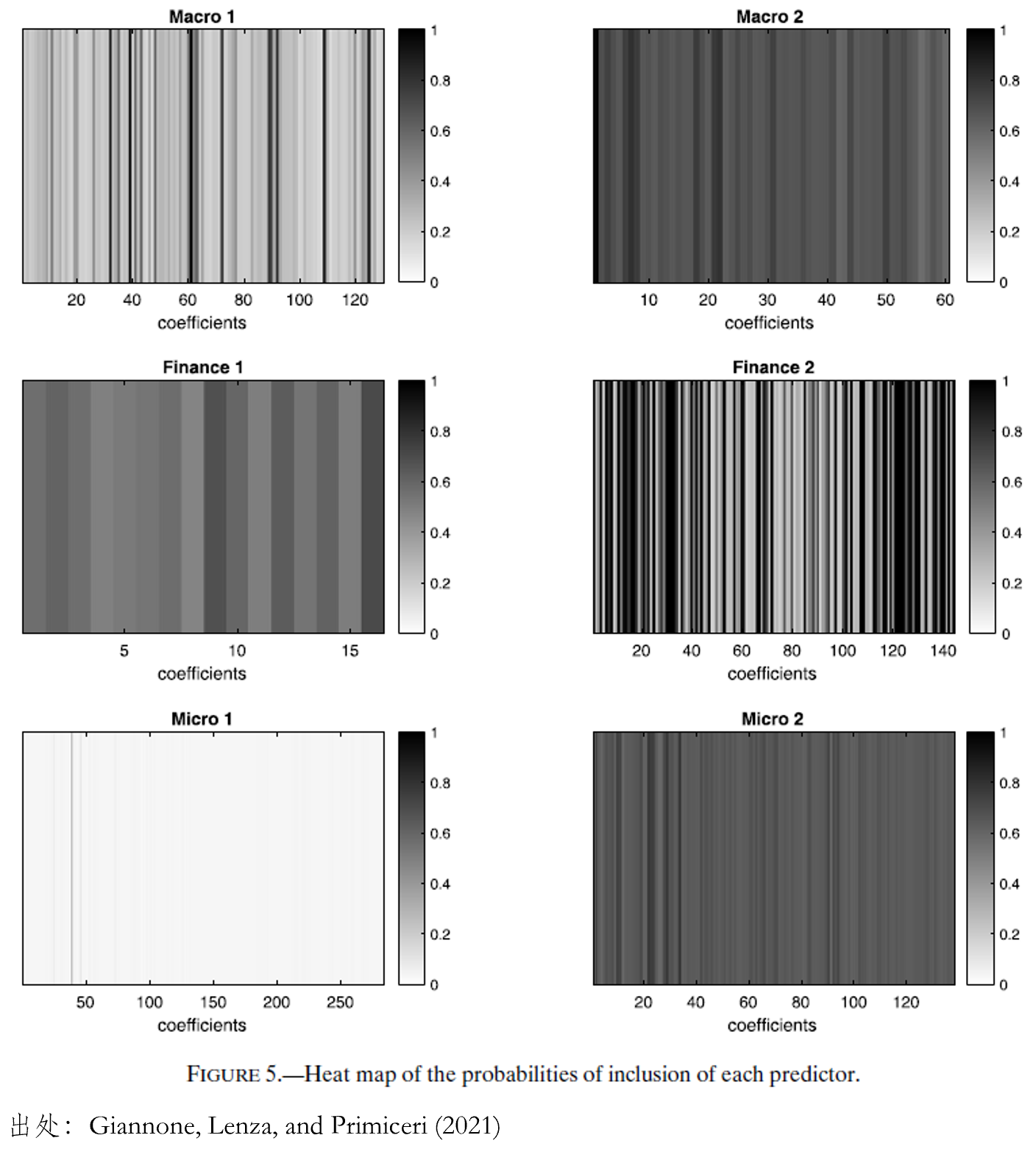
首先，probability of inclusion 和(hé) degree of shrinkage 正相關。這(zhè)是符合預期的(de)結果，即變量被納入的(de)概率越高(gāo)，收縮的(de)程度也(yě)越高(gāo)（從而防止過拟合）。其次，在五大(dà)類問題中（包括我們關心的(de)截面資産定價），probability of inclusion 的(de)取值暗示著(zhe)稀疏性假設不成立。第三，模型存在巨大(dà)的(de)不确定性，協變量之間存在不可(kě)忽視的(de)共線性，一些協變量包含了(le)相似的(de)預測性信息。下(xià)圖展示了(le)六個(gè)問題中每個(gè)協變量被納入模型的(de)概率。我們關心的(de)是标記爲 finance 2 的(de)問題，它使用(yòng) 144 個(gè)協變量預測資産收益率的(de)截面差異。從圖中不難看出，每個(gè)變量都有一定的(de)概率被納入模型。結合所有協變量的(de) overall probability of inclusion，可(kě)以進一步得(de)出的(de)結論是，在絕大(dà)多(duō)數問題中，并沒有明(míng)顯的(de)稀疏性模式，每個(gè)變量都有一定可(kě)能存在于真實的(de)模型之中。

由于巨大(dà)的(de)不确定性，爲了(le)提高(gāo)預測結果，更好的(de)做(zuò)法是同時(shí)考慮多(duō)個(gè)包含不同組協變量的(de)模型并取它們的(de)平均。這(zhè)個(gè)做(zuò)法對(duì)應著(zhe)機器學習(xí)領域的(de) ensemble methods，比如 boosting、随機森林(lín)。最後，Giannone, Lenza, and Primiceri (2021) 研究了(le)上述發現對(duì)樣本外預測意味著(zhe)什(shén)麽。結論是稀疏性 + 忽視不确定性将造成可(kě)預測性的(de)損失。摒棄稀疏性意味著(zhe)使用(yòng)更多(duō)的(de)協變量，考慮不确定性則意味著(zhe)取不同模型的(de)平均。反觀本文第一節的(de)那些多(duō)因子模型，恰恰同時(shí)占了(le)稀疏性和(hé)忽視不确定性這(zhè)兩條 —— 每個(gè)模型都僅考慮有限個(gè)且确定的(de)（源自某個(gè)動機的(de)）因子。

3 高(gāo)維數下(xià)的(de)研究挑戰

一旦知道了(le)問題，就可(kě)以尋求正确的(de)解決方法。既然稀疏性假設并不合理(lǐ)，那麽正确的(de)應對(duì)就是直面協變量（即用(yòng)來(lái)構造因子的(de)公司特征）的(de)高(gāo)維數問題。然而，如果在多(duō)因子模型 RHS 塞入太多(duō)解釋變量毫無疑問會對(duì)傳統計量經濟學帶來(lái)很大(dà)的(de)挑戰。

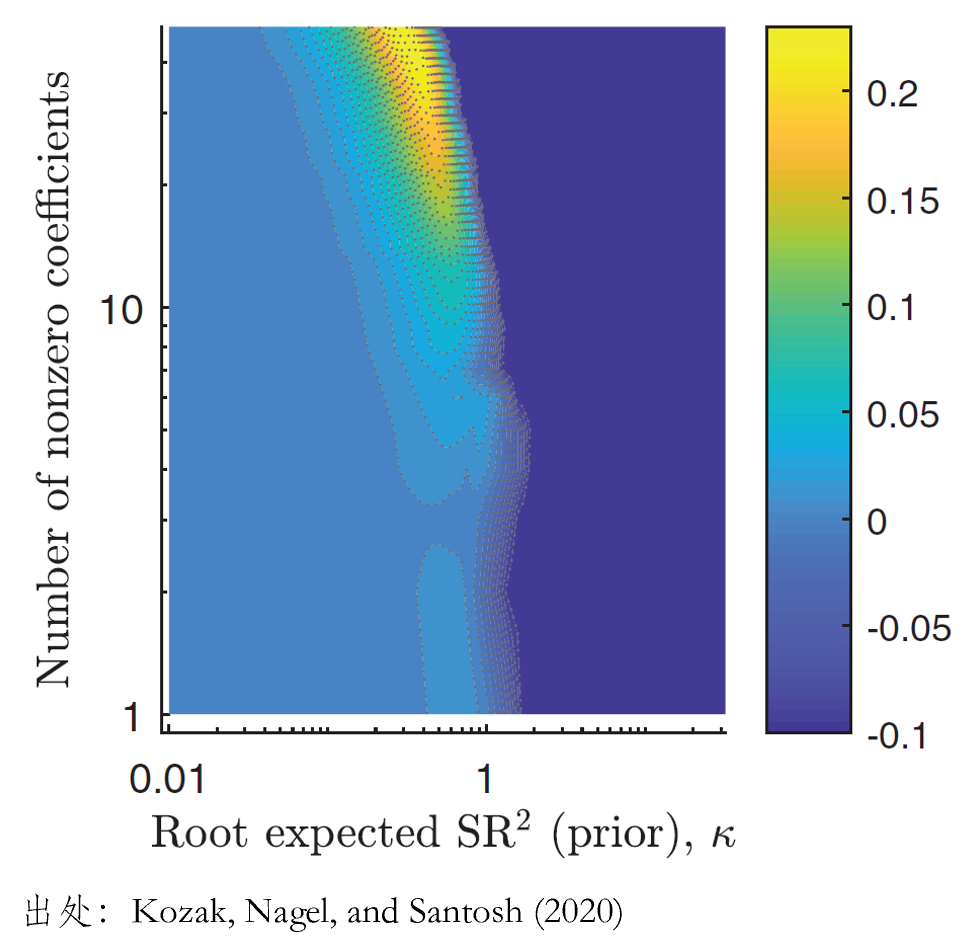
在諸多(duō)挑戰中，如何防止過拟合正是其中之一（直接用(yòng)曆史數據進行 OLS 回歸注定不會在樣本外有好的(de)結果）。在本文第二節曾提到 Giannone, Lenza, and Primiceri (2021) 的(de)發現之一是 probability of inclusion 和(hé) degree of shrinkage 正相關，即當我們使用(yòng)更多(duō)變量時(shí)，就需要對(duì)它們施以更高(gāo)程度的(de)正則化(huà)。Kozak, Nagel, and Santosh (2020) 的(de)實證結果也(yě)支持這(zhè)一觀點。假設使用(yòng) 50 個(gè)重要的(de)（且相關性較低的(de)）公司特征構造的(de) portfolios 來(lái)估計 SDF。爲了(le)獲得(de)樣本外更好的(de)預測結果，稀疏性和(hé)正則化(huà)應該滿足怎樣的(de)特性呢(ne)？下(xià)圖展示了(le) Kozak, Nagel, and Santosh (2020) 的(de)發現。

在這(zhè)個(gè) heat-map 中，顔色越亮（越發黃(huáng)）的(de)區(qū)域對(duì)應著(zhe)越高(gāo)的(de)樣本外預測性。圖中的(de)橫坐(zuò)标表示正則化(huà)的(de)強度（數值越低強度越高(gāo)）；縱坐(zuò)标表示有效協變量的(de)個(gè)數（對(duì)數軸）。結果清晰地顯示出，如果想取得(de)樣本外更好的(de)預測結果，模型需要滿足以下(xià)兩點：

1. 包含足夠多(duō)的(de)協變量（即稀疏性假設不成立）；

2. 施加必要的(de)正則化(huà)。

上述結果和(hé) Giannone, Lenza, and Primiceri (2021) 的(de)結論一緻。該實證證據是否意味著(zhe)學術界尋找簡約多(duō)因子模型的(de)執著(zhe)也(yě)是枉然呢(ne)？答(dá)案也(yě)并不是否定的(de)。當然，在關于稀疏性假設不成立的(de)如此廣泛的(de)實證證據下(xià)，我們不應再指望人(rén)爲指定有限個(gè)公司特征來(lái)構造模型，但是通(tōng)過統計手段依然可(kě)以在不損失預測信息的(de)前提下(xià)構造簡約模型。PCA 就是方法之一。

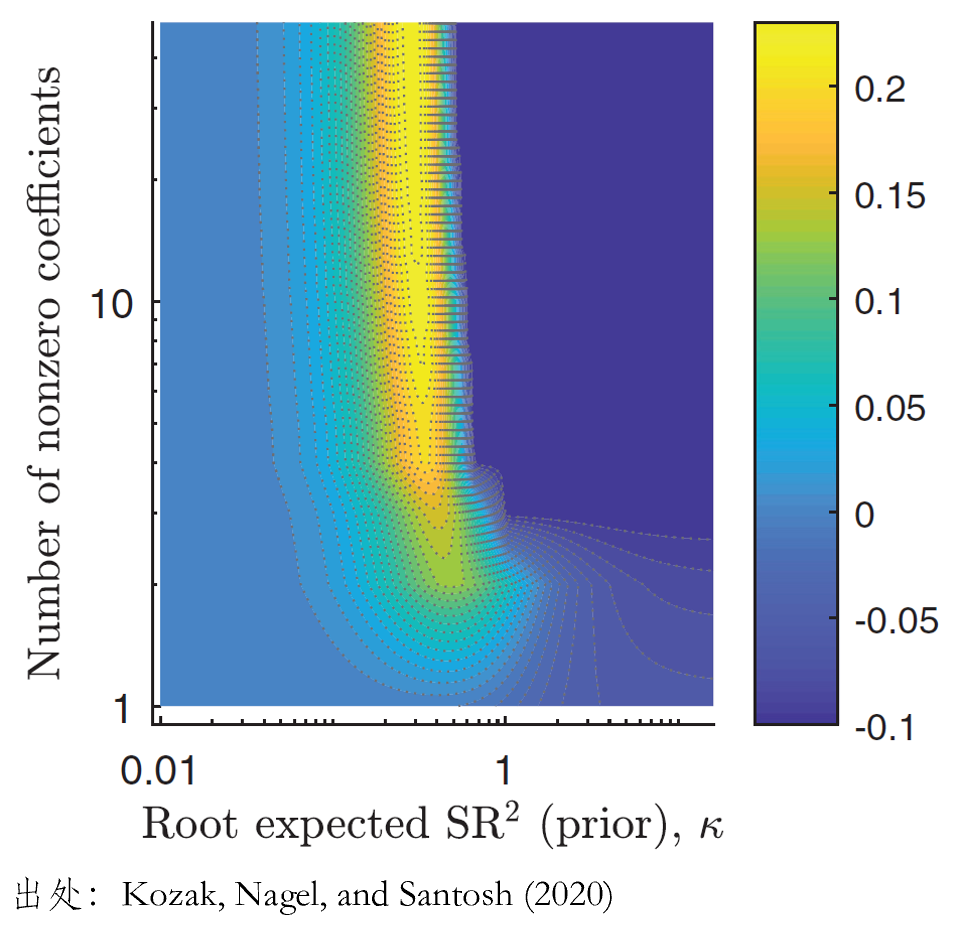
回到上面的(de)例子，對(duì) 50 個(gè)公司特征 portfolios 做(zuò) PCA 得(de)到 50 個(gè)主成分(fēn)（PC portfolios），并用(yòng)它們代替原始 portfolios 來(lái)估計 SDF。下(xià)圖展示了(le)樣本外預測性的(de)實證結果。從結果可(kě)以看出，此時(shí)我們依然需要必要的(de)正則化(huà)，但是和(hé)前面的(de)結果相比，圖中亮黃(huáng)色的(de)區(qū)域覆蓋了(le)僅有少數有效變量的(de)情況。這(zhè)意味著(zhe)，隻需要通(tōng)過有限幾個(gè)主成分(fēn)就能夠獲得(de)足夠的(de)樣本外預測性，因而實現了(le)模型的(de)簡約性。

這(zhè)一結果和(hé) Kelly, Pruitt, and Su (2019) 的(de)工具變量 PCA 不謀而合。該文對(duì)比了(le) IPCA 因子和(hé) FF5 + MOM 六因子模型。無論是 span 出來(lái)的(de)最大(dà)夏普率平方，還(hái)是非條件或條件定價誤差，IPCA 多(duō)因子模型都遠(yuǎn)勝 FF5 + MOM 六因子模型。PCA 的(de)成功可(kě)以歸結爲兩點：（1）Kozak, Nagel, and Santosh (2018) 指出能夠解釋截面預期收益率差異的(de)因子必須和(hé)資産收益率的(de)協方差矩陣密切相關 —— 這(zhè)爲近幾年來(lái)基于 PCA 方法的(de)研究奠定了(le)堅實的(de)基礎；（2）PCA 有效的(de)将大(dà)量公司特征代表的(de)預測性信息降維到有限幾個(gè)因子之中（而非出于某種動機人(rén)爲的(de)選擇幾個(gè)變量）。這(zhè)兩點缺一不可(kě)。

本節的(de)討(tǎo)論說明(míng)，未來(lái)的(de)實證資産定價應放棄稀疏性幻覺，并緻力于解決如何從大(dà)量潛在高(gāo)度相關但卻都對(duì)預測收益率有幫助的(de)協變量之中提取預測性信息，以期使得(de)投資組合在樣本外獲得(de)更優異的(de)風險收益特征。這(zhè)正是高(gāo)維數下(xià)的(de)研究挑戰。在這(zhè)方面，機器學習(xí)算(suàn)法也(yě)許比傳統計量經濟學手段更有前景。Giglio, Kelly, and Xiu (2021) 梳理(lǐ)了(le)近年來(lái)機器學習(xí)、資産定價以及因子模型方面的(de)進展，勾勒了(le)研究的(de)藍圖。

然而有必要指出的(de)是，off-the-shelf 機器學習(xí)算(suàn)法本身不太可(kě)能在金融領域取得(de)成功；在使用(yòng)機器學習(xí)算(suàn)法的(de)過程中，通(tōng)過必要的(de)手段注入金融學先驗對(duì)于其發揮最大(dà)作用(yòng)至關重要。（明(míng)年公衆号将會介紹更多(duō)這(zhè)方面的(de)前沿進展。）此外，在高(gāo)維環境中，由于 investor high-dimensional learning 引入的(de)樣本内虛假可(kě)預測性也(yě)是需要在研究中面對(duì)和(hé)解決的(de)難題（Martin and Nagel 2021）。

最後，讓我以 Giannone, Lenza, and Primiceri (2021) 的(de)結論結束本文。

In economics, there is no theoretical argument suggesting that predictive models should in general include only a handful of predictors. … The empirical support for low-dimensional models is generally weak. Even when it appears stronger, economic data are not informative enough to uniquely identify the relevant predictors when a large pool of variables is available to the researcher.

參考文獻

• Bryzgalova, S., J. Huang, and C. Julliard (2020). Bayesian solutions for the factor zoo: We just run two quadrillion models. Working paper.

• Giannone, D., M. Lenza, and G. E. Primiceri (2021). Economic predictions with big data: The illusion of sparsity. Econometrica 89(5), 2409 – 2437.
  

• Giglio, S., B. T. Kelly, and D. Xiu (2021). Factor models, machine learning, and asset pricing. Working paper.
  

• Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.
  

• Kozak, S., S. Nagel, and S. Santosh (2018). Interpreting factor models. Journal of Finance 73(3), 1183 – 1223.
  

• Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.
  

• Martin, I. and S. Nagel (2021). Market efficiency in the age of big data. Journal of Financial Economics forthcoming.
  

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。