主動風險預算(suàn)初探

作者：石川

摘要：主動風險預算(suàn)策略需要加入人(rén)爲的(de)判斷。這(zhè)個(gè)判斷需要針對(duì)未來(lái)建模、而非針對(duì)曆史拟合，方能有效。

1 風險平價和(hé)風險預算(suàn)

前文《你真的(de)搞懂(dǒng)了(le)風險平價嗎？》指出當投資品的(de)收益率之間獨立，且夏普率相同時(shí)，等風險投資組合（equally-weighted risk contributions portfolio，簡稱 EWRCP）實際上就是在最大(dà)化(huà)投資組合的(de)夏普率。在實際投資中，風險平價策略一般被用(yòng)來(lái)做(zuò)大(dà)類資産配置（如股票(piào)、債券、商品等），而這(zhè)些不同大(dà)類的(de)投資品之間相關性先天較低，因此 EWRCP 模型的(de)第一個(gè)假設 —— 投資品收益率獨立可(kě)算(suàn)是勉強滿足。但是該模型的(de)第二個(gè)假設 —— 不同投資品的(de)夏普率相同，往往和(hé)實際情況相左。考慮到這(zhè)個(gè)問題，可(kě)以将風險平價改成風險預算(suàn)（risk budgeting）。具體的(de)，我們不把投資組合的(de)風險平均的(de)分(fēn)配在不同大(dà)類的(de)投資品間，而是按照(zhào)它們的(de)夏普率的(de)平方來(lái)分(fēn)配風險，簡稱 SSWRCP（Sharpe Ratio-squared-weighted risk contributions portfolio）。

令 Σ 表示投資品的(de)協方差矩陣、SR_i = μ_i/σ_i 表示投資品 i 的(de)夏普率、σ_p 表示投資組合的(de)波動率、ω 爲投資組合的(de)權重向量。很容易證明(míng)（如下(xià)圖推導），當投資品相互獨立時(shí)（協方差矩陣是對(duì)角陣），根據夏普率平方分(fēn)配風險得(de)到的(de)投資組合（即 SSWRCP）也(yě)正是在最大(dà)化(huà)組合的(de)夏普率。

由上述推導可(kě)知，SSWRCP 的(de)最優解中，投資品的(de)權重 ω_i 和(hé) μ_i/(σ_i)^2 成正比，而這(zhè)個(gè)比例正是大(dà)名鼎鼎的(de)凱利準則（Kelly Criterion）。在投資品相互獨立的(de)假設下(xià)，按此權重配置每個(gè)投資品保證了(le)投資組合的(de)夏普率最大(dà)。

2 主動風險預算(suàn)

在使用(yòng) SSWRCP 時(shí)，一個(gè)重要的(de)假設是投資品的(de)夏普率已知。然而，事後（ex-post）夏普率是無法預測的(de)，我們能夠使用(yòng)的(de)隻有事前（ex-ante）夏普率，即根據曆史數據計算(suàn)出每個(gè)投資品的(de)（超額）收益率和(hé)波動率，再計算(suàn)出夏普率。

縱觀各大(dà)類投資品，它們的(de)表現都有周期。當經濟環境不利于該類資産時(shí)，它會出現持續的(de)下(xià)跌。如果在計算(suàn)事前夏普率的(de)時(shí)間窗(chuāng)口内某投資品的(de)收益率均值爲負，那麽得(de)到的(de)夏普率也(yě)是負數。顯然，沒有任何道理(lǐ)将這(zhè)樣一個(gè)投資品輸入到 SSWRCP 中，因此隻能暫時(shí)把它排除在外，而這(zhè)事實上引入了(le)擇時(shí)。我們稱加入了(le)擇時(shí)的(de)風險預算(suàn)爲主動風險預算(suàn)（active risk budgeting）。

主動風險預算(suàn)通(tōng)過擇時(shí)旨在規避不同類投資品連續下(xià)跌的(de)風險，它的(de)假設是過去的(de)下(xià)跌趨勢會延續。但是，一旦擇時(shí)錯誤，它也(yě)會錯失掉投資品反彈帶來(lái)的(de)上漲。此外，較買入持有策略，任何擇時(shí)都引入了(le)額外的(de)不确定性。對(duì)于投資組合來(lái)說，該不确定性能否會貢獻 α 是一個(gè)未知數。下(xià)文對(duì)主動風險預算(suàn)做(zuò)一些簡單的(de)實證初探。

3 構建投資策略

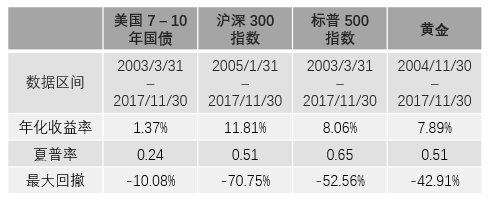
我們選擇滬深 300 指數（A）、美(měi)國 7-10 年國債（IEF）、标普 500 指數（SPX）和(hé)黃(huáng)金（GLD）作爲投資标的(de)，數據區(qū)間和(hé)投資品的(de)表現如下(xià)表所示。整個(gè)回測期從 2003 年 3 月(yuè) 31 日至 2017 年 11 月(yuè) 30 日。

對(duì)于主動風險預算(suàn)策略，構建如下(xià)：

由上述說明(míng)可(kě)知，根據投資組合的(de)約束條件不同，我們有兩個(gè)版本的(de)主動風險預算(suàn)策略。爲了(le)檢查主動風險預算(suàn)的(de)效果，我們将該策略和(hé)簡單多(duō)樣化(huà)策略（也(yě)考慮兩個(gè)版本）比較。在簡單多(duō)樣化(huà)策略不做(zuò)任何擇時(shí)，按資金量對(duì)所有可(kě)交易的(de)投資品等權配置。以上策略中，均不考慮交易成本。下(xià)面就來(lái)看看實證結果。

4 實證結果

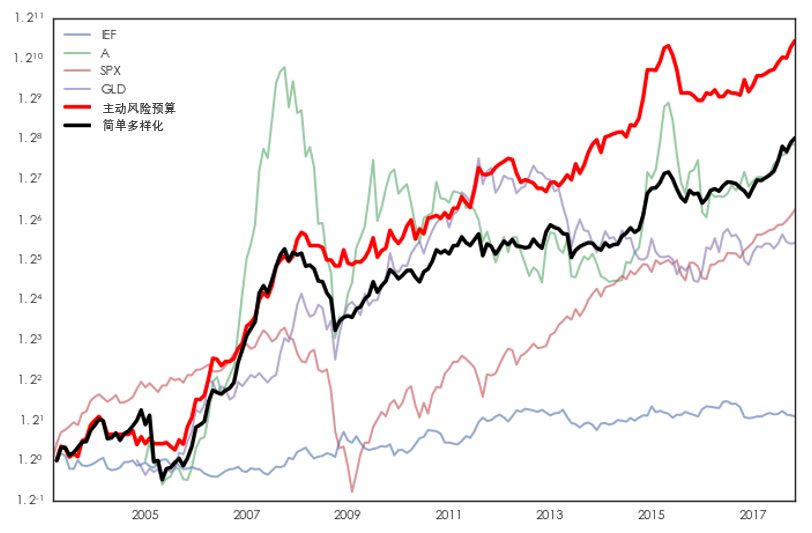
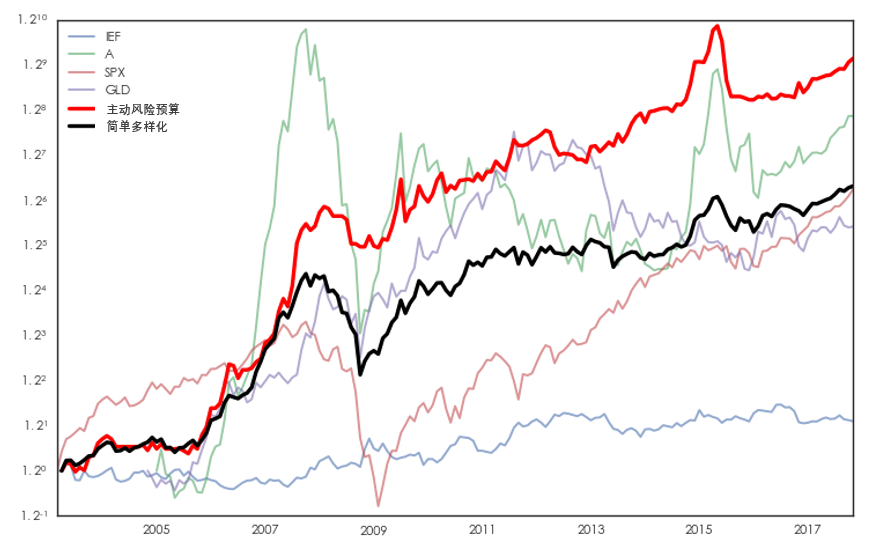
首先來(lái)看在第一種約束條件下(xià) —— 即投資組合的(de)月(yuè)收益波動率爲 4% —— 兩個(gè)策略的(de)比較。下(xià)圖展示了(le)兩個(gè)策略（紅色粗實線爲主動風險預算(suàn)、黑(hēi)色粗實線爲簡單多(duō)樣化(huà)）的(de)淨值比較，以及四種标的(de)投資品。

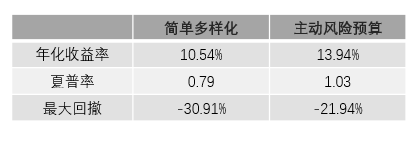
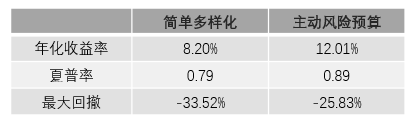
這(zhè)兩個(gè)策略的(de)具體收益、風險數據如下(xià)表所示。

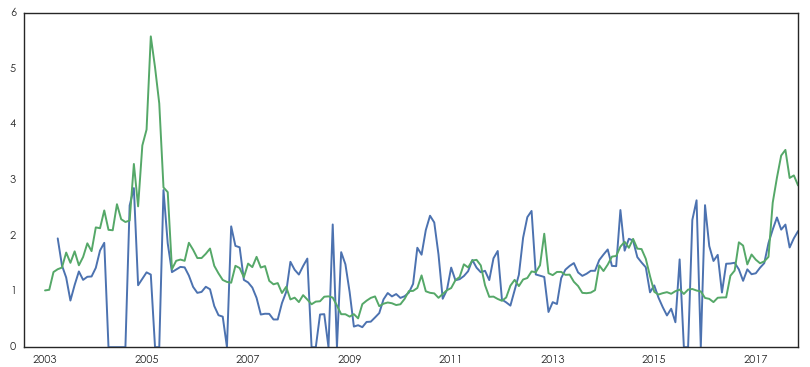
該結果說明(míng)，無論從收益率、夏普率還(hái)是最大(dà)回撤來(lái)說，主動風險預算(suàn)策略都戰勝了(le)簡單多(duō)樣化(huà)。但是，我們不能忽視另外一個(gè)因素：杠杆的(de)應用(yòng)。下(xià)圖顯示了(le)這(zhè)兩個(gè)策略在回測期内杠杆随時(shí)間的(de)變化(huà)（藍色爲主動風險預算(suàn)；綠色爲簡單多(duō)樣化(huà)）：

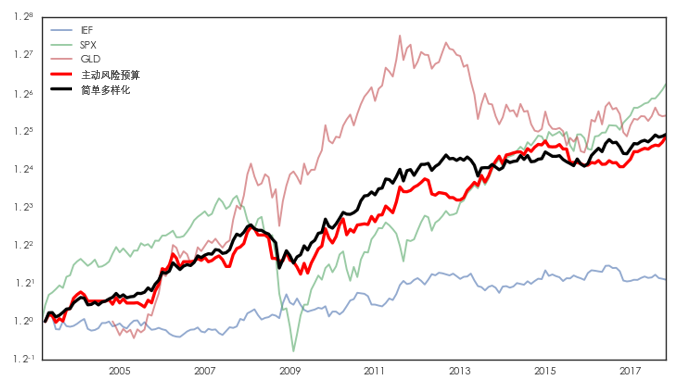
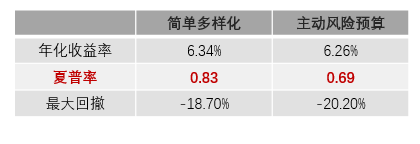
不難看出，上面兩個(gè)策略都需要使用(yòng)杠杆。在回測期的(de)很多(duō)時(shí)間段，它們的(de)杠杆率都超過 1，而上面的(de)實證假設了(le)加杠杆是不需要成本的(de)，這(zhè)顯然是不合理(lǐ)的(de)。假設我們不能加杠杆，即考慮第二種約束條件 —— 要求每期都滿倉配置。在該條件下(xià)，兩種策略的(de)表現如下(xià)：

從夏普率來(lái)看，去杠杆對(duì)簡單多(duō)樣化(huà)策略并沒有影(yǐng)響，但是卻顯著的(de)降低了(le)主動風險預算(suàn)的(de)夏普率（雖然它仍然優于簡單多(duō)樣化(huà)策略）。雖然主動風險預算(suàn)策略在兩種不同的(de)約束條件下(xià)都戰勝了(le)簡單多(duō)樣化(huà)，但我們必須意識到的(de)是由于 A 股的(de)存在（滬深 300）以及它的(de)兩撥極其鮮明(míng)的(de)牛熊市，任何擇時(shí)策略隻要牛市抓得(de)好、熊市跑得(de)快(kuài)，那它就不會太差。而主動風險預算(suàn)策略較簡單多(duō)樣化(huà)而言無疑占了(le)先手。如果我們去掉滬深 300 指數，僅考慮其他(tā)三個(gè)投資标的(de)，則在不考慮杠杆的(de)情況下(xià)，這(zhè)兩個(gè)策略的(de)表現如下(xià) —— 簡單多(duō)樣化(huà)好于主動風險預算(suàn)，主動的(de)擇時(shí)并沒有帶來(lái)主動的(de) α。

5 任重道遠(yuǎn)

風險平價（以及由此衍生出來(lái)的(de)風險預算(suàn)）源于橋水(shuǐ)基金的(de)全天候策略。該策略的(de)出發點是不預測未來(lái)的(de)經濟環境。本文研究的(de)主動風險預算(suàn)中，基于曆史數據對(duì)未來(lái)進行了(le)擇時(shí)，假設未來(lái)可(kě)以延續曆史。從結果來(lái)看，它能跑赢簡單多(duō)樣化(huà)多(duō)少占了(le) A 股的(de)便宜，并不令人(rén)信服。反觀簡單多(duō)樣化(huà)，由于它不擇時(shí)、對(duì)曆史無拟合，無疑在樣本外适應性更強。

任何“主動”策略都需要加入人(rén)爲的(de)判斷。這(zhè)個(gè)判斷需要針對(duì)未來(lái)建模、而非針對(duì)曆史來(lái)拟合。在《你真的(de)搞懂(dǒng)了(le)風險平價嗎？》，我們在假設已知投資品事後夏普率下(xià)，說明(míng)了(le) SSWRCP 的(de)有效性。因此，在實際投資中，應考慮從經濟學的(de)邏輯出發對(duì)不同投資品的(de)未來(lái)收益風險情況進行分(fēn)析。在國内券商的(de)最新報告中，我們看到有一些類似的(de)分(fēn)析，并将分(fēn)析結果結合 Black-Litterman 模型（見《Black-Litterman 模型 —— 貝葉斯框架下(xià)的(de)資産配置利器》）進行風險預算(suàn)，取得(de)了(le)不錯的(de)效果。在今後的(de)文章(zhāng)中，我們也(yě)會對(duì)這(zhè)方面做(zuò)一些探討(tǎo)。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。