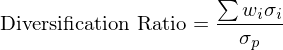還(hái)在對(duì)著(zhe)一階矩做(zuò)因子擇時(shí)？不妨試試二階矩

作者：石川

摘要：Fergis et al. (2019) 提出防禦性因子擇時(shí)，使用(yòng)三個(gè)維度的(de)擇時(shí)指标，有效降低因子投資組合在極端市場(chǎng)環境下(xià)的(de)風險。

1 引言

因子擇時(shí)（factor timing）是進行因子投資的(de)人(rén)繞不過的(de)課題，但如何擇時(shí)才能在樣本外取得(de)更好的(de)效果尚無定論。然而，這(zhè)絲毫不影(yǐng)響人(rén)們對(duì)因子擇時(shí)的(de)熱(rè)情，無論是學術界還(hái)是業界都對(duì)它進行了(le)大(dà)量的(de)實證研究。究其原因，隻因擇時(shí)成功能帶來(lái)的(de)收益太誘人(rén)。

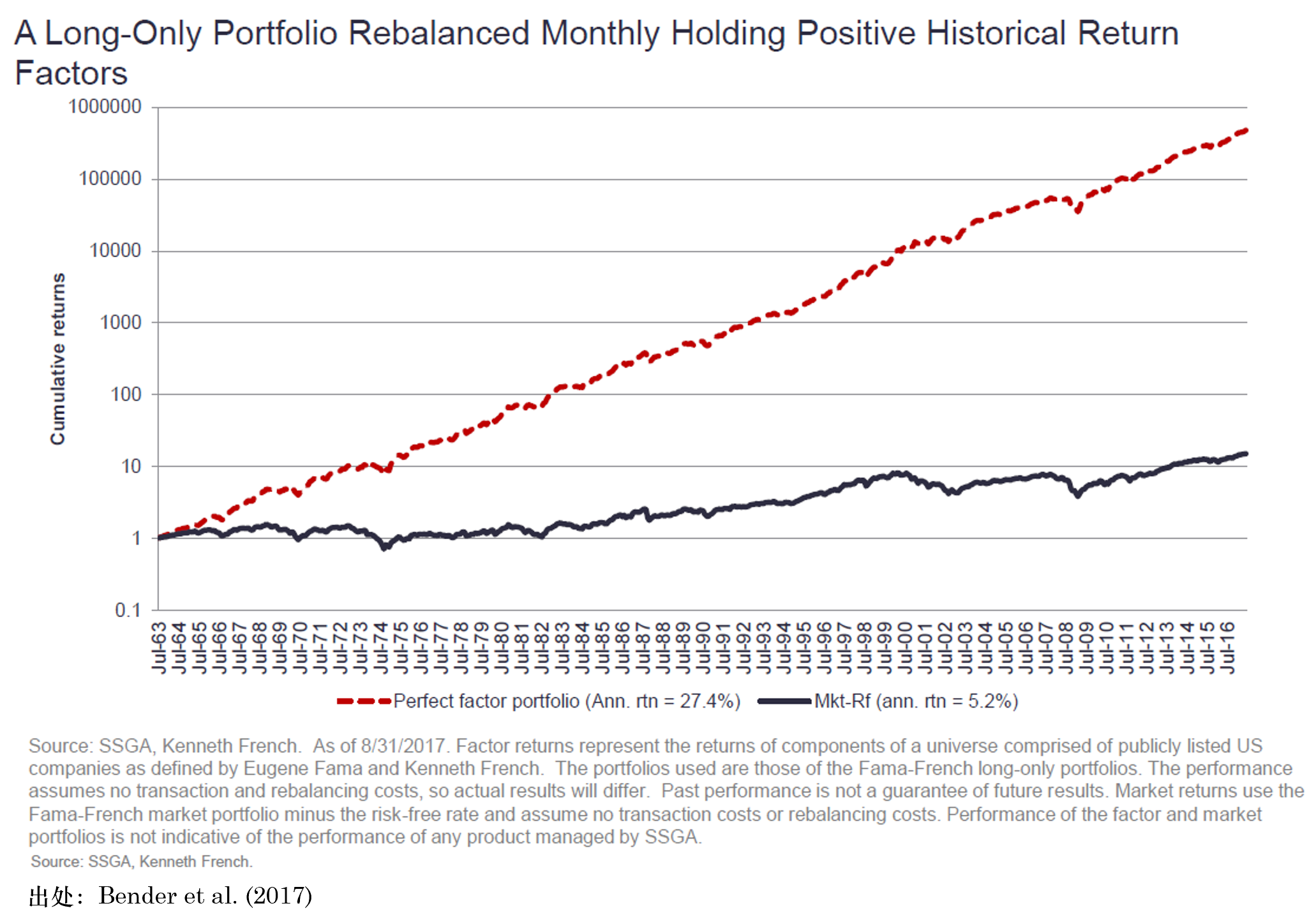
在 2017 年 Jacobs Levy Center 的(de)年會上，來(lái)自 State Street Global Advisors 的(de) Jennifer Bender 做(zuò)了(le)題爲 The promises and pitfalls of factor timing 的(de)報告（Bender et al. 2017）。下(xià)圖正是來(lái)自該報告，它假想了(le)在開天眼前提下(xià)，正确的(de)因子擇時(shí)（每次調倉時(shí)正确挑出下(xià)一期收益最高(gāo)的(de)因子）能夠獲得(de)的(de)超高(gāo)收益。

這(zhè)篇報告後被發表于 2018 年度 Journal of Portfolio Management（JPM）的(de) Quantitative Special Issue（Bender et al. 2018）。就因子擇時(shí)這(zhè)個(gè)問題，Bender et al. (2017, 2018) 是來(lái)自業界的(de)比較客觀的(de)聲音(yīn)，值得(de)仔細讀一讀。不過，它并不是本文的(de)重點，所以對(duì)它的(de)介紹到此結束。

在介紹本文的(de)重點之前，再來(lái)看看兩位大(dà)佬掐架（熟悉這(zhè)段的(de)朋友請跳過）：來(lái)自 Research Affiliates 的(de) Robert Arnott 以及來(lái)自 AQR 的(de) Cliff Asness。自 2016 年以來(lái)，Robert Arnott 發表了(le)一系列因子擇時(shí)的(de)文章(zhāng)，題目都非常“嚣張”，比如 Timing 'Smart Beta' Strategies? Of Course! Buy Low, Sell High!（Arnott et al. 2016）和(hé) Forecasting Factor and Smart Beta Returns (Hint: History Is Worse than Useless)（Arnott et al. 2017）。Arnott 提倡使用(yòng)因子估值（factor valuation）來(lái)擇時(shí) —— 當因子便宜的(de)時(shí)候配置、當因子昂貴的(de)時(shí)候擱置。Arnott 通(tōng)過實證結果證明(míng)了(le)其主張在主流的(de)因子上都是有效的(de)。

針對(duì)按估值進行因子擇時(shí)是否靠譜這(zhè)個(gè)問題，我和(hé)合夥人(rén)進行了(le)激烈的(de)探討(tǎo)，最後得(de)到的(de)看法是：在便宜時(shí)候配置因子等價于在整個(gè)多(duō)因子組合中提高(gāo)了(le)對(duì)價值因子的(de)暴露；因爲價值因子是有效的(de)，因此如此“擇時(shí)”自然有效。一旦未來(lái)價值因子失效，那麽這(zhè)種擇時(shí)法會因爲在其上的(de)過高(gāo)暴露而受損。因此，按估值擇時(shí)是否合理(lǐ)、怎麽才能更好的(de)規避在價值因子上的(de)暴露是需要進一步研究的(de)問題。如果說 Arnott et al. (2016) 這(zhè)篇文章(zhāng)隻是抛出了(le)估值擇時(shí)說，那麽 Arnott et al. (2017) 則更是使用(yòng)了(le) History is worse than useless 這(zhè)樣刺眼的(de)标題直接抨擊了(le)因子擇時(shí)中的(de)另一思路 —— 按因子動量擇時(shí)：

Selecting strategies or factors based on past performance, regardless of the length of the sample, will not help investors earn a superior return and is actually more likely to hurt them. —— Arnott et al. (2017)

面對(duì)如此“挑釁”，另一位大(dà)佬 Asness 坐(zuò)不住了(le)，他(tā)在多(duō)個(gè)場(chǎng)合多(duō)次抨擊了(le) Arnott 的(de)觀點。在 2017 年，Asness 領銜在 JPM 上發表了(le)一篇題爲 Contrarian Factor Timing is Deceptively Difficult（Asness et al. 2017） 的(de)文章(zhāng)，回擊了(le)因子估值擇時(shí)。該文的(de)論點之一也(yě)是估值擇時(shí)有效本質是因爲價值因子有效：

At first glance, valuation-based timing of styles appears promising, which is not surprising because it is a simple consequence of the efficacy of the value strategy itself. Yet when the authors implement value timing in a multi-style framework that already includes the value style, they find somewhat disappointing results. Because value timing of factors is correlated to the standard value factor, it adds further value exposure.

除此之外，在 JPM 2019 年度最新一期的(de) Quantitative Special Issue 上（全刊爲因子投資專題），來(lái)自 AQR 的(de) Tarun Gupta 和(hé) Bryan Kelly 發表了(le)一篇題爲 Factor Momentum Everywhere 的(de)文章(zhāng)，指出在全球的(de) 65 個(gè)選股因子上觀察到了(le)穩健的(de)動量效應、通(tōng)過動量擇時(shí)可(kě)以顯著提高(gāo)收益：

Factor momentum adds significant incremental performance to investment strategies that employ traditional momentum, industry momentum, value, and other commonly studied factors.

這(zhè)篇文章(zhāng)雖然不直接出自 Asness，但畢竟也(yě)是 AQR 出品，并作爲 JPM 2019 因子投資特刊的(de)首篇文章(zhāng)被放在了(le)最醒目的(de)位置，足見其地位。至于 Asness 怒怼 Arnott 的(de)其他(tā)故事，我的(de)好友徐楊在《多(duō)因子策略的(de)五大(dà)討(tǎo)論》中有過生動的(de)描述，頗爲精彩。毫無疑問，因子擇時(shí)在因子投資中争議(yì)巨大(dà)。但本文無意加入這(zhè)場(chǎng)争論，而是想介紹 JPM 2019 因子投資特刊中的(de)另外一篇文章(zhāng) —— Defensive factor timing（防禦性因子擇時(shí)，下(xià)稱 DFT）。

2 防禦性因子擇時(shí)

無論是根據估值還(hái)是動量做(zuò)因子擇時(shí)，其核心都是想獲得(de)更高(gāo)的(de)收益。較簡單多(duō)樣化(huà)或風險平價等配置因子的(de)方法，這(zhè)些方法的(de)難點在于必須判斷因子收益率的(de)一階矩 —— 期望。然而外推猜收益談何容易？正因如此，來(lái)自 BlackRock 的(de)團隊“另辟蹊徑”，提出了(le)防禦性因子擇時(shí)（Fergis et al. 2019）。它正是本節以及後面兩小節要介紹的(de)内容。防禦性因子擇時(shí)的(de)目的(de)是降低風險。與一般的(de)因子擇時(shí)預測因子收益率不同，DFT 關注的(de)是因子收益率的(de)二階矩及高(gāo)階矩，即風險。當市場(chǎng)整體風險偏好驟降、不同因子之間相關性顯著上升、以及單因子變得(de)極度昂貴時(shí)，防禦性因子擇時(shí)主動降低因子投資組合的(de)倉位，以此減少資産損失。Fergis et al. (2019) 同時(shí)指出，由于防禦性因子擇時(shí)的(de)目的(de)是規避巨大(dà)的(de)市場(chǎng)風險，因此它對(duì)于因子投資組合倉位的(de)調整也(yě)注定是一個(gè)低頻(pín)事件。

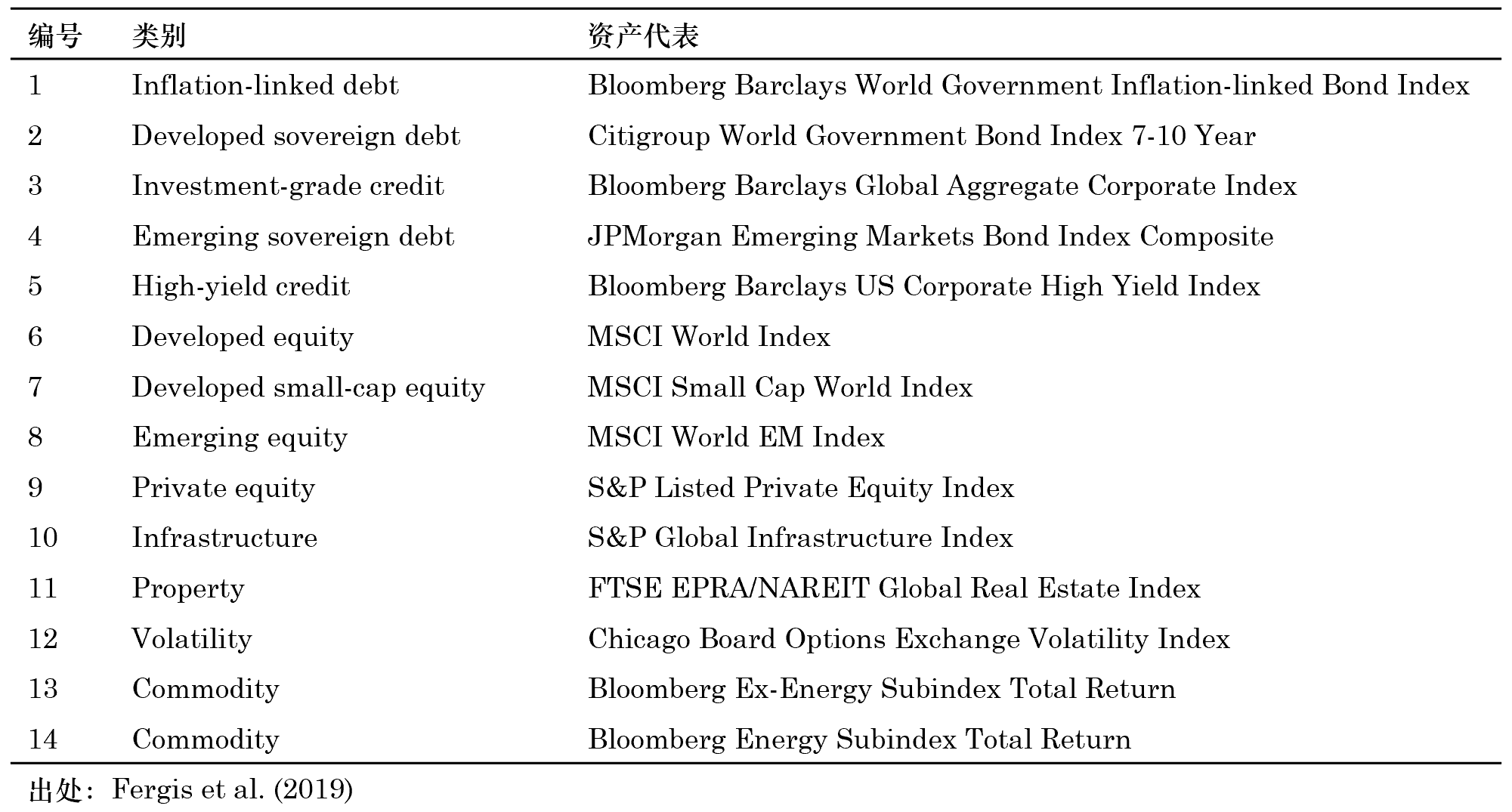
Fergis et al. (2019) 的(de)另外一個(gè)不同之處是，它關注的(de)不單單是我們常說的(de)股票(piào)市場(chǎng)中的(de)因子（本文第一節中提到的(de)那些文獻以及大(dà)佬掐架針對(duì)的(de)也(yě)主要是股票(piào)中的(de)風格因子）。相反的(de)，Fergis et al. (2019) 著(zhe)眼于不同類資産（股票(piào)、債券、商品、房(fáng)地産等）所暴露在的(de)風險因子上。具體的(de)，Fergis et al. (2019) 一文考慮了(le) 14 類資産：

如何确定這(zhè)些不同類資産所背後共同的(de)因子呢(ne)？最直接的(de)辦法是進行 PCA。考慮到通(tōng)過統計手段找到的(de)因子缺乏必要的(de)經濟學解釋，Fergis et al. (2019) 追随 Chen, Roll and Ross (1986) 的(de)思路、選用(yòng)宏觀經濟指标作爲這(zhè)些資産所面對(duì)的(de)共同風險因子。這(zhè)些指标包括：經濟增長(cháng)、實際利率、通(tōng)脹、信貸、新興市場(chǎng)以及流動性。使用(yòng)宏觀經濟因子的(de)好處是：

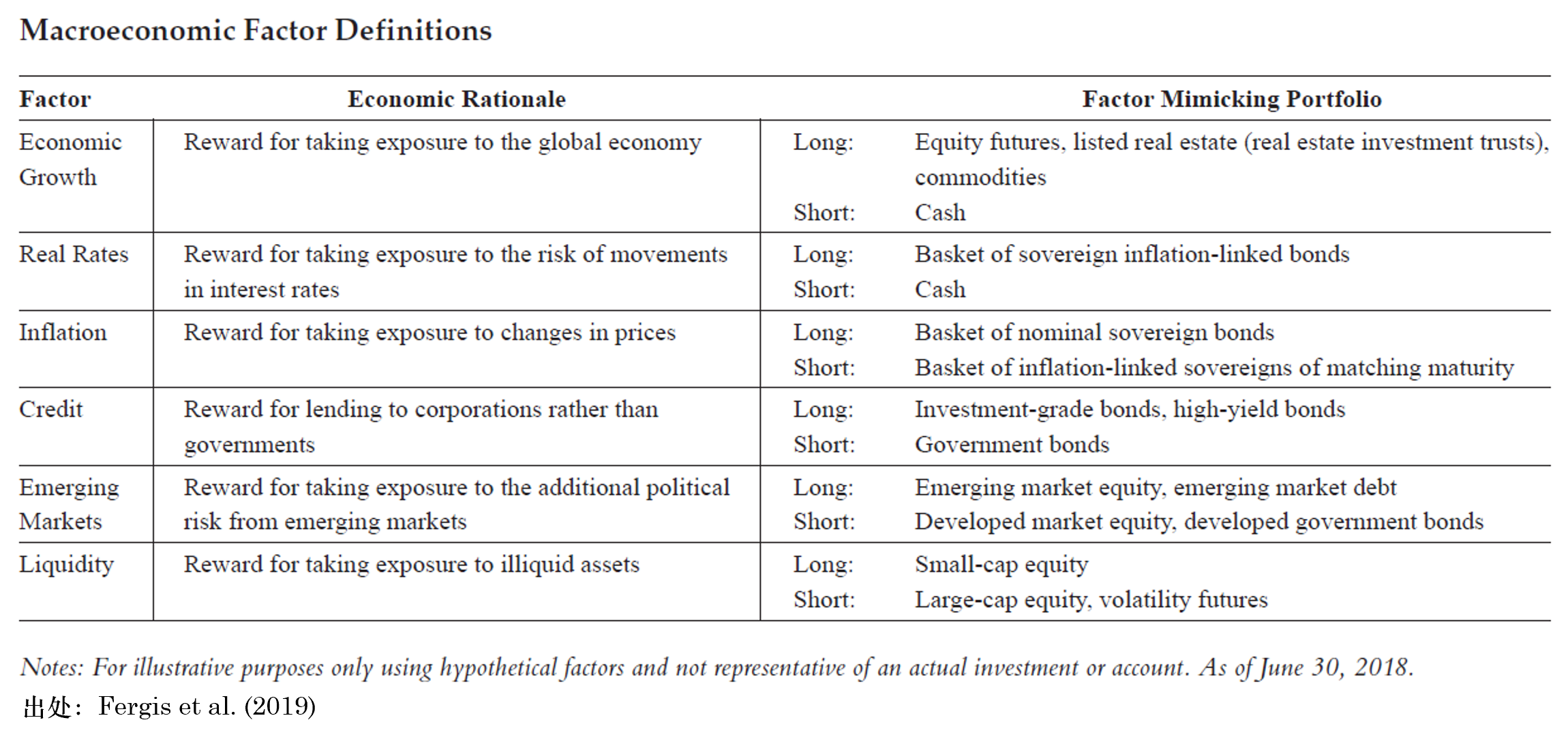
然而，使用(yòng)宏觀經濟因子必須面對(duì)的(de)一個(gè)問題是這(zhè)些因子的(de)風險以及收益是無法直接被觀測到的(de)（比如我們沒法說 GDP 增長(cháng)的(de)收益是多(duō)少）。爲了(le)解決這(zhè)個(gè)難題，就不得(de)不請出因子投資中的(de)一個(gè)重要概念：Factor Mimicking Portfolio。當風險因子是諸如宏觀經濟指标的(de)時(shí)候，由于無法直接衡量其波動或者收益，需要使用(yòng)适當的(de)資産構建出一個(gè)多(duō)、空對(duì)沖的(de)投資組合，使其在該因子上的(de)暴露最純粹，并利用(yòng)這(zhè)個(gè)投資組合的(de)收益率和(hé)波動來(lái)衡量該因子的(de)風險和(hé)收益。這(zhè)個(gè)投資組合就稱爲 factor mimicking portfolio。針對(duì)六大(dà)宏觀經濟因子，Fergis et al. (2019) 構建的(de) factor mimicking portfolios 如下(xià)。

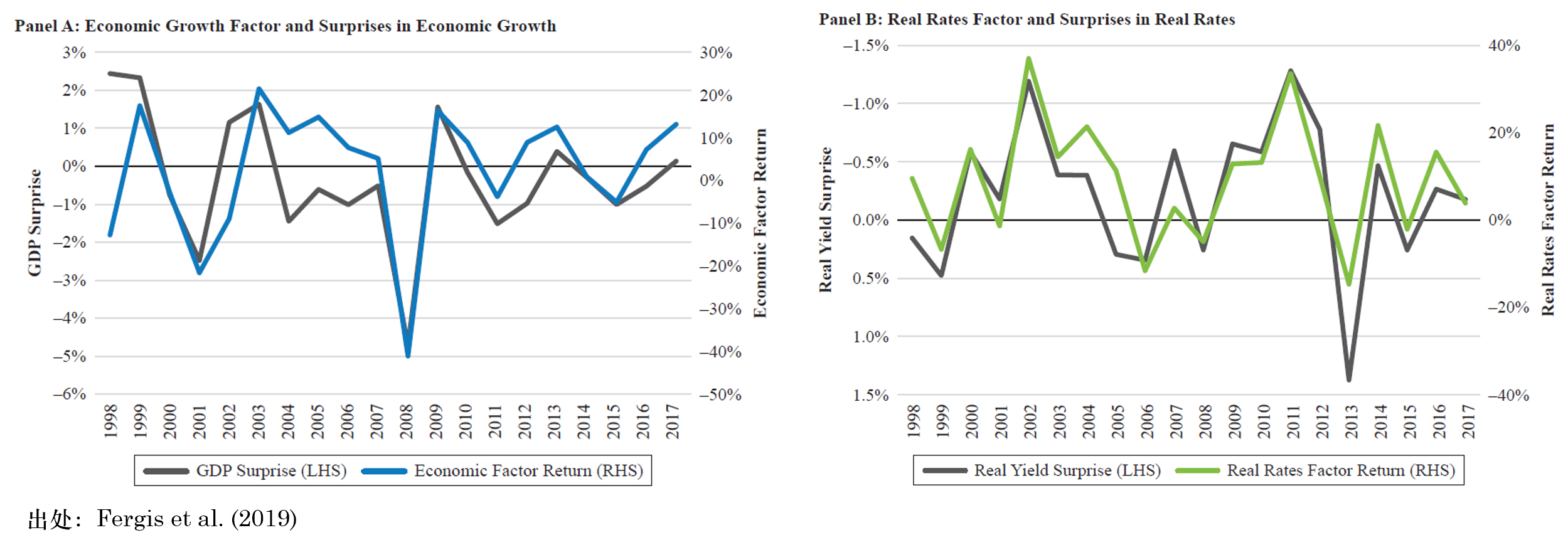
下(xià)圖顯示了(le)經濟增長(cháng)和(hé)實際利率兩個(gè)宏觀經濟因子和(hé)它們各自的(de) factor mimicking portfolios 在時(shí)序上的(de)相關性。不難看出，factor mimicking portfolios 很好的(de)反映出這(zhè)些因子的(de)變化(huà)。

使用(yòng)以上六大(dà)宏觀經濟指标的(de) factor mimicking portfolios 作爲待配置的(de)因子，Fergis et al. (2019) 進行了(le)防禦性因子擇時(shí)的(de)實證研究。作爲配置基準，Fergis et al. (2019) 将最終的(de)投資組合年化(huà)波動率限制在 10%，并按照(zhào)以下(xià)方案配置了(le)這(zhè)六個(gè)因子、構建了(le)多(duō)因子組合：經濟增長(cháng)和(hé)實際利率兩個(gè)因子各貢獻 30% 的(de)風險、其餘四個(gè)因子各貢獻 10% 的(de)風險。下(xià)面就來(lái)看看 Fergis et al. (2019) 用(yòng)來(lái)描述極端風險的(de)擇時(shí)指标。

3 擇時(shí)指标

極端市場(chǎng)風險來(lái)自三個(gè)方面：

Fergis et al. (2019) 使用(yòng)不同的(de)指标來(lái)監測上述風險。當前兩種極端風險之一出現時(shí)，因子投資組合的(de)整體倉位減少 20% 以降低風險可(kě)能造成的(de)大(dà)幅回撤；當第三種風險出現時(shí)，投資組合會在該因子上進行 5% 的(de)減倉。雖然 Fergis et al. (2019) 也(yě)考慮了(le)因子估值，但是它并沒有主張當某個(gè)因子便宜時(shí)爲其加倉，而僅是把它當做(zuò)抵禦風險的(de)手段。從 Fergis et al. (2019) 提出的(de)框架來(lái)看，前兩種風險對(duì)于防禦性因子擇時(shí)的(de)重要性遠(yuǎn)超過因子估值本身。因此下(xià)文著(zhe)重介紹它們。對(duì)于因子估值，請參考 Fergis et al. (2019) ，本文不再贅述。

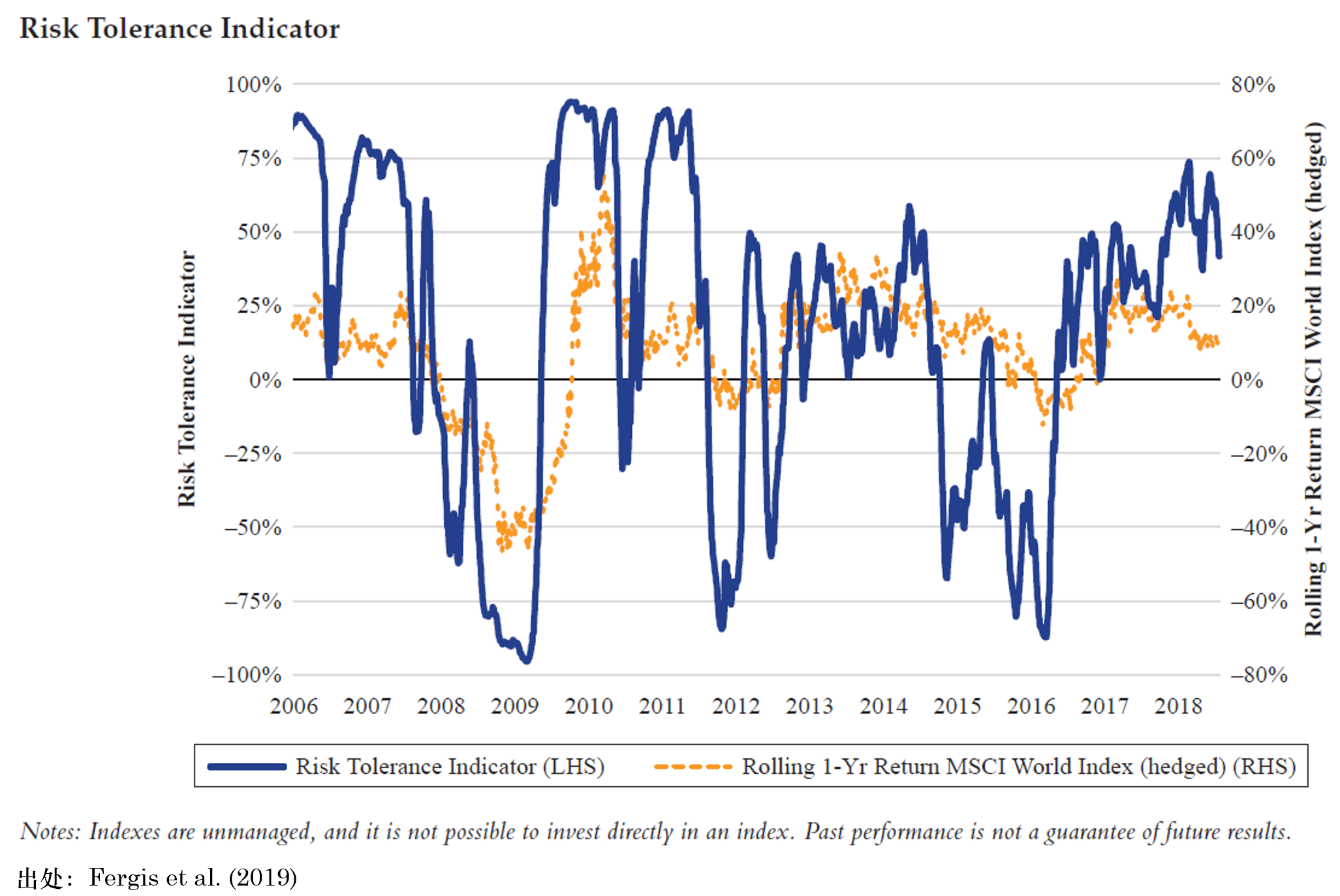
首先來(lái)看看市場(chǎng)風險偏好。Fergis et al. (2019) 使用(yòng)前述 14 種資産的(de)波動率和(hé)收益率計算(suàn)秩相關系數（rank correlation coefficient），以此構建了(le)一個(gè) Risk Tolerance Indicator（RTI）。這(zhè)背後的(de)依據是：市場(chǎng)風險偏好的(de)高(gāo)、低可(kě)以由不同資産的(de)收益率和(hé)它的(de)風險水(shuǐ)平的(de)一緻程度所反應。當風險偏好高(gāo)時(shí)，高(gāo)風險資産應該比低風險資産有更高(gāo)的(de)收益率；當風險偏好低時(shí)，高(gāo)風險資産應比低風險資産有更大(dà)的(de)跌幅。秩相關系數的(de)優勢是考察兩個(gè)變量（這(zhè)裏是收益率和(hé)波動率）的(de)單調相關性，而不假設變量之間的(de)線性或非線性關系。

令 q(R) 和(hé) q(σ) 分(fēn)别代表不同資産收益率和(hé)波動率的(de)排序序列，則 RTI 的(de)定義爲：

根據定義，RTI 的(de)取值範圍是 -1 到 1 之間，越大(dà)說明(míng)風險偏好越高(gāo)、越低說明(míng)風險容忍度越低。使用(yòng)秩相關系數來(lái)描述市場(chǎng)情緒并不是什(shén)麽新鮮事物(wù)，很多(duō)國内外的(de)研究報告中都對(duì)它進行過充分(fēn)的(de)說明(míng)（例子）。在實證中，Fergis et al. (2019) 采用(yòng) 14 種資産滾動三個(gè)月(yuè)的(de)周頻(pín)收益率計算(suàn) RTI。下(xià)圖爲 RTI 和(hé) MSCI World Index 一年滾動收益率之間的(de)關系，RTI 在 2008 年金融危機和(hé) 2010、2012 年歐洲主權債務危機時(shí)都給出了(le)明(míng)确的(de)警示信号。

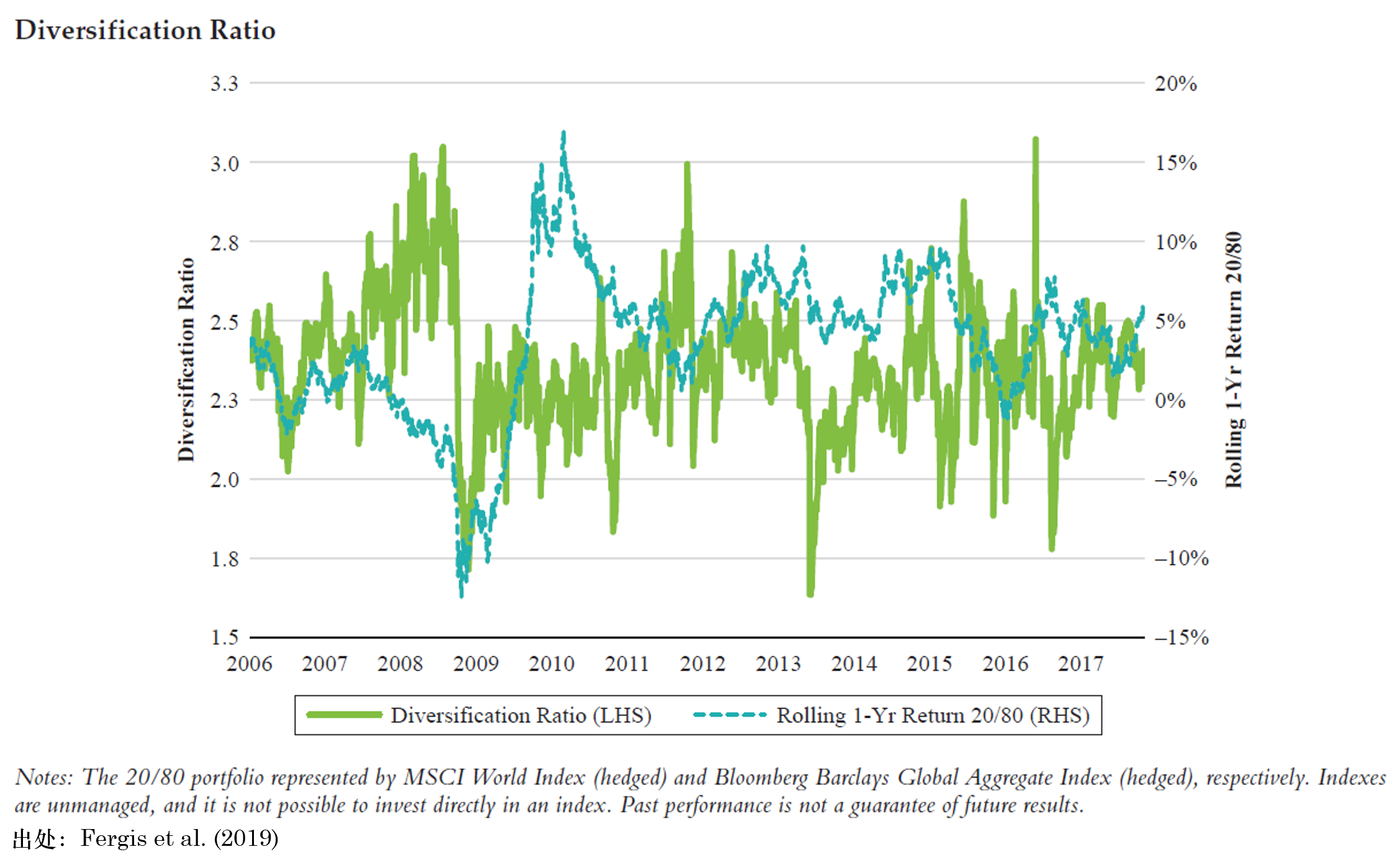
再來(lái)看看相關性。爲了(le)監控因子之間相關性激增的(de)風險，Fergis et al. (2019) 使用(yòng)了(le) Diversification Ratio（DR）這(zhè)個(gè)概念，它是各因子自身波動率按其權重的(de)加權與投資組合波動率之比：

由定義可(kě)知，DR 越大(dà)說明(míng)因子之間的(de)相關性越低，越能夠分(fēn)散化(huà)風險；越小則意味著(zhe)因子之間的(de)相關性上升。在實證期内，DR 和(hé)某個(gè)代表性的(de) 20/80 stock/bond portfolio 的(de)時(shí)序如下(xià)圖所示。

4 擇時(shí)案例

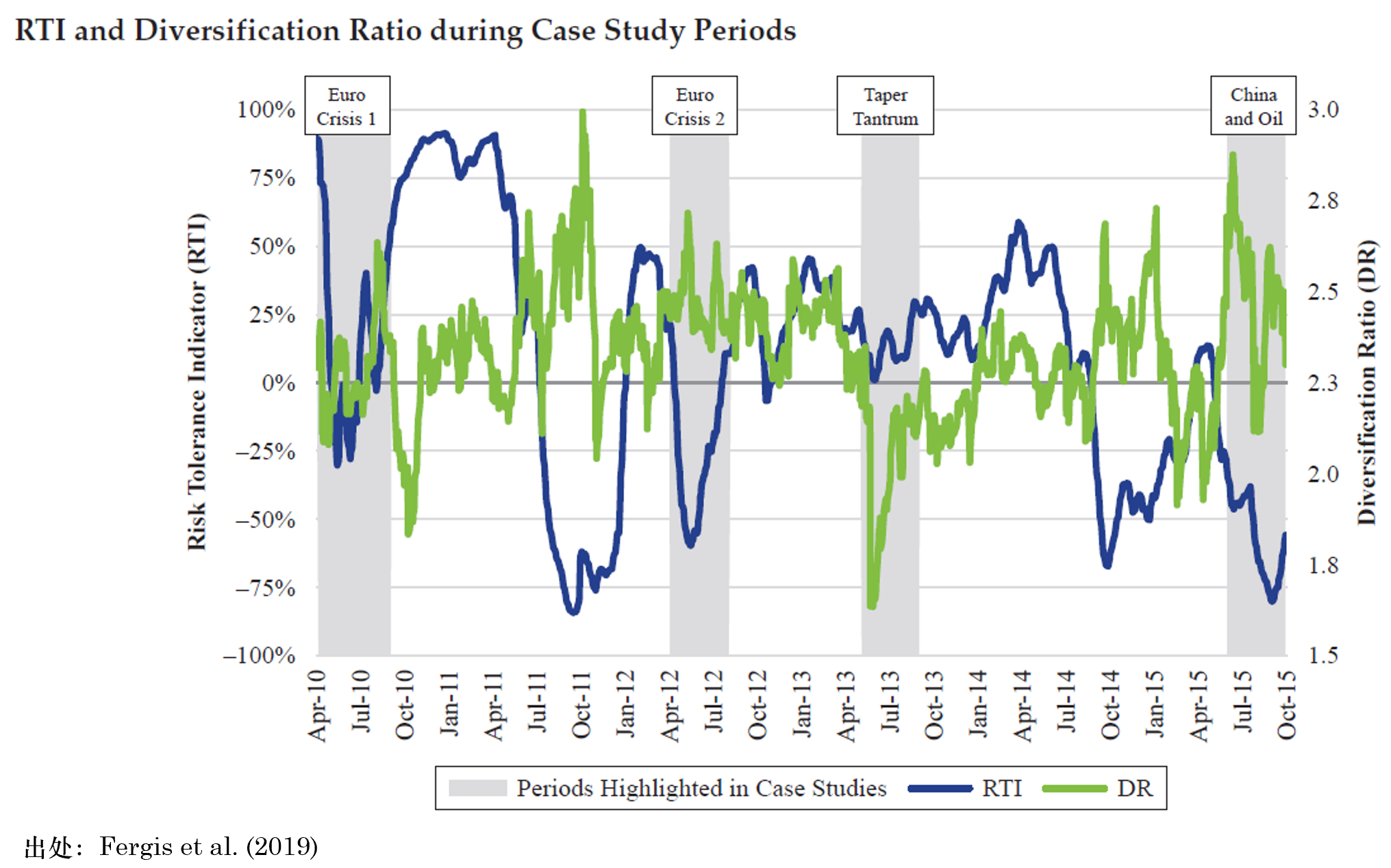
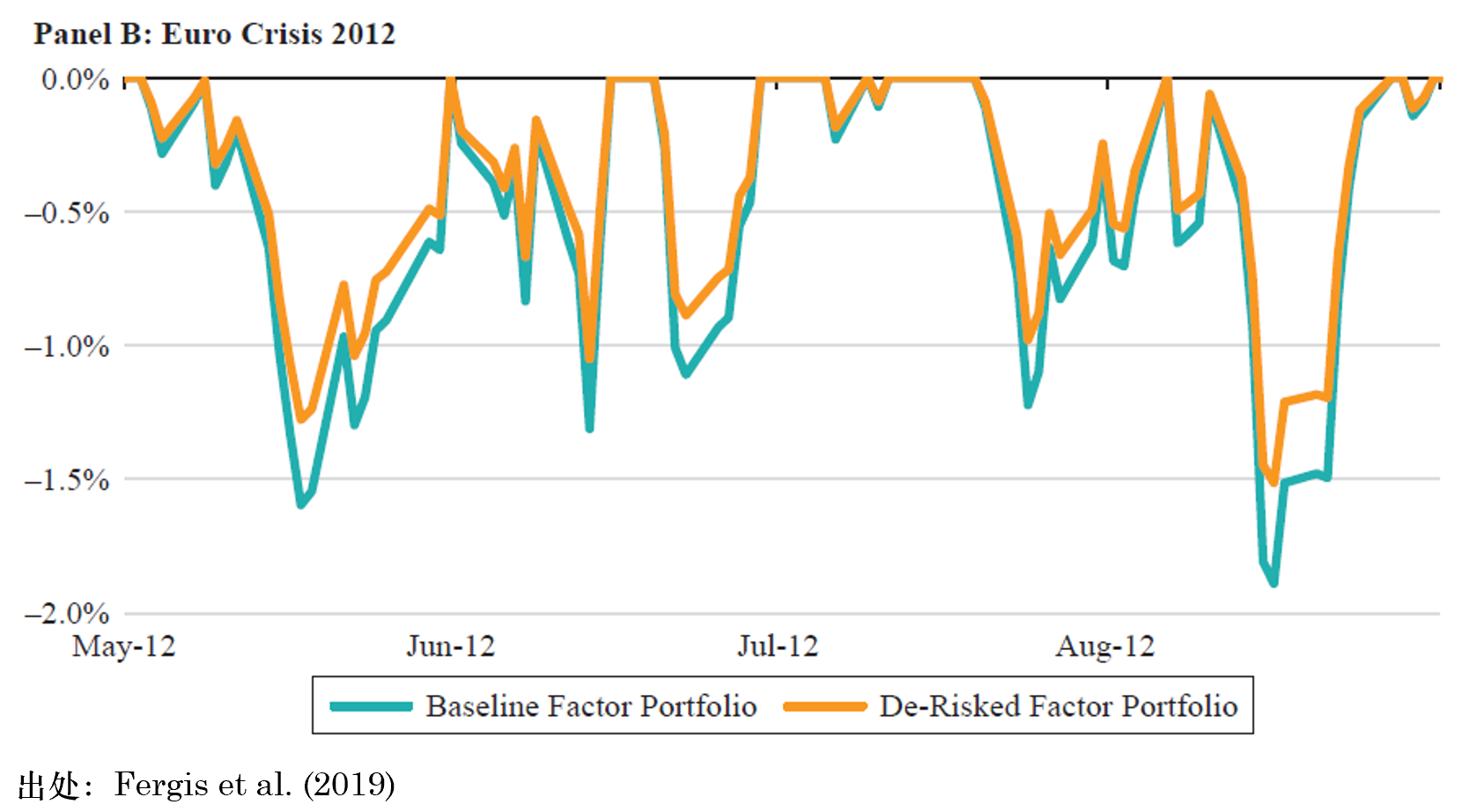
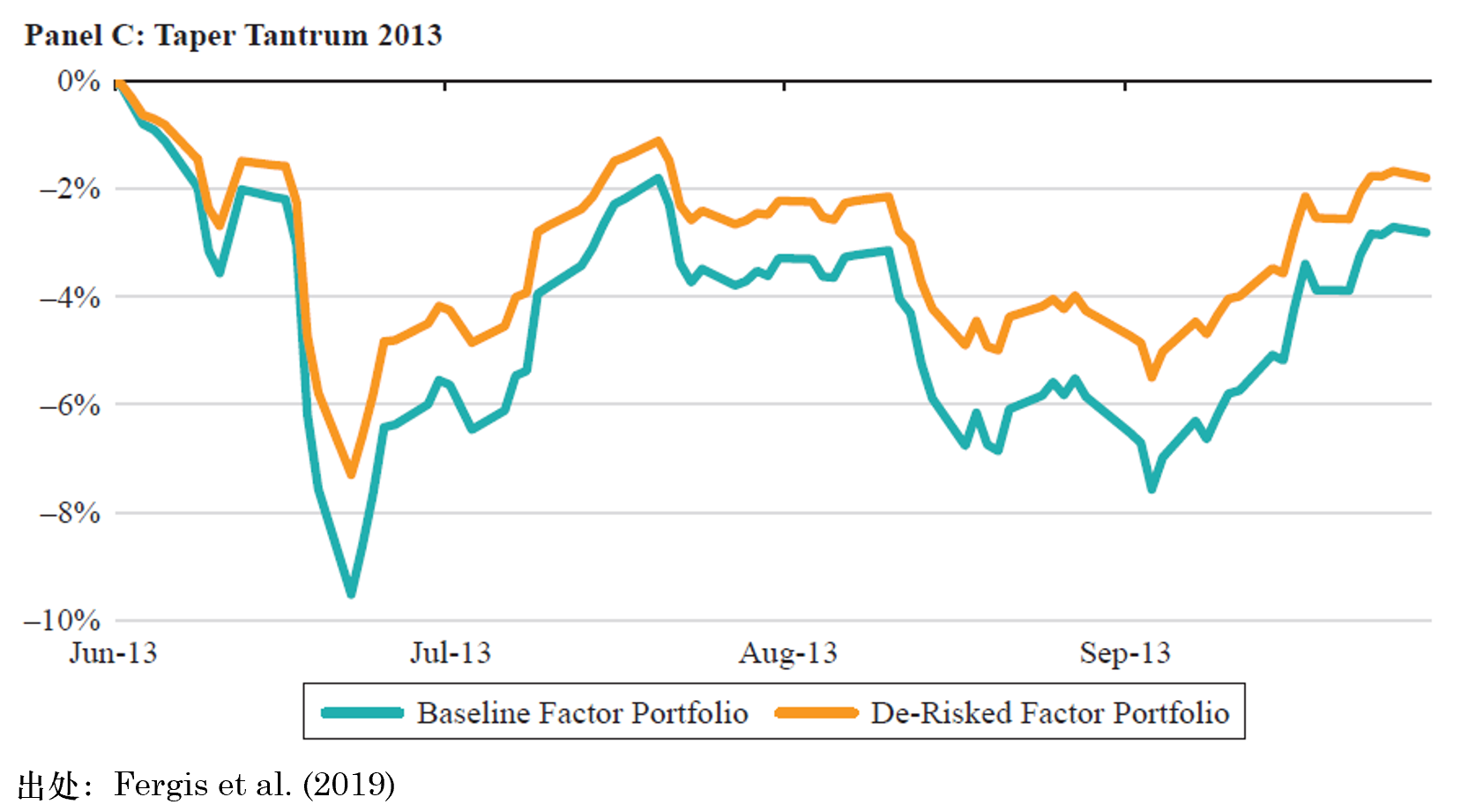
Fergis et al. (2019) 使用(yòng)提出的(de)三類擇時(shí)指标 —— RTI、DR 以及因子估值 —— 介紹了(le)四個(gè)防禦性因子擇時(shí)案例（下(xià)圖）。本小節介紹其中的(de)兩個(gè)，即 Euro Crisis 2 和(hé) Taper Tantrum。

先來(lái)看看“Euro Crisis 2”。2012 年 Q2，由希臘和(hé)西班牙引發的(de)一系列問題使得(de)全球市場(chǎng)的(de)神經極度緊繃。RTI 指标從四月(yuè)底的(de) 20% 驟降至六月(yuè)中旬的(de) -60%。在這(zhè)種大(dà)環境下(xià)，防禦性因子擇時(shí)自 2012 年五月(yuè)将多(duō)因子投資組合的(de)倉位下(xià)降 20%，直至同年八月(yuè) RTI 恢複到 0% 的(de)水(shuǐ)平才重新提高(gāo)到之前的(de)倉位。在市場(chǎng)極度動蕩的(de)四個(gè)月(yuè)内，該主動風控将投資組合的(de)最大(dà)回撤從 -1.9% 降低至 -1.5%。

再來(lái)看看“Taper Tantrum”。2013 年夏天，時(shí)任美(měi)聯儲主席伯南(nán)克宣布美(měi)聯儲将會逐漸削減（taper）購(gòu)債規模。聽(tīng)到這(zhè)個(gè)消息後，投資者開始瘋狂抛售債券、債市收益率大(dà)幅上行，而債券價格的(de)下(xià)跌也(yě)傳導到其他(tā)資産，導緻不同類資産的(de)下(xià)跌。這(zhè)一事件被稱爲“減碼恐慌”（taper tantrum）。在這(zhè)期間，RTI 指标卻意外沒有任何表示。所幸的(de)是，DR 指标發揮了(le)作用(yòng)。它的(de)急跌顯示出因子之間的(de)相關性迅速提升，從而啓動了(le)防禦性因子擇時(shí)。自 2013 年六月(yuè)，多(duō)因子投資組合的(de)倉位被降低 20% 以抵禦風險，直至同年九月(yuè) DR 恢複到之前的(de)水(shuǐ)平，倉位才提高(gāo)到基準水(shuǐ)平。在這(zhè)期間，防禦性因子擇時(shí)将投資組合的(de)回撤從 -9.5% 降低至 -7.3%。

這(zhè)個(gè)例子不僅說明(míng) DR 指标在抵禦風險時(shí)的(de)作用(yòng)，更說明(míng)了(le)同時(shí)使用(yòng)多(duō)個(gè)低相關的(de)風控指标對(duì)于抵禦風險至關重要。如果模型中僅有 RTI，它将無法捕捉 Taper Tantrum 事件。以上就是對(duì) Fergis et al. (2019) 一文的(de)簡要解讀。簡單總結一下(xià)：它使用(yòng)六個(gè)宏觀經濟因子來(lái)刻畫(huà) 14 類資産收益率的(de)共同的(de)變化(huà)，再結合三個(gè)角度的(de)擇時(shí)指标對(duì)這(zhè)六個(gè)因子進行防禦性擇時(shí)，最終的(de)目的(de)是在市場(chǎng)極端風險出現時(shí)有效降低多(duō)因子投資組合的(de)損失。

5 結語

讀過 Fergis et al. (2019) 之後，我最大(dà)的(de)感觸就是大(dà)寫的(de)兩個(gè)字：實用(yòng)。這(zhè)篇文章(zhāng)中并沒有高(gāo)深的(de)數學 —— RTI、DR 這(zhè)些指标的(de)計算(suàn)方法都很簡單、也(yě)早已被用(yòng)在不同的(de)投資實踐中。然而，和(hé) Bender et al. (2017, 2018) 一樣，Fergis et al. (2019) 也(yě)讓我們看到海外頂級機構是如何站在實踐的(de)角度進行因子擇時(shí)的(de)研究。

除此之外，該文的(de)“實用(yòng)性”還(hái)表現在以下(xià)兩個(gè)方面。首先是針對(duì)不同宏觀經濟指标構建的(de) factor mimicking portfolios。通(tōng)過對(duì)這(zhè)些投資組合收益和(hé)風險的(de)追蹤，可(kě)以有效的(de)評價宏觀經濟風險，從而幫助我們進行風險控制。第二點是該文做(zuò)因子擇時(shí)的(de)出發點是對(duì)大(dà)類資産進行風險控制。如今，因子投資早已深入人(rén)心，而因子的(de)概念也(yě)早已從狹隘的(de)選股指标上升到進行大(dà)類資産配置的(de)有效手段。最近，MSCI 就高(gāo)調推出了(le) Multi-Asset Class Factor Model（MAC），指導從戰略和(hé)戰術層面進行不同目的(de)的(de)資産配置，而 MAC 模型的(de) Tier 1 因子既包括傳統意義上的(de) Equity、Commodity 大(dà)類資産也(yě)包括像利率、通(tōng)脹等這(zhè)些導緻資産收益率共同波動的(de)宏觀驅動因素。

廣義的(de)大(dà)類資産因子配置已經成爲投資界的(de)主流；越來(lái)越多(duō)的(de)機構在資産配置時(shí)不再僅關注資産的(de)類别，而是聚焦于資産收益背後的(de)不同驅動因素（比如債券不再被當作一個(gè)固定收益資産類别，而是被視作在 interest rate、credit、以及 inflation 因子上有不同的(de)暴露和(hé)行爲） —— 那些才是真正的(de)因子，比如本文中的(de)六個(gè)宏觀經濟因子，以及 MSCI MAC 模型中的(de) Tier 1。這(zhè)将凸顯防禦性因子擇時(shí)的(de)價值。

參考文獻

Arnott, R. D., N. Beck, V. Kalesnik, and J. West (2016). Timing 'Smart Beta' Strategies? Of Course! Buy Low, Sell High! Working paper.

Arnott, R. D., N. Beck, V. Kalesnik (2017). Forecasting Factor and Smart Beta Returns (Hint: History Is Worse than Useless). Working paper.

Asness, C., S. Chandra, A. Ilmanen, and R. Israel (2017). Contrarian factor timing is deceptively difficult. The Journal of Portfolio Management 43(5), 72 – 87.

Bender, J., X. Sun, R. Thomas, and V. Zdorovtsov (2017). The promises and pitfalls of factor timing. Jacobs Levy Equity Management Center 2017 Conference.

Bender, J., X. Sun, R. Thomas, and V. Zdorovtsov (2018). The promises and pitfalls of factor timing. The Journal of Portfolio Management 44(4), 79 – 92.

Chen, N., R. Roll, and S. A. Ross (1986). Economic forces and the stock market. Journal of Business 59(3), 383 – 403.

Fergis, K., K. Gallagher, P. Hodges, and K. Hogan (2019). Defensive factor timing. The Journal of Portfolio Management 45(3), 50 – 68.

Gupta, T. and B. Kelly (2019). Factor momentum everywhere. The Journal of Portfolio Management 45(3), 13 – 36.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。