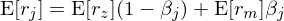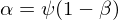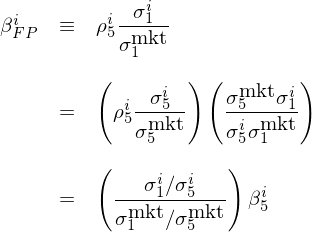BAB vs BABAB

作者：石川

摘要：Betting Against Beta 這(zhè)篇構築在 Black CAPM 模型上的(de)實證資産定價文章(zhāng)是 AQR 最著名的(de)代表作之一。然而，有人(rén)對(duì)它提出了(le)強烈的(de)質疑。

1 Black CAPM

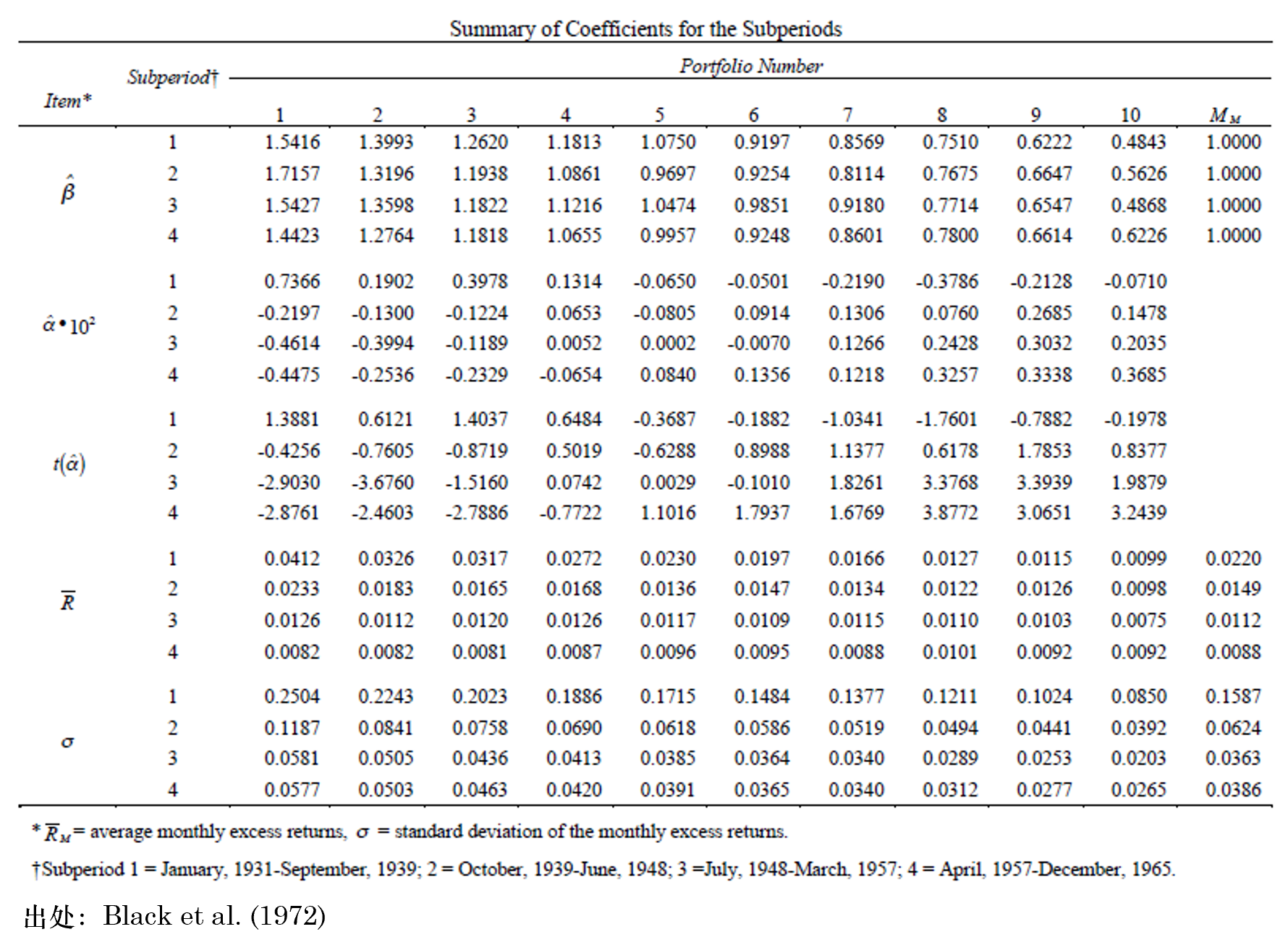
1972 年，Fischer Black、Michael Jensen 和(hé) Myron Scholes 從實際市場(chǎng)數據中觀察到股票(piào)收益率和(hé)它們的(de)  β  畫(huà)出來(lái)的(de) Security Market Line（SML）遠(yuǎn)比 CAPM 預測的(de)要更平緩，這(zhè)說明(míng)風險和(hé)收益的(de)關系不能很好的(de)滿足 CAPM。Black et al. (1972) 從時(shí)間序列回歸和(hé)截面回歸兩個(gè)維度實證了(le)上述猜想，并提出了(le)新的(de) CAPM 模型。

Black et al. (1972) 按照(zhào)股票(piào)的(de) β 大(dà)小把股票(piào)分(fēn)成十組（第一組中 β最大(dà)），然後在時(shí)序上回歸（檢驗時(shí)考慮了(le)各種偏差和(hé)誤差的(de)影(yǐng)響），得(de)到了(le)如下(xià)結果。按照(zhào) CAPM，回歸的(de)截距項（即 α）應該爲 0，然而Black et al. (1972) 觀察到在不同的(de)曆史時(shí)期，α 顯著不爲 0 且和(hé) β 呈負相關 —— 高(gāo) β 的(de)股票(piào)往往有負 α。

觀察到實際數據和(hé) CAPM 之間的(de)背離，Black et al. (1972) 抛棄了(le) CAPM 中的(de)無風險利率并提出了(le)一個(gè)雙因子模型：

上式中小寫字母 r 表示股票(piào)或者組合的(de)絕對(duì)收益。由于第二個(gè)因子 r_z 和(hé)  β 有關，因此它被稱爲 β 因子。由于 r_z 和(hé) r_m 的(de)協方差爲零，r_z 代表著(zhe)一個(gè) β 中性組合的(de)收益率。這(zhè)個(gè)改進的(de) CAPM 模型被後人(rén)稱爲 Black CAPM 模型（或 zero-beta CAPM 模型），它比最初的(de) CAPM 更加符合實際數據，因此應用(yòng)更加廣泛。

2 Betting Against Beta

在 Black CAPM 被提出的(de) 40 年之後，來(lái)自 AQR 的(de) Andrea Frazzini 和(hé) Lasse Heje Pedersen 在 Journal of Financial Economics 上發表了(le)一篇題爲 Betting Against Beta 的(de)文章(zhāng)（Frazzini and Pedersen 2014，下(xià)稱 FP），從另外的(de)角度解釋了(le) α 和(hé) β 之間的(de)負相關。他(tā)們指出在實際投資中，不同的(de)投資者受到不同資金使用(yòng)的(de)限制。爲了(le)追求更高(gāo)的(de)收益，一些投資者（特别是機構）會把有限的(de)資金投資于高(gāo)風險的(de)投資品，比如高(gāo) β 的(de)股票(piào)，這(zhè)便造成了(le)它們 α 的(de)下(xià)降。FP 用(yòng) ψ 來(lái)表示資金限制強弱程度，并得(de)出 α 和(hé) β 的(de)關系如下(xià)：

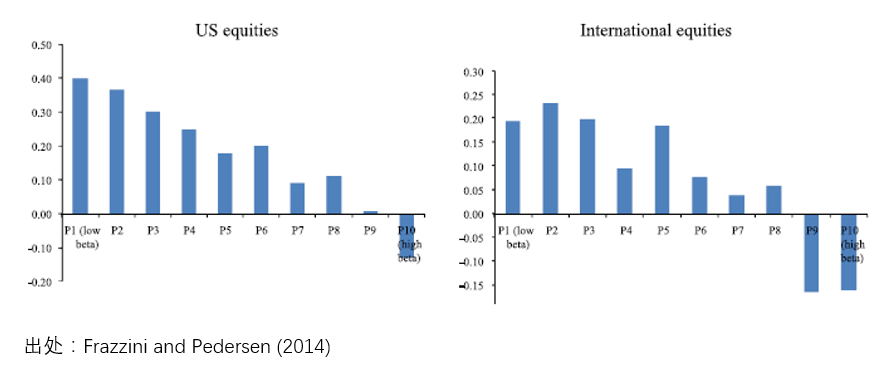
Frazzini and Pedersen (2014) 在不同的(de)市場(chǎng)中（包括股票(piào)、商品、債券、外彙）實證了(le)他(tā)們的(de)模型。下(xià)圖顯示了(le)在美(měi)國股票(piào)和(hé)全球股票(piào)市場(chǎng)中，按照(zhào) β 的(de)高(gāo)低将股票(piào)分(fēn)成十檔，每一檔的(de)超額收益（超額收益是總收益減去一些常見因子能夠解釋的(de)部分(fēn)）。他(tā)們針對(duì)這(zhè)個(gè)現象提出了(le) Betting Against Beta 策略（下(xià)稱 BAB）、構建投資組合、賺取其他(tā)因子無法解釋的(de)超額收益。

由于低 Beta 作爲一個(gè)因子早已深入人(rén)心，Betting Against Beta 一經發表，便在學術界和(hé)業界産生了(le)巨大(dà)的(de)反響。自 2014 年以來(lái)，它的(de)被引用(yòng)量在所有 Journal of Financial Economics 的(de)文章(zhāng)中高(gāo)居第二位，僅僅次于排名第一的(de) Fama-French 五因子模型。而在業界，它成爲防禦型投資策略當仁不讓的(de)傑出代表，得(de)到了(le)大(dà)量機構投資者的(de)追捧。

3 Betting Against Betting Against Beta

正所謂“人(rén)紅是非多(duō)”，面對(duì) BAB 因子在紙面上（on paper）獲得(de)的(de)非凡超額收益，有人(rén)就提出了(le)尖銳的(de)質疑。2018 年，Robert Novy-Marx 和(hé) Mihail Velikov 撰寫了(le)一篇題爲 Betting Against Betting Against Beta （BABAB）的(de)文章(zhāng)（Novy-Marx and Velikov 2018），指出 FP 在構建 BAB 因子時(shí)有三個(gè)地方“不走尋常路”，從而導緻了(le)其 on paper 的(de)超高(gāo)收益，而這(zhè)些收益在實際投資中無法兌現。這(zhè)三個(gè)地方是：

上述的(de)第三方面 —— 計算(suàn) β 的(de)方法 —— 對(duì)學術界的(de)影(yǐng)響很大(dà)。自 BAB 發表之後，很多(duō)研究也(yě)采用(yòng)同樣的(de)思路計算(suàn) β 值。在該方法中，FP 使用(yòng)一年滾動窗(chuāng)口計算(suàn)市場(chǎng)和(hé)個(gè)股收益率的(de)标準差，而采用(yòng)五年滾窗(chuāng)口計算(suàn)二者之間的(de)相關系數；FP 指出這(zhè)麽做(zuò)的(de)原因是，相對(duì)于波動率，相關系數的(de)變化(huà)更加緩慢(màn)。當采用(yòng)傳統方法計算(suàn) β 時(shí)，相關系數和(hé)标準差采用(yòng)的(de)是同樣長(cháng)度的(de)時(shí)間窗(chuāng)口。通(tōng)過簡單的(de)運算(suàn)，不難看出 FP 計算(suàn)的(de) β 值（記爲 β_FP）和(hé)傳統 β 值的(de)關系：

上式中，ρ 表示相關系數，σ 代表标準差，上标 i 代表個(gè)股 i，mkt 代表市場(chǎng)，下(xià)标 1 和(hé) 5 分(fēn)别代表一年和(hé)五年的(de)滾動窗(chuāng)口。該關系式說明(míng)，采用(yòng) FP 方法計算(suàn)出的(de) β 等價于傳統方法計算(suàn)的(de) β 乘以一個(gè)系數；該系數是個(gè)股一年波動率和(hé)五年波動率的(de)之比和(hé)市場(chǎng)一年波動率和(hé)五年波動率之比的(de)相對(duì)大(dà)小。

Novy-Marx and Velikov (2018) 指出，該系數對(duì) β_FP 的(de)計算(suàn)在時(shí)序上有很大(dà)的(de)影(yǐng)響：當市場(chǎng)自身處于高(gāo)波動時(shí)，個(gè)股雖然也(yě)是高(gāo)波動，但是實證數據表明(míng)個(gè)股的(de) σ_1/σ_5 和(hé)市場(chǎng)的(de) σ_1/σ_5 之間的(de)彈性小于 1，因此該系數小于 1；與之相反的(de)，當市場(chǎng)自身處于低波動時(shí)，二者之間的(de)彈性大(dà)于 1。這(zhè)說明(míng)當市場(chǎng)處于高(gāo)波動時(shí)，使用(yòng) FP 方法計算(suàn)的(de)個(gè)股 β 比傳統方法計算(suàn)的(de) β 更低；而當市場(chǎng)處于低波動時(shí)，使用(yòng) FP 方法得(de)到的(de) β 比傳統方法得(de)到的(de) β 更高(gāo)。這(zhè)進一步造成，将 β_FP 按照(zhào)個(gè)股市值加權後，得(de)到的(de)市場(chǎng)的(de) β 并不等于 1。下(xià)一節使用(yòng) A 股數據對(duì)此上述結論進行簡單實證。

4 簡單實證

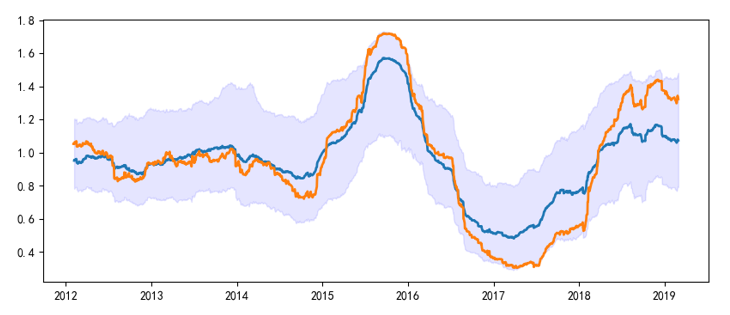
實證中選擇的(de)時(shí)間區(qū)間爲 2010 年 1 月(yuè) 1 日到 2019 年 2 月(yuè) 28 日。爲了(le)簡化(huà)實證，我從上證指數中選出了(le) 830 支在整個(gè)範圍内均有交易數據的(de)個(gè)股（以此排除上市、退市等的(de)影(yǐng)響）。使用(yòng)個(gè)股的(de)收益率和(hé)市值即可(kě)以構建出這(zhè) 830 支股票(piào)對(duì)應的(de)“市場(chǎng)”的(de)收益率時(shí)間序列，從而計算(suàn)個(gè)股的(de) β。由于數據不足 10 年，因此實證中并沒有采用(yòng) FP 中的(de)一年和(hé)五年時(shí)間窗(chuāng)口，而是使用(yòng)半年和(hé)兩年爲窗(chuāng)口分(fēn)别計算(suàn)标準差和(hé)相關系數。首先來(lái)看看個(gè)股的(de) σ_S/σ_L 和(hé)市場(chǎng)的(de) σ_S/σ_L 之間的(de)關系（其中 S 代表半年的(de)短窗(chuāng)口、L 代表兩年的(de)長(cháng)窗(chuāng)口）。下(xià)圖中，藍色實線是個(gè)股 σ_S/σ_L 中位數、陰影(yǐng)區(qū)域爲 5% 到 95% 分(fēn)位數；黃(huáng)色曲線是市場(chǎng) σ_S/σ_L。不難看出，當市場(chǎng) σ_S/σ_L 較大(dà)時(shí)（意味著(zhe)市場(chǎng)處于高(gāo)波動），大(dà)部分(fēn)個(gè)股的(de) σ_S/σ_L 在黃(huáng)色曲線之下(xià)；而當市場(chǎng) σ_S/σ_L 較小時(shí)（意味著(zhe)市場(chǎng)處于低波動），大(dà)部分(fēn)個(gè)股的(de) σ_S/σ_L 在黃(huáng)色曲線之上。這(zhè)個(gè)結果和(hé) Novy-Marx and Velikov (2018) 針對(duì)美(měi)股的(de)實證結果相同。

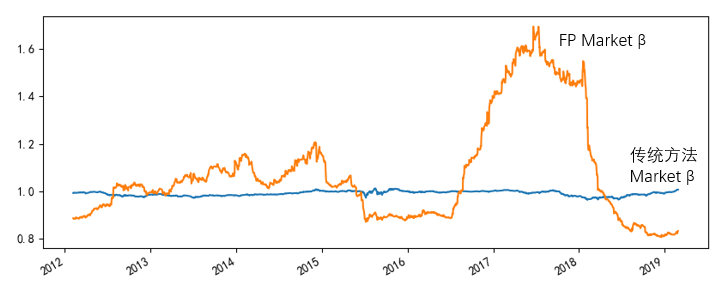
再來(lái)看看市值加權的(de) β_FP 得(de)到的(de)市場(chǎng) β 如何随時(shí)間變化(huà)。理(lǐ)論上，當采用(yòng)了(le)正确的(de)方法計算(suàn)個(gè)股的(de) β 後，市場(chǎng)的(de) β 應該等于 1。下(xià)圖中，藍色曲線是通(tōng)過傳統方法 —— 即使用(yòng)兩年窗(chuāng)口計算(suàn)标準差和(hé)相關系數 —— 得(de)到的(de)個(gè)股 β 後再通(tōng)過市值加權得(de)到的(de)市場(chǎng) β，它的(de)取值基本上沒有偏離 1.0；而黃(huáng)色曲線爲使用(yòng)個(gè)股 β_FP 得(de)到的(de)市場(chǎng) β，它在大(dà)多(duō)數時(shí)間顯著的(de)偏離 1.0。

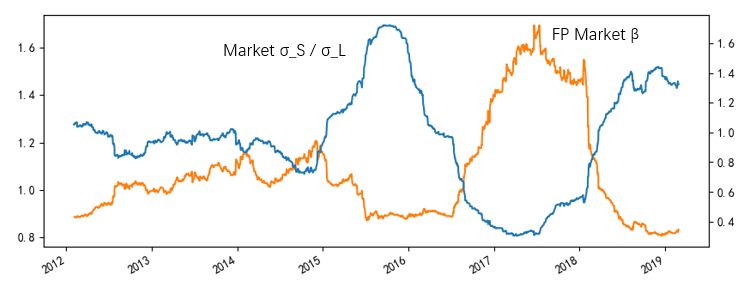
從個(gè)股 σ_S/σ_L 和(hé)市場(chǎng) σ_S/σ_L 的(de)關系出發可(kě)知：當市場(chǎng)處于高(gāo)波動時(shí)，β_FP 小于傳統方法計算(suàn)出的(de) β；當市場(chǎng)處于低波動時(shí)，β_FP 大(dà)于傳統方法計算(suàn)出的(de) β。因此，我們預期使用(yòng) β_FP 得(de)到的(de)市場(chǎng) β 和(hé)市場(chǎng) σ_S/σ_L 的(de)取值在時(shí)序上呈現負相關。下(xià)圖證實了(le)這(zhè)種猜想。

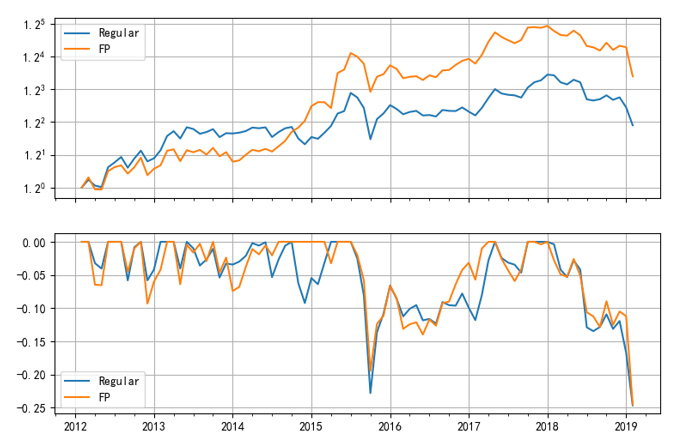
以上實證結果說明(míng)，使用(yòng) FP 方法和(hé)使用(yòng)傳統方法得(de)到的(de)個(gè)股 β 有很大(dà)差異。這(zhè)會造成以該 β 值作爲因子來(lái)選股出現不同的(de)結果。由于計算(suàn) β 需要至少兩年的(de)數據，因此下(xià)面來(lái)考察從 2012 年到 2019 年上述兩種不同 β 計算(suàn)方法的(de)選股結果。下(xià)圖顯示，使用(yòng) β_FP 戰勝了(le)傳統 β：β_FP 因子獲得(de)年化(huà)收益率 9.27%、夏普率 0.59；而傳統 β 因子僅獲得(de)年化(huà)收益率 5.08% 和(hé)夏普率 0.40。

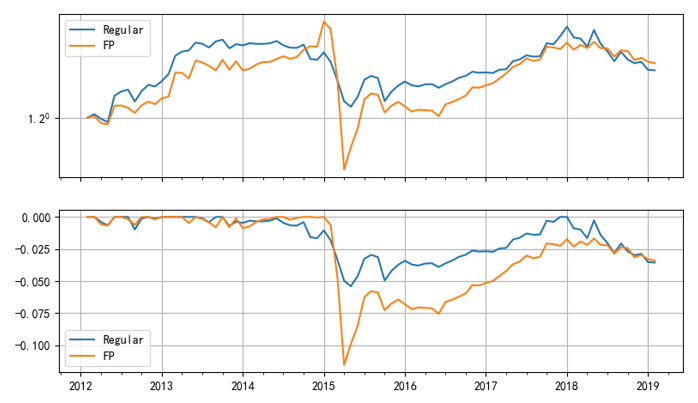
不過，先别著(zhe)急下(xià)結論！我并沒有說明(míng)因子投資組合是如何構建的(de)。該因子投資組合是按照(zhào) β 從小到大(dà)排序，首尾各取 100 支等權配置，每月(yuè)末調倉。等權配置增加了(le)在小市值上的(de)暴露；如果按照(zhào)市值加權構建投資組合會如何呢(ne)？下(xià)圖給出了(le)實證結果：β_FP 因子獲得(de)年化(huà)收益率 0.65%、夏普率 0.18；而傳統 β 因子獲得(de)年化(huà)收益率 0.56% 和(hé)夏普率 0.25。當排除了(le)小市值影(yǐng)響後，傳統 β 因子戰勝了(le) β_FP 因子。這(zhè)個(gè)結果和(hé) Novy-Marx and Velikov (2018) 對(duì) BAB 的(de)第一條質疑相一緻。

最後想指出的(de)是，上述結果僅僅是對(duì) BAB 做(zuò)的(de)一點非常有限的(de)實證，從該結果中我們還(hái)遠(yuǎn)不能得(de)到任何确定性的(de)結論。如何計算(suàn) β，這(zhè)個(gè)最簡單的(de)問題，似乎也(yě)并不是那麽容易回答(dá)。

5 結語

大(dà)量的(de)實證數據顯示，市場(chǎng) β 和(hé) α 确實存在負相關；Fischer Black 40 年前的(de)智慧也(yě)依舊(jiù)閃亮。然而，Novy-Marx and Velikov (2018) 指出，我們應該時(shí)刻保持警惕，搞清楚使用(yòng)“特殊”方法計算(suàn)的(de)因子、構建的(de)投資組合是否意外的(de)暴露在别的(de)地方并影(yǐng)響對(duì)因子有效與否的(de)判斷。

最後再來(lái)自我檢討(tǎo)一下(xià)。我幾年前第一次讀 BAB 的(de)時(shí)候，就被裏面計算(suàn) β 的(de)方法深深說服，沒有努力去思考背後的(de)邏輯是否成立。Novy-Marx and Velikov (2018) 的(de)分(fēn)析說明(míng)，即便 BAB 是來(lái)自研究能力超一流的(de) AQR、發表于金融領域頂刊之一的(de) JFE，我們也(yě)不應該想當然的(de)拿來(lái)主義。近日，AQR 這(zhè)個(gè)投資界的(de)“學術天團”爲了(le)慶祝其成立二十周年，特意甄選了(le) 20 篇他(tā)們所著的(de)最具代表性的(de)學術論文、出版了(le)《20 for Twenty》一書(shū)，BAB 赫然在列。Cliff Asness 對(duì)這(zhè)篇文章(zhāng)的(de)一句話(huà)點評是：

Fischer Black was right about the security market line (among many other things).

看完了(le) BABAB，我想：Fischer Black 的(de)确是對(duì)的(de)，但是 BAB 也(yě)許未必。Don't get me wrong！我依然是 AQR 的(de)忠實粉絲，也(yě)非常佩服他(tā)們的(de)學術能力和(hé)分(fēn)享意識，隻不過正确的(de)态度應是時(shí)刻保持獨立思考，因爲剖析一個(gè)因子成與敗背後的(de)真正原因始終是我們自己的(de)責任。

參考文獻

Black, F., M. C. Jensen, and M. Scholes (1972). The Capital Asset Pricing Model: Some Empirical Tests. In Studies in the Theory of Capital Markets. M. C. Jensen (editor), New York: Praeger, 79 – 121.

Frazzini, A. and L. H. Pedersen (2014). Betting against beta. Journal of Financial Economics 111(1), 1 – 25.

Novy-Marx, R. and M. Velikov (2018). Betting Against Betting Against Beta. Working paper.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。