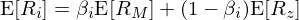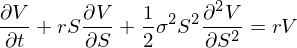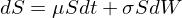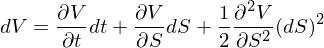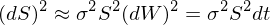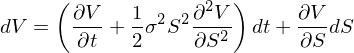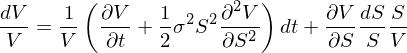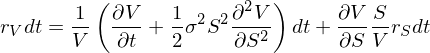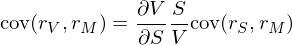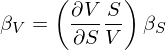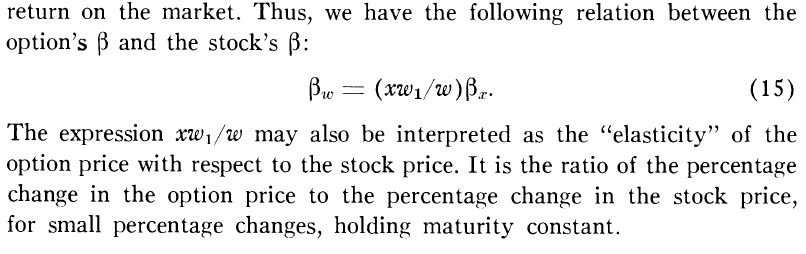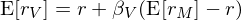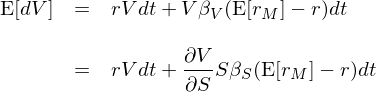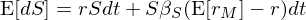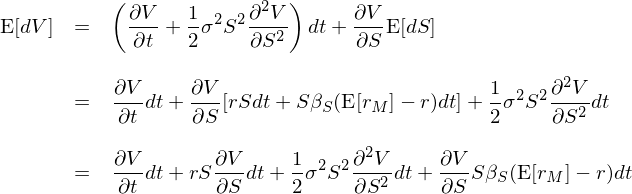Fischer Black

作者：石川

摘要：他(tā)是華爾街(jiē)的(de)第一個(gè)寬客，他(tā)的(de)一生就是一部金融工程發展史。

0 引言

他(tā)是華爾街(jiē)的(de)第一個(gè)寬客；他(tā)的(de)一生就是一部金融工程發展史；他(tā)将 CAPM 視作人(rén)生信條，一生在動态均衡下(xià)研究定價問題；以他(tā)名字命名的(de)公式遍及資産定價，期權定價，固定收益衍生品定價，以及資産配置各個(gè)領域。由于英年早逝，他(tā)遺憾無緣諾貝爾獎，但他(tā)的(de)名字被金融領域的(de)所有人(rén)銘記。上面這(zhè)段話(huà)是在我看完 Perry Mehrling 爲 Fischer Black 寫的(de)傳記 Fischer Black and the Revolutionary Idea of Finance 之後寫下(xià)的(de)感悟。

這(zhè)本書(shū)以介紹 Fischer Black 爲契機，生動的(de)呈現出金融領域的(de)各位大(dà)咖（Emanuel Derman、Eugene Fama、Michael Jensen、Harry Markowitz、Robert Merton、Paul Samuelson、William Sharpe、Jack Treynor……）之間的(de)淵源以及他(tā)們各自精彩絕倫的(de)理(lǐ)論發現；各學派（芝加哥(gē)、麻省理(lǐ)工、哈佛、斯坦福等）思想之間的(de)區(qū)别；以及像富國銀行、高(gāo)盛集團這(zhè)些巨頭在金融工程發展初期就大(dà)膽嘗試、勇于創新的(de)魄力。

毫無疑問，這(zhè)是一部描繪金融工程發展史的(de)鴻篇巨作（花費 7 年完成）；而之所以能夠如此，隻因爲 Fischer Black 在曆史的(de)洪流中留下(xià)了(le)太過深刻的(de)足迹，他(tā)的(de)那些足迹涉及這(zhè)些人(rén)、這(zhè)些學校和(hé)這(zhè)些機構。其實，我最初讀這(zhè)本書(shū)是在兩年前，當時(shí)就對(duì) Fischer Black 佩服的(de)五體投地并成了(le)他(tā)的(de)腦(nǎo)殘粉。最近又機緣巧合聽(tīng)到了(le) Fischer Black 的(de)名字，便勾起了(le)昔日的(de)回憶，于是決定以這(zhè)篇小文回顧下(xià)他(tā)對(duì)金融領域的(de)貢獻。

1 Black CAPM

說起 Black 最被人(rén)熟知的(de)成就，那自然是大(dà)名鼎鼎的(de)期權定價公式。然而，我會把關于期權定價的(de)介紹放到下(xià)一節。本小節，讓我們先來(lái)說說同樣對(duì)市場(chǎng)影(yǐng)響深遠(yuǎn)的(de) Black CAPM。在上一節提到的(de) Black 傳記一書(shū)的(de)封皮上，頁面上方的(de)公式正是 Black CAPM。關于傳統 CAPM，各位小夥伴都已經熟悉了(le)，公衆号之前的(de)文章(zhāng)《CAPM 的(de)一小段曆史》也(yě)做(zuò)過介紹。CAPM 中最大(dà)的(de)假設之一是投資者可(kě)以按照(zhào)無風險利率自由借貸。然而這(zhè)個(gè)假設在現實中往往過于嚴苛。爲此， Black (1972) 和(hé) Black, Jensen and Scholes (1972) 舍棄了(le)該假設并提出了(le)另外一個(gè)版本的(de) CAPM，後被稱作 Black CAPM。它在市場(chǎng)因子之外又加入了(le)第二個(gè)因子，是一個(gè)兩因子模型：

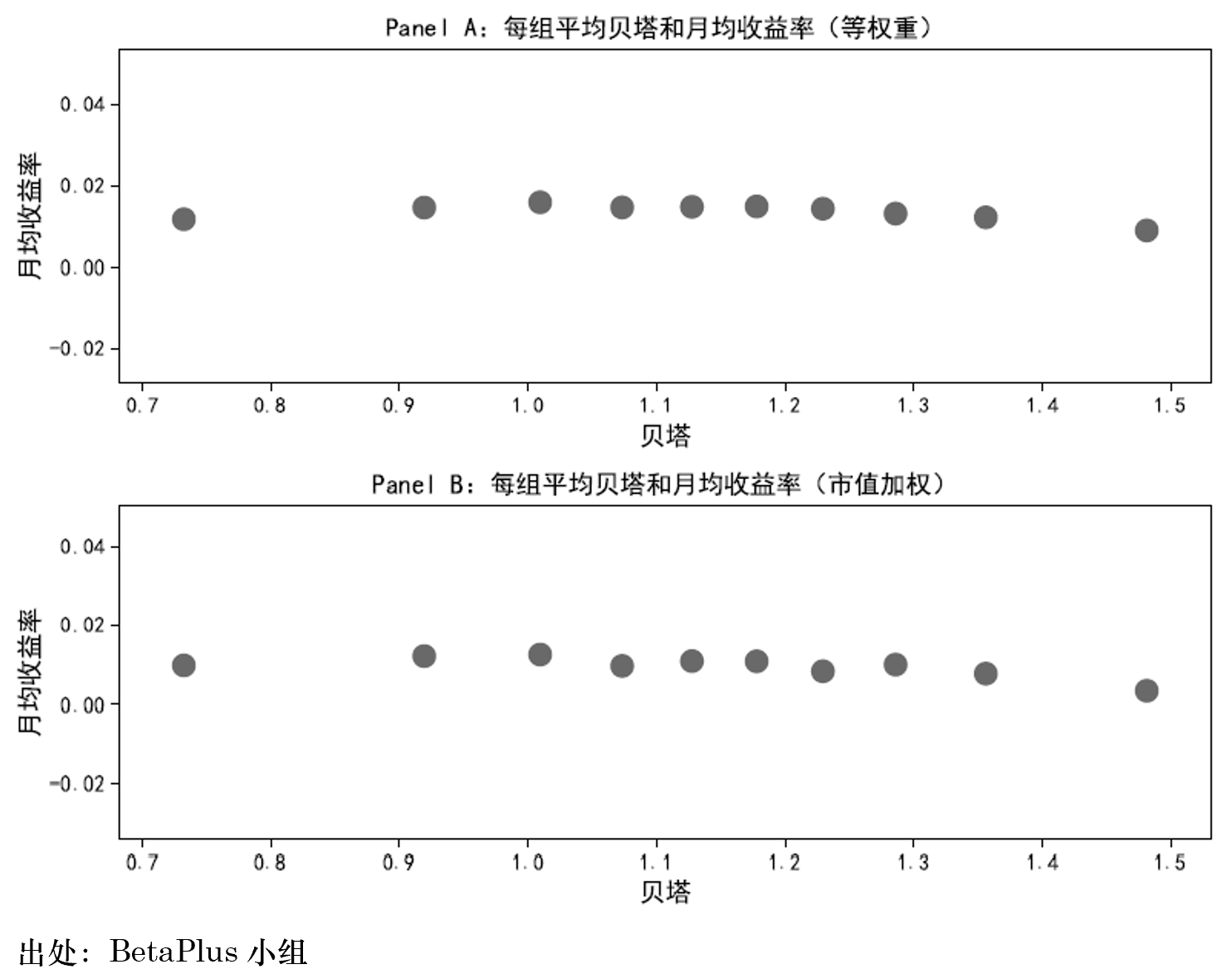
式中 E[R_z] 是第二個(gè)因子的(de)預期收益率。由于該因子的(de)系數是 1 - β_i，因而被稱爲 β 因子，其收益率 R_z 和(hé)市場(chǎng)組合的(de)收益率 R_M 的(de)協方差爲零，即 cov(R_z, R_M) = 0。如果考察資産超額收益 E[R_i] - r_f 和(hé)其 β_i 的(de)關系，則傳統 CAPM 模型暗示這(zhè)二者關系之間的(de)斜率爲市場(chǎng)組合的(de)預期超額收益 E[R_M] - r_f。反觀兩因子的(de) Black CAPM 模型，随著(zhe) (1 - β_i)E[R_z] 這(zhè)一項的(de)加入且這(zhè)一項的(de)收益率和(hé)資産的(de) β_i 成反比，因此 Black CAPM 隐含的(de)資産預期收益 E[R_i] 和(hé) β_i 之間的(de)關系相比傳統 CAPM 模型則更加平坦，而這(zhè)也(yě)恰恰更符合實證數據的(de)結果。

上圖是來(lái)自 A 股市場(chǎng)的(de)實證。将股票(piào)按照(zhào)其 β_i 的(de)高(gāo)低劃分(fēn)成十組，并統計每組的(de)（月(yuè)）預期收益率。不出意外，這(zhè)十組的(de)預期收益并沒有像傳統 CAPM 暗示的(de)那樣随 β_i 單調上升，而是更符合 Black CAPM 所反映的(de)關系。由于更加符合實證數據，Black CAPM 比傳統 CAPM 得(de)到了(le)更廣泛的(de)應用(yòng)，也(yě)拉開了(le)研究的(de)大(dà)潮。後面的(de)故事人(rén)們都知道了(le)，在 Black CAPM 被提出的(de) 40 年之後，Frazzini and Pedersen (2014) 在前人(rén)的(de)基礎上發表了(le)著名的(de) Betting against beta（BAB）。他(tā)們指出在實際投資中，不同的(de)投資者受到不同資金使用(yòng)的(de)限制。在這(zhè)種背景下(xià)，爲了(le)追求更高(gāo)的(de)收益，一些投資者（特别是機構）會把有限的(de)資金投資于高(gāo)風險的(de)投資品，比如高(gāo) β 的(de)股票(piào)，這(zhè)便造成了(le)它們超額收益 α 的(de)下(xià)降。BAB 的(de)故事無需多(duō)表，感興趣的(de)小夥伴可(kě)參考《BAB vs BABAB》。

2 從 CAPM 到期權定價

1967 年 3 月(yuè)下(xià)旬的(de)某天，Fischer Black、Michael Jensen 和(hé) William Sharpe 在芝加哥(gē)機場(chǎng)附近的(de)一個(gè)小旅館的(de)房(fáng)間裏進行了(le)一次頗有意義的(de)會面。他(tā)們三人(rén)當初討(tǎo)論的(de)問題是共同基金的(de)業績評價問題，即研究主動基金經理(lǐ)能否戰勝市場(chǎng)。對(duì)于 Black 來(lái)說，這(zhè)是他(tā)和(hé) CAPM 以及有效市場(chǎng)假說的(de)第一次邂逅。也(yě)正是自那一天起，CAPM 思想開始令 Black 著(zhe)迷。OK，鋪墊完了(le)，接下(xià)來(lái)讓我們說說期權定價。Black 傳記封皮下(xià)方的(de)那個(gè)公式正是由 Black and Scholes (1973) 提出的(de)期權定價公式。不過本小節關注的(de)是 Black-Scholes 偏微分(fēn)方程（PDE）：

上式中 r 爲無風險收益率；V 和(hé) S 分(fēn)别爲期權和(hé)股票(piào)的(de)價格；股票(piào)價格 S 滿足如下(xià)幾何布朗運動（需要背景知識的(de)小夥伴請參考《布朗運動、伊藤引理(lǐ)、BS 公式（前篇、後篇）》）：

在 Black and Scholes (1973) 這(zhè)篇文章(zhāng)中，Black 在推導完 PDE 并給出期權定價公式後，也(yě)從 CAPM 出發推導出了(le)上述 PDE，足見其對(duì) CAPM 思想的(de)執著(zhe)。

如何推導呢(ne)？由于 V 是 S 的(de)函數，由伊藤引理(lǐ)可(kě)知：

由于 S 滿足幾何布朗運動，将 dS 的(de)表達式兩邊取平方、利用(yòng)布朗運動二次變分(fēn)性質 (dW)^2 = dt、最後略去高(gāo)階小量有：

将上式代入 dV 表達式的(de)右側得(de)到下(xià)式（記該式爲 *，下(xià)文還(hái)會用(yòng)到）：

(*) 式兩邊同時(shí)除以 V：

在無窮小的(de)時(shí)間間隔 dt 内，由定義可(kě)知，dV/V 是 dt 内期權的(de)收益率，等于 (r_V)dt；同理(lǐ)，dS/S 是 dt 内股票(piào)的(de)收益率，等于 (r_S)dt。将這(zhè)二者替換上式中的(de) dV/V 以及 dS/S：

上式兩邊同時(shí)消去 dt，并同時(shí)和(hé)市場(chǎng)收益 r_M 計算(suàn)協方差；需要注意的(de)是，上式右側第一項中的(de)變量和(hé)偏導數在時(shí)刻 t 均是已知的(de)，因此是一個(gè)常數，隻有右側第二項才是随機項。因此，求和(hé) r_M 求協方差有：

顯然，上式兩邊同時(shí)除以 var(r_M) 就可(kě)以得(de)到喜聞樂(yuè)見的(de) β 形式：

這(zhè)正是 Black and Scholes (1973) 中的(de)公式（15）：

接下(xià)來(lái)，對(duì) V 應用(yòng) CAPM，該期權的(de)預期收益率爲：

将 dV/V = (r_V)dt 代入上式，并利用(yòng) β_V 和(hé) β_S 之間的(de)關系（記爲 I 式）：

類似的(de)，對(duì)股票(piào) S 應用(yòng) CAPM 則有：

對(duì) (*) 式兩邊取期望（該式右側第一項爲常數、期望就是它本身），并利用(yòng)上述 E[dS] 的(de)表達式可(kě)得(de)（記爲 II 式）：

至此，我們得(de)到了(le)兩個(gè) E[dV] 的(de)表達式（I、II）。比較它們的(de)右側可(kě)知 (I) 的(de)第二項和(hé) (II) 的(de)最後一項一樣，可(kě)以抵消。在剩餘項中都除以 dt，最後聯立 (I) 和(hé) (II) 相等得(de)到：

這(zhè)正是 Black-Scholes 偏微分(fēn)方程。

3 Black-Litterman

Black 的(de)思想之所以閃耀著(zhe)不朽的(de)光(guāng)芒是因爲他(tā)永遠(yuǎn)思考理(lǐ)論與實際如何聯系；理(lǐ)論必須是爲了(le)解決實際的(de)金融問題服務的(de)。這(zhè)也(yě)解釋了(le)爲什(shén)麽他(tā)會從 UChicago 和(hé) MIT 離開，前往業界加盟高(gāo)盛。在高(gāo)盛，Black 和(hé) Emanuel Derman 以及 William Toy 提出了(le)關于短期利率的(de) Black-Derman-Toy 模型，可(kě)以用(yòng)來(lái)對(duì)固定收益衍生品定價。當然，Black 在高(gāo)盛的(de)另一項研究成果則更被人(rén)們所熟知，那就是 Black-Litterman 資産配置模型（見《Black-Litterman 模型 —— 貝葉斯框架下(xià)的(de)資産配置利器》）。

Black-Litterman 模型可(kě)以被視作是 Black 在探索一般均衡的(de)實踐中的(de)一個(gè)小的(de)裏程碑。該模型在數學上的(de)本質是一種貝葉斯收縮。它從市場(chǎng)的(de)供需出發，認爲投資品在整個(gè)市場(chǎng)中按其市值的(de)占比體現了(le)當前市場(chǎng)供需關系的(de)均衡狀态。投資品市值與市場(chǎng)總市值的(de)比值就是該投資品在這(zhè)個(gè)市場(chǎng)均衡組合中的(de)權重。在這(zhè)個(gè)基礎上，該模型進一步假設各投資品在市場(chǎng)組合中的(de)配置比例是由投資者追求效用(yòng)的(de)最大(dà)化(huà)所緻，并由此反推出市場(chǎng)均衡狀态下(xià)各投資品的(de)收益率，把它作爲預期收益率的(de)先驗。

另一方面，Black-Litterman 模型将新息定義爲投資者對(duì)于投資品收益率相對(duì)強弱的(de)主動判斷（稱爲 views，即觀點）。最後，在貝葉斯框架下(xià)，将先驗和(hé)新息結合起來(lái)，就得(de)到預期收益率的(de)後驗。将其代入到 mean-variance optimization（MVO）中就能求出最優的(de)資産配置。Black-Litterman 資産配置模型解決了(le) MVO 模型在應用(yòng)中的(de)兩個(gè)痛點：（1）投資品的(de)期望收益率很難預測；（2）模型對(duì)輸入參數太敏感，導緻投資者無法理(lǐ)解模型給出的(de)最佳投資組合中投資品的(de)配置權重。Black-Litterman 模型從市場(chǎng)均衡配置出發，有效的(de)結合了(le)投資者對(duì)投資品的(de)主動判斷，求出的(de)配置結果符合投資者的(de)預期。在華爾街(jiē)，Black-Litterman 模型在高(gāo)盛以及其他(tā)金融機構都有著(zhe)廣泛的(de)應用(yòng)。

4 Noise

1985 年，Fischer Black 當選美(měi)國金融協會（AFA）主席。依照(zhào) AFA 目前的(de)慣例，每位主席任期一年，且在卸任時(shí)發表主席演講。而 Black 演講的(de)題目則是 Noise（Black 1986）。比起 Black CAPM、Black-Scholes 期權定價公式以及 Black-Litterman 資産定價模型，Noise 這(zhè)篇演講無疑更貼近我們每一個(gè)人(rén)。

金融市場(chǎng)的(de)信噪比很低。大(dà)量的(de)噪聲包圍著(zhe)微弱的(de)信号，使得(de)從它們之中剝離出信号難上加難。在 Black 看來(lái)，噪聲交易者的(de)存在爲市場(chǎng)提供了(le)流動性，是市場(chǎng)充滿活力的(de)原因也(yě)是市場(chǎng)的(de)必要組成部分(fēn)。但另一方面，由于噪聲交易者根據“噪聲”而非“信息”來(lái)交易，因此資産的(de)價格中同時(shí)反映出信息和(hé)噪聲。Black 關于噪聲交易者的(de)觀點與 Robert Shiller 一緻。後者提出的(de)噪聲交易者模型則拉開了(le)行爲金融學的(de)序幕。然而，與 Shiller 因這(zhè)個(gè)觀點而堅定的(de)認爲市場(chǎng)是非有效不同，Black 在演講中抛出的(de)觀點則要溫和(hé)一些。他(tā)認爲在絕大(dà)多(duō)數情況下(xià)，價格以 2 爲系數圍繞著(zhe)價值波動。這(zhè)大(dà)概和(hé)他(tā)金融學術生涯早期受到源自芝加哥(gē)大(dà)學的(de)有效市場(chǎng)假說的(de)影(yǐng)響有關。

We might define an efficient market as one in which price is within a factor of 2 of value, i.e., the price is more than half of value and less than twice value. The factor of 2 is arbitrary, of course. Intuitively, though, it seems reasonable to me, in the light of sources of uncertainty about value and the strength of the forces tending to cause price to return to value. By this definition, I think almost all markets are efficient almost all of the time. "Almost all" means at least 90%.

在 Noise 這(zhè)篇演講中，給我留下(xià)印象最深刻的(de)一句話(huà)是下(xià)面這(zhè)句：

Noise causes markets to be somewhat inefficient, but often prevents us from taking advantage of inefficiencies.

這(zhè)讓我想起之前讀到的(de) Statman (2018) 這(zhè)篇題爲 Behavioral Efficient Markets 的(de)論文。該文曾獲得(de) The 20th Annual Bernstein Fabozzi/Jacobs Levy Awards 最佳論文獎。它認爲有效市場(chǎng)假說包括 price-equals-value market hypothesis 和(hé) hard-to-beat market hypothesis 兩層含義。這(zhè)兩層含義完美(měi)的(de)對(duì)應著(zhe) Black 上面那句話(huà)的(de)前、後半句。正如人(rén)們觀察到的(de)那樣，在市場(chǎng)中，資産價格并不總是等于其内在價值（盡管内在價值是難以觀測的(de)），而是可(kě)以偏離價值。這(zhè)意味著(zhe) price-equals-value market hypothesis 通(tōng)常不成立，說明(míng)了(le)市場(chǎng)在一定程度上是非有效的(de)。而另一方面，市場(chǎng)又确實很難被戰勝。從這(zhè)個(gè)意義上說，hard-to-beat market hypothesis 是成立的(de)。

5 遺憾

1959 年，Fischer Black 從 Harvard 本科畢業。在申請研究生時(shí)，他(tā)唯一感興趣的(de)方向其實是物(wù)理(lǐ)學。然而，在讀了(le)一年之後，他(tā)便被人(rén)工智能所吸引而更換了(le)方向。但即便到此時(shí)，金融依然尚未和(hé)他(tā)産生交集。Black 的(de)博士生涯頗具坎坷，但最終還(hái)是在幾經波折之後于 1964 年獲得(de) Harvard 應用(yòng)數學的(de)博士學位。從 Harvard 畢業之後，他(tā)加入了(le) Arthur D. Little 這(zhè)個(gè)成立于 1886 年的(de)、世界上最古老的(de)管理(lǐ)咨詢公司。而正是在 Arthur D. Little，他(tā)遇到了(le)将其帶入金融領域、也(yě)是後來(lái)對(duì)他(tā)的(de)研究思想産生巨大(dà)影(yǐng)響的(de)人(rén) —— Jack Treynor。從此，Black 便在金融領域開啓了(le)開挂的(de)人(rén)生……

1997 年，諾貝爾經濟學獎授予了(le) Myron Scholes 和(hé) Robert Merton，以表彰他(tā)們在期權定價上的(de)發現。令人(rén)感到遺憾的(de)是，由于 Black 英年早逝、加上諾獎不頒發給已故學者，因此他(tā)未能獲獎。但諾獎委員(yuán)會還(hái)是在當年的(de)獲獎公告中特地強調了(le) Fischer Black 所發揮的(de)關鍵作用(yòng)（以下(xià)爲節選，公告全文中超過 10 次提及了(le) Fischer Black 的(de)名字），以此表達對(duì)他(tā)的(de)肯定。

盡管如此，還(hái)是有大(dà)佬對(duì)諾獎委員(yuán)會表達了(le)不滿。Emanuel Derman 在 My life as a quant（寬客人(rén)生）中就表達了(le)以下(xià)的(de)觀點。金融圈内所有人(rén)都認爲期權定價公式獲得(de)諾獎隻是早晚的(de)事兒(ér)。而且，人(rén)們也(yě)知道 Black 于 1994 年不幸被診斷出緻命的(de)喉癌。因此，人(rén)們都迫切希望諾獎委員(yuán)會能及時(shí)把經濟學獎頒給期權定價公式，以免留下(xià)遺憾。然而，諾獎委員(yuán)會似乎不願意把諾貝爾獎頒給在業界工作的(de)人(rén)，特别是一個(gè)來(lái)自投行的(de)人(rén)。雖然這(zhè)僅僅是猜測，但它還(hái)是令人(rén)唏噓不已。

不過，學術界對(duì)業界的(de)“不屑”可(kě)能也(yě)由來(lái)已久。Black 和(hé) Scholes 早在 1970 年 11 月(yuè)就将期權定價論文提交到 Journal of Political Economy，當時(shí) Black 還(hái)在 Arthur D. Little 工作。由于文章(zhāng)在當初來(lái)看有些晦澀難懂(dǒng)，再加上第一作者來(lái)自一個(gè)咨詢公司而非金融名校，該文在開始時(shí)反複被拒。所幸，最後“金子還(hái)是發光(guāng)了(le)”。該文被 Merton Miller（Eugene Fama 的(de)導師）留意到，并一眼看出了(le)它的(de)重要性。在 Miller 的(de)推薦下(xià)，該文最終被錄用(yòng)和(hé)發表。

1994 年，Fischer Black 被 IAFE 授予年度金融工程師稱号（該獎項自 1993 年設立，第一個(gè)獲獎者是 Robert Merton），以表彰他(tā)對(duì)金融工程實踐應用(yòng)方面的(de)卓越貢獻。毫無疑問，Fischer Black 的(de)一生是傳奇的(de)一生，他(tā)也(yě)絕對(duì)無愧于華爾街(jiē)第一寬客的(de)頭銜。他(tā)對(duì)均衡模型的(de)畢生追求在金融領域創造了(le)一個(gè)又一個(gè)經典，永遠(yuǎn)被後人(rén)銘記。最後，讓我用(yòng) Black 自己的(de)話(huà)來(lái)結束本文，并向他(tā)緻敬。

I like the beauty and symmetry in Mr. Treynor's equilibrium models so much that I started designing them myself. I worked on models in several areas：Monetary theory, Business cycles, Options and warrants. For 20 years, I have been struggling to show people the beauty in these models to pass on knowledge I received from Mr. Treynor. In monetary theory —— the theory of how money is related to economic activity —— I am still struggling. In business cycle theory —— the theory of fluctuation in the economy —— I am still struggling. In options and warrants, though, people see the beauty.

世上再無 Black。

參考文獻

Black, F. (1972). Capital market equilibrium with restricted borrowing. Journal of Business 45(3), 444 – 455.

Black, F. (1986). Noise. Journal of Finance 41(3), 528 – 543.

Black, F., M. C. Jensen, and M. Scholes (1972). The capital asset pricing model: Some empirical tests. In M. C. Jensen (Eds), Studies in the Theory of Capital Markets. New York, NY: Praeger.

Black, F. and R. Litterman (1992). Global portfolio optimization. Financial Analysts Journal 48(5), 28 – 43.

Black, F. and M. Scholes (1973). The pricing of options and corporate liabilities. Journal of Political Economy 81(3), 637 – 645.

Frazzini, A. and L. H. Pedersen (2014). Betting against beta. Journal of Financial Economics 111(1), 1 – 25.

Statman, M. (2018). Behavioral efficient markets. The Journal of Portfolio Management 44(3), 76 – 87.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。