一個(gè)策略的(de)自白

作者：石川

0 引言

我是一個(gè)策略。我的(de)管理(lǐ)人(rén)付出了(le)很多(duō)的(de)努力、使用(yòng)科學的(de)方法打造我。我曆經模型提出、數據收集、回測驗證、過拟合評價、模拟盤檢驗等多(duō)道工序，最終變成了(le)現在的(de)樣子。我在樣本外的(de)實盤中日複一日、年複一年地按照(zhào)管理(lǐ)人(rén)設想的(de)方式運轉。從未出過差錯。但是最近，我的(de)管理(lǐ)人(rén)在使用(yòng)我以及和(hé)别人(rén)討(tǎo)論我的(de)時(shí)候，有些做(zuò)法讓我覺著(zhe)很費解。這(zhè)些做(zuò)法包括“随機模式誤解 + 小數定律偏誤”、“吃(chī)補藥”、“過度關注最大(dà)回撤”以及“擇時(shí)”。

Something is Not Right。

我希望和(hé)我的(de)管理(lǐ)人(rén)說說心裏話(huà)。

1 随機模式誤解 + 小數定律偏誤

長(cháng)期來(lái)看，我的(de)夏普率大(dà)概穩定的(de)維持在 1.5 左右。然而最近一段時(shí)間無疑是我的(de)“高(gāo)光(guāng)時(shí)刻”。最近兩個(gè)月(yuè)我的(de)夏普率高(gāo)達 3.0，這(zhè)讓我的(de)管理(lǐ)人(rén)很高(gāo)興，非常高(gāo)興，非常非常高(gāo)興。但我卻覺著(zhe)他(tā)這(zhè)種情緒很危險。我希望告訴他(tā)千萬不要誤入 Tversky and Kahneman (1971) 指出的(de)“小數定律偏誤”。這(zhè)兩位心理(lǐ)學大(dà)咖通(tōng)過研究發現了(le)人(rén)們習(xí)慣犯以下(xià)兩種錯誤：

除此之外，在通(tōng)常情況下(xià)，人(rén)們會低估随機模式出現的(de)頻(pín)率。這(zhè)一現象往往和(hé)小數定律偏誤疊加，造成對(duì)總體錯誤的(de)認知。舉個(gè)例子。在一個(gè)遊戲中，參與者被要求猜測五輪扔硬币的(de)結果（fair coin，正反面出現概率各爲 50%，以 1 代表正面、0 代表反面）。最終得(de)到的(de)結果是，有 121 人(rén)猜測結果是 11010，35 人(rén)猜測結果爲 10101，而 1 人(rén)猜測結果是 11111。11010 和(hé) 10101 裏面都有三個(gè) 1，但猜前者的(de)人(rén)數卻更多(duō)，隻因它看上去更随機一些，而非像 10101 那樣 1 和(hé) 0 完美(měi)交錯。而 11111 僅有 1 人(rén)猜測這(zhè)說明(míng)人(rén)們認爲随機結果不應如此一緻。但事實上，這(zhè)三種結果的(de)概率完全相同，都是 (1/2)^5 不是嗎？

在另一個(gè)實驗中，263 名大(dà)學生在統計課上被要求判斷 10 次扔硬币中出現連續正面，或連續反面的(de)最大(dà)次數。比如，如果某次結果是 1101000110，那麽最大(dà)的(de)就是連續 3 個(gè)反面。在這(zhè)些學生中，僅有 13% 的(de)學生猜測最大(dà)連續結果的(de)次數超過 4。然而事實卻是，在 10 次扔硬币中，出現 4 次或 4 次以上連續結果（正或反）的(de)概率高(gāo)達 47%，遠(yuǎn)超過 13%。大(dà)多(duō)數人(rén)并不能正确認識到随機數據中出現連續相同結果的(de)概率有多(duō)高(gāo)。一旦連續結果出現，人(rén)們傾向認爲這(zhè)并非随機結果，而是有潛在的(de)原因。

而對(duì)随機模式的(de)誤解也(yě)會随著(zhe)遊戲次數的(de)增加（即數據量的(de)增加）而加重。有一個(gè)教授，曾經做(zuò)過一個(gè)非常有意思的(de)實驗。他(tā)讓學生盡可(kě)能随機的(de)給出長(cháng)度爲 100 的(de) 0、1 序列（模拟扔硬币的(de)結果）。與此同時(shí)，他(tā)使用(yòng)電腦(nǎo)的(de)随機數也(yě)生成一個(gè)長(cháng)度爲 100 的(de)序列。使用(yòng)統計檢驗兩個(gè)序列發現，學生并不能很好的(de)産生真正的(de)随機序列。

當随機序列的(de)長(cháng)度變爲 100 時(shí)，在通(tōng)常的(de)情況下(xià)是可(kě)以出現 6 到 8 個(gè)連續的(de) 0 或者 1 的(de)（即在随機生成的(de)序列中，你可(kě)以在局部看到 00000000 或者 1111111 這(zhè)樣的(de)排列）。但是，人(rén)們産生的(de)“随機”序列卻遠(yuǎn)比真實的(de)有序的(de)多(duō)。如果你也(yě)對(duì)這(zhè)個(gè)實驗感興趣，不妨訪問下(xià)面這(zhè)個(gè)網站：

http://faculty.rhodes.edu/wetzel/random/mainbody.html

以上例子均說明(míng)，人(rén)們對(duì)于随機序列産生的(de)結果往往沒有很好的(de)認知。很多(duō)看似不可(kě)能的(de)結果 —— 比如連續的(de) 0 或者 1 —— 其實都是總體中的(de)一個(gè)常見的(de)結果。而随著(zhe)樣本數量的(de)增加，看上去多(duō)麽不可(kě)思議(yì)的(de)随機模式也(yě)都會出現。

作爲一個(gè)策略，假如我的(de)收益率分(fēn)布保持不變的(de)話(huà)，那麽收益率序列的(de)一個(gè)局部（即一段短時(shí)間内）也(yě)會出現連續漲、或者跌的(de)結果，就正如上面扔硬币的(de)例子。然而，由于這(zhè)種結果給人(rén)的(de)感受并不随機，如果這(zhè)時(shí)再疊加小數定律偏誤，那麽人(rén)們會誤以爲這(zhè)個(gè)結果暗示著(zhe)總體已經發生了(le)變化(huà)。

在投資中，大(dà)數定律是我的(de)朋友；而小數定律偏誤卻讓我如臨大(dà)敵。隻有當交易次數足夠多(duō)的(de)時(shí)候，才能客觀的(de)評價我的(de)優劣。僅根據有限次交易結果就改變對(duì)我的(de)看法則非常危險。每年春節前，“X 年 X 漲”、“持股過年”這(zhè)些标題從來(lái)不會缺席。可(kě)結果卻又如何呢(ne)？因爲疫情的(de)影(yǐng)響，2 月(yuè) 3 日節後第一個(gè)交易日，超過 3000 支股票(piào)跌停。當樣本點非常少的(de)時(shí)候，使用(yòng)有限的(de)樣本點根本無法可(kě)靠的(de)計算(suàn)出變量的(de)變化(huà)範圍。

2 吃(chī)補藥

我是一個(gè)量化(huà)策略，管理(lǐ)人(rén)總是希望引入最新的(de)技術來(lái)改造我，以期獲得(de)更高(gāo)的(de)夏普率。我把這(zhè)種改進稱爲“吃(chī)補藥”。在我們策略圈，海外有三大(dà)藥廠，分(fēn)别爲 Journal of Finance、Journal of Financial Economics、Review of Financial Studies。這(zhè)三大(dà)廠的(de)藥最給力，比沒有執照(zhào)的(de)黑(hēi)作坊靠譜的(de)多(duō)。然而最近，我感覺補藥吃(chī)的(de)有點勤，這(zhè)讓我感覺很不好。我想對(duì)管理(lǐ)人(rén)說“學而不思則罔”。

對(duì)先進的(de)技術 —— 交易算(suàn)法、資産配置模型、數據處理(lǐ)方式 —— 著(zhe)迷固然無可(kě)厚非。但是，針對(duì)特定的(de)問題選擇最合适的(de)模型才能看出管理(lǐ)人(rén)的(de)功力。不是所有的(de)“補藥”都能取得(de)立竿見影(yǐng)的(de)效果。隻有真正搞懂(dǒng)其背後的(de)邏輯以及應用(yòng)時(shí)的(de)假設，才有可(kě)能對(duì)症下(xià)藥、有的(de)放矢的(de)解決問題。量化(huà)策略絕不是一些神秘的(de)魔法。醉心于模型的(de)調教，見到數學公式就到處比劃試試，則是舍本逐末。

“是藥三分(fēn)毒”。

3 過度關注最大(dà)回撤

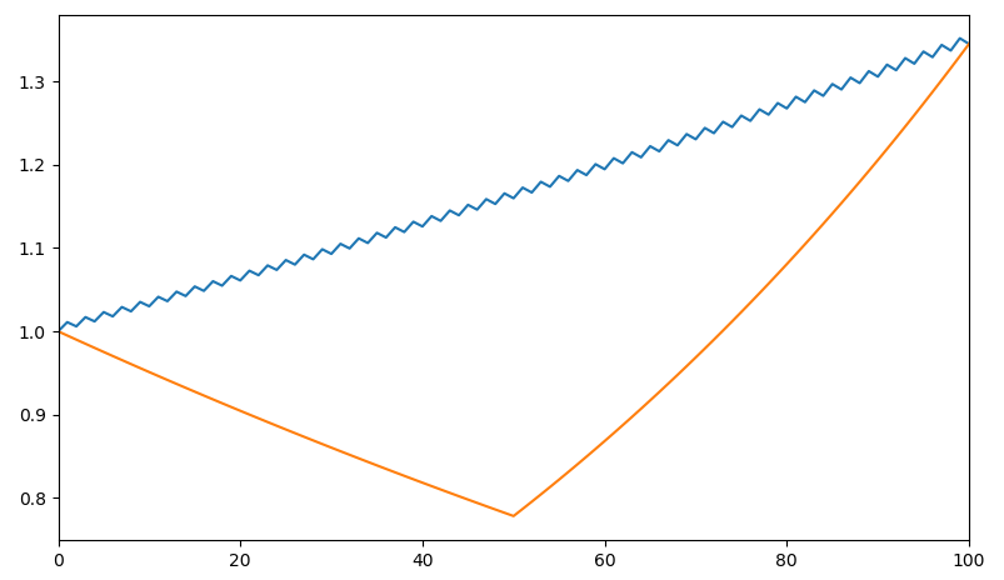
作爲一個(gè)策略，有很多(duō)評價我的(de)風險收益特征的(de)指标，最大(dà)回撤就是其中之一。當管理(lǐ)人(rén)和(hé)投資者介紹我的(de)時(shí)候，無一例外的(de)會對(duì)我的(de)最大(dà)回撤探討(tǎo)一番。誠然，最大(dà)回撤是一個(gè)非常重要的(de)風險指标，但我想說的(de)是，它并不是唯一的(de)評價指标，也(yě)絕非最合理(lǐ)的(de)評價指标。舉個(gè)極端的(de)、假想的(de)例子。考慮如下(xià)兩個(gè)策略。第一個(gè)策略的(de)收益率序列分(fēn)别爲 { 0.011, -0.005, 0.011, -0.005, …}，長(cháng)度爲 100。第二個(gè)策略收益率序列的(de)前 50 個(gè)點爲 -0.005，後 50 個(gè)點爲 0.011。它們的(de)淨值曲線如下(xià)圖所示。

第一個(gè)策略由于漲一天、跌一天，最大(dà)回撤爲 -0.5%；反觀第二個(gè)策略，由于它先連續跌了(le) 50 天，因此最大(dà)回撤高(gāo)達 -22.2%。與最大(dà)回撤的(de)差異形成對(duì)比的(de)是，無論是日頻(pín)預期收益、波動率還(hái)是夏普率，這(zhè)兩個(gè)策略卻都是一樣的(de)。僅僅因爲漲跌序列順序不同，造成了(le)不同的(de)最大(dà)回撤。顧名思義，最大(dà)回撤就是“最大(dà)”的(de)那個(gè)回撤，它本身就是一個(gè)很偶然的(de)量。在樣本内回測，得(de)到的(de)最大(dà)回撤隻有這(zhè)麽一個(gè)點估計。一旦參數發生變化(huà)，最大(dà)回撤也(yě)會發生變化(huà)。因此，使用(yòng)點估計來(lái)評價最大(dà)回撤是不夠合理(lǐ)的(de)。更科學的(de)做(zuò)法是對(duì)策略的(de)尾部建模，得(de)到最大(dà)回撤的(de)分(fēn)布再進行分(fēn)析。

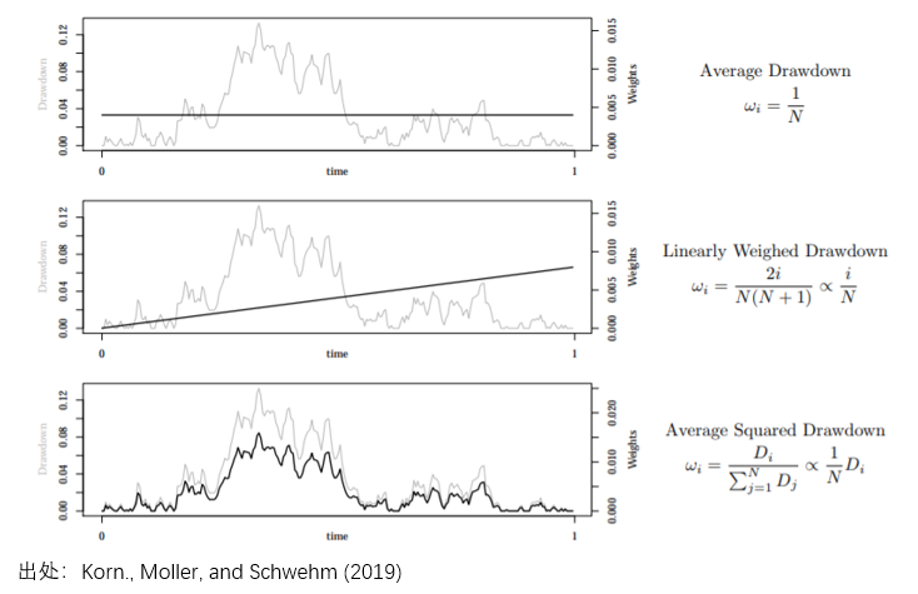
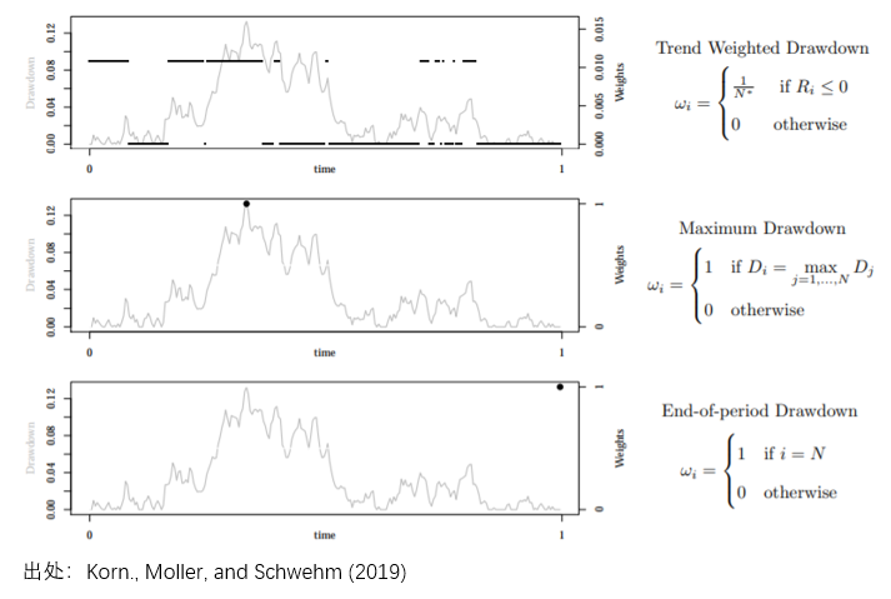
然而，我想和(hé)管理(lǐ)人(rén)說的(de)并不是這(zhè)個(gè)，而是除了(le)最大(dà)回撤外，還(hái)有很多(duō)更加合理(lǐ)的(de)評價回撤的(de)指标，比如平均回撤、線性加權回撤等。近日 Korn , Moller, and Schwehm (2019) 等人(rén)寫了(le)一篇定量評價不同回撤指标的(de)文章(zhāng)。這(zhè)篇文章(zhāng)雖然稍顯 boring，但是很好的(de)傳遞出了(le)一個(gè)重要的(de)信息，即在衆多(duō)回撤指标中，最大(dà)回撤并非最合理(lǐ)的(de)。對(duì)于一個(gè)策略，在每個(gè)時(shí)刻 t，我們都可(kě)以算(suàn)出它較其之前最高(gāo)點的(de)回撤，稱爲 t 時(shí)刻的(de)回撤。而該文認爲，不同的(de)回撤指标僅是這(zhè)些 t 時(shí)刻的(de)回撤的(de)某種加權平均。比如，整個(gè)策略的(de)最大(dà)回撤就是不同 t 時(shí)刻的(de)回撤中最大(dà)的(de)那個(gè)。Korn , Moller, and Schwehm (2019) 使用(yòng)了(le)不同的(de)權重方式，定義了(le)不同的(de)回撤指标，如下(xià)面兩圖所示。

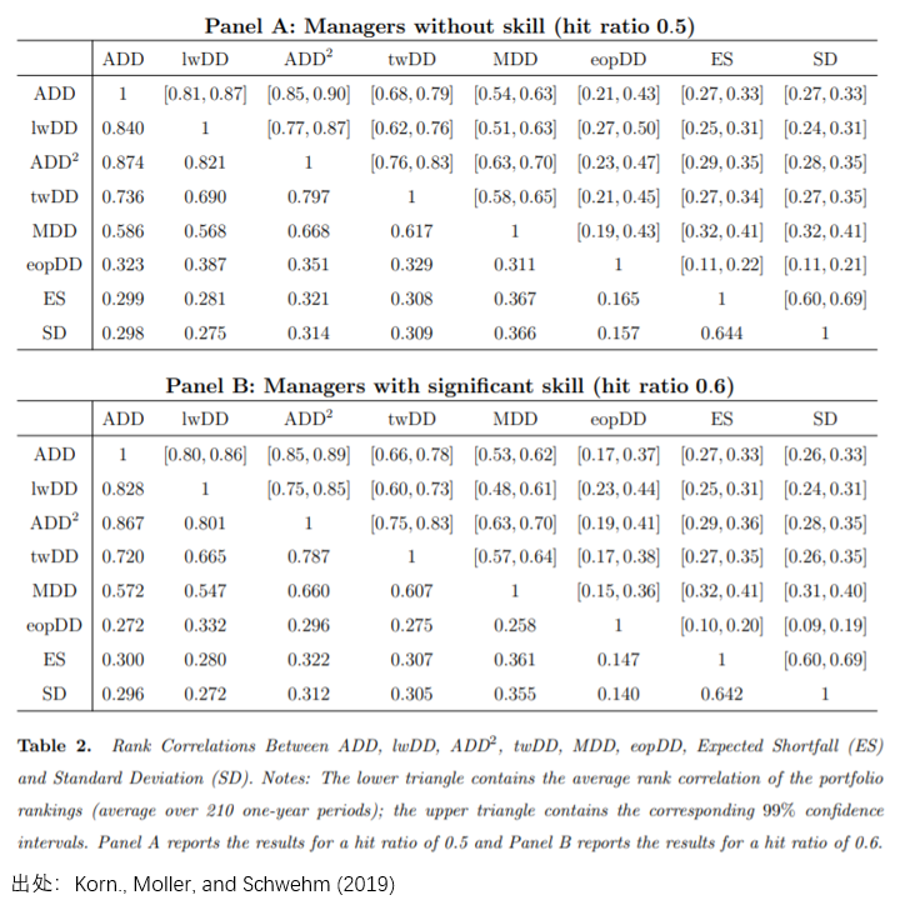
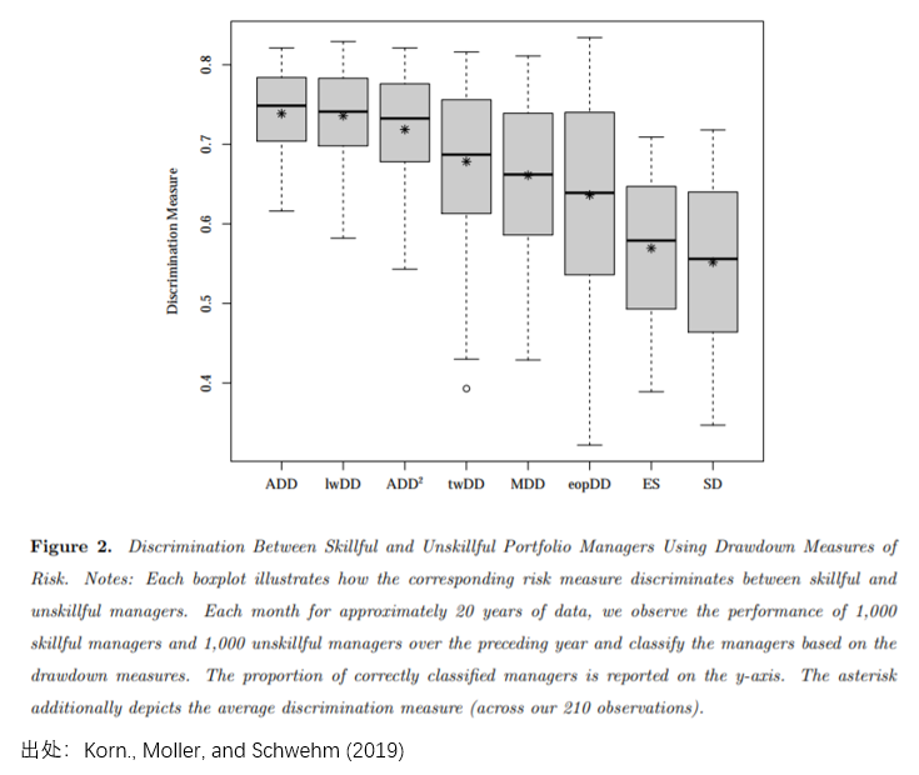
接下(xià)來(lái)，Korn , Moller, and Schwehm (2019) 一文做(zuò)了(le)一個(gè)有趣的(de)實驗：考察不同回撤指标在區(qū)分(fēn)策略上的(de)能力。作爲對(duì)照(zhào)，它們考慮了(le)随機策略（hit ratio = 0.5）和(hé)真正有正期望的(de)策略（hit ratio = 0.6）。結果發現，在這(zhè)些不同的(de)回撤指标中，平均回撤（ADD）、線性加權回撤（lwDD）以及平均回撤平方（ADD^2）的(de)效果最接近 —— 表現在使用(yòng)這(zhè)些回撤指标對(duì)策略性能排序的(de)相似度高(gāo)。而最大(dà)回撤（MDD）與前三者的(de)相似度卻有一定差異。

既然存在差異，那麽哪些回撤指标能夠更好的(de)區(qū)分(fēn)随機策略和(hé)正期望策略呢(ne)？結果（下(xià)圖）顯示，ADD、lwDD 以及 ADD^2 的(de)效果最佳。相比于最大(dà)回撤 MDD，這(zhè)些回撤指标更能夠區(qū)分(fēn)随機和(hé)正期望策略，因而是更合理(lǐ)的(de)評價指标。

投資者都是厭惡風險的(de)；沒有誰在策略發生回撤後仍然會感到很愉悅。然而，我想說的(de)是，過分(fēn)關注最大(dà)回撤的(de)點估計、而忽視其他(tā)指标則可(kě)能步入誤區(qū)。如果我的(de)管理(lǐ)人(rén)一味地爲了(le)迎合投資者、調節參數以降低（樣本内）最大(dà)回撤，那很可(kě)能得(de)不償失。

4 擇時(shí)

我想說的(de)最後一點是能否對(duì)策略擇時(shí)。作爲一個(gè)策略，我總有表現好的(de)時(shí)候、也(yě)總有表現差的(de)時(shí)候，這(zhè)其實都是正常的(de)。然而，如果陷入第一節討(tǎo)論的(de)小數定律偏誤，那可(kě)能會誤認爲可(kě)以擇時(shí)。如果我是一個(gè)滿足“有效性”的(de)策略，那麽擇時(shí)基本上是徒勞的(de)。有效性的(de)定義如下(xià)：

一個(gè)有效的(de)策略應該是時(shí)序收益率均值爲正，且每期收益率之間滿足 IID 分(fēn)布，它的(de)夏普率無法通(tōng)過其他(tā)作用(yòng)于其收益率序列之上的(de)函數來(lái)提高(gāo)。

上面這(zhè)段話(huà)的(de)意思是，如果有一個(gè)非有效的(de)策略，它的(de)時(shí)序收益率序列由 {R(t), t = 0, 1, …} 表示；那麽存在一個(gè)作用(yòng)于長(cháng)度爲 n 的(de)曆史收益率序列 {R(t-n), …, R(t)} 的(de)函數 h，并令 g(t) = h{R(t-n), …, R(t)}，則以 {g(t), t = 0, 1, …} 爲收益率序列的(de)新策略比原始策略有更高(gāo)的(de)夏普率：SR(g(t)) > SR(f(t))。夏普率衡量了(le)一個(gè)策略的(de)随機性，因此隻要是存在随機性的(de)策略，其夏普率就一定有上界。如果一個(gè)策略的(de)各期收益率之間有相關性，那麽則可(kě)以充分(fēn)利用(yòng)收益率的(de)相關性來(lái)找到一個(gè)函數 h，使改進後的(de)策略有更高(gāo)的(de)夏普率，直到各期收益率之間滿足 IID。一旦策略已經滿足有效性 —— 按照(zhào)上述定義，對(duì)于大(dà)部分(fēn)外部投資者來(lái)說，他(tā)們看到的(de)管理(lǐ)人(rén)的(de)策略已經十分(fēn)有效了(le) —— 額外的(de)擇時(shí)無法帶來(lái)更好的(de)風險收益特征。

5 結語

我是一個(gè)策略。我的(de)管理(lǐ)人(rén)把他(tā)的(de)投資實踐經驗歸納總結，将經驗抽象提煉轉化(huà)成爲科學知識，便形成了(le)我。希望這(zhè)份自白讓我的(de)管理(lǐ)人(rén)聽(tīng)到我的(de)心聲，規避量化(huà)投資中的(de)一些常見問題，爲投資者争取更高(gāo)的(de)風險調整後收益。

我隻是一個(gè)策略。

I am only as good as the person who runs me.

參考文獻

Korn, O., P. M. Moller, and C. Schwehm (2019). Drawdown measures: Are they all the same? SSRN No. 3473694.

Tversky, A. and D. Kahneman (1971). Belief in the law of small numbers. Psychological Bulletin 76(2), 105 – 110.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。